Suboptimal foraging behavior: A new perspective on gambling

Abstract

Why do people gamble? Conventional views hold that gambling may be motivated by irrational beliefs, risk-seeking, impulsive temperament, or dysfunction within the same reward circuitry affected by drugs of abuse. An alternate, unexplored perspective is that gambling is an extension of natural foraging behavior to a financial environment. However, when these foraging algorithms are applied to stochastic gambling outcomes, undesirable results may occur. To test this hypothesis, we recruited participants based on their frequency of gambling – yearly (or less), monthly, and weekly – and investigated how gambling frequency related to irrational beliefs, risk-taking/impulsivity, and foraging behavior. We found that increased gambling frequency corresponded to greater gambling-related beliefs, more exploratory choices on an explore/exploit foraging task, and fewer points earned on a patchy foraging task. Gambling-related beliefs negatively related to performance on the patchy foraging task, indicating that individuals with more gambling-related cognitions tended to leave a patch too quickly. This indicates that frequent gamblers have reduced foraging ability to maximize rewards; however, gambling frequency- and by extension, poor foraging ability- was not related to risk-taking or impulsive behavior. These results suggest that gambling reflects the application of a dysfunctional foraging process to financial outcomes.

Introduction

Gambling is a popular activity around the world. In the U.S., an estimated 77% of individuals gambled in 2012 (Welte et al. 2014), which generated massive revenues for state- and privately-owned gambling operations. However, for the individual, the odds of winning are unfavorable and gambling typically produces a net loss. Considering the well-known odds of winning in legalized gambling games, rational people would not gamble if winning money was the goal (Walker 1992). So why do people gamble? There are several perspectives on this question that regard gambling as an irrational behavior because unlike natural reward-seeking behaviors, such as foraging for food, gambling does not maximize rewards. In fact, probabilistic rewards cannot be maximized (except on average) by adaptive behavior, but that knowledge conflicts with our behavioral intuitions. Standard psychological and neurological perspectives on gambling do not consider the possibility that gambling might reflect variations or disruptions in mechanisms that evolved to support adaptive behavior in the natural world, which may be maladaptive when applied to unpredictable monetary gambling outcomes.

Gambling research tends to be informed by one of three common perspectives. First, the cognitive psychological perspective proposes that people gamble simply because they are not rational (Walker 1992). This hypothesis is based on research in which gamblers were asked to think aloud while gambling (e.g., Ladouceur et al. 1988, Walker 1992, Delfabbro and Winefield 2000), which found that gamblers often express irrational beliefs, such as believing they can influence or predict the outcome of a gamble (i.e., illusion of control). According to this perspective, these cognitive biases maintain gambling behavior even when wins are infrequent (Gilovich 1983, Walker 1992, Delfabbro and Winefield 2000). Five common gambling-related cognitions and expectancies have been identified based on the thinking aloud method, and a self-report Gambling-Related Cognition Scale (GRCS) was developed to screen individuals for gambling-related cognitions (Raylu and Oei 2004). These cognitions tend to be stronger in individuals with problem gambling and may influence the development and maintenance of problem gambling (Raylu and Oei 2004).

Second, the personality-trait perspective proposes that gambling is an expression of risk-taking and impulsivity. Gambling means risking something of value in the hope of gaining something of greater value (Potenza 2006), and risk-taking behavior tends to co-occur with impulsive personality traits (Stanford et al. 1996, Zuckerman and Kuhlman 2000). Non-problem gambling behavior, as well as problem gambling, has been associated with self-reported impulsivity (Mishra et al. 2010, MacLaren et al. 2011). Indeed, problem gambling was characterized as an impulse control disorder in the DSM-IV (APA 2000). Furthermore, impulsivity and gambling attitudes and beliefs have been associated with greater risk-taking on the Balloon Analogue Risk Task (BART), which is a laboratory-based task designed to measure behavioral risk-taking and self-control (Lejuez et al. 2003).

Third, the neurobiological perspective proposes that gambling is driven by reward and motivational processes mediated by dopaminergic pathways in the brain. In this perspective, gambling triggers dopamine release similar to natural rewards and drugs of abuse; thus, gambling behavior can be maintained by a schedule of reinforcement and gambling has its own addiction liability (for review, see Zack and Poulos 2009). In fact, pathological gambling shares so many characteristic traits with drug addiction that the DSM-V now classifies pathological gambling as a behavioral disorder similar to substance-related disorders (APA 2013). More evidence of the relationship between gambling and dopamine release comes from the sudden development of pathological gambling in Parkinson’s patients treated with dopamine agonists (Grosset et al. 2006, Dagher and Robbins 2009).

While not an exhaustive list of all possible explanations for gambling behavior, these three perspectives are common in the gambling literature and provide important insights into how gambling is currently conceptualized by the research community. But a potentially important perspective is missing: As the neurobiological perspective suggests, gambling stimulates the dopaminergic system, which drives emotional and motivational aspects of behavior. However, this system did not evolve to support gambling or drug-seeking behavior, but rather it evolved to incentivize and reinforce behaviors promoting survival and reproduction, such as foraging for food and finding mates (Kelley and Berridge 2002). A critical difference between natural rewards and gambling rewards is that in nature, foragers are often able to use recent reward history to make predictions about proximate future rewards, and adjust their behavior to maximize expected rewards and minimize the cost of obtaining them. Conversely, gambling rewards are stochastic; therefore, adaptive behavioral strategies that rely on the temporal correlations among outcomes observed in the real world may prove maladaptive in purely stochastic environments. Yet, a forager’s instinct is to make future predictions based on the outcomes of past experiences. It may be this instinct that gives rise to the “illusion of control” and other gambling-related cognitions.

Although foraging paradigms have only recently been applied to human behavior (e.g., (Rutledge et al. 2009), the study of foraging is fundamental to the investigation of natural animal behavior (Charnov 1976, Stephens and Krebs 1986). A large body of field and laboratory research demonstrates that foraging behavior is conserved across a wide range of species and can be predicted by mathematical models of optimal foraging behavior (Cassini et al. 1993, Hayden et al. 2011, Katz et al. 2013). Generally, foraging theory divides foraging into two main classes of decision problems: 1) patch-leaving, that is when to exit a depleting patch and search for a new one; and 2) prey choice, whether to accept or reject individual resources when they are encountered. Optimal foraging models posit that foragers solve these problems by maximizing the rate of resource intake relative to time and energy costs and the richness of the environment (Stephens and Krebs 1986).

The patch-leaving problem is particularly relevant to gambling because it requires balancing immediate but diminishing rewards against delayed but potentially larger rewards, a process that may require self-control. Two of the most well-established patch foraging paradigms are the multi-armed bandit task (Sutton and Barto 1998) and the patchy-foraging task (Stephens and Krebs 1986). In the multi-armed bandit task, the forager must explore the environment to discover the hidden value and location of rewards and exploit the option with the greatest value. In an uncertain environment where the value of rewards can change quickly, the challenge is deciding when to explore or exploit in order to maximize long-term rewards. In the patchy-foraging task, rewards are clumped in discrete locations (i.e., patches) and decrease over time as they are exploited (analogous to food being depleted as it is consumed). Eventually, the forager must leave to find a new patch; however, it takes time to travel from patch to patch. Foragers must balance the motivation to obtain an immediate (yet diminishing) reward with the costs in time and energy needed to move to a new patch in order to maximize long-term rate of reward.

Foraging behavior is an expression of a natural instinct to maximize reward rates relative to the costs to obtain those rewards, and centers around common phenomena like diminishing returns and environmental uncertainty. Although foraging paradigms have not previously been used in gambling research, gambling could be contextualized as natural foraging behavior gone awry, or a natural foraging behavior that struggles to cope with unnatural stochastic outcomes. Here, we probed how gambling frequency (yearly, monthly, and weekly gamblers) relates to standard explanatory measures, such as irrational beliefs and risk-taking/impulsive behavior, compared to measures derived from foraging theory. We hypothesized that gambling frequency would vary with risk-taking behavior, impulsivity and gambling-related cognitions, based on previous research (see above). Furthermore, we hypothesized that weekly gamblers would make fewer exploratory choices on the multi-armed bandit task and stay longer in patches in the patchy-foraging task, based on evidence from the neurobiological perspective that suggests problem gambling is related to a diminished sensitivity to outcomes and perseverative behavior (e.g., de Ruiter et al. 2009).

Method

Participants

Participants aged 18 to 55 years were recruited from the Durham/Chapel Hill/Raleigh community of North Carolina. Participants were eligible for the study if they had gambled at least once in their lifetime and were in general good health. Exclusion criteria consisted of significant health problems, current use of psychoactive medication, positive breath alcohol concentration on the study day, positive urine drug screen on the study day, a positive urine pregnancy test for women, treatment for drug or alcohol abuse/dependence in the past 6 months, and seeking treatment or currently in treatment for problem gambling. Prospective participants were identified by their typical frequency of gambling and were recruited into three gambling-frequency groups: yearly gamblers (who reported infrequent gambling), monthly gamblers, and weekly gamblers. This included any type of gambling (e.g., lottery tickets/scratch-off games, sports bets, casino visits, online gambling, etc.). Participants provided written informed consent, and this study was approved by the Institutional Review Board at Duke University.

Questionnaires

South Oaks Gambling Screen (SOGS)

This 20-item questionnaire is used to screen for pathological gambling. A score of 5 or more is considered evidence of pathological gambling (Lesieur and Blume 1987). The SOGS also queries frequency (not at all, less than 1×/week, or 1×/week or more) of different types of gambling (e.g., cards, sports bet, casino, lotteries).

Barratt Impulsiveness Scale (BIS)

This 30-item questionnaire measures the personality and behavioral constructs of impulsivity (Patton et al. 1995). It consists of three subscales: attentional (e.g., “I don’t pay attention”), motor (e.g., “I do things without thinking”), and non-planning (e.g., “I plan tasks carefully”) impulsivity, as well as a total score. Higher scores indicate greater impulsivity.

Quick Delay Questionnaire (QDQ)

This 10-item questionnaire assesses two types of delay-related behavior: delay aversion (e.g., “I hate waiting for things”) and delay discounting (e.g., “The future is not important to me – I only consider the immediate consequences of my actions”) (Clare et al. 2010). Higher scores indicate more delay aversion and discounting.

Risk Attitude Scale (RAS)

This 40-item questionnaire assesses risk taking across five domains: financial investment, gambling, health/safety, ethics, recreational, social (Weber et al. 2002). Participants completed the entire questionnaire, but only the gambling domain subscale (e.g., “What is your likelihood of gambling a week’s income at a casino?”) is included in the current set of results. Higher scores indicate greater likelihood of risky behavior.

Gambling Related Cognitions Scale (GRCS)

This 23-item questionnaire measures a range of gambling-related cognitions, including interpretive control/bias (e.g., “Relating my winnings to my skill and ability makes me continue gambling”), illusion of control (e.g., “Praying helps me win”), predictive control (e.g., “When I have a win once, I will definitely win again”), gambling-related expectancies (e.g., “Gambling makes me happier”), and a perceived inability to stop (e.g., “I will never be able to stop gambling”) (Raylu and Oei 2004). Higher scores indicate stronger gambling-related cognitions.

Tasks

4-Armed Bandit Task (4ABT)

This task measures exploratory and exploitative behavior, and this version of the task was modeled after (Daw et al. 2006) and has been described elsewhere (Addicott et al. 2013). In brief, four slot machines were depicted on a computer screen and participants selected one to play using a number pad. Then, the selection was highlighted and the number of points paid off was displayed onscreen. The number of points paid off by each slot machine changed gradually from trial to trial, independently of other slot machines. The point values were calculated previously using a biased random walk, and every participant received the same pattern of point values. Choices on each trial were classified as exploratory or exploitative according to a behavioral model based on a softmax rule and Kalman filter (Anderson and Moore 1979, Daw et al. 2006). On each trial, choice of the slot machine with the highest estimated action value in the model was coded as exploitative, and all other choices were coded as exploratory (see Addicott et al. 2013 for complete details). The task consisted of 300 trials and lasted approximately 10 minutes. The primary dependent variables were the total points and the percentage of exploratory trials.

Patchy-foraging Task (PFT)

This task measures reward persistence and was modeled after (Hayden et al. 2011). Here, two patches (i.e., berry bushes) were depicted on a computer screen: the current patch and the next patch. The travel time to the next patch (5, 10, or 20 seconds) was also shown. On each trial, participants selected one patch using a number pad. When the current patch was selected, the number of points awarded for that selection was shown on screen for 1.5 seconds. The points awarded for the current patch began at 5 and decreased by a random integer between 0 and 1 for every selection. Point values decreased from 5 to 0 after approximately 20 selections. When the next patch was selected, there was an immediate time-out for the duration of the travel time, and then the participant could choose between the current patch and the next patch again. There was an unlimited number of patches, but a finite amount of time to perform the task (8 minutes).

Optimal patch leave time was calculated using the marginal value theorem and simulated data. The marginal value theorem states that a forager should leave a patch when the rate of return in that patch equals the average rate of return in the greater environment (Charnov 1976). The optimal patch leave time equals the maximum value for the ratio: reward amount/(travel time to patch + foraging time in patch), and this was estimated for each travel time (5, 10, 20 sec). Then, the sum of the differences between the average leave time for each delay and the optimal leave time for that delay was calculated for each participant. Positive values indicate the patch was left later than optimal, negative values indicate the patch was left earlier than optimal. The primary dependent variables were the total points and the sum difference from optimal leave time.

Balloon Analogue Risk Task (BART)

This task measures risk-taking and was modeled after (Lejuez et al. 2003). In this version, a balloon is depicted on a computer screen along with the words “pump”, “stop”, and the total accumulated points. Participants are instructed to pump the balloon for points using a number pad. Each time the balloon is pumped, it appears larger and its point value increases. However, if the balloon pops, all the points for that balloon are lost. Balloons could pop on any pump, but the probability of popping increased as the number of pumps increased. The participant can stop and collect the points for a balloon at any time before it pops. After a balloon pops or its points are banked, a new balloon appears and the participant can make another selection. The balloons had an average break-point of 4 pumps. There were an unlimited number of balloons, but a finite amount of time to perform the task (12 minutes). The primary dependent variables were the total points and the average number of pumps on banked balloons.

Risk Preference Task (RPT)

This task measures preference for risky gambles and was modeled after (Sonuga-Barke 2002). Here, participants make a choice between a certain outcome and a gamble. The values of the certain outcomes were 3, 4, 5, 6, and 7 points and each certain outcome value was used in 10 or 11 trials. The accompanying risky gambles were drawn from a set of three possible winning probabilities (25%, 50%, and 75%) with seven ratios of the expected value of the gamble (EV_G) to the value of the certain option (V_C). The EV_G/V_C ratios were 0.5, 1, 1.3, 1.6, 1.9, 2.5, and 4. After making a selection, the participant was shown the number of points they won and the number of points they could have won if they had chosen the other option. There were 52 trials and the task lasted approximately 10 minutes. The dependent variables were the total points and the percentage of risky gambles chosen.

CANTAB (Cambridge Cognition Ltd)

Three tasks from the CANTAB suite were included to measure executive function and performance. The Paired Associates Learning (PAL) task measures visual memory and learning, the Intra-Extra Dimensional Set Shift (IED) task measures rule acquisition and flexibility of attention, and the Spatial Working Memory (SWM) task measures retention of visuospatial information. The dependent variables were the number of errors made in each of the three tasks. The numbers of errors on the PAL and IED were adjusted for each stage of the task not attempted because of a failure to complete a previous stage. Participants with significantly outlying number of errors in one or more task were excluded from the analyses.

The task instructions given to participants are described in the Supplementary Information. These questionnaires and tasks were part of a larger battery of measures used in an investigation on the interaction between gambling traits and smoking status. Only the relevant methods are described here.

Procedure

Following an initial screening session to determine eligibility, participants completed a series of questionnaires and computer tasks. The order of the questionnaires and computer tasks were counterbalanced across participants. The study period lasted approximately 3 hours.

Participants were compensated for their time and were told they could earn up to $10 bonus pay based on the points they earned on the computer tasks. For every computer task, participants were instructed to try to earn as many points as possible. At the end of the study, all participants were informed that they had earned the bonus pay.

Data Analysis

Differences in demographic and questionnaire data across groups were analyzed using Chi-square tests and 1-way Analysis of Variance (ANOVA) with post hoc Bonferroni correction for the number of group comparisons. Behavioral performance was analyzed across groups using 1-way ANOVAs and post hoc Bonferroni correction for the number of group comparisons. Correlations between questionnaire data and task performance were analyzed with Spearman’s rho, which maintains a more robust control of Type I errors than Pearson’s r when one or more variable has a non-normal distribution (Bishara and Hittner 2012). Correlations between questionnaire data and task performance were corrected for multiple comparisons using Bonferroni correction. Lastly, we pursued a regression approach with variable selection using elastic net regularization (Zou and Hastie 2005). Elastic net regularization modifies standard least squares regression by parametrically balancing model parsimony against goodness of fit. That is, the elastic net penalty, a mixture of sparse and ridge regression, favors the best-fitting model involving the fewest regressors. Regression coefficients for small or unneeded variables are thus regularized to 0, resulting in a variable selection mechanism free from many of the biases of stepwise methods and with better generalization performance to unseen data (Hastie et al. 2009). Specifically, the elastic net method minimizes the penalized sum of squares

$$\sum _i{(y_i-{(X\beta )}_i)}^2+\lambda ((1-\alpha )\sum _j|{\beta }_j|+\alpha \sum _j{\beta }_j^2)$$

Here, λ controls the over regularization strength, the tradeoff between goodness of fit and parsimony, while α controls the tradeoff between the sum of absolute coefficients (sparse or LASSO) penalty and the sum of squared coefficients (ridge) penalty. We fit such a model to our data, asking which of our behavioral and self-report metrics were most beneficial in predicting gambling frequency and GRCS scores. Plots of regression coefficient against λ/model size were similar for all values of α, so here we report the results for α = 0. To determine the best value of λ (i.e., model parsimony), we performed 10-fold cross-validation. That is, our data were divided into 10 partitions, the model was subsequently trained on 9 of these, and its validity assessed by predictive performance on the final, held-out partition. This process was then repeated 10 times, each time using one of the partitions as held-out data, and the results averaged. From this, we indicate both the value of λ that resulted in best model performance (best model) and the largest value of λ that resulted in performance within one standard error of this value (most parsimonious model).

Numeric variables underwent z-score transformation prior to being included in the model. All analyses were performed using SPSS (version 22; Chicago, IL). One participant was excluded from all analyses due to significantly outlying number of errors in the CANTAB, and another participant’s CANTAB data was lost due to a computer error and this participant was dropped from all analyses. Tests of normality were performed to identify outliers and potentially non-strategic (i.e., random) behavior on each of the tasks. Distributions were examined on secondary performance outcomes, consisting of the r²-values of correlations between patch delay and patch leave time for the PFT, accuracy of a risk preference parameter (beta) in predicting participants’ choices in the RPT (Huettel et al. 2006), the total number of balloons for the BART, and the absolute difference in the number of exploratory trials (coded by the mathematical model) and the number of switch trials (defined simply as a different slot machine selected on trial n than on trial n-1) for the 4ABT. Random selection of slot machines vitiates the accuracy of the mathematical model (which assumes the player is selecting targets using rational, goal-directed behavior). One weekly and two yearly gamblers had significantly outlying values (i.e., > 3 standard deviations from the mean) in the difference between explore and switch trials and were removed from the 4ABT analyses. No other significant behavioral outliers were found.

Results

Participants

A total of 60 participants completed the study and provided useable data (40% male, aged Mean ± SD 34 ± 10 years). Participants were grouped according to gambling frequency, and participant characteristics are shown in Table 1. There were no differences in age, sex, or racial distribution across groups. However, yearly gamblers had more years of education than weekly gamblers (15 vs 13 years, respectively; p = 0.018). The gambling-related cognition scores increased across groups (F_2,59=8.3, p < 0.001) and weekly gamblers had significantly higher scores than yearly gamblers (p < 0.001); however, there were no differences in the gambling subscale scores of the RAS, the BIS total score (or its subscale scores), or the QDQ.

Table 1.

Participant Characteristics. Mean (SD).

	Yearly	Monthly	Weekly	Significance
n	24	14	22
Age	32 (9)	33 (10)	37 (11)	n.s.
Sex (M/F)	9/15	6/8	9/13	n.s.
Race (C/A/AA/O)	10/1/12/1	8/1/4/1	2/1/18/1	n.s.
Education	15 (3)	15 (2)	13 (2)	F(2,59)=4.3, p = 0.018; posthoc: yearly > weekly, p = 0.024
GRCS Total	7.1 (3.1)	8.7 (3.3)	11.9 (5.3)	F(2,59)=8.3, p < 0.001; posthoc: weekly > yearly, p< 0.001
RAS Gambling	5.3 (2.7)	6.6 (3.1)	6.3 (3.0)	n.s.
BIS Total	59.7 (12.3)	61.9 (9.1)	61.4 (9.7)	n.s.
QDQ	22.4 (5.9)	22.9 (5.4)	24.5 (6.7)	n.s.

M: male, F: female, C: Caucasian, A: Asian, AA: African American, O: other, n.s.: not significant

According to the SOGS, the most common types of gambling among the participants were playing the lottery (85% of participants), visiting casinos (77%), playing slot machines (77%), and playing card games (67%). Of these, Chi-square tests revealed that weekly gamblers reported playing the lottery (p = 0.008) and visiting casinos (p = 0.003) more frequently than the other two groups.

Two weekly gamblers had SOGS scores > 5, indicating probable pathological gambling at some point in their lifetime.

Behavior

Performance outcomes on the 4ABT, PFT, BART, and RPT across the three groups are shown in Figure 1. In the 4ABT, there was a step-wise increase in the percent exploratory choices made across the three groups (F_2,56 = 5.7, p = 0.006), and weekly gamblers made significantly more exploratory choices than yearly gamblers (p = 0.005). Overall, an increase in exploratory choices in the 4ABT was associated with a decrease in total points because points are maximized by exploiting slot machines with the greatest expected value. As such, there was a trend towards a step-wise decrease in the total points across the three groups (F_2,56 = 3.1, p = 0.054). Weekly gamblers had fewer points than the yearly gamblers (p = 0.049).

Figure 1.

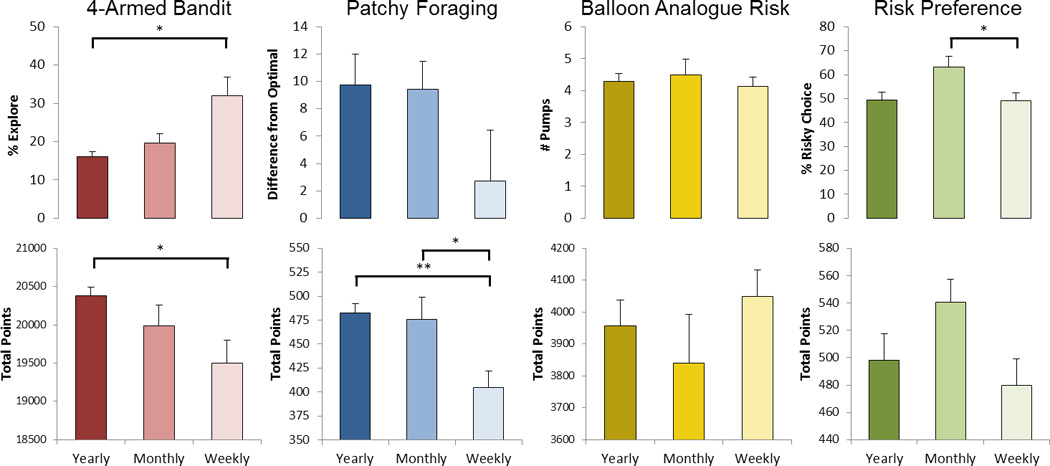
Average behavioral performance and total points earned on the 4-Armed Bandit, Patchy Foraging, Balloon Analogue Risk, and Risky Preference Tasks across the three gambling-frequency groups. Error bars are S.E.M. *p < 0.05, **p < 0.005.

Post hoc tests were conducted on two qualitative variables in order to better characterize group differences in performance. First, the learning rate is the rate at which values of the slot machines are updated (i.e., the sensitivity to the most recent pay-off of each slot machine), and is optimally determined by the Kalman filter. Second, the range in action values is the difference between the estimated value of the chosen option and the maximum estimated pay-out during exploration of other options. One-way ANOVAs of the average learning rates and average ranges in action values revealed no differences in these measures across groups. This suggests there were no qualitative differences in performance across groups.

In the PFT, participants completed an average of 11.7 ± 3 trials and there was no difference in the number of trials completed across groups. There was a step-wise decrease in the total number of points earned across the three groups (F_2,59 = 7.7, p < 0.001); the weekly gamblers earned fewer points than both the monthly (p = 0.015) and yearly gamblers (p = 0.002). Performance on the PFT (difference from optimal leave time) also decreased across groups, although not significantly. This decrease is somewhat misleading, since points should increase as the difference from optimal leave time decreases. However, the sum difference from optimal includes negative values when participants in a group left earlier than optimal. Thus, weekly gamblers have a smaller sum difference despite having a slightly greater absolute difference compared to the other groups (absolute difference from optimal = 12, 10, and 15 for yearly, monthly, and weekly gamblers, respectively) and this is reflected in their total points.

Post hoc tests were performed on the average leave time in each delay condition. A 3 (delay to next patch) × 3 (gambling frequency group) repeated-measures ANOVA revealed an interaction effect (F_4,114) = 4.16, p = 0.003). This effect was due to a significant increase from the patch leave time for the 5 sec to the 20 sec delay conditions among the yearly (paired-samples: t₂₃ = 5.64, p < 0.001) and monthly gamblers (t₁₃ = 3.45, p = 0.004), but not among the weekly gamblers (t₂₁ = 0.55, p = 0.589), see Figure 2. In other words, unlike the yearly and monthly gamblers, weekly gamblers did not adjust their patch leave time according to the length of the delay to the next patch.

Figure 2.

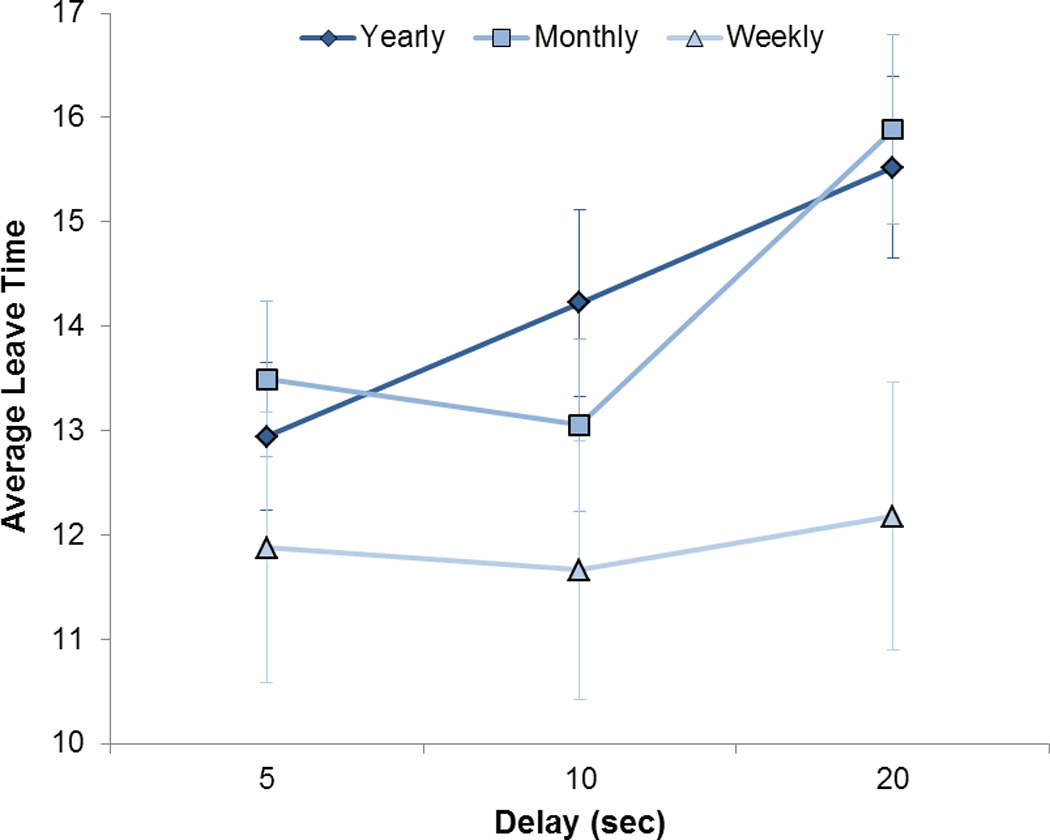
Average patch leave time (i.e., number of choices to remain at current patch) for each delay (in seconds) to the next patch across the three gambling-frequency groups. The yearly and monthly gamblers had significantly longer patch leave times in the 20 sec delay condition compared to the 5 sec delay condition (p’s < 0.005). The weekly gamblers had similar patch leave times across the delay conditions. Error bars are S.E.M.

In the BART, participants completed an average of 29.6 ± 10 trials and there was no difference in the number of trials across groups. There was an average of 4.3 pumps on banked trials, and participants earned an average of 3963 points. The number of pumps was negatively associated with the total points earned. Neither number of pumps or total points differed across groups.

In the RPT, there was a significant difference in the number of risky options chosen across groups (F_2,59 = 3.7, p = 0.031). Unexpectedly, there was no difference between yearly and weekly gamblers, but monthly gamblers chose more risky options than weekly gamblers (p = 0.043). Overall, the number of risky gambles accepted was associated with an increased number of points; however, the total points did not differ across groups.

Lastly, we explored the effect of smoking status and education level on behavioral outcomes using a multivariate general linear model; smoking status and education level were included as covariates of no interest. The 4ABT percent exploratory choices remained significant (F_2,56 = 4.2, p = 0.020) but the significance of the 4ABT total points decreased (F_2,56 = 1.8, p = 0.171). The PFT total points remained significant (F_2,59 = 4.1, p = 0.022), as did the RPT percent risky choice (F2,59 = 3.4, p = 0.040). Other outcomes remained nonsignificant. The number of errors on the three CANTAB measures did not differ across groups. See Table 2 for a summary of CANTAB performance.

Table 2.

Results of the CANTAB. Mean (SD).

	Yearly	Monthly	Weekly	Significance
CANTAB PAL adjusted errors	12 (12)	9 (9)	16 (13)	n.s.
CANTAB IED adjusted errors	32 (20)	27 (23)	43 (42)	n.s.
CANTAB SWM errors	23 (17)	19 (18)	26 (16)	n.s.

n.s: not significant

Relationships between self-reported traits and behavioral performance

Task performance and scores on the 4ABT, PFT, BART, and RPT (eight dependent variables in all) were correlated separately with the self-report GRCS, BIS, RAS gambling, and QDQ measures (correction for 8 comparisons = p < 0.006). The only significant correlation was between the GRCS and the PFT difference from optimal (rho = −.40, p = 0.001), see Figure 3.

Figure 3.

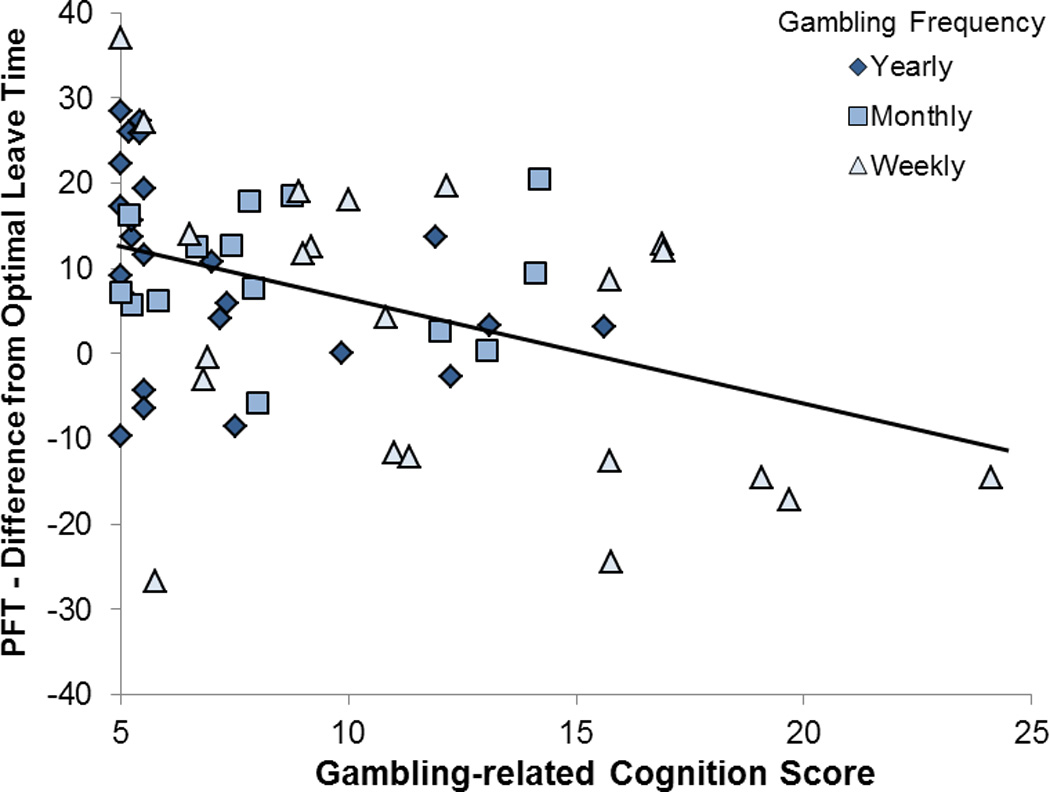
Correlation between Gambling-related Cognition Scores and Patchy Foraging Task performance. Performance is represented as the difference between individual’s average leave time (measured in the number of selections to stay at the current bush) and the optimal leave time derived using the marginal value theorem. Spearman’s rho = −.40, p = 0.001.

Lastly, all performance and self-report measures were included as potential regressors in an elastic net model in order to directly compare the foraging and impulsivity gambling perspectives and determine which of these best predicted gambling frequency and GRCS scores. The elastic net model automatically performs variable selection, without many of the detrimental biases of stepwise regression, while providing information about the order in which predictors should enter the model. For the gambling frequency model, the optimal value of the regularization parameter,, was 0.760 and the most parsimonious value of λ giving the same predictive error (to within one standard error) was 0.800. These values are indicated by vertical lines in Figure 4a, which shows that PFT total points were the only relevant predictor in the gambling frequency model. For the GRCS model, the optimal value of λ was 0.300 and the most parsimonious value was 0.940. These values are indicated by vertical lines in Figure 4b, which shows that the RAS gambling self-report score, the PFT difference from optimal performance, the PFT total points, and the QDQ were the relevant predictors in the GRCS model. That is, when given the option of choosing from among the behavioral and self-report measures, the elastic net procedure reliably selected performance measures based on natural foraging behaviors before other behavioral measures, suggesting that these tasks better assessed underlying factors predicting real-world gambling behavior and beliefs.

Figure 4.

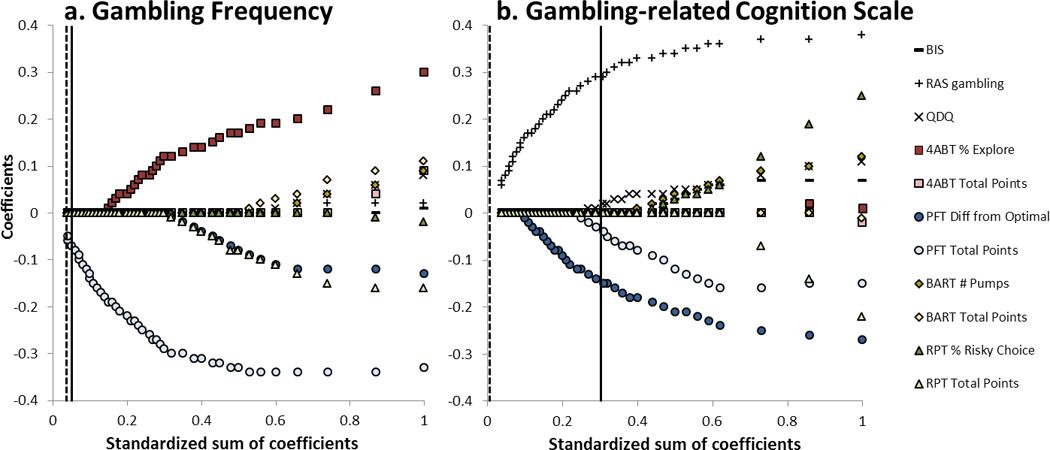
Results of the elastic net model for a) gambling frequency, and b) gambling-related cognition scale scores. Values indicate the strength of regression effects (y-axis) for each variable as a function of model parsimony (x-axis). As values increase along the x-axis, the model becomes less parsimonious and additional variables enter the model (lines diverging from 0 along the y-axis). At a given parsimony (x-axis position), the y-axis value of the variable lines indicates the strength of that regression coefficient in the model. The solid vertical line indicates the optimal model, and the dashed vertical line indicates the most parsimonious model within one standard error. Only coefficients with nonzero values between these vertical lines should be considered to have relevance for predictive performance in the model.

Discussion

There are many perspectives on the question of why people gamble, and most of these perspectives consider gambling to be an inherently irrational behavior. An unexplored alternative is that gambling frequency is related to natural variations in foraging behaviors, and there may be environmental or genetic differences that inform or influence one’s foraging ability and success, which in turn affects one’s propensity for gambling. We tested two perspectives on why people gamble (e.g., they are motivated by gambling-related beliefs or risk-taking/impulsive traits) against an alternative foraging model. We hypothesized that participants who gambled most frequently would exhibit the most gambling-related cognitions, impulsivity, risk-taking, and perseverative foraging behavior. Our results supported the cognitive psychological perspective, in that weekly gamblers had significantly more gambling-related cognitions than yearly gamblers. However, we did not find evidence for the personality trait perspective: there was no step-wise increase in impulsivity or risk-taking measures across yearly, monthly, and weekly gamblers. We did find support for the sub-optimal foraging perspective, although not in the direction we had anticipated. Rather than being more perseverative, as hypothesized, weekly gamblers were more exploratory and left patches with diminishing reward values more quickly than the other groups. Conversely, the yearly gamblers tended to exploit more and stay at patches longer than optimal, but the weekly gamblers earned the fewest number of points on the foraging tasks. Rather than being dysfunctional, this variation in foraging behavior across individuals may be an adaptation that can improve an individual’s survival likelihood by promoting lesser-used strategies, or strategies that may change in fitness strength when the environment changes from stable to volatile. Future studies could investigate genetic and environmental influences on foraging behaviors in relation to gambling frequency and the risk of developing pathological gambling.

In our foraging perspective, we propose that gambling could be related to either 1) a dysregulation in the dopaminergic system that drives motivational behaviors, or 2) a healthy dopaminergic system that struggles to maximize unpredictable outcomes. Support for the latter would be suggested by optimal foraging performance but poor performance on risk-taking tasks with unpredictable outcomes, which was not found to be the case. Our results provide support for a dysregulated motivational system, one that drives sub-optimal foraging behavior. Weekly gamblers tended to switched targets on the 4ABT at the expense of points. Rather than being motivated by points, this “channel-surfing” may be information-seeking behavior, motivated by a desire to know what else is available in the environment. Weekly gamblers also earned the fewest points on the PFT, and earlier patch-leaving was related to higher GRCS scores. While the exact nature of this relationship remains unclear, it is possible that gambling-related cognitions arise from an instinct to look for patterns and to make predictions in order to maximize rewards as they commonly occur in nature. This instinct could bias individuals towards seeking reward patterns and feeling a sense of control over gambling outcomes. However, our results suggest a complex relationship between foraging behavior, gambling-related cognitions, and gambling frequency. Our weekly gamblers tended to have higher scores on the GRCS, although some weekly gamblers declared no gambling-related cognitions yet performed sub-optimally on the PFT as well. Rather than gambling-related cognitions mediating the relationship between foraging behavior and gambling behavior, perhaps gambling-related beliefs are epiphenomenal cognitive justifications for maladaptive decision making. Future research could address these issues by investigating the effects of correcting gambling-related cognitions (via education and increased awareness of stochastic reward structure) on changes in foraging behavior.

According to the elastic net analyses, the foraging paradigms were stronger predictors of gambling frequency and gambling-related cognitions than the risk-taking/impulsivity paradigms. This further supports our hypothesis that gambling behavior is rooted in suboptimal foraging behavior. An important difference between the foraging paradigms and the risk-taking/impulsivity paradigms is the reward structure. Because of these differences, each task requires a different strategy to maximize rewards. In the BART and RPT, rewards vary in magnitude and probability, and “risky” selections are those that favor a small probability of a large reward; however, BART total points were negatively associated with risky decisions, but RPT total points positively associated with risky decisions. For the BART, we limited the duration of the task, not the number of balloons, which could have affected the optimal strategy. However, the limited duration parallels the design of the PFT, in that participants can choose to remain in one patch (or one balloon) to earn points, or leave for the next one. Yet, surprisingly, we did not find similar results across the two tasks.

In the foraging tasks, rewards only varied in magnitude. In order to maximize rewards in both the 4ABT and PFT, the player needs a running estimate of the average number of points available in the overall environment (i.e., the average of all slot machine and patch options). The player should then stay at the current slot machine or patch while its points are better than the overall average, and leave when its points are worse than the overall average. Thus, the player must be sensitive to the range of points available and the rate of change over time, unlike in the BART and PFT where outcomes on each trial are independent of other trial outcomes. When investigating gambling behavior, it seems logical to use paradigms with probabilistic rewards, similar to real-world games of chance, and of course, some reward outcomes in real-world foraging are probabilistic as well. However, based on the results of this study, we propose that it is the individual’s ability to track outcomes over time and make advantageous stay/switch or explore/exploit decisions for short- and long-term gain (i.e., essential foraging decisions) that moderates gambling behavior. We suspect that one of the major contributing factors to the success of these foraging-type tasks over the impulsivity/risky choice paradigms is precisely this dimension of time: foraging behavior, like most decision behaviors, takes place repeatedly, as a sequence of decisions over time. Risky choice and impulsivity paradigms, by contrast, focus on biases most sharply associated with single decisions (repeated multiple times per task). However, our outcomes of interest fundamentally involve the rate at which participants choose to gamble, and decisions to gamble or not gamble are not made in isolation, but repeatedly over time.

The majority of research on gambling has focused on differences between problem gamblers versus non-problem gamblers or other controls. Many studies have shown an association between problem gambling and risk-taking and/or impulsivity (Mishra et al. 2010, MacLaren et al. 2011). While our hypotheses were informed by this research, our sample consisted of non-problem gamblers (with the exception of 2 participants, although they were not seeking treatment for problem gambling at the time of the study); which may be why we did not replicate those results. Alternatively, impulsivity and risk-taking are common among individuals with substance dependence (de Wit 2009) and may be expressed in problem gamblers as part of a general addiction phenotype. Individuals with problem gambling tend to have co-morbid substance dependence and other psychiatric disorders (Kessler et al. 2008). It may be the case that impulsivity/risk-taking co-occur with many types of problematic behaviors, but do not motivate gambling, specifically. Of course, more research is necessary to investigate whether problem gamblers also exhibit sub-optimal foraging behaviors, and these paradigms may provide a new avenue for researching and understanding maladaptive reward-seeking behaviors.

The psychobiological foundations of addiction are believed to originate in neural systems designed for foraging behaviors and for the encoding of emotional states (Panksepp 2010) and the dopaminergic system in particular underlies many reward-driven and motivational behaviors. In related research using a 2-armed bandit model of foraging behaviors, dopamine function has been proposed to modulate energy expenditure along an explore/exploit axis and a conserve/expend axis, in that diminished dopamine function favors exploitation and energy conservation while enhanced dopamine function favors exploration and energy expenditure (Beeler et al. 2012). If a healthy dopaminergic system is necessary for an optimal explore/exploit trade-off in foraging paradigms, then perhaps foraging paradigms could benefit addiction research by providing a behavioral assessment of dopamine function. Drugs of abuse acutely enhance dopamine levels but chronic abuse can decrease dopamine function (Volkow et al. 2009), and decreased dopamine function might predict increased exploitative behavior in foraging tasks. Along these lines, we previously found that nicotine-dependent smokers exploited more than nonsmokers in a multi-armed bandit task (Addicott et al. 2013). By extension, we hypothesized that individuals at increased risk for pathological gambling would exploit more than healthy controls, although this was not the case among our sample of non-problem, frequent gamblers. However, there have been very few studies conducted on the effects of pathological conditions on foraging behavior, and more research is needed to understand the complex relationship between dopamine function and foraging behavior among human subjects with and without dopamine-related pathologies.

Our study is not without limitations. First, we were not able to balance the sample sizes across groups due to a short recruitment period. Our results indicated that the monthly gamblers had greater risk preference than the other two groups, and this outcome could be related to the smaller sample size, and greater performance variability, of the monthly group. Second, we relied on the SOGS to assess gambling history; however, the SOGS was designed for clinical populations and other assessments may be more appropriate for non-problem gamblers. Third, none of our tasks represented a realistic gambling scenario, where the probability of winning is low and financial loss occurs. It is possible that we did not find effects of risk preference for this reason. Lastly, we did not recruit a random sample of participants, individuals who reported never gambling were excluded, and yearly, monthly, and weekly gamblers were recruited in approximately equal proportions. In addition, an equal number of smokers (≥ 10 cigarettes per day) and nonsmokers were recruited for each gambling frequency group. Thus, our sample does not represent the general population and future studies are needed to determine the generalizability of our results.

In summary, we investigated several perspectives on the question of why people gamble. Our results supported the cognitive psychological perspective that suggests frequent gambling is motivated and/or maintained by gambling-related cognitions. Conversely, our results did not support the popular personality-trait perspective that suggests frequent gambling is related to risk-taking and impulsivity. However, risk-taking and impulsivity may be characteristics of pathological gamblers, while our sample largely consisted of non-problem gamblers. We also proposed and showed support for a new, sub-optimal foraging perspective on gambling. Frequent gamblers exhibited more exploratory behavior and shorter latencies to target switching at the expense of maximizing their earned points. Foraging behavior is an instinctive ability to maximize rewards while minimizing the time and cost of obtaining those rewards; this behavior is believed to be regulated by dopamine-driven motivational systems. As such, foraging paradigms may be useful for future research on gambling and other addictions.