Requirement for transient metal ions revealed through computational analysis for DNA polymerase going in reverse

Significance

DNA polymerases use a general two-metal ion mechanism for DNA synthesis. Recent time-lapse crystallographic studies identified additional adjunct metal ions in the polymerase active site. One of these ions correlates with appearance of pyrophosphate and was proposed to be involved in pyrophosphorolysis (reverse reaction of DNA synthesis). Because DNA polymerases can use pyrophosphorolysis to remove chain-terminating nucleotides during chemotherapies, a better understanding of this reaction is warranted. Through site-directed mutagenesis, pyrophosphorolysis measurements, and computational analysis, we examine the role of metal ions in the reverse reaction. The results indicate that the product-associated metal ion facilitates pyrophosphorolysis during the early stages of the reaction but deters the reaction at later stages, suggesting dynamic metal behavior that can modulate the chemical equilibrium.

Abstract

DNA polymerases facilitate faithful insertion of nucleotides, a central reaction occurring during DNA replication and repair. DNA synthesis (forward reaction) is “balanced,” as dictated by the chemical equilibrium by the reverse reaction of pyrophosphorolysis. Two closely spaced divalent metal ions (catalytic and nucleotide-binding metals) provide the scaffold for these reactions. The catalytic metal lowers the pK_a of O3′ of the growing primer terminus, and the nucleotide-binding metal facilitates substrate binding. Recent time-lapse crystallographic studies of DNA polymerases have identified an additional metal ion (product metal) associated with pyrophosphate formation, leading to the suggestion of its possible involvement in the reverse reaction. Here, we establish a rationale for a role of the product metal using quantum mechanical/molecular mechanical calculations of the reverse reaction in the confines of the DNA polymerase β active site. Additionally, site-directed mutagenesis identifies essential residues and metal-binding sites necessary for pyrophosphorolysis. The results indicate that the catalytic metal site must be occupied by a magnesium ion for pyrophosphorolysis to occur. Critically, the product metal site is occupied by a magnesium ion early in the pyrophosphorolysis reaction path but must be removed later. The proposed dynamic nature of the active site metal ions is consistent with crystallographic structures. The transition barrier for pyrophosphorolysis was estimated to be significantly higher than that for the forward reaction, consistent with kinetic activity measurements of the respective reactions. These observations provide a framework to understand how ions and active site changes could modulate the internal chemical equilibrium of a reaction that is central to genome stability.

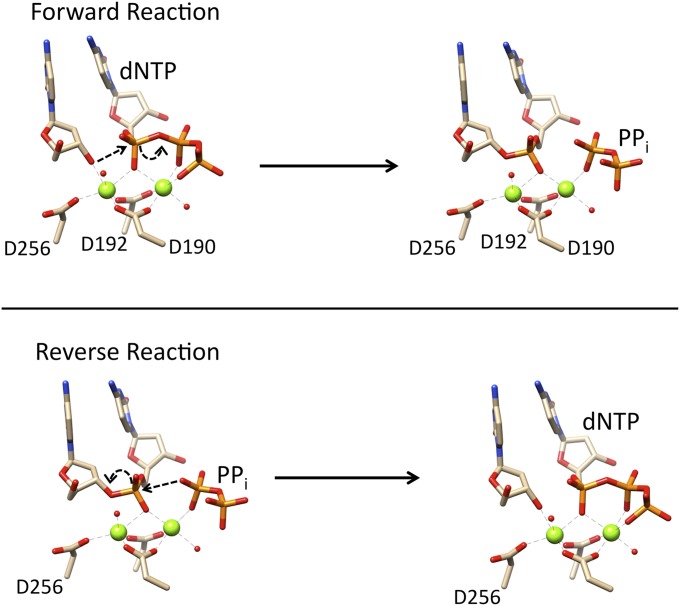
DNA polymerases are responsible for high-fidelity DNA synthesis during replication and repair of the genome (1). Although there are at least 17 human DNA polymerases, they all use a general nucleotidyl transferase DNA synthesis reaction. This reaction requires deoxynucleoside triphosphates (dNTPs), divalent metal ions, and DNA substrate with a primer 3′-OH annealed to a coding template strand. An inline nucleophilic attack of the primer 3′-oxyanion on P_α of the incoming dNTP results in products with DNA extended by one nucleotide [i.e., deoxynucleoside monophosphate (dNMP)] and pyrophosphate (PP_i). If the enzyme does not release PP_i, pyrophosphorolysis (reverse reaction) can generate dNTP and a DNA strand that is one nucleotide shorter (Fig. 1) (2).

Fig. 1.

Proposed two-metal reaction schemes for the forward reaction of nucleotide incorporation and the reverse reaction of pyrophosphorolysis by pol β. The conserved active site carboxylates that coordinate two magnesium ions (green spheres) are shown. The metal nearest Asp256 (D256) is the catalytic metal, and the metal that coordinates Asp190 (D190) and Asp192 (D192) is the nucleotide-binding metal. Two water molecules coordinating the metal ions are also shown (small red spheres).

Although the forward DNA synthesis reaction is preferred, the pyrophosphorolysis reaction can be biologically significant. Because DNA polymerases are an attractive chemotherapeutic target, chain-terminating nucleoside drugs are often used in a strategy of blocking DNA synthesis (3–5). However, drug resistance to chain-terminating agents is influenced by the ability of a stalled DNA polymerase to remove chain-terminating nucleotides through pyrophosphorolysis (6–8). Additionally, pyrophosphorolysis has been reported to remove misinserted nucleotides opposite specific DNA lesions as a proofreading activity (9). Accordingly, a better understanding of the mechanism of this reaction will hasten drug design and intervention. Although the biological implications are significant, a detailed chemical description of the reverse reaction is currently lacking.

DNA polymerase (pol) β has served as a model eukaryotic DNA polymerase for computational, structural, mechanistic, kinetic, and biological studies (10–12). Based on the structure of DNA bound to the exonuclease site of Escherichia coli DNA polymerase I, a general two-metal ion mechanism for the nucleotidyl transferase (nuclease and DNA synthesis) reaction was proposed 25 y ago (13). High-resolution crystallographic structures of a precatalytic ternary complex of pol β are consistent with the two-metal ion mechanism (14, 15). The active site metal ions are referred to as the catalytic (M_c) and nucleotide (M_n) metals. The metal ions coordinate the primer terminus nucleophilic oxygen (i.e., O3′), oxygens of each phosphate of the incoming nucleotide, and active site aspartate residues Asp190, Asp192, and Asp256 (Fig. 1). The catalytic metal ion lowers the pK_a of the primer terminus, whereas the nucleotide metal ion balances the developing negative charge during chemistry.

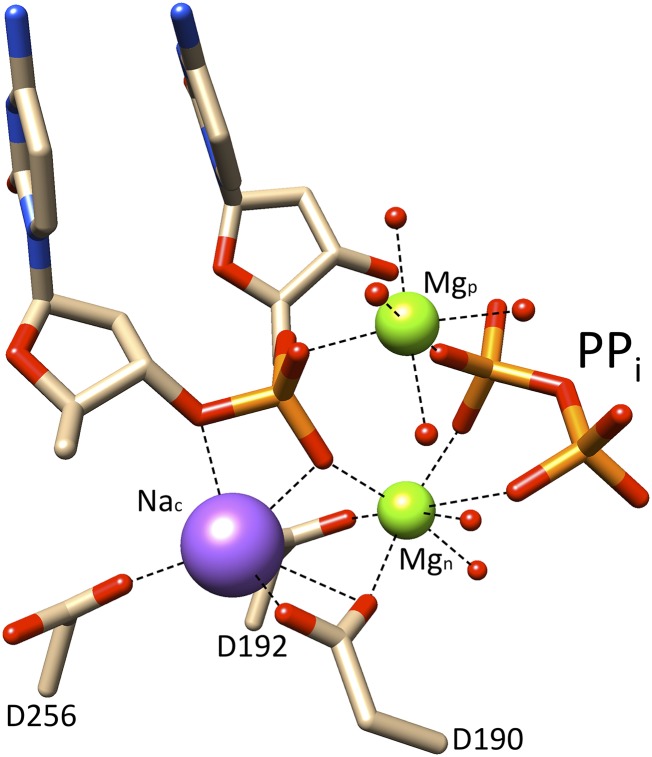
Recent time-lapse crystallography snapshots of postcatalytic events (i.e., with products) revealed that a Na⁺ ion replaces Mg²⁺ at the catalytic metal ion site and that a new Mg²⁺-binding site (M_p) associated with the nascent products (Fig. 2, extended DNA and PP_i) forms transiently (16). The product-associated metal ion has also been observed in structures of pol η (17) and pol β with alternate substrates (18, 19). It was proposed that the product metal ion may play a role in modulating charge distribution during the reverse reaction (16). To probe this possibility, we used a quantum mechanical/molecular mechanical (QM/MM) computational approach (20, 21) that has become an instrumental tool in mechanistic studies on enzyme catalysis. The results provide evidence that transient metal ions mediate charge distribution within the polymerase active site during chemistry that can alter the internal chemical equilibrium between the forward and reverse reactions.

Fig. 2.

The product metal-binding site. The product metal (Mg_p) coordinates the products of the forward reaction (i.e., nonbridging oxygens on the incorporated dCMP and PP_i). A sodium ion (Na_c) occupies the catalytic metal ion site in this product ternary complex structure (PDB ID code 4KLG). Metal-coordinating water molecules are shown as small red spheres.

Results

QM/MM Calculations.

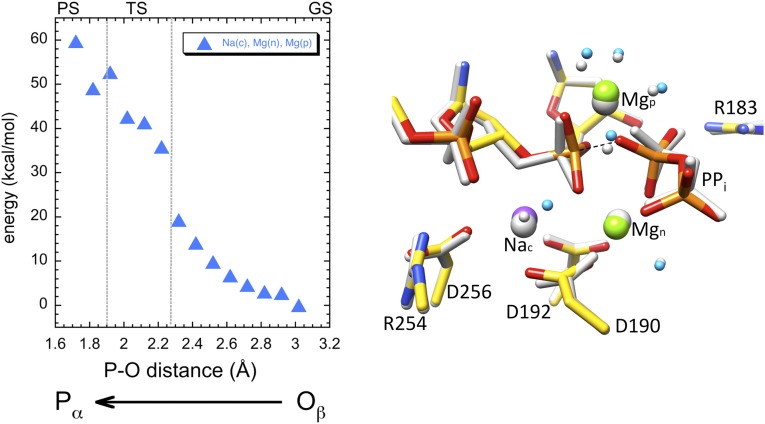
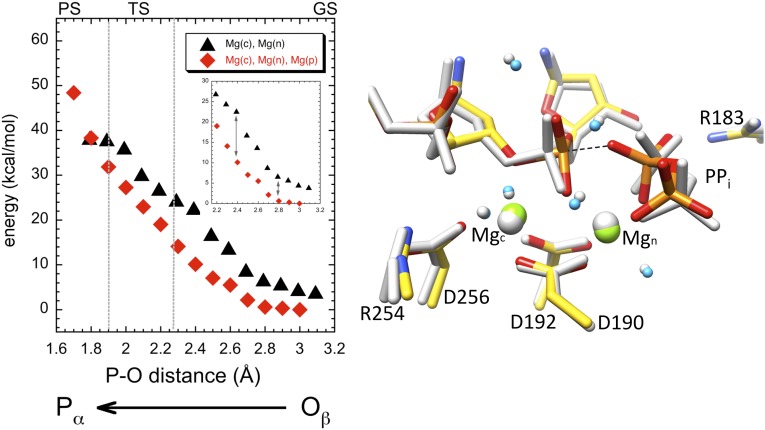
The energy profile and transition state determined previously for the forward DNA synthesis reaction (22–24) were used here as a frame of reference, where the energy at the transition state corresponded to ∼18 kcal/mol and the transition state was at an O3′–P_α distance of ∼2.2 Å. With this in mind, we initially examined the energy profile of the reverse reaction for the Na_cMg_nMg_p system based on the product complex observed immediately following catalysis (Fig. 3, Left) (16). As the distance between the PP_i nucleophilic oxygen and P_α was decreased, the energy profile resembled that of the forward reaction while these atoms were >2.3 Å apart. However, as this distance was further decreased, the energy for the reverse reaction became unrealistic during what would traditionally be the transition state. In the final calculation at a P_α–O_β distance of 1.7 Å, the three reactive atoms O3′–P_α–O_β were in positions similar to those for the transition state of the forward reaction (Fig. 3, Right) (22). However, the energy at this point (∼60 kcal/mol) was unreasonably high, and the profile indicated the system was essentially locked with no possible products. The product metal ion/oxygen coordination was maintained by the system throughout the entire energy profile calculations. The presence of the product metal ion appeared to block the reaction at P_α–O_β distances expected of the transition state.

Fig. 3.

QM/MM calculation for the Na_cMg_nMg_p system. Energy profile for the system that mimics an intermediate crystallographic substrate/product complex is shown in the Left panel. The calculated energy is plotted against the Pα–O_β distance as the reaction coordinate (i.e., the oxygen closest on PP_i to the primer terminal phosphate). The approximate ground, transition, and products states (GS, TS, and PS) of the reverse reaction are indicated. The starting (gray) and final (color) structures in the QM system are shown in the Right panel. Hydrogens are not shown for clarity, and the dotted line represents a pseudobond between P_α and O_β in the final configuration.

Because these results indicated the Na_cMg_nMg_p system does not yield an energetically realistic path for pyrophosphorolysis, we next determined whether a Mg²⁺ in the catalytic metal ion-binding site, as observed in certain crystallographic structures, could favorably influence the energy profile of the reverse reaction. Therefore, the Na⁺ in the catalytic metal ion site was substituted with a Mg²⁺ in preparing the Mg_cMg_nMg_p system (Fig. 4, Left), and the calculations repeated. The configuration with the lowest energy for this system was found at the P_α–O_β distance of 3.0 Å, and this was selected to be the starting point for this system (Fig. 4, gray structure). All magnesium ions were octahedrally coordinated in the starting configuration of the QM component. In this configuration, the distance between the magnesium ions at the catalytic and nucleotide metal sites was 3.62 Å, and the product metal was 4.99 Å distant from the nucleotide metal.

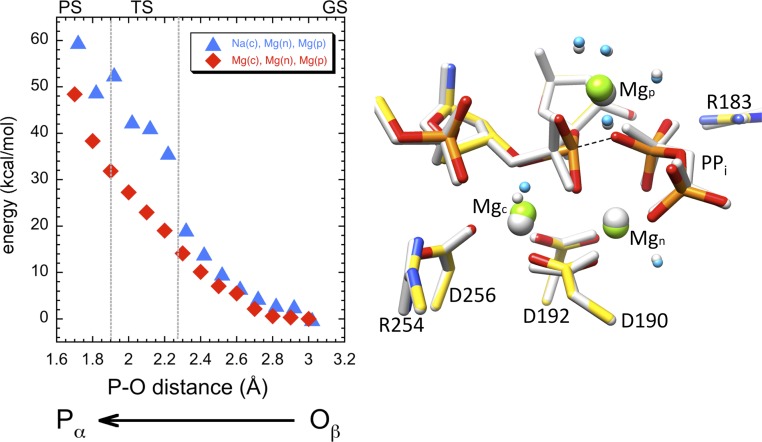
Fig. 4.

QM/MM calculation for the Mg_cMg_nMg_p system. This is similar to Fig. 3, except with magnesium in the catalytic metal site and reoptimizing the system at the initial MD level before starting QM/MM optimizations. The energy profile (Left) of the Na_cMg_nMg_p system is also shown here for comparison (blue triangles). The starting (gray) and final (color) structures in the QM system are shown in the Right panel.

As with the first calculation, the energy profile indicated a catalytically unrealistic reaction path (Fig. 4, Left). When the P_α–O_β distance was 1.7 Å, the energy of the system (∼50 kcal/mol) was far too high to be relevant; the final structure (Fig. 4, colored structure) was similar to that for the Na_cMg_nMg_p system (Fig. 3). Interestingly, the energy in the vicinity of a possible transition state for the Mg_cMg_nMg_p system was lowered by the presence of the Mg_c, indicating the possible requirement of Mg²⁺ in the catalytic metal ion position. Thus, both of these systems were inappropriate for mediating the reverse reaction, in part because the product metal ion appeared to be blocking the reaction late in these reaction paths.

A two-metal ion mechanism was originally proposed in the nucleotidyl transferase process (13). To examine whether Mg²⁺ at these two metal ion-binding sites (catalytic and nucleotide) might be sufficient for pyrophosphorolysis, we modified the potentially reactive core so as to prepare a Mg_cMg_n system by removing Mg_p and replacing it with a water molecule. After constrained and then unconstrained molecular dynamics (MD) to achieve equilibrium, a QM/MM initial system was defined from the final optimized configuration of the classical trajectory. Several additional water molecules (six) that coordinated the pyrophosphate and the primer terminus phosphate were included in the QM component (Fig. 5, structure representation). In the optimized QM/MM reference system, the P_α–O_β distance was 3.6 Å. This was the largest separation for these atoms for all systems studied. In the other systems for which the product metal was present, this distance was 0.7 Å shorter. The two magnesium ions were separated by 3.56 Å and maintained octahedral coordination, as in the two systems described above.

Fig. 5.

QM/MM calculation for the Mg_cMg_n system. This system was created after exchanging the positions of Mg_p in the Mg_c, Mg_n, Mg_p system with that of the oxygen of a remote water molecule and reoptimizing the system in the beginning at the MD level before starting QM/MM optimizations. The energy profile (Left) of the Mg_cMg_nMg_p (red diamonds) is also shown for comparison. In the Inset, the early gain in energy for the three-metal system is emphasized. The starting (gray) and final (color) structures in the QM system are shown in the Right panel.

The energy profiles for the Mg_cMg_n system is shown in Fig. 5. Although there were subtle differences in the energy along the reaction path, the overall features of the energy profile with this system (Fig. 5, Left) were similar to those observed in the other two systems. Importantly, the reverse reaction was not observed, thereby indicating that the mechanism of the reverse reaction is not simply the same as the forward reaction.

For the three systems described thus far, an instructive comparison of the energy profiles is provided in Figs. 4 and 5. When Mg²⁺ occupies the product metal ion site, the energy barrier in the early part of the reaction path (P_α–O_β distances from 2.9 to 2.4 Å) is 8–10 kcal/mol lower than for the two-metal ion system (Fig. 5, Left Inset). Thus, the results for the early portion of these profiles suggested a beneficial effect of Mg²⁺ in the product metal ion site during the initial attack of the PP_i oxygen on the primer terminus phosphate (i.e., P_α). However, it becomes inhibitory when these atoms approach 2.3 Å. A similar inhibition phenomenon occurs when Na⁺ occupies the catalytic metal site. Fig. 4 indicates that additional energy is required, as the P_α–O_β distance is reduced below 2.4 Å when Na⁺, a weak Lewis acid, is in the catalytic metal ion-binding site. From this comparison, we deduce that Mg²⁺, a stronger Lewis acid, is required in the catalytic site. A product Mg²⁺ ion lowers the activation energy in the early part of the reaction path but must be displaced midpath in order for the reaction to proceed beyond the transition state (∼2.4 Å). It appears that the “strong” coordination (strict octahedral geometry and ligand distances) exhibited by Mg²⁺ in the product metal site as the reaction approaches the transition state region does not permit the reaction to proceed, thereby precluding Mg²⁺ in the catalytic site facilitating product departure.

Pol β Pyrophosphorolysis Solution Assay.

In light of the results described so far, we decided to confirm that pol β is capable of catalyzing the reverse reaction. A qualitative assay to measure pyrophosphorolysis activity in solution with nicked DNA as substrate demonstrated that the wild-type enzyme can remove 3′-nucleotides from the substrate in a short period (Fig. 6). In a single-turnover assay system, where the enzyme concentration exceeded the substrate concentration, removal of the 3′-nucleotide occurred at a rate of 0.03/s. This rate of the reverse reaction is over two orders of magnitude less than that of the forward reaction (i.e., the insertion of a single nucleotide into a gapped substrate) (25).

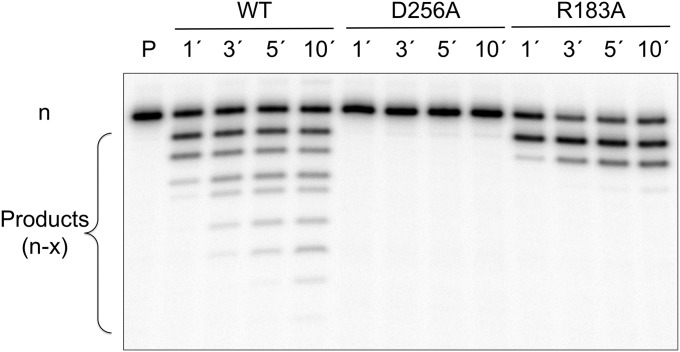
Fig. 6.

Pyrophosphorolysis. The reverse reaction (pyrophosphorolysis) was assayed under single-turnover conditions (E>>DNA) using a 5′-[³²P] nicked DNA substrate with wild-type (WT) pol β or D256A and R183A mutants. Reactions were initiated with MgCl₂/PP_i and stopped after 1, 3, 5, or 10 min. The products were separated on a 16% denaturing gel as outlined in Materials and Methods. The first lane (P) represents the full-length primer (n), whereas the shorter products (n–x) represent continued pyrophosphorolysis reactions generating additional products. Loss of pyrophosphorolysis activity by removing a catalytic metal-binding ligand through D256A mutation indicates that the catalytic metal is essential for the reverse reaction. Likewise, removing a hydrogen bond with PP_i through R183A substitution dramatically decreases pyrophosphorolysis.

A crystallographic structure of the ternary substrate precatalytic complex indicated that the catalytic metal site was empty for the alanine mutant of Asp256 (24). We found that the reverse reaction was also lost with this mutant (Fig. 6), suggesting that there is a stringent requirement for the catalytic metal ion during pyrophosphorolysis. Additionally, because Arg183 interacts directly with the PP_i product and stabilizes it in the active site (16), the effect of loss of this interaction was experimentally determined for the reverse reaction. As expected, the results indicated that loss of the Arg183 interaction severely limits the reverse reaction (Fig. 6).

Assuming that the experimentally determined rate measured for the forward and reverse reactions represent chemistry, the experimental free energy difference (3.6 kcal/mol) is similar to the calculated difference (4 kcal/mol; see QM/MM System to Probe a Transient Product Metal). However, because the computational uncertainty is similar to the calculated difference, the chemical equilibrium constant could be significantly different from the simple ratio of the observed forward and reverse rate constants (26–30).

QM/MM System to Probe a Transient Product Metal.

Time-lapse X-ray crystallographic structural snapshots had suggested that the occupancy of the product metal site is transient. The product metal is not observed until a significant population of PP_i is formed and dissociates before PP_i dissociation (16). To better understand these crystallographic results, we needed to develop a QM component that could reflect the transient nature of this metal. However, it is problematic to recreate transient occupation of the product metal site with an optimum number of QM atoms selected; the expansion of the QM system size to permit movement of the product metal would be computationally prohibitive. Therefore, we chose an alternate approach to mimic the transient nature of the product metal. We reduced the rigidity imposed by the Mg²⁺ ion at the product metal site by substituting it with Na⁺. This substitution of Na⁺ allows an extended coordination distance and prevents the restrictive nature imposed by magnesium to preserve its coordination sphere. In addition, because we computationally observed a beneficial effect of Mg²⁺ at the catalytic metal site, we switched the catalytic site sodium to a magnesium ion. Thus, the original Na_cMg_nMg_p system became Mg_cMg_nNa_p. After equilibration, this system has a relaxed metal ion–oxygen coordination sphere at the product site that reflects the transient nature of a metal ion at this site. In the equilibrated system, Na⁺ has oxygen coordination distances that are longer (∼2.4 Å) than those for Mg²⁺ (∼2.1 Å) (31).

First, to test the idea of using this new system in a full QM/MM calculation, we reoptimized the original Na_cMg_nMg_p geometry at the P_α–O_β distance of 1.7 Å for the new Mg_cMg_nNa_p system and found that the system spontaneously converted to the product state for the reverse reaction (Fig. 7, green triangle). This indicated that the new system was not trapped in a dead end complex and was capable of yielding products. Next, an unconstrained optimization of the original Na_cMg_nMg_p system in its geometry at a P_α–O_β distance of 1.7 Å spontaneously resulted in a state similar to that of the starting point of the reaction path (SI Appendix, Fig. S1, open triangle at a P_α–O_β distance of 2.9 Å). Thus, because a product state could be observed in the Mg_cMg_nNa_p system, we extended the QM/MM examination to all geometries in the energy profile of the Mg_cMg_nNa_p system.

Fig. 7.

Influence of Na_p late in the reaction coordinate. The Na_c of the Na_cMg_nMg_p system was replaced with a magnesium ion and Mg_p with a sodium ion (i.e., swapping the two ions occupied at catalytic and product metal ion sites as shown in the Right panel) in the final conformation (P_α–O_β = 1.7 Å) shown in Fig. 3. Relaxing the resultant system using a QM/MM reoptimization yielded a triphosphate product conformation (green triangle).

The energy profile for the Mg_cMg_nNa_p system is shown in Fig. 8 (green circles). When the catalytic metal site is occupied by Mg²⁺ and the product metal site by Na⁺, a complete reaction profile with a broad transition state (2.0–2.2 Å) is observed, with an activation barrier of ∼22 kcal/mol. Fig. 8 also provides comparison of the two-metal (Mg_cMg_n) and three-metal (Mg_cMg_nMg_p) ion systems for the reverse reaction with that of a system in which a third metal (a sodium that mimics a transient metal) occupies the product metal site. A metal ion in the product metal site substantially lowers the energy in the initial phase of the reaction path. Importantly, the transient nature of the product metal ion (i.e., replacement with a sodium ion) facilitates the product state by producing a catalytically competent reaction path. Nevertheless, the energy barrier at the transition state of the reverse reaction is higher than that reported for the forward reaction (22–24) (i.e., ∼22 vs. ∼18 kcal/mol). In addition, a weak coordination for the water molecules solvating Na⁺ is observed (Fig. 8) in comparison with that of the Mg²⁺ at the product metal ion site.

Fig. 8.

QM/MM calculation for the Mg_cMg_nNa_p system. All QM/MM optimized configurations in Fig. 3 were subjected to the swapping of the metal ions occupied at catalytic and product metal-binding sites to create this system. The energy profile (Left) for the reoptimized structures for the Mg_cMg_nNa_p system (green circles) is compared with the Mg_cMg_nMg_p and Mg_cMg_n systems (red diamonds and black squares, respectively). The Inset shows the energy profiles for the transition region. A structural state (Right) that resembles the expected triphosphate product (in color) is compared with an early configuration in the reaction coordinates (gray).

Charge Calculations and the Mechanism of Transient Metal Effects on the Reverse Reaction.

The QM component in these studies consisted of 113 atoms. A substantial number of atoms in this quantum subsystem are buried. It is generally recognized that charge calculations using electrostatic potential fitting schemes, such as Merz–Singh–Kollman (32), Chelp (33), and ChelpG (34), can become unreliable for buried charges (35). Therefore, we selected an atomic charge method that yields a stable charge distribution for atoms. The CM5 charge model (35), an extension of Hirshfeld population analysis proposed by the Truhlar group and that is adapted to accommodate buried atoms properly, was used for calculating QM component charges. We subsequently performed a QM cluster calculation on the QM atoms (including protons at the pseudoatom positions in the boundaries) in the presence of the charge distribution of the MM atoms, so as to preserve the surrounding QM/MM environment that significantly influences the QM component. The resultant electrostatic charges obtained from the CM5 charge scheme are tabulated (SI Appendix, Table S1 A–D; the atom identities are given in SI Appendix, Table S1E). For clarity, we present the atomic charge differences (current – initial value) at each selected step.

The charge variations during the reaction profiles can be used to examine the redistribution of the electron density during the course of the reaction (SI Appendix, Fig. S2). In the initial portion of the reaction path (2.9–2.4 Å), the variations of charge for all four systems were similar. Interestingly, however, in the Mg_cMg_nNa_p system, for which the reverse reaction was observed, a relatively larger charge variation was found for the new primer O3′ product (atom 62, variation of about 0.24e for Mg_cMg_nNa_p versus 0.09e–0.14e for the other three systems) of the sugar ring. This oxygen atom became more negative as the transition state developed and resolved. The result in this case was reminiscent of the charge variation found for the same oxygen atom during the forward reaction (24), except in this case the oxygen becomes more negative instead of less negative (as in the forward reaction) after the transition state. This charge variation is mediated by the catalytic magnesium ion, explaining the requirement for magnesium at the catalytic site (Fig. 9). Participation of water molecules in charge redistribution was significant, as revealed by the relatively larger charge variation of several of the water molecules (water oxygen atoms 96 and 99), again especially in the Mg_cMg_nNa_p case for which the reverse reaction was observed.

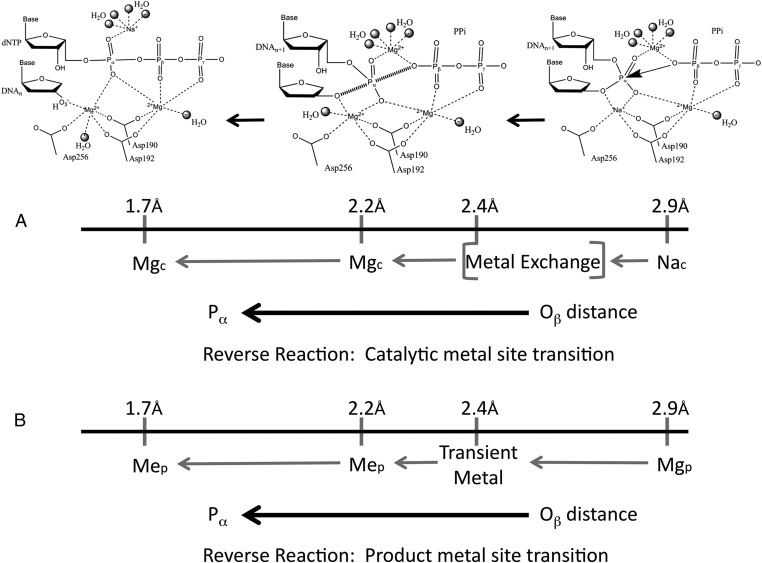
Fig. 9.

Reaction path and various metal ion-binding site occupancies during the course of the pyrophosphorolysis reaction. The starting configuration (Top Right) of the reverse reaction is the product structure of the nucleotide incorporation reaction. A sodium ion is observed in the catalytic metal-binding site. In the transition state (Top Middle), the catalytic metal site requires a magnesium ion. The conversion of PP_i to dNTP is found in the product state of the pyrophosphorolysis reaction (Top Left). Shown are potential metal ion occupancies at (A) the catalytic metal ion-binding site and (B) the product metal ion-binding site for various segments of the reaction path to facilitate pyrophosphorolysis.

Discussion

It is a basic tenant of the theory of enzyme action that the enzyme catalyzes both the forward and reverse reaction. Thus, for forward reactions that do not have a large negative free energy change, the reverse reaction can become an important condition-dependent consideration. Such is the likely case for the pol β chemical nucleotide insertion (forward) and pyrophosphoroylsis (reverse) reactions. We have previously used QM/MM methods to complement our experimental structural studies of the forward chemical nucleotide insertion for pol β (22–24). Given the substantial evidence that the reverse reaction occurs and the recent identification of an adjunct third metal transiently observed during substrate/product interconversion (16), we embarked on a series of QM/MM simulations that model the reverse reaction. A logical progression of calculations Na_cMg_nMg_p, Mg_cMg_nMg_p, and then Mg_cMg_n did not provide a productive path; that is, the transition barriers were too large to be feasible. However, when we used the geometries generated by the Na_cMg_nMg_p system to optimize energies and geometries for an Mg_cMg_nNa_c system, a reasonable path for pyrophosphorolysis that is energetically feasible was found that also accommodates the transient nature of the product metal.

Transient Metals and the Reverse Reaction.

The calculations indicate that pyrophosphorolysis requires a temporal order of metal binding in the catalytic and product metal sites (Fig. 9). Starting with the crystallographic ternary product structure (Fig. 3, structural image), magnesium in the product metal site is beneficial as the P_α–O_β distance is reduced from 2.9 to 2.4 Å. This is evident by comparing the energy of the Mg_cMg_n system with that of the Mg_cMg_nMg_p system; the latter system was 8–10 kcal/mol more favorable (Fig. 4). After this point in the reaction path, the presence of magnesium in the product metal site was inhibitory. This inhibition arises from the Mg²⁺ sterically blocking bond formation in the computational studies, thus indicating the product metal must be transiently bound during catalysis. Substituting a sodium ion for the magnesium ion permits the reaction to proceed given the “loosened” ligand coordination of sodium compared with magnesium. An additional critical observation is that the reaction can only proceed when the catalytic metal site contains a magnesium ion. Regarding the catalytic metal site, the crystallographic ternary product structure contains a sodium ion in this site (Fig. 3, structural image). As the P_α–O_β distance is reduced from 2.9 to 2.4 Å, the energy with either sodium or magnesium in the catalytic site was similar (Fig. 4). After this point, however, magnesium in the catalytic site was favorable. This was evident when the inhibitory effect of magnesium in the product metal site was removed by substituting with sodium at this site (Fig. 8). This transient behavior of the active site metals during the reverse reaction is illustrated in Fig. 9.

Overview.

The notion that transient metal ions could be important in the DNA polymerase catalytic cycle had not occurred to us until time-lapse crystallographic structural intermediates revealed a new metal-binding site accompanying product formation was transient in nature (i.e., not observed in pre- or postcatalytic structures) (16). Previous work had noted that sodium easily exchanged for magnesium at the catalytic metal-binding site (15, 16). The sodium exchange for the catalytic metal ion is probably facilitated by the loss of a metal-binding ligand (primer O3′) as DNA is extended by a nucleotide in the forward reaction. The calculations provide an additional feature of the catalytic site metal ion exchange; when a sodium ion occupies the catalytic metal site, the reverse reaction was blocked. Accordingly, loss of the catalytic magnesium ion after insertion (forward reaction) commits the reaction forward.

In hindsight, the dynamic nature of the metals is not surprising. During the course of the chemical reaction, developing negatively charged ligands must be neutralized in the product state. Thus, metal–ligand interactions in the ground state are broken during the course of the reaction, and new product ligands generate new metal interactions. This appears to be the situation with a metal ion at the product metal-binding site described here. Because products must be released for catalytic cycling, the stabilizing influence of the product metal ion must be removed to permit product dissociation.

Given the positive charge of a metal ion in the context of the active site, it is likely that a transient metal would have a significant impact on charge distribution during the reaction. In this way, the impact of the metal ions in the QM/MM systems used here can be rationalized. For the reverse reaction, the switch from Mg²⁺ to Na⁺ at the product site mimics the transient nature of this metal. Likewise, Mg²⁺ at the catalytic site is absolutely required, indicating that magnesium must rebind to this site for pyrophosphorolysis to occur. Although the mechanism of the ion exchange at these two sites originates for different reasons, the transient feature of active site metals can provide catalytic versatility (i.e., modulate the active site chemical equilibrium) and may be a general strategy used by other metal-dependent enzymes. Nonetheless, metal ion transitions during the course of a reaction present a computational challenge and opportunity.

Because many DNA polymerases undergo subdomain motions that accompany substrate binding, the active site also transitions from an open, solvent-exposed state to a closed, less solvent-accessible state (11). In this context, it should be noted that these calculations are performed in an environment of the closed polymerase active site and are thus sensitive to the internal chemical equilibrium at the enzyme active site. As described above, active site metals can modulate the internal equilibrium in the closed polymerase state. Open/closed enzyme conformational changes would be expected to also alter the overall equilibrium. For example, rapid reopening after DNA synthesis that permits PP_i dissociation would “pull” the reaction forward, thereby increasing the observed equilibrium constant toward DNA synthesis.

Because protein dynamics are not considered here, it is important to acknowledge the technical limitations of the present work. Chung et al. (36), in their review of the method used here, note the challenging task to carry out stable geometry optimization of a complex system with an enormous number of degrees of freedom that leads to a great number of potential conformations. By necessity, our sampling is limited but, we believe in this case, is adequate for the current exploration. In addition, the QM/MM methodology that was developed to treat the essential parts of the enzymatic reaction by QM can give rise to potential errors due to insufficient size of the QM system, treatments of the QM and MM boundaries, and electrostatic interactions between the QM and MM systems. Previously, Ryde and coworkers (37) reported that the mean absolute errors emanating from systems could be as much as 7 kcal/mol. Despite these potential errors, the magnitude of which is difficult to systematically estimate, the current level of methodology is quite useful for combining with crystallography and experimental measurements when considering mechanistic possibilities.

Conclusions

We have performed a series of QM/MM calculations and pyrophosphorolysis assays to examine the effect of the product metal ion on the pyrophosphorolysis reaction catalyzed by pol β. This adjunct metal was observed near the end of the nucleotide insertion reaction in the recent time-lapse crystallographic structures (16–19). Our results from QM/MM calculations indicate that the pyrophosphorolysis reaction is dependent on a magnesium ion in the catalytic metal site. Additionally, a magnesium or sodium ion in the product site reduces the activation barrier in the initial portion of the pyrophosphorolysis reaction coordinate. However, continued occupancy of the product site by a magnesium ion shows a strong inhibitory effect as the reaction proceeds into the anticipated transition state region; that is, P_α–O_β distances are less than 2.4 Å and must be removed for the pyrophosphorolysis reaction to proceed. The calculated transition state energy barrier for the pyrophosphorolysis reaction is within a range (∼22 kcal/mol) that is generally consistent with our solution kinetics studies. These observations provide a framework to understand how ions and active site charge distribution modulate the chemical equilibrium of a reaction that is central to genome stability.

Materials and Methods

Pyrophosphorolysis Solution Assays.

Bacterially expressed wild-type human pol β and mutants (D256A and R183A) were purified as described previously (38). Reactions were conducted in 50 mM Mes, 25 mM Tris, 25 mM ethanolamine (pH 7.5 adjusted at 37 °C) containing 100 mM KCl, 1 mM DTT, and 100 µg/mL BSA. Pol β (2 µM) was preincubated with nicked DNA (200 nM) for 5 min at 37 °C. The reaction was initiated by manual mixing with a prewarmed solution of 20 mM Mg²⁺ and 2 mM PP_i (1:1, vol/vol) (final enzyme, DNA, MgCl₂, and PP_i concentrations were 1 µM, 100 nM, 10 mM, and 1 mM, respectively). Aliquots (10 µL) were removed at various times and quenched in an equal volume of 0.3 M EDTA, pH 8.0. Reaction substrates and products were resolved on 16% (wt/vol) denaturing (8 M urea) polyacrylamide gels and visualized by phosphorimagery using a Typhoon 8600 (GE Healthcare) imager and ImageQuant software.

Computational Procedure for QM/MM Calculations.

Initial structures for theoretical calculations were prepared using a recent high-resolution crystallographic structure of the ternary product complex [Protein Data Bank (PDB) ID code 4KLG] where the catalytic metal site is occupied by a sodium ion and magnesium ions occupy the nucleotide and product metal sites. MD simulations were carried out in a completely solvated aqueous medium after hydrogens and neutralizing sodium ions were added. Positions of all crystallographic water molecules were preserved initially. The pyrophosphate charge was taken to be –3, and the phosphate on the pyrophosphate near the newly formed DNA primer terminus was assumed to be completely deprotonated. All MD trajectory calculations were carried out with the Amber12SB force field using the particle mesh Ewald MD module of Amber.12 (39). Water molecules were represented by the transferable intermolecular potential 3P model (40). Long-range interactions were treated with the particle mesh Ewald method (41). After initial isothermal-isobaric trajectory at 10K to adjust the density of the system near 1.0 g/cm³, a 20-ns constant volume/constant temperature (T = 300K) equilibrium simulation with the sequentially decreasing harmonic constraint force constants (from 50 to 0.1 kcal/mol/nm) applied to the protein, DNA, and metal ions in the crystallographic structure ensures that the system coordinates represent a precatalytic state. Before QM/MM calculations, we optimized several configurations selected from MD simulations and used the lowest energy system as the starting configuration for the reaction path calculation; other configurations are within 3 kcal/mol to this lowest energy conformation. The lowest energy configuration was used for the reaction path calculation. The system with a magnesium ion at the active site was prepared from the same coordinates (PDB ID code 4KLG). A two-metal system originates from this system where the product metal and a distal water molecule exchange their positions and the geometry reoptimized.

The QM/MM systems were prepared from the final optimized structures of the above systems. The quantum region included parts of Arg183, Asp190, Asp192, Arg254, and Asp256 from pol β; the former primer terminal nucleotide including the 5′-phosphate group; the newly extended primer terminal nucleotide; and the three metal ions in the catalytic, nucleotide, and product metal positions. In addition, there were six water molecules solvating the metal ions included in the QM region. Except for the system without a product metal, all systems contained 113 QM atoms; in the two-metal system, there were 112 QM atoms. Atoms within 10 Å of the quantum atoms were treated using the Amber force field and allowed to move. The rest of the atoms remained frozen during the optimizations. Altogether, each system contained over 10,100 atoms in the MM region. The charges of the QM region with Na_cMg_nMg_p, Mg_cMg_nMg_p, Mg_cMg_nNa_p, and Mg_cMg_n systems were –1, 0, –1, and –2, respectively.

The reaction scheme for bond formation (and bond breaking) was studied using the hybrid QM/MM potential with the ONIOM(MO:MM) framework (42) implemented in the Gaussian-09-D1 (43). The QM region was treated using B3LYP exchange-correlation function and 6–31+g* basis set. The classical region was handled using the Amber ff12SB force field (39). Calculations were performed within the electronic embedding scheme (42, 43) to accommodate the polarization of the QM region by the partial charges in the MM region. The only reaction coordinate present in the current protocol was the distance between the phosphorous atom of the phosphate group of the primer terminus and the nearest oxygen atom of PP_i.