Detecting Glaucoma Progression From Localized Rates of Retinal Changes in Parametric and Nonparametric Statistical Framework With Type I Error Control

Abstract

Purpose.

We evaluated three new pixelwise rates of retinal height changes (PixR) strategies to reduce false-positive errors while detecting glaucomatous progression.

Methods.

Diagnostic accuracy of nonparametric PixR-NP cluster test (CT), PixR-NP single threshold test (STT), and parametric PixR-P STT were compared to statistic image mapping (SIM) using the Heidelberg Retina Tomograph. We included 36 progressing eyes, 210 nonprogressing patient eyes, and 21 longitudinal normal eyes from the University of California, San Diego (UCSD) Diagnostic Innovations in Glaucoma Study. Multiple comparison problem due to simultaneous testing of retinal locations was addressed in PixR-NP CT by controlling family-wise error rate (FWER) and in STT methods by Lehmann-Romano's k-FWER. For STT methods, progression was defined as an observed progression rate (ratio of number of pixels with significant rate of decrease; i.e., red-pixels, to disk size) > 2.5%. Progression criterion for CT and SIM methods was presence of one or more significant (P < 1%) red-pixel clusters within disk.

Results.

Specificity in normals: CT = 81% (90%), PixR-NP STT = 90%, PixR-P STT = 90%, SIM = 90%. Sensitivity in progressing eyes: CT = 86% (86%), PixR-NP STT = 75%, PixR-P STT = 81%, SIM = 39%. Specificity in nonprogressing patient eyes: CT = 49% (55%), PixR-NP STT = 56%, PixR-P STT = 50%, SIM = 79%. Progression detected by PixR in nonprogressing patient eyes was associated with early signs of visual field change that did not yet meet our definition of glaucomatous progression.

Conclusions.

The PixR provided higher sensitivity in progressing eyes and similar specificity in normals than SIM, suggesting that PixR strategies can improve our ability to detect glaucomatous progression. Longer follow-up is necessary to determine whether nonprogressing eyes identified as progressing by these methods will develop glaucomatous progression. (ClinicalTrials.gov number, NCT00221897.)

We present three new methods to detect glaucoma progression from localized rates of retinal changes with control for overall false detection errors. These methods using HRT exams detected a higher portion of nonprogressing patient eyes with subtle and/or early stages of visual function progression.

Introduction

Glaucoma is a progressive optic neuropathy that results in progressive loss of retinal nerve fibers and death of retinal ganglion cells.^1,2 The loss of retinal nerve fibers causes characteristic changes in the appearance of the retinal nerve fiber layer as localized or diffuse defects and changes in the configuration of the optic disk.³ Detecting structural glaucomatous change over time, therefore, is a central aspect of detecting glaucomatous progression and management of glaucoma.¹ Progressive retinal changes are observable in vivo using various optical imaging modalities. In this work, we focus on detecting glaucomatous progression from localized rates of structural changes using the Heidelberg RetinaTomograph (HRT; Heidelberg Engineering, GmbH, Germany).

Techniques, such as the HRT topographic change analysis (TCA),⁴ statistic image mapping of the retina (SIM),⁵ and proper orthogonal decomposition framework (POD),^6,7 can detect retinal locations with glaucomatous change over time from serial HRT exams. The TCA and POD methods detect changes in retinal locations in each HRT follow-up exam with respect to a baseline and SIM detects retinal locations with significant rate of change during follow-up. Simultaneous assessment of thousands of retinal locations for progression increases the family-wise or overall false-positive detection errors. This tendency of multiple simultaneous tests to increase the overall false-positive errors or type I statistical errors is known as the multiple comparison problem.^8–13 Patterson et al.⁵ pointed out the multiple comparison problem in retinal imaging when retinal locations are evaluated collectively to detect glaucomatous progression as in HRT TCA, and developed the SIM method based on a nonparametric statistical technique. The SIM evaluates the statistical significance of rate of change at each retinal location as well as controls the overall type I error due to simultaneous assessment of spatial extents of changes (cluster size) using a statistical procedure known as resampling. During resampling, the observed retinal measurements of an eye are treated as its sampling population and new unique samples are drawn from this population. In general, the following procedures are available for resampling: bootstrap (sampling with replacement),¹⁴ jackknife (leaving one observation out at a time),¹⁵ permutation (sampling without replacement),^16,17 and subsampling (resampling fewer samples).¹⁸

In glaucoma research, the resampling approach has been used for assessing the effect of number scans acquired per exam on the estimates of optic disk stereometric parameters,¹⁹ parameter selection for glaucoma detection using a linear discriminant function,²⁰ detecting glaucomatous changes over time using time-domain optical coherence tomography (O'Leary D, et al., IOVS 2007;48:ARVO E-Abstract 3335), evaluating HRT stereometric parameters and topographic change analysis probability maps (Artes PH, et al., IOVS 2008;49:ARVO E-Abstract 5430), data simulations to evaluate longitudinal glaucomatous changes in visual fields²¹ and optic nerve head,²² detecting glaucomatous progression of visual fields^23,24 (O'Leary D, et al., NAPS Abstract, 2011), and is increasingly utilized for nonparametric statistical analysis in glaucoma research.^25–27

The SIM controls the overall false-positive detection only among the spatial extents (or clusters) of progression in neighboring retinal locations (i.e., only during cluster-level testing) and does not control among individual retinal locations (i.e., not during pixel-level testing). Lack of control for overall false-positive detection among retinal locations may reduce the confidence on the assessment of progression in retinal locations reported in the glaucoma progression maps for visual inspection, and may decrease the sensitivity of detecting progression using the clusters of changes due to possible increase in the number of false-positive locations in individual clusters.

In this study, we introduced the following three new parametric and nonparametric statistical strategies called pixelwise rates of retinal changes (PixR) to control overall false-positive detection of progression among individual retinal locations and compare their diagnostic accuracy for detection of glaucoma progression to SIM: (1) PixR nonparametric cluster test (PixR-NP CT) is a nonparametric test that directly extends SIM by controlling overall false-positive errors at pixel- and cluster-level using Bonferroni correction or family-wise error rate (FWER), (2) PixR nonparametric single threshold test (PixR-NP STT) is a nonparametric test that controls overall false-positive errors at the pixel-level using a k–FWER procedure by Lehmann and Romano,²⁸ which is less conservative than Bonferroni correction, and (3) PixR parametric single threshold test (PixR-P STT) controls overall false-positive errors at the pixel-level in a parametric framework using the k-FWER procedure.

Methods

Subjects

We included 267 eyes from 187 eligible participants with good quality HRT images from the University of California, San Diego (UCSD) Diagnostic Innovations in Glaucoma Study (DIGS). For eligibility, the study eyes were required to have at least four good quality HRT-II exams, at least five good quality Standard Automated Perimetry visual field exams (SAP; Humphrey HFA-II; Carl Zeiss Meditec, Dublin, CA) and at least two good quality stereophotographs of the optic disk (TRC-SS; Topcon Instruments Corp. of America, Paramus, NJ). Visual fields included for assessing progression were acquired using either full threshold or SITA standard threshold test strategy and using either 30-2 or 24-2 testing algorithm. For data quality, HRT-II exams with mean pixel height standard deviation (MPHSD) < 50 μm, even image exposure and with good centering were considered to be of acceptable quality after quality review by the UCSD Imaging Data Evaluation and Assessment Center according to standard protocols²⁹; SAP visual field exams with fewer than 25% false-positives, false-negatives, and fixation losses, and no observable testing artifacts were considered to be reliable; and stereophotographs assessed as fair to excellent quality by trained graders were considered to be of acceptable quality. Median (interquartile range) MPHSD for the HRT exams was 15 (12–21) μm.

The study eyes comprised of three categories, namely, progressing eyes for assessing sensitivity of detecting progression, nonprogressing patient eyes, and longitudinal normal eyes for assessing specificity of detecting progression.

Glaucomatous progression was defined based on either progressive visual field loss or optic disk changes from stereophotograph assessment. Progressive visual field loss was defined based on likely progression by SAP Guided Progression Analysis (GPA; Humphrey Field Analyzer, software ver. 4.2; Carl Zeiss Meditec). Progressive changes in stereophotographic appearance of the optic disk between the baseline and the last stereophotograph of each eye (patient name, diagnosis, and temporal order of stereophotographs were masked) were assessed by two observers based on a decrease in the neuroretinal rim width, appearance of a new retinal nerve fiber layer (RNFL) defect, or increase in the size of a preexisting RNFL defect. Any differences in assessment between these two observers were adjudicated by a third observer. For each eye, the baseline visual field exams for SAP GPA and the baseline stereophotograph for grading optic disk progression were chosen to be within six months from the HRT-II baseline exam date. Similarly, the last SAP exam and the last stereophotograph were chosen to be within six months of the last HRT-II exam.

A total of 36 eyes from 33 participants progressed by stereophotographs and/or showed likely progression by SAP GPA, while 210 patient eyes from 148 participants were nonprogressing eyes that did not progress by stereophoto assessment or by the SAP GPA likely progression criterion, and 21 eyes from 20 participants were longitudinal normal eyes with no history of IOP > 22 mm Hg and with all HRT exams acquired within a short duration (median of 0.5 years). A detailed demographic summary of the study eyes is presented in Table 1.

Table 1.

Demographics of the Progressing Eyes, Longitudinal Normal Eyes, and Nonprogressing Patient Eyes From the UCSD Diagnostic Innovations in Glaucoma Study

	Progressing Eyes	Longitudinal Normal Eyes	Nonprogressing Patient Eyes
No. of eyes (No. of subjects)	36 (33)	21 (20)	210 (148)
Age, y
Mean (95% CI)	64.7 (61.6, 67.7)	57.4 (49.7, 65.1)	61.4 (59.4, 63.4)
Median (range)	65.0 (48.3, 83.3)	57.0 (24.6, 86.5)	64.4 (18.1, 85.5)
Interquartile range	(57.0, 71.8)	(47.9, 67.9)	(53.2, 69.7)
No. of HRT exams
Median (range)	5 (4–8)	4 (4–8)	4 (4–8)
Interquartile range	(4.5–6)	(4–4)	(4–5)
HRT follow-up, y
Median (range)	4.1 (2.4, 7.0)	0.5 (0.2, 8.0)	3.6 (1.7–7.4)
Interquartile range	(3.7, 5.8)	(0.4, 0.7)	(2.9–4.5)
SAP mean deviation at baseline, dB
Mean (95% CI)	−3.65 (−5.45, −1.84)	−0.34 (−0.80, 0.13)	−1.72 (−2.16, −1.28)
Median (range)	−2.15 (−21.74, 1.72)	−0.25 (−2.81, 1.31)	−0.95 (−30.13, 2.20)
Interquartile range	(−4.16, −0.41)	(−0.88, 0.23)	(−2.35, −0.07)
SAP PSD at baseline, dB
Mean (95% CI)	4.19 (2.87, 5.51)	1.63 (1.45, 1.81)	2.47 (2.18, 2.76)
Median (range)	2.30 (0.99, 13.18)	1.53 (1.09, 2.84)	1.73 (0.85, 13.32)
Interquartile range	(1.73, 4.45)	(1.42, 1.77)	(1.45, 2.50)
% abnormal disk from photo evaluation at baseline	77.1%, 27 of 35 eyes*	4.8%, 1 of 21 eyes	45.2%, 95 of 210 eyes
% abnormal visual field at baseline	52.8%, 19 of 36 eyes	4.8%, 1 of 21 eyes	32.9%, 69 of 210 eyes
% of abnormal disk from photo evaluation and abnormal visual field at baseline	42.9%, 15 of 35 eyes*	0.0%, 0 of 21 eyes	19.5%, 41 of 210 eyes

^* One of the eyes that progressed by SAP GPA of the 36 progressors did not have a baseline stereophotograph within 6 months from the HRT-II baseline date.

The UCSD Institutional Review Board approved the study methodologies, and all methods adhered to the Declaration of Helsinki guidelines for research in human subjects and the Health Insurance Portability and Accountability Act (HIPAA).

New Strategies

Section 1: PixR Nonparametric Cluster Test (PixR-NP CT).

Part A: Regression Model.

Progressive structural changes due to loss of retinal nerve fibers are observable as progressive reduction of retinal height in HRT topographies. Therefore, to characterize the rate of retinal changes, a simple linear regression h_f(ℓ) = β₀(ℓ) + β₁(ℓ) × T_f + ε_f(ℓ) was fit at each retinal location with pixel coordinate ℓ in the HRT topographic series. Point estimates b₀ and b₁, respectively, of the regression coefficients β₀ and β₁ were estimated using the method of least squares³⁰; h_f is the retinal height (in μm) at follow-up time T_f (in months) and ε_f is the regression error (distributional characteristics given in Part B).

Part B: Assessing the Significance of Rate of Change Using Permutation Tests.

The rate of retinal height change at each location ℓ is given by its respective regression coefficient β₁(ℓ) corresponding to time factor T_f. Therefore, the significance of the observed rate of retinal height decrease at each location was assessed using a null hypothesis of H₀(ℓ): β₁(ℓ) = 0 against a directional or one-sided alternative hypothesis H_a(ℓ): β₁(ℓ) > 0. The hypotheses were tested using a studentized test statistic t(ℓ) = β₁(ℓ)/se(β₁[ℓ]) at each HRT pixel, where se(β₁) is the standard error of the regression coefficient β₁ estimated assuming a normal distribution of β₁³⁰. A studentized or pivotal test statistic guarantees good performance under resampling.^13,31,32

To evaluate the null hypothesis at each pixel, the sampling distribution of the test statistic t(ℓ) under the null hypothesis, known as a null-distribution (i.e., distribution of t[ℓ] when β₁[ℓ] = 0), is required. The null-distribution of the test statistic t(ℓ) was built at each retinal location ℓ from several unique pseudo-topographic series of the eye. The pseudo-topographic series were generated under the null hypothesis using the permutation resampling technique as follows.^{14,16,33–35}

To simulate topographic sequences under the null hypothesis, first, regression residuals under the null condition (i.e., when b₁[ℓ] = 0) were estimated at each retinal location in the observed topographic series as e_f,H0(ℓ) = h_f(ℓ) − b₀(ℓ), with point estimates of regression coefficients b₀(ℓ) and b₁(ℓ) estimated using the method of least squares. At each pixel, error terms under the null condition {e_f,H0(ℓ): f = 1, …, F} were assumed to be independent and identically distributed (i.e., errors were not autocorrelated and were with constant variance) over time T_f with no other distributional assumptions. Under the assumption of independent and identical distribution of model errors, the error terms e_f,HO(ℓ) over time T_f satisfy the exchangeability criterion for resampling^36–39 and, therefore, are exchangeable under the null hypothesis. Error terms e_f,H0(ℓ) were randomly permuted and 999 unique pseudo-topographic series were constructed under the null hypothesis as 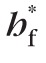(ℓ) = b₀(ℓ) + 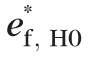(ℓ)^32,35; where, { 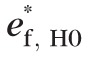(ℓ): f = 1, …, F} is a unique random permutation of the residuals { 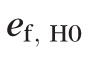(ℓ): f = 1, …, F} at location ℓ and F is the number of follow-up exams. Resampling under the null hypothesis or a restricted model also is known as wild bootstrap.⁴⁰

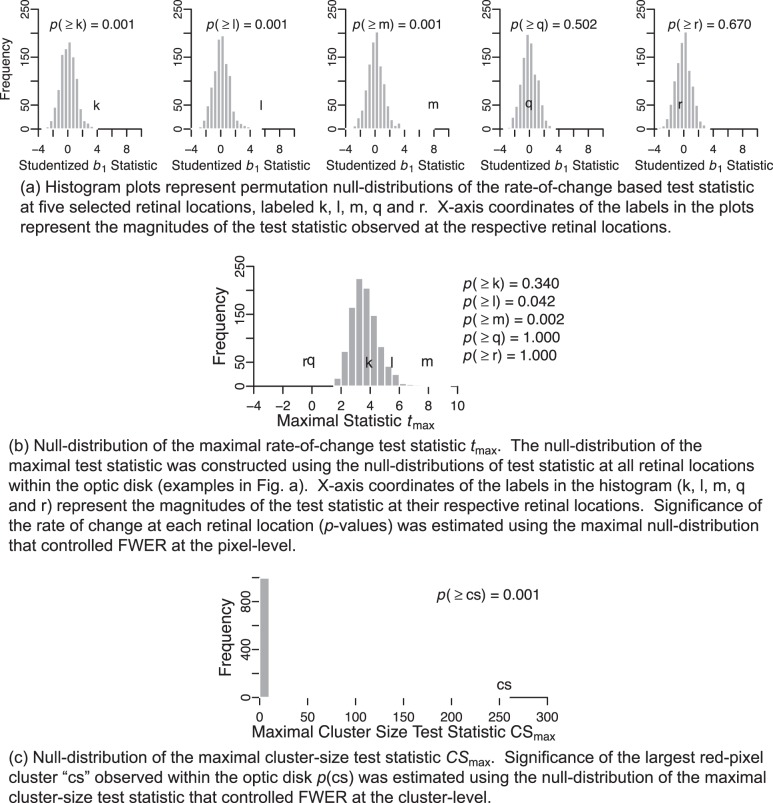
For each retinal location, a null-distribution of the rate-of-change based test statistic t(ℓ) was built using a collection of 1000 test statistics. Each null-distribution comprised of one test statistic estimated from the observed retinal topographic series and 999 test statistics estimated from 999 unique pseudo-topographic series of the respective eye when there is no significant rate of change. Figures 1 and 2, respectively, show examples of a normal eye and a progressing eye. Figure 3 shows a procedural example of building a null-distribution of the test statistic t(ℓ) in one retinal location (labeled k) in the progressing eye shown in Figure 2. Figure 4a shows permutation null-distributions of the test statistic at five selected retinal locations in the example progressing eye.

Figure 1.

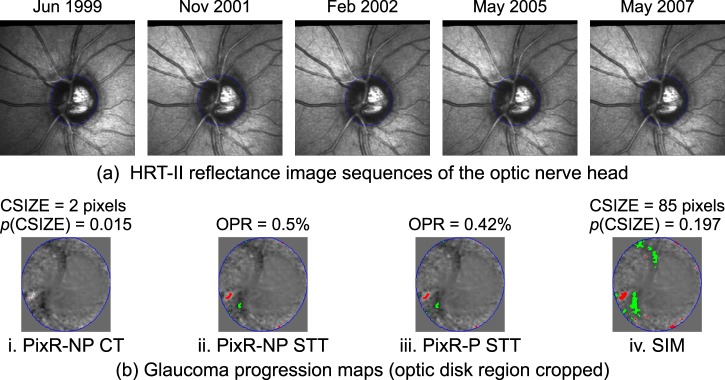
Glaucoma progression maps of the PixR strategies (bi–iii) and SIM (biv) generated from the HRT topographic series of an example normal eye (for visual clarity, reflectance images are shown in [a]). The glaucoma progression maps represent locations with significant rate of retinal height decrease (red-pixels) and increase (green-pixels) with normalized slope statistics in the background. CSIZE, size of the largest red-pixel cluster within the optic disk (in number of pixels); OPR, observed progression rate within the optic disk margin (in %); NP, nonparametric; P, parametric.

Figure 2.

Glaucomatous progression maps of the PixR strategies (bi–iii) and SIM (biv) of an example progressing eye (a). The glaucoma progression maps represent locations with significant rate of retinal height decrease (red-pixels) and increase (green-pixels) with normalized slope statistics in the background.

Figure 3.

Procedural example for building a null distribution of the rate-of-change based b₁ test statistic at a retinal location labeled k (e, f) in the progressing eye in Figure 2. The null distribution comprised of one test statistic estimated from the observed topographic series (a) and 999 test statistics estimated from 999 pseudo-topographic series (c, d) at location k. The pseudo-topographic series were constructed by resampling residual errors under the null-condition (b–d) at location k.

Figure 4.

Null distribution of the maximal rate-of-change test statistic t_max (b) and maximal cluster-size test statistic CS_max (c) constructed to control FWER at pixel-level and cluster-level, respectively, for the example progressing eye in Figure 2. Permutation null-distributions of the studentized b₁ statistic at selected retinal locations (HRT pixels) within the optic disk are shown in (a).

Part C: Family-Wise Type I Error Control.

In this study, significance of the rate of change at each retinal location within the optic disk margin was used to detect glaucomatous progression (Figs. 1b, 2b). More formally, glaucomatous progression was inferred from a collection or a family of all hypothesis tests within the optic disk F = {H₀(ℓ): ℓ = 1, …, N}, where H₀(ℓ) is the null hypothesis at location ℓ and N is the total number of retinal locations within the disk. Because of the multiplicity of retinal locations simultaneously tested to assess glaucomatous progression, it is essential to control the overall type I error or false-positive detections (a multiple comparison problem^8–13,41). In PixR-NP CT, family-wise type I error was controlled at pixel-level and cluster-level by controlling a family-wise error rate using Bonferroni correction.^10,41

Part C1: Pixel-Level Type I Error Control.

Let, 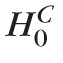= 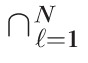H₀(ℓ) represent the complete null hypothesis for the family F (i.e., a hypothesis that all retinal locations are true negatives with no significant rate of change). To control type I error at the pixel-level for the family of tests F, an FWER or the probability of committing at least one type I error¹² was controlled at a level of significance α_p. Therefore, probability P(at least one false-positive retinal location| 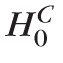) ≤ α_p.

In terms of the test statistic: P( 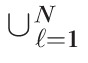[t(ℓ) ≥ t_cutoff| 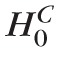] ≤ α_p), or

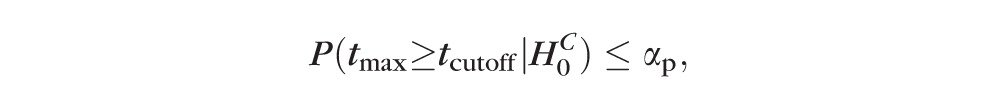where

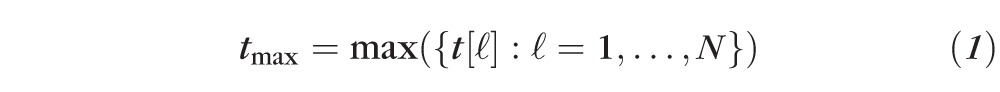Therefore, the critical value t_cutoff of the maximal rate-of-change test statistic t_max controls FWER at the chosen level of significance α_p. By using the critical value t_cutoff to determine the significance of rate of change at each retinal location, the overall false-positive detections (FWER) can be controlled at level α_p. The null-distribution of the maximal test statistic t_max is required to estimate the critical value t_cutoff. The critical value t_cutoff was estimated as the (1 − α_p)th percentile value in the null-distribution of the maximal test statistic.

The null-distribution of the maximal test statistic t_max was built for each study eye using a collection of the maximum value of the test statistic (estimated as in Equation 1) in each of the 1000 unique pseudo-topographic series simulated in Part B. We preserved the observed dependence structure of retinal measurements and, thereby, preserved the statistical dependence structure among retinal measurements in each pseudo-topographic series by using the same temporal resampling order for all retinal locations in a given pseudo-topographic series. Figure 4b shows the null-distribution of the maximal rate-of-change test statistic t_max and P values for the rate of change at selected retinal locations in the example progressing eye.

Using the null-distribution of the maximal test statistic, P values P(t[ℓ]) adjusted for family-wise type I error at level α_p were estimated for each retinal location ℓ. Therefore, locations with P(t[ℓ]) < α_p were considered to have significant rate of retinal height decrease. In this work, at pixel-level, we controlled family-wise type I error at a standard level of significance for one-tailed tests α_p = 2.5%. Glaucoma progression maps indicating locations with significant rate of retinal height decrease (called red-pixels with negative rate of change) and increase (called green-pixels with positive rate of change) were generated. Red-pixels corresponded to glaucomatous progression or noise and green-pixels corresponded to treatment effects or noise. Figures 1bi and 2bi show examples of glaucoma progression maps generated by the PixR-NP CT method.

Part C2: Cluster-Level Type I Error Control.

To assess glaucomatous progression in an eye, all spatial extents or clusters of red-pixels (with 8-connectivity) were identified after overall type I error control at pixel-level. Let {CS_k: k = 1, …, M} equal the cluster sizes (size in number of pixels) of all the red-pixel clusters observed within the optic disk in a pseudo-topographic series. The probability of incorrectly inferring at least one red-pixel cluster as significant (i.e., FWER at cluster-level) was controlled at a level α_c.

Probability P(at least one false-positive red-pixel cluster| 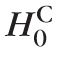) ≤ α_c, or

Thus, similar to the pixel-level type I error control, the significance of an observed red-pixel cluster P(CS_k) was determined using a null-distribution of the maximal cluster-size test statistic. The null-distribution of the maximal cluster-size test statistic for each study eye comprised of the size of the largest cluster of red-pixels within the optic disk in each of the pseudo-topographic series, given by { 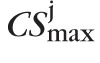: j = 1, …, 1000} = 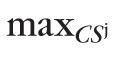({ 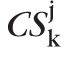: k = 1, …, M_j; and j = 1, …, 1000}), where is the size of the largest red-pixel cluster in the jth pseudo-topographic series and M_j is the number of red-pixel clusters observed in the jth pseudo-topographic series. Figure 4c shows the null-distribution of the maximal cluster-size test statistic CS_max for the example progressing eye.

Part D: Criterion of Glaucoma Progression.

Because we controlled the probability of making at least one false detection at cluster-level, glaucomatous progression was defined as a presence of at least one red-pixel cluster within the optic disk in the observed topographic series with probability P(cluster size CS_k) < α_c. A stricter cluster-level significance α_c = 1% was chosen similar to SIM.

Section 2: PixR Nonparametric Single Threshold Test (PixR-NP STT).

The linear regression model, test statistic t(ℓ), and permutation testing steps in PixR-NP STT are same as those of PixR-NP CT described in Section 1, Parts A and B.

PixR-NP CT uses Bonferroni correction, which provides conservative control of family-wise type I errors and, therefore, may increase type II errors and reduce the power to detect true changes (e.g., see Fig. 2bi versus Fig. 2bii). Therefore, in PixR-NP STT, we allowed up to k type I errors (instead of at most one type I error allowed by Bonferroni correction) by controlling a generalized FWER or k-FWER²⁸ at the pixel-level.

Probability P(at most k false-positive retinal locations | ) ≤ α_p.

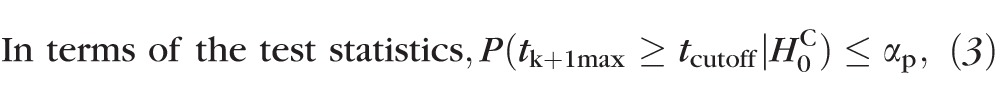where, t_k+1max is the (k + 1)th largest test statistic among all retinal locations in a topographic series. Therefore, significance of retinal height changes P(t(ℓ)) were estimated using a null-distribution of the (k + 1)th largest test statistic given by { 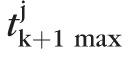: j = 1, …, 1000}, where 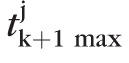is the (k + 1)th largest test statistic in the jth pseudo-topographic series of the eye. The critical value t_cutoff estimated from the null-distribution of the (k + 1)th largest test statistic controls the probability of making at most k false-positive errors at a level of significance α_p. Figure 5 shows the null-distribution of the (k + 1)th largest test statistic t_k+1max and P values for the rate of change at selected retinal locations in the example progressing eye.

Figure 5.

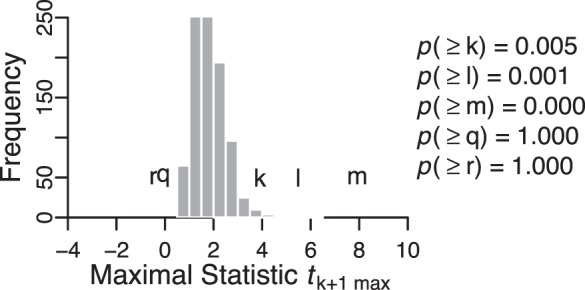
Null-distribution of the maximal rate-of-change test statistic t_{k+1 max} constructed to control the Lehmann-Romano generalized k-FWER at pixel-level for the example progressing eye in Figure 2. The maximal null-distribution was estimated using null-distributions of the test statistic at all retinal locations within the optic disk. Examples of null-distribution at selected retinal locations, labeled k, l, m, q and r, are shown in Figure 4a. X-axis coordinates of the labels (k, l, m, q, r) represent the magnitudes of the observed test statistic at their respective retinal locations relative to the maximal null-distribution of the test statistic. Significance of the rate of change at each retinal location (P values) was estimated using the maximal null-distribution that controlled for type I error at the pixel-level using the generalized family-wise error rate. P values estimated using the k-FWER method are lower than those of the FWER approach (P values in Fig. 5 versus Fig. 4b) indicating that the k-FWER approach is less conservative than the FWER Bonferroni approach.

In PixR-NP STT, we set k to be 2.5% of total number of retinal locations within the optic disk (i.e., k = 2.5% of N) and a level of significance of α_p = 1%. Thus, retinal locations with P(t[ℓ]) < α_p were considered to have significant rates of retinal height changes. Red- and green-pixels were identified as in PixR-NP CT. A measure of observed progression rate was estimated as a ratio of number of red-pixels to the total number of pixels within the optic disk margin. Because we allowed up to k false-positive errors (k = 2.5% of N), the upper bound for the anticipated false-positive rate was k/N × 100 = 2.5%. Therefore, glaucomatous progression was detected by PixR-NP STT when the observed progression rate is greater than the anticipated false-positive rate of 2.5%.

Section 3: PixR Parametric Single Threshold Test (PixR-P STT).

The PixR-P STT test is a parametric version of the PixR-NP STT method. As in PixR-NP CT, the linear least-squares regression model h_f(ℓ) and the test statistic t(ℓ) described in Section 1, PartA were used to assess the rate of change at each retinal location. The regression error terms were assumed to be independent (i.e., no autocorrelation) and normally distributed ε_f ∼ N(0, σ²) with a constant variance σ² over time (i.e., homoscedastic).

Significance of the rate of change at each retinal location P(t[ℓ]) was estimated using a directional t-test (MATLAB function “glmfit” in Statistics Toolbox, ver. 2010b; Mathworks, Inc., Natick, MA). Pixel-level type I error was controlled using the less conservative k-FWER procedure as in PixR-NP STT, but in a parametric framework.²⁸ For k-FWER control, we allowed up to k type I errors at a level of significance α_p with k as 2.5% of number of retinal locations (pixels) within the optic disk margin. The level of significance α_p was determined empirically, such that the diagnostic performance of the PixR-P STT is similar to that of the PixR-NP STT method. To control k-FWER at level α_p, a common P value threshold was estimated as (k + 1) × α_p/N using the single-step k-FWER method by Lehmann and Romano.²⁸ Retinal locations with P value P(t[ℓ]) less than the k-FWER-based P value threshold were considered to have significant rates of retinal height changes. Red- and green-pixels were identified as in PixR-NP CT based on the significance of the rate of retinal height decrease and increase, respectively. A measure of observed progression rate was estimated as a ratio of number of red-pixels to the total number of pixels within the optic disk margin. Because, k-FWER control provides an upper bound for the number of false-positives as k (2.5% of number of locations within disk), glaucomatous progression was detected by PixR-P STT when the observed progression rate was greater than 2.5%.

Statistic Image Mapping (SIM)

The SIM method has been described in detail previously.⁵ In brief, a standardized slope test statistic was estimated as S(ℓ) = |b₁(ℓ)/ŝ(b₁[ℓ])|, where |.| operator gives the absolute value and ŝ(b₁[ℓ]) is a smoothed standard error estimate of the regression coefficient b₁(ℓ). The spatially smoothed standard error estimate ŝ(b₁[ℓ]) was computed by spatially filtering standard error estimates of the regression coefficient b₁ using a Gaussian kernel of size 17 × 17 pixels and standard deviation of 2.354 pixels. Pseudo-topographic series were generated from the raw topographic retinal measurements using the permutation resampling procedure (not under the null hypothesis). Pixel-level changes were estimated using a probability suprathreshold or a global threshold of α_p = 5% and family-wise type I error was controlled only at the cluster-level at a level of significance α_c = 1%. Glaucomatous progression was detected when there was at least one red-pixel cluster within the disk with P < α_c.

All computational analyses were conducted using a MATLAB distributed computing server (Mathworks, Inc.) in the Triton Compute Cluster at the San Diego Supercomputer Center (SDSC), San Diego, California.

Results

Table 2 presents the diagnostic accuracy of the PixR and SIM techniques. The PixR strategies (PixR-NP CT, PixR-NP STT, and PixR-P STT) provided high sensitivity (86%, 75%, and 81%, respectively) and high specificity in the longitudinal normal eyes (81%, 90%, and 90%, respectively). With an empirically determined level of significance α_p = 25%, the parametric PixR-P STT was able to provide a similar diagnostic accuracy as the nonparametric PixR-NP STT, but with reduced computational demands. The SIM method provided similar specificity (90%) and lower sensitivity (39%) than the PixR strategies. The SIM had the highest specificity in the nonprogressing eyes (79%) followed by PixR-NP STT (56%), PixR-P STT (50%), and PixR-NP CT (49%). When the specificity of PixR-NP CT in the longitudinal normal eyes was set to 90% (by changing α_c from 1% to 0.8%) similar to all other methods, sensitivity was 86%, and specificity in the nonprogressing patient eyes was 55% for PixR-NP CT.

Table 2.

Diagnostic Accuracy of the SIM Method and the New PixR Strategies for Detecting Glaucomatous Progression

Techniques	Test Type	Sensitivity (95% CI) in Progressing Eyes, n = 36 Eyes	Specificity (95% CI) in Longitudinal Normal Eyes, n = 21 Eyes	Specificity (95% CI) in Nonprogressing Eyes, n = 210 Eyes
SIM Patterson et al.5	Nonparametric test by resampling raw measurements	39% (22–56)	90% (76–100)	79% (73–84)
PixR-NP Cluster Test, PixR-NP CT	Nonparametric test by resampling regression residuals under the null hypothesis	86% (73–99)	81% (62–100)	49% (42–56)
	At 90% specificity in the longitudinal normal eyes	86% (73–99)	90% (76–100)	55% (48–62)
PixR-NP Single Threshold, PixR-NP STT	Nonparametric test by resampling regression residuals under the null hypothesis	75% (59–91)	90% (76–100)	56% (49–63)
PixR-P Single Threshold, PixR-P STT	Parametric test	81% (66–95)	90% (76–100)	50% (43–57)

Figures 1 and 2, respectively, show the glaucomatous progression maps generated by each of the methods for an example normal eye and a progressing eye. In contrast to the other methods, PixR-NP CT that uses Bonferroni correction for type I error control detected fewer retinal changes in the normal eye (Fig. 1bi versus Figs. 1bii, 1biii) and the progressing eye (Figs. 2bi versus Figs. 2bii, 2biii). However, the overall diagnostic accuracy of PixR-NP CT was comparable to that of PixR-NP STT and PixR-P STT.

For permutation testing in the nonparametric PixR-NP and SIM methods, 999 unique pseudo-topographic series were simulated by Monte Carlo sampling of all possible unique permutations of the observed topographies series of each eye. Figure 3 shows a procedural example of building a null-distribution of the test statistic at each retinal location. Figure 4 illustrates the construction of null distributions of the maximal rate-of-change and maximal cluster-size test statistics required to control FWER in the PixR-NP CT method. Figure 5 shows the null-distribution of the k-maximal rate-of-change test statistic required for controlling k-FWER in the PixR-NP STT method. By comparing the null distributions of the maximal rate-of-change test statistic and the P values at selected retinal locations in Figure 4b versus Figure 5, it can be observed that the k-FWER procedure is less conservative than the FWER or Bonferroni procedure. For example, at the retinal location labeled k, the FWER and k-FWER procedures provided a P value of P(k) = 0.340 and P(k) = 0.005, respectively.

In this study, we defined progressive visual field loss based on “likely progression” by SAP GPA indicative of significant visual function degradation seen in three or more test points on three consecutive follow-up tests. We evaluated whether HRT-based techniques are detecting subtle and/or early stages of progression in a subset of the nonprogressing patient eyes that have not yet met the criteria of “likely progression” on SAP GPA. We defined three categories of visual field changes in the nonprogressing patients and found that PixR methods identified more of these eyes as progressing than SIM (Table 3). Specifically, of 54 nonprogressing eyes with “possible progression” by SAP GPA (defined as significant change in three or more test points on two consecutive follow-up tests), progression was detected by SIM in 15 eyes, by PixR-NP CT in 31 eyes, by PixR-NP STT in 27 eyes, and by PixR-P STT in 29 eyes. A second subset of seven eyes developed “possible progression” by SAP GPA within one year after the last HRT follow-up exam. Of these seven eyes, progression was detected by SIM in two eyes and by all PixR strategies in five eyes. A third subset of 17 eyes developed at least two progression points (possible and/or likely), including at least one likely progressing point in SAP GPA. Of these 17 eyes, progression was detected by SIM in 1 eye, by PixR-NP CT in 11 eyes, by PixR-NP STT in 5 eyes, and by PixR-P STT in 6 eyes.

Table 3.

Detection of Progression by the SIM Method and PixR Strategies in a Subset of 78 Nonprogressing Eyes That Developed “Possible Progression” by SAP GPA

Techniques	Nonprogressing Eyes With “Possible Progression” by SAP GPA Within the HRT Follow-up Duration, n = 54 Eyes (%)	Nonprogressing Eyes With “Possible Progression” by SAP GPA Within 1 Year After the Last HRT Follow-up, n = 7 Eyes (%)	Nonprogressing Eyes With at Least 2 Progression Points, Possible and/or Likely, Including at Least 1 Likely Progression Point in SAP GPA Within the HRT Follow-up Duration, n = 17 Eyes (%)
SIM	15 (27.8)	2 (28.6)	1 (5.9)
PixR-NP cluster test, PixR-NP CT	31 (57.4)	5 (71.4)	11 (64.7)
PixR-NP single threshold, PixR-NP STT	27 (50.0)	5 (71.4)	5 (29.4)
PixR-P single threshold, PixR-P STT	29 (53.7)	5 (71.4)	6 (35.3)

Discussion

At high specificity (90%) in the longitudinal normal eyes, the nonparametric PixR-NP CT strategy provided higher sensitivity (86%) than SIM (39%), suggesting that this method may improve our ability to detect glaucomatous structural change. Moreover, our results suggested that this technique detected a larger proportion of eyes with more subtle visual field changes than SIM (Table 3).

The PixR-NP CT method was extended directly from SIM by controlling the overall false detection errors among retinal locations as well as among clusters or spatial extents of progression, and by building nonparametric distributions for hypothesis testing using pseudo-topographic series of each study eye simulated without any significant retinal change over time (i.e., under null hypothesis). The parametric PixR-P STT and nonparametric PixR-NP STT provided high sensitivity (≥75%) and specificity (90%) in normals. In contrast to the nonparametric PixR-NP STT method, the parametric PixR-P STT method requires significantly less computational resources with the promise of providing a similar diagnostic accuracy.

The SIM method provided higher specificity for the nonprogressing patient eyes (79%) than the PixR strategies (specificities ranging from 49%–56%), indicating that the PixR strategies detected progression more often than SIM. Given the high specificity reported by PixR in normal eyes, it is likely that a subset of these patient eyes are progressing, but do not yet meet the threshold definition for progression by stereophotography and visual field-guided progression analysis used in this study. These results are also supported by the moderate specificity in this same group of nonprogressing patient eyes (at 86% specificity in the longitudinal normal eyes) provided by the HRT TCA (57%)⁴² and the POD framework (43%–51%)⁷ in previous studies. Moreover, our post hoc analysis (Table 3) of the nonprogressing patient eyes suggested that HRT techniques are detecting subtle and/or early stages of visual function progression. Longer follow-up is needed to determine whether the progression detected by PixR in the nonprogressing patient eyes later develops into GPA “likely progression.”

For statistical tests, the SIM method uses a level of significance (LOS) α_p = 5% (two-tailed) at each pixel location and addresses the multiple comparison problem at the cluster-level (using Bonferroni correction) at an LOS α_c = 1%.⁵ For PixR-NP CT, we used the same LOS as SIM, namely α_p = 2.5% (one-tailed) at pixel-level and α_c = 1% at cluster-level. In contrast to SIM and PixR-NP CT methods, we used a less conservative Lehman-Romano's k-FWER procedure for addressing multiple comparison problem at pixel-level in PixR-NP STT and PixR-P STT methods. Similar to the standard LOS for one-tailed tests, we chose the number of false-positive errors k allowed by the k-FWER procedure to be 2.5% (of retinal locations within the disk margin). For the PixR-NP STT method, because we allowed up to k errors, we chose a stricter level of significance of α_p = 1% (one-tailed) to address the multiple comparison problem. In the parametric PixR-P STT method, probabilities of progression were estimated parametrically using t-tests. Therefore, we empirically determined that at a liberal level of significance α_p = 25% (one-tailed), the PixR-P STT parametric method is able to achieve a similar diagnostic accuracy as the PixR-NP STT nonparametric method. Differences in the LOS between parametric and nonparametric PixR STT methods highlight likely significant differences between their respective k-maximal test statistic distributions. Further study of these techniques and progression criteria using independent population groups will be useful to identify limitations and avenues for improvement of these techniques.

In PixR-NP CT, type I error is controlled using Bonferroni correction, which places higher confidence on retinal locations marked as progressing in glaucoma progression maps. However, at the pixel-level, Bonferroni correction is conservative because thousands of locations are tested simultaneously and increases type II or false-negative errors. Therefore, a generalized family-wise error rate or k-FWER method was used in PixR-NP STT and PixR-P STT methods to control type I error while maximizing the detection power (or reducing type II error; see Fig. 2bi versus Fig. 2bii). Because the number of clusters is fewer than the number of locations, SIM circumvents the issue of increased type II error at pixel-level by controlling type I error only at the cluster-level.^42–44 Entirely avoiding type I control at pixel-level, however, may affect the diagnostic accuracy of the cluster-based progression criterion because of the increased number and increased chances of false progressing locations present in the cluster-level analysis. Thus, the sensitivity of SIM is likely to be influenced by the spatial extent (or cluster-size) of glaucomatous progression.⁴⁵ For example, glaucomatous progression with smaller spatial extents may be missed by the cluster-level test alone because of the increased type I error propagated from the pixel-level to the cluster-level test. Therefore, before cluster-level analysis in SIM, the suprathreshold or the common global probability threshold at pixel-level should be adjusted depending on the anticipated spatial extent of changes (i.e., large diffuse changes versus regional changes with smaller spatial extent).^45,46 For optimal control of false change locations, empirically derived thresholds of rate of change may be used during pixel-level analysis ⁴⁷ with the difficulty that the absolute rate of change may vary by region.

Among the nonparametric procedures, permutation tests are exact; that is, the probability of incorrectly rejecting a test at a significance level α is exactly α.⁴⁸ In practice, building the full permutation distribution comprising of all unique permutations of the observed measurements is computationally demanding. For example, as pointed by Patterson et al.,⁵ an eye with four HRT exams will have 369,600 unique permutations at each retinal location. Therefore, approximate permutation distributions were built by Monte Carlo sampling of the full permutation distribution. The Monte Carlo permutation test, however, also provides an exact or at least an asymptotically exact control of type I error at the chosen significance level α.^31,49,50 In contrast, bootstrap control of type I error is only asymptotically exact. Therefore, Monte Carlo permutation tests are more suitable for detecting glaucomatous progression.

It is likely that retinal measurements in an observed topographic series, for example in a progressing eye, may exhibit significant rates of retinal changes. Pseudo-topographic series simulated from the observed retinal measurements, however, should reflect the null hypothesis of no change. Simulating pseudo-topographic series by resampling residuals under the null hypothesis ensures that the test statistic distribution built from the pseudo-topographic series follows null hypothesis even when the underlying population that generated the observed topographic series does not satisfy the null hypothesis (e.g., in a progressing eye). Thus, as suggested by the Hall-Willson guidelines for resampling-based testing^51,52 and Westfall-Young guidelines for multiple testing,¹³ pseudo-topographic series not generated under the null hypothesis may result in loss of power; however, loss of power is minimized when a studentized test statistic is used for hypothesis testing.³² Further, because overall type I error control requires a joint distribution (i.e., maximal null-distribution) of the test statistics, centering the test statistics under the null hypothesis is likely an optimal choice to address multiple comparison problem in retinal imaging. In PixR strategies, pseudo-topographic series for each study eye were generated by resampling residuals under the null hypothesis. Other promising approaches for building null-distributions are generating pseudo-topographic series using physiology-based simulations⁵³ and by generating pseudo follow-up exams with no changes using the baseline subspace of the proper orthogonal decomposition framework.⁷

Resampling residuals in the nonparametric PixR strategies was based on the assumption of exchangeability of residuals under the null hypothesis. Exchangeability was justified by the assumption of independence (i.e., no autocorrelation) and identical distribution (i.e., constant error variance over time) of the regression errors.³⁶ When regression errors are autocorrelated or when error variance is not constant over time (heteroscedasticity), resampling residuals over time will not preserve the observed temporal (time) dependence structure or autocorrelation in pseudo-topographic series. This may result in inaccurate null distributions and affect the exactness of the tests. Therefore, though permutation tests are exact and do not assume normality of distribution, likely heteroscedasticity (e.g., due to changes in disease severity) or autocorrelated errors in topographic series may violate the exchangeability criterion required for resampling and may affect its performance.⁵⁴ One of the sources of autocorrelated errors is methodological due to omission of one or more key predictor variables, such as the IOP at each follow-up, in the regression model.³⁰ Model errors autocorrelated over time in a retinal time series of an eye can be modeled as a moving-average process.⁵⁵ In addition to autocorrelated errors, there is an obvious autocorrelation of retinal height measurements in the time series of an eye due to repeated measurements in each retinal location in each eye over time. Retinal measurements autocorrelated over time within an eye can be modeled as an autoregressive process.⁵⁵ Possible variation of autocorrelation among retinal locations and among eyes, as well as presence of glaucomatous progression should be factored while building such retinal time series models. Further studies are necessary to characterize fully sources of autocorrelation of retinal measurements in optical retinal images acquired over time. Upon characterizing autocorrelation and heteroscedasticity in the optic nerve head time series, several procedures are available to account for autocorrelation and heteroscedasticity during resampling.^30,56–60

Similar to the temporal (time) autocorrelation of retinal measurements at a given retinal location, it also is essential to preserve the spatial dependence or correlation among retinal measurements in pseudo-topographic series similar to that of the observed topographic series.³⁶ This is due to the fact that spatial information from all retinal locations are combined to control family-wise type I error by building a null distribution of the maximal rate-of-change test statistic and maximal cluster-size test statistic. In the nonparametric PixR-NP methods, the observed spatial correlation among retinal measurements in each eye were preserved in all simulated pseudo-topographic series by using the same temporal resampling order at each retinal location.

The second guideline of Hall-Wilson recommends using a pivotal or studentized statistic for testing a single hypothesis, which does not significantly affect the power of a test, but influence convergence accuracy of the test statistic.^13,51 Therefore, a single hypothesis evaluating a simple linear regression is not affected in the absence of a pivotal statistic.³³ Westfall-Young,¹³ however, recommends a pivotal statistic for multiple comparison problems. In PixR methods, a studentized test statistic based on the regression coefficient (β₁/SE[β₁], where SE is the standard error) was used for hypothesis testing. When a nonstudentized test statistic (β₁) was used in PixR-NP CT, sensitivity decreased to 44% (95% confidence interval [CI] = 27%–62%) with the same specificity in normals of 81% (62%–100%). Although pivotal statistic does not have a significant effect on the diagnostic accuracy of an individual hypothesis test, it is evident from the diagnostic accuracy of PixR-NP CT that a pivotal statistic facilitates improved diagnostic accuracy for multiple comparison problems by providing a uniform type I error rate in all retinal locations.³⁶ A uniform type I error rate is achieved in all retinal locations because the distribution of a pivotal statistic is independent of the data generating distribution at each retinal location and, therefore, is comparable across retinal locations during type I error control (for building the null-distribution of the maximal test statistic). Further, use of a pivotal statistic assures an asymptotically exact Monte Carlo permutation test.^31,49 To standardize the test statistic in the nonparametric PixR methods, the standard errors of the regression coefficients SE(β₁) were estimated in a parametric setup to reduce computational demands. Improved standard error estimates can be obtained by using a second level of bootstrap for each pseudo-topographic series.¹⁴

For multiple testing procedures such as PixR, a subset pivotality criterion based on the joint distribution of the test statistics at individual retinal location is suggested to achieve a strong control of the family-wise error rate.¹³ While detecting localized glaucomatous progression, the subset pivotality guideline for multiple testing is trivially satisfied because the significance of the rate of change observed in a retinal location is not dependent on the significance of other retinal locations (e.g., in contrast, tests for spatial correlation among retinal locations do not satisfy the subset pivotality guideline^13,36,61). Therefore, the nonparametric PixR-NP CT method provides a strong control of the family-wise error rate.

For parametric cluster-level analysis, a parametric null distribution of the cluster-size statistic is required, which is not yet established for optical images of the retina. Therefore, at present, glaucomatous progression is detected in the parametric PixR-P strategy using inferences at the pixel-level only. Based on random field theory, parametric distribution of the cluster size statistic has been developed in neuroimaging.^62,63 It has potential for use with the parametric PixR-P strategy and may facilitate real-time inferences on cluster-size statistics from retinal images.

One of the limitations of the methods presented is the assumption of linearity in the progression of structural changes. In future studies, we will investigate suitable nonlinear multiple regression models with additional predictor variables, such as the IOP at each follow-up for the PixR strategies. Another limitation is that we used HRT exams acquired within a short interval (median follow-up of 0.5 years) in longitudinal normal eyes to assess specificity. The shorter follow-up duration provides confidence that there is no significant glaucomatous progression without requiring SAP GPA and/or manual assessment of stereophotographs. Further studies, however, are necessary to assess the performance of these techniques using longer longitudinal series acquired over a longer follow-up duration from healthy normal eyes to assess the effects of long-term variability as well as the effects of age-related changes on detecting progression.

In conclusion, by reducing false-positive errors using FWER or Lehmann-Romano's k-FWER strategies, the PixR provided higher diagnostic accuracy for detecting glaucoma progression than SIM. Moreover, in nonprogressing patient eyes, retrospective inspection indicated that PixR techniques are detecting a higher proportion of subtle and/or early stages of visual function progression than SIM. The PixR strategies show promise for improving our ability to detect glaucoma progression.