ION MANIPULATIONS IN STRUCTURES FOR LOSSLESS ION MANIPULATIONS (SLIM): COMPUTATIONAL EVALUATION OF A 90° TURN AND A SWITCH

Abstract

The process of redirecting ions through 90° turns and ‘tee’ switches utilizing Structures for Lossless Ion Manipulations (SLIM) was evaluated at 4 Torr pressure using SIMION simulations and theoretical methods. The nature of pseudo-potential in SLIM-tee structures has also been explored. Simulations show that 100% transmission efficiency in SLIM devices can be achieved with guard electrode voltages lower than ~10 V. The ion plume width in these conditions is ~1.6 mm while at lower guard voltages lead to greater plume widths. Theoretical calculations show marginal loss of ion mobility resolving power (<5%) during ion turn due to the finite plume widths (i.e. race track effect). More robust SLIM designs that reduce the race track effect while maximizing ion transmission are also reported. In addition to static turns, the dynamic switching of ions into orthogonal channels was also evaluated both using SIMION ion trajectory simulations and experimentally. Simulations and theoretical calculations were in close agreement with experimental results and were used to develop more refined SLIM designs.

INTRODUCTION

Ion Mobility Spectrometry/Mass Spectrometry (IMS/MS) using conventional drift tubes has increasingly contributed to MS applications^1-9, and has great potential for enabling more sophisticated analyses in conjunction with more complex ion manipulations. Gas phase ion manipulations are attractive due to their speed, but currently more extended sequences of manipulations have remained largely unexplored due to ion losses and challenges in the fabrication of platforms that are both effective and practical. Ion funnels¹, for example, have enabled efficient ion confinement, focusing and transport.^2-6 Ion mobility multi-pass cyclic designs^{7, 8} have demonstrated for extended mobility separations, but signal intensity and/or resolution losses are both important aspects of performance, and can be problematic. There is continuing interest in improved ion mobility based separations,¹⁰ and somewhat more complex manipulations have been implemented to e.g. study structural changes of polyatomic ions using IMS-IMS.⁹ In addition to travelling wave based mobility separations^11-14, overtone mobility separations^15-17 have been explored both experimentally, theoretically and through modeling/simulation. In addition to IMS separations, other types of ion manipulations (e.g., involving gas phase reactions) are of growing interest,^{18, 19} but their use at present is largely precluded by increasingly significant ion losses with each additional step.

Recently demonstrated “Structures for Lossless Ion Manipulations” (SLIM) can be readily fabricated using printed-circuit board (PCB) technologies and have the potential to enable extended sequences of gas phase ion manipulations.^20-22 SLIM use RF and DC potentials applied to arrays of planar electrodes to confine and move ions in gases at moderate to low pressures (e.g., a few Torr in initial reports). One of the basic SLIM components initially implemented enabled linear ion transport, and utilized computational modeling of potentials and ion trajectories to design a simple SLIM IMS module and optimize its performance.²³ Another SLIM component demonstrated²⁰ was the ‘tee’ switch for controlled direction of ion motion to either a linear path or through a 90° turn.^{20, 22} However the underlying principles for optimized turning and the potential “race track” effect on IMS resolving power were not discussed in detail.

Here we discuss key fundamental considerations for turning and switching ions. The effective potentials in the SLIM switch component are calculated. The effect of the potentials on the ion plume widths, ion transmission efficiency and IMS resolution is presented. The race track effect (and the resulting ion packet ‘broadening’ after a turn) is characterized theoretically and experimentally, for a single turn and then extended to include scenarios with multiple turns. In addition, fundamental considerations for dynamic (or time synchronized) ion switching²⁰ into orthogonal channels are discussed. Finally we discuss the theoretical/computational methods and their relationship with experiments in SLIM development.

METHODS

SIMION 8.1 (Scientific Instruments Services (SIS) Inc., NJ, USA) was used to study ion motion. The SDS collision model^{23, 24} was used to model the ion drift at 4 Torr N₂. The geometries simulated were based upon SLIM PCB components developed for experimental studies, and were generated using Eagle CAD software (CAD Soft Inc., Germany). The geometry and electrode potentials (RF and DC) were imported into a custom program to calculate the overall effective potential. The effective potential²⁵ (V*) was derived according to the equation: $V^{\ast }(r,z)=\frac{q{E}_{RF}^2(r,z)}{4m{\omega }^2}$; where q = z.e is the ion charge; E_RF(r, z) is the amplitude of the RF electric field; m is the ion mass, and ω is the angular frequency of the RF field. The DC gradient was superimposed on V* to generate full effective potentials. The voltages assigned in the simulations were guided by experimental observations, and also provided feedback to suggest alternative experimental arrangements.^{20, 22} The voltages applied to the SLIM-tee electrodes are detailed in Figure 1.

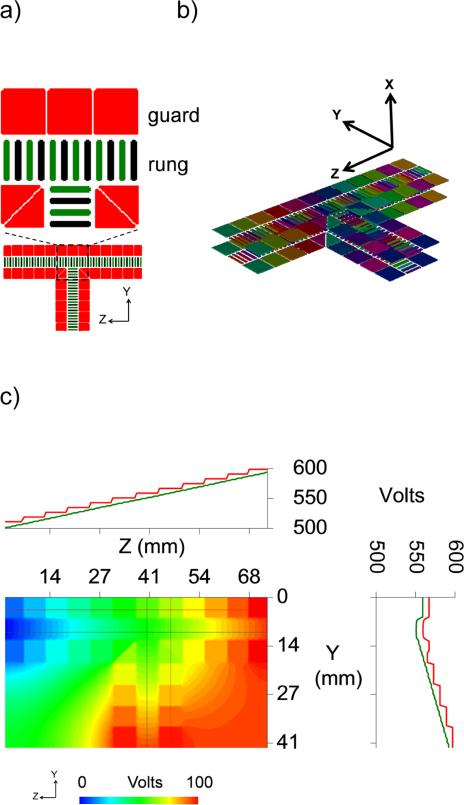
Figure 1.

a) SLIM “tee” switch unit with inset showing zoomed view of the intersection region. Green and black colored electrodes represent the “rung” electrodes with positive and negative phase of RF respectively. b) 3D view of the SLIM tee with co-ordinate system c) Contour plot showing the DC voltages applied in the SLIM tee for turning ions, with the “guard” electrode biased 5 V above their corresponding first rung electrode. The profile along the Z-axis show the voltage at y = 5 mm (red, along the guard) and at Y = 10 mm (green, along the rungs). The profile along the Y-axis show the voltages at Z = 46 mm (red, along the guards) and at Z = 40 mm (green, along the rungs).

Positive ions from an Agilent tuning mix (Agilent Technologies, Santa Clara, USA) were formed by ESI by infusing the sample solution at a rate of 300 nL/min through an emitter into a 500 μm (i.d.) stainless steel capillary MS inlet heated to 120 °C. Ion drift measurements utilized an ion funnel trap to accumulate and release ions to SLIM.^{3, 26, 27} Ions were ejected from the ion funnel trap into the SLIM tee switch at 4 Torr in ~160 μs wide pulses to perform ion turns and dynamic ion switch experiment. Ions exiting the SLIM were collected using a rear ion funnel and then transferred to a TOF MS for detection (model 6224 TOF, Agilent Technologies, Santa Clara, CA, USA). The total length of the SLIM and rear ion funnel provided an ion drift length of 64.5 cm, with constant IMS electric field throughout. The ion flight path length from the source to the tee switch intersection was ~30 cm, and this value was utilized for simulations. The detailed experimental arrangement for lossless switching, turning, controlled trapping and release of the ions is further elaborated elsewhere.^{18, 20, 22} Selected ions were switched into orthogonal channels and trapped for 5 ms, while the ions that were not switched were routed into the IMS detector to obtain the straight-path spectrum. The dynamically selected ions were allowed to drift along the orthogonal path for a short distance and were then trapped by applying a higher voltage at a downstream point in the orthogonal portion of the SLIM tee. After a 5 ms trapping period, the ions were routed, from the orthogonal path, back into the straight channel to obtain the “switched” spectrum. The switching efficiency and selectivity were evaluated under different conditions by comparing the ion intensities of the selected species from the “straight” spectrum and “switched” paths.

RESULTS AND DISCUSSION

Figure 1a shows the electrode arrangement for the SLIM switch component used for performing ion turns (detailed dimensions are in Supplementary Information Figure S1). Alternating RF phases were applied to adjacent “rung” electrodes, resulting in a pseudo-potential field that effectively repels ions approaching the rung electrodes (and the PCB surfaces). The guard electrodes flank the rung electrodes on both sides and are capable of providing lateral confinement to allow for lossless ion confinement within the SLIM component.^20-23 Figure 1b shows a SIMION screenshot of the 3D SLIM tee component used in the simulations. Figure 1c shows the DC voltages applied to the rung and guard electrodes to turn ions in the tee. The contour plot shows a map of applied potentials on one of the two parallel SLIM tee switches. The adjacent graphs show the applied voltage profiles for the rung and guard electrodes. For example, the voltages at the location of the horizontal red line at Y = 3 mm on the contour graph are represented in the top graph by the stepped voltage profile along the Z-direction (i.e., the voltages applied to the series of guard electrodes). Similarly, the voltages at the location of the horizontal green line at Y = 10 mm in the contour plot are represented in the graph by the profile of voltages on the rung electrodes. Additionally, voltage profiles along the Y-axis are shown at Z = 46 mm (vertical red line along the guard electrodes) and at Z = 40 mm (green, along the rung electrodes). The guard electrodes are biased 5 V higher than the first of the adjacent rung electrodes. However, since there are four rung electrodes for each guard in these initial SLIM designs, the result is a stepped voltage profile with a 5V guard bias at the first rung electrode and small stepwise increases for the subsequent three rung electrodes. The effective potentials experienced by the ions were calculated as described above.

At ~4 Torr pressure ion motion is quickly damped due to ion/molecule collisions. Ions are expected to follow the electric field lines in the direction of the decreasing potential gradient. Ion confinement is determined by the potential minima in the lateral direction as well as the Brownian motion or diffusion at these pressures. These factors largely determine the width of the ion plume and are discussed below in regard to ion motion inside the SLIM tee, and particularly at the intersection region where the electrode orientation changes by 90°. Potential issues anticipated include the impact of changes in rung electrode orientation (where the rung electrode at the junction is adjacent to another rung electrode having the same RF phase) and the potential for reduced ion confinement.

Ion Movement Through 90° Turns

Figure 2a shows the calculated effective potential contours in the YZ and XY planes that serves to move ions through a 90° turn, superimposed with a single ion trajectory (starting at the bottom and ending at the lowest point in the effective potential; top left). In the XY plane, the potential trapping well between the boards has a bimodal shape, which results when the spacing of the surfaces becomes large enough to be influenced by the guard potentials and their DC field penetration into the RF trapping region in between the surfaces.^{21, 23} The result of this is the creation of two off-axis potential minima located at approximately X=1.0 mm and −1.0 mm from the axis and equidistant from the two boards (see Supplementary Information Figure S2), rather than a single minimum at the mid-point between the two surfaces. The net effective potential diagram in the YZ plane (Figure 2a) is shown for 1.4 mm from one of the surfaces (i.e. at X = 1.0 mm from the central axis between the two surfaces).

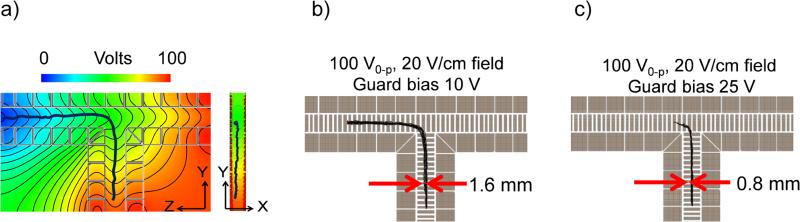
Figure 2.

a) Left panel shows the contours of effective potential (100 V_0-p, 1 MHz rf, 5 V guard bias, m/z 622, +1) in the YZ plane at the potential minima point between the surfaces (X = 1 mm from the center of X = 1.4 mm for SLIM surface) and right panel shows the potential contour between the surfaces (Supplementary Information Figure S2 shows the potential profile between the surfaces). A single ion trajectory (dark-blue line) calculated by SIMION and the board layout are superimposed for clarity. The ion plume width from simulations (not shown) was ~2 mm. b) SIMION simulation of ion turn (m/z 622) in SLIM tee at 10 V guard bias resulting in a plume width ~1.6 mm. c) SIMION simulation of ion turn (m/z 622) in SLIM tee at 25 V guard bias resulting in an ion plume width of ~0.8 mm, but where significant ion losses occur at the turn.

SIMION simulations for a population of 1000 ions showed lossless ion transmission under these conditions. However, ion transmission through the tee can be affected by other factors. The effect of DC field penetration due to guard bias is particularly important as it may affect the behavior of ions at the intersection region of the tee. Higher guard bias leads to better ion confinement and a narrower plume width (1.6 mm at 10 V bias, 0.8 mm at 25 V bias, as shown in Figure 2b and 2c, and 2 mm at 5 V bias). However, at the turn location there are rung electrodes in the presently considered design having an orthogonal orientation, and which thus have the same RF phase as the nearest rung electrode in the orthogonal channel. The same RF phase on adjacent electrodes reduces the pseudo-potential well, and affects ion transmission. At a lower RF trapping potential, the DC field penetration from guard electrode may potentially ‘push’ ions even closer to the rung electrodes, resulting in ion losses at the turn. For a 25 V guard bias, the ion plume experiences losses at the turn location due to the lower confining potential from the rung electrodes with the same RF phase as the rung electrode located just before the turn (Figure 2c). However, at the lower guard bias (10 V) the weaker DC field eliminates ion losses to the electrode surfaces at the turn regions (Figure 2b). Under these conditions the plume width is almost two-fold greater. At a 5 V bias the plume width is 2.5-fold greater than for a 25 V bias, which may also adversely impact the IMS resolving power.

Ions travelling through the 90° turn can experience a ‘race track’ effect, wherein the ions located closer to the center of the turning arc take a shorter time to cover the arc length compared to ions farther away from the center. This effect is further amplified by the greater field gradient for the shorter inner path; ions not only have a shorter path to complete the turn, but move faster than ions taking the longer path. Thus, a wider ion plume is anticipated to result in a greater race track effect, and a greater potential for loss of resolution in ion mobility separations. Similarly, an abrupt (i.e. sharp) turn that minimizes the difference between the shorter and longer (i.e. inner and outer) paths will minimize this effect. Since the plume widths are finite, the race track effect cannot be mitigated altogether (Supplementary Information Figure S3 further illustrates the effect during ion turns), but it can be minimized, ideally to an extent that any loss of mobility resolution will be insignificant. To more quantitatively evaluate the extent of the race track effect on mobility resolving power, both a theoretical evaluation and ion trajectory simulations were used, as discussed below.

The arrival time (T_f) of an ion in the plane immediately following a turn can be expressed in terms of the ion arrival time at the plane preceding the turn (T), the radius of curvature (r_o), the velocity of the ion (v_ion) and the displacement of the ion from the primary turning arc or path (y). Here y can vary from −w/2 to w/2, where w is the width of the ion plume in the plane of ion turning (see Figure S3 in Supplementary Information). The plume arrival time distribution can be considered Gaussian. Also, the plume shape in the plane of the turn can be considered Gaussian truncated at plume width w.

$$T_f=T+\frac{(r_o+y)\pi }{2v_{ion}}=T+\frac{r_o\pi }{2v_{ion}}+\frac{y\pi }{2v_{ion}}$$ (1)

T and y may be regarded as random variables and the terms r_o and v_ion can be regarded as constant by neglecting the effects of diffusion and the consequent intermixing of ion trajectories due to Brownian motion. Since the drift time required to execute the turn is much lower than the initial flight time, it is reasonable to assume that the contribution due to diffusion at the turn is much smaller. Though this analysis is essentially 2D, it has no deviation from a real 3D analysis since the 90° turn itself occurs over a plane. Since, by symmetry, the mean of y is 0, the mean arrival time, ${\overline{T}}_f$, at the plane following the turn is given by:

$${\overline{T}}_f=\overline{T}+\frac{r_o\pi }{2v_{ion}}$$ (2)

where $\overline{T}$ is the mean arrival time at the plane preceding the turn. Since T and y are taken to be uncorrelated, the variance of T_f can be written as

$$Var\left(T_f\right)=Var\left(T\right)+{\left(\frac{\pi }{2v_{ion}}\right)}^{2}Var\left(y\right)$$ (3)

such that the standard deviation (σ_f) and full width at half maximum (FWHM_f) of the arrival time distribution in the plane following the turn are, respectively:

$${\sigma }_f=\sqrt{{\sigma }^2+{\left(\frac{\pi }{2v_{ion}}\right)}^2{\left({\sigma }_y\right)}^2}$$ (4)

$$FWH{M}_f=\sqrt{FWH{M}^2+{\left(\frac{\pi }{2v_{ion}}\right)}^2{\left(FWH{M}_y\right)}^2}$$ (5)

Here σ and FWHM are the standard deviation and full width at half maximum of the arrival time distribution of the ion packet (i.e. peak) before the turn. The FWHM_y is the full width at half maximum of the packet width in the plane of turning. The FWHM of the arrival time distribution after the turn (FWHM_f) is therefore dependent on the width of the ion packet in the plane of turning and also, through an inverse relationship, on the speed of ions. The velocity of the ions is determined by the reduced ion mobility (K₀) and the applied drift field (E₀), where $K=\left(\frac{760}{p}\right)K_0$, and is given by

$$v_{ion}=K.E_0$$ (6)

Substituting Equation 6 into Equation 5 and substituting in turn the resultant equation into the expression for resolving power (average drift time over full width at half maximum), the ion mobility resolving power after the turn can be written as:

$$R=\frac{{\overline{T}}_f}{FWH{M}_f}=\frac{\overline{T}+\frac{r_o\pi }{2K.E_0}}{\sqrt{FWH{M}^2+{\left(\frac{\pi }{2K.E_0}\right)}^2{\left(FWH{M}_y\right)}^2}}$$ (7)

It should be noted that in the plane immediately following the turn, the ion arrival time will be correlated with the displacement of the ions from the primary turning arc. If this correlation were preserved, then the decrease in resolving power at subsequent turns would be somewhat greater than that implied by equation 7, however, diffusion will tend to reduce this effect. Ion trajectory simulations (SIMION) were used to illustrate the net effects due to drift and diffusion at the turn and comparison with theoretical estimates.

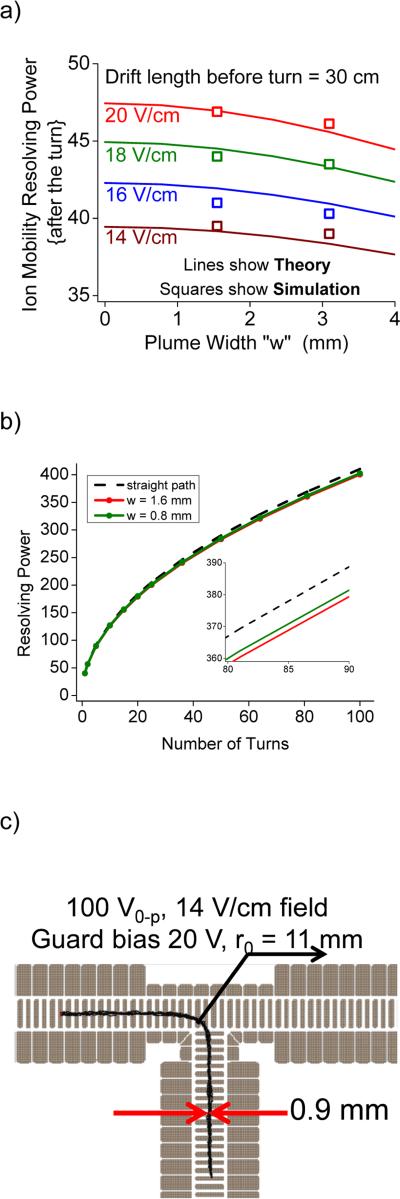
SIMION simulations were used to estimate the radius of curvature (r_o). The mean ion trajectory obtained from SIMION (Supplementary Information Figure S4, left panel) was used to obtain the turning arc of ions and the radius of curvature in SLIM. The drift length of the ions before executing the turn was 30 cm (consistent with experimental studies with ion turning in SLIM). Figure 3 shows the calculated resolving power (R) after turning as a function of the ion plume spatial width (up to 4 mm; $\mathrm{w}=\frac{\ln \left(100\right)}{\ln \left(2\right)}FWH{M}_y$) at drift fields from 14 V/cm to 20 V/cm. Supplementary Information Figure S4 (right panel) shows the radii of curvature for the turns used in Equation 7. The current SLIM devices used for experiments have a rung electrode width of 5 mm. The plume widths normally observed (using ion trajectory simulations) with this rung electrode configuration were <2 mm for relative guard bias voltages of 5 V and higher. For SLIM designs with rung electrodes width of 10 mm the simulations indicated that the plume width would be larger. Simulations were used to study the significance of race track effect in conjunction with the theoretical approach. The simulations accounted for both the race track effect and diffusion on peak broadening. To minimize the computational cost, the simulations of the 90° turns were performed on a single SLIM tee component (i.e. without actually simulating the upstream 30 cm linear SLIM section). Instead, the effect of the upstream optics was incorporated using appropriate initial conditions of the ion plume within SIMION. The initial plume distribution was considered to be Gaussian. The simulation physical plume width was calculated in the form of the standard deviation using the expression $\sigma =\sqrt{2D{t}_{birth}}$, where the “time of birth” of ions (t_birth) is defined in the SIMION particle definitions. t_birth is calculated as the time taken by the ion to traverse 30 cm (corresponding to the experimental distance between ion funnel trap and the switch intersection region). The initial position of the peak centroid in the SLIM was such that the leading edge of the ion plume was a few millimeters from the SLIM tee intersection. Ion statistics were recorded immediately after the turn and the mean arrival time and FWHM were used to calculate the final resolving power. Figure 3a shows the resolving power after the turn for simulations of ion turning in a SLIM-tee with 10 mm and 5 mm rung electrodes which generated ion plume widths of 3.1 mm and 1.6 mm respectively. The guard bias was 10V in both cases. The loss of resolving power due to the turn (i.e. compared to a straight path or a turn with an infinitesimally small plume width) as predicted by theory and simulation at w = 1.6 mm plume width was ~4%. As apparent, the loss of resolving power due to turns in SLIM devices was generally less than the experimental variation over short drift regions.²² The effect of the diffusion and race track effect at the turn, therefore, is minimal. For longer separations before a turn the loss of resolving power, while higher than experimental variation, would still be less than 5%. The race track effect during ion turns for comparatively small beam widths can therefore be considered negligible, and was confirmed so in previously reported experiments.²²

Figure 3.

a) Theoretical and simulated resolving power obtained after a turn for typical ion plume widths observed for the present SLIM. Lines show theory and squares show simulation at a plume width of 1.6 mm and 3.1 mm. b) Resolving power in a cyclical separator with multiple turns. c) SLIM-tee deisng with segmented guard electrodes that provides lossless transmission at higher guard biases. The thinner plumes help reduce loss of resolving power.

Since the turning of ions can avoid significant losses of mobility resolving power in SLIM, the feasibility of greatly extended path configurations involving multiple ion turns, e.g. in a cyclic multi-pass SLIM ion mobility separation module, for achieving very large resolving powers is of interest. To explore this ability, the cumulative effect of multiple turns on the resolving power was calculated by extending Equation 7. If ‘N’ is designated as the number of turns and the drift time for every turn is T₁, then the resolving power after N turns can be calculated as shown in Equation 8.

$$R_N=\frac{\left[T_1+\frac{\pi r_0}{2K{E}_0}\right]\sqrt{N}}{\sqrt{\left[{\left(FWH{M}_1\right)}^2+{\left(\frac{\pi }{2K{E}_0}FWH{M}_y\right)}^2\right]}}$$ (8)

In typical designs of SLIM developed thus far, the plume widths are in the range of a few millimeters. Figure 3b shows the resolving power for a straight path and the effect of multiple turns on the resolving power for plume widths of 1.6 mm and 0.8 mm. While the effect of the turn is minimal and is not observable at lower drift lengths (or low number of turns), at >60 turns significant but small effects on the resolving power are increasingly evident (compare black dotted line vs. red line in Figure 3b, inset shows a zoomed in version of the graph).

In order to recover this marginal (but otherwise acceptable) loss of resolving power at every turn, alternate designs potentially resulting in even more efficient turns were explored. From the theoretical development discussed above (Equation 7 and Figure 3a), the width of the ion plume has a major effect on the loss of resolving power in the turn. The ability to achieve a thinner ion plume width in the current design is limited by the maximum guard voltage avoiding ion losses (Figure 2). While the voltage applied to the guards prevents lateral ions losses (i.e. ejection from the SLIM), much higher voltages can lead to ion losses to the rung electrodes, particularly at the turn due to the lower RF pseudo-potential well depth arising from the proximity of electrodes with the same RF phase. Designs effective with greater guard bias provide a tighter ion packet, thus minimizing the race track effect. Simulations for SLIM designs with segmented guard electrodes (i.e. with improved granularity in the applied voltages as shown in Figure 3c) showed that finer control over the voltages allows application of higher guard biases without causing ion losses. At 14 V/cm field, the ions could execute lossless turns at a much higher guard bias (+20 V) when the guards were segmented to a width corresponding to the span of two rung electrodes. The resulting plume width of 0.9 mm reduced the loss of resolving power after the turn by 25%. Further segmentation of the guards (to one per each rung electrode) would be ideal. However the limitations on the dimensions of electronic components and the electrodes on the PCB presently make such designs impractical.

Another approach for reducing the loss of resolving power in turns can be based upon greater field penetration from the orthogonal region into the straight section, to focus ions closer to the middle of the straight section to facilitate sharper (i.e. more abrupt) turns. This can be achieved by using longer electrodes at the intersection and/or using an “insert” electrode at the intersection (Supplementary Information S5). However, this provides only a marginal gain of resolving power at the expense of ion losses at the turn due to the greater DC field penetration and consequent greater loss of RF well depth at the intersection due to the proximity of same polarity electrodes. Thus, the “ion trajectory” simulations can be used to not only provide guidance for efficient SLIM designs, but also to quickly identify designs needing further refinement (for e.g. by additionally segmenting the guards in the case of elongated or insert electrode designs).

Dynamic Switching

In addition to the continuous (static) 90° turning of ions, the dynamic (fast) switching of ions to an orthogonal channel was also evaluated.²⁰ During dynamic switching, ion packets can ideally be selected for transfer into an orthogonal channel (e.g. for ‘ion fractionation’ after IMS). At the SLIM-tee intersection region, the rung electrode at the orthogonal portion of the turn was biased 10 V above the corresponding rung electrode in the straight portion, to maintain linear ion path. The switching was achieved effectively by creating an orthogonal gradient at the SLIM-tee intersection region. This gradient was created either by lowering the first rung electrode in the orthogonal portion of SLIM-tee by 20 V below the corresponding electrode in the straight path or by raising the voltage on the guard electrode at the intersection by more than 100 V to push ions into the orthogonal path. Experimental tuning indicated that either of these schemes is robust in terms of effectively switching ions into the orthogonal path. In either of these cases, the orthogonal gradient used was ~133 V/cm for effective ion switching.

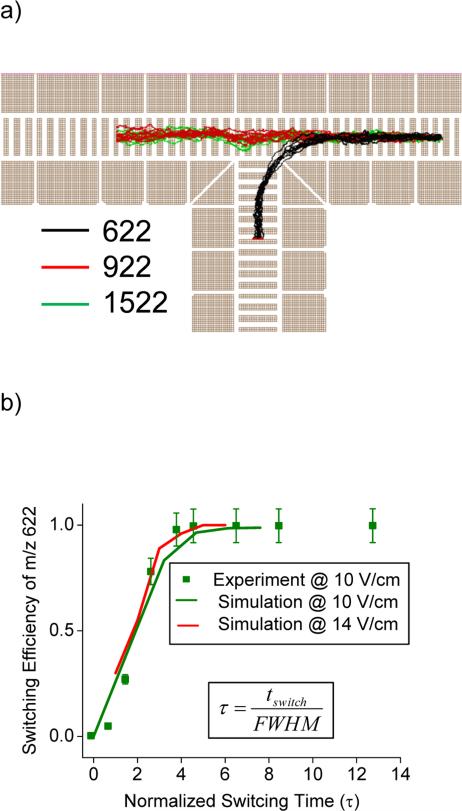
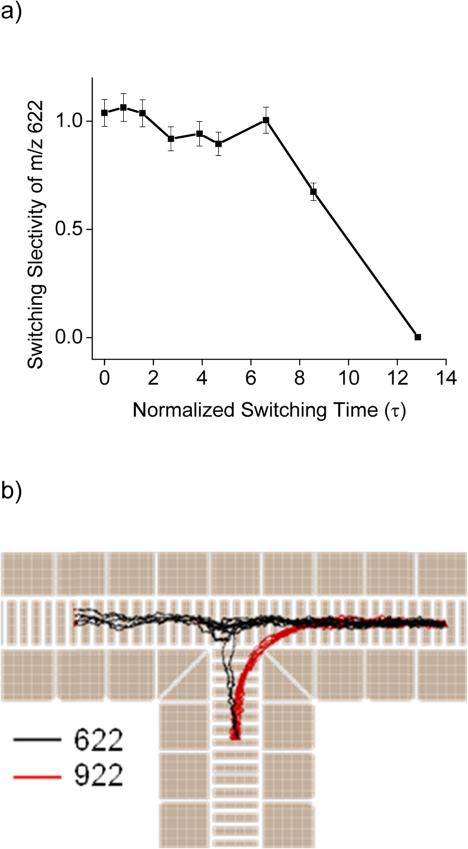
As indicated above, ion path switching can be performed to direct selected mobilities into orthogonal SLIM channels for further ion processing, as shown in Figure 4a, by timing the switching voltages for specific mobilities. The straight trajectories correspond to m/z 922 (K₀ = 0.97 cm²/Vs) and 1222 (K₀ = 0.85 cm²/Vs) ions of the Agilent Tune Mix, whereas m/z 622 (K₀ = 1.17 cm₂/Vs) was switched to the orthogonal channel by applying a switching pulse of 1250 μs when m/z 622 ions were at the switch intersection (9640 μs after the ion release from the ion funnel trap, flight path to reach tee intersection was 30 cm, E₀ = 14 V/cm, p = 4 Torr). The plume width in the dynamic switching simulation was modeled by defining the peak physical width as an initial condition in the SIMION particle definitions. This was calculated using the expression $\sigma =\sqrt{2Dt}$, where “ t ” is the time of flight of the ions prior to entering the simulated region. Also, simulations and experiments were performed at E₀ = 10 V/cm drift field, with corresponding arrival time and switching conditions. Experimentally, the switching pulse widths used were between 648 μs and 6744 μs, and were applied 13446 μs (or 83 TOF pulses, each TOF pulse is 162 μs) after ion release from ion funnel trap; at 10 V/cm drift field. Figure 5b shows the experimental and simulated switching efficiency for peak m/z 622 as a function of normalized switching time $(\tau =\frac{t_{switch}}{FWHM})$ for different drift field conditions of 10 V/cm and 14 V/cm. Effectively complete selection of mobility separated ions are expected to require extended switching times due to the Gaussian nature of the peak distribution, and was evaluated for simulations of m/z 622 and m/z 922 species. Such expectations revealed from simulations are closely correlated with experimental observations as seen from Figure 4b. For very fast switching (τ < 4), ions not selected for the turn (i.e. switched) proceeded in the straight path. Isolation of a given species obviously requires sufficient resolving power with details depending on the mixture complexity. At very wide pulse widths (extended switching times of τ > 7) the switch behaves as static turn.

Figure 4.

a) SIMION simulation of ion switching (m/z 622). b) The switching efficiency as a function of normalized switching time. Squares show experiment at 10 V/cm. Lines show simulations at 10 V/cm and 14 V/cm.

Figure 5.

a) Switching selectivity of m/z 622 from experiment b) SIMION simulation of selective switching of m/z 922 at τ = 10.

Experimental characterization of switching selectivity for m/z 622 (ratio of relative peak intensity due to switching of m/z 622 and the relative intensity of the total switched signal intensity for m/z 622 and the contribution due to unintended switching of m/z 922) shows that at τ > 7 there is significant cross contamination in the switched signal attributed to unintended switching of m/z 922 in addition to m/z 622 (Figure 5a). Simulations also point out to areas where additional refinement of the SLIM design and operating parameters can improve performance over that realized in this initial design. For example a simulation where m/z 922 is being switched into orthogonal channel, at τ = 10, we observed cross contamination with m/z 622 leaking into the orthogonal section (Figure 5b). Simulations have helped guide selection of experimental parameters (switching times, voltages, etc.) and predict achievable performance, allowing accelerated SLIM device development from such predictive modeling capabilities, and particularly benefiting the development and design of additional complex gas phase ion manipulations.

CONCLUSIONS AND FUTURE DIRECTIONS

The redirecting of ions through 90° turns utilizing a SLIM tee/switch component was evaluated using theoretical and simulation methods, and correlated well with experimental observations. Thus, the effective potentials and trajectories calculated for the SLIM guided selection of the parameters necessary for lossless ion turning and switching; of practical importance due to the large number of potential variables (e.g. electrode voltage biases). We have found that the loss of mobility resolving power due to the turns should generally be insignificant for the ion plume widths typically observed, and as long as plume width is small (<2 mm), thus allowing for greatly extending the ion path lengths using multiple turns. Simulations also indicate that dynamic ion switching can be performed losslessly and with high selectivity using suitable switching parameters. These calculations and simulations correlated well with experimental observations, thus encouraging the development of more complex SLIM devices.