Millisecond Dynamics of the Small Domain Generate the Kinetic Cooperativity Effect in Human Pancreatic Glucokinase

Abstract

The hallmark of glucokinase (GCK), which catalyzes the phosphorylation of glucose during glycolysis, is its kinetic cooperativity whose understanding at atomic detail has remained open since its discovery over 40 years ago. Here, we show that the origin of kinetic cooperativity is rooted in intramolecular protein dynamics using kinetic CPMG-NMR data of 17 isoleucine side-chains distributed over all parts of GCK. Residues of glucose-free GCK located in the small domain display a distinct exchange behavior involving multiple conformers that are substantially populated (p > 17%) with a k_ex = 509 ± 51 s⁻¹, whereas in the glucose-bound form these exchange processes are quenched. This exchange process directly competes with the enzymatic turnover rate at physiological glucose concentrations, thereby generating the sigmoidal rate dependence that defines kinetic cooperativity.

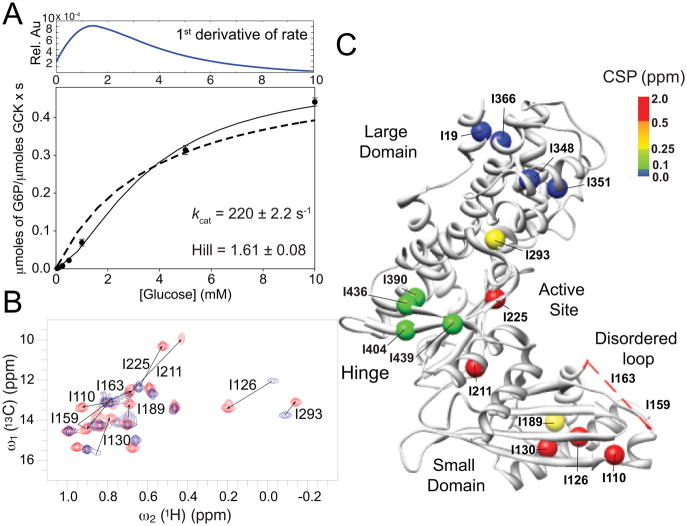
Elucidation of mechanisms by which allostery and cooperativity is achieved in proteins for the regulation of their function remains a fundamental question as it has important practical implications, for example, for the design of small molecule activators and inhibitors. Human glucokinase (GCK), which is a 53 kDa monomeric enzyme, displays a special case of allosteric regulation known as kinetic cooperativity and it has become a model system to study this phenomenon [1, 2]. GCK acts as the primary glucose sensor in the human body and, in the presence of ATP, it catalyzes the first step in glycolysis; phosphorylation of glucose at the 6′ position [3]. Precise regulation of glucose concentration in the blood stream is accomplished via glucokinase’s sigmoidal response of its enzymatic rate to increasing glucose content known as kinetic cooperativity (Figure 1A) [1–3]. The sigmoidal rate has its steepest slope at a glucose concentration in the low millimolar range, which is close to the average glucose concentration in the blood stream (Figure 1A, top panel). In this way, GCK can respond sensitively to increases in glucose concentration after the uptake of glucose-containing food, without completely depleting glucose levels.

Figure 1.

Enzyme glucokinase (GCK), its kinetic cooperativity, and NMR 2D ¹H-¹³C HMQC-TROSY spectra. A. Kinetic cooperativity profile of GCK during glucose phosphorylation at 313 K, which is the same temperature used for all NMR experiments with a turnover rate constant k_cat = 220 s⁻¹. The first derivative of the fitted kinetic cooperativity profile is plotted in the upper panel. For comparison, a fit to Michaelis-Menten kinetics is indicated as a dotted line. B. 2D ¹H-¹³C HMQC-TROSY spectra of unliganded [¹³CH₃-methyl] Ile-δ1 labeled GCK (blue) and glucose-bound GCK (red) recorded at 700 MHz and 313 K. Significant chemical shift perturbations are indicated by arrows connecting cross-peaks belonging to the two states and they are labeled with the corresponding amino acid number (see also Figure S2). C. X-ray crystal structure of unliganded GCK (PDB ID: 1V4T) mapping the positions of all Ile methyls as spheres, which are colored based upon the chemical shift perturbation between unliganded and glucose-bound GCK as indicated by the color scale [5]. The amino-acid region 151 – 179, which lacks electron density in the unliganded structure and contains Ile-159 and Ile-163, is shown as a red dashed line.

Several X-ray crystal structures are available for the glucose bound and the unliganded states of GCK, which exhibit, among other features, different opening angles between the large and the small domain (Figure 1C, Figure 3). In the bound form, GCK is closed and the protein segment with amino-acid sequence 151 – 179 forms a β-hairpin that stabilizes glucose at its binding site (PDB ID: 3IDH) [4]. By contrast, in the unliganded form (PDB ID: 1V4T) [5] GCK is open and amino acids 151 – 179 do not show electron density forming a disordered loop, which could be characterized by solution NMR [6].

Figure 3.

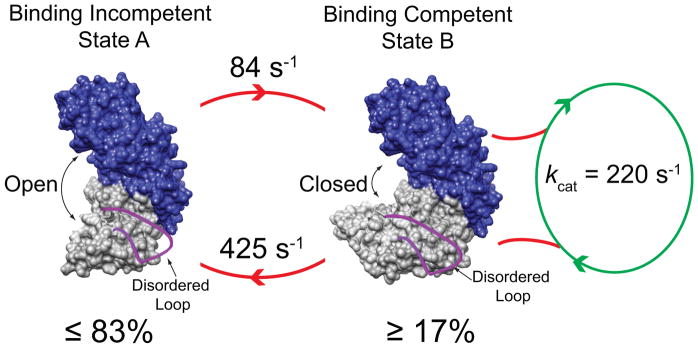
Schematic model for the origin of kinetic cooperativity of GCK by the interconversion of a binding competent (right) and incompetent state (left), whereby the loop 151 – 179 (red) is disordered in both conformations.

Advances in experimental techniques, accompanied by progress in biomolecular computation, have led to a more general view of protein structure in terms of conformational ensembles. This development has also influenced the formulation of mechanisms by which allostery is achieved thermodynamically, whereby small molecules control enzymatic function via the modulation of conformational distributions or population shifts [7–10], thus expanding the repertoire of classical models of allostery and binding cooperativity [11,12].

Understanding of kinetic cooperativity must not only take into account the underlying conformational ensembles, but also the precise motional timescales involved [13–19]. This is because cooperativity is encountered for GCK only in the reaction velocity and not in substrate binding (GCK has only a single glucose binding site) and, hence, it represents a kinetic rather than a thermodynamic phenomenon. Theoretical models proposed since the 1970s postulate that cooperativity depends upon the presence of multiple conformations that interconvert on timescales comparable to the turnover rate constant, which is approximately 60 s⁻¹ at room temperature and higher at elevated temperature. However, experimental evidence has remained sparse [13–19].

Nuclear magnetic resonance (NMR) Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion experiments provide quantitative information about enzyme dynamics to better understand the role of dynamics for catalysis and regulation [20–28]. CPMG experiments report on motions occurring in the 100 – 2000 s⁻¹ regime, which covers the timescales previously predicted to give rise to kinetic cooperativity [13–19]. For larger proteins, such as GCK, CPMG experiments can be applied to methyl groups of selectively labeled amino acids by taking advantage of their favorable spectroscopic properties in terms of sensitivity and linewidths [29]. All 17 Ile side-chains labeled in their ¹³CH₃-methyl δ1 position could be observed in the 2D ¹H-¹³C HMQC-TROSY spectra [22] of glucose-bound form and they were previously assigned by site-selective mutagenesis. However, in the unliganded state most of the residues of the small domain were undetectable. Their disappearance, preventing more detailed analysis, was explained by the presence of conformational exchange on the millisecond timescale [6].

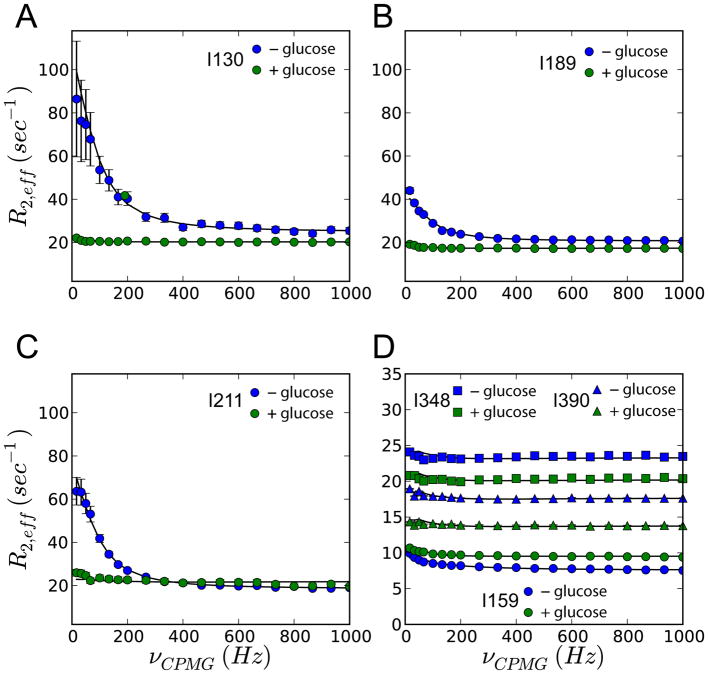
Here, we report the observation and quantification of the dynamics of all 17 Ile side-chains in both the unliganded and the glucose-bound state of GCK by CPMG relaxation dispersion. This was made possible by >80% perdeuteration of the sample using glycerol-D₈ as the sole carbon source and long induction times at 20°C. Figure 1B shows the superposition of the 2D ¹H-¹³C TROSY-HMQC spectra of GCK in the unliganded and glucose-bound forms with all isoleucine cross-peaks now being observable in both states (Figure S2). Application of methyl-CPMG relaxation experiments [30] to ¹³CHD₂ groups at Ile-δ1 positions in its unliganded and glucose-bound state leads to the relaxation dispersion profiles depicted in Figure 2.

Figure 2.

CPMG relaxation dispersion experiments show changes in the methyl dynamics following glucose binding. Dispersion profiles of residues representing small domain (A–C), disordered loop (D; circles), large domain (D; squares) and hinge region (D; triangles) in the absence (blue) and presence of glucose (green). The data were analysed using the ChemEx software by numerically solving the Bloch-McConnell equations [31] as described in Supporting Information.

Residue-specific analysis of chemical shift perturbations (CSP) upon glucose binding shows that residues belonging to the same regions behave similarly. Large domain Ile residues, such as I19, I348, I351, I366 (Figure 1C and Figure S3), experience very small ¹³C chemical shift changes, whereas hinge residues I390, I404, I436, and I439 display CSPs in the medium range (0.1 – 0.25 ppm). The most prominent CSPs are seen for residues that are either located in close vicinity of glucose, such as I211, I225, and I293, or residues that are located in the small domain far from the glucose binding site, such as I126, I130, I189, I110, I159, and I163 (0.25 – 2 ppm).

CPMG relaxation dispersion data also reveal differential behavior for residues belonging to the different regions. The strongest dispersions, as characterized by R_ex, the difference in effective relaxation rates (R_2,eff) at low and high CPMG refocusing frequencies, are found for small domain residues I126, I130, I189, I211 of unliganded GCK (R_ex = 5–60 s⁻¹) (Figure 2A–C and Figure S4). Residues I110, I126, I130, I189, I211, and I293 can be globally fit to a two-state exchange model, yielding k_ex = k_AB + k_BA = 509 ± 51 s⁻¹ and an excited-state population of 16.5 ± 1.7 %, which corresponds to intermediate exchange, thus explaining the strong line broadening observed in the methyl-TROSY spectrum (Figure S5). This corresponds to forward and reverse kinetic rates of 84 ± 8 s⁻¹ and 425 ± 43 s⁻¹, respectively. Addition of glucose quenches the millisecond dynamics of the small domain (Figure 2A–C, and Figure S4 green curves). Some residues belonging to other regions of the enzyme experience dynamics on a faster timescale and are not affected by glucose (Figure 2D).

Interestingly, the disordered region spanning residues 151 – 179 in the small domain with the two NMR reporters I159 and I163 shows essentially no millisecond exchange with R_ex values smaller than 3.8 s⁻¹ (Table S2). Hence, the disordered loop does not sense the intermediate exchange experienced by the other Ile residues of the small domain. This region remains disordered in all dominant substates of unliganded GCK and does not visit, to any significant extent, other conformations, including the β-hairpin conformation it occupies in the glucose-bound state. By contrast, the other small domain residues exchange between two or more folded conformational states.

Because of the motional broadening of the NMR spectrum [32], high-resolution NMR information is unavailable for the conformational substates. However, the CPMG fitting results yield average proton chemical shift changes Δω = 0.11 ppm, which is consistent with the average proton chemical shift change observed between the unliganded and the glucose-bound state of GCK for the small-domain residues that are not in close vicinity to the glucose binding site (Table S1). Therefore, these chemical shift changes, despite their small magnitude, are not incompatible with large conformational changes, similar to those observed between the closed glucose-bound state (PDB ID: 3IDH) and the open, unliganded state (PDB ID: 1V4T).

The turnover rate constant of GCK measured at the same temperature as the NMR experiments (313 K) is 220 s⁻¹ representing the slowest step in the reaction after glucose and ATP binding has occurred. Kinetic cooperativity is retained at this temperature with a Hill coefficient of 1.6. This turnover value defines the conformational exchange rates that can contribute to the kinetic cooperativity of the enzyme (Figure 1A). Conformational exchange processes that are comparable or slower than the turnover rate constant can produce deviation from Michaelis-Menten kinetics, i.e. kinetic cooperativity, since the enzyme has sufficient time between two successive catalytic events to populate the open, inactive state. Return to the active state happens spontaneously with a rate constant of 84 s⁻¹ that may be modulated by the presence of substrates (Figure 3). Interestingly, conformational exchange on the millisecond timescale is largely quenched for an activated variant of GCK (Figure S6), which does not display significant kinetic cooperativity, further corroborating the relevance of the observed wild-type dynamics for kinetic cooperativity.

It is well possible that the equilibrium dynamic events in the small domain are accompanied by a change in the opening angle between the small and large domains while the loop remains disordered. This could be addressed by characterizing the long-range distance distribution between parts of the two domains that are not in the vicinity of the binding site, e.g., by FRET measurements. The population of the binding-incompetent state must be significant to produce the strong kinetic cooperativity effect observed in Figure 1A. Our estimate of 83% is consistent with previous global fit analysis of fluorescence spectroscopic studies, which yielded a similar alternative conformation population [33]. The two-state model used here, while sufficient to explain our data, is likely to be an oversimplified representation of the real unliganded glucokinase ensemble.

Our results are consistent with the following model of GCK function: after phosphorylation of glucose, the β-hairpin 151 – 179 becomes disordered, which allows the release of phosphorylated glucose and ADP, while the large and small domains remain in a closed conformation. This arrangement is similar to the crystal structure of glucose-bound GCK (PDB ID: 3IDH), except that the loop is disordered. Next, the population of unliganded enzyme gradually transitions from the closed state to an open state, which is possibly glucose-binding incompetent, on an intermediate timescale (425 s⁻¹), while the loop 151 – 179 remains disordered. The inactive state could be structurally related to the open state (PDB ID: 1V4T), which shows a small domain topology that differs from that of the closed state (PDB ID: 3IDH).

This study shows how for this critical enzyme conformational heterogeneity and conformer interconversion on the proper timescale provide an elegant means for the precise regulation of its activity. Future work will focus on the structural and mechanistic role of activating and inactivating mutants on kinetic cooperativity many of which cause hyperinsulinima and diabetes.

Experimental Section

The complete description of the experimental procedures can be found in Supporting Information.