Cortical surface segmentation and mapping

Abstract

Segmentation and mapping of the human cerebral cortex from magnetic resonance (MR) images plays an important role in neuro-science and medicine. This paper describes a comprehensive approach for cortical reconstruction, flattening, and sulcal segmentation. Robustness to imaging artifacts and anatomical consistency are key achievements in an overall approach that is nearly fully automatic and computationally fast. Results demonstrating the application of this approach to a study of cortical thickness changes in aging are presented.

Introduction

Reconstructing and mapping the cerebral cortex is a critical part of many neuroscientific studies and is often involved in neuro-surgical planning. Visualizing the location of gyri and sulci assists in defining location of brain function on the cortex (Thompson et al., 2001; Van Essen et al., 2001), which can be used to learn more about brain function or to avoid critical areas in neurosurgery. Morphometric measurements such as volume (Kim et al., 2000), surface area (Magnotta et al., 1999), thickness (Kruggel and von Cramon, 2000; Yezzi and Prince, 2003), and sulcal depth (Manceaux-Demiau et al., 1998) can be used to provide valuable information about cortical characteristics in both health and disease. In addition, cortical reconstruction is important for functional brain mapping (Dale and Sereno, 1993), surgical planning (Grimson et al., 1998), and cortical unfolding or flattening (Drury et al., 1996; Fischl et al., 1999).

The CRUISE method, Cortical Reconstruction Using Implicit Surface Evolution, is at the core of the described approach. It comprises a collection of algorithms designed to find three surfaces representing the cortex: the inner surface (the gray matter (GM)/white matter (WM) interface), the pial surface (the GM/cerebrospinal fluid (CSF) interface), and the central surface (the geometric center between the inner and pial surfaces). The CRUISE approach was developed in our research group and originally reported in (Xu et al., 1999), and several improvements have been made over the years (Han et al., 2001a,b, 2002, 2003; Pham et al., 2002). A detailed paper describing CRUISE has been submitted separately to NeuroImage. The present paper provides a synthesis of the key ideas in CRUISE together with surface-based methods that follow CRUISE, including sulcal segmentation (Rettmann et al., 2002), spherical mapping (Tosun and Prince, 2001), and partial flattening for visualization and common coordinates (Tosun et al., 2003, 2004). Together, these methods comprise an overall approach to cortical mapping that we describe herein.

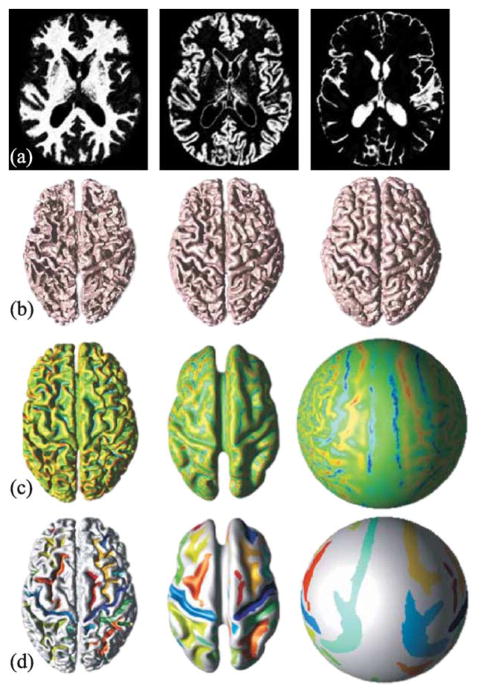
There are four major goals (or endpoints) in the approach we describe, as illustrated in Fig. 1. Starting from a volumetric MR image, the first goal is to find a fuzzy classification of the WM, GM, and CSF in the cerebrum. A fuzzy classification yields three membership functions, cross-sections of which are shown in Fig. 1a. These soft classifications can be thought of as partial volume images or posterior probability functions. The second goal is to reconstruct anatomically feasible surfaces representing the inner, central, and pial surfaces bounding the cortex, as shown in Fig. 1b. These surfaces can be used to compute thickness and volume, and the central surface is used as a 2-D approximation of the 3-D cortex itself.

Fig. 1.

Four main goals: (a) fuzzy classification; (b) nested cortical surface reconstruction; (c) partial inflation and spherical mapping (displaying mean curvature); and (d) sulcal segmentation.

The third goal of the described approach, illustrated in Fig. 1c, is to provide both partially flattened and spherical mappings of the central surface of the cortex. These maps serve to help visualize data defined on the cortex and to provide spherical coordinates throughout the cortex. It has also been found that partially flattened cortices provide a useful geometry in which to register brains from different individuals (Tosun et al., 2003, 2004). The fourth goal of our approach is to segment the sulci present in the central surface, as shown in Fig. 1d. The segmented sulci can be labeled and used for registration, for displaying geometry or function, or for computing regional morphometric changes due to aging or disease. In short, the sulci represent important landmarks for cortical localization.

In the following sections, we take the reader through some of the mathematics that are at the core of our algorithms. Novel visualizations are used to illustrate and motivate the core concepts. This exposition does not represent a resource sufficient to carry out an implementation of our approach (although details present in cited papers should provide enough information). Rather, it serves as a basis for improved understanding, perhaps leading to new creativity, improved methods, and ideas for novel applications in which our approach can be put to use.

White matter segmentation

The cortical GM surrounds the WM in the cerebrum, and the two can generally be visually distinguished in T1-weighted MR images, as shown in Fig. 2a. If the WM were segmented, then the WM/GM (inner cortical) surface would be the surface surrounding the WM segmented volume. Looking at the image, one might surmise that a simple intensity threshold or isosurface could be used to find the WM boundary as shown in Fig. 2e; but if one wants an accurate, reproducible representation, several additional steps are required.

Fig. 2.

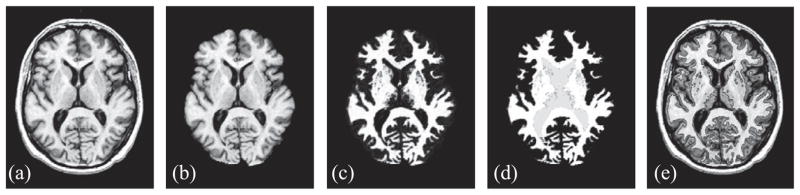
Cross-sectional view of (a) T1-weighted MR image, (b) initial preprocessing to extract cerebral volume, (c) WM membership function, (d) WM membership after removing subcortical structures and topology correction, (e) WM isosurface at 0.5 overlaid on original MR image.

There are four specific issues that are not addressed by a thresholding or isosurface in finding the inner cortical surface. First, the tissues outside the cerebrum (marrow, fat, skin) may have intensities similar to white matter. Simple thresholding will detect these components as well as the WM. A second issue is that noise, intensity inhomogeneities, and partial volume effects are common in MR images. A simple thresholding will fail unless these artifacts are addressed. A third issue is that there are subcortical structures within the WM that are clearly not part of the cortical WM/GM interface. The fourth problem with thresholding is that it does not take topology into consideration. The issue of topology is important for cortical surface reconstruction because the actual physical topology of a cortical surface is believed to be fixed across individuals and equivalent to a sphere.

The initial steps of CRUISE seek to localize the three major tissue classes and generate an initial estimate of the GM/WM interface while addressing all of the aforementioned issues. The results of the major processing steps are shown in Fig. 2. The cerebral extraction was performed using methods outlined in Goldszal et al. (1998).

Tissue classification

After extracting the cerebral volume, our Fuzzy And Noise Tolerant Adaptive Segmentation Method (FANTASM) is used to identify the spatial distribution of GM, WM, and CSF within the image volume. Because the cortex is thin relative to the voxel size of most MR acquisitions, FANTASM computes a “soft” or “fuzzy” tissue classification, which retains more information from the original image than traditional hard segmentations. The tissue classification is additionally robust to both noise and intensity inhomogeneities. We briefly describe FANTASM here.

Let Ω be the set of voxel indices, C be the number of tissue classes, and y_j, j ∈ Ω be the observed (preprocessed) MR image values. The goal of FANTASM is to find intensity centroids v_k, k =1,…, C, a gain field g_j, j ∈ Ω and membership functions u_jk, j ∈ Ω, k =1,…, C that will minimize the following objective function

$$J_{\text{FANTASM}}=\sum _{j\in \mathit{\Omega }}\sum _{k=1}^C{u}_{jk}^q{\Vert y_j-g_j{v}_k\Vert }^2+{\lambda }_1\sum _{j\in \mathit{\Omega }}\sum _{r=1}^3{(D_r\ast g)}_j^2+{\lambda }_2\sum _{j\in \mathit{\Omega }}\sum _{r=1}^3\sum _{s=1}^3{(D_r\ast D_s\ast g)}_j^2+\frac{\beta }{2}\sum _{j\in \mathit{\Omega }}\sum _{k=1}^C{u}_{jk}^q\sum _{l\in N_j}\sum _{m\ne k}{u}_{lm}^q$$ (1)

The parameter q, which must satisfy q > 1 (and is set to 2 in this work), determines the amount of “fuzziness” of the resulting classification (Bezdek et al., 1993). The expressions D_r*g and D_r* D_s*g present first and second order finite differences applied to the gain field. The first term is data-driven and is primarily responsible for clustering the intensity values within the image. The second and third terms are regularization terms on the gain field to insure it is spatially smooth and slowly varying. The final term constrains the membership functions to also be spatially smooth, thereby reducing the effects of noise. The parameters β, λ₁, and λ₂ are weights that determine the amount of smoothness in resulting membership functions (β) and the gain field (λ₁ and λ₂). Details of the notation and mathematics can be found in Pham and Prince (1999) and Pham (2001). By modeling the effects of inhomogeneities and noise all within a single objective function, we are able to effectively compensate for each of these artifacts while simultaneously computing our tissue classification using an iterative optimization algorithm. Fig. 1a shows the membership functions for WM, GM, and CSF (going left to right) computed using FANTASM.

Automatic editing of the WM membership function

AutoFill consists of a sequence of image processing operations that automatically fills the ventricles and subcortical GM structures (e.g., putamen, thalamus) within the WM membership function (Han et al., 2001a). Figs. 2c–d show cross-sectional views of the WM membership function before and after AutoFill processing.

AutoFill uses the fact that the subcortical GM together with the ventricles form concavities inside the WM that open from the bottom of the brain. We first find the ventricles using a standard 3-D geometric deformable model (GDM), initialized using a small sphere positioned at the centroid of the CSF membership volume. The ventricles are then used as “seeds” to fill the WM membership function using 2D region-growing in successive coronal slices. A putamen mask generated from a Talairach normalization is used to roughly constrain the region growing. Once processed, the outside of the WM membership approximates the inner cortical surface, connecting the two hemispheres around the corpus callosum (superior connection) and through the brain stem at the level of the diencephalon (inferior connection).

Topology correction of WM isosurface

Because of noise and partial volume averaging, an isosurface generated from the AutoFill processed WM membership function typically contains hundreds of handles (like that on a coffee cup). We designed a Graph-based topology correction algorithm (GTCA) in order to remove all the handles from the WM membership function volume before its isosurface is computed (Han et al., 2002). Before summarizing the GTCA method, we want to emphasize that all isosurfaces in this work are computed using a connectivity consistent Marching Cubes (CCMC) algorithm (Han et al., 2003), which guarantees that the extracted isosurface has a topology consistent with the digital topology principles used in GTCA. We note that other topology correction methods can also be found in the literature (Kriegeskorte and Goebel, 2001; Shattuck and Leahy, 2001).

GTCA relies on digital topology principles and graph analysis to detect and remove handles (Han et al., 2002). An input WM membership function volume is first thresholded (at membership value 0.5) to create a binary volume consisting of object (or foreground) and background. The binary volume is further processed to keep only the largest connected object component while clearing the other object components to background. Internal cavities of the resulting object are filled if they exist. A morphological opening operation is then performed, which divides the object into body parts (voxels that remain after the opening operator) and residue parts (voxels that are removed by the opening). A conditional topological expansion procedure then replaces residue parts that do not involve handles. A graph is then constructed by analyzing the connectivity of the body and residue pieces, and one or more residue pieces are removed to break the cycles in the graph, thereby removing handles in the volume. GTCA alternates between the above process which directly cuts handles in the foreground and an alternative process which inverts the foreground and background of the binary volume and thus fills the tunnels in the background. The two processes are first applied at a fine scale (as determined by the size of the morphological opening operator) and the scale is sequentially increased if necessary until all the handles/tunnels are removed. In this way, the topology correction attempts to only make the smallest possible changes to the input WM volume.

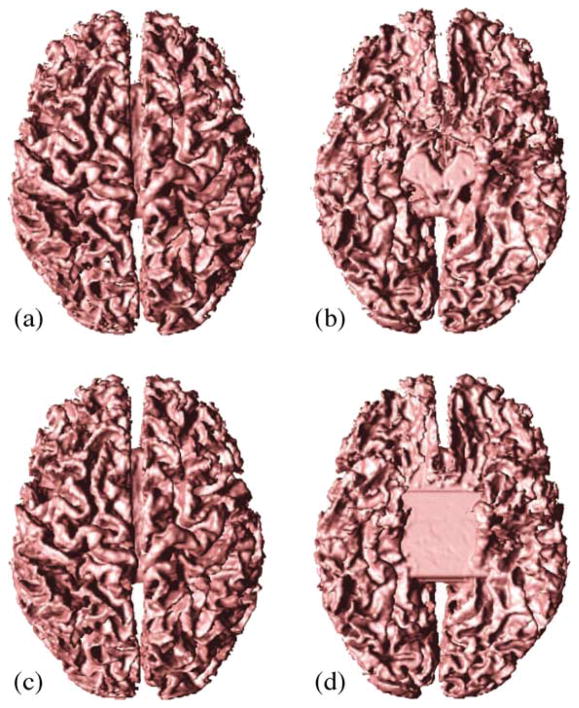
Fig. 3 shows the effects of AutoFill and topology correction. Note how AutoFill has removed the cavity at the bottom of the brain. In Fig. 4, we show magnified views of the WM isosurface before and after topology correction. All handles seen in Fig. 4a are removed in Fig. 4b. The two surfaces are otherwise identical.

Fig. 3.

WM isosurface: (a) top and (b) bottom views; Isosurface after Autofill and topology correction: (c) top and (d) bottom views.

Fig. 4.

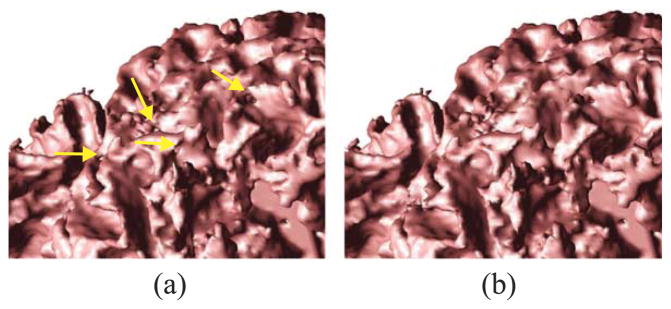
WM boundary surface obtained (a) before and (b) after topology correction.

Nested surfaces

The isosurface generated after topology correction of the filled WM volume is topologically correct and is close to the GM/WM interface. It serves as an initialization in a nested surface reconstruction step for finding the three cortical surfaces of interests (cf. Fig. 1b).

The nested surface reconstruction step applies a deformable model method to deform the initial topology-correct WM boundary surface to find the three cortical surfaces in sequence. The particular deformable model method we use is a topology-preserving geometric deformable model (TGDM) method developed by our research group (Han et al., 2003) that guarantees the topological consistency of the final surfaces while avoiding the self-intersection problem in traditional deformable model methods. There is, however, a difficulty in accurately locating the central and pial surfaces within tight cortical folds due to the partial volume effects. We address this by processing the GM membership function to recover the pial boundaries in these areas.

Anatomically consistent enhancement (ACE)

Partial volume averaging at voxels of cortical GM, particularly in sulci where the cortex is “back-to-back,” can cause widely inaccurate estimates of both the central and pial surfaces. To address this problem, we have designed a procedure called anatomically consistent enhancement (ACE) to modify the initial fuzzy GM segmentation before proceeding to the surface reconstruction. The goal of ACE is to provide a GM representation that has evidence of sulci where it might not otherwise exist due to the partial volume effect. Accordingly, ACE modifies the initial GM segmentation to create a thin, digital separation between sulcal GM banks. In implementation, ACE is computed by first locating (automatically) the exterior skeleton of the shape defined by the GM/WM interface and then resetting the GM membership function at the skeletal points to zero while adding its original value to the CSF membership function. The use of the conventional Euclidean skeleton, however, has the drawback of often cutting into actual GM when the two GM banks of a sulcus are asymmetric, as seen in Figs. 5a–b. This problem can be addressed by incorporating the presence of CSF in the definition of distance used to compute the outer skeleton. Such a (weighted) distance will shift the skeleton toward CSF regions, and thus better preserves the asymmetric sulcal banks as shown in Fig. 5c.

Fig. 5.

Magnified views of (a) original GM membership function, (b) ACE result using Euclidean skeleton, and (c) ACE result using weighted-distance skeleton.

The weighted distance function, denoted by D(x), is derived by applying a non-uniform speed function, F(x), in the following Eikonal equation:

$$\begin{array}{ll}F(\mathit{x})\Vert \nabla D(\mathit{x})\Vert \hfill & =1\text{in}\mathit{\Omega },\hfill \\ D(\mathit{x})\hfill & =0\text{for}\mathit{x}\in \mathit{\Gamma },\hfill \end{array}$$ (2)

where Ω is the image domain and Γ is the GM/WM interface, for which we use the 0.5-isosurface of the WM membership function. In particular, we choose

$$F(\mathit{x})=1-0.9u_{\mathit{csf}}(\mathit{x}),$$ (3)

where u_csf (x) is the CSF fuzzy membership function. The reduced speed inside CSF regions causes the measured distance to be larger than the usual Euclidean distance, and thus shifts the skeleton to these regions.

A cross-sectional view of a GM membership function before and after ACE modification is shown in Fig. 6. In most cases where sulcal banks are back-to-back and no CSF was apparent in the original GM membership image, there is now a noticeable gap between the banks in the modified membership image. There are also several examples showing a “gentle reinforcement” of weak sulci, preserving the location of the sulcal gap and the nonuniform cortical thickness on opposite banks.

Fig. 6.

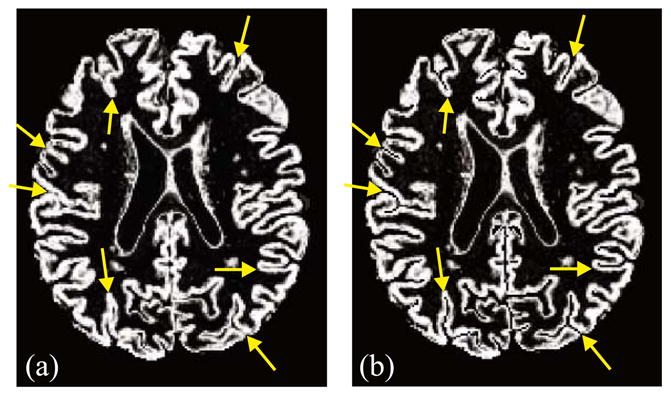
A 2D cross-section of: (a) original GM membership function and (b) the ACE enhanced GM membership function.

Nested cortical surface reconstruction

Three instances of TGDM are targeted at the three different cortical surfaces, as illustrated in Fig. 7. The result of a previous surface is used as the new initialization for the next surface. Each step differs in its initialization and in the specific choice of the speed functions in a generic TGDM evolution equation:

$${\mathit{\Phi }}_t(\mathit{x},t)={\omega }_{\kappa }\kappa (\mathit{x})\Vert \nabla \mathit{\Phi }(\mathit{x},t)\Vert +{\omega }_{R}R(\mathit{x})\Vert \nabla \mathit{\Phi }(\mathit{x},t)\Vert +{\omega }_{\overrightarrow{v}}\overrightarrow{v}(\mathit{x})·\nabla \mathit{\Phi }(\mathit{x},t).$$ (4)

Fig. 7.

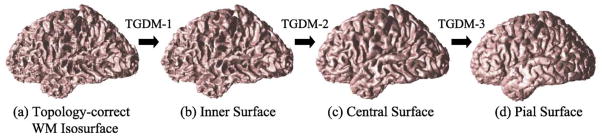
Nested cortical surface reconstruction.

In this context, Φ (x,t) is a signed distance function (also known as the level set function) whose zero-level set corresponds to the implicitly embedded deforming surface. Φ_t denotes the partial derivative of Φ with respect to its time variable, and ΔΦ is the spatial gradient of Φ. κ(x), R(x), and v⃗ (x) are three types of speed functions that control the evolution of the level set function. ω_R, ω_k, and ω_v⃗ are the weights that cause the respective speeds to be emphasized differently.

In our cortical surface reconstruction method, κ(x) is always chosen to be the mean curvature function of the level sets of Φ. R(x) and v⃗(x) are derived from the processed fuzzy membership functions. The details can be found in Han et al. (2001b). To ensure the proper nesting of the reconstructed surfaces, we impose an additional constraint when implementing the second (central surface) and third (pial surface) TGDM, which requires that the evolving surface stay outside of the initial surface. This constraint guarantees that the estimated central cortical surface is not inside the inner cortical surface at any point, and the pial surface is not inside the central surface.

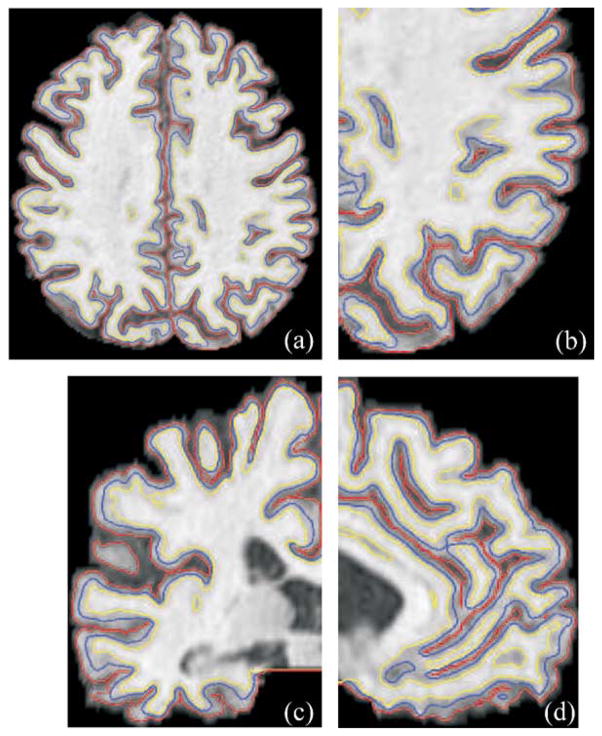
An example of the nested cortical surface reconstruction results is illustrated in Fig. 8. The three surfaces are properly nested and accurately follow the convoluted cortical folds.

Fig. 8.

(a) Three reconstructed surfaces displayed on an axial slice of the original MR data. (b) A zoom of the bottom-right corner of (a). (c), (d) Zoomed views on coronal and sagittal slices, respectively. Yellow: inner; blue: central; red: pial.

Surface inflation and spherical mapping

In this section, we describe an approach for creating a standardized partially flattened cortex (PFC) from a central surface cortex reconstruction. The PFC is an intermediate data structure that is used for visualization, cortex-to-cortex registration, creating correspondences between cortices, and mapping each cortex to an atlas. This atlas can have anatomical labels as well as a spherical map, thereby providing both a cortical parcellation and spherical coordinates for every cortex. Our approach combines parametric relaxation, iterated closest point registration, and conformal mapping, as now briefly described.

Surface inflation

Cortices from different individuals are similar at a coarse scale, but not at a fine scale. Accordingly, it makes sense in population-based analysis to find a coarse representation of each cortex. Fig. 1c shows an example of an original central cortical surface and both a coarse partially flattened map and a spherical map. To obtain a coarser shape and a more regular mesh structure, the central surface mesh is smoothed using the following relaxation operator (Drury et al., 1996)

$$v_i^{t+1}=(1-\lambda )v_i^t+\lambda {\overline{v}}_i^t,$$ (5)

where v_i is the position of the i^th vertex, t is the iteration number, λ ∈ [0,1] is a smoothing parameter, and v̄_i is the average vertex position, defined in Tosun et al. (2003, 2004). This process progressively simplifies the surface in each step, making the resulting surface more like a sphere with each iteration.

In order to be able to compare partially flattened surfaces across individuals, we stop the relaxation process when the shapes are similar, as judged by evaluating the L₂ norm of mean curvature H, defined as (Smith et al., 2000)

$${\Vert H\Vert }_2=\sqrt{\frac{1}{4\pi }\int H^2\mathrm{d}A.}$$ (6)

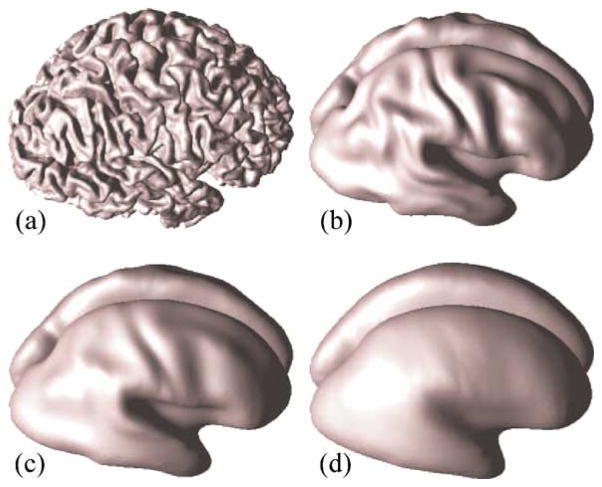
Several partially flattened surfaces are shown in Fig. 9. We choose to stop inflation when ||H||₂ ≤ 3.25, so that PFC shapes are like those in Fig. 9b.

Fig. 9.

Surface inflation: (a) Original cortical surface, (b) ||H||₂ = 3.25, (c) ||H||₂ = 2.5, (d) ||H||₂ = 2.0.

Cortex registration

Cortices from different subjects can be registered to each other (and to an atlas) using their PFC representations. Let V and W be two PFCs with vertices ${\{v_i\}}_{i=1}^N$ and ${\{w_j\}}_{j=1}^M$, respectively. We use a global 3-D rigid body surface-based registration algorithm based on the iterative closest point algorithm (ICP) (Besl and McKay, 1992) to register these surfaces. Our modification to ICP acknowledges the fact that V and W are triangulated surfaces rather than simple point sets. This means that the closest point to v_i ∈ V on W may not be a vertex, but may instead be a point on a triangular element defined by the vertices in W.

We identify the closest point to v_i ∈ V on the surface W by 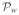(v_i) where 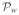(·) is the projection (onto W) operator. Similarly, the closest point to w_j ∈ W on the surface V is given by (w_j), where 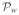(·) is the projection (onto V) operator. This identification yields the correspondence pairs (v_i, 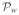(v_i)), i = 1,…, N and (w_j, 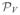(w_j)), j = 1,…, M. In order to reduce possible directional bias, we define the modified ICP objective function in a bilateral fashion, as follows

$$f(\mathcal{R};V,W)=\frac{1}{N+M}\times \left(\sum _{i=1}^N\Vert v_i-{\mathcal{P}}_{\mathcal{R}(W)}(v_i)\Vert +\sum _{j=1}^M\Vert \mathcal{R}(w_j)-{\mathcal{P}}_V(\mathcal{R}(w_j))\Vert \right).$$ (7)

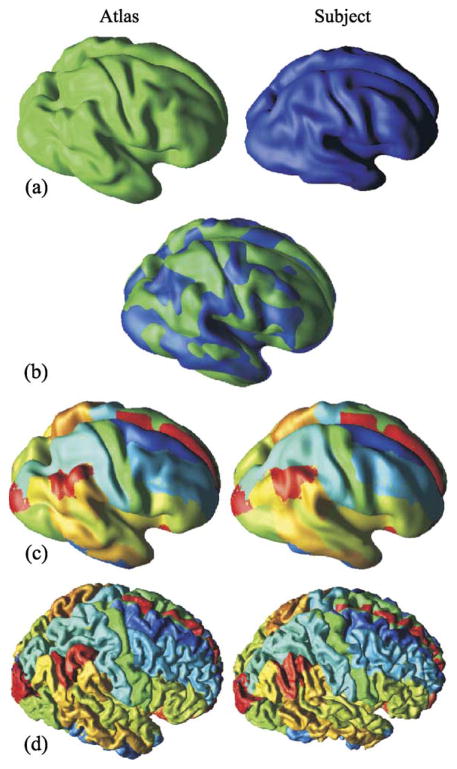
The fact that W is being moved is reflected in this expression by the use of the rigid body transformation operator 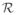(·). Registration of a subject to an atlas (Kabani et al., 1998) is illustrated in Fig. 10. The most prominent anatomical details representing the major sulci are preserved on the PFC representations. These major anatomical features are the key features that drive the surface registration algorithm, and since these features are quite stable across individuals, the rigid body registration is quite successful as illustrated in Fig. 10.

Fig. 10.

A subject is registered to an atlas. (a) Original PFCs; (b) superposed PFCs after registration; labels on atlas are transferred to subject on (c) PFC and (d) original central surface.

Spherical mapping

The PFC representation has been utilized for visualization and for cortical registration (Fischl et al., 1999; Sereno et al., 1996). For quantitative evaluation, however, it is necessary to establish a coordinate system on the cortex so that features can be identified more rigorously (Angenent et al., 1999; Drury et al., 1996; Fischl et al., 1999; Hurdal et al., 1999; MacDonald et al., 2000; Thompson et al., 2000). Spherical coordinates are appropriate since the topology of the sphere is the same as that of the cortical surface. Two general approaches have been explored in the past: (1) iterative relaxation followed by radial projection to the sphere (Fischl et al., 1999; Sereno et al., 1996) and (2) conformal mapping (Angenent et al., 1999).

We employ a single optimized, conformal map that takes the PFC of our atlas to the sphere. In this way, the PFC of a subject brain, after registration to the PFC of our atlas, can be rapidly mapped to the sphere using the atlas’s conformal map. As illustrated in Fig. 11, our spherical mapping process begins at the stage of a PFC. The first step is to bring each vertex to the complex plane using the conformal flattening technique described in Angenent et al. (1999), as shown in Fig. 11b. A Möbius transform then adjusts the points on the complex plane in order to line up the hemispheres and minimize area distortion, where optimization on both hemispheres is carried out simultaneously (cf., (Tosun and Prince, 2001; Tosun et al., 2003, 2004)). The area distortion measure is minimized within the group of Möbius transformations

Fig. 11.

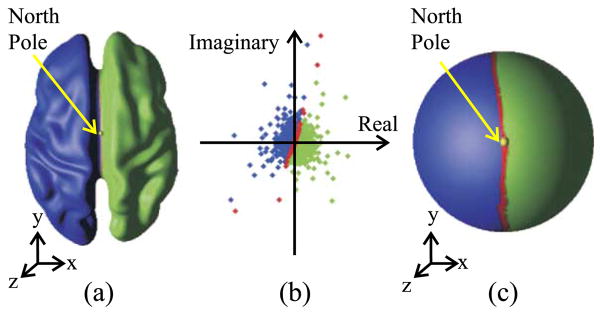
(a) Hemispherical cut path colored by red on the original surface with the north pole point marked by yellow, (b) the original flat map, and (c) the spherical map (scaled for display purposes). Hemispherical cut path (red); Left cortical hemisphere (blue); Right cortical hemisphere (green); North pole point (yellow).

$$\left\{r\frac{\rho (z-s)+1}{\rho (z-s)-1}:r\in ℝ,s\in ℂ,\rho \in ℂ\right\},$$

using the conjugate gradient algorithm, where z ∈ 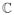is the resulting location of the triangle mesh vertex on the complex plane after conformal flattening. An inverse stereographic projection then brings the points on the complex plane to the sphere, as shown in Fig. 11c. This particular Möbius transformation maps each cortical hemisphere to one half of the unit sphere such that the hemispherical cut (the red path in Fig. 11) maps to a great circle on the unit sphere with consistent left/right and anterior/posterior orientations. Details of the proposed spherical mapping technique can be found in (Tosun and Prince, 2001; Tosun et al., 2003, 2004). We note that the composition of the conformal flattening with a Möbius transformation followed by the inverse stereographic projection is still conformal. By using barycentric coordinates within the triangles on the atlas cortex, there exists a mathematical map from each registered PFC to the sphere.

Sulcal segmentation

The goal of sulcal segmentation is to extract the buried cortical regions surrounding each of the sulcal spaces. We define these regions as “sulcal regions”, and refer to the regions of cortex that are not buried in the folds as “gyral regions”. These structures are depicted in Fig. 12a. A classification of points on the surface as either gyral or sulcal is not, however, sufficient to obtain a distinct region corresponding to each sulcus as sulci are frequently separated by a ridge buried within the cortical folds. This is illustrated in Fig. 12b with a simplified representation of two sulcal regions in three-dimensions. This entire buried region is classified as sulcal, but our aim is to obtain distinct regions corresponding to each of the two folds as illustrated in Fig. 12b, where one of the sulcal regions is represented as a solid line and the other as a dashed line. An intuitive approach for obtaining this segmentation is to apply the watershed algorithm on the buried regions of cortex. In the watershed algorithm, a catchment basin (CB) is produced corresponding to each local minima and, as illustrated in the figure, would provide an appropriate segmentation of sulcal regions. The main challenge lies in defining a suitable function describing the “height” of the cortex, from which the watershed can be computed. We utilize a measure of geodesic depth—i.e. depth along the surface—to construct this height function.

Fig. 12.

(a) Simplified cross-section of cortical surface illustrating “sulcal regions”. (b) An illustration of how the watershed algorithm can be used to segment sulcal regions.

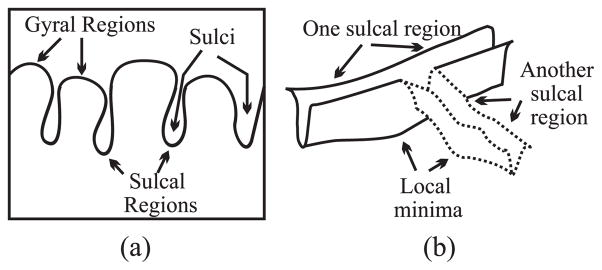
Our approach for generating a sulcal segmentation from a cortical surface consists of four parts: sulcal/gyral classification, geodesic depth calculation, watershed implementation, and catchment basin merging. The result of each of these steps is illustrated in Fig. 13 on the partially flattened cortical surface. We note that all processing is done on the original cortical surface—the partially flattened surface is used for visualization only. We now describe each of the steps of the sulcal segmentation procedure. A more detailed description of the entire procedure can be found in (Rettmann et al., 2002).

Fig. 13.

(a) Shrink-wrap surface, (b) sulcal/gyral classification, (c) geodesic depth, (d) catchment basins, (e) sulcal segmentation on partially flattened cortical surface, and (f) sulcal segmentation on cortical surface.

Sulcal/gyral classification

Our first goal is to classify the cortical surface into sulcal and gyral regions. We accomplish this by first defining and finding an outer cortical surface—i.e., that part of the cortex that one could see, if the cerebral cortex were isolated and separated into hemispheres. This is accomplished by computing a “shrink-wrap” surface for each hemisphere—i.e., a surface that tightly surrounds the cortical surface but does not enter into the cortical folds. The left and right cortical hemispheres are automatically identified by defining a cut around the corpus callosum using the knowledge of the locations of the anterior and posterior commissures. Focusing on one cortical hemisphere, the shrink-wrap is implemented by initializing a deformable surface model as an ellipsoidal shape around the hemisphere and applying appropriate internal and external forces (Rettmann et al., 2002). The result of this procedure is illustrated in Fig. 13a where a cross-section of the shrink-wrap (in blue) is shown along with the original cortical surface (in white).

Sulcal and gyral regions are then readily defined by computing the Euclidean distance from each vertex on the cortical surface to the closest point on the shrink-wrap for the corresponding hemisphere. A vertex is defined to be in a sulcal region if this distance is greater than 2 mm, otherwise it is in a gyral region. The resultant classification is shown in Fig. 13b where the sulcal regions are shown in red and the gyral regions in blue.

Geodesic depth calculation

To compute the geodesic depth within sulcal regions, we first define all gyral regions to have zero geodesic depth. The geodesic depth from the gyral regions to all vertices in sulcal regions can be calculated by solving the following Eikonal equation for T (Kimmel and Sethian, 1998):

$$\begin{array}{ll}\mid \nabla T(\mathit{x})\mid \hfill & =\mathit{1}\mathit{in}\mathit{\Omega },\hfill \\ T(\mathit{x})\hfill & =\mathit{0}\mathit{in}\mathit{\Gamma },\hfill \end{array}$$ (8)

where Ω is the set of vertices and triangles in sulcal regions—a continuous domain—and Γ is the set of vertices and triangles in gyral regions. The desired function T(x) is the time it takes to travel from Γ to x; because unit speed propagation is assumed, T is equivalent to geodesic distance. This equation can be solved using the fast marching (FM) method originally developed in Sethian (1996) and extended to triangulated domains in Kimmel and Sethian (1998).

The fast marching method yields the times T at which a unit speed wave originating from the boundary of the gyral regions reaches the vertices in sulcal regions. We then define the geodesic depth for each vertex a on the cortical surface

$$g(a)=\{\begin{array}{ll}T(a)\hfill & \text{if}a\in S\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (9)

Where 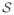is defined to be the set of all vertices in sulcal regions. The geodesic depth map is displayed in Fig. 13c where large depths are shown in red and yellow and small depths in blue and green.

Watershed algorithm

The maximum geodesic depth is given by

$$g_{max}=\underset{a\in \mathcal{S}}{max}g(a).$$

The height function over which we wish to compute the watershed is then given by

$$f(a)=g_{max}-g(a),a\in \mathcal{S}.$$ (10)

The goal of the watershed algorithm is to label each vertex on the mesh according to its “catchment basin”. We use the watershed by immersion algorithm (Vincent and Soille, 1991) which begins with the smallest height, identifies minima as they arise, and properly associates vertices with minima during the “immersion” until all vertices are labeled. All vertices associated with a minima form a catchment basin and the result of the watershed algorithm is shown in Fig. 13d. From this figure, it is clear that an oversegmentation has occurred—i.e. several CBs represent each sulcal region. This is addressed by a CB merging algorithm designed to combine appropriate CBs to form regions corresponding to each cortical sulcus.

Merging of catchment basins

Oversegmentation occurs in the watershed algorithm because small ridges in the sulcal regions result in the formation of separate CBs. Our merging algorithm is based on two criteria—the height of the ridge separating the CBs and the size of the CB. If the height of the ridge separating two CBs is small, they are merged together. Additionally, small CBs are either removed (if they have no adjacent CBs) or are merged with a larger, adjacent CB. Details of this algorithm can be found in Rettmann et al. (2002). The result of the merging algorithm followed by the size filter is shown on both the partially flattened and original cortical surfaces in Figs. 13e–f. These images illustrate that a distinct region is segmented corresponding to each cortical fold.

Study on cortical thickness

Cortical thickness is an important metric for analyzing the 3-D structure of the cortex. The cortical GM is bounded by the CSF on the outside, and by the WM on the inside. Therefore, with accurate estimates of the GM/WM interface (inner) and GM/CSF interface (pial) surfaces, we can compute the thickness of the cortex. We adopt a simple thickness measure as in Zeng et al. (1999). That is, at each grid point between the inner and pial surfaces, the thickness is defined to be the sum of the distances from the point to the inner and the pial surfaces. A cross-section from the thickness volume of a sample subject is shown in Fig. 14a.

Fig. 14.

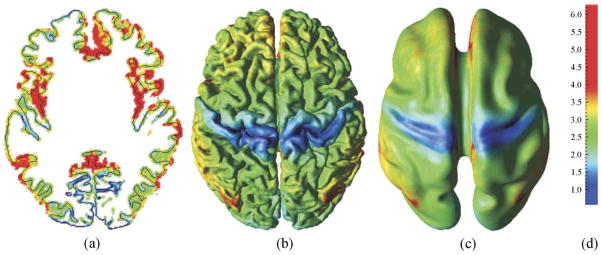
(a) Central surface of a sample subject superposed on a 2-D cross-section of its thickness volume; average brain template for cortical thickness displayed on (b) the atlas’s cortical surface and (c) the atlas’s partially flattened surface; (d) Colormap (in mm).

In this study, we analyze the cortical thickness of 35 individuals at three different time points for a total of 105 data sets. All data were obtained from the Baltimore Longitudinal Study of Aging database (Resnick et al., 2000; Shock et al., 1984). The three data sets analyzed for each individual correspond to years 1, 3, and 5 of the BLSA study. This group consists of 19 women and 16 men ranging in ages from 59 to 84. We conduct both cross-sectional as well as longitudinal analyses of the mean thickness for the entire cortex, the sulcal regions, and the gyral regions. In addition, an average brain template for cortical thickness is constructed.

Thickness on average brain template

Partially flattened surfaces of the 105 data sets (3 scans for each of the 35 subjects) and the cortex registration algorithm were utilized to construct an average brain template for cortical thickness. We randomly picked one of the 105 data sets as the atlas brain. Since the partially flattened surfaces of different cortices have a very similar shape, it is possible to map the thickness measures from each data set to the atlas’s partially flattened surface. To obtain this mapping, the partially flattened surface from each data set is first registered to the atlas’s partially flattened surface using the registration algorithm described in Cortex registration. Next, focusing on a single data set, the mesh nodes of the partially flattened surface of the atlas are projected onto the registered partially flattened surface of that data set. The thickness measures from the data set are then interpolated for each mesh node on the atlas’s surface. This procedure is followed for each of the 105 data sets. At the end, an average over all data sets is computed for each mesh node on the atlas’s surface yielding an average brain template for cortical thickness.

This average thickness is shown on the atlas’s cortical surface in Fig. 14b and the atlas’s partially flattened map in Fig. 14c. The thickness values fall predominantly in the range of 1–5 mm with a mean of 2.80 mm, which is in agreement with other published results (Beatty, 2001; Griffin, 1994). In addition, the postcentral gyrus is clearly thinner than other regions of the cortex which is consistent with other findings that some of the thinnest cortical regions occur in sensory cortex (Fischl and Dale, 2000).

Cross-sectional and longitudinal analyses

In this section, we describe both cross-sectional as well as longitudinal analyses aimed at evaluating the effects of age on cortical thickness. The cross-sectional analysis assesses age-associated differences in thickness across the group of 35 individuals spanning an age range of 26 years. The longitudinal analysis assesses changes in mean thickness within individuals over the 4-year interval. We consider three measurements: the mean global thickness, the mean sulcal thickness, and the mean gyral thickness. The mean global thickness is computed as the average thickness values over all vertices on the cortical surface. As described in Automatic editing of the WM membership function, surface elements that reside on the artificial surface created by AutoFill joining the hemispheres below the corpus callosum are not part of the cortical surface. Accordingly, we formed a mask for each MR image data set marking the regions that were modified by AutoFill. Vertices within the mask were excluded from the mean thickness calculation. The mean sulcal thickness is computed as the average thickness of all points lying in one of the final segmented sulcal regions as described in Sulcal segmentation. Similarly, the mean gyral thickness is the average thickness of all points that do not lie within a segmented sulcal region.

In the cross-sectional analysis, the scans for each year were analyzed separately. Thus, we obtained individual results for the set of scans obtained at year 1, year 3, and year 5 of the BLSA study. We should, however, observe similar trends between the three analyses as they are the same subjects only at different time points. For each year, we compute the correlation coefficients between the mean thickness measurements and age. All computations were done using SAS version 8.02 (SAS Institute, Cary, NC). The results of this analysis are reported in Table 1. From this table, we see that all thickness measurements for all years have a negative correlation with age indicating that older individuals have thinner cortices than younger individuals. These results are significant for all but two of the measurements (P < 0.05). In the analysis, we also observed that the mean sulcal thickness is less than the mean gyral thickness which is consistent with other published results (Fischl and Dale, 2000). This was observed in the analyses for all 3 years and the differences were shown to be significant (P < 0.01 paired t test). The results of this analysis show that older individuals have thinner cortices than younger individuals, which could indicate that the cortex is thinning with age.

Table 1.

Correlations between age and mean thickness

Region	Year 1	Year 3	Year 5
Global	−0.41*	−0.34*	−0.33*
Sulcal	−0.41*	−0.39*	−0.40*
Gyral	−0.40*	−0.31	−0.30

^*P < 0.05.

In the longitudinal analysis, we tested for changes in mean thickness within individuals over the 4-year time span. We did not obtain significant results in this analysis; however, this could be due to the small sample size and relatively short time interval. We are currently investigating this question in a more extensive analysis using the entire database from the BLSA, which consists of 158 subjects scanned up to 10 years at present. This data set will provide both more statistical power (due to a larger N) as well as a longer time span to measure possible change. We expect this data set will be a rich resource for answering both questions on cortical thickness changes as well as other morphometric changes associated with aging.