Cortical reconstruction using implicit surface evolution: Accuracy and precision analysis

Abstract

Two different studies were conducted to assess the accuracy and precision of an algorithm developed for automatic reconstruction of the cerebral cortex from T1-weighted magnetic resonance (MR) brain images. Repeated scans of three different brains were used to quantify the precision of the algorithm, and manually selected landmarks on different sulcal regions throughout the cortex were used to analyze the accuracy of the three reconstructed surfaces: inner, central, and pial. We conclude that the algorithm can find these surfaces in a robust fashion and with subvoxel accuracy, typically with an accuracy of one third of a voxel, although this varies with brain region and cortical geometry. Parameters were adjusted on the basis of this analysis in order to improve the algorithm’s overall performance.

Introduction

Many brain mapping procedures require automated methods to find and mathematically represent the cerebral cortex in volumetric MR images. Such reconstructions are used for characterization and analysis of the two-dimensional (2-D) geometry of the cortex— e.g., computing curvatures (Cachia et al., 2001; Zeng et al., 1999), geodesic distances (Cachia et al., 2002; Rettmann et al., 2002), thickness and volume (Fischl and Dale, 2000; MacDonald et al., 2000; Miller et al., 2000; Magnotta et al., 1999; Kruggel and von Cramon, 2000; Tosun et al., 2001; Crespo-Facorro et al., 1999; Kim et al., 2000; Jones et al., 2000; Kabani et al., 2001; Yezzi and Prince, 2003; Lerch and Evans, 2005), segmenting sulci and gyri (Cachia et al., 2002; Rettmann et al., 2002; Behnke et al., 2003), surface flattening (Carman et al., 1995; Drury et al., 1996; Timsari and Leahy, 2000), and spherical mapping (Fischl et al., 1999; Tosun et al., 2004b; Angenent et al., 1999).

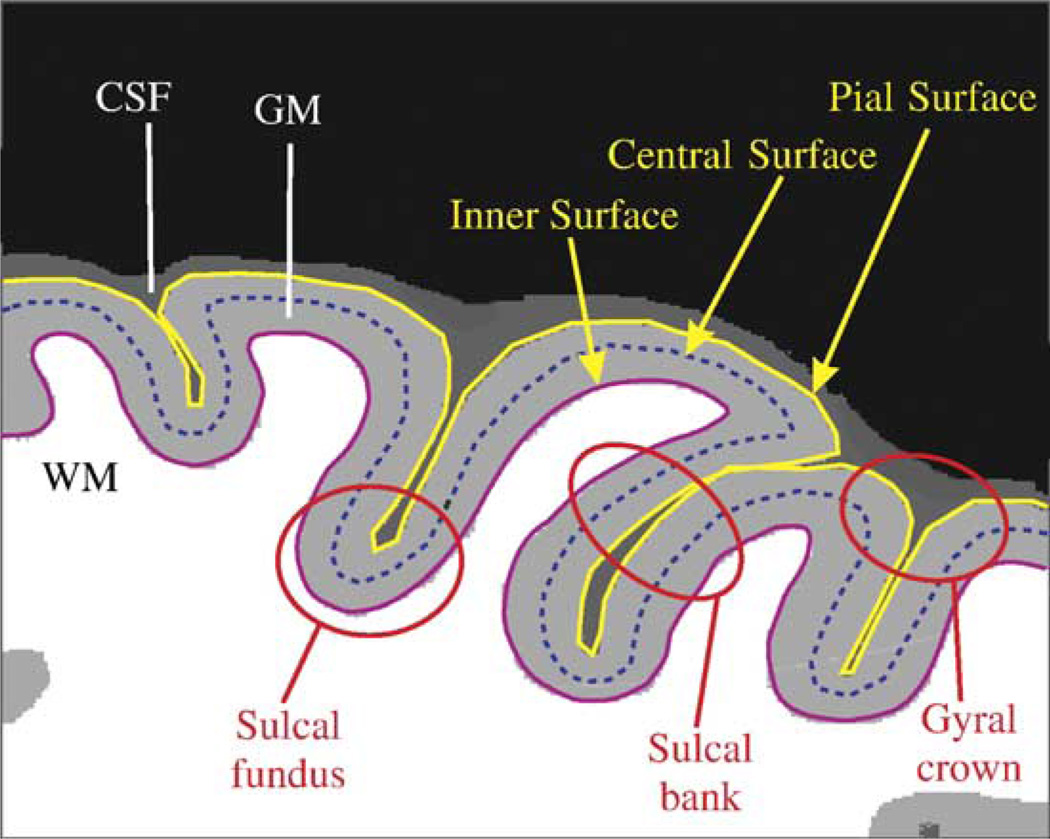
The cerebral cortex is a thin, folded sheet of gray matter (GM). As illustrated in Fig. 1, the cortical GM is bounded by the cerebrospinal fluid (CSF) on the outside, and by the white matter (WM) on the inside. The boundary between GM and WM forms the inner surface, and the boundary between GM and CSF forms the pial surface. It is useful to define the central surface as well; it lies at the geometric center between the inner and pial surfaces, representing an overall 2-D approximation to the three dimensional (3-D) cortical sheet. Many approaches have been proposed in the literature for the reconstruction of these surfaces from MR brain images (Mangin et al., 1995; Teo et al., 1997; Davatzikos and Bryan, 1996; Sandor and Leahy, 1997; Joshi et al., 1999; Dale et al., 1999; Zeng et al., 1999; Xu et al., 1999; MacDonald et al., 2000; Kriegeskorte and Goebel, 2001; Shattuck and Leahy, 2002). These approaches mostly differ in their ability to capture the convoluted cortical geometry, reconstruction accuracy, and robustness against imaging artifacts. We have developed a 3-D reconstruction method, called Cortical Reconstruction Using Implicit Surface Evolution (CRUISE), for automatic reconstruction of these three nested cortical surfaces from T1-weighted volumetric axially acquired MR brain images (Han et al., 2001b, 2004).

Fig. 1.

A cartoon drawing illustrating the definition of the three nested cortical surfaces—”inner”, “central”, and “pial”—and the definition of the three cortical geometries—”sulcal fundus”, “sulcal bank”, and “gyral crown”.

This paper presents two different studies – a repeatability analysis and a landmark accuracy study – characterizing the precision and accuracy of CRUISE algorithms. The goal of these studies is to evaluate the performance of CRUISE (in accuracy and precision) and to suggest optimal parameters for CRUISE algorithms. We note that a preliminary version of this work has appeared as a conference paper (Tosun et al., 2004a). The organization of this paper is as follows. CRUISE: cortical reconstruction using implicit surface evolution briefly describes the CRUISE algorithms and the relation between its parameters and the location of the reconstructed surfaces. The precision and accuracy analysis is described in Repeatability analysis and Landmark accuracy study on inner and pial surfaces, respectively. Based on the results reported in Landmark accuracy study on inner and pial surfaces, Parameter adjustment and evaluation describes an approach to adjust the parameters used in CRUISE algorithms. The paper is summarized and suggestions for future work are given in Discussion and future work.

CRUISE: cortical reconstruction using implicit surface evolution

The general approach we use to find cortical surfaces from MR image data is described in Xu et al. (1999). As described in Han et al. (2001a,b, 2002, 2003), several improvements to this initial approach have been made over the past several years. CRUISE is the current embodiment of this basic approach together with the improvements, and is described in Han et al. (2004). CRUISE is a data-driven method combining a robust fuzzy segmentation method, an efficient topology correction algorithm, and a geometric deformable surface model. The algorithm has been targeted toward and evaluated on the Baltimore Longitudinal Study of Aging MR imaging studies (Resnick et al., 2000). A given data set comprises a volumetric SPGR series (Wang and Rieder, 1990) acquired axially on a GE Signa 1.5 T scanner with the following parameters: TE = 5, TR = 35, FOV = 24, flip angle = 45°, slice thickness = 1.5, gap = 0, matrix = 256 × 256, NEX = 1. Thus, the native voxel size is 0.9375 mm × 0.9375 mm × 1.5 mm. We now briefly describe CRUISE, the algorithm whose performance is evaluated in subsequent sections of this paper.

The first processing step in CRUISE is to re-slice the image volume to horizontal cross-sections parallel to the plane passing through the anterior and posterior commissures, followed by the skull-stripping process to remove the cerebellum, extracranial tissue, and brain stem (at the level of the diencephalon) as described in (Talairach and Tournoux, 1988; Goldszal et al., 1998). In particular, removal of extracranial tissue was accomplished by a sequential application of morphological operators, thresholding, seeding, region growing, and manual editing, as follows. First, the brain tissue was detached from the surrounding dura by a 3-D morphological erosion operator with a spherical structuring element of radius 2 mm. Then, a 3-D seeded region growing extracted the brain tissue. The tissue lost in the erosion step was recaptured by a 3-D morphological dilation operator with a spherical structuring element of radius 4 mm. Since the CSF/dura interface is difficult to determine reliably with the SPGR pulse sequence, a limitation of these automated steps is that an undetermined amount of sulcal CSF is typically removed. In addition, some manual editing was necessary to extract the sagittal sinus anteriorly and posteriorly, to eliminate extracranial tissues mesial to the temporal lobes, to remove portions of the dura posteriorly, and to edit out the cerebellum and brainstem. These steps required some manual interaction including identification of the anterior and posterior commissures. The remaining image volume is then resampled to obtain isotropic voxels each having size 0.9375 mm × 0.9375 mm × 0.9375 mm using cubic B-spline interpolation in order to simplify numerical implementation, make subsequent processing less sensitive to orientation, and avoid computational errors due to non-isotropic voxels.

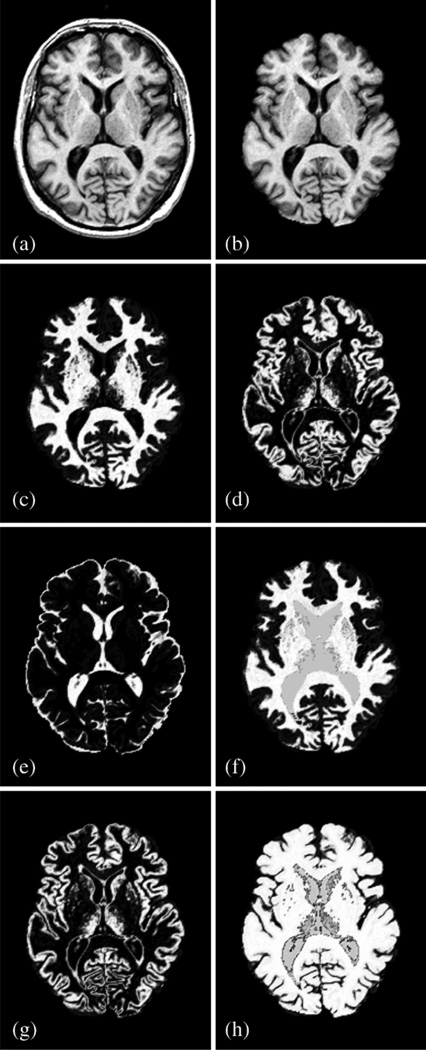
The next step in processing this “skull-stripped” MR image volume is to apply a fuzzy segmentation algorithm (Pham and Prince, 1999; Pham, 2001), yielding three membership function image volumes representing the fractions of WM, GM, and CSF within each image voxel, denoted by µ_WM, µ_GM, and µ_CSF, while compensating for intensity inhomogeneity artifacts inherent in MR images, and smoothing noise. A sample axial cross-section from a T1-weighted MR image volume and a skull-stripped MR image volume are shown in Figs. 2a–b, and cross-sections of the computed membership functions are shown in Figs. 2c–e.

Fig. 2.

Cross-sectional view of (a) T1-weighted MR image volume; (b) skull-stripped MR image volume; (c) WM membership µ_WM; (d) GM membership µ_GM; (e) CSF membership µ_CSF; (f) AutoFill-edited WM membership μ̂_WM; (g) ACE-edited GM membership μ̂_GM; (h) sum of AutoFill-edited WM membership and ACE-edited GM membership μ̂_WM + μ̂_GM.

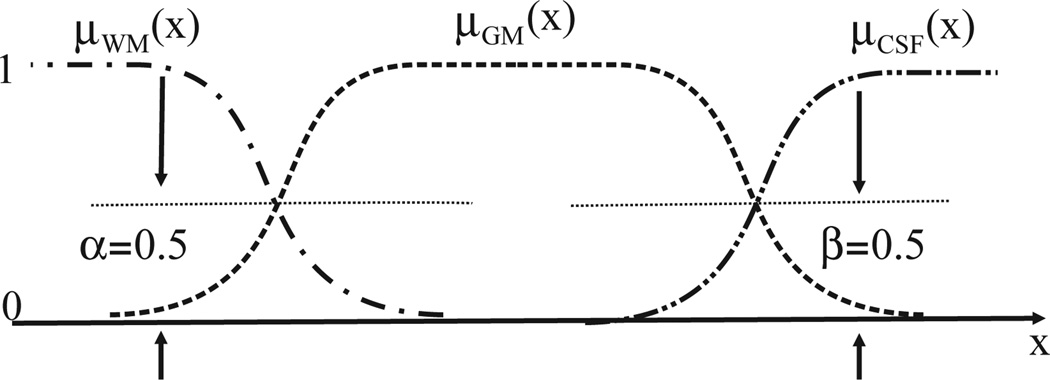
Fig. 3 illustrates idealized, one-dimensional (1-D) profiles of the membership functions, µ_WM, µ_GM, and µ_CSF, along a line passing through cortical gray matter. From left to right, these profiles indicate the presence of first white matter, then gray matter, then cerebrospinal fluid. Here, α is a threshold that is used to locate the interface defined between WM and GM tissues. Ideally, GM/ WM interface voxels contain both WM and GM, and the voxels inside the GM/WM interface have larger WM fraction than GM fraction. Therefore, an isosurface of the WM membership function at an isolevel α = 0.5 provides a good approximation to the GM/ WM interface. It is apparent from Fig. 2c, however, that such an isosurface will include non-cortical surfaces such as the subcortical interfaces near the brainstem and within the ventricles.

Fig. 3.

One-dimensional (1-D) profiles of WM, GM and CSF membership functions.

To prevent undesirable parts of the WM membership isosurface from being generated, an automatic method called AutoFill (Han et al., 2001a) is used to edit µ_WM in order to fill the concavities corresponding to the ventricles and the subcortical GM structures such as the putamen and caudate nucleus with white matter. The AutoFill-edited white matter membership is denoted by μ̂_WM, an example of which is shown in Fig. 2f The largest triangle mesh surface of the α = 0.5 isosurface of μ̂_WM is a close approximation to the GM/WM interface within each cortical hemisphere, and it connects the two hemispheres across the corpus callosum at the top and through the brainstem at the bottom. A graph-based topology correction algorithm (GTCA) (Han et al., 2002) followed by a topology-preserving geometric deformable surface model (TGDM) (Han et al., 2003) is used to estimate a topologically correct and slightly smoothed “inner surface” on the GM/WM interface, as shown in Figs. 4a and 4d. The smooth, artificial surface on the bottom of the brain is caused by AutoFill editing.

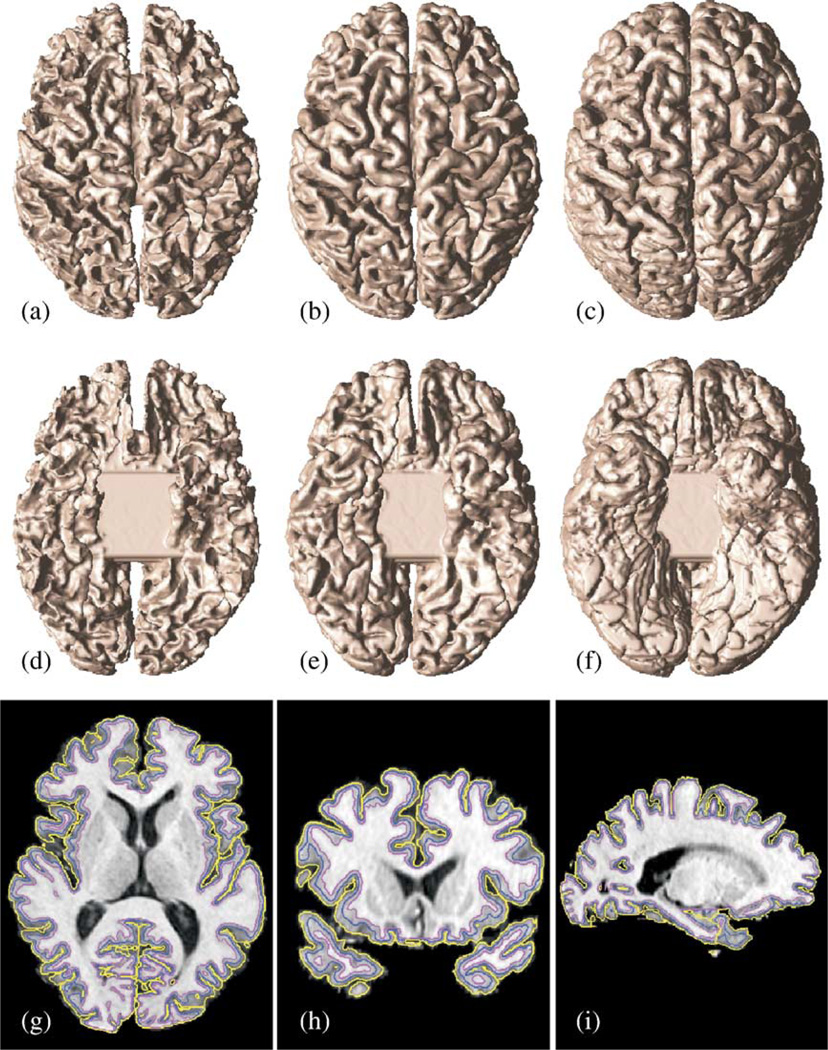
Fig. 4.

Topologically correct cortical surfaces of a sample brain: (a) inner surface top view; (b) central surface top view; (c) pial surface top view; (d) inner surface bottom view; (e) central surface bottom view; (f) pial surface bottom view. Estimated surfaces displayed as contours superposed on the skull-stripped MR image (g) axial, (h) coronal, and (i) sagittal cross-sections. (inner: magenta, central: blue, and pial: yellow.)

The inner surface serves as an initial surface for finding both the central surface that lies at the geometric center of the GM tissue and the pial surface that lies at the GM/CSF tissue interface. These surfaces are difficult to find due to the effect of partial volume averaging, which makes adjacent GM banks within narrow sulci barely distinguishable. In particular, within each sulcal fold, two GM banks separated by CSF should be clearly defined; but evidence of CSF is often missing in tight sulci. To compensate for this effect, CRUISE uses anatomically consistent enhancement (ACE) (Xu et al., 2000; Han et al., 2001b), which automatically edits the gray matter membership function, creating thin (artificial) CSF separations within sulci. An ACE-edited gray matter membership function, denoted by μ̂_GM, is shown in Fig. 2g. This image shows sulcal CSF where the original GM membership function (Fig. 2d) does not.

The ACE-edited GM membership function is used in two ways to find the central and pial surfaces. First, a generalized gradient vector flow (GGVF) external force (Xu et al., 1999) is computed directly from μ̂_GM, as if it were an edge map itself. A TGDM deformable surface is then initialized at the inner surface and is driven toward the central surface using the GGVF forces. This yields a central surface, as shown in Figs. 4b and 4e. To find the pial surface, it is observed that the β = 0.5 isosurface of μ̂_WM + μ̂_GM (shown in Fig. 2h) is a very good approximation to the pial surface. Accordingly, a region-based TGDM deformable surface model (Han et al., 2001b) is used to drive the central surface toward the β = 0.5 isosurface of μ̂_WM + μ̂_GM, yielding an estimate of the pial surface, as shown in Figs. 4c and 4f.

Connectivity consistent marching cubes (CCMC) algorithm described in (Han et al., 2003) is used to compute the isosurfaces from the results of each deformable model. When surfaces are computed using geometric deformable models such as TGDM, they contain no self-intersections. Also, in the TGDM deformable surface models described above, an extra constraint is used to ensure that the central surface is outside the inner surface and the pial surface is outside the central surface. Thus, the three cortical surfaces shown in Figs. 4a – f contain no self intersections, and they are properly nested with no mutual intersections. Figs. 4g – i show the contours of these nested cortical surfaces superposed on skullstripped MR image cross-sections. Visual inspection reveals excellent fidelity of both the inner and central surfaces, with occasional large errors on the pial surface. It is the goal of the present paper to give quantitative measures to the accuracy and precision of CRUISE on reconstructing these three nested surfaces.

Repeatability analysis

The first study is focused on the robustness of CRUISE against imaging noise and artifacts to assess the precision on reconstructing the nested surfaces. This is accomplished by conducting a repeatability study using three subjects each scanned twice within a short time interval during which the subject was repositioned in the scanner. Ideally, our surfaces should be reproduced with high precision in successive scans of the same subject’s brain. For longitudinal analysis, repeatability is a critical feature of a cortical reconstruction algorithm, since detection of subtle changes is the main objective. The goal of the repeatability analysis is to measure the differences in surface reconstruction from repeated scans of the same subject, and to identify the regions where large differences are observed. A preliminary repeatability analysis was reported in Han et al. (2004); the present paper provides a complete description of the analysis and provides additional results.

Surface masking

CRUISE was applied to each of the six MR image data sets (the original and repeat scan MR images of the three individual subjects) to generate six sets of nested cortical surfaces. Surfaces reconstructed from the MR image data sets are represented by triangle meshes comprising approximately 300,000 vertices each. Our aim is to measure how well CRUISE can reproduce the cortical geometry despite changes in patient position and the introduction of different MR noise and artifacts in the repeat scan. Therefore, surface elements that do not correspond to cortex are ignored in the analysis.

Surface elements that do not belong to cortex reside on the artificial surface created by AutoFill joining the hemispheres below the corpus callosum (see Figs. 2c and 2f and Figs. 4d – f). Accordingly, we formed a mask for each MR image data set marking the regions that were modified by AutoFill. The modified regions were identified automatically by subtracting the original WM membership function µ_WM from the AutoFill-edited WM membership function μ̂_WM. A binarized version of this difference volume was then used to identify the triangle mesh vertices not corresponding to cortical geometry. Vertices so identified are excluded from the entire analysis given below, from 3-D surface alignment to distance analysis, including all statistical performance analysis.

3-D surface alignment

We are interested in shape differences between the two repeat scans; a rigid body difference should not matter. Therefore, the repeat scan surface W is first aligned with the original surface V in order to remove a shift or rotation that inevitably took place between the two scans. Although a 3-D volumetric registration approach could be used to align the original and repeat scan volumetric MR image data sets, since our primary objective is to measure differences between the surfaces, a 3-D surface registration approach is used instead to avoid possible surface differences due to the volume registration errors. Specifically, we use a global 3-D rigid body surface-based registration algorithm based on iterative closest point algorithm (ICP) (Besl and McKay, 1992). At each iteration, ICP first finds the closest point correspondences between the point sets, and then finds a rigid body transformation of one point set in order to minimize the average distance of the corresponding points. These steps are repeated until convergence. The reason that we applied ICP to directly align the surfaces instead of using a volume registration method is because here we are interested in comparing the shapes of the estimated cortical surfaces. Directly aligning the surfaces removes the possibility that errors we report would be, in part, due to errors in volume registration. ICP is an iterative method for aligning two point sets.

The surfaces V and W are represented by vertices – ${\left\{v_i\right\}}_{\mathrm{i}=1}^N$ in V and ${\left\{w_j\right\}}_{j=1}^M$ in W – connected by triangular surface elements. Ordinarily, ICP ignores the fact that V and W are surfaces when creating correspondences. Instead, it finds a mapping ℐ(i) that gives the point w_ℐ(i)∈W corresponding to the closest vertex v_i ∈ V. Accordingly, the pair [v_i, w_ℐ(i)] forms a correspondence pair, and ICP finds the rigid body transformation ℛ(·) of points in W that minimizes the average distance between correspondences, given by

$$f(ℛ;V,W)=\frac{1}{N}\sum _{i=1}^N\Vert v_i-ℛ(w_{ℐ(i)})\Vert ,$$ (1)

where ‖·‖ gives the length of a vector.

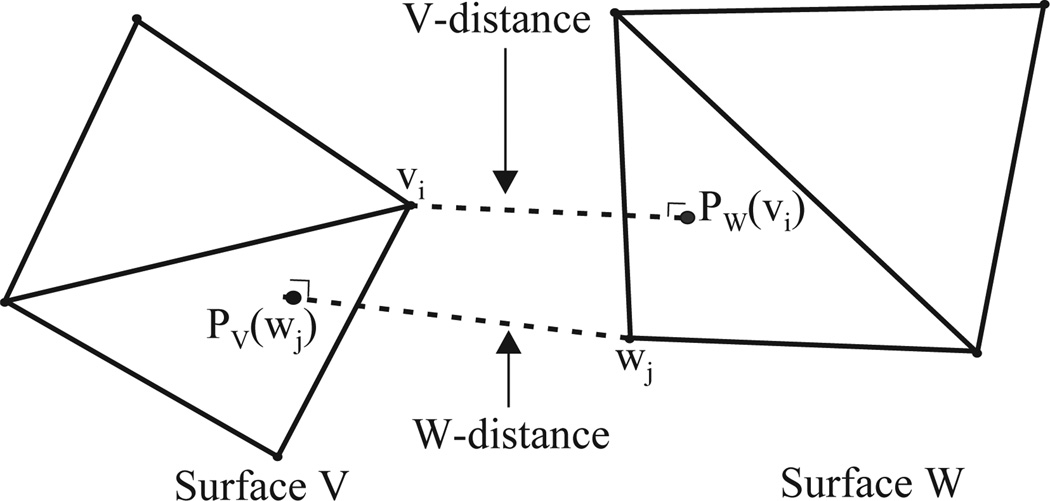
Our modification to ICP acknowledges the fact that V and W are triangulated surfaces rather than simple point sets. This means that the closest point to v_i ∈ V on W may not be a vertex, but may instead be a point on a triangular element defined by the vertices in W. This situation is illustrated in Fig. 5. In our modification to ICP, correspondence pairs are identified by projection operators. In particular, we identify the closest point to v_i ∈ V on the surface W by the projection 𝒫_W(v_i), where 𝒫_W(·) is the projection (onto W) operator. Similarly, the closest point to w_j ∈ W on the surface V is given by 𝒫_V(w_j), where 𝒫_V(·) is the projection (onto V) operator. This identification yields the correspondence pairs [v_i, 𝒫_W(v_i)], i = 1, …,N and [w_j, 𝒫_V(w_j)], j = 1, …, M. In order to reduce possible directional bias, we define the modified ICP objective function in a bilateral fashion, as follows

$$f(ℛ;V,W)=\frac{1}{N+M}\times (\sum _{i=1}^N\Vert v_i-{𝒫}_{ℛ(W)}(v_i)\Vert +\sum _{j=1}^M\Vert ℛ(w_j)-{𝒫}_V(ℛ(w_j))\Vert ).$$ (2)

Fig. 5.

Illustration of the ICP “correspondence pairs”, and the distance measures.

The fact that W is being moved under a rigid body transformation is reflected in this expression by the use of the rigid body transformation operator ℛ(·)

One additional aspect should be clarified. Each cortical segmentation produces three cortical surfaces - inner, central, and pial - and all three should be aligned before computing shape differences. It is possible to align each surface separately using modified ICP; but we elected to align them all together in one larger modified ICP algorithm. To achieve this, it is necessary to modify the projection operators so that they yield points on corresponding surfaces. For example, if v_j represents an inner vertex, the projection 𝒫_W(v_j) yields a point on the inner surface of the model W. We have modified ICP for this nested surface approach.

Distance measures

After the nested surface model W has been transformed into alignment with V, we are in position to quantify the distance between the two surfaces. One good measure of this distance is the modified ICP objective function, Eq. (2). We use Eq. (2) as a measure of absolute distance (AD) between two surfaces V and ℛ(W), where W is aligned with a (optimal, after ICP) rigid body transformation ℛ.

To provide a thorough analysis on the absolute distance measure, two distance measures defined from one surface to the other are used. The first distance function “W -distance” is defined on the mesh nodes ${\{ℛ(w_j)\}}_{j=1}^M$ of the surface ℛ(W), as the norm of the difference vector between correspondence pair [ℛ(w_j), 𝒫_V(ℛ(w_j)), j = 1,…,M. In an analogous fashion, the second distance function “V-distance” is defined on the mesh nodes ${\left\{v_i\right\}}_{i=1}^N$ of the surface V, as the norm of the difference vector between correspondence pair [v_j, 𝒫_ℛ(W)(v_i)], i = 1,…,N. W-distance and V-distance measures are illustrated in Fig. 5.

W-distance and V-distance measures are small when the surfaces are very similar and grow larger as the surfaces become dissimilar. Differences in the smoothness of the two surfaces could conceivably make W-distance and V-distance measures substantially different (although we do not expect this in a repeatability analysis, where the CRUISE algorithm uses the same parameters in each trial). It is useful to identify a signed distance (SD)—for example, to see whether one surface is always inside the other. To provide a signed distance, the inner product of the difference vector with the outward normal vector of the surface on which the distance measure is defined is computed. If the inner product is positive, then the signed distance is positive, and if the inner product is negative, then the signed distance is negative.

Results

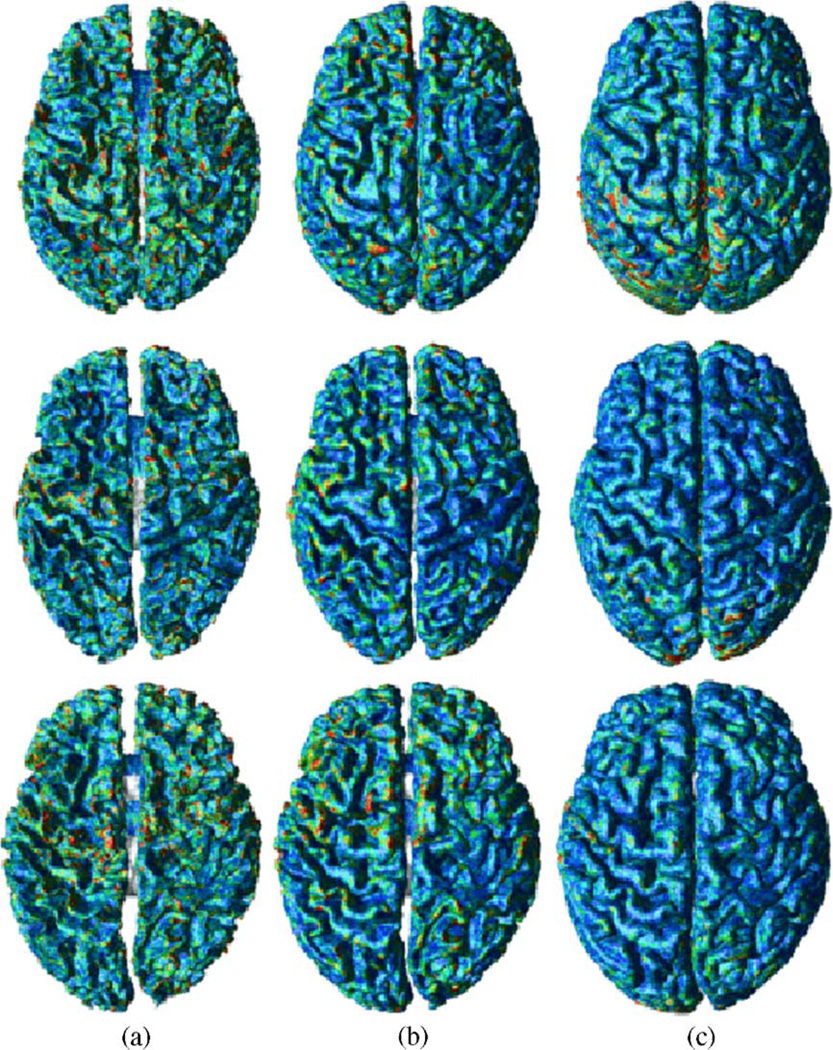
In Table 1, statistics of the combined distance measure (incorporating both W-distance and V-distance) are reported, and W-distance measures on the nested cortical surfaces of the three subjects are displayed in Fig. 6. No specific pattern was observed on any of the nested surfaces of the three individual subjects analyzed in this study.

Table 1.

Repeatability analysis: Statistics of the combined distance measure incorporating both W-distance and V-distance (in mm)

V	W	Surface	Signed distance (SD)		Absolute Distance (AD)
			Mean	stdev	Mean	stdev	>1 mm	>2 mm
A1	A2	Inner	0.05	0.45	0.33	0.32	3.7%	0.3%
B1	B2	Inner	0.03	0.39	0.27	0.28	2.2%	0.3%
C1	C2	Inner	0.05	0.46	0.32	0.34	3.9%	0.5%
All Inner Points			0.04	0.43	0.31	0.32	3.3%	0.4%
A1	A2	Pial	−0.06	0.42	0.30	0.31	3.4%	0.3%
B1	B2	Pial	−0.08	0.38	0.26	0.30	2.8%	0.4%
C1	C2	Pial	−0.06	0.37	0.25	0.28	2.4%	0.3%
All Pial Points			−0.07	0.39	0.27	0.30	2.8%	0.4%
A1	A2	Central	0.01	0.37	0.26	0.27	2.1%	0.2%
B1	B2	Central	0.00	0.34	0.23	0.26	1.7%	0.2%
C1	C2	Central	0.01	0.39	0.26	0.29	2.5%	0.3%
All Central Points			0.01	0.37	0.25	0.27	2.1%	0.3%

A, B, C: different subjects.

Fig. 6.

W-distance measure (in mm) on (a) inner, (b) central, and (c) pial surfaces of the three subjects. (Surface points masked out (see Surface masking) are colored in white, all distances above 1 mm are colored in red, and the distance in the range [0 mm–1 mm] are colored by a colormap linearly from dark blue to red.)

Overall, the mean signed distances for any surface are just a few hundredths of a mm. This indicates that the corresponding surfaces are well aligned and there are no gross geometric errors between the two scans. The overall mean absolute distances are in the range 0.23 – 0.33 mm, which is slightly less than one third of a voxel size. We conclude that CRUISE has sub-voxel precision on locating the nested cortical surfaces. Smaller means and standard deviations are observed on the central surface compared with those for the inner and pial surfaces. This adds strength to the claim that the central surface can be found in a more robust fashion (Xu et al., 1999).

Although the average and the standard deviations are reasonably small, there are regions where the aligned surfaces are separated by large distances. Table 1 indicates the percentage of analyzed surface (ignores “AutoFill-edited WM points”) where the absolute distance is larger than 1.0 and 2.0 mm. This is between 1.7 and 3.7% of the surface where AD > 1.0 mm and 0.2–0.5% of the surface where AD > 2.0 mm, which is small, but of concern in longitudinal analysis where the sought changes might be in the neighborhood of these small percentages. We analyzed many of these regions manually, and found that large separations can occur because of differences in skull-stripping, AutoFill editing, topology correction, and ACE editing. Skull stripping is particularly problematic because user interaction can erroneously remove GM or leave dura, which can affect the positioning of all three surfaces, particularly the central and pial surfaces. The remaining sources of errors are noise spikes present in one data set but not the other and subtle differences in partial volume averaging due to the slight positioning differences between the two scans. ACE-related differences are only present on the central and pial surfaces.

Landmark accuracy study on inner and pial surfaces

Accurate representation of the cerebral cortex is crucial in characterization and analysis of the geometry of the cortex. In this section, we evaluate the reconstruction accuracy of CRUISE in addition to its robustness against imaging artifacts. A landmark accuracy study on the central surface using a set of 50 manually selected central surface landmarks – 5 on each hemisphere of 5 brains – was reported in our previous work (Han et al., 2004; Xu et al., 1999). The distance from each landmark to the central surface estimated by our algorithm served as a measure of accuracy. Overall, the mean landmark error was 0.51 mm with a standard deviation of 0.41 mm, illustrating subvoxel accuracy in our reconstruction of the central surface (see Han et al., 2004).

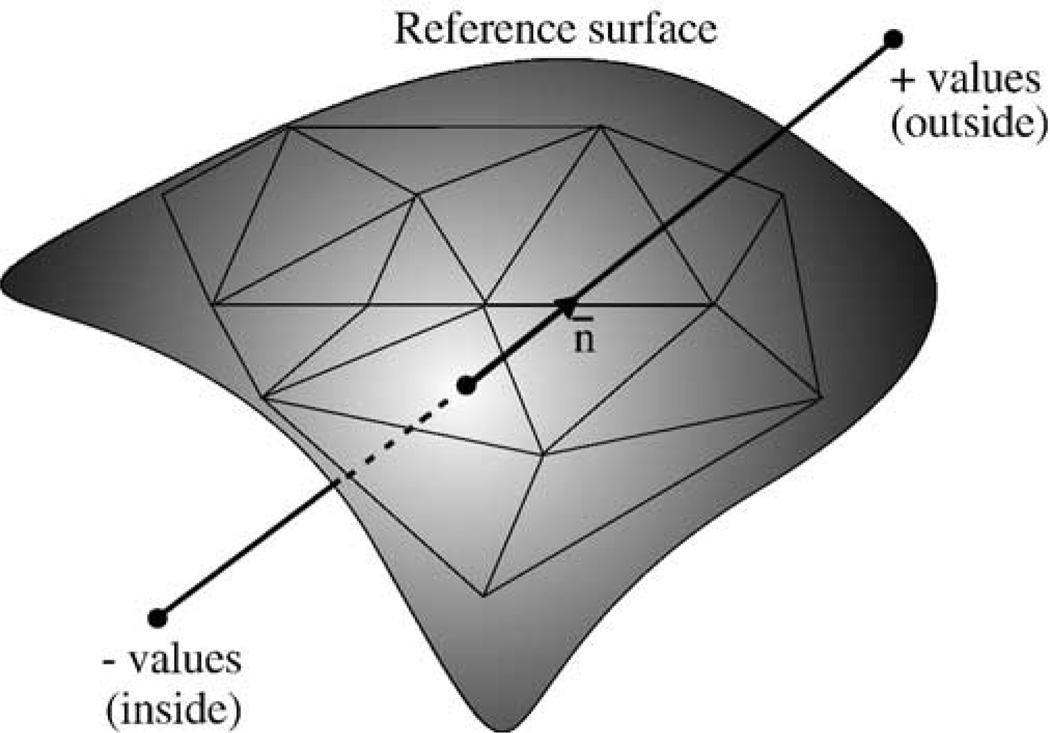
The focus of the landmark accuracy study presented in this paper is to quantify the accuracy of the inner and pial surfaces estimated by the CRUISE algorithm. In addition, we assess how the accuracy varies both across the surface as well as within different cortical geometries. Twelve raters¹ participated in this study. Each rater identified a series of landmarks at the GM/WM and GM/CSF tissue interfaces on the skull-stripped MR brain image volumes. The landmarks effectively yield a rater implied surface at the corresponding cortical layer. Throughout this study, we refer to these surfaces as the implied surfaces and the estimated (inner and pial) surfaces generated by CRUISE as the reference surfaces. To quantify the level of agreement between the reference and implied surfaces, we define a landmark offset measure as the signed minimum distance from a given landmark to the corresponding reference surface, using negative and positive values to indicate the landmark point being inside or outside the reference surface, respectively. Fig. 7 illustrates the landmark offset from a given landmark to the reference surface. These measures will be used to quantify the accuracy of the estimated inner and pial surfaces and to infer any systematic bias of CRUISE in either the inward or outward directions.

Fig. 7.

Illustration of the “landmark offset”.

The CRUISE reference surfaces are defined primarily by the 0.5 isolevels of the μ̂_WM and μ̂_GM + μ̂_WM functions as described in CRUISE: cortical reconstruction using implicit surface evolution. Thus, in addition to the landmark offset measurement, the values of surface defining membership function at the landmarks (μ̂_WM for the inner surface, and μ̂_WM + μ̂_GM for the pial surface) could provide insight into a systematic bias of the CRUISE estimated surfaces. For example, if the membership values at the landmarks were consistently higher than 0.5 for both inner and pial surfaces, this would indicate an outward bias of the CRUISE estimated surfaces. This is made clear by referring back to Fig. 3. Consider the isosurfaces that would be generated at higher μ̂_WM and µ_GM + μ̂_WM isolevel values—i.e., α > 0.5 and β > 0.5 respectively. The isosurfaces estimated at these isolevels would give an inner surface and a pial surface inside the surfaces estimated at α = 0.5 and β = 0.5 indicating an outward bias of the CRUISE estimated surfaces. We are particularly interested in these measures because α and β are easily changed to improve the performance of CRUISE.

The landmark accuracy study consisted of three steps. First, we conducted an analysis of both the landmark offsets and the membership function values at the landmarks. This analysis quantifies the accuracy of the CRUISE estimated surfaces as well as any systematic bias. In the second step, we selected new threshold values of α and β according to the observed landmark offset and membership function values. These values were selected so that they best fit the raters’ data from step one. In the third step, we repeated the landmark accuracy study with the new thresholds. The following is a complete description of the landmark picking procedure, the analysis, and the results.

Interactive program for landmark picking

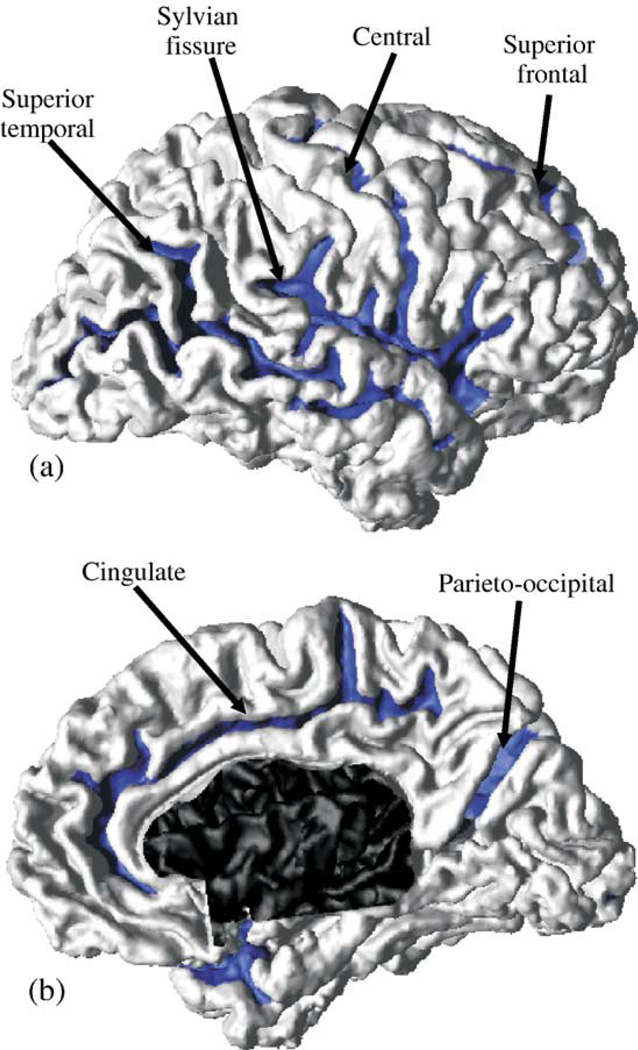
Our initial landmark accuracy study on the central surface (Han et al., 2004; Xu et al., 1999) included only one rater who picked a single landmark in each region-of-interest at integer number coordinates. Since the landmarks were manually picked, there is always uncertainty about the validity of the result as the level of measured errors approaches the inherent variability of the rater. To minimize this uncertainty, we designed a new landmark accuracy study for the inner and pial surfaces with an extended number of landmarks and raters, using two different MR brain image volumes. Landmarks are located on the GM/WM and GM/CSF interfaces in six cortical regions where each region is defined by a cortical sulcus. These include the sylvian fissure (SYLV), superior frontal (SF), superior temporal (ST), cingulate (CING), and parieto-occipital (PO) sulci of each cortical hemisphere, and the central (CS) sulcus of the left hemisphere. These sulcal regions are colored on the right hemisphere of one cortical surface in Fig. 8. Within each region, landmarks are defined on the three cortical geometries—”sulcal fundus”, “sulcal bank”, and “gyral crown”. Sulcal fundus points lie along the bottom of a cortical fold, sulcal bank points lie along the sides of a fold, and gyral crown points lie along the top of a fold, as illustrated in Fig. 1.

Fig. 8.

The location of the sulcal regions labeled on (a) the lateral surface and (b) the medial surface of one cortical surface.

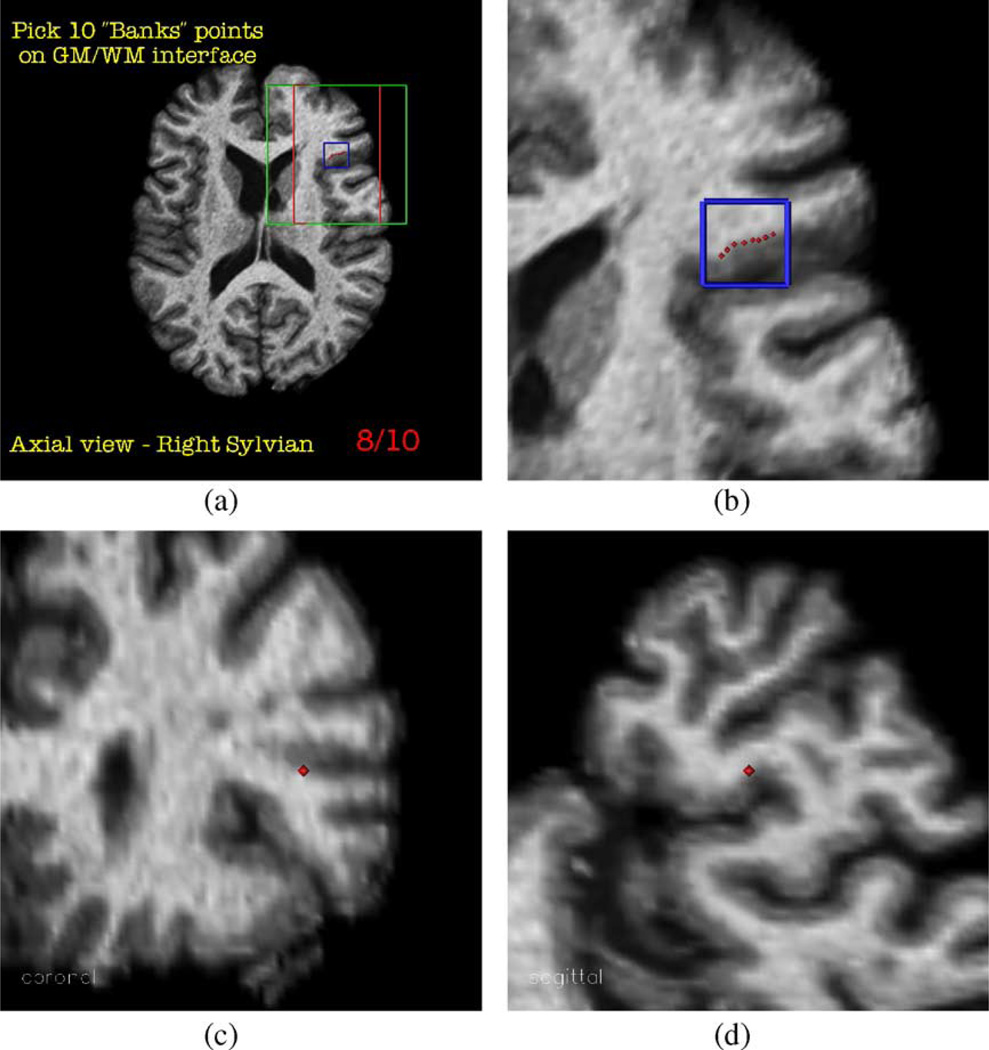
A visualization program was written using Open Visualization Data Explorer 4.2.0, IBM Visualization Software to pick landmarks inside a region-of-interest box on the pre-selected axial cross-sections of the raw MR image volume. We chose to pick landmarks by viewing axial cross-sections, the orientation on which the MR images were acquired. A total of 66 axial cross-sections were pre-selected, each corresponding to one of the eleven sulcal regions, one of the three cortical geometries, and one of the tissue interfaces. The purpose of the visualization program is to provide a standard way of picking the landmarks so that a statistical analysis approach could be used to compare the data of different raters. The interface had two primary displays. The first display, shown in Fig. 9(a), provided the information required to pick the landmarks on that axial cross-section. This included information on which tissue interface the landmarks should be selected, the number of landmarks to select, and the cortical geometry type. In addition, a counter was incremented after each landmark selection indicating the number of picks remaining. A blue box outlined a 10 voxel × 10 voxel region in which the rater was required to pick the landmarks. In the second primary display, shown in Fig. 9(b), an enlarged view around the 10 voxel × 10 voxel outlined by the blue box from the first display was shown. The interface allowed the rater to adjust several parameters including the center and size of the enlarged view in the second display as well as the colormap scaling to improve the contrast between different cortical tissues. The rater was able to select between two possible colormaps—linear or logarithmic. In the linear map, each colormap level corresponds to a constant intensity range in the image. The second colormap utilizes logarithmic scaling providing more contrast at low intensities. Each landmark was selected in this second primary display with a right mouse click and the selected point was marked in red in all displays. In order to get a sense of the location of the point in 3-D, the two orthogonal cross-sections through this point were also displayed, as shown in Figs. 9c – d. The landmark was automatically recorded as the physical position of the selected point with floating number coordinates and landmarks identified by a given rater were forced to be at least 0.50 mm apart from each other. The rater also had the flexibility of removing any of the previously recorded landmarks. All raters were asked to use the same linux workstation with fixed monitor settings, but encouraged to vary the brightness and contrast colormap table as desired. This encouraged raters to concentrate on picking landmarks on the desired tissue interface, and not simply to pick intensity edges that they might observe on a static display with fixed lighting conditions.

Fig. 9.

Interactive program for landmark picking: (a) an example axial cross-section, (b) enlarged view around designated region for landmark picking, and (c–d) orthogonal cross-sections through the last selected point.

Data

Twelve raters participated in the landmark accuracy study and the study was carried out using two different MR image volumes. First six raters picked landmarks on both image volumes and the remaining raters picked landmarks on only the first image volume. Ten landmarks were picked on each of 66 pre-selected axial cross-sections. Each rater picked a total of 330 landmarks equally distributed across the different sulcal regions and different geometry groups on each cortical tissue interface. It took approximately 1 h and 30 min per brain to pick the landmarks, with a substantial portion of this time required for adjusting the parameters of the colormap scaling function for the best contrast.

Two measures were computed in this study—landmark offset and surface defining membership function value (SDMFV). The SDMFV at each landmark point is defined as the value of the AutoFill-edited WM membership function, μ̂_WM, for the inner surface and the sum of the ACE-edited GM and AutoFill-edited WM membership functions, μ̂_GM + μ̂_WM, for the pial surface. To measure the landmark offset, first the minimum absolute distance (AD) from landmark point to the corresponding reference surface is computed, and then the absolute distance measurement is signed according to the sign convention illustrated in Fig. 7, which gives the signed distance (SD) from the landmark point to the corresponding reference surface.

The landmark offset measure calculation requires finding the closest point on the reference surface to the landmark point. Since each landmark point is categorized by the sulcal region in which it is picked, we restricted the distance calculation in the sulcal region of interest. To identify the reference surface points in the sulcal regions analyzed in this study, we utilized the sulcal segmentation method described in Rettmann et al. (2002), and the assisted sulcal labeling program described in Rettmann et al. (2005). Presumably the 10 voxel × 10 voxel box provided to the rater in each preselected axial cross-section includes only points within a given sulcal region, however, due to the highly convoluted nature of the cortex in 3-D, the landmark point and its corresponding closest point might not be in the same sulcal region. For less than 2.0% of the landmark points, the closest point on the corresponding reference surface had a non-matching sulcal label. reference surface either had a non-sulcal region label or had a different sulcal region label than the given landmark point’s. These landmark points were excluded from the entire analysis presented below.

Data analysis

We first tested the effects of variable intensity inhomogeneity and colormap scaling by comparing the algorithm versus rater across the two different subjects, the three different cortical geometries (sulcal fundus, sulcal bank, and gyral crown), and eleven different sulcal regions. In this study, we analyzed the GM/ WM and GM/CSF interface data separately.

Statistical analyses were performed using R version 2.0.0 (The R Development Core Team, 2003). The effects of “rater”, “subject”, “sulcus”, and “geometry” on dependent SD and SDMFV measures were analyzed in a series of multivariate analyses of variance (MANOVA), with “subject”, “sulcus”, and “geometry” used as nested grouping factors and “rater” as a repeated factor. The first MANOVA focused on the effects of “rater”, “subject”, “sulcus”, and “geometry” on SD and SDMFV measures. Bartlett’s test showed statistically significant (1% level) evidence against the null hypothesis that the covariance matrices are homogeneous. Two-tailed hypotheses were tested using Pillai’s trace criteria since it is robust to violations of assumptions concerning homogeneity of the covariance matrix. MANOVA revealed a significant effect of “rater”, “sulcus”, and “geometry”, but “subject” failed to reach significance for both GM/WM and GM/CSF interface data. The threshold for significance was set at P < 0.01.

We conducted follow-up univariate analyses using Type III sums of squares to elucidate these effects. The second MANOVA focused on the effects of “rater”, “subject”, “sulcus”, and “geometry” on the dependent measures of raters 1–6. Results revealed no significant effect of “subject”, but group differences in “rater”, “sulcus”, and “geometry”. A third MANOVA focused on the effects of “rater”, “sulcus”, and “geometry” on the dependent measures of raters 7–12, and revealed significant group differences. Significant differences in the performance of the algorithm relative to rater across different aspects of the cortical geometry and across different sulcal regions may reflect variability in noise, intensity inhomogeneity, abnormalities in the original MR brain volume, and colormap scaling function for the different brain features. On the other hand, the absence of an effect for “subject” reflects the intra-rater consistency of picking landmarks in different MR images. A final MANOVA focused on the dependent SD and SDMFV measures of each rater separately and tested the effects of “sulcus”, “geometry”, and, if applicable, “subject”. The results revealed significant “sulcus” and “geometry” group differences, but not significant group difference of “subject” for both GM/WM and GM/CSF interface data of the raters 1, 2, and 3.

Landmark offset on the inner surface

The landmark offset statistics on the inner surface for different sulcal regions and different cortical geometries are shown in Table 2. The overall mean landmark offset is −0.34 mm with a standard deviation of 0.63 mm, which can be interpreted as about one third mm accuracy on the inner surface estimation. Only 15% of the landmarks are farther than 1.0 mm from the estimated inner surfaces, and about 1.0% of the landmarks are farther than 2.0 mm from the estimated inner surfaces, indicating that gross errors are not common.

Table 2.

Landmark offset Statistics on Inner Surface (mean ± stdev in mm)

	Subject I (12 raters)		Subject II (6 raters)		Both subjects (12 raters)
	SD	AD	SD	AD	SD	AD	>1	>2
Sulcus
LCS	−0.50 ± 0.57	0.59 ± 0.48	−0.82 ± 0.63	0.89 ± 0.54	−0.60 ± 0.61	0.69 ± 0.52	23%	2.4%
LSYLV	−0.04 ± 1.00	0.80 ± 0.63	−0.63 ± 0.63	0.68 ± 0.58	−0.24 ± 0.95	0.76 ± 0.62	28%	5.5%
LST	−0.19 ± 0.51	0.44 ± 0.33	−0.30 ± 0.63	0.56 ± 0.42	−0.23 ± 0.56	0.48 ± 0.36	8%	0.4%
LSF	−0.18 ± 0.49	0.41 ± 0.33	−0.27 ± 0.45	0.42 ± 0.31	−0.21 ± 0.48	0.41 ± 0.32	6%	0.0%
LCING	0.25 ± 0.67	0.54 ± 0.47	−0.23 ± 0.52	0.44 ± 0.35	0.10 ± 0.67	0.51 ± 0.44	13%	0.2%
LPO	−0.59 ± 0.55	0.62 ± 0.51	−0.50 ± 0.45	0.56 ± 0.37	−0.56 ± 0.52	0.60 ± 0.47	18%	1.7%
RSYLV	−0.40 ± 0.44	0.47 ± 0.36	−0.78 ± 0.53	0.85 ± 0.42	−0.52 ± 0.51	0.60 ± 0.42	20%	0.2%
RST	−0.42 ± 0.54	0.58 ± 0.37	−0.27 ± 0.63	0.53 ± 0.43	−0.37 ± 0.58	0.56 ± 0.39	16%	0.2%
RSF	−0.14 ± 0.43	0.36 ± 0.27	−0.48 ± 0.45	0.54 ± 0.38	−0.24 ± 0.46	0.41 ± 0.32	6%	0.0%
RCING	−0.35 ± 0.46	0.45 ± 0.37	−0.56 ± 0.61	0.63 ± 0.53	−0.42 ± 0.53	0.51 ± 0.44	12%	0.6%
RPO	−0.46 ± 0.67	0.63 ± 0.50	−0.27 ± 0.48	0.44 ± 0.33	−0.40 ± 0.62	0.57 ± 0.46	18%	0.9%
Geometry
Sulcal fundus	−0.53 ± 0.57	0.61 ± 0.49	−0.64 ± 0.51	0.68 ± 0.46	−0.57 ± 0.55	0.63 ± 0.48	21%	1.6%
Sulcal bank	−0.33 ± 0.51	0.49 ± 0.37	−0.38 ± 0.53	0.50 ± 0.43	−0.35 ± 0.52	0.49 ± 0.39	10%	0.6%
Gyral crown	0.04 ± 0.68	0.50 ± 0.46	−0.36 ± 0.67	0.60 ± 0.47	−0.09 ± 0.70	0.54 ± 0.47	15%	1.1%
All	−0.27 ± 0.64	0.53 ± 0.45	−0.47 ± 0.59	0.60 ± 0.46	0.34 ± 0.63	0.55 ± 0.45	15%	1.1%

In addition to variance on SD measure with cortical geometry and position, we looked at the correlation between SD measure and the inner cortical surface orientation relative to the normal direction of axial cross-sections. For each landmark point, the relative orientation of the inner cortical surface was quantified using the angle between the inner cortical surface patch around the closest surface point to that landmark point and the axial cross-section on which the landmark point was selected. The correlation coefficient between SD measures and the relative inner cortical surface orientation is −0.164. This statistically significant negative correlation (P <0.01) indicates that the accuracy is better when the local surface patch is perpendicular to the axial cross-section. This could indicate that raters are able to better localize interfaces that are perpendicular to the viewing plane. It is also possible that this is related to the underlying data resolution, which is poorest in (approximately) the direction orthogonal to our axial cross sections.

Landmark offset on the pial surface

The landmark offset statistics on the pial surface are also shown in Table 3. The overall mean landmark offset is −0.32 mm with a standard deviation of 0.49 mm, and only 8% of the landmarks are farther than 1.0 mm from the estimated pial surfaces. Smaller standard deviations of the pial surface landmark offsets compared with inner surface landmark offsets indicate a higher stability for the pial surface. The higher stability on the pial surface could be due to the ACE-processing in the CRUISE algorithm (see CRUISE: cortical reconstruction using implicit surface evolution). In ACE-processed regions, ACE is more dominant than the membership isolevel criterion in defining the surface location (Han et al., 2003). A smaller mean landmark offset and standard deviation is observed at the ACE-processed regions as compared with the mean landmark offset and standard deviation of the regions not processed by ACE (see Table 3). This suggests that the GM/CSF interface defined by ACE is more in accordance with the rater implied surfaces. A study similar to the one described in the previous section was carried out to assess the correlation between the SD measure and the relative orientation of the pial cortical surface but the estimated correlation coefficient (0.040) is not statistically significant.

Table 3.

Landmark offsets on Pial Surface (mean ± stdev in mm)

	Subject I (12 raters)		Subject II (6 raters)		Both subjects (12 raters)
	SD	AD	SD	AD	SD	AD	>1	>2
Sulcus
LCS	−0.35 ± 0.47	0.45 ± 0.38	−0.27 ± 0.50	0.47 ± 0.31	−0.33 ± 0.48	0.46 ± 0.35	6%	0.0%
LSYLV	−0.19 ± 0.48	0.39 ± 0.33	−0.26 ± 0.44	0.41 ± 0.31	−0.21 ± 0.47	0.40 ± 0.32	5%	0.0%
LST	−0.45 ± 0.51	0.54 ± 0.42	−0.39 ± 0.75	0.67 ± 0.51	−0.43 ± 0.60	0.58 ± 0.45	15%	1.3%
LSF	−0.32 ± 0.54	0.46 ± 0.43	−0.04 ± 0.57	0.43 ± 0.37	−0.23 ± 0.56	0.45 ± 0.41	8%	0.4%
LCING	−0.25 ± 0.34	0.33 ± 0.25	−0.34 ± 0.62	0.52 ± 0.48	−0.28 ± 0.45	0.39 ± 0.36	6%	0.2%
LPO	−0.41 ± 0.41	0.45 ± 0.38	−0.35 ± 0.47	0.47 ± 0.34	−0.39 ± 0.43	0.45 ± 0.37	8%	0.2%
RSYLV	−0.54 ± 0.42	0.56 ± 0.38	−0.34 ± 0.44	0.44 ± 0.34	−0.47 ± 0.43	0.52 ± 0.37	14%	0.0%
RST	−0.25 ± 0.46	0.42 ± 0.31	−0.31 ± 0.48	0.44 ± 0.36	−0.27 ± 0.47	0.43 ± 0.33	6%	0.0%
RSF	−0.25 ± 0.40	0.35 ± 0.32	−0.30 ± 0.48	0.45 ± 0.35	−0.27 ± 0.43	0.38 ± 0.33	5%	0.0%
RCING	−0.42 ± 0.51	0.48 ± 0.45	−0.26 ± 0.62	0.50 ± 0.44	−0.36 ± 0.56	0.49 ± 0.45	17%	0.0%
RPO	−0.39 ± 0.40	0.44 ± 0.33	−0.19 ± 0.53	0.45 ± 0.34	−0.32 ± 0.46	0.44 ± 0.34	6%	0.0%
Geometry
Sulcal fundus	−0.49 ± 0.47	0.53 ± 0.42	−0.48 ± 0.55	0.58 ± 0.45	−0.49 ± 0.50	0.55 ± 0.43	14%	0.4%
Sulcal bank	−0.37 ± 0.42	0.44 ± 0.35	−0.19 ± 0.47	0.40 ± 0.32	−0.31 ± 0.45	0.43 ± 0.34	6%	0.1%
Gyral crown	−0.18 ± 0.44	0.36 ± 0.32	−0.15 ± 0.56	0.45 ± 0.36	−0.17 ± 0.48	0.39 ± 0.33	5%	0.1%
nonACE	−0.47 ± 0.50	0.54 ± 0.43	−0.49 ± 0.51	0.57 ± 0.42	−0.48 ± 0.51	0.55 ± 0.43	14%	0.4%
ACE	−0.23 ± 0.38	0.35 ± 0.28	−0.01 ± 0.47	0.36 ± 0.30	−0.17 ± 0.42	0.35 ± 0.29	3%	0.0%
All	−0.35 ± 0.46	0.44 ± 0.37	−0.28 ± 0.55	0.48 ± 0.39	−0.32 ± 0.49	0.45 ± 0.38	8%	0.2%

Consistent negative mean landmark offsets (more pronounced on the sulcal fundus regions for both the GM/WM and GM/CSF interface data) and the mean SDMFVs greater than 0.5 (reported in Tables 4 and 5) may be interpreted as an outward bias of CRUISE. To address this observation, a simple parameter adjustment study is described in Parameter adjustment and evaluation.

Table 4.

Membership Values (μ̂_WM) at GM/WM Interface Landmarks (mean ± stdev)

	Subject I (12 raters)	Subject II (6 raters)	Both Subjects (12 raters)
Sulcus
LCS	0.70 ± 0.21	0.80 ± 0.18	0.74 ± 0.20
LSYLV	0.58 ± 0.30	0.73 ± 0.22	0.63 ± 0.28
LST	0.62 ± 0.25	0.65 ± 0.24	0.63 ± 0.25
LSF	0.61 ± 0.20	0.64 ± 0.23	0.62 ± 0.21
LCING	0.48 ± 0.24	0.63 ± 0.23	0.52 ± 0.25
LPO	0.75 ± 0.18	0.75 ±0.19	0.75 ± 0.18
RSYLV	0.70 ± 0.21	0.81 ± 0.19	0.73 ± 0.21
RST	0.72 ± 0.20	0.65 ± 0.26	0.70 ± 0.23
RSF	0.61 ± 0.19	0.72 ± 0.20	0.64 ± 0.20
RCING	0.70 ± 0.19	0.71 ± 0.24	0.70 ± 0.21
RPO	0.68 ± 0.25	0.67 ± 0.22	0.68 ± 0.24
Geometry
Sulcal fundus	0.71 ± 0.22	0.76 ± 0.20	0.73 ± 0.21
Sulcal bank	0.67 ± 0.22	0.68 ± 0.22	0.67 ± 0.22
Gyral crown	0.57 ± 0.25	0.68 ± 0.25	0.61 ± 0.25
All	0.65 ± 0.23	0.70 ± 0.23	0.67 ± 0.23

Table 5.

Membership values (subμ̂WM + μ̂_GM) at GM/CSF Interface Landmarks (mean ± stdev)

	Subject I (12 raters)	Subject II (6 raters)	Both subjects (12 raters)
Sulcus
LCS	0.70 ± 0.19	0.62 ± 0.25	0.68 ± 0.22
LSYLV	0.60 ± 0.22	0.60 ± 0.23	0.60 ± 0.23
LST	0.74 ± 0.15	0.65 ± 0.29	0.71 ± 0.21
LSF	0.71 ± 0.23	0.54 ± 0.28	0.66 ± 0.26
LCING	0.60 ± 0.20	0.64 ± 0.24	0.62 ± 0.22
LPO	0.79 ± 0.15	0.65 ± 0.26	0.75 ± 0.20
RSYLV	0.77 ± 0.14	0.67 ± 0.24	0.73 ± 0.18
RST	0.66 ± 0.21	0.64 ± 0.23	0.66 ± 0.22
RSF	0.64 ± 0.22	0.66 ± 0.25	0.65 ± 0.23
RCING	0.72 ± 0.19	0.62 ± 0.28	0.68 ± 0.23
RPO	0.70 ± 0.18	0.60 ± 0.27	0.67 ± 0.22
Geometry
Sulcal fundus	0.76 ± 0.19	0.68 ± 0.24	0.73 ± 0.21
Sulcal bank	0.68 ± 0.19	0.60 ± 0.25	0.65 ± 0.22
Gyral crown	0.64 ± 0.21	0.61 ± 0.28	0.63 ± 0.23
nonACE	0.71 ± 0.19	0.71 ± 0.22	0.71 ± 0.21
ACE	0.68 ± 0.21	0.52 ± 0.26	0.63 ± 0.24
All	0.70 ± 0.20	0.63 ± 0.26	0.67 ± 0.22

Parameter adjustment and evaluation

In Landmark accuracy study on inner and pial surfaces, we reported the landmark offsets on the inner and pial surfaces. We observed consistent negative mean landmark offsets on both the inner and pial surfaces, which indicates an outward bias of CRUISE. Based on the observed SDMFV at the landmarks (cf. Tables 4 and 5), we wanted to estimate the α and β thresholds that best fit the landmark data and repeat the landmark accuracy analysis with the surfaces estimated with the new α and β thresholds. For this purpose, we needed to divide the landmark data into two groups; the first group (training data) was used to estimate the new α and β thresholds, and the second group (test data) was used to repeat the analysis to quantify any such improvement.

We wanted the training data to represent both MR brain images and all possible cortical geometry and sulcus factors used in the analysis presented in Landmark accuracy study on inner and pial surfaces. Only the first six raters picked landmarks on both MR brain images, hence, the training data should be a subset of these raters’ data. The grouping was based on the intra-rater consistency on picking landmarks reported in Landmark accuracy study on inner and pial surfaces. Therefore, data of the raters 1, 2, and 3 formed the training data, and the rest of the data were used to test the new α and β thresholds.

SDMFV statistics for the training data are reported in Table 6. Although we observed that the α and β thresholds should be functions of the cortical geometry – i.e., the ideal thresholds are different for different parts of the brain – in this study, we chose a simpler approach and set α and β to the observed mean SDMFV, and repeated our previous analysis with these thresholds.

Table 6.

Membership function value statistics for the training data—3 raters, 2 subjects (mean ± stdev)

Region	Measure	Sulcal fundus	Sulcal banks	Gyral crown	All
Inner surface	μ̂WM	0.75 ± 0.21	0.68 ± 0.24	0.63 ± 0.28	0.69 ± 0.25
Pial surface	μ̂WM + μ̂GM	0.56 ± 0.28	0.54 ± 0.27	0.56 ± 0.27	0.55 ± 0.27
Pial surface—nonACE	μ̂WM + μ̂GM	0.75 ± 0.20	0.68 ± 0.22	0.65 ± 0.24	0.69 ± 0.22
Pial surface—ACE	μ̂WM + μ̂GM	0.42 ± 0.25	0.41 ± 0.24	0.40 ± 0.25	0.41 ± 0.25
Pial surface	μ̂WM + μ̂GM	0.70 ± 0.23	0.62 ± 0.24	0.62 ± 0.25	0.65 ± 0.24

The average of μ̂_WM measure at the GM/WM landmarks of the training group is 0.69. The inner surface was estimated using the new α = 0.69 threshold and the repeated landmark offset statistics for the GM/WM landmarks of the test group are given in Table 7. For comparison reasons, we also included the landmark offset statistics of the test group for the inner surface estimated using α = 0.5. Although the landmark offset measure is improved by 55% in the sulcal fundus region and by 92% in the sulcal bank region, we see a degradation of landmark offset measure in the gyral crown region. The average inner surface accuracy over all cortical geometries is 0.04 mm.

Table 7.

Landmark offsetson Inner Surface for Test Data—9 raters, 2 subjects (mean ± stdev in mm)

Geometry	α	SD	AD	>1	>2
Sulcal fundus	0.50	−0.56 ± 0.56	0.62 ± 0.49	20%	1.9%
Sulcal bank	0.50	−0.36 ± 0.49	0.48 ± 0.37	8%	0.6%
Gyral crown	0.50	−0.07 ± 0.66	0.49 ± 0.44	14%	0.6%
All	0.50	−0.33 ± 0.61	0.53 ± 0.44	14%	1.0%
Sulcal fundus	0.69	−0.25 ± 0.54	0.45 ± 0.39	8%	0.7%
Sulcal bank	0.69	−0.03 ± 0.57	0.38 ± 0.42	5%	1.6%
Gyral crown	0.69	0.40 ± 0.89	0.68 ± 0.70	19%	7.0%
All	0.69	0.04 ± 0.73	0.50 ± 0.54	10%	3.1%

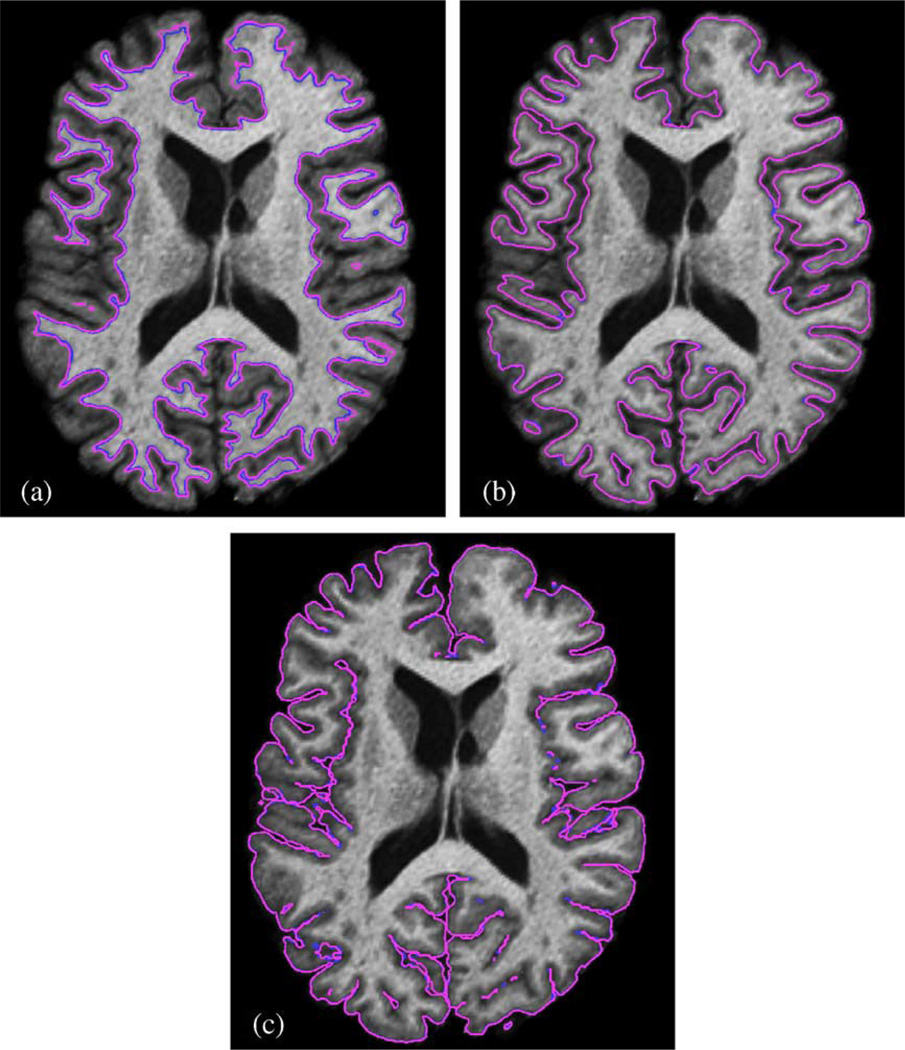
The TGDM to estimate the central surfaces was initialized at the inner surface estimated by α = 0.69 threshold and the new central surfaces were used as the initial condition for the TGDM with the new β threshold to estimate the new pial surfaces (see CRUISE: cortical reconstruction using implicit surface evolution). β threshold was set to the average of μ̂_WM + μ̂_GM measure at the GM/CSF landmarks of the training group; β = 0.55. The statistics of the landmark offset measure on the new pial surfaces are reported in Table 8 with the landmark offset measure statistics on the old pial surfaces for comparison purposes. By adjusting the β threshold, 10%–41% improvement on the landmark offset measure is observed on different geometry groups. A sample axial cross-section from the first MR image volume with surfaces estimated with the original and the new α and β thresholds are shown in Fig. 10. Based on the visual inspection, a better performance has been achieved both on the inner and pial surfaces with the use of the new threshold values; however, the new threshold values have no substantial effect on the central surface estimation.

Table 8.

Landmark offsets on Pial Surface for Test Data—9 raters, 2 subjects (mean ± stdev in mm)

Geometry	α	β	SD	AD	>1	>2
Sulcal fundus	0.50	0.50	−0.51 ± 0.50	0.56 ± 0.45	15%	0.4%
Sulcal bank	0.50	0.50	−0.33 ± 0.43	0.42 ± 0.34	6%	0.1%
Gyral crown	0.50	0.50	−0.17 ± 0.48	0.39 ± 0.33	5%	0.1%
nonACE	0.50	0.50	−0.49 ± 0.52	0.56 ± 0.44	15%	0.4%
ACE	0.50	0.50	−0.18 ± 0.40	0.34 ± 0.27	2%	0.0%
All	0.50	0.50	−0.34 ± 0.49	0.45 ± 0.38	9%	0.2%
Sulcal fundus	0.69	0.55	−0.46 ± 0.50	0.52 ± 0.44	14%	0.8%
Sulcal bank	0.69	0.55	−0.25 ± 0.43	0.38 ± 0.32	5%	0.1%
Gyral crown	0.69	0.55	−0.10 ± 0.48	0.38 ± 0.32	4%	0.1%
nonACE	0.69	0.55	−0.40 ± 0.53	0.51 ± 0.42	12%	0.6%
ACE	0.69	0.55	−0.12 ± 0.41	0.34 ± 0.27	2%	0.0%
All	0.69	0.55	−0.27 ± 0.50	0.43 ± 0.37	8%	0.3%
Sulcal fundus	0.69	0.65	−0.35 ± 0.52	0.48 ± 0.40	11%	0.4%
Sulcal bank	0.69	0.65	−0.14 ± 0.42	0.34 ± 0.29	3%	0.1%
Gyral crown	0.69	0.65	−0.14 ± 0.42	0.34 ± 0.29	3%	0.1%
nonACE	0.69	0.65	−0.27 ± 0.53	0.45 ± 0.39	9%	0.4%
ACE	0.69	0.65	0.00 ± 0.44	0.35 ± 0.27	3%	0.0%
All	0.69	0.65	−0.14 ± 0.51	0.40 ± 0.34	6%	0.2%
Sulcal fundus	0.69	0.69	−0.31 ± 0.52	0.47 ± 0.39	10%	0.3%
Sulcal bank	0.69	0.69	−0.08 ± 0.42	0.33 ± 0.28	3%	0.0%
Gyral crown	0.69	0.69	0.13 ± 0.50	0.41 ± 0.32	6%	0.1%
nonACE	0.69	0.69	−0.21 ± 0.54	0.44 ± 0.38	9%	0.2%
ACE	0.69	0.69	0.05 ± 0.46	0.36 ± 0.28	3%	0.0%
All	0.69	0.69	−0.09 ± 0.52	0.40 ± 0.34	6%	0.1%

Fig. 10.

A sample MR image cross-section with (a) inner, (b) central, and (c) pial surfaces of the first subject (blue (α = 0.5 and β = 0.5), red (α = 0.69 and β = 0.55)).

By setting β threshold to the average of μ̂_WM + μ̂_GM measure over all training group landmarks, we make the assumption that the pial surface is determined solely by the isosurface of the μ̂_WM + μ̂_GM function everywhere in the cortex. However, it is quite evident from difference between the average μ̂_WM + μ̂_GM measure on regions not edited by ACE and regions edited by ACE (cf. Table 6) that the ACE stopping criterion is more dominant than the isolevel criterion. To address this issue, we explored two approaches. First, since the raters selected landmarks on the original MR image volumes without any ACE editing, instead of the μ̂_WM + μ̂_GM measure, we used the μ̂_WM + µ_GM measure and set the β threshold to its average at the training landmarks; β = 0.65 as reported in Table 6. 18%–58% improvement is observed on different geometry regions. The results are reported in Table 8. We observed perfect accuracy in the regions edited by the ACE algorithm with this new β threshold adjustment. In the second approach, we only used the training group landmarks on the regions not edited by the ACE algorithm, but still used the μ̂_WM + μ̂_GM measure. This time, the β threshold is set to 0.69 (see Table 6), and the resultant landmark offset measure statistics are given in Table 8. This threshold adjustment yields 24%–76% improvement on the landmark offset measure and the average pial surface accuracy over all cortical geometries is 0.09 mm.

Different percentile improvements on the different geometry groups, and occasional degradation support the claim that the α and β thresholds should be defined as functions of the cortical geometry. In future work, we will investigate the features that can be extracted from the membership functions so that the α and β can be defined as functions of cortical geometry, but still yield topologically correct nested cortical surfaces.

In order to see the effect of the α and β thresholds on estimating the central surface, we repeated the landmark accuracy study reported in (Han et al., 2004) on the new central surfaces estimated by using the new thresholds. Slight differences were observed on the reported values, but no substantial improvement or change was noted. These results show the robustness of the central surface reconstruction with respect to the α and β thresholds, which supports our previous claim about the stability of the central surface and how well it captures the geometry of the cortex compared with the inner and pial surfaces (Xu et al., 1999).

The repeatability analysis on the nested cortical surfaces was also carried out using the new thresholds. Although slight differences were observed in the reported values, no substantial improvement or change was noted.

Discussion and future work

The purpose of this work was to evaluate the accuracy and precision of the CRUISE algorithms developed for the automatic reconstruction of the nested surfaces of the cerebral cortex from MR image volumes. This was accomplished by conducting two different studies. Our first conclusion is that the nested cortical surfaces – inner, central, and pial – can be found in a robust fashion using the CRUISE algorithms. Second, the three nested cortical surfaces can be found with subvoxel accuracy, typically with an accuracy of one third of a voxel. In this work, the performance of the CRUISE algorithm was tested on a single BLSA data set. The MR acquisition protocol that is used in the BLSA is based on a well-established MR pulse sequence that is very common in neuroscience research, and is capable of being implemented on all MR scanners. Although performance will differ when the algorithm is applied to data having different acquisition protocols, we believe that acquisition parameters can be adjusted on modern scanners to achieve equal or superior performance to that described herein. Currently, we utilize “rater implied surfaces”, derived from rater selected landmarks, to quantify the accuracy of CRUISE. In future work, we plan to create a nested surface truth model from the visible human cyrosection and MR image data (Spitzer et al., 1996), and validate our methods against these data.

The nested surfaces can be reliably used for analysis of the cortex geometry; however, the reported accuracy levels can be of concern in longitudinal analysis since the sought changes might be in the neighborhood of the observed errors. A simple experiment to improve CRUISE by selecting new threshold values which were more in accordance with the rater implied surfaces was presented in Parameter adjustment and evaluation. Our statistics on SD and SDMFV suggest that the positioning of tissue interfaces with respect to the membership function values varies spatially. In future research, we expect to show that a variable threshold scheme – e.g., varying α and β thresholds as functions of cortical geometry or position – will provide even higher accuracy in the CRUISE reconstruction algorithm. Alternative segmentation methods may also yield new ways to further improve CRUISE.