Spatial Moran Models I. Stochastic Tunneling in the Neutral Case

Abstract

We consider a multistage cancer model in which cells are arranged in a d-dimensional integer lattice. Starting with all wild-type cells, we prove results about the distribution of the first time when two neutral mutations have accumulated in some cell in dimensions d ≥ 2, extending work done by Komarova [12] for d = 1.

1 Introduction

The accumulation of mutations is important not only for cancer initiation, progression, and metastasis, but also for the emergence of acquired resistance against chemotherapeutics, radiation therapy, or targeted drugs. For this reason there is a large and growing literature on the waiting time τ_k until some cell has acquired k prespecified mutations. In all the models we consider, type i individuals mutate to type (i + 1) at rate u_i+1. The dynamics considered have most often been studied in multi-type Moran models with a homogeneously mixing population of constant size. Here we will concentrate on how results change when one considers a spatial Moran models, and as is the case for much earlier work we will concentrate on the behavior of τ₂.

We suppose that cells of type 0 and type 1 have relative fitness 1 and λ. Since we will only consider the waiting time for the first type 2, the relative fitness of type 2’s is not important. In this work we will consider situation in which λ is so close to 1 that the mutations are essentially neutral. For cancer applications, this is a restrictive assumption, and it will be removed in the companion paper (part II) by Durrett, Foo and Leder [6]. However, the current result applies to the important case of tumor suppressor genes. In that case, when both copies of the gene are inactivated trouble develops, but while there is one working copy the cell can function normally.

We begin by recalling results for the Moran model in a homogeneously mixing population of size N. Here and in what follows the mutation rates u_i and selection coefficient λ depend on N, even though this is not indicated in the notation, and we write a_N ≪ b_N if a_N/b_N → 0 as N → ∞. The next result made its first appearance on page 16230 of Nowak et al [17]. Since then it has appeared in print a number of times: [14], [18], [10], [11], and in Nowak’s excellent book [16] on Evolutionary Dynamics.

Theorem 1

In the neutral case of the Moran model, λ = 1, if we assume that

$$\frac{1}{\sqrt{u_2}}\ll N\ll \frac{1}{u_1}$$ (1)

and let u₁, u₂ → 0 then we have

$$P({\tau }_2>t/N{u}_1{u}_2^{1/2})\to exp(-t)$$

The same conclusion holds if $\mid \lambda -1\mid \ll u_2^{1/2}$.

Durrett and Schmidt [7] applied these ideas to study regulatory sequence evolution and to expose flaws in Michael Behe’s arguments for intelligent design. Durrett, Schmidt, and Schweinsberg [8], see also Schweinsberg [19], generalized this result to cover τ_k.

The conditions in the result may look mysterious but they can be derived by simple reasoning. Here and throughout the paper and f(u) ~ g(u) means f(u)/g(u) → 1 as u → 0. Suppose first that λ = 1.

• (A1)If we start the Moran model with k ≪ N type 1’s and the rest type 0, then the 1’s behave like a critical branching process. The time needed for the 1’s to die out is O(k) and the number of type-1 births before they die out is O(k²). Thus we expect the first type 2 to occur in a type 1 family that reaches size $k_1=O(1/\sqrt{u_2})$, and hence has $O(k_1^2)=O(1/u_2)$ births. The condition $1/\sqrt{u_2}\ll N$ in (1) guarantees k₁ ≪ N.
• (A2)
  Since the voter model is a martingale, the probability a type-1 mutation creates a family that reaches size $1/\sqrt{u_2}$ is $\sqrt{u_2}$. More to the point a simple computation (consider what happens at the first jump) shows that the probability a type-1 family gives rise to a type-2 before it dies out is $~\sqrt{u_2}$. Since mutations to type 1 occur at times of a rate Nu₁ Poisson process and with probability $~\sqrt{u_2}$ give rise to a type 2, it follows that if ρ₂ is the birth time of the type-1 mutant that first gives rise to a type 2 then

  $$P({\rho }_2>t/N{u}_1{u}_2^{1/2})\to exp(-t).$$

  To complete the proof we need to show that τ₂ − ρ₂ ≪ ρ₂, and for this we need the condition N ≪ 1/u₁ in (1).

• (A3)By the discussion of (A1), the first mutation will occur in a family that reaches a size $O(1/\sqrt{u_2})$. If $\mid \lambda -1\mid \ll u_2^{1/2}$, then computations with Girsanov’s formula show that (in the limit u₂ → 0) the behavior of the Moran model, while it is $O(1/\sqrt{u_2})$, is indistinguishable from the case with no drift.

The assumption of a homogeneously mixing cell populations simplifies calculations considerably, but is not realistic for solid tumors. For this reason, Komarova [12] considered a spatial model, which is very similar to one introduced much earlier by Williams and Bjerknes [20]. Due to work of Bramson and Griffeath [2, 3], the second model is known to probabilists as the biased voter model.

In the usual formulation of the biased voter model, each site on the d-dimensional integer lattice 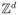can be in state 0 or 1 indicating the presence of a cell with relative fitness 1 or λ > 1. Cells give birth at a rate equal to their fitness, and the offspring replaces a nearest neighbor chosen at random. When λ = 1 this is the voter model which was introduced independently by Clifford and Sudbury [4] and Holley and Liggett [9]. For a summary of what is known see Liggett [15].

In the biased voter model births drive the process. In Komarova’s version cells die at rate 1 and are replaced by a copy of a nearest neighbor chosen with probability proportional to its fitness. A site with n_i neighbors in state i makes

$$\begin{array}{cc}\text{transitions}& \text{at}\text{rate}\\ 0\to 1& \lambda n_1/(\lambda n_1+n_0)\\ 1\to 0& n_0/(\lambda n_1+n_0)\end{array}$$

In d = 1 if the set of sites in state 1 is an interval [ℓ, r] with ℓ < r then any site that can change has n₁ = n₀ = 1 so Komarova’s model is a time change of the biased voter model. In d ≥ 2 this is not exactly true. However, we are interested in values of λ = 1 + s where s = 0.02 or even less, so we expect the two models to have very similar behavior. In any case, the difference between the two models is much less than their difference from reality, so we will choose to study the biased voter, whose duality with branching coalescing random walk (to be described below) gives us a powerful tool for doing computations.

Since we want a finite cell population we will restrict our process to be a subset of (−L/2, L/2]^d. Komarova [12] uses “Dirichlet boundary conditions”, i.e., she assumes her space is an interval with no cells outside, but this is awkward because the set of type 1 cells may reach one end of the interval and then no further changes happen at that end. To avoid this, we will use periodic boundary conditions, i.e., we consider ( 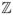mod L)^d. The resulting toroidal geometry is a little strange for studying cancer. However, using ( 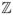mod L)^d has the advantage that the space looks the same seen from any point. Our results will show that for the parameter values the first type 2 will arise when the radius of the set of sites occupied by 1’s is ≪ L so the boundary conditions do not matter.

Let ${\xi }_s^0$ be the set of cells equal to 1 in the voter model with no mutations from 0 to 1 on 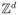starting from a single type 1 at 0. Let | ${\xi }_s^0$| be the number of cells in ${\xi }_s^0$, and let

$${\nu }_d=1-Eexp\left(-u_2{\int }_0^{T_0}\mid {\xi }_s^0\mid ds\right).$$ (2)

This quantity, which is defined for the voter model without mutation, calculates the probability, which depends on the dimension d, that a mutation to type 1 gives rise to a type 2 before its family dies out. To see why this is true note that the integral ${\int }_0^{T_0}\mid {\xi }_s^0\mid ds$ gives the total number of man-hours in the type 1 family, and conditional on this the number of mutations that will occur is Poisson with mean $u_2{\int }_0^{T_0}\mid {\xi }_s^0\mid ds$.

Since mutations to type 1 in a population of N cells occur at rate Nu₁ this suggests that

$$P({\tau }_2>t)\to exp(-N{u}_1{\nu }_{d}t).$$ (3)

As we will explain in a moment, there is a constant γ_d so that ν_d ~ γ_dh_d(u₂) as u₂ → 0 where

$$h_d(u)=\{\begin{array}{ll}{u}^{1/3}\hfill & d=1,\hfill \\ u^{1/2}{log}^{1/2}(1/u)\hfill & d=2,\hfill \\ u^{1/2}\hfill & d\ge 3.\hfill \end{array}$$ (4)

To state the result we need one more definition:

$$g_d(u)=\{\begin{array}{ll}{u}^{1/3}\hfill & d=1,\hfill \\ {log}^{-1/2}(1/u)\hfill & d=2,\hfill \\ 1\hfill & d\ge 3.\hfill \end{array}$$ (5)

Theorem 2

In the neutral case of the biased voter model, λ = 1, if we assume

$$\frac{1}{h_d(u_2)}\ll N\ll \frac{g_d(u_2)}{u_1},$$ (6)

then there are constants λ_d given in (12) and (13) so that as u₁, u₂ → 0

$$P({\tau }_2>t/N{u}_1{\gamma }_d{h}_d(u_2))\to exp(-t).$$

The same conclusion holds if |λ − 1| ≪ h_d(u₂).

In d = 1 this result was proved by Komarova [12], see her equation (62) and assumption (60), then change notation u₁ → u, u₂ → u₁. See also her survey paper [13]. Note that when d ≥ 3 the order of magnitude of the waiting time and the assumptions are the same as in Theorem 1. In d = 2 there are logarithmic corrections to the behavior in Theorem 1, so only in the case of d = 1 (which is relevant to cancer in the mammary ducts) does space make a substantial change in the waiting time.

The reasons for the conditions in Theorem 2 are the same as in Theorem 1.

• (B1)We will see that the mutation to type-2 will occur in a type-1 family that reaches size k = O(1/h_d(u₂)). The left hand assumption in (6) implies that k ≪ N, so the type 2 mutant arises before the 1’s reach fixation.
• (B2)
  Let ρ₂ be the time of the first type 1 mutation that begins the family that eventually leads to a type 2. Since mutations to type 1 occur at rate Nu₁ and lead to a type 2 with probability ν_d, it is easy to see that

  $$P({\rho }_2>t)\to exp(-N{u}_1{\nu }_{d}t)$$

  so to prove the result we need to show that with high probability τ₂ − ρ₂ ≪ ρ₂. As the reader will see, this is guaranteed by the right-hand assumption in (6).

• (B3)As in the discussion of Theorem 1, once we know that the mutation to type-2 will occur in a type-1 family that reaches size k = O(1/h_d(u₂)), it follows that if |λ − 1| ≪ h_d(u₂) then (in the limit u₂ → 0) the behavior of the size of the biased voter | ${\xi }_t^0$| is, while it is O(1/h_d(u₂)), indistinguishable from the case with no drift.

2 The Key to the Proof

The size of the voter model, when $\mid {\xi }_t^0\mid >0$, is a time change of symmetric simple random walk, with jumps happening at two times the size of the boundary | $\partial {\xi }_t^0$|, which is the number of nearest neighbor pairs with $x\in {\xi }_t^0$ and $y\notin {\xi }_t^0$. The one dimensional case is easy because when ${\xi }_t^0\ne \varnothing$ the boundary $\mid \partial {\xi }_t^0\mid =2$. The key to the study of the process in d ≥ 2 is the observation that there are constants β_d so that

$$\mid \partial {\xi }_t^0\mid {~}_p\{\begin{array}{ll}2d{\beta }_d\mid {\xi }_t^0\mid \hfill & d\ge 3,\hfill \\ 4{\beta }_2\mid {\xi }_t^0\mid /log(\mid {\xi }_t^0\mid )\hfill & d=2.\hfill \end{array}$$ (7)

where $\mid \partial {\xi }_t^0\mid {~}_{p}f(\mid {\xi }_t^0\mid )$ means that when | ${\xi }_t^0$| is large, $\mid \partial {\xi }_t^0\mid /f(\mid {\xi }_t^0\mid )$ is close to 1 with high probability.

The intuition behind this result is that the voter model is dual to a collection of coalescing random walks, so in d ≥ 3 neighbors of points in ${\xi }_t^0$ will be unoccupied with probability ≈ β_d, the probability two simple random walks started at 0 and e₁ = (1, 0, … 0) never hit. In dimension d = 2, the recurrence of random walks implies that when $\mid {\xi }_t^0\mid =k$ is large, most neighbors of points in ${\xi }_t^0$ will be occupied, but due to the fat tail of the recurrence time sites will be vacant with probability ~β₂/log k, where β₂ = π.

Before we try to explain why (7) is true, we will list an important consequence. Let T_k be the first time $\mid {\xi }_t^0\mid =k$. Let

$$a_n=\{\begin{array}{ll}{n}^2\hfill & d=1,\hfill \\ 2\mathit{n}logn\hfill & d=2,\hfill \\ n\hfill & d\ge 3.\hfill \end{array}$$

Lemma 1

Let ${\xi }_t^0$ be the unbiased voter model (i.e., λ = 1) starting from a single occupied site.

$$\left(\frac{\mid {\xi }_{T_{n\epsilon }+a_{n}t}^0\mid }{n}|T_{n\epsilon }<\infty \right)\Rightarrow (Y_t\mid Y_0=\epsilon ),$$ (8)

where ⇒ indicates convergence in distribution of the stochastic processes and the limit has

$$d{Y}_t=\{\begin{array}{ll}\sqrt{2}d{B}_t\hfill & d=1,\hfill \\ \sqrt{2{\beta }_d{Y}_t}d{B}_t\hfill & d\ge 2.\hfill \end{array}$$

where B_t is a one dimensional Brownian motion. In d = 1 the process is stopped when it hits 0. In d ≥ 2, 0 is an absorbing boundary so we don’t need to stop the process.

In d = 1 this result is trivial. If one accepts (7) then (8) can be proved easily by computing infinitesimal means and variances and using standard weak convergence results. In d ≥ 2, (7) and (8) are almost consequences of work of Cox, Durrett, and Perkins [5]. They speed up time at rate a_n, scale space by $1/\sqrt{a_n}$, and assign each point occupied in the voter model mass 1/n to define a measure-valued diffusion Xⁿ which they prove converges to super-Brownian motion. See their Theorem 1.2. (Their scaling is a little different in d = 2 but this makes no difference to the limit.)

Let $V_{n,s}^{\prime }(x)$ be the fraction of sites adjacent to x in state 0 at time s (with the prime indicating that we multiply this by log n in d = 2, see page 196). A key step in the proof in [5] is to show, see (I1) on page 202, that for nice test functions ϕ

$$E\left[{\left({\int }_0^T{X}_s^n(\{V_{n,s}^{\prime }-{\beta }_d\}{\varphi }^2)ds\right)}^2\right]\to 0$$ (9)

where $X_s^n(f)$ denote the integral of the function f against the measure $X_s^n$. The result in (9) shows that when we integrate in time and average in space (multiplying by a test function to localize the average) then (7) is true.

From the convergence of the measure valued diffusion Xⁿ to super-Brownian motion, (8) follows by considering the total mass. Earlier we said (8) is almost a consequence of [5], since they start their process from an initial measure (i.e., O(n) initial 1’s) while consider a single occupied site and condition on reaching nε. However, this defect can be remedied by citing the work of Bramson, Cox, and LeGall [1], who have a result, Theorem 4 on page 1012 that implies (8) in d ≥ 2.

The result in (8) is enough for Section 3, but for the calculations in Section 4 we will need a version of (7). In that section we will compute under the assumption that if $\mid {\xi }_t^0\mid =k$

$$\mid \partial {\xi }_t^0\mid =\{\begin{array}{ll}2d{\beta }_{d}k\hfill & d\ge 3,\hfill \\ 4{\beta }_{2}k/logk\hfill & d=2.\hfill \end{array}$$ (10)

If one wants to give a rigorous proof of the estimates there, then small values of k, can be treated with the inequalities

$$C{k}^{1/d}\le \mid \partial {\xi }_t^0\mid \le 2dk,$$

and one can control large values of k using (9) and estimates such as (J1) and (J2) on page 208 of [5]. We will assume (10) in order to avoid getting bogged down in technicalities.

3 Proof, part I

Let ${\nu }_d^{\epsilon }$ be the probability defined in (2) ignoring mutations to type 2 that occur before T_nε. The size of the voter model, | ${\xi }_t^0$|, is a martingale, so if we let P₁ to denote the law of the voter model starting from one occupied site P₁(T_nε < ∞) = 1/nε. Applying (8) now,

$${\nu }_d^{\epsilon }~\frac{1}{n\epsilon }·\left[1-E_{\epsilon }exp\left(-{na}_n{u}_2{\int }_0^{T_0}{Y}_{s}ds\right)\right].$$ (11)

where T₀ = min{t : Y_t = 0}, E_ε is the expected value for (Y_t|Y₀ = ε). We have

$${na}_n=\{\begin{array}{ll}{n}^3\hfill & d=1,\hfill \\ 2n^{2}logn\hfill & d=2,\hfill \\ n^2\hfill & d\ge 3.\hfill \end{array}$$

so if we set n = 1/h_d(u₂) then (4) implies na_nu₂ → 1 and using (11) gives

$${\nu }_d^{\epsilon }~h_d(u_2)·\left[\frac{1-E_{\epsilon }exp\left(-{\int }_0^{T_0}{Y}_{s}ds\right)}{\epsilon }\right].$$

Thus the type-2 mutation will occur in a family that reaches sizes O(1/h_d(u₂)), and we must assume 1/h_d(u₂) ≪ N.

If we ignore the time to reach size 1/h_d(u₂), the time needed to generate the type-2 mutation is, by (8), of order

$$a(1/h_d(u_2))~\{\begin{array}{ll}{u}_2^{-2/3}\hfill & d=1,\hfill \\ 2u_2^{-1/2}{log}^{1/2}(1/u_2)\hfill & d=2,\hfill \\ u_2^{-1/2}\hfill & d\ge 3.\hfill \end{array}$$

where we have written a(n) for a_n for readability. Thus for (B2) we need a(1/h_d(u₂)) ≪ 1/Nu₁h_d(u₂), which means N ≪ g_d(u₂)/u₁.

The next order of business is to compute ν_d. Stochastic calculus (or calculations with infinitesimal generators) tells us that

$$v(x)=E_{x}exp\left(-{\int }_0^{T_0}{Y}_{s}ds\right)$$

is the unique function on [0, ∞) with values in [0, 1], v(0) = 1 and

$$v^{″}-xv=0\text{in}d=1{\beta }_{d}x{v}^{″}-xv=0\text{in}d\ge 2.$$

In d = 1 all solutions have the form:

$$v(x)=\alpha Ai(x)+\beta Bi(x),$$

where Ai and Bi are Airy functions

$$\begin{array}{l}Ai(x)=\frac{1}{\pi }{\int }_0^{\infty }cos\left(\frac{t^3}{3}+xt\right)dt,\\ Bi(x)=\frac{1}{\pi }{\int }_0^{\infty }exp\left(-\frac{t^3}{3}+xt\right)+sin\left(\frac{t^3}{3}+xt\right)dt.\end{array}$$

Since Bi is unbounded and Ai is decreasing on [0, ∞), we take β = 0 and set α = 3^2/3Γ(2/3) to satisfy the boundary condition, v(0) = 1. Letting ε → 0 we conclude that

$${\gamma }_1=-\alpha A{i}^{\prime }(0)=3^{1/3}\mathrm{\Gamma }(2/3)/\mathrm{\Gamma }(1/3).$$ (12)

In d ≥ 2, $v(x)=exp(-{\beta }_d^{-1/2}x)$, and we have

$${\gamma }_d={\beta }_d^{-1/2}.$$ (13)

4 Proof, part II: Missing details for λ = 1

In the previous section we have calculated the probability ${\nu }_d^{\epsilon }$ that a type 1 family reaches size ε/h_d(u₂) and then gives rise to a type 2. To let ε → 0 and prove Theorem 2 we need to consider the possibility of a mutation to type 2 in a family that (i) never reaches size nε, or (ii) will reach nε but hasn’t yet. To have a convenient name we will call these small families. Families of the first kind arise at rate Nu₁(1 − 1/nε) and families of the second kind arise at rate Nu₁/nε. We will now calculate the expected rate at which type-2’s are born from these small families. In the proof of Theorem 2, we will let ε → 0 slowly as n → ∞ so we can and will assume nε → ∞.

Consider the voter model ${\xi }_t^0$ starting from a single 1 at the origin at time 0. Let V_k be the total time spent at level k, i.e., |{ $t:\mid {\xi }_t^0\mid =k$}| and let N_k be the total number of returns to level k before leaving the interval (0, nε). Recalling our assumption in (10), we let q(k) the rate jumps occur at level k.

Let S_k be the embedded discrete time chain, which is a simple random walk, and let $T_k^{+}=min\{n\ge 1:S_n=k\}$.

$$\begin{array}{l}{E}_1\left({\int }_0^{T_0}\mid {\xi }_s^0\mid ds|T_0<T_{n\epsilon }\right)=E_1\left(\sum _{k=1}^{n\epsilon }k{V}_k|T_0<T_{n\epsilon }\right)\\ =E_1\left(\sum _{k=1}^{n\epsilon }\frac{k{N}_k}{q(k)}|T_0<T_{n\epsilon }\right)=\sum _{k=1}^{n\epsilon }\frac{{\overline{P}}_1(T_k<\infty )}{{\overline{P}}_k(T_k^{+}>T_0)}\frac{k}{q(k)},\end{array}$$ (14)

where the bar indicates conditioning on T₀ < T_nε. A similar argument shows that

$$E_1\left({\int }_0^{T_{n\epsilon }}\mid {\xi }_s^0\mid ds|T_{n\epsilon }<T_0\right)=\sum _{k=1}^{n\epsilon }\frac{1}{{\widehat{P}}_k(T_k^{+}>T_{n\epsilon })}\frac{k}{q(k)},$$ (15)

where the hat indicates conditioning on T_nε < T₀.

The three conditional probabilities we need can be computed using facts about simple random walk that follow from the fact that it is a martingale.

$${\overline{P}}_1(T_k<\infty )=\frac{P_1(T_k<\infty )P_k(T_0<T_{n\epsilon })}{P_1(T_0<T_{n\epsilon })}=\frac{(1/k)(1-k/n\epsilon )}{(1-1/n\epsilon )}.$$ (16)

For the next two we note that the first step has to be in the correct direction for these events to happen.

$${\overline{P}}_k(T_k^{+}>T_0)=\frac{(1/2)(1/k)}{(1-k/n\epsilon )}.$$ (17)

$${\widehat{P}}_k(T_k^{+}>T_{n\epsilon })=\frac{(1/2)(\frac{1}{n\epsilon -k})}{(k/n\epsilon )}.$$ (18)

Thus the expected total man-hours ${\int }_0^{T_0}\mid {\xi }_s^0\mid ds$ for a family that will die out before reaching size nε is

$$~\frac{2}{(1-1/n\epsilon )}\sum _{k=1}^{n\epsilon }{(1-k/n\epsilon )}^2\frac{k}{q(k)},$$ (19)

and in families that have yet to reach size nε,

$$\frac{2}{n\epsilon }\sum _{k=1}^{n\epsilon }(n\epsilon -k)\frac{k^2}{q(k)}.$$ (20)

The next result shows that the contribution of small families are indeed negligible. Note that in all three cases the order of magnitude of the contributions from small families is the same as the overall rate, but contains a constant that → 0 as ε → 0.

Lemma 2

The expected total man-hours in small families is

$$\le \{\begin{array}{ll}N{u}_1{u}_2^{1/3}·\frac{{\epsilon }^2}{4}\hfill & d=1,\hfill \\ N{u}_1{u}_2^{1/2}{log}^{1/2}(1/u_2)·\frac{7\epsilon }{24{\beta }_2}\hfill & d=2,\hfill \\ N{u}_1{u}_2^{1/2}·\frac{\epsilon }{2d{\beta }_d}\hfill & d\ge 3.\hfill \end{array}$$

Proof

In one dimension, q(k) = 2. The sum in (19) is dominated by

$${\int }_0^{n\epsilon }{(1-x/n\epsilon )}^{2}xdx=\frac{1}{{(n\epsilon )}^2}{\int }_0^{n\epsilon }{y}^2(n\epsilon -y)dy=\frac{{(n\epsilon )}^2}{12}.$$

Thus, families of the first kind produce type 2’s at rate ≤ Nu₁u₂(nε)²/12. The expression in (20) is dominated by

$$\frac{2}{n\epsilon }{\int }_0^{n\epsilon }(n\epsilon -x)x^{2}dx=\frac{{(n\epsilon )}^3}{6}.$$

Thus, families of the second kind produce type-2’s at rate ≤ Nu₁u₂(nε)²/6. Adding the last two conclusions gives the result for d = 1.

In d ≥ 3, (10) implies q(k) = 2dβ_dk, so (19) becomes

$$\frac{1}{d{\beta }_d}\sum _{k=1}^{n\epsilon }{(1-k/n\epsilon )}^2.$$

The sum is bounded above by the integral

$${\int }_0^{n\epsilon }{(1-x/n\epsilon )}^{2}dx=\frac{n\epsilon }{3},$$

so with our choice of $n=u_2^{-1/2}$, families of the first kind produce type 2’s at rate bounded above by $N{u}_1{u}_2^{1/2}\epsilon /(3d{\beta }_d)$. Setting q(k) = 2dβ_dk, (20) becomes

$$\frac{1}{d{\beta }_{d}n\epsilon }\sum _{k=1}^{n\epsilon }(n\epsilon -k)k.$$

The sum is bounded above by the integral

$${\int }_0^{n\epsilon }(n\epsilon -x)xdx=\frac{{(n\epsilon )}^3}{6}.$$

Thus, families of the second kind produce type-2’s at $\text{rate}\le N{u}_1{u}_2^{1/2}\epsilon /(6d{\beta }_d)$. Adding the last two conclusions gives the result for d ≥ 3.

In d = 2, (10) implies q(k) = 4β₂k/log k, so (19) becomes

$$\frac{1}{2{\beta }_2}\sum _{k=1}^{n\epsilon }{(1-k/n\epsilon )}^{2}logk.$$

Each term in the sum is bounded above by log(nε), so the sum is less than nε log nε. Since $n=u_2^{-1/2}{log}^{-1/2}(1/u_2)$, families of the first kind produce type 2’s at rate bounded above by

$$\begin{array}{l}N{u}_1{u}_2·\frac{1}{2{\beta }_2}n\epsilon log(n\epsilon )=N{u}_1{u}_2·\frac{1}{2{\beta }_2}\epsilon u_2^{-1/2}{log}^{-1/2}(1/u_2)·\frac{1}{2}log(1/u_2)\\ =\frac{\epsilon }{4{\beta }_2}N{u}_1{u}_2^{1/2}{log}^{1/2}(1/u_2).\end{array}$$

Taking q(k) = 4β₂k/log k, (20) becomes

$$\frac{1}{2{\beta }_{2}n\epsilon }\left(\sum _{k=1}^{n\epsilon }(n\epsilon -k)\mathit{k}logk\right).$$

The sum is bounded above by

$${\int }_0^{n\epsilon }(n\epsilon -x)xlog(n\epsilon )dx\le \frac{{(n\epsilon )}^3}{6}log(n\epsilon ).$$

Thus families of the second kind produce type 2’s at rate bounded above by

$$\begin{array}{l}\frac{N{u}_1{u}_2}{n\epsilon }·\frac{1}{2{\beta }_{2}n\epsilon }·\frac{{(n\epsilon )}^3}{6}log(n\epsilon )=\frac{1}{12{\beta }_2}N{u}_1{u}_2·n\epsilon log(n\epsilon )\\ =\frac{\epsilon }{24{\beta }_2}N{u}_1{u}_2^{1/2}{log}^{1/2}(1/u_2).\end{array}$$

Adding the last two conclusions gives the result for d = 2 and completes the proof.

5 Proof, part III: Almost neutral mutations

In the biased voter model, whose law we denote by P^λ, jumps occur at rate 1 + λ times the size of the boundary. To compensate for this we need to run the unbiased (λ = 1) voter at rate (1 + λ)/2. If we do this, call the resulting law P̃⁰, and let ω_T is a realization of ${\xi }_t^0$ run up to time T then the Radon-Nikodym derivative

$$\frac{d{P}^{\lambda }}{d{\stackrel{\sim }{P}}^0}({\omega }_T)={\left(\frac{2\lambda }{\lambda +1}\right)}^{n_{+}}{\left(\frac{2}{\lambda +1}\right)}^{n_{-}},$$

where n₊ and n₋ are the number of up jumps in ω_t when 0 ≤ t ≤ T.

If ${max}_{t\le T}\mid {\xi }_t^0\mid =O(K)$ then the difference 0 ≤ n₊ − n₋ = O(K). Since under P̃₀, | ${\xi }_t^0$| is a time change of simple random walk, we see that the total number of jumps n₊ + n₋ = O(K²). Taking K = 1/h_d(u₂) and assuming |λ − 1| ≪ h_d(u₂), when u₂ is small the Radon Nikodym derivative is

$$\begin{array}{l}={\left(1+\frac{\lambda -1}{\lambda +1}\right)}^{n_{+}}{\left(1-\frac{\lambda -1}{\lambda +1}\right)}^{n_{-}}\\ ={\left(1+\frac{\lambda -1}{\lambda +1}\right)}^{n_{+}-n_{-}}{\left(1-\frac{{(\lambda -1)}^2}{{(\lambda +1)}^2}\right)}^{n_{+}+n_{-}}\approx 1.\end{array}$$

The last result implies that (8) extends to almost neutral mutations, and the computations in Section 2 are valid. To extend the part of the proof in Section 3, we need to check that (16)–(18) are true asymptotically for almost neutral mutations. To do this we recall that if a < x < b

$$P_x^{\lambda }(T_b<T_a)=\frac{{\theta }^x-{\theta }^a}{{\theta }^b-{\theta }^a}\text{where}\theta =1/\lambda .$$ (21)

When 0 ≤ a < x ≤ b = O(1/h_d(u₂)) and |λ − 1| ≪ h_d(u₂) we have

$$P_x^{\lambda }(T_b<T_a)\approx \frac{x-a}{b-a}.$$

To show that the sums come out the same we need the following uniform version which follows from (21). If |λ − 1|h_d(u₂) → 0 then for any C fixed

$$\underset{0\le -a,b\le C/h_d(u_2)}{sup}\left|\frac{P_0^{\lambda }(T_b<T_a)}{-a/(b-a)}-1\right|\to 0.$$