Abstract
Recently we have analyzed light transmission and spectral selectivity by optical channels in Müller cells and other transparent cells, proposing a model of their structure, formed by specialized intermediate filaments [1,2]. Our model represents each optical channel by an axially symmetric tube with conductive walls. Presently, we analyze the planar polarization selectivity in long nanostructures, using the previously developed approach extended to structures of the elliptic cross-section. We find that the output light polarization angle depends on the a/b ratio, with a and b the semiaxes of the ellipse. Experimental tests used a Cr nano-strip device to evaluate the transmitted light polarization. The model adapted to the experimental geometry provided an accurate fit of the experimental results.
Graphical Abstract
Igor V. Khmelinskii
I. Introduction
The celestial distribution of the angle of the skylight polarization, being the same under all possible sky conditions (clear, fog, clouds, etc), is used for the orientation by polarization-sensitive animals, including many vertebrates [3](Horváth et al., 2014). There is considerable behavioral and physiological evidence for polarization-based navigation in vertebrates, including fish, reptiles and birds, but not in mammals, while it is known that mammals, including humans, can still perceive the polarization of light to some extent (Muheim, 2011; Wehner, 2014) [4,5]. The search for the physical mechanisms of the polarization sensitivity has taken two different paths: some researchers are looking for optical polarizing filters in front of the photoreceptors, while others suggest that photoreceptor cells themselves may have different intrinsic sensitivity to differently polarized light (Wehner, 2014)[5].
Photoreceptors would be intrinsically sensitive to polarization if they had some dichroic absorbance at the molecular level. Indeed, it was shown for the invertebrate rabdomeric photoreceptors that their chromophore is preferentially aligned along the axis of the microvillus and immobilized, allowing for robust polarization sensitivity (Wehner, 2014)[5]. On the other hand, the first spectroscopic measurements found rhodopsin dipoles in the vertebrate photoreceptors free to rotate within the photoreceptor membrane without any preferred orientation to the incident light, thus rejecting the possibility for their polarization sensitivity (Brown 1972; Cone 1972)[6,7]. These earlier results have been criticized later. Namely, a preferred orientation of rhodopsin was discovered in some fish species (anchovy cone photoreceptor outer segments), where it is contained in transversely-oriented lamellar membranes [8,9,10](Fineran and Nicol 1978; Zueva, 1981; Kondrashev et al., 2012). Additionally, rhodopsin mobility was significantly restricted in some species [11](Govardovskii et al., 2009), explained by its possible oligomerisation [12] (Roberts, 2014). These data suggest that the photoreceptors may be intrinsically sensitive to polarization, at least in some vertebrate species.
On the other hand, the same anchovy and some other fish have specialized guanine crystals surrounding the outer segments that may work as polarized light reflectors [13,14](Denton and Nicol 1965, Brady et al. 2013). The suggested polarization sensitivity in birds is due to specialized oil droplets present in the optic path of only one of the cone photoreceptors in the specialized cone pair [15,16,17,18](Young and Martin 1984; Cameron and Pugh, 1991; Zueva at al. 2003; Åkesson, 2014). All of these additional elements present in the optical path may work as specialized filters. Here we suggest a novel possibility that the specialized optical channels inside the transparent cells may work as additional polarization filters in front of the photoreceptors.
We have earlier proposed that bundles of nanoscale filaments (with each fiber 10–12 nm in diameter) in the transparent cells of the optical tract may directly participate in the transmission of light energy, and developed a physical model of the light energy transfer in long carbon-based conductive nanostructures [1,2]. We developed a quantum mechanism (QM) of the electromagnetic field (EMF) transmission by a waveguide [1, 2], a capillary with conductive walls, with the diameter significantly smaller than the EMF wavelength. We suggested that the intermediate filaments found in the transparent cells may be the ideal match to the nanotube-based model, because of their diameter (10–12 nm) and because their axial structure resembles that of nanotubes, with a low-density core and high-density walls, according to the X-ray diffraction data [19] (Strelkov et al., 2003). Thus, our models provide the theoretical background for the experimental results obtained earlier by different authors that implicate the specialized intermediate filaments in the cell transparency [1,2]. Note that genetic deletions or mutations, or chemical modifications of these intermediate filaments may lead to transparency loss [20,21,22,23,24], underlining the importance of their structure for their light-guiding properties.
Interestingly, the retinal Müller cells (MC) and their intermediate filaments should be included into the optical path before photoreceptors in vertebrates, as they were found to transfer light to the cones in their inverted retina [25] (Franze et al., 2007). We found [1, 2] that the QM reproduces the high efficiency of the EMF transmission by the nanoscale tubes, provided their shape is optimized. We also proposed that such mechanism may explain light transparency of the MC, without the exact knowledge of the waveguide chemical structure [1,2]. Generically, we model each of the waveguides/channels in the bundle by an axisymmetric tube with conductive walls. Note that extended π-conjugated carbon systems are electric superconductors, typical examples being single-wall carbon nanotubes and graphene [32–37].
The optical selectivity in different nanoscale systems has been explored quite intensively before [37–49]. Recently we applied an approach proposed by Makarov et al. [1] to explore spectral selectivity in axisymmetric nanoscale waveguides [2]. We reported that the transmission spectra of the model waveguides have a well-defined spectral band, its width dependent on the waveguide diameter and wall thickness. Thus, we concluded that the MC waveguides composed of bundles of specialized intermediate filaments may transmit visible light within a determined spectral range, dependent on the geometrical parameters of the individual filaments. Presently, we extend the modeling approaches developed earlier [1,2] to explore the planar polarization selectivity in the optical waveguides (including the specialized intermediate filaments in Müller cells, etc), allowing them to function in the optical tract as polarization filters in front of the photoreceptors. Generally, polarization selectivity arises in less-than-axially-symmetric waveguides. In particular, here we analyze light polarization in the waveguides with elliptical cross-section in function of the a/b ratio, a and b being the semiaxes of the ellipse, by using both the perturbation theory and the numerical analysis of the complete model.
II. The Theoretical Model and Methods
Recently, we presented the basic theoretical description of the light (Electromagnetic ield, EMF) transmission by nanochannels [1]. Since the diameter of the intermediate filaments is about 10 – 20 nm, the EMF can not be transmitted by such channels in the classic description of the Maxwell theory. Therefore, we proposed that the EMF transmission by such channels should be described by the Quantum Mechanism (QM) based on the Quantum Confinement (QC) of the excitations in long structures of small transverse size [1]. In the first approximation, we described these channels as long hollow cylinders structure with conductive walls. A well-known example of such molecular systems that we already considered is given by the single-wall carbon nanotubes (SWCNT), which are electrically conductive due to an extended conjugated π-electronic system of their carbon backbone [1]. Thus, the external EMF interacts with the intermediate filaments, inducing formation of the excited electronic states, delocalized over the entire length of the filament. Due to the geometry of the intermediate filaments, the excited states mainly emit in the two end zones of the filament, with the photons immediately reabsorbed by the photosensor cell [1]. Alternatively, the excitation may be transferred directly from the filament to the sensor cell chromophores, without generation of a photon. Presently, we use the main ideas of the previously developed theoretic description [1].
In the present study, we extend the earlier developed modeling approaches describing light transmission by intermediate filaments, present, for example, in Müller cells. This section analyzes the polarization selectivity of the optical channels in Müller cells and other biological systems using the earlier developed models and methods, including a model for the EMF transmission by optical channels [1,2]. Note that the channel diameter and wall thickness are much smaller than the wavelength of light, with the wall thickness and the diameter of the optical channel being the model parameters. This model employs quantum confinement (QC) to describe the EMF transmission by the optical channels [1,2]. Presently we use the same model to analyze the polarization selectivity of the optical channels in function of their geometric parameters. We analyze a waveguide with a coaxial elliptical cross-section using both the perturbation theory and the direct numerical analysis. Note that both of the these theoretical approaches were initially proposed earlier [1,2].
A. The quantum confinement model
Presently we extend the earlier developed theoretical models [1,2] to the waveguides with an elliptic tube symmetry, analyzing the light transmission by a coaxial waveguide with an elliptic cross-section (see Figure AI.1), where the ellipse is described by
| (1) |
Here aext and bext are the semiaxes of the external ellipse, aint and bint are the semiaxes of the internal ellipse, with , L is the length of the device. The Laplace operator in the elliptic cylinder reference system (ξ,η,z; ECRS) may be represented as shown in the Appendix, while the Schrödinger equation for the electron in the ECRS is given by:
| (2) |
or
| (3) |
where
| (4) |
| (5) |
above, ξ is a positive real value, η ∈ [0, 2π], and
| (6) |
We analyzed the problem for the following boundary conditions:
| (7) |
The solution of the z-dependent part is given by:
| (8) |
| (9) |
Thus, we obtain the complete wavefunction in the form:
| (10) |
The Ψ(ξ, η) functions may be determined approximately for small eccentricities, i.e. for a/b − 1 << 1, using the perturbation theory. Alternatively, the problem may be solved numerically for any a/b value. Next, we describe both approaches.
B. The Perturbation Theory Approach
The Laplace operator in the elliptical system may be presented as a sum of two terms [56] (see the Appendix):
| (11) |
where
| (12) |
Note that the first term coincides with the Laplace operator in the cylindrical reference system (CRS), while the second term adds the contributions unique to the elliptic cylinder reference system (ECRS). We used both terms in the perturbation-theory analysis. The following relations represent the perturbation operator in terms of the CRS variables:
| (13) |
| (14) |
Thus, we may obtain the expressions for ξ, η of the ECRS in terms of ρ, φ of the CRS. The solutions of the Schrödinger equation with the Laplace operator (12a) have been obtained earlier, and were used here [1]. Using the zero-order set of the electronic states in the axisymmetric system, their energies, and the previously proposed methods to calculate the light transmission efficiency [1], we calculated numerically the polarization factor of the transmitted light in function of a/b. We made these calculations in the first-order perturbation theory, with the perturbed states and the perturbation matrix elements given by:
| (15) |
These calculations were performed using the earlier developed methods, with appropriate modifications to the respective homemade FORTRAN code [1,2]. The simulations used two different parameter sets of the optical channel: 3.0 or 4.0 nm wall thickness, 5 nm internal radius, 10.0 µm channel length, and 34700 or 19500 cm−1 energy of the transmitted light. The results were presented in terms of the relationship:
| (16) |
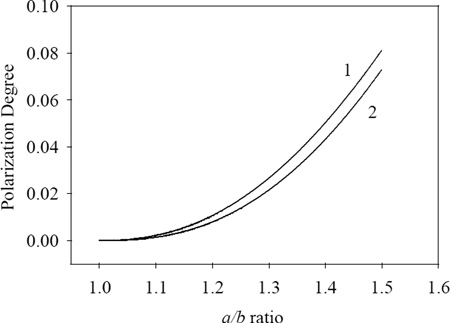
where Wa is the calculated output energy with the polarization parallel to the larger axis and Wb is the calculated output energy with the polarization perpendicular to the larger axis, both obtained for the input light with P = 0. The a/b ratio varied from 1.0 to 1.5, with Fig. 1 showing the results obtained for the two model systems.
Figure 1.
Perturbation-theory calculations for the elliptic-tube model: (1) 3.0 nm wall thickness, 5 nm internal radius, 10.0 µm channel length, 34700 cm−1 energy of the incident EMF radiation; (2) 4.0 nm wall thickness, 5 nm internal radius, 10.0 µm channel length, 19500 cm−1 energy of the incident EMF radiation.
Fig. 1 shows that the polarization angle increases from zero to about 0.08, being larger for the higher-energy radiation, although the calculated difference between the two parameter sets is less than 0.01. We shall discuss these results in detail below.
C. The Numerical Analysis
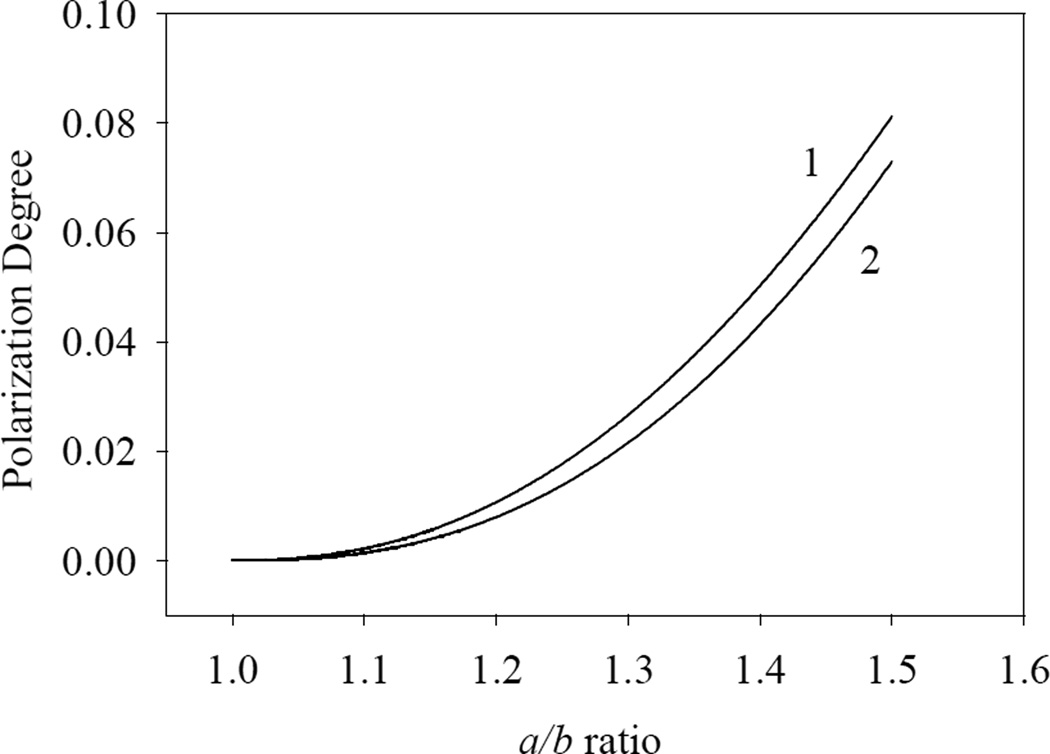
The Eq. (3,a) was solved numerically using the finite-difference methods as described earlier [1]. Fig. 2 shows the polarization angle calculated for the same two parameter sets, in function of the a/b ratio.
Figure 2.
Numerical analysis of the elliptic-tube model: (1) 3.0 nm wall thickness, 5 nm internal radius, 10.0 µm channel length, 34700 cm−1 energy of the incident EMF radiation; (2) 4.0 nm wall thickness, 5 nm internal radius, 10.0 µm channel length, 19500 cm−1 energy of the incident EMF radiation.
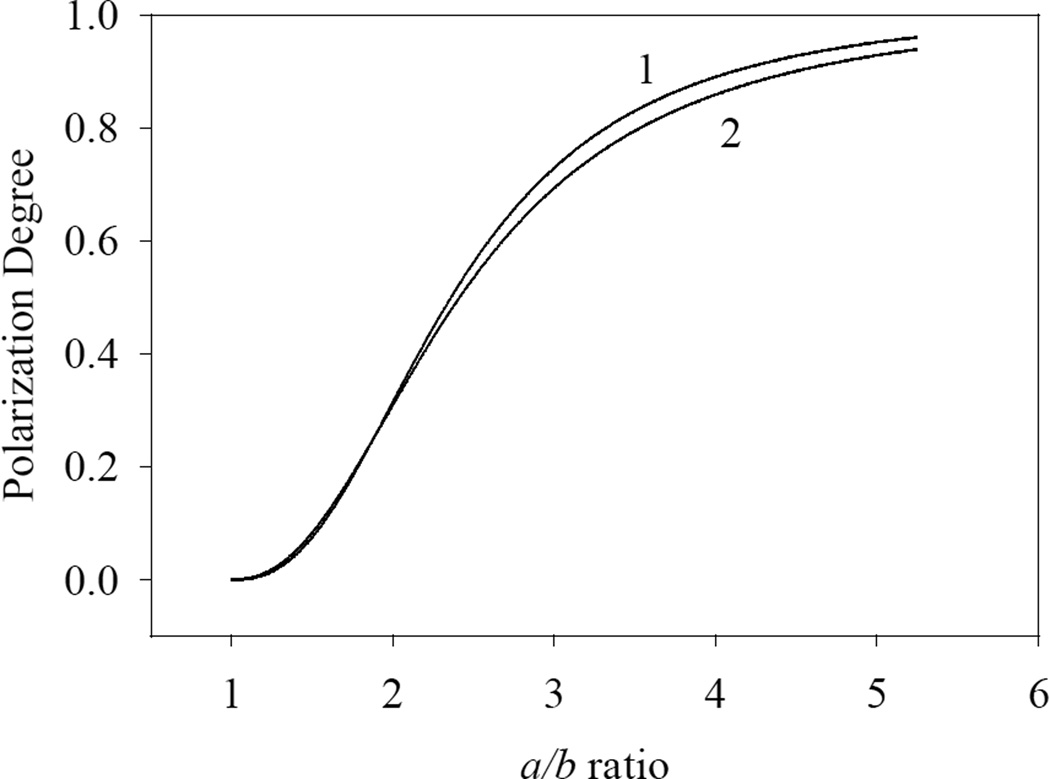
Fig. 2 shows that the polarization angle achieves values close to unity for both of the parameter sets at the a/b ratio of 5.5. We compared the results obtained in the two approaches for a/b < 1.5. The values calculated by the perturbation theory are typically slightly smaller than those obtained by the numerical analysis, with the maximum relative differences below 1%. Therefore, the perturbation theory adequately describes the degree of polarization at a/b < 1.5.
III. Experiments on a Thin-film Waveguide
We discussed above the theoretical models analyzing the polarization selectivity of the optical waveguides. The model was primarily addressing the intermediate filaments, existing in the structure of the light-transmitting cells, such as the Müller cells. Presently we are unable to perform experiments on biological objects; therefore, we measured the angle of polarization experimentally on a thin-film model waveguide, a Cr metal track deposited on AlN substrate with 0.1×1.0 cm size and variable thickness, in the nanometer range. Two fiber-optical lightguides were connected to the track at both ends, normal to the track surface. The effective diameter of the light-guides was 1.0 mm, equal to the track width. The transmission spectra of the Cr tracks were recorded with a polarizer in the beam path.
A. Experimental Methods and Techniques
The experimental setup described earlier [2] was partially modified for the present measurements. Commercial AlN substrates 12.5 mm in diameter and 1.5 mm thick (Valley Design Corp.) were used to deposit rectangular Cr tracks 0.1×1.0 cm2 in size with the preset thickness in the nm range. Commercial Cr targets (Sigma/Aldrich) were used to produce nanotracks on a commercial sputtering/thermo-evaporation Benchtop Turbo deposition system (Denton Vacuum). A copper foil mask was used to deposit the Cr tracks of the required geometry. The track thickness was controlled by XRD, with the XPert MRD system (PANalytic) calibrated using standard nanofilms of the same material. The estimated absolute uncertainty of the Cr track thickness was 7%; the relative uncertainties were much smaller, determined by the shutter opening times of the deposition system.
The transmission spectra were recorded on a Hitachi U-3900H UV-Visible Spectrophotometer. The spectral peak maxima and widths were located using the PeakFit software (Sigmaplot). The AlN substrates with the deposited Cr tracks were mounted into the sample holder. Two multimode fiber-optic light-guides with 1.0 mm diameter were also mounted on the same sample holder, normal to the track. The light-guides were transparent in the range from 800 to 445 nm.
Thus, one end of each of the light-guides was in direct contact to the Cr track, while the other one was mounted into a home-made fiber-optic adaptor, connecting the experimental assembly to the spectrophotometer, with a linear polarizer installed into the input beam path. The blank scan made with the two sample ends of the light-guides connected directly to each other was subtracted from the experimental spectra.
B. Experimental Results and Analysis
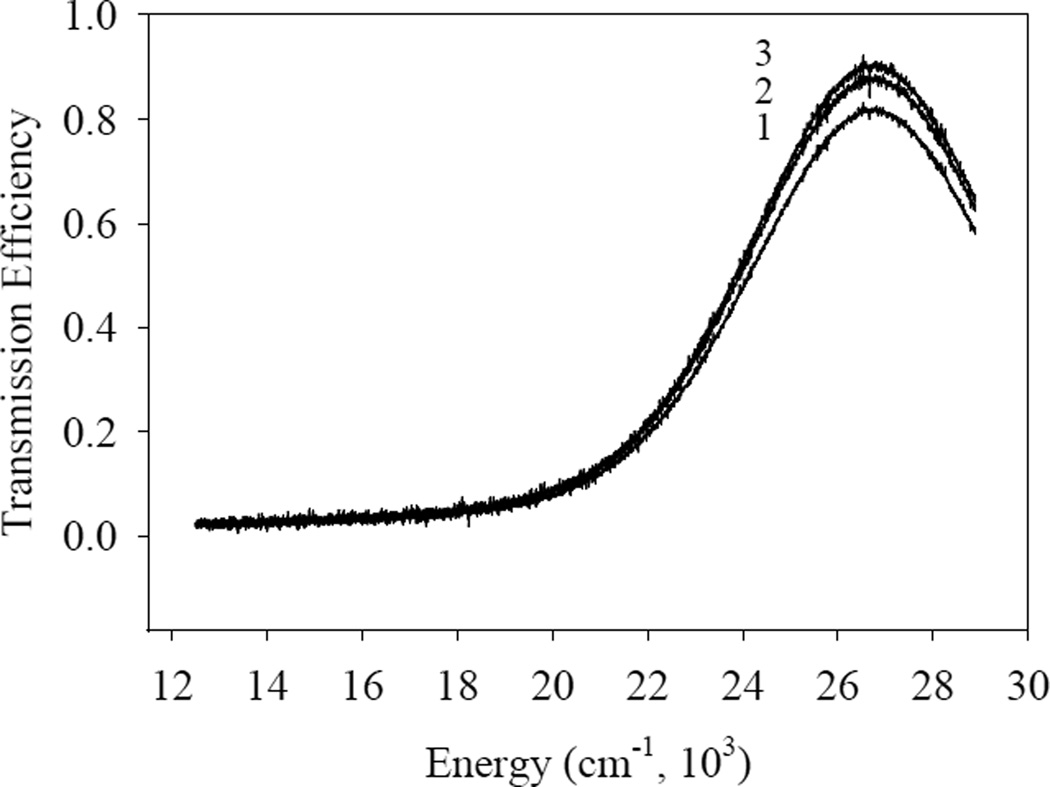
We tested two different Cr tracks: a) 0.1×1.0 cm2 × 6.4 nm; and (b) 0.1 × 1.0 cm2 × 8.3 nm. Fig. 3 shows the spectra of the sample (a) without polarizer at different distances between the ends of the two light-guides connected to the sample.
Figure 3.
Transmission spectra of the 0.1×1.0 cm2 ×6.4 nm Cr sample: (1) 9 mm distance between the input and output light guides; (2) 7 mm distance; (3) 5 mm distance.
We see that the transmitted light intensity is only weakly dependent on the distance between the ends. We therefore conclude that the entire surface of the Cr track emits light almost homogeneously in function of the distance from the input light-guide.
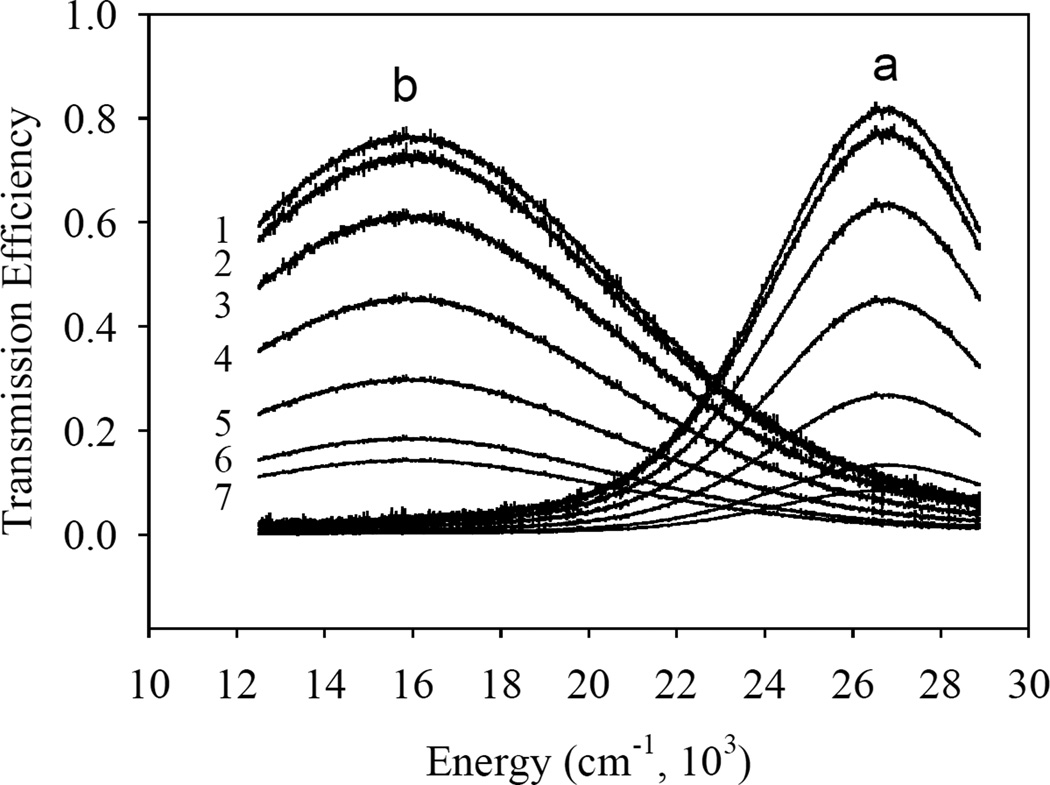
Fig. 4 shows the transmission spectra of the samples (a) and (b), recorded with the polarizer in the beam path, at different angles, with the zero angle corresponding to the electric field vector E parallel to the track axis.
Figure 4.
Transmission spectra of the (a) 0.1×1.0 cm2 × 6.4 nm and (b) 0.1×1.0 cm2 × 8.3 nm Cr tracks on the AlN substrate recorded with the polarizer at different angles: (1) 0°; (2) 15°; (3) 30°; (4) 45°; (5) 60°; (6) 75°; (7) 90°.
Comparing the spectra of the Fig. 4, we conclude that the polarization efficiencies of the Cr tracks are quite high, with the thinner sample (a) having a slightly higher polarization efficiency.
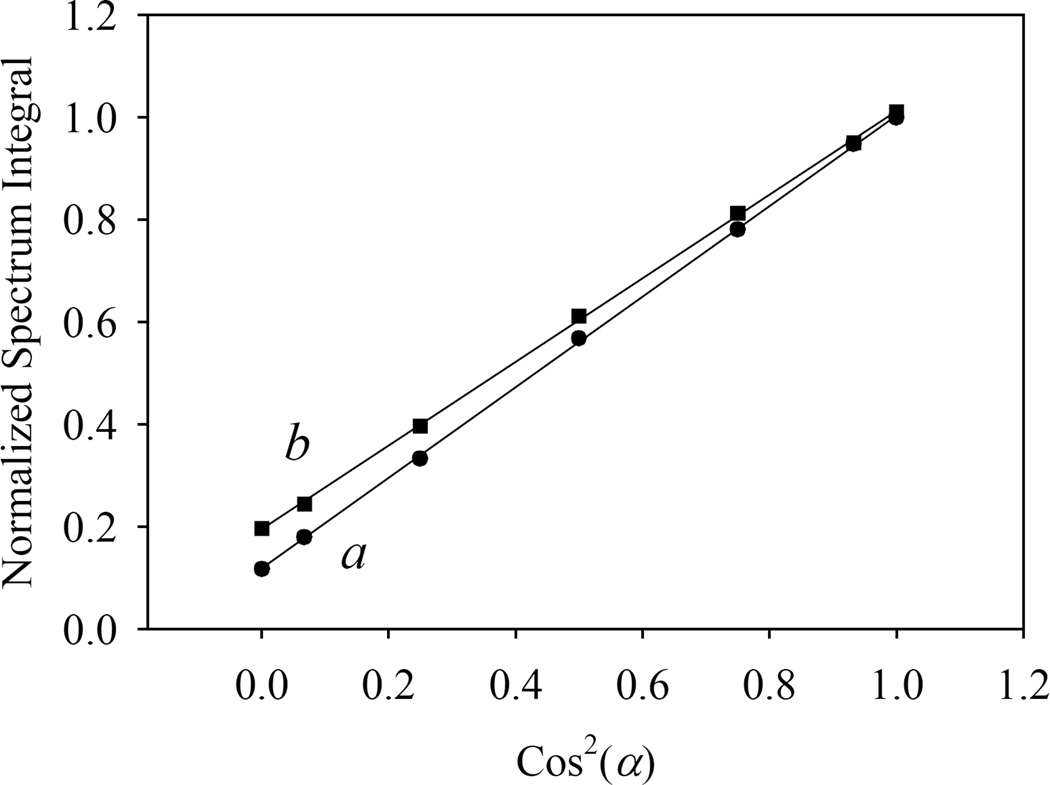
Thus, the Cr sample tracks are efficient light polarizers. Recalling that the transmission of a linear polarizer varies as Cos2(α), α being the angle between the electric of linearly-polarized light and the polarization direction, we plotted the integrated transmission spectra in function of Cos2(α), with the results shown in Fig. 5.
Figure 5.
The integrated transmission spectra vs. the theoretical Cos2(α) factor, describing the intensity in function of the polarizer angle, for the two samples: (a) 0.1×1.0 cm2 × 6.4 nm and (b) 0.1×1.0 cm2 × 8.3 nm.
The data of Fig. 5 were fitted by linear functions (y = ax + b) with the parameters: a = 0.886, b = 0.117; and a = 0.817, b = 0.195, respectively, and very good quality fits (R2 > 0.9997), showing that the results follow the Cos2(α) behavior expected for the linearly polarized light.
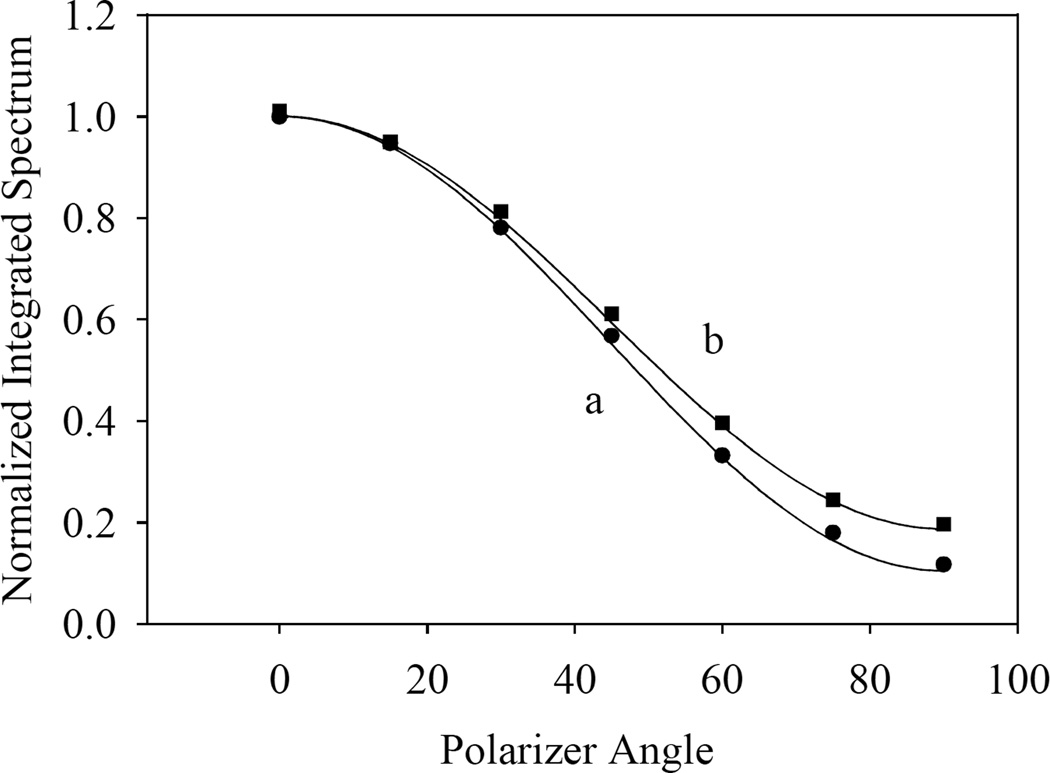
Now, we modified the earlier developed theoretical model [1,2] in order to accommodate waveguides of rectangular cross-section, using the same physical ideas, with the band width in the absorption spectrum determined by the interactions between the discrete quantum states and the quasi-continuum conduction zone, and by the density of states in the latter. The home-made FORTRAN code [1,2] was suitably modified to accommodate rectangular waveguides. Fig. 6 shows that model calculations reproduce the experimental results quite well.
Figure 6.
The integrated transmission spectra vs. the polarizer angle for both samples (a) 0.1×1.0 cm2 × 6.4 nm and (b) 0.1×1.0 cm2 × 8.3 nm. The experimental points are compared to the model calculations (lines).
We conclude this section by stating that nanosized waveguides have intrinsic polarization selectivity, provided they are not cylindrically symmetrical, as seen both in model calculations and in the experimental study of the rectangular Cr tracks. We believe that the same mechanism of the polarization selectivity may operate in the optical channels of live cells build of bundles of the elliptic intermediate filaments.
IV. Discussion
We investigated the polarization selectivity of the nanosized optical waveguides theorically, and tested it experimentally on a model strip nanostructure. The polarization selectivity for the transmitted light arises when we consider a waveguide with an elliptic cross-section, being absent for a waveguide of a cylindrical cross-section. Note that the transversal dimensions of the waveguide are much smaller than the wavelength of the light, transmitted in the form of an excited state (exciton) from one end of the waveguide to the other. Presently we considered a model based on quantum confinement in nanostructured conductive materials [1,2]. This model was used to explore the EMF energy transmission by cylindrical channels and more complex systems with axial symmetry; the same approach was presently used to analyze the spectral selectivity of long optical nanochannels. Note that the light transmission by nanowires, nanotubes and similar systems has been partially analyzed using the plasmon-polaron theory [50– 52], with the transmission spectrum also dependent on the wire radius. The transmission spectra of the nanowires were significantly wider [50–52] than those obtained previously [1,2] for the thin-walled tubes, while comparable to those obtained for the thick-walled tubes [2]. This result is dependent on the γ, in the classical case of the plasmon-polaron theory, this parameter describes the friction coefficient describing the electron motion in such systems; in the QM description, this parameter describes the relaxation rate of the excited electronic state. The parameter γ increases with the wall thickness of the nanotubes [1,2], resulting, as already mentioned, in the spectral widths of the plasmon excitations being comparable to the spectra obtained for the thick-walled tubes, as calculated using the QM mechanism [2].
The polarization selectivity of the optical channels made of filaments was analyzed in the present study using the quantum confinement approach for nanotubes with elliptic cross-section. We found that such channels produce polarization degrees in excess of 95% for an ellipse with a/b = 5.5, functioning as an efficient polarizer.
Our theoretical model was primarily addressing biological systems transparent to light, including bundles of intermediate filaments in Müller cells. We proposed [1,2] that intermediate filaments are built of electrically conductive proteins [53,54]. Indeed, the structure of protein molecules was found to facilitate long-range electron transfer in solutions and even in dry solid state, transmitting electric currents much higher than those recorded for saturated organic substances with comparable thickness. In fact, proteins demonstrate the electrical conductivity comparable to that of nanowires made of carbon nanotubes [53]. Taking into account the information on the electric conductivity of proteins and the experimental data obtained in the present study, we conclude that the intermediate filaments with non-circular cross-section should have some polarization selectivity as regards light/excitation transmission. Thus, the currently proposed quantum confinement model should appropriately describe the intermediate filaments, wire-like biological structures built of proteins and present in many types of cells. We believe that the intermediate filaments found in transparent cells should be described quite well by the nanotube-based model, due to their small diameter (usually, 10 to 12 nm) and because their cross-section closely resembles that of a thick-walled nanotube, with the lower-density core and the higher-density walls, according to the X-ray diffraction data [19]. Note that SWCNTs are indeed an efficient EMF polarizer, in full agreement with the presently discussed theoretic ideas [58]. While the sensitivity of the vertebrate eye is well-documented behaviorally, the physical basis of its polarization sensitivity is still under investigation. There is a possibility of the optical polarizing filters existing in front of the photoreceptors, or else the photoreceptors themselves may have an intrinsic polarization sensitivity [5] (Wehner, 2014). Currently, we have reasons to believe that nature may use both possibilities in different vertebrate species. Here we suggest a novel mechanism of the polarization-dependent filtering by specialized nanofilaments existing in the retina, namely the intermediate filaments in the Müller cells, which transmit light to the cone photoreceptors in the vertebrate retina [25; 55] (Franze, 2007; Agte et al., 2011). The mechanism discussed in the present study is radically different from those proposed previously in the literature; however, it is a definite possibility. We believe that this mechanism may also be at work in other transparent biological systems with specialized filaments.
V. Conclusions
We report that the model device shown in Fig. A1 has the polarization selectivity as regards the transmission of light. The polarization degree of the transmitted light strongly depends on the a/b ratio, transforming strongly elliptic nanofibers into efficient optical polarization filters. We believe that similar structures exist in nature, including intermediate fiber bundles in Müller cells, conducting light from the internal surface of the retina to the sensory photoreceptor cells (cones).
Presently we discussed the polarization selectivity of the specialized intermediate filaments in the Müller cells. As we proposed, apparently all of the biological objects that are transparent to visible light have bundles of intermediate filaments that may directly transmit the light energy through the cell avoiding light absorption by various chromophores present in other cellular structures. We infer that some of these light-transmitting intermediate filaments may be polarization-selective, provided they have an elliptic cross-section. To illustrate the developed theoretical models, we tested the polarization selectivity of nanometer-thick macroscopically-sized rectangular Cr strips. The models modified to accommodate waveguides of rectangular cross-section describe the experimental data with good accuracy. We believe that the proposed mechanism of the polarization selectivity may be at work in transparent live cells that transmit light over bundles of intermediate filaments.
Highlights.
Development of a new theoretical models of light polarization paaed by nano channels;
Development of quantum models of light polarization transmitted by intermediate filaments;
Development of theory of experimental methods to prove theoretical models.
Acknowledgements
V. M. is grateful for the NASA EPSCoR grant PR NASA EPSCoR (NASA Cooperative Agreement NNX13AB22A), and M. I. is grateful for the NIH grant G12 MD007583 that partly supported the present research.
Appendix
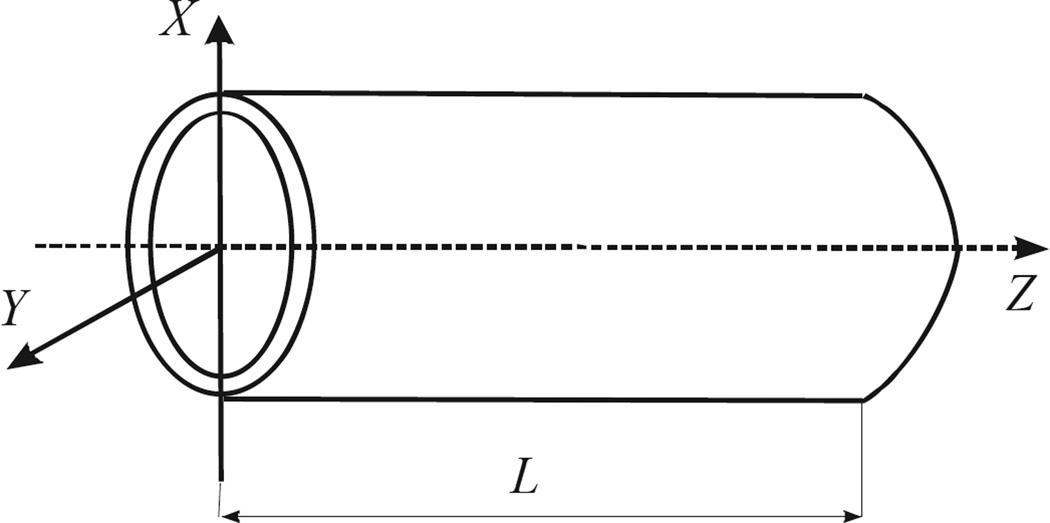
Presently, we analyzed the light transmission by a co-axial cylindrical system with the elliptic cross-section (Fig. A1). The geometry is described by the equations:
| (A1) |
Here aext, bext are the semiaxes of the external, and aint, bint of the internal ellipse (Fig. A1), , L is the length of the device.
The Laplace operator in the ECRS referential (ξ,η,,z) may be presented as follows:
| (A2) |
The latter relationship may be rewritten using the variables of the CRS referential (ρ,φ,z), using the following relations coupling the two reference systems:
| (A3) |
Thus, the Laplace operator in the ECRS expressed in terms of the derivatives calculated in the CRS is given by [56]:
| (A4) |
Thus, the latter operator is a sum of two terms:
| (A5) |
where
| (A6) |
The operator (A2) was used in the numerical analysis of the problem using finite difference methods [57], while the operator (A5) was used in the perturbation-theory approach.
Figure A1. The model system: a thick-walled elliptic cylinder.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Makarov VI, Zueva L, Khmelinskii I, Inyushin M. On the Mechanism of Light Transmission by Müller Cells. http://arxiv.org/abs/1503.02923. [Google Scholar]
- 2.Khmelinskii I, Zueva L, Inyushin M, Makarov VI. Model of Spectral Selectivity of Müller Cell Optical Channels, Submitted to J. Chem. Phys. 2015 Apr 1; [Google Scholar]
- 3.Horváth G, Barta A, Hegedüs R. Polarization of the Sky. In: Horváth, editor. Polarized Light and Polarization Vision in Animal Sciences. Springer: Series in Vision Research 2; 2014. [Google Scholar]
- 4.Muheim R. Behavioral and physiological mechanisms of polarized light sensitivity in birds. Philos Trans R Soc Lond B Biol Sci. 2011 Mar 12;366(1565):763–771. doi: 10.1098/rstb.2010.0196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wehner R. Polarization Vision: A Discovery Story. In: Horváth, editor. Polarized Light and Polarization Vision in Animal Sciences. Springer: Series in Vision Research 2; 2014. [Google Scholar]
- 6.Brown PK. Nat New Biol. 1972;236:35–38. doi: 10.1038/newbio236035a0. [DOI] [PubMed] [Google Scholar]
- 7.Cone RA. Nat New Biol. 1972;236:39–43. doi: 10.1038/newbio236039a0. [DOI] [PubMed] [Google Scholar]
- 8.Fineran BA, Nicol JAC. Philos Trans R Soc Lond B. 1978;283:25–60. [Google Scholar]
- 9.Zueva LV. J. Evol. Biochem. Physiol. 1981;17:420–425. [Google Scholar]
- 10.Kondrashev SL, Gnyubkina VP, Zueva LV. Vision Res. 2012;68:19–27. doi: 10.1016/j.visres.2012.07.005. [DOI] [PubMed] [Google Scholar]
- 11.Govardovskii VI, Korenyak DA, Shukolyukov SA, Zueva LV. Mol. Vis. 2009;15:1717–1729. [PMC free article] [PubMed] [Google Scholar]
- 12.Roberts NW. Polarization Vision of Fishes. In: Horváth, editor. Polarized Light and Polarization Vision in Animal Sciences. Springer: Series in Vision Research 2; 2014. [Google Scholar]
- 13.Denton EJ, Nicol JAC. J. Mar. Biol. Assoc. UK. 1965;45:705–709. [Google Scholar]
- 14.Brady PC, Travis KA, Maginnis T, Cummings ME. Proc Natl Acad Sci USA. 2013;110:9764–9769. doi: 10.1073/pnas.1222125110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Young SR, Martin GR. Vis Res. 1984;24:129–113. doi: 10.1016/0042-6989(84)90098-1. [DOI] [PubMed] [Google Scholar]
- 16.Cameron DA, Pugh EN. Nature. 1991;353:161–164. doi: 10.1038/353161a0. [DOI] [PubMed] [Google Scholar]
- 17.Zueva LV, Golubeva TB, Kerov VS, Zuev AV. J. Evol. Biochem. Physiol. 2003;39:724–731. Translated from russian Zhurnal Evolutionnoi Biokhimii I Fiziologii, 2003, v.39, N6: 586–591. [PubMed] [Google Scholar]; Zueva LV, Govardovskii VI. J. Evol. Biochem. Physiol. 1991;27:506–512. [Google Scholar]
- 18.Åkesson S. The Ecology of Polarization Vision in Bird. In: Horváth, editor. Polarized Light and Polarization Vision in Animal Sciences. Springer: Series in Vision Research 2; 2014. [Google Scholar]
- 19.Strelkov SV, Herrmann H, Aebi U. Bioessays. 2003;25:243–251. doi: 10.1002/bies.10246. [DOI] [PubMed] [Google Scholar]
- 20.Bloemendal H. Proctor lecture. Disorganization of membranes and abnormal intermediate filament assembly lead to cataract. Invest Ophthalmol Vis Sci. 1991;32:445–455. [PubMed] [Google Scholar]
- 21.Matsushima H, David LL, Hiraoka T, Clark JL. Exp Eye Res. 1997;64:387–395. doi: 10.1006/exer.1996.0220. [DOI] [PubMed] [Google Scholar]
- 22.Clark JL, Matsushima H, David LL, Clark JM. Eye (Lond) 1999;13(Pt 3b):417–424. doi: 10.1038/eye.1999.116. [DOI] [PubMed] [Google Scholar]
- 23.Alizadeh A, Clark J, Seeberger T, Hess J, Blankenship T, FitzGerald PG. Invest Ophthalmol Vis Sci. 2003;44:5252–5258. doi: 10.1167/iovs.03-0224. [DOI] [PubMed] [Google Scholar]
- 24.Oka M, Kudo H, Sugama N, Asami Y, Takehana M. Mol. Vis. 2008;25:815–822. [PMC free article] [PubMed] [Google Scholar]
- 25.Franze K, Grosche J, Skatchkov SN, Schinkinger S, Schild D, Uckermann O, Travis K, Reichenbach A, Guck J. Proc Natl Acad Sci USA. 2007;104:8287–8292. doi: 10.1073/pnas.0611180104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mintmire JW, White CT. Phys Rev Lett. 1998;81:2506. [Google Scholar]
- 27.Frank S, Poncharal P, Wang ZL, de Heer WA. Science. 1998;280:1744. doi: 10.1126/science.280.5370.1744. [DOI] [PubMed] [Google Scholar]
- 28.Sinnott SB, Andreys R. Sciences. 2001;26:145. [Google Scholar]
- 29.Kataura H, Kumazawa Y, Maniwa Y, Umezu I, Suzuki S, Ohtsuka Y, Achiba Y. Synthetic Metals. 1999;103:2555. [Google Scholar]
- 30.Iakoubovskii K, Matsui H, Matsuzaki H, Okamoto H, Miyata Y. Journal of Physical Chemistry B. 2006;110:17420. doi: 10.1021/jp062653t. PMID 16942079. [DOI] [PubMed] [Google Scholar]
- 31.Iakoubovskii K, Minami N, Kazaoui S, Ueno T, Miyata Y, Yanagi K, Kataura H, Ohshima S, Saito T. Journal of Physical Chemistry C. 2008;112:11194. doi: 10.1021/jp062653t. [DOI] [PubMed] [Google Scholar]
- 32.Mintmire JW, White CT. Phys Rev Lett. 1998;81:2506. [Google Scholar]
- 33.Frank S, Poncharal P, Wang ZL, de Heer WA. Science. 1998;280:1744. doi: 10.1126/science.280.5370.1744. [DOI] [PubMed] [Google Scholar]
- 34.Sinnott SB, Andreys R. Critical Reviews in Solid State and Materials Sciences. 2001;26:145. [Google Scholar]
- 35.Kataura H, Kumazawa Y, Maniwa Y, Umezu I, Suzuki S, Ohtsuka Y, Achiba Y. Synthetic Metals. 1999;103:2555. [Google Scholar]
- 36.Iakoubovskii K, Matsui H, Matsuzaki H, Okamoto H, Miyata Y. Journal of Physical Chemistry B. 2006;110:17420. doi: 10.1021/jp062653t. [DOI] [PubMed] [Google Scholar]
- 37.Iakoubovskii K, Minami N, Kazaoui S, Ueno T, Miyata Y, Yanagi K, Kataura H, Ohshima S, Saito T. Journal of Physical Chemistry, C. 2008;112:11194. doi: 10.1021/jp062653t. [DOI] [PubMed] [Google Scholar]
- 38.Amanda JH, Van Duyne RP. J. Am. Chem. Soc. 2002;124:10596–10604. doi: 10.1021/ja020393x. [DOI] [PubMed] [Google Scholar]
- 39.Nien Li-Wei, Chao Bo-Kai, Li Jia-Han, Hsueh Chun-Hway. Plasmonics. 2015;10:553–561. [Google Scholar]
- 40.SSulaiman A, Kausar MZ, Reza AW, Latef TA, Ullah MH, Karim ME. Sensors. 2015;15:8787–8831. doi: 10.3390/s150408787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Reza AW. Sensors. 2015;15:8787–8831. doi: 10.3390/s150408787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Chen Li, Zhou W, Qiang Z, Brown GJ. Spectral Selectivity of Photonic Crystal Infrared Photodetectors. Dhar Nibir K, Dutta Achyut K, Islam M. Saif., editors. Nanomaterial Synthesis and Integration for Sensors, Electronics, Photonics, and Electro-Optics. Proceedings of SPIE. 2006;6370:63701I. Proc. of SPIE, Vol. 6370 63701I-1. [Google Scholar]
- 43.Krier A. Mid-infrared semiconductor optoelectronics. London: Springer; 2006. [Google Scholar]
- 44.Lin SY, Fleming JG, Li ZY, El-Kady I, Biswas R, Ho KM. Journal of Optical Society America B. 2003;20:1538. [Google Scholar]
- 45.Xi Y-G, Wang X, Hu X-H, Liu X-H, Zi J. Chinese Physics Letters. 2002;19:1819. [Google Scholar]
- 46.David SV, Hayden BY, Gallant JL. Journal of Neurophysiology. 2006;96:3492. doi: 10.1152/jn.00575.2006. [DOI] [PubMed] [Google Scholar]
- 47.Adelson EH, Bergen JR. J. Opt. Soc. Am. 1985;A2:284. doi: 10.1364/josaa.2.000284. [DOI] [PubMed] [Google Scholar]
- 48.Freeman RG, Grabar KC, Allison KJ, Bright, Davis RM, Guthrie JA, Hommer AP, Jackson MB, Smith MA, Walter PC, Natan DG. M Science. 1995;267:1629–1632. doi: 10.1126/science.267.5204.1629. [DOI] [PubMed] [Google Scholar]
- 49.McFarland AD, van Duyne RP. Nano Letters. 2003;3:1057–1062. [Google Scholar]
- 50.Zayats AV, Smolyaninov II. J. Opt. A: Pure Appl. Opt. 2003;5(56959):S16–S50. PII: S1464-4258(03)56959-8. [Google Scholar]
- 51.Oulton RF, Sorger VJ, Zentgraf T, Ma RM, Gladden C, Dai L, Bartal G, Zhang X. Nature. 2009;461:629. doi: 10.1038/nature08364. [DOI] [PubMed] [Google Scholar]
- 52.Chen J, Perebeinos V, Freitag M, Tsang J, Fu O, Liu J, Avouris P. Science. 2005;310:1171. doi: 10.1126/science.1119177. [DOI] [PubMed] [Google Scholar]
- 53.Ron I, Pecht I, Sheves M, Cahen DI. Acc Chem Res. 2010;43:945–953. doi: 10.1021/ar900161u. (ISSN: 1520–4898) [DOI] [PubMed] [Google Scholar]
- 54.Gerster D, Reichert J, Bi H, Barth JV, Kaniber SM, Holleitner AW, Visoly-Fisher I, Sergani S, Carmeli I. Nature Nanotechnology. 2012;7:673–676. doi: 10.1038/nnano.2012.165. [DOI] [PubMed] [Google Scholar]
- 55.Agte S, Junek S, Matthias S, Ulbricht E, Erdmann I, Wurm A, Schild D, Käs JA, Reichenbach A. Biophys J. 2011;101:2611–2619. doi: 10.1016/j.bpj.2011.09.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Korotun AV. Solid State Physics (Russian) 2014;56:1107–1200. [Google Scholar]
- 57.Krissinel EB, Shohirev NV. Solution of Non Stationary Diffusion Equation by Finite Difference Method. Novosibirsk: AS USSR, SB, IChK&C, NSU, Scientific Council SB AN USSR, Mathematical Methods in Chemistry; 1987. Reprint. [Google Scholar]
- 58.Nojeh A, Ioakeimidi K, Sheikhaei S, Pease RFW. Photoemission from single-walled carbon nanotubes. J. Appl. Phys. 2008;104:054308. [Google Scholar]