Balanced SSFP-like steady-state imaging using small-tip fast recovery (STFR) with a spectral pre-winding pulse

Abstract

Purpose

Small-tip fast recovery (STFR) imaging has been proposed recently as a potential alternative to balanced steady-state free precession (bSSFP). STFR relies on a tailored “tip-up” RF pulse to achieve comparable signal level as bSSFP, but with reduced banding artifacts and transient oscillations, and is compatible with magnetization-preparation pulses. Previous STFR implementations used 2D or 3D pulses spatially tailored to the accumulated phase calculated from a B0 field map, making the steady-state STFR signal contain some T2* weighting. Here we propose to replace the spatially tailored pulse with a recently introduced spectrally selective “pre-winding” pulse that is precomputed to a target frequency range. The proposed “spectral-STFR” sequence produces T2/T1-weighted images similar to bSSFP, but with reduced banding and potentially other benefits.

Theory and Methods

We investigated the steady-state signal properties of spectral-STFR using simulations, and phantom and human volunteer experiments.

Results

Our simulation and experimental results showed that the spectral-STFR sequence has similar signal level and tissue contrast as bSSFP, but has a wider passband and more consistent banding profiles across different tissues (e.g., less hyperintense signal at band edges for low flip angles). Care is needed in designing the spectral RF pulse to ensure that the small tip angle approximation holds during RF transmission.

Conclusion

Spectral-STFR has similar tissue contrast as bSSFP but a wider passband and more consistent CSF/brain tissue contrast across the passband. The spectral-STFR sequence is a potential alternative to bSSFP in some applications. Compared to a spatially tailored STFR sequence, spectral-STFR can be pre-computed, is easier to implement in practice, and potentially has more uniform image contrast and minimal T2* weighting.

Introduction

Balanced steady-state free precession (bSSFP) is a rapid imaging sequence that has high signal-to-noise ratio (SNR) efficiency and useful tissue contrast, but suffers from banding and other artifacts (7), and is generally incompatible with magnetization-preparation pulses. Small-tip fast recovery (STFR) imaging has been proposed recently as a potential alternative to bSSFP (5, 9, 10). STFR relies on a tailored tip-up RF pulse (Fig. 1) and a gradient crusher to achieve comparable signal level as bSSFP, but with potential for reduced banding artifacts and transient oscillations. In addition, unlike bSSFP, STFR is compatible with magnetization preparation pulses, such as fat saturation or magnetization transfer pulses (13).

Figure 1.

Proposed spectral-STFR pulse sequence. Spectral pre-winding pulses are used for both tip-down and tip-up excitations in this paper. (a) Steady-state spin path. The tip-down pulse “prephases” the spins to have a phase equal to the negative of half the accumulated free precession phase −θ_f/2 = ωT_free/2, where T_free is the free precession time. After readout, the spin is tipped back to the z-axis by a pulse tailored to the phase θ_f/2. (b) Pulse sequence timing diagram.

However, previous STFR implementations used spatially tailored pulses that introduce some T2* weighting (10), unlike bSSFP that refocuses microscopic B0 inhomogeneities and therefore produces more pure T2 (and T1) tissue contrast. Here we propose to modify the STFR sequence using a spectral tip-up pulse, specifically the “pre-winding” RF pulse proposed recently by Asslander et al. (1). This modification removes the intra-voxel dephasing-induced T2* weighting in spatial-STFR, making the contrast more similar to bSSFP, and has the additional advantage that tip-up pulses can be precomputed to a target frequency range and do not rely on detailed patient-specific fieldmap (B0) information. This paper compares this new “spectral-STFR” sequence with bSSFP in terms of (1) signal level, (2) brain tissue contrast, and (3) off-resonance signal (banding) profile, using Bloch simulations and phantom and in vivo imaging experiments.

Theory

In (5,9), we described the theory and implementation of STFR in detail. There are two key ideas in STFR: First, after readout, a tip-up radio-frequency (RF) pulse tailored to the accumulated phase during free precession is transmitted to bring spins back to the longitudinal-axis, which “fast recovers” the transverse magnetization and preserves it as longitudinal magnetization for the next TR. Second, after the tip-up pulse, an unbalanced gradient is played out to dephase residual transverse spins (9). Figure 1 shows the spin path and an example sequence diagram of the proposed spectral-STFR sequence, where α (red waveform) and -β (blue waveform) correspond to the tip-down and tip-up parts, respectively. We use an unspoiled sequence (constant RF phase over time) here since it is less sensitive to phase mismatch between pre-winding pulse and actual accumulated phase than RF-spoiled STFR (9).

Unlike bSSFP, which typically has short slice-selective RF pulses that can be approximated by instantaneous rotations, the relatively long RF pulses in spectral-STFR can incur significant signal decay (“finite RF pulse effects” (2)). This T2 decay mechanism is exacerbated by the fact that the instantaneous flip angle during RF excitation can go well beyond the final target angle. Since the detailed shape of the spectral RF pulse will vary depending on, e.g., target bandwidth and details of the pulse design implementation (as described below), we did not derive an analytic signal model for spectral-STFR but instead rely on Bloch simulations for steady-state signal calculations.

Methods

Spectral RF pulse design

We use spectral pre-winding pulses for both tip-down and tip-up excitations in our current implementation. The tip-down pulse is tailored to the following spectrum: d(Δω) = sin αe^{(iΔωT_free/2)} where α is the flip angle (uniform for all spins), Δω is a vector containing the range of target off-resonance frequencies ¹, and T_free is the free precession time between tip-down and tip-up excitations. After readout, the spins will have phase −ΔωT_free/2, and a tip-up pulse is tailored to this to bring all spins back to the longitudinal axis. The tip-up pulse is designed by first designing an intermediate tip-down pulse with negative B0 field map, and then negating and time-reversing this intermediate pulse (5). The target excitation pattern for this intermediate pulse is determined by Bloch simulation of the tip-down and free precession. The effective flip angle of the tip-up pulse is usually smaller than the tip-down pulse in STFR due to T2 decay during the free precession, leading to a lower RF power for the tip-up pulse. Note that in previous spatial designs, d is a function of position, but here d is a function only of off-resonance frequency.

We compute the RF waveform under the small tip angle approximation (6, 12); specifically, we solve $\widehat{b}=\underset{b∊{\mathbb{C}}^{N_s}}{\text{argmin}}\parallel \mathit{A}\mathit{b}-\mathit{d}\left(\omega \right){\parallel }_2^2+\mu {\mathit{b}}^{\prime }\mathit{b}$, where µ is the Tikhonov Regularization parameter controlling the tradeoff between RF power and excitation accuracy. A is the small tip system matrix with a_ij = ıγM₀e^{ıΔω_i(t_j−T))}. Unlike the conventional small tip angle system matrix (12), there is no phase encoding term ık_j · r_j in A here since all gradients are set to zero for spectral selectivity.

Simulations

We designed spectral pre-winding RF pulses with 10° flip angle and +/−75 Hz target bandwidth. We evaluated the RF pulse design for different Tikhonov regularization parameters. We also simulated the steady-state signals for spectral-STFR and bSSFP using T1/T2 values for gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) (8), over a 300 Hz bandwidth with 4.9 ms readout time to compare the banding profile and tissue contrast.

Imaging experiments

To evaluate the steady state signal level and demonstrate the banding reduction of STFR, we acquired RF-spoiled gradient echo (SPGR), bSSFP and spectral-STFR images of a GE resolution phantom using a GE 3.0 T scanner and a birdcage T/R headcoil. We designed a spectral-STFR pulse covering the B0 bandwidth (BW) in the target slices (−75 Hz to 75 Hz). Spectral-STFR used a 10° flip angle, which is expected to produce similar signal as bSSFP with 20° flip angle (9). The pulse lengths were 2 ms for each RF pulse, and a 3D readout was used with 256×256×65 sampling, 24×24×32 cm field of view (FOV), and 62.5 KHz receive bandwidth, resulting in a 4.9 ms readout time, including dephasing, rephasing, and phase encoding gradients, and 10 ms TR, which also includes a crusher after the tip-up pulse. We used a large readout FOV in z to eliminate aliasing from untargeted slices since the spectral pre-winding pulse is not spatially selective. For comparison, SPGR/bSSFP images were acquired with the same resolution, 10°/20° flip angle, and 10 ms/7 ms TR.

A healthy volunteer was imaged with the same hardware setup as the phantom experiments. We acquired a low resolution 3D B0 map solely to estimate and specify the target off-resonance range. We designed a spectral-STFR sequence (10° flip angle) targeted to −120 to +50 Hz. The pulse lengths were 2 ms for each RF pulse. We determined that the specific absorption rate (SAR) of our sequence was moderate; specifically the integrated total RF power of our spectrally tailored pulse was approximately equal to a 35° sinc pulse of time-bandwidth 6 and duration 1.2 ms. The 3D readout was the same as in the phantom experiment. For comparison, bSSFP images were acquired with the same resolution, 20° flip angle, and 7 ms TR.

Results

Figure 2 demonstrates the impact of regularization parameter choice on the spectral pulse. Although the final excitation flip angle is small in our implementation (e.g., 10° in this simulation), the instantaneous flip angle during RF transmission can be large (Fig. 2 (c)). Therefore, the small tip approximation can be inaccurate for this pulse design. To keep the small tip approximation accurate, we used a large regularization parameter that keeps the flip angle relatively small during the whole excitation process. With relatively large regularization (a), the small tip approximation matches the Bloch simulation very well, but both deviate somewhat from the target. With small regularization (b), the small tip prediction matches the target, but the actual excitation does not match the target. All experiments in this study used µ = 0.6.

Figure 2.

Effect of regularization parameter µ on spectral pre-winding RF pulse waveforms. (a) Large µ (0.6) can suppress the b1 magnitude and keep the small tip angle approximation accurate (i.e., small difference between the small tip angle approximation and Bloch simulation). (b) With small µ (0.02), the excitation predicted by the small tip model matches the target, but the actual excitation pattern has large deviations from the target since the small tip approximation does not hold for the entire RF transmission window. (c) Actual flip angle of a spin during the RF pulse can be larger than the final target flip angle. Small regularization leads to higher intermediate flip angle and therefore less accurate excitation. We designed pulses with µ = 0.6 in this study.

Figure 3(a) shows the simulated steady-state signal for spectral-STFR and bSSFP for gray matter (GM), white matter (WM), and CSF over a 300 Hz bandwidth with 4.9 ms readout time. In this figure, the sequence was designed for 150 Hz target bandwidth, with µ = 0.6. The flip angles are 10° and 20° for spectral-STFR and bSSFP, respectively. Both sequences have high CSF signal, as expected. Spectral-STFR has wider passband (≈ 50% increase in FWHM). The banding shape of spectral-STFR is more consistent across different tissues, e.g., the CSF signal near the band edge is less hyperintense relative to the corresponding bSSFP curve. Figure 3(b) shows the simulated banding profile for fat. Fat can have high signal depending on its off-resonance, which is a potential drawback of spectral-STFR. Potential ways to suppress the fat signal are discussed further below.

Figure 3.

Simulated steady-state banding profile of (a) spectral-STFR and bSSFP for WM, GM, and CSF, using T1 and T2 values from (8), and (b) spectral-STFR for fat with T1 and T2 values from (4). RF pulses were designed for 150 (+/−75) Hz target bandwidth, 4.9 ms Tfree, and β = 0.6. In general, spectral-STFR and bSSFP have similar tissue contrast (e.g., high CSF signal). Spectral-STFR has wider passband than bSSFP. The banding shape for spectral-STFR is similar for different tissue types, indicating a relatively consistent tissue contrast across the frequency band. Fat can have high signal in spectral-STFR.

Figure 4 shows the field map, SPGR, bSSFP, and the spectral-STFR image for 4 slices spanning 4 cm in the phantom. As predicted from simulation, the banding artifacts observed in bSSFP are successfully reduced in the STFR images, and the STFR signal is relatively uniform across the passband.

Figure 4.

Comparison of SPGR, bSSFP, and spectral-STFR imaging in a phantom. (a) B0 map. (b) Steady-state images, displayed on a common grayscale. Spectral-STFR (bottom row) reduces the banding artifact seen in bSSFP (middle row), and has a relatively uniform signal with varying off-resonance. Both bSSFP and STFR generally achieve higher signal than SPGR (top row).

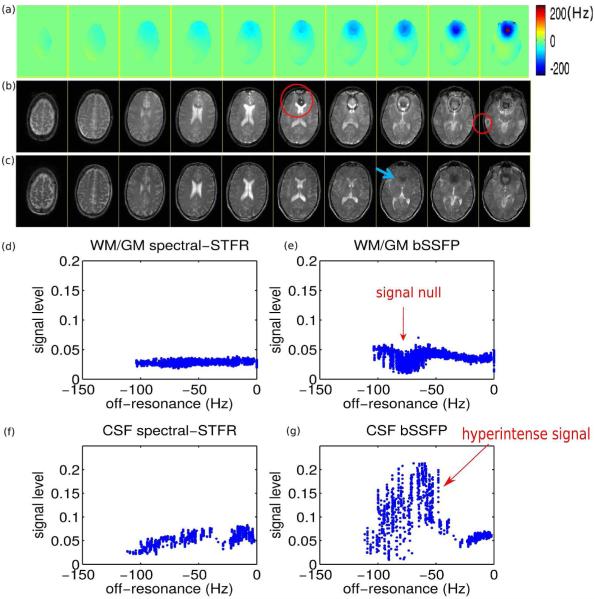
Finally, Fig. 5 shows the field map, bSSFP image, and spectral-STFR image for 10 slices spanning 7 cm in a volunteer. The banding artifacts observed in bSSFP that are within our target frequency range have been successfully removed in the STFR images. As off-resonance goes beyond the target range, signal drop occurs (e.g., blue arrow), but the rate of this drop across the object is smaller than the bSSFP signal drop, agreeing with our simulations (Fig. 3). The fat signal in spectral-STFR varies more across the object compared to bSSFP, also in agreement with simulations.

Figure 5.

Comparison between bSSFP and spectral-STFR imaging: representative human volunteer imaging results. (a) B0 field map, and (b) bSSFP and (c) spectral-STFR images. Spectral-STFR has similar image contrast as bSSFP, but no hyperintense CSF signal near the edge of the bands. In addition, spectral-STFR successfully reduces the banding artifacts (e.g, red circle) within the target frequency range. Signal drop-out occurs when off-resonance goes beyond the target range (e.g., blue arrow). (d-g) Plots of signal level versus off-resonance frequency in CSF and WM/GM ROIs (segmented manually from slices 6-8). The center of target bandwidth is −35 Hz and 0 Hz for spectral-STFR and bSSFP, respectively. Balanced SSFP shows signal drop near −70 Hz, which is corrected at the corresponding frequency (-105 Hz) in spectral-STFR. The CSF signal variation of spectral-STFR is much smaller than bSSFP near the edge, agreeing with the simulation in Fig. 3. The fat signal near the skull shows high variability in the spectral-STFR images, as expected from the simulation results in Fig. 3(b).

Discussion

The key to the proposed spectral-STFR sequence is to design a spectral pre-winding pulse that can successfully prephase the spins over a wide bandwidth. With the same pulse design method, the only way to increase the target bandwidth is to reduce the readout time, leading to lower resolution, lower SNR, or increased number of TRs. There are several potential improvements of the pulse design method. As shown above, the actual flip angle during RF transmission can be large enough to significantly violate the small tip angle approximation, so a large tip design may therefore generate better results. We have evaluated the large tip design method proposed by Grissom (3) that combines optimal control with a linearization of the Bloch equation. Using this method, we can design pulses that target wider bandwidths (result not shown); however we found that the final pulse is sensitive to how the algorithm is initialized (initial pulse). In (3), a scaled small tip design pulse was used as the initial pulse. We have found that if we use a large regularization parameter in designing the initial pulse, the resulting large tip design does not improve the result significantly compared to the initial pulse. If we use a small regularization parameter, the large tip design step can significantly improve the result and perfectly match the target phase pattern, but leads to high RF power and low steady-state signal (not shown). The fact that a high power pulse leads to a lower steady-state signal for short T2 species may be useful to enhance image contrast (e.g., increase the contrast between CSF and WM/GM, or between CSF and cranial nerves). However, the general problem of enforcing the RF power constraint while designing a pulse that matches the target phase remains an open problem.

In this paper we used non-spatially-selective RF pulses for both tip-down and tip-up excitations, however it is possible to limit the FOV by using a spatially selective tip-down excitation (e.g., a conventional slice-selective RF pulse) followed by a spectral tip-up pulse. In this case it is necessary to use RF-spoiling to suppress unwanted SSFP-echo signal created by the non-spatially-selective tip-up pulse (5). Another way to limit the FOV may be to use a slab saturation pulse between time-points (3) and (4) in Fig. 1(b). Thirdly, in Cartesian imaging sequences (e.g., spin-warp or EPI) the FOV in the frequency encoding direction is limited by the readout bandwidth.

This paper considered the excitation accuracy following a single shot only, however it may be possible to design the RF pulses for optimal steady-state signal across the target off-resonance bandwidth. For example, in (5, 9) we showed that the steady-state signal is relatively insensitive to flip angle over a certain range (e.g., 10° to 25° for gray matter and white matter). We can therefore partially relax the magnitude (flip angle) constraint or limit the maximum deviation (11) in the pulse design, which may improve steady-state accuracy. Also, a joint pulse design that considers both tip-down and tip-up pulses in one RF pulse design step may be helpful (9).

We observed in our simulations (Fig. 3(b)) and our in vivo experiments (Fig. 5) that fat signal varies significantly with off-resonance, which is a potential disadvantage of our sequence. However, since a key advantage of STFR is the ability to incorporate magnetization-preparation pulses (between time-points (3) and (4) in Fig. 1(b)), as demonstrated in (13), we can incorporate fat-suppression pulses to suppress the fat signal. In our in vivo experiment, the peak of the measured 10 second SAR average is 0.8 W/Kg on our GE scanner, which is well below the 6.4 W/Kg limit. The integrated RF power of a 6 ms SLR fat saturation pulse is only half the integrated power of our spectral-prewinding pulses. So adding this fat saturation pulse to our sequence will not violate the SAR limit. However, adding magnetization preparation pulses can increase the length of the sequence and therefore reduce the SNR efficiency. Alternatively, we may change the readout time to shift fat to the null of its banding profile, but it may be difficult to place fat in a signal null over the whole brain imaging due to B0 inhomogeneity.

Some differences between spectral-STFR and bSSFP should be noted. First, for a given readout duration and acquisition matrix, the total acquisition time for spectral-STFR will be longer, due to the tip-up RF pulses. Second, we observe in our in vivo results that blood signal in large vessels is suppressed in spectral-STFR relative to bSSFP. One possible cause for this is that the phase of flowing blood spins at the beginning and end of the free precession interval may not be consistent, i.e., the phase at end of Tfree may deviate from the predicted phase based on the local off-resonance frequency at the position of the spin at the beginning of the readout interval. Another possibility is that the imaging gradients induce flow-related spin phase due to non-zero gradient first moments, also causing the spin phase at end of Tfree to deviate from the tip-up target excitation phase. This may be problematic for applications that rely on bright blood signal, such as cardiac functional imaging or phase-contrast velocity mapping.

Although the spectral pre-winding pulse does not need spatial off-resonance information, a B0 field map may still need to be acquired in practice to estimate the center of target off-resonance frequency. However, this field map can be in very low resolution. Also, if the scanner can auto-shim the center off-resonance close to 0 in the target region, the B0 field map acquisition step can be avoided.

Finally, we note that the GRASS sequence can also be an alternative to bSSFP in some applications, and produces bright CSF like bSSFP. However, since GRASS relies on multiple-TR echo pathways to form its T2 and T1-weighted steady-state signal, we expect that GRASS is generally less compatible with magnetization preparation compared to STFR. In addition, GRASS is relatively sensitive to flow and motion, which limits its applications. Also, we observed in simulation that for the sequence used in this paper, spectral-STFR has 30% higher signal than GRASS.

Conclusion

We have proposed a new steady-state MRI imaging sequence that combines STFR and a spectrally tailored pulse, and that may offer an alternative to bSSFP in some applications. We have demonstrated that the resulting spectral-STFR sequence has similar tissue contrast as bSSFP but has increased passband width, and more consistent CSF/brain tissue contrast across the passband.