Evaluating the effect of horizontal transmission on the stability of plasmids under different selection regimes

Abstract

In theory, plasmids can only be maintained in a population when the rate of horizontal gene transfer is larger than the combined effect of segregational loss and the decrease of fitness associated with plasmid carriage. Recent advances in genome sequencing have shown, however, that a large fraction of plasmids do not carry the genes necessary for conjugation or mobilization. So, how are so-called non-transmissible plasmids able to persist? In order to address this question, we examined a previously published evolutionary model based on the interaction between P. aeruginosa and the non-transmissible plasmid pNUK73. Both our in silico and in vitro results demonstrated that, although compensatory adaptation can decrease the rate of plasmid decay, the conditions for the maintenance of a non-transmissible plasmid are very stringent if the genes it carries are not beneficial to the bacterial host. This result suggests that apparently non-transmissible plasmids may still experience episodes of horizontal gene transfer occurring at very low frequencies, and that these scattered transmission events are sufficient to stabilize these plasmids. We conclude by discussing different genomic and microbiological approaches that could allow for the detection of these rare transmission events and thus to obtain a reliable estimate of the rate of horizontal gene transfer.

Introduction

Plasmids are accessory genetic elements able to transfer horizontally between bacteria. They carry genes that help their host adapt to new niches and stresses, playing a key role in bacterial evolution.¹ Plasmids frequently code for antibiotic resistance genes, being responsible for the spread of antibiotic resistance and multiresistance among pathogenic bacteria, which is currently a major concern for public health.^2,3

One of the central questions about plasmid biology is how plasmids can be stably maintained in bacterial populations in the long term.⁴ This is challenging to understand due to factors that hinder plasmid survival. Specifically, (i) plasmids produce a cost to the host bacteria,⁵ causing a competitive disadvantage and (ii) plasmids can be lost during cell division (even if it is at a very low rate).⁶ Taken together, these 2 factors predict a constant decline of the plasmid frequency in the population over time.⁷ However, there are factors that counteract the effect of cost and segregational loss and contribute to plasmid maintenance in bacterial populations, such as (i) selection for plasmid-encoded traits, (ii) horizontal transfer of the plasmid between bacteria (mainly by conjugation) and (iii) compensatory mutations alleviating the cost produced by the plasmid.^4,8 The balance among all these factors determines the fate of a given plasmid in a bacterial population.⁹

Previous theoretical studies have argued that plasmids can only be maintained in a bacterial population when they are able to conjugate.^8,10,11 However, recent advances in genome sequencing have shown that, paradoxically, a large fraction of plasmids seem to be “non-transmissible” by conjugation according to their sequence.¹² The mechanisms that allow non-transmissible plasmids to persist are poorly understood. In a recent study we used mathematical modeling, functional genomics and experimental evolution to investigate this problem.¹³ We developed a model system based on the opportunistic pathogen Pseudomonas aeruginosa PAO1 carrying the small non-conjugative plasmid pNUK73, which produces a particularly big fitness cost in this strain (approximately 20% reduction in relative fitness). pNUK73 confers resistance to neomycin, producing an increase in the minimal inhibitory concentration (MIC) of approximately 60-fold in PAO1. After 30 daily passages (300 generations) the plasmid-bearing subpopulation presented compensatory mutations that completely compensated for the cost of plasmid carriage. These mutations putatively inactivated 3 particular chromosomal genes: a helicase carrying an UvrD-like helicase C-terminal domain (PA1372) and 2 contiguous putative serine/threonine protein kinases (PA4673.15 and PA4673.16).

However, the plasmid-free subpopulation was also adapting to the environmental conditions and therefore their fitness also increased relative to the parental strain. This was due to the acquisition of generally beneficial mutations for adaptation to the laboratory conditions. These mutations targeted primarily the diguanylate cyclase gene wspF (PA3703) in our experimental system. Thus, the plasmid-bearing lineage continued to go extinct, albeit at a slower rate. As a result, the population size of the plasmid-bearing lineage was too small for the generally beneficial mutations to fix. The plasmid-bearing populations could be rescued, however, by adding antibiotics. This led to an increase in plasmid-bearing cells population size which allowed generally beneficial mutations to fix. Therefore, we found that positive selection and compensatory adaptation interact to stabilize pNUK73: positive selection increases the probability of compensatory adaptation by increasing the population size of plasmid-bearing lineages, improving therefore the chances of new adaptive mutations in the plasmid-bearing cells. Compensatory adaptation, in turn, increases the effect of positive selection on plasmid stability by slowing the rate at which the plasmid is lost between episodes of positive selection.

Our previous results show that compensation and positive selection help stabilize non-transmissible plasmids over a few hundreds of generations. However, the long-term maintenance of these plasmids remains challenging to understand.¹³ In this commentary we expand the results of our population genetics model to analyze the effects of different regimes of selection as well as the impact of horizontal gene transfer in the long-term stability of these plasmids.

Modeling Plasmid Stability Under Different Selective Regimes

The mechanisms that drive plasmid dynamics in a population, for instance conjugation and segregational loss, are noisy processes that can be studied using a stochastic modeling approach.^14,15 The mathematical model presented in San Millan et al. 2014 is a mean field approximation of this stochastic process.¹³ We use this approach because it allows us to numerically simulate a system of ordinary differential equations to identify the ecological and evolutionary forces that drive plasmid dynamics. For instance, this simple population genetics model predicts that a consequence of having a dynamic population structure with different bacterial types having different stability patterns is that the rate of decay of the plasmid in a mixed population also has to be a dynamic property of the system. Furthermore, differences in susceptibility patterns for different bacterial types imply that the use of antibiotics has the effect of modifying allele frequency in the population and, as a result, the plasmid can become more stable after being exposed to antibiotics.

In our previous work we observed that rare events of selection slowed down plasmid loss but could not halt it completely. Here we used the same model based on pNUK73 and P. aeruginosa to investigate the effect of different selective regimes in the stability of the plasmid and try to find the conditions necessary for long term maintenance. In order to quantify the stability of the plasmid we will use the time elapsed before the plasmid frequency in the population is below a threshold represented with a parameter ϵ > 0 (in the numerical simulations presented in this paper we considered 1%, but found no qualitative differences when evaluating different values of ϵ). Now, let us denote with T the duration of the observation (in our evolutionary experiment T = 32 days) and with t* the interval of time before the frequency of plasmid-bearing cells is below ϵ. We say the plasmid persists when t* > T, that is when the frequency of plasmid-bearing cells at the end of the experiment is larger than ϵ. Figure 1 shows that if we vary the strength (the antibiotic dose) and the frequency (interval of time between periodic exposures) of the selective pressure, there is a region (at high-doses and high-frequencies) in the dose-frequency plane where a non-transmissible plasmid can be maintained indefinitely. Furthermore, if the selective pressure is applied frequently, very low concentrations are able to maintain the plasmid in the population. In agreement with this prediction, a recent experimental study shows that very low concentrations of antibiotics or heavy metals are sufficient to maintain resistance plasmids.¹⁶ Conversely, if the dose is too low or the interval of time between antibiotic exposures too far in between, the plasmid becomes unstable (Fig. 1).

Figure 1.

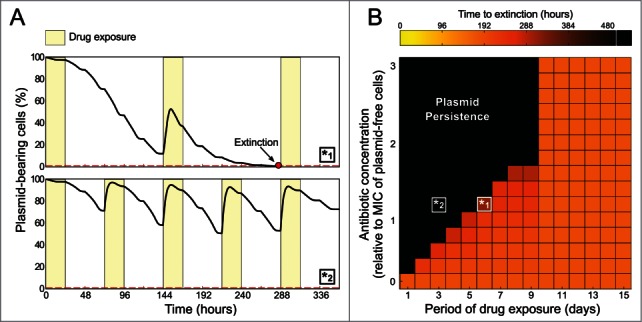
Stability of plasmid pNUK73 under different antibiotic regimes. Numerical simulations of the evolutionary model presented in San Millan et al. 2014 with parameter values determined from experimental data and an extinction threshold of ϵ = 0.01. (A) Frequency of plasmid bearing cells under 2 different selection regimes: same antibiotic dose (25% above the MIC of the plasmid-free cells) but with different frequencies of drug exposure (antibiotic use is represented with yellow bars). Note how when the antibiotic is used once weekly the plasmid-bearing population is driven to extinction (red dot), while if the drug is used twice-weekly the plasmid is able to persist indefinitely. (B) Heat map representing the time to extinction of the plasmid-bearing population when exposed to increasing drug concentrations and different periods of drug exposure (from daily exposure, every 2, d etc.). Note that plasmid persistence is observed only at certain combinations of dose and frequency of antibiotic exposure (black region). The positive selection regimes used to obtain the time-series illustrated in (A) are represented with white boxes in the period-dose plane.

Effect of Horizontal Gene Transfer on Plasmid Stabilization

In our previous work we demonstrated that compensatory adaptation and positive selection interact to stabilize non-conjugative plasmids on a time scale of hundreds of generations. Moreover, in the previous section of this paper we showed, using the same model, that very low concentrations of frequent positive selection could theoretically stabilize non-transmissible plasmids in the short term. However, the maintenance of these plasmids over longer time scales remains enigmatic for several reasons. First, although compensatory adaptation removes the cost of plasmid carriage rapidly, it is only under episodes of early positive selection that the plasmid-bearing lines are able to reach the same fitness as the plasmid-free cells, removing the effective cost of plasmid carriage (by acquiring extra general beneficial mutations). Second, even if plasmid-bearing cells have no competitive disadvantage compared to plasmid-free cells, segregational loss will gradually reduce the frequency of plasmids in the population (as observed in our experiments). Third, plasmid-encoded genes could theoretically move to the chromosome if they were under constant selection, rendering the plasmid redundant. And fourth, even if the pervasive presence of positive selection can explain the maintenance of part of the non-transmissible plasmids, it could not justify the persistence of the small non-transmissible cryptic plasmids carrying no selectable genes, which are also common in nature.^18,19 So, how are non-transmissible plasmids maintained in the population in the long-term?

The study by Smillie et al. (2010) that predicted that approximately 50% of plasmids are non-transmissible by conjugation is based on detecting the presence of genes involved in conjugation and mobilization on the plasmids.¹² Therefore, and as the authors of this study have pointed out, these analyses may underestimate the potential for the horizontal spread of plasmids by other means, such as transduction or natural transformation.¹² In addition, some of the plasmids lacking conjugation-related genes may still be able to undergo conjugation by co-integration into conjugative elements (also known as conduction⁷).

We modified our mathematical model to include horizontal transmission of the plasmid. In particular, we considered that plasmid mobilization occurs through conjugation and, similar to previously published models,^9,14,20 we included a mass action term representing the rate at which plasmid-free cells acquire plasmids from plasmid-bearing donor cells. In our model, the parameter β ≥ 0 will denote the rate of conjugation. Although we are modeling the horizontal transmission by conjugation, we argue that modeling other forms of horizontal gene transfer of the plasmid such as transduction or transformation will produce similar results.

In agreement with previous studies,^8,11 our numerical simulations show we can stabilize a plasmid in a selection regime where the plasmid would be unstable by considering a non-zero probability of horizontal transmission. For instance, if we numerically simulate our model considering a daily usage of antibiotics, then we can identify a range of drug concentrations where the plasmid is unstable if the rate of horizontal transmission is below a certain threshold. Indeed, Figure 2A shows how the plasmid-bearing population is driven to extinction in less than 12 d if we consider the plasmid is non-conjugative (that is, β = 0) but with a horizontal transmission rate as low as β = 5 × 10⁻¹¹ the plasmid-bearing subpopulation recovers and fixes.

Figure 2.

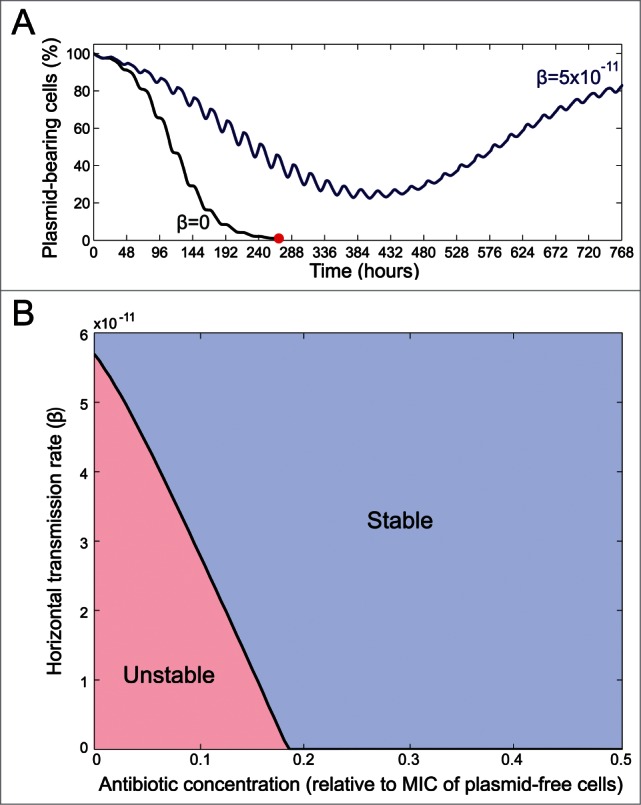
Effects of horizontal gene transfer and positive selection on plasmid stability. Theoretical scenario where antibiotics are used every day at a constant dose and where the rate of horizontal transmission (β) is allowed to change. (A) Comparison between plasmid dynamics for a non-conjugative plasmid (black line) and (blue line) when the rate of horizontal transmission is low (but non-zero) and the antibiotic is deployed at a dose corresponding to 12.5% the MIC of the plasmid-free cells. Note how if β = 5 × 10⁻¹¹ the plasmid-bearing population recovers after an initial decrease in frequency, but if β = 0 the plasmid-bearing population is driven to extinction. (B) By numerically simulating our evolutionary model under different rates of conjugation and intensities of positive selection we can characterize different plasmid stability regions.

The minimum horizontal transmission rate that stabilizes the plasmid can be estimated numerically for different antibiotic concentrations (it is important to highlight that these values should not to be considered as quantitative predictions of the model, as this would be beyond the objectives of this simple model). Of course, at high antibiotic concentrations (close or above the MIC of plasmid-free subpopulation), selection for the plasmid is so high that even a non-conjugative plasmid can be maintained in the population during the duration of our experiment. But, interestingly, the critical value of β that maintains the plasmid is relatively low even when selection for the plasmid is zero, a prediction in agreement with a recently published mathematical analysis showing that a plasmid carrying deleterious genes can still present a non-zero fixation probability.²¹ This result is based on the observation that when the frequency of plasmid-bearing cells is low, then almost all individuals in the population are potential recipients of the plasmid and thus the probability of a horizontal transmission event occurring is increased.

Conclusion

In summary, both our theoretical model and our experimental results support the tenet that it is very difficult for strictly non-transmissible plasmids to persist over the long-term in a bacterial population. These findings tantalizingly suggest that such plasmids may need to experience episodes of horizontal gene transfer in order to persist.

It is possible that some apparently non-conjugative plasmids actually do conjugate.⁷ In addition, although conjugation is arguably the main route for plasmid horizontal transfer, transformation and especially transduction may play an important role in lower rates of plasmid dissemination.¹² It is therefore possible that all plasmids are transmissible, only at extremely different rates. The frequency of transmission will probably determine the fate of the plasmid and will depend on multiple factors such as the genetic composition of the plasmid itself (presence of conjugative genes), the host bacterium genetic background (coexistence of other mobile elements such as plasmids or phages) and environmental factors (inducing or facilitating conjugation or transduction). Further studies will be required to assess the mobility of the a priori non-transmissible plasmids and to identify the underlying horizontal transfer mechanism. In order to achieve this goal, we could use stochastic models of plasmid dynamics to assess the temporal variability observed in the data and use fluctuations in plasmid-bearing frequencies to make inferences about different mechanisms of horizontal transfer driving plasmid dynamics. Furthermore, we conceive 2 possible approaches to determine the actual potential and frequency of transmission of these plasmids:

• –First, the direct experimental observation of plasmid transmission between donor and recipient strains in vitro or in vivo. This is the classical approach used to determine the transfer rate of conjugative elements and has already been successfully applied to the phage-mediated mobilization of plasmids and to plasmid transformation.^22-24 The main advantage of this method is that one can directly observe the transfer events and accurately quantify the frequencies under very controlled experimental conditions. The principal disadvantage of this approach is that the experimental settings usually differ to the real world conditions, and this may bias the results. Also, these methods are time-consuming and low-throughput, since each plasmid-host combination has to be tested individually.
• –Second, the use of ‘phylodynamic’ approaches to measure rate of transmission of elements between strains. Phylodynamic methods have played a big role in our understanding of the transmission of viruses between humans.^25,26 This approach is based on inferring viral transmission dynamics from viral genomic data, using bioinformatics and sophisticated statistical methods. The movement of mobile genetic elements between bacterial strains is analogous to the viral transmission among patients so phylodynamic methods could be adapted to analyze this problem. This approach presents several benefits: the utilization of the increasingly available bacterial and plasmid genomes and existing statistical methods, the possibility of integrating temporal dynamics and ecological contexts in the analysis of the spread of the plasmid (coalescent theory analysis²⁵) and the potential for high-throughput analysis. The main problem of this approach could be that the resolution of the method is hampered by low mutation rate. While viruses mutate at a much higher rate than their human hosts, bacteria and plasmid have much lower mutation rates than viruses, and this could decrease the power of this approach. Finally, alternative approaches such as network modeling coupled with phylogenetic analysis could also provide valuable information about the rate of transmission of plasmids between bacterial strains.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Acknowledgments

We would like to thank Ben S Cooper for his help developing the mathematical model. We thank Karl Heilbron for his helpful comments on the manuscript.