Understanding variation in disease risk: the elusive concept of frailty

Abstract

The concept of frailty plays a major role in the statistical field of survival analysis. Frailty variation refers to differences in risk between individuals which go beyond known or measured risk factors. In other words, frailty variation is unobserved heterogeneity. Although understanding frailty is of interest in its own right, the literature on survival analysis has demonstrated that existence of frailty variation can lead to surprising artefacts in statistical estimation that are important to examine. We present literature that demonstrates the presence and significance of frailty variation between individuals. We discuss the practical content of frailty variation, and show the link between frailty and biological concepts like (epi)genetics and heterogeneity in disease risk. There are numerous suggestions in the literature that a good deal of this variation may be due to randomness, in addition to genetic and/or environmental factors. Heterogeneity often manifests itself as clustering of cases in families more than would be expected by chance. We emphasize that apparently moderate familial relative risks can only be explained by strong underlying variation in disease risk between families and individuals. Finally, we highlight the potential impact of frailty variation in the interpretation of standard epidemiological measures such as hazard and incidence rates.

Key Messages.

• Variation in risk of disease often goes far beyond what is captured by measured risk factors.

• Heterogeneity in risk may be established early in life, and stochastic variation in these processes could be a major contributor in this regard.

• Even a moderate familial relative risk points to the existence of large variations in disease risk between families, and Individuals, across the population.

• Failing to take into account the unobserved heterogeneity between individuals may lead to erroneous interpretations of standard epidemiological measures such as age-incidence curves and hazard ratios.

Introduction

In epidemiology and clinical science, it is often tacitly assumed that the risk of a certain disease is similar among individuals across the population at equal levels of known risk factors. It is often presumed, for instance, that all individuals are vulnerable to the same risk factors, and to the same degree. Differences between individuals tend to be ignored unless they can be expressed in terms of known risk factors such as known genetic properties. However, the fact of the matter is that individuals are generally highly dissimilar also for many unknown, or just partly known, reasons. Indeed, the extent of this heterogeneity is probably not generally appreciated.

Heterogeneity which is unknown, or not represented in available data, is often referred to as frailty, a quantity that varies between individuals. The term frailty comes from the statistical field of survival analysis, where there is a strong interest in this type of heterogeneity. Frailty is usually modelled by assuming that the hazard rate (baseline hazard) for an average individual, $\alpha (t)$, is multiplied by a frailty factor Z that renders the level for a specific individual, i.e. the individual hazard rate is;

$$\lambda \left(t\right)=Z\alpha (t).$$

When we integrate out the variation in Z to get the (observable) population hazard rate, the resultant function is quite different from the baseline hazard α(t). A number of various distributions exists for the frailty Z.^1,2 Note that the baseline hazard may be a function of observed individual covariates, e.g. through a Cox model, and that including a frailty term may improve the fit of such a model.³

A number of diseases exhibit incidence rates that peak at young ages, including cancers like childhood leukaemia and Hodgkin lymphoma, but also schizophrenia, which has recently been analysed from a frailty point of view.⁴ In several cases frailty variation is a reasonable explanation for an early peak in incidence, especially when the disease has a strong heritability, which is the case for diseases like schizophrenia and testicular cancer. The frailty approach has yielded particularly fruitful insights for testicular cancer.^5–8 Furthermore, the so-called frailty models form a basis for the analysis of familial association in cancer incidence.^7–9

One goal of the present paper is to point out the ubiquity of heterogeneity, or varying frailty. We shall also emphasize the role of stochasticity. Furthermore, we will discuss how important indications of frailty variation may be deduced from data on familial disease association. Indeed, moderate familial association implies surprisingly strong variation in risk between individual families. Although understanding frailty variation is important in its own right, it may also be essential in order to correctly interpret statistical analyses in epidemiological studies. Finally, we will cover an issue that has been pointed out in the statistical literature: that not taking into account unobserved frailty variation in statistical analyses may lead to misleading comparisons of hazard rates and incidence rates resulting in, among other things, an artificial cross-over effect.

Heterogeneity between individuals may be high

Individual variation in susceptibility

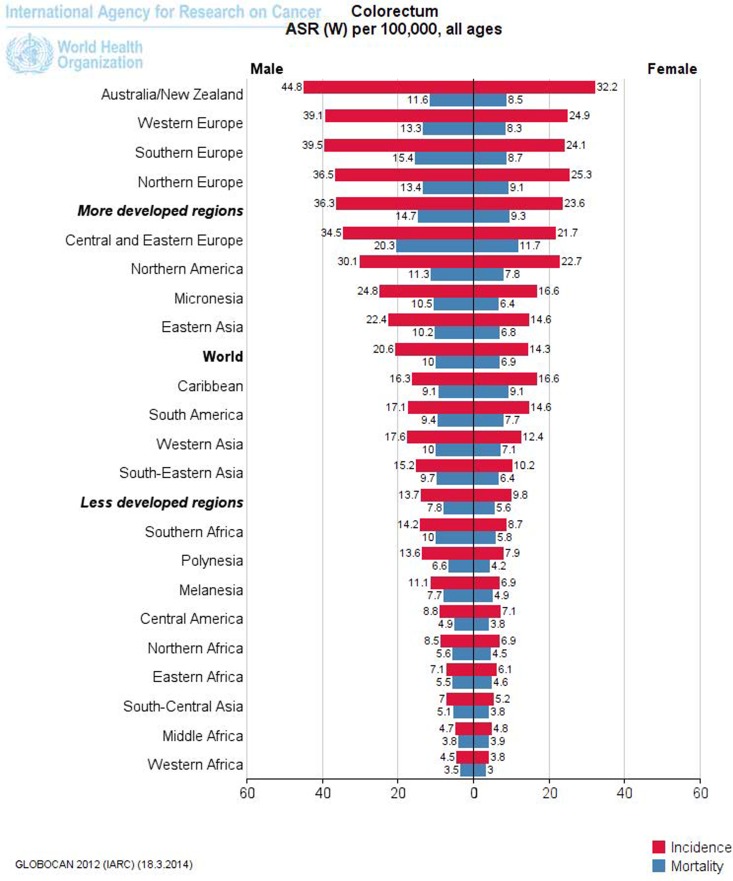
It is often obvious that disease risk is a fluid phenomenon, dependent on environmental and lifestyle risk factors, genes, age and the country of residence, among other things. For example, the risk of being diagnosed with colorectal cancer (CRC) varies widely across different countries; it has increased sharply (in fact more than tripled) in the past few decades in many industrialized countries, and it varies substantially between different countries worldwide. This means that the risk of CRC is not a given quantity, but rather something that varies widely. It would follow that the individual risk of CRC is also a fluid phenomenon; that it varies considerably between individuals even when the outer circumstances are similar. Furthermore, there are large differences in risk across regions (Figure 1).¹⁰ Therefore, it seems logical that the risk will not be homogeneous within regions (especially given the arbitrariness of many borders).¹¹ In short, the variation in risk between regions strongly suggests a considerable variation within regions. This kind of variation has been clearly demonstrated for the USA with regard to the dependence on race of CRC incidence.¹² However, it is highly likely that there are other variations based on both known and unknown risk factors. Large variations in the susceptibility to CRC have been estimated in Norway,¹³ and it has been estimated that only 12% of the US population is susceptible to colon cancer.¹⁴

Figure 1.

Age-standardized rates (ASR) of colorectal cancer, standardized with respect to the world (W) population, in various regions for 2012. Picture constructed by Globocan¹⁰.

Some of the biomedical literature has indicated that there is a high degree of variation in individual cancer susceptibility, thereby supportingthe presence of frailty variation. An interesting paper is that of Balmain et al.¹⁵ where they indicate a strong variation in susceptibility to breast cancer. They studied a population without high-risk individuals (individuals with BRCA1 and BRCA2 mutations excluded), and still suggest a 40-fold difference in the risk of breast cancer between the top 20% and bottom 20% of the study population. Their model also suggests that more than 50% of cancers occur in the 12% of the population that is most susceptible. Peto and Mack¹⁶ reached similar conclusions by studying the relatives of breast cancer patients.They observed a very strong familial risk in monozygotic twins which could only be explained by a large individual variation in risk. They make the following statement: ‘Our most surprising conclusion is that a high proportion of all breast cancers, and perhaps the majority, arise in women at very high risk’. Also, the increased risk of a another breast malignancy after ductal carcinoma in situ of the breast, even after adjustment for type of treatment, points to a large variation between individuals in susceptibility to this disease.¹⁷

Regarding CRC, Win et al.¹⁸ suggest that ‘the risk of developing CRC varies approximately 20-fold between the people in the lowest quartile (average 1.25% lifetime risk of CRC) vs the highest quartile for familial risk profile (average 25% risk)’. Another study of colorectal cancer in DNA mismatch repair gene mutation carriers showed a U-formed distribution in risk distinguishing a high-risk group from a moderate risk-group.¹⁹

It is important to be aware that even for cancers with strong attributable risk factors, frailty remains a large component. In lung cancer, for instance, there are strong indications that some people are much more vulnerable to the damage inflicted by smoking than others, with just 10–15% of smokers developing lung cancer.²⁰

Susceptibility may be established early in life

The notion of ‘early life programming’ has become popular. This idea was formulated in the Forsdahl-Barker hypothesis, which states that the risk of many diseases is strongly influenced by what happens very early in life, e.g. at or prior to birth. Forsdahl²¹ showed a strong correlation between mortality rates for arteriosclerotic heart disease in people aged 40–69 years, and infant mortality in the same birth cohorts within Norwegian counties. Earlier works include that of Ravelli et al.²²who observed babies born to women who were pregnant during the Dutch famine. They found that the weight of these children later in life depended on which trimester the famine affected. Kermack et al. found an association between childhood and adult mortality for different birth cohorts.^23,24 Barker et al. studied heart disease and found that areas in England that had the highest coronary heart disease mortality in the 1980s also had the highest child mortality rates 70 years earlier.^25,26 Since then, many papers have been published indicating a relationship between early life conditions and disease risk later in life,²⁷ including the recent paper by Eriksson et al.²⁸ who assert in the title that ‘Boys live dangerously in the womb’.

Epigenetics is the study of changes in gene expression that are not caused by alterations in the nucleotide sequence of the genome, and examples of cellular mechanisms producing such changes are DNA methylation and histone modification. Epigenetic processes are involved in both mitotic and meiotic cell division, as discussed by Davey Smith.²⁹ In the former, they ensure the transmission of cellular traits, essential for development from the pluripotent zygote to the formed organism. Although it is not clearly established what happens epigenetically during meiosis, these mechanisms clearly play a role in mediating transgenerational inheritance as addressed by Heard and Martienssen.³⁰

Forsdahl-Barker type effects have been tied to such epigenetic alterations.^31,32 Painter et al. showed that the children of those exposed to the Dutch famine in utero during World War II (WWII) were also at increased risk for ill health, which indicates that epigenetic effects in utero can even have transgenerational consequences.³³ Studies from The Netherlands and Scandinavia have shown a decreased risk of testicular cancer for birth cohorts born during WWII compared to those born before and after.^34,35

All these examples suggest that epigenetic alterations early in life may lead to a large degree of heterogeneity between adult individuals in a population.

Different types of variation

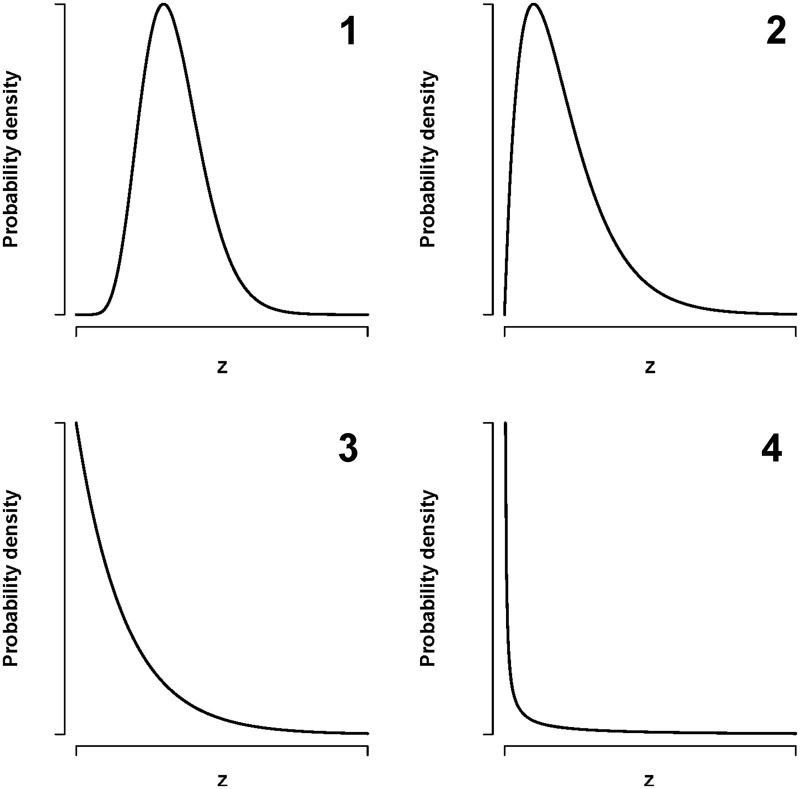
Figure 2 illustrates various ways in which frailty, $Z$, can be distributed between individuals. Panel 1 indicates a frailty that is quite similar across individuals, with some variation. Panel 2 shows a situation where most individuals have a relatively similar frailty, but there are some individuals who deviate quite a lot (the upper tail). This is expressed even more clearly in panel 3, where many individuals have a frailty close to zero whereas there are a number of individuals with high frailty. An even stronger variation is illustrated in panel 4, where most individuals have frailty close to zero but some individuals have a very high frailty. All these types of variation could actually occur. The examples given in this paper show that even the types of variation shown in panels 3 and 4 could be common. However, another issue is how frailty develops over time. One view is that there is a rather small variation in frailty at an early age, which increases over time as the result of the varying stresses of life. An alternative view argues that much of the variation in frailty between individuals is determined very early in life, maybe even prior to birth.

Figure 2.

Various types of possible distributions of the frailty (unexplained risk), $Z$, at an early age. The panels illustrate: (1) small variation in frailty between individuals, (2) large group have moderate frailty, and a smaller group of individuals have a high frailty, (3) very skewed: many individuals have a low frailty and a small group have a high frailty, (4) most individuals have close to zero frailty and a few individuals have a high frailty.

Genetic variation and rare variants

Over past years, genome-wide association (GWA) studies have led to new discoveries about genes and pathways involved in common diseases and other complex traits.³⁶ However, most of the associated single nucleotide polymorphisms (SNPs) have small effect sizes and the proportion of heritability is modest, which has led people to think that rare mutations might be responsible for many diseases.³⁷ Rare gene combinations are difficult to discover in GWA studies, which may explain the apparent lack of genetic effects.^38,39 Also, other authors explain how disease susceptibility may be an effect of common low-penetrance genes or rare gene combinations.^40,41 On the other hand, there are examples of common SNPs explaining a large fraction of the heritability of complex traits in human populations, such as height, by considering all SNPs simultaneously.⁴²

A simple polygenic model, where the risk (or liability) is a linear combination of a (possibly large) number of factors with no single factor dominating, will often be assumed to give a normally distributed risk like that in panel 1 of Figure 2. On the other hand, rare variants make it more likely that we will get skewed variations of the type seen in panels 3 and 4.⁴¹

Heterogeneity may be due to stochastic processes

Randomness and chaos

Heterogeneity, or varying frailty, between individuals may have a number of different explanations: environment, genetics or epigenetics; or it may be a purely stochastic phenomenon. There is a growing recognition in biology that both stochastic variation and chaotic variation are important. By stochastic variation we mean a purely random phenomenon, but it is well known that unpredictable variation may also be produced by deterministic mathematical relations if they are nonlinear; this is often termed chaos. This mathematical theory and its implication for biology and other fields are discussed in detail in a book by Strogatz.⁴³ A characteristic of the chaos phenomenon is that small variations in starting conditions may yield very big differences in the end product; even simple nonlinear equations may have this effect. Hence, dynamic systems may develop in a very complex and unpredictable way. This is seen in many fields, like meteorology, physics and economics and is likely to play a considerable role in biology as well. The sensitive dependence on initial conditions is often popularized by the term ‘butterfly effect’, where one imagines that a butterfly flapping its wings may produce a hurricane on the other side of the world several weeks later. Although randomness and chaos are different mathematical phenomena, they are also related and a mixture of both might be present.Often they cannot be clearly distinguished. In general, random and chaotic variation is to be expected on purely mathematical principles.

Many studies point to large individual differences that do not have obvious explanations, where the above discussion could be relevant. Kirkwood and Finch⁴⁴ show that even genetically identical (i.e. isogenic) worms have great variation in their lifetimes. They stress the random and unpredictable nature of cell damage that occurs with ageing. Epigenetic factors are also likely contributors to these time-dependent processes.

Le and Cheng⁴⁵ studied the problem of why genetically identical cells in the body vary widely in their storage of fat, even when there is no difference in the expression of the particular genes that affect this storage. They found that the differences between cells were due to variation occurring in a cascade of events within an insulin-signalling pathway. These variations were slight at the beginning of the cascade, but led to very different results at the end. Possibly this is an example of chaos; cascade phenomena would be expected to be nonlinear with complex feedback dynamics.

In an interesting Nature letter, Frank and Nowak⁴⁶ suggest a model where random mutations at a very young age can produce a developmental disposition to cancer.The idea is that during the gestational phase, stem cells may mutate and then multiply randomly with long-lasting effects. If the mutation rate is high enough, this initial random variation could be a dominant feature in later life.^47,48

A classic paper by Gärtner, on the importance of apparently random variation in biology, was recently reprinted in the International Journal of Epidemiology with a series of commentaries that discuss the nature of this variation, whether it is due for example to epigenetic effects, and whether nonlinearity could be a source.^49–56

The examples given here show that great individual variation in genetically identical organisms may simply be an accumulation of purely random variation combined with nonlinear dynamics.

Davey Smith offered a fascinating discussion of the importance of randomness in epidemiology.⁵⁷ He asserted that epidemiology cannot capture the pervasive randomness which averages out at the population level. Our point here, though, is that when time is considered, there are tell-tale indications of random variation.

Epigenetic stochasticity

During recent years, there has been growing recognition that environmental exposure affects cancer susceptibility through epigenetic changes, in addition to the traditional gene-environment interactions that can promote mutations. This is particularly relevant in the developmental origins of health and disease hypothesis.⁵⁸ Some authors argue for a paradigm shift, where the old view on the importance of DNA mutations is down-weighted and supplemented by the modern view of epigenetic modifications.⁵⁹ There are, however, indications of an important stochastic component to these modifications, and it has even been speculated that the majority of important epigenetic changes may not be due to the environment, but to random events early in life.⁵⁹ This might explain the large variation that is often observed between genetically identical individuals.⁶⁰

Familial cancer risk points to large individual heterogeneity

For many diseases there is a familial association in risk more than can be explained by chance. A surprising and counter-intuitive issue is that even a moderate familial association points towards a large variation in risk between families. Hence, the existence of a familial association is another argument for the presence of considerable individual heterogeneity in risk.

There is generally a familial association when it comes to cancer risk. For example, in breast cancer some mutations in the genes BRCA1 and BRCA2 confer a very high risk in the specific family. But even in the absence of such ‘important’ genes, sizeable familial association is still observed. Johns and Houlston⁶¹ pointed out that having a first-degree relative with CRC is associated with more than a doubling of one’s risk for the disease, whereas the risk is increased more than 4-fold when one has two first-degree relatives with CRC. The risk of testicular cancer for a brother of a case is increased about 6-fold.^7,8 Tumours of the nervous system also show a strong heritability (standardized incidence ratios around 2, but up to 27 for the rare multiplex families).⁶²

Even familial risks that appear modest, like the relative risk of about 2 seen for relatives of breast or colon cancer patients, still imply a large variation in risk between individuals.^62–64 This has also been pointed out by Moger et al.⁷ and by Aalen⁶⁵ in a cardiovascular disease setting. In fact the variation in individual risk when even small familial risks are observed will typically be of the type in panels 3 and 4 of Figure 2. An interesting quote from Hopper⁶³ stresses this surprising fact:

Even for a disease for which there is only what one might consider in epidemiological terms ‘modest’ familial aggregation (such as a 2-fold increased risk for close relatives of affected), people of the same age and sex must differ greatly in their familial risks of disease (e.g. a 20-fold or more difference in risk between the quarter of the population at lowest familial risk and the quarter of the population at greatest familial risk). This familial risk gradient is in addition to differences due to ‘non-familial’ environmental or lifestyle factors that are specific to individuals. Finding the causes of even a modest proportion of familial aggregation of a disease could be a major step in understanding the causes of the disease itself.

Let us consider a very simple situation: assume that the population is divided into two groups of equal size, and such that the probability of acquiring a specific disease is 1% in one group and 20% in the other. All the members of a given family belong to the same group, be it the high-risk or low-risk group. Consider that the familial relative risk is defined as follows: the conditional probability of developing the disease if a specific family member has acquired it, divided by the average risk of getting the disease. In our example the familial relative risk equals 1.82. Hence a relative risk of 20 at the individual level translates into a very modest familial risk, just as suggested by Hopper.⁶³

Since familial relationships are important for disease risk, it is useful to use study designs that to some extent control for such relationships. Within-pair twin studies are useful in this regard.⁶⁶

Statistical models for familial risk

In order to get a deeper understanding, one has to consider statistical models. The familial risk association depends on two conditions, namely the correlation between the risk factors within a family, and the variation in risk within the population associated with these factors. Assume that the risk depends exponentially on normally distributed risk factors with a correlation ρ, and that s denotes the relative risk associated with a change in the risk factor from mean –2 standard deviations (SD) to mean + 2SD. The familial relative risk, r, associated with a diseased sibling is given by:

$$r=\text{exp}\left\{\rho {\left(\ln s\right)}^2/16\right\},$$ (1)

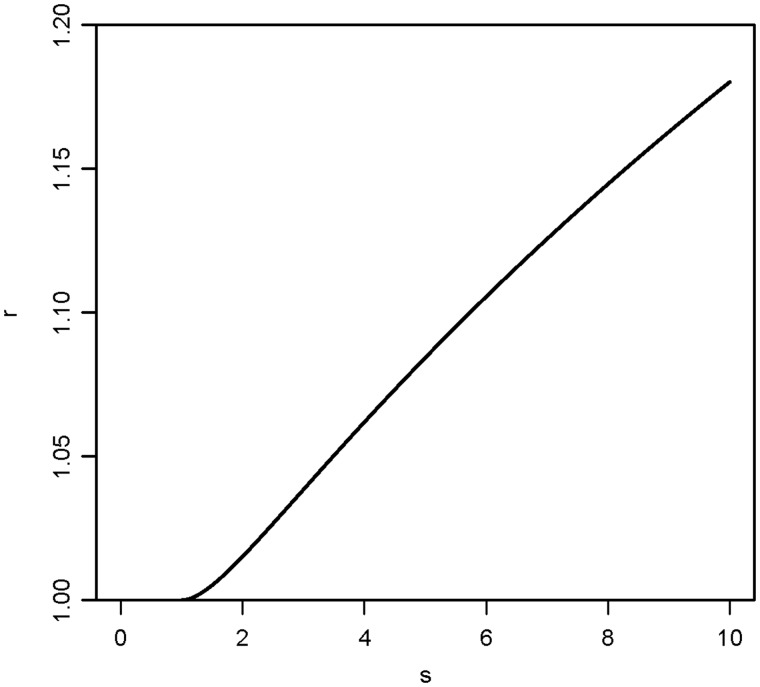
which is a special case of a more general formula given by Aalen.⁶⁵ Assume for instance that ρ = 0.5 which is a very strong familial correlation. Then formula (1) as a function of s is plotted in Figure 3. One sees that even for s = 10, which represents a very strong effect of the risk factor, the value of r is still less than 1.2. Hence, for simple polygenetic inheritance at the risk factor level, the familial relative risk associated with even strong risk factors is very moderate.

Figure 3.

The familial relative risk, r, associated with a diseased sibling as a function of s according to formula (1) in the text, where s denotes the relative risk associated with a change in a risk factor from mean minus two standard deviations to mean plus two standard deviations. The familial correlation, $\rho$, is set to 0.5. Based on normally distributed variation in risk.

In practice, familial association will have several sources, partly genetic and partly a shared environment or culture, or attitude toward various risk behaviours. It can be shown that known environmental influences contribute only very slightly to the observed familial risk association. However, measured risk factors could be poor surrogates for risk factors that are stronger, more strongly familial, and the effect could be somewhat prone to measurement error, for example. ⁶⁴

Formula (1) presumes a normal distribution of the risk factor(s), which one would usually assume for simple polygenetic inheritance. Some skewness might be introduced, which might appear more realistic if some genes have a stronger effect than others, for example due to higher penetrance. To investigate the effect of introducing additional skewness in the distribution of the risk factor(s) into the model, we shall assume that two individuals have a common risk component which is gamma distributed with shape parameter $\delta$. Following Aalen,⁶⁵ the modified familial relative risk, r_F, is given by:

$$r_F={\left\{1+\frac{\ln r}{\delta -2{(\delta \ln r)}^{1/2}}\right\}}^{\delta }.$$ (2)

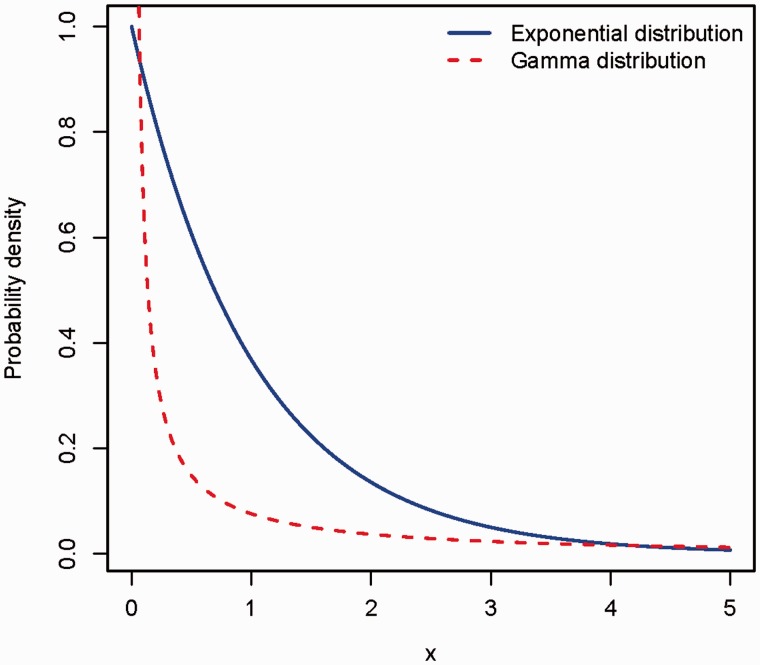
Note that when the shape parameter $\delta$ goes to infinity, this expression will converge to r (because an infinite $\delta$ implies a normal distribution for the common component). Plots of formula (2) as a function of $\delta$ and r are given in Figure 4. The major deviation occurs for $\delta =1$ which corresponds to an exponential distribution of the common familial risk. This represents a high degree of skewness (Figure 5). It means that members of a minority of families have a much higher risk than others. However, the familial relative risk still appears to be moderate. Figure 5 also includes an illustration of an even more skewed gamma distribution.

Figure 4.

The modified familial relative risk, $r_F$, associated with a diseased sibling as a function of r according to formula (2) in the text, where the two individuals in the family have a common risk component that is gamma distributed with shape parameter $\delta$. Here r is the familial relative risk from formula (1), that is the familial relative risk without the skewness introduced by the common, gamma distributed component. $r_F$ is plotted for given values of $\delta$. Note that $\delta \to \infty$ implies $r_F=r$.

Figure 5.

Probability density for a random variable X, following either the exponential distribution (solid line) or the gamma distribution with shape parameter 0.5 (dashed line).

Similar results are presented in the work of Moger et al.⁷ where a totally different mathematical model also indicated that even a very skewed familial frailty distribution would result in very moderate familial relative risks. The paper presents the following useful formula:

$$R=C{V}^2+1$$

where CV is the coefficient of variation of the probability of being susceptible, as it varies between families, and R is the relative risk of another member of the family acquiring the disease if there is already a case in the family. From the above formula it is seen that assuming, for example, R = 2 implies CV = 1. This means that the standard deviation equals the expectation. If the distribution comes from the gamma family, then it has to be an exponential distribution. If CV is greater than 1, then the shape parameter of the gamma distribution is less than 1, which yields an extremely skewed distribution (Figure 5). In fact the cases discussed here correspond to panels 3 and 4 of Figure 2.

The conclusion from this brief review of familial association is that a familial relative risk of 2 or above is a strong indication of wide variation in individual familial risk and of the existence of high risk groups of individuals.

The competing explanations: frailty selection vs biological mechanism

Frailty explanations of observed incidence rates will typically attribute certain findings to statistical selection effects. A disease where frailty is likely to play a role is testicular cancer. The age-incidence curve of this disease is typical of cancer forms originating in early (fetal) life, reaching a peak at a rather young age (approximately 30 years) and then declining sharply. A reasonable explanation for this observation is that some men are susceptible to acquiring testicular cancer, and do so relatively early. This leads to an increasing age-incidence rate at quite young ages. The subsequent declining incidence of testicular cancer with age is presumed to be due to high-risk individuals being selected out from the population after they acquire the disease.⁵ The individual risk of testicular cancer is thus increasing throughout life for susceptible individuals, whereas the age-incidence rate observed in the population is peaking due to selection effects. This fits well with biological evidence suggesting that testicular cancer may be caused by cellular damage during fetal life, which has been used as a basis for a so-called frailty analysis of incidence.⁵ The origin of testicular cancer is believed to be carcinoma in situ cells, the malignant transformation of which is initiated during early development from primordial germ cells, or gonocytes that fail either to end their proliferation or to undergo proper differentiation.⁶⁷ Since the incidence rate of testicular cancer also has increased substantially during past decades, this damage appears to have become more prevalent over time. It should be noted that this kind of statistical explanation typically competes with a biological mechanistic one. It has also been suggested that the decline in the risk of testicular cancer with age could be due to a declining testosterone level. Although the surge in testosterone level during puberty is important for the transformation of dormant carcinoma in situ cells to invasive testicular cancer, there is no evidence that individual testosterone level is a risk factor for testicular cancer.⁶⁸ Furthermore, the decline in testosterone is rather modest from the age of 30 years.

On the other hand, there are clearly cases where frailty is not the major cause of the decline in risk. One example is retinoblastoma, where there are almost no cases in individuals over 10 years of age. The likely explanation is that the retinoblasts are fully differentiated at the age of 10, and thus thereafter are not susceptible to malignant transformation.⁶⁹ However, in his seminal study on retinoblastoma, Knudson actually took varying frailty into account.⁷⁰ Long before the Rb1 gene was identified, he separated a very frail group (those with an inherited germ line mutation) from a less frail group (those who had the non-hereditary form), and used this to formulate his famous two-hit hypothesis. The case of retinoblastoma is thus an example of how the consideration of varying frailty combined with biological knowledge may provide valuable insights.

Competing frailty and biological mechanistic explanations are often suggested, and it may not be obvious which one is correct. Part of the difficulty is that when frailty is estimated from single event data (e.g. the single occurrence of a specific type of cancer for an individual), there will necessarily be uncertainty. A much more precise assessment of frailty can be done in a setting where there are repeated events (e.g. cancer in both breasts, kidneys or testicles), or when studying cancer incidence in families, e.g. testicular cancer among brothers.^7,8

Interpretation of epidemiological measures

Taking heterogeneity, or varying frailty, between individuals into account can be of crucial importance for the understanding of epidemiological features in a population. There is a natural tendency to assume that hazard rates and incidence rates can be taken at face value. Although these concepts appear to be simple, their interpretation can still be very difficult. The statistical interest in frailty stems in part from the fact that it can lead to curious statistical artefacts.

Cross-over effects

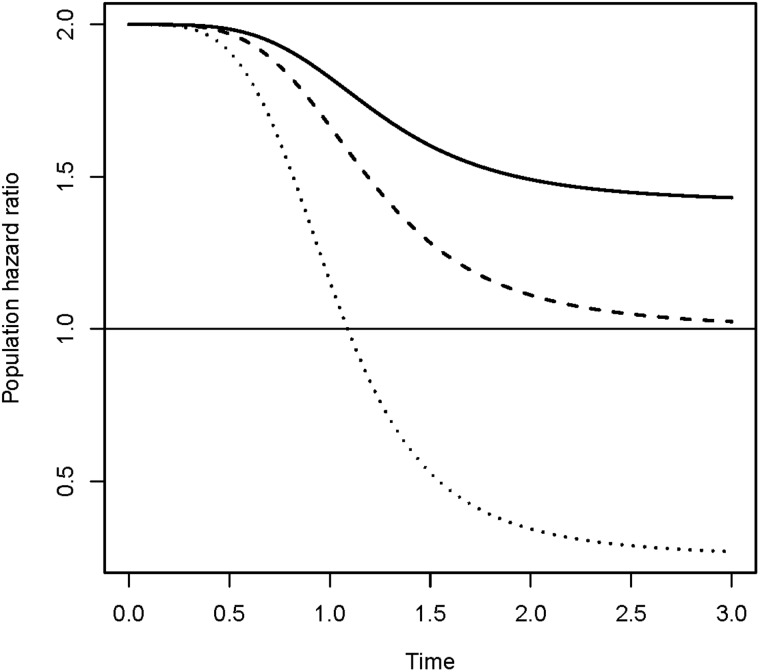
Consider two groups of individuals with hazard rates $\alpha (t)$ and$2\alpha (t)$, such that the hazard ratio is 2. In each of these groups there would necessarily be some unobserved heterogeneity between individuals. By introducing equally distributed frailty variables in the two groups, a decreasing hazard ratio over time may be obtained. Depending on the choice of frailty distribution, the hazard ratio may even cross over and become lower than 1, such that the high-risk group appears to become the low-risk group (Figure 6). The decrease (and possible cross-over) of the hazard ratio over time is a frailty effect. Individuals in the high-risk group will on average experience events earlier than those in the low-risk group. This causes the proportion of highly susceptible individuals in the high-risk group to decrease faster than in the low-risk group, leaving an increasing proportion of less susceptible individuals. Thus, the hazard ratio will decrease. If, for instance, the population contains a non-susceptible subgroup, then the susceptible individuals in the high-risk group would be exhausted earlier than in the low-risk group, causing the relative risk to cross over and become lower than 1, even if the hazard ratio stays constant on the individual level. This means that when frailty is not observed and cannot be accounted for, a wrong conclusion could be drawn regarding the true relationship between two groups. This is in fact a time-dependent version of Simpson’s paradox, which means that the observed relationship (concerning risk of disease, for example) between two groups is reversed at an aggregate level compared with what would be observed at a more detailed level if covariates could be conditioned on.

Figure 6.

Assume that the hazard rates in two risk groups are $\alpha \left(t\right)$ and $2\alpha \left(t\right)$ respectively. When frailty variables are introduced, the observed relative risk declines over time as shown in the figure. Three frailty distributions are used; one leads to a crossover of the hazard ratio. This case corresponds to a frailty distribution with a positive probability of zero frailty (i.e. a non-susceptible group). See Aalen et al.², Chapter 6, for technical details.

Likely cross-over phenomena are observed in practice, for example in the work of Gulsvik et al. where it is shown that high serum cholesterol appears as a ‘protective’ factor with respect to general mortality at old age.⁷¹ This could be a frailty artefact, especially since statin treatments has been shown to reduce disease incidence of cardiovascular disease in the elderly.⁷² A strongly reduced risk with age was also seen for smokers compared with never smokers in the paper by Gulsvik et al. which could be, at least partially, a frailty phenomenon.⁷¹ Increasing reverse causation with age could also contribute to explaining such results.

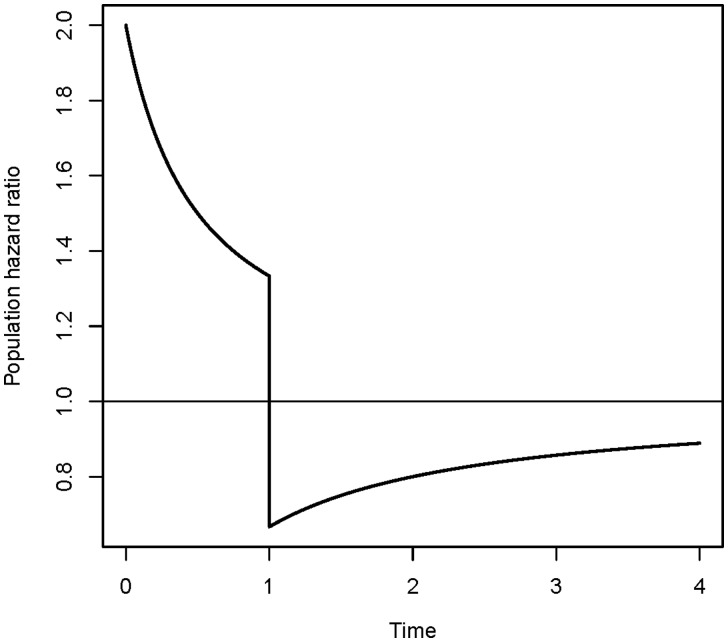
Another interesting effect of frailty occurs when discontinuing treatment in a clinical trial. Let us assume that the treatment group has hazard rate $\alpha (t)$ and the control group has hazard rate$2\alpha (t)$, presuming the treatment is effective. At the start of the study, the hazard ratio is 2. Because the treatment is effective, patients in the control group will on average have events earlier than in the treatment group, and the hazard ratio will decrease with time. At some point the difference between the hazard rates is so small that it is decided treatment is no longer effective, and it is stopped. A possible consequence of this decision is that the hazard ratio drops below 1, and it appears protective to be a member of the control group (Figure 7). In the control group the frailest individuals would already have had an event at this point and, at the time of discontinuing the treatment, there would be a higher proportion of less frail individuals in the control group. In the treatment group, frail individuals that would already have had an event if they had not been treated, have a very high risk immediately after the treatment is stopped. Not being aware of a possible frailty effect may lead to a wrong impression of the effect of discontinuing a treatment for an individual.

Figure 7.

Effect of discontinuing treatment. A control group with hazard rate $2\alpha \left(t\right)$ is compared with a treatment group with hazard rate $\alpha \left(t\right)$. Treatment is discontinued at time point 1.

False protectivity

In a competing risks framework, two (or more) events compete in determining the failure of an individual. The failure rate of each cause is expressed in terms of a cause-specific hazard rate. As in the example above, the hazard rates may be influenced by frailties. If these frailties are correlated, then one may observe a false protectivity.⁷³ If a covariate has a detrimental effect on one of the two competing risks, it may, at the population level, appear to be protective in the other cause-specific hazard rate.

Frailty and models of carcinogenesis

The famous multi-stage model of Armitage and Doll set the stage for a mathematical approach to understanding cancer incidence,⁷⁴ and it continues to play a fundamental role in our understanding of the carcinogenic process. This was exemplified by the re-publication of the original article in the International Journal of Epidemiology at its 50-year anniversary in 2004.⁷⁵ In a commentary to this reprint, Doll points out his views on the random nature of cancer development.⁷⁶ Since the Armitage-Doll model was first suggested, however, more sophisticated models have been published. Moolgavkar and Knudson proposed a two-hit model (combined with clonal expansion of initiated cells),⁷⁷ andexplained peaking incidence rates of certain cancers by the varying (decreasing) number of stem cells susceptible to mutation. Their model has later been expanded to allow for a cell to undergo several transitions before going into the clonal expansion phase,⁷⁸ as well as other further developments of the model.^47,79,80 All these models were created to facilitate the understanding of cancer development on an individual level. Meza et al. studied the effect of gestational mutations on cancer risk, and stated that: ‘Even with identical gestational mutation rates in all individuals in a population, at birth individuals are at different risk because of random variation in the number of mutated cells at birth’.⁴⁷ Heidenreich modelled risk functions (at certain ages) for liver cancer by treating the two-stage clonal expansion model as fully stochastic, and demonstrated that this leads to heterogeneity in a population even when considering genetically identical individuals.^81,82 Taking varying frailty into account (i.e. heterogeneity in risk between individuals), a Weibull hazard rate, as suggested by the Armitage-Doll model, is a sensible approximation to the carcinogenic process within an individual.⁸³ A mathematical formulation is that, on the individual level, the hazard rate of an event is given as a product of the Weibull hazard and an individual frailty factor. The frailty component may include both underlying heritable predispositions and an increased susceptibility due to purely random events. As opposed to the exhaustion of susceptible stem cells within the individual, the model considers the exhaustion of initially highly susceptible individuals as an explanation of a peaking age-incidence curve. This approach may also be modified in several ways, including taking into account an expanding host tissue during, for example, puberty.⁸⁴ An important element is thus to combine models of carcinogenesis with a realistic understanding of individual differences,^6,84,85 to better understand features of population age-incidence rates.

Interpretation of incidence rates

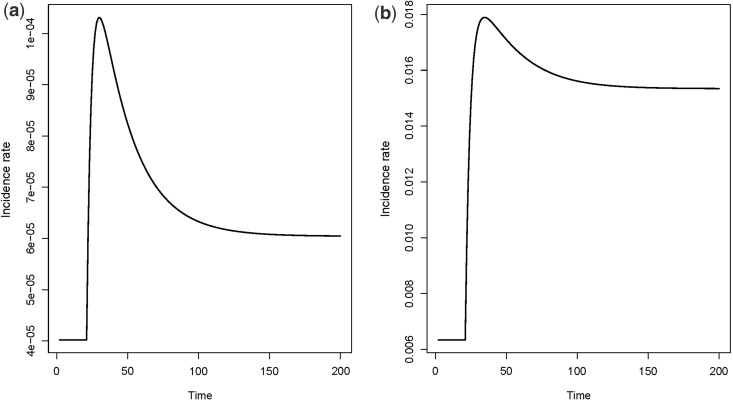
It turns out that changes in epidemiological incidence rates over calendar time also can be wrongly interpreted if one does not take into consideration the possible heterogeneity between individuals. Consider the simple Armitage-Doll multistage model of carcinogenesis, which states that a cell has to go through a certain number of transitions to reach malignancy. As an example, consider the simple version of a multistage model as shown in Figure 8. Assume that the transition rates are not the same for all individuals, but that there is a strong variation in susceptibility. Consider for instance a population where only a small subgroup is susceptible to the cancer in question, and the majority has a zero rate of cancer initiation (transition from a normal cell to an intermediate cell). If the initiation rate increases abruptly at a given point in (calendar) time, the incidence rate may increase to a peak, then drop and stabilize on a higher level. This is illustrated in Figure 9a, for the simple multistage model in Figure 8, with only 1% of the population being susceptible. The same point, with 90% being susceptible, is illustrated in Figure 9b. Although a simplification, the abrupt increase in the initiation rate could be the result of a risk factor that becomes more pronounced in the population at a given time.

Figure 8.

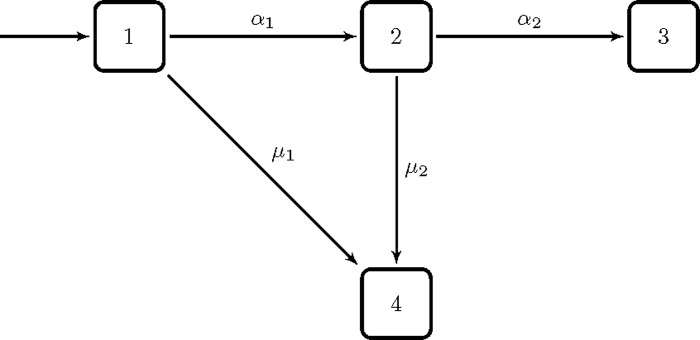
Simple illustration of an Armitage-Doll multi-stage model of carcinogenesis. The states represent the stages of the carcinogenic process. State one is the healthy state, state two is an intermediate state, and in state three a malignant cell has developed. State four is a censored state. The $\alpha$s and $\mu$s are transition rates.

Figure 9.

Incidence rates for the model in Figure 8. Assume that 10,000 individuals enter state one per time unit. The transition rates are ${\alpha }_1=0.01$ for time $<20$, and ${\alpha }_1=0.03$ for time $\ge 20$. Also, ${\alpha }_2=0.02$, ${\mu }_1=0.01$ and ${\mu }_2=0.05$ a) 1% of the population is susceptible, i.e. having ${\alpha }_1\ne 0$. b) 90% of the population is susceptible, i.e. having ${\alpha }_1\ne 0$.

The above example is simple, but illustrates that changes in the prevalence of risk factors may have an impact on observed incidence rates, even a long time after the change occurred. Whereas the real biological change here was an abrupt increase in the prevalence of a risk factor, the observed incidence rates gave the impression of a risk that first increased and then decreased. It is of course more likely that the presence of risk factors changes gradually over time, and this will have a similar effect on observed incidence rates as in the above example. The idea is that the increase in the prevalence of the risk factor over time could cause cancers that would not have emerged earlier to appear, even a long time after the external risk factor has ceased to change, and the observed incidence rate will thus continue to change after the prevalence of the risk factor has stabilized. If a cell requires more events to become malignant, changes in prevalence of different risk factors may affect the transition rates to various states. This could possibly also lead to multimodal shapes of hazard rates.

The point we are making is that changes in the incidence rate may not be a simple reflection of what is happening at a biological level. It is well known that underlying effects will be smoothed out in the observed incidence. But in addition to this, frailty may produce incidence rates with aspects that are unrepresentative of the underlying changes. Care should be taken before drawing conclusions on an individual level based on observations in a population.

Conclusion

We have pointed out a number of findings that indicate the presence of a considerable individual variation in the risk of cancer and other diseases that goes beyond what is due to measured risk factors. Varying frailty may create artefacts when studying incidence rates and other epidemiological measures, such as a decline in incidence due to the frailest individuals experiencing the event early.

Familial associations in disease that appear moderate may be the result of a large underlying variation in risk between individuals. This and other aspects of individual variation point towards caution in interpretation. The presence of individual heterogeneity cannot be ignored. It may be necessary to perform mathematical modelling to get a proper understanding of the nature and magnitude of the phenomenon of frailty in any given study population.

Funding

This work was partially supported by a grant from the Norwegian Research Council (191460/V50), and by the Norwegian Cancer Society, project/grant number 171851.

Conflict of interest: None declared.