Abstract
The strategy for evaluating template-based models submitted to CASP has continuously evolved from CASP1 to CASP5, leading to a standard procedure that has been used in all subsequent editions. The established approach includes methods for calculating the quality of each individual model, for assigning scores based on the distribution of the results for each target and for computing the statistical significance of the differences in scores between prediction methods. These data are made available to the assessor of the template-based modeling category, who uses them as a starting point for further evaluations and analyses. This article describes the detailed workflow of the procedure, provides justifications for a number of choices that are customarily made for CASP data evaluation, and reports the results of the analysis of template-based predictions at CASP8.
Keywords: CASP, protein structure prediction, template-based protein modeling, numerical evaluation measures
INTRODUCTION
The CASP experiments have been instrumental in fostering the development of novel prediction methods and in establishing reliable measures for numerical assessment of the submitted three-dimensional models of proteins. Different evaluation criteria have been tested in CASP throughout the years; some of those have been identified as suitable for an automated standard analysis. The Protein Structure Prediction Center performs numerical evaluation of the CASP models according to these established criteria1 and makes the results available to the community via the CASP web site. These data are usually the assessors’ starting point for the official analysis of the structure prediction results.
Several numerical evaluation measures can give a reasonable estimate of the similarity between a model and the corresponding experimental structure. Not in all cases can they be directly and automatically used for ranking models according to their accuracy. For example, models of targets for which no clear evolutionarily related templates can be identified might be quite far from the experimental structure and thereby achieve very low scores. On the other hand, careful visual inspection might highlight cases where these models, although far from being perfect, do correctly reproduce important features of the target protein—overall fold, proper secondary structure arrangements, correct inter-residue contacts, and so forth. For template-based predictions, though, numerical scores are sufficiently informative to confidently compare the quality of the models and therefore evaluate the effectiveness of the corresponding prediction methods.
This article discusses the standard measures that the template-based modeling (TBM) assessors used in previous CASPs to assess model quality and compare group performance. We also describe here the results of their application to the CASP8 predictions for the TBM category.
METHODS: STANDARD EVALUATION MEASURES AND PROCEDURES
The most relevant issue that every CASP assessor has to deal with is the choice of a scoring scheme and of the appropriate metrics for comparing models and targets. Although no measure is better than the others in all cases, a number of them are sufficiently reliable to provide correct model quality estimates and have indeed been extensively used in CASP.
RMSD
The root mean square deviation (RMSD) was the metric used in CASP1-32–4 and its use is still very widespread among computational biologists due to its conceptual simplicity. It is a very effective measure for comparing rather similar conformations, such as different experimental determinations of the same protein in different conditions or different models in an NMR ensemble. RMSD is, however, not ideal for comparing cases when the structures are substantially different for several reasons. First, its quadratic nature can penalize errors very severely, that is, a few local structural differences can result in high RMSD values. Second, it obviously depends on the number of equivalent atom pairs, and thus tends to increase with protein size. Finally, and probably most importantly, the end user of a model is typically more interested in which regions are sufficiently close to the native structure than in how incorrect the very wrong parts of a model are—that affect the RMSD most dramatically.
GDT-TS and GDT-HA
To overcome the RMSD shortcomings, a new threshold-based measure, GDT-TS,5 was developed and first used by the comparative modeling (CM) assessor in CASP4.6,7 GDT-TS is the average maximum number of residues in the predictions deviating from the corresponding residues in the target by no more than a specified Cα distance cut-off for four different LGA8 sequence-dependent superpositions with distance thresholds of 1, 2, 4, and 8 Å. By averaging over a relatively wide range of distance cut-offs, GDT-TS rewards models with a roughly correct fold, while scoring highest those perfectly reproducing the target main chain conformation. For the purpose of automatic evaluation of the overall quality of a model, GDT-TS proved to be one of the most appropriate measures and has been used by the assessors of all CASP experiments after CASP4. In CASP6 and CASP7, a modification of GDT-TS, GDT-HA, was also used by the assessors for the analysis of high accuracy template-based modeling targets.9,10 GDT-HA uses thresholds of 0.5, 1, 2, and 4 Å, thus allowing a better detection of small differences in the model backbone quality.
AL0
Another historical accuracy measure in CASP is the AL0 score, representing the percentage of correctly aligned residues after the LGA sequence-independent superposition of the model and the experimental structure with a threshold of 5 Å. A residue in the model is considered correctly aligned if its Cα atom is within 3.8 Å from the position of the corresponding experimental atom and no other Cα atom is closer. Even though conceptually different from GDT-TS, these two measures are highly correlated.
Other evaluation measures
In recent years, other measures11–14 have been developed that take into account the peculiarities of the comparison between a model and a structure as opposed to the comparison of two experimental structures. Each of these measures has its value and indeed some of them have been used in CASP6-8 assessments.
Z-scores
In the numerical evaluation procedure of the CASP models, GDT-TS, GDT-HA, AL0, and other related parameters are computed for each model. Each prediction method could therefore be ranked after combining the values of the submitted models over all targets. The weakness of such a procedure is due to the fact that it treats all targets equally. Different targets can have different difficulties and therefore the same difference in scores between models for two different targets should not be assigned the same weight. The problem was addressed by the CM assessor in CASP4 by introducing Z-scores.7 This strategy implicitly takes into account the predictive difficulty of a target, as the normalized score reflects relative quality of the model with respect to the results of other predictors. Noticeably, the Z-scores can be computed also for non-normal distributions, although in this case the standard normal probability table could not be used and is indeed not used in CASP. The use of Z-scores instead of raw scores proved to be very effective for analyzing relative model quality, although the results should be taken with a grain of salt for some targets for which very few groups generated good models as this can lead to an overestimation of their performance.
Ranking procedures
Although using Z-scores for analyzing model quality and relative group performance became a common practice in CASP, the specific details of the scoring schemes are left to the assessors. In previous CASPs, the approaches used by the TBM assessors—formerly CM and fold recognition (FR) assessors—slightly differed in the choices for the following alternatives:
Use all submitted models for calculating means and standard deviations needed for the Z-score computations versus ignore outliers from the datasets (and if so—how are outliers defined?).
Set negative Z-scores to zero or not.
Use the sum of Z-scores versus use the average over the number of predicted targets for ranking.
Use Z-scores from a single evaluation measure as the basis for the ranking scheme versus combine Z-scores from independent evaluation measures.
There are both advantages and potential pitfalls in these choices as we will briefly discuss below.
One of the potential problems in the use of the Z-scores is that the basic statistical parameters of the distribution of the selected evaluation score might be influenced by some extremely bad models. These can arise, for example, because of bugs in some of the servers participating in the experiment or unintentional human errors. In particular, very short “models” consisting of just a few residues can be found among the CASP predictions. To eliminate the effect of these unrealistic models on the scoring system, outliers might be excluded from the datasets used for calculating final mean and standard deviation values. The CASP6 FR assessor considered models shorter than 20 residues as outliers.15 All other TBM assessors (starting from CASP5) chose to curate the data by removing models whose score is lower than the mean of the distribution of all the values for the specific target by more than two standard deviations.
One of the aims of CASP is to foster the development of novel methods in the field. Previous assessors evaluated that some scoring schemes might be less appropriate than others for encouraging predictors to test riskier approaches. For example, the scoring scheme based on combining all Z-scores can prevent predictors from submitting models for more challenging targets. Indeed, incorrect models—more likely to appear in these cases—would obtain negative Z-scores leading to a lower overall score for the submitting group. One way to avoid this potential problem is to set negative Z-scores to 0, in other words to assign incorrect models the average score for that target. This technique was suggested by the CM assessor in CASP4,7 and was used by all but the CASP6 FR assessor since.
For ranking purposes, Z-scores of the models submitted by each group need to be summed or averaged over the number of predicted domains. This choice is clearly irrelevant if all groups predict the same set of targets. When this is not the case, the ranking can be affected by this choice. Summing penalizes groups who did not submit models for all targets, while averaging might penalize those who submit a larger number of targets, even if negative Z-scores are set to 0. The CM assessors in CASP4-77,9,16,17 preferred averaging the scores (not considering groups who submitted a very small number of predictions), while the FR assessors in CASP518 and CASP615 tried both averaging and summing approaches.
A combination of the Z-scores derived from several measures was used by the FR assessors in CASP518 and CASP615 while Z-scores from a single measure, always GDT-TS, were used by the CM assessors in CASP4-7.7,9,16,17 The GTD-TS, AL0, GDT-HA measures are all strongly correlated, and the value of computing them mostly resides in highlighting potential inconsistencies among them.
Model_1
CASP rules allow up to five models to be submitted for same target. Predictors are informed that only the model designated as first will be used in standard ranking as any other choice would lead to unfair comparisons. “Selecting the best of the five models” strategy would provide an advantage to groups submitting more predictions as they would be more likely to submit a better model just because of larger sampling. On the other hand, the “averaging over all predictions” strategy might disadvantage groups using this possibility to test novel and riskier methods.
Statistical comparison of group performance
A sensitive and important issue concerns the evaluation of the statistical significance of the difference in the scores of different groups. The CASP5 CM assessor introduced the use of a paired t-test between the results of each pair of groups.16 Notice that groups are not ranked according to the t-test and each pair is compared independently therefore there is no multiple testing issue. One potential problem is that the t-test is based upon an assumption of normality of the distributions to be compared and one should verify that this is the case in the experiment. If not, a nonparametric test—such as the Wilcoxon signed rank test—should be used.
CASP8 evaluation of template-based models
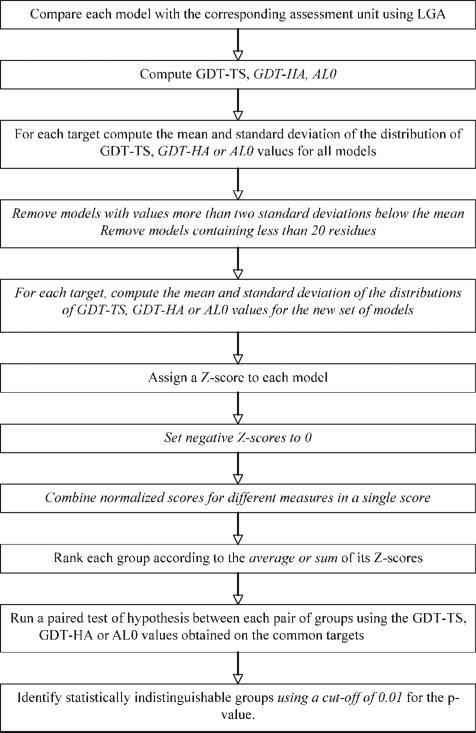
The overall evaluation procedure is summarized in Figure 1. Once the parameters used in the evaluation (highlighted in italic) are selected, the calculations are straightforward and the results are provided to the template-based modeling assessor as soon as the target structures and their dissection in prediction units19 are available.
Figure 1.
Flowchart of the procedure used for evaluation. Steps in italics depend upon the assessor preference.
In the analysis of CASP8 template-based models described here, we adopted the parameters most often used by the assessors in the previous CASPs.
GDT-TS measure was used as the basic measure for comparing models and experimental structures. The GDT-TS values are computed using LGA in sequence-dependent mode.*
Models shorter than 20 residues were removed from the dataset. If several independent segments were submitted for the same prediction unit, the frame with the largest number of residues was selected as the representative model.
Z-scores were calculated based on the GDT-TS (and other) measures without further data curation (data reported on the web). The Z-scores reported in this article were calculated after removal of the models with values more than two standard deviations below the mean.
Negative Z-scores were set to zero.
Groups were ranked according to the average of GDT-TS-based Z-scores for the models designated as first by the predictors.
The normality of the GDT-TS distributions for each target was evaluated using the Shapiro Wilk test.20
The statistical significance of the differences between the GDT-TS values of the models was assessed with a suitable paired test of hypothesis for all pairs of groups on the common set of predicted targets.
It should be noted that in CASP8 targets were split in the two categories: (1) targets for prediction by all groups (human/server targets) and (2) targets for server prediction (server only targets). All in all, the TBM category encompassed 154 assessment units,19 64 of which were human/server domains and the remaining 90 were server only. All groups (server and human-expert) were ranked according to their results on the subset of 64 human/server domains, while server groups were also ranked on the complete list of 154 domains.
RESULTS
As an illustration of the evaluation strategy described in Methods, we show here the results of the automatic analysis performed on the template-based predictions in CASP8. Since they are reported here, these data will not be included in the TBM assessor paper21 that will instead concentrate on more detailed evaluations of the structural features of the submitted models.
Table I shows the correlation between the Z-scores obtained using GDT-TS, GDT-HA, and AL0 for the groups participating in CASP8. They are highly correlated for both sets of targets (“Human and Server” and “Server only”), therefore in the following we will only discuss the results of GDT-TS. The results obtained using the other scoring schemes are available on the CASP web site.
Table I.
Agreement Between Group Rankings Based on Different Model Quality Measures
| Dataset | ρ | ||
|---|---|---|---|
| All groups | Mean AL0 Z-score | Mean GDT-TS Z-score | 0.97 |
| Human and server targets | Mean AL0 Z-score | Mean GDT-HA Z-score | 0.96 |
| Mean GDT-TS Z-score | Mean GDT-HA Z-score | 0.99 | |
| Server groups | Mean AL0 Z-score | Mean GDT-TS Z-score | 0.97 |
| All targets (human and server plus server only) | Mean AL0 Z-score | Mean GDT-HA Z-score | 0.95 |
| Mean GDT-TS Z-score | Mean GDT-HA Z-score | 0.98 |
Spearman's correlation (ρ) between the Z-scores obtained by each group using different measures. The data are reported for both the “human and server” subset and for the complete set of targets.
Table II illustrates the results obtained by all the groups submitting predictions. The server results are evaluated on the complete set of assessment units, while the results of all groups are computed for the subset of “Human and Server” targets.
Table II.
Average Z-Scores Based on GDT-TS for Individual Prediction Groups
| “Human and Server” target subset |
All targets |
||||||
|---|---|---|---|---|---|---|---|
| Rank | Group name | Group id | No. of targets | Mean Z-score | No. of targets | Mean Z-score | Rank (servers only) |
| 1 | IBT_LT | 283 | 64 | 1.11 | |||
| 2 | DBAKER | 489 | 64 | 1.03 | |||
| 3 | Zhang | 71 | 64 | 0.94 | |||
| 4 | Zhang-Server | 426 | 64 | 0.84 | 154 | 0.89 | 1 |
| 5 | KudlatyPredHuman | 267 | 18 | 0.83 | |||
| 6 | TASSER | 57 | 64 | 0.83 | |||
| 7 | fams-ace2 | 434 | 64 | 0.83 | |||
| 8 | ZicoFullSTP | 196 | 64 | 0.81 | |||
| 9 | SAM-T08-human | 46 | 62 | 0.80 | |||
| 10 | Zico | 299 | 64 | 0.78 | |||
| 11 | MULTICOM | 453 | 64 | 0.78 | |||
| 12 | GeneSilico | 371 | 64 | 0.76 | |||
| 13 | ZicoFullSTPFullData | 138 | 64 | 0.75 | |||
| 14 | LEE-SERVER | 293 | 9 | 0.75 | 97 | 0.80 | 2 |
| 15 | McGuffin | 379 | 63 | 0.73 | |||
| 16 | 3DShot1 | 282 | 64 | 0.73 | |||
| 17 | Sternberg | 202 | 64 | 0.72 | |||
| 18 | Jones-UCL | 387 | 64 | 0.72 | |||
| 19 | mufold | 310 | 61 | 0.71 | |||
| 20 | FAMS-multi | 266 | 64 | 0.70 | |||
| 21 | Elofsson | 200 | 64 | 0.68 | |||
| 22 | Chicken_George | 81 | 64 | 0.67 | |||
| 23 | 3DShotMQ | 419 | 64 | 0.66 | |||
| 24 | Bates_BMM | 178 | 64 | 0.65 | |||
| 25 | SAMUDRALA | 34 | 53 | 0.63 | |||
| 26 | HHpred5 | 12 | 64 | 0.61 | 154 | 0.64 | 5 |
| 27 | LevittGroup | 442 | 62 | 0.61 | |||
| 28 | BAKER-ROBETTA | 425 | 64 | 0.60 | 154 | 0.57 | 8 |
| 29 | RAPTOR | 438 | 64 | 0.59 | 154 | 0.69 | 3 |
| 30 | LEE | 407 | 64 | 0.59 | |||
| 31 | MidwayFolding | 208 | 63 | 0.57 | |||
| 32 | Phyre_de_novo | 322 | 64 | 0.56 | 154 | 0.67 | 4 |
| 33 | Ozkan-Shell | 485 | 24 | 0.55 | |||
| 34 | HHpred4 | 122 | 64 | 0.54 | 154 | 0.56 | 10 |
| 35 | ABIpro | 340 | 64 | 0.54 | |||
| 36 | sessions | 139 | 4 | 0.52 | |||
| 37 | MUSTER | 408 | 64 | 0.51 | 154 | 0.47 | 20 |
| 38 | METATASSER | 182 | 64 | 0.51 | 154 | 0.62 | 7 |
| 39 | Pcons_multi | 429 | 62 | 0.50 | 151 | 0.51 | 13 |
| 40 | pro-sp3-TASSER | 409 | 64 | 0.50 | 154 | 0.63 | 6 |
| 41 | TsaiLab | 230 | 4 | 0.49 | |||
| 42 | fais@hgc | 198 | 51 | 0.48 | |||
| 43 | A-TASSER | 149 | 64 | 0.47 | |||
| 44 | ricardo | 403 | 12 | 0.46 | |||
| 45 | circle | 396 | 61 | 0.45 | 150 | 0.40 | 25 |
| 46 | HHpred2 | 154 | 64 | 0.45 | 154 | 0.50 | 15 |
| 47 | MULTICOM-CLUSTER | 20 | 64 | 0.43 | 154 | 0.56 | 11 |
| 48 | SAM-T08-server | 256 | 64 | 0.43 | 154 | 0.48 | 17 |
| 49 | YASARA | 147 | 15 | 0.42 | 74 | 0.41 | 24 |
| 50 | FEIG | 166 | 64 | 0.41 | 154 | 0.47 | 18 |
| 51 | GS-KudlatyPred | 279 | 63 | 0.41 | 153 | 0.49 | 16 |
| 52 | Phyre2 | 235 | 64 | 0.40 | 154 | 0.34 | 34 |
| 53 | SHORTLE | 253 | 42 | 0.40 | |||
| 54 | CBSU | 353 | 36 | 0.39 | |||
| 55 | FAMSD | 140 | 64 | 0.39 | 154 | 0.47 | 19 |
| 56 | MULTICOM-REFINE | 13 | 64 | 0.39 | 154 | 0.56 | 9 |
| 57 | POEMQA | 124 | 63 | 0.38 | |||
| 58 | MUProt | 443 | 64 | 0.38 | 154 | 0.54 | 12 |
| 59 | CpHModels | 193 | 59 | 0.38 | 146 | 0.33 | 37 |
| 60 | COMA-M | 174 | 63 | 0.37 | 153 | 0.45 | 22 |
| 61 | Phragment | 270 | 64 | 0.37 | 154 | 0.32 | 40 |
| 62 | FFASsuboptimal | 142 | 60 | 0.36 | 150 | 0.36 | 32 |
| 63 | EB_AMU_Physics | 337 | 61 | 0.35 | |||
| 64 | Jiang_Zhu | 369 | 64 | 0.35 | |||
| 65 | MULTICOM-RANK | 131 | 64 | 0.35 | 154 | 0.51 | 14 |
| 66 | TJ_Jiang | 384 | 64 | 0.35 | |||
| 67 | reivilo | 22 | 1 | 0.34 | |||
| 68 | FALCON | 351 | 64 | 0.34 | 154 | 0.39 | 26 |
| 69 | 3D-JIGSAW_AEP | 296 | 63 | 0.34 | 153 | 0.33 | 38 |
| 70 | PS2-manual | 23 | 61 | 0.34 | |||
| 71 | PSI | 385 | 64 | 0.34 | 154 | 0.35 | 33 |
| 72 | NirBenTal | 354 | 11 | 0.33 | |||
| 73 | Pcons_dot_net | 436 | 59 | 0.32 | 144 | 0.37 | 28 |
| 74 | PS2-server | 48 | 61 | 0.32 | 151 | 0.42 | 23 |
| 75 | 3DShot2 | 427 | 64 | 0.32 | 154 | 0.34 | 35 |
| 76 | nFOLD3 | 100 | 63 | 0.32 | 151 | 0.31 | 42 |
| 77 | AMU-Biology | 475 | 59 | 0.32 | |||
| 78 | FrankensteinLong | 172 | 45 | 0.31 | |||
| 79 | MULTICOM-CMFR | 69 | 64 | 0.31 | 154 | 0.46 | 21 |
| 80 | jacobson | 470 | 1 | 0.31 | |||
| 81 | FALCON_CONSENSUS | 220 | 63 | 0.31 | 153 | 0.32 | 41 |
| 82 | Softberry | 113 | 64 | 0.30 | |||
| 83 | Poing | 186 | 64 | 0.30 | 154 | 0.29 | 45 |
| 84 | fais-server | 116 | 59 | 0.29 | 148 | 0.37 | 27 |
| 85 | keasar-server | 415 | 58 | 0.29 | 140 | 0.37 | 29 |
| 86 | Frankenstein | 85 | 56 | 0.28 | 131 | 0.28 | 48 |
| 87 | FFASstandard | 7 | 60 | 0.28 | 148 | 0.33 | 39 |
| 88 | taylor | 356 | 12 | 0.28 | |||
| 89 | COMA | 234 | 63 | 0.28 | 153 | 0.34 | 36 |
| 90 | Bilab-UT | 325 | 64 | 0.27 | |||
| 91 | FFASflextemplate | 247 | 59 | 0.27 | 147 | 0.29 | 46 |
| 92 | pipe_int | 135 | 60 | 0.26 | 143 | 0.36 | 30 |
| 93 | Hao_Kihara | 284 | 62 | 0.26 | |||
| 94 | GeneSilicoMetaServer | 297 | 59 | 0.26 | 147 | 0.27 | 51 |
| 95 | Pcons_local | 143 | 60 | 0.26 | 145 | 0.28 | 47 |
| 96 | 3D-JIGSAW_V3 | 449 | 63 | 0.26 | 153 | 0.31 | 43 |
| 97 | mGenTHREADER | 349 | 64 | 0.26 | 154 | 0.30 | 44 |
| 98 | Abagyan | 458 | 6 | 0.25 | |||
| 99 | SAINT1 | 119 | 35 | 0.25 | |||
| 100 | GS-MetaServer2 | 153 | 60 | 0.24 | 146 | 0.27 | 49 |
| 101 | PRI-Yang-KiharA | 39 | 64 | 0.24 | |||
| 102 | BioSerf | 495 | 64 | 0.23 | 152 | 0.36 | 31 |
| 103 | keasar | 114 | 63 | 0.22 | |||
| 104 | Kolinski | 493 | 64 | 0.22 | |||
| 105 | mti | 289 | 6 | 0.22 | |||
| 106 | POEM | 207 | 64 | 0.21 | |||
| 107 | ACOMPMOD | 2 | 60 | 0.20 | 143 | 0.17 | 58 |
| 108 | FUGUE_KM | 19 | 55 | 0.20 | 141 | 0.15 | 60 |
| 109 | SAM-T02-server | 421 | 60 | 0.19 | 148 | 0.19 | 56 |
| 110 | Zhou-SPARKS | 481 | 40 | 0.19 | |||
| 111 | tripos_08 | 83 | 27 | 0.19 | |||
| 112 | fleil | 70 | 64 | 0.18 | |||
| 113 | SAM-T06-server | 477 | 64 | 0.18 | 154 | 0.21 | 53 |
| 114 | 3Dpro | 157 | 58 | 0.17 | 147 | 0.18 | 57 |
| 115 | JIVE08 | 330 | 40 | 0.17 | |||
| 116 | RBO-Proteus | 479 | 63 | 0.16 | 153 | 0.19 | 55 |
| 117 | Wolfson-FOBIA | 10 | 7 | 0.15 | |||
| 118 | mumssp | 345 | 5 | 0.14 | |||
| 119 | FOLDpro | 164 | 64 | 0.14 | 154 | 0.09 | 64 |
| 120 | forecast | 316 | 64 | 0.13 | 151 | 0.23 | 52 |
| 121 | Fiser-M4T | 394 | 25 | 0.12 | 93 | 0.27 | 50 |
| 122 | Sasaki-Cetin-Sasai | 461 | 40 | 0.12 | |||
| 123 | Pushchino | 243 | 47 | 0.10 | 127 | 0.21 | 54 |
| 124 | SMEG-CCP | 14 | 62 | 0.10 | |||
| 125 | panther_server | 318 | 48 | 0.10 | 129 | 0.13 | 62 |
| 126 | LOOPP_Server | 454 | 56 | 0.09 | 135 | 0.17 | 59 |
| 127 | Wolynes | 93 | 27 | 0.08 | |||
| 128 | Handl-Lovell | 29 | 18 | 0.07 | |||
| 129 | ProtAnG | 110 | 38 | 0.07 | |||
| 130 | huber-torda-server | 281 | 42 | 0.07 | 92 | 0.13 | 63 |
| 131 | xianmingpan | 463 | 54 | 0.06 | |||
| 132 | MUFOLD-MD | 404 | 62 | 0.06 | 150 | 0.09 | 65 |
| 133 | DelCLab | 373 | 60 | 0.05 | |||
| 134 | mariner1 | 450 | 58 | 0.04 | 143 | 0.07 | 67 |
| 135 | MUFOLD-Server | 462 | 64 | 0.04 | 154 | 0.15 | 61 |
| 136 | StruPPi | 183 | 63 | 0.03 | |||
| 137 | TWPPLAB | 420 | 64 | 0.03 | |||
| 138 | RPFM | 5 | 10 | 0.02 | |||
| 139 | OLGAFS | 213 | 43 | 0.02 | 125 | 0.08 | 66 |
| 140 | NIM2 | 55 | 10 | 0.02 | |||
| 141 | POISE | 170 | 11 | 0.01 | |||
| 142 | rehtnap | 95 | 48 | 0.01 | 131 | 0.04 | 68 |
| 143 | FLOUDAS | 236 | 36 | 0.01 | |||
| 144 | Distill | 73 | 62 | 0.01 | 152 | 0.02 | 69 |
| 145 | ProteinShop | 399 | 6 | 0.01 | |||
| 146 | MeilerLabRene | 211 | 45 | 0.01 | |||
| 147 | schenk-torda-server | 262 | 56 | 0.01 | 136 | 0.00 | 70 |
| 148 | DistillSN | 272 | 59 | 0.00 | |||
| 149 | mahmood-torda-server | 53 | 39 | 0.00 | 73 | 0.00 | 71 |
| 150 | Scheraga | 324 | 35 | 0.00 | |||
| 151 | psiphifoldings | 63 | 30 | 0.00 | |||
| 152 | igor | 188 | 13 | 0.00 | |||
| 153 | ShakAbInitio | 104 | 7 | 0.00 | |||
| 154 | dill_ucsf | 414 | 7 | 0.00 | |||
| 155 | Linnolt-UH-CMB | 382 | 5 | 0.00 | |||
| 156 | HCA | 402 | 5 | 0.00 | |||
| 157 | PHAISTOS | 459 | 5 | 0.00 | |||
| 158 | BHAGEERATH | 274 | 3 | 0.00 | 5 | 0.00 | 72 |
| 159 | PZ-UAM | 18 | 2 | 0.00 | |||
Mean Z-score of the participating groups after setting negative Z-scores to 0. Data for human predictors are computed on the subset of “Human and server” targets, while the results of the servers are reported for both this subset (to allow a proper comparison with human groups) and for the whole set of assessment units. Data are ranked according to the Z-scores on the “Human and Server” subset, the rank of servers on the complete set of targets is reported in the last column.
For conciseness, the average Z-score presented in the table refers to the case where negative values were set to 0. However, the overall conclusions are not affected by this choice (data not shown).
The Shapiro Wilk test established that only seven of the 154 GDT-TS distributions were likely to be normal at the 1% confidence level. A non-Gaussian distribution of the GDT-TS scores might arise if groups of predictors used different templates for building their models, or if some groups were unable to detect a possible template and used less reliable template-free methods. The TBM assessor manuscript discusses this point in more detail.21
We applied both the t-test and Wilcoxon test to the data and the results were essentially identical: statistically indistinguishable groups were such by both analyses (data not shown). We report in Tables III and IV the results of the Wilcoxon signed rank test for the 20 best ranking groups in the “Human and Server” and “All targets” categories, respectively.
Table III.
Statistical Comparisons Among the Top 20 Groups on the “Human and Server” Subset of Targets
| 283 | 489 | 71 | 426 | 57 | 434 | 196 | 46 | 299 | 453 | 371 | 138 | 379 | 282 | 202 | 387 | 310 | 266 | 200 | 81 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 283 | 64 | 64 | 64 | 64 | 64 | 64 | 62 | 64 | 64 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 489 | 5.11E-01 | 64 | 64 | 64 | 64 | 64 | 62 | 64 | 64 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 71 | 4.21E-01 | 7.47E-01 | 64 | 64 | 64 | 64 | 62 | 64 | 64 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 426 | 1.67E-01 | 3.56E-01 | 1.03E-02 | 64 | 64 | 64 | 62 | 64 | 64 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 57 | 1.81E-01 | 3.15E-01 | 3.81E-01 | 9.68E-01 | 64 | 64 | 62 | 64 | 64 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 434 | 1.46E-01 | 3.35E-01 | 2.29E-02 | 8.26E-01 | 9.56E-01 | 64 | 62 | 64 | 64 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 196 | 5.06E-02 | 1.21E-01 | 2.86E-02 | 2.43E-01 | 2.71E-01 | 1.98E-01 | 62 | 64 | 64 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 46 | 8.82E-02 | 1.85E-01 | 1.44E-01 | 6.87E-01 | 8.44E-01 | 5.67E-01 | 4.63E-01 | 62 | 62 | 62 | 62 | 61 | 62 | 62 | 62 | 59 | 62 | 62 | 62 | |
| 299 | 3.10E-02 | 8.32E-02 | 1.32E-02 | 1.76E-01 | 1.78E-01 | 1.19E-01 | 9.10E-01 | 3.80E-01 | 64 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 453 | 4.27E-02 | 9.20E-02 | 1.08E-02 | 1.34E-01 | 2.06E-01 | 1.17E-01 | 6.39E-01 | 2.51E-01 | 6.68E-01 | 64 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 371 | 3.69E-02 | 1.14E-01 | 8.67E-03 | 2.04E-01 | 4.10E-01 | 1.14E-01 | 8.13E-01 | 2.94E-01 | 7.41E-01 | 5.20E-01 | 64 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 138 | 1.91E-02 | 4.21E-02 | 6.04E-03 | 7.44E-02 | 8.17E-02 | 5.25E-02 | 4.70E-01 | 1.92E-01 | 3.99E-01 | 9.27E-01 | 4.28E-01 | 63 | 64 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 379 | 7.04E-02 | 1.54E-01 | 4.20E-04 | 1.33E-01 | 4.86E-01 | 8.60E-02 | 7.89E-01 | 3.88E-01 | 7.30E-01 | 4.96E-01 | 9.73E-01 | 4.71E-01 | 63 | 63 | 63 | 60 | 63 | 63 | 63 | |
| 282 | 1.86E-02 | 8.97E-02 | 2.11E-03 | 6.27E-02 | 2.45E-01 | 5.90E-02 | 8.75E-01 | 2.51E-01 | 9.34E-01 | 7.64E-01 | 6.38E-01 | 6.85E-01 | 6.80E-01 | 64 | 64 | 61 | 64 | 64 | 64 | |
| 202 | 8.57E-03 | 3.92E-02 | 8.05E-03 | 9.08E-02 | 9.52E-02 | 7.27E-02 | 6.69E-01 | 2.96E-01 | 6.99E-01 | 9.85E-01 | 4.90E-01 | 9.60E-01 | 3.05E-01 | 6.92E-01 | 64 | 61 | 64 | 64 | 64 | |
| 387 | 1.22E-02 | 2.99E-02 | 1.22E-03 | 2.00E-02 | 6.69E-02 | 1.97E-02 | 3.76E-01 | 9.05E-02 | 3.81E-01 | 6.95E-01 | 1.15E-01 | 7.30E-01 | 1.40E-01 | 4.06E-01 | 6.65E-01 | 61 | 64 | 64 | 64 | |
| 310 | 7.93E-03 | 2.77E-02 | 1.69E-03 | 4.58E-02 | 8.56E-02 | 3.05E-02 | 4.90E-01 | 1.26E-01 | 4.94E-01 | 7.18E-01 | 2.67E-01 | 7.97E-01 | 2.93E-01 | 4.57E-01 | 7.41E-01 | 8.97E-01 | 61 | 61 | 61 | |
| 266 | 2.44E-02 | 8.36E-02 | 2.84E-04 | 5.71E-02 | 2.33E-01 | 2.62E-02 | 9.52E-01 | 2.27E-01 | 9.86E-01 | 7.10E-01 | 6.62E-01 | 6.20E-01 | 4.85E-01 | 8.90E-01 | 6.09E-01 | 2.34E-01 | 4.43E-01 | 64 | 64 | |
| 200 | 1.08E-02 | 2.50E-02 | 1.24E-03 | 1.80E-02 | 3.27E-02 | 1.32E-02 | 1.97E-01 | 3.60E-02 | 2.42E-01 | 5.02E-01 | 1.20E-01 | 5.23E-01 | 1.62E-01 | 2.73E-01 | 6.23E-01 | 8.75E-01 | 8.54E-01 | 2.23E-01 | 64 | |
| 81 | 1.87E-02 | 4.28E-02 | 2.39E-04 | 5.81E-03 | 4.48E-02 | 6.32E-03 | 2.01E-01 | 6.44E-02 | 2.25E-01 | 5.04E-01 | 1.67E-01 | 5.45E-01 | 1.35E-01 | 2.70E-01 | 6.17E-01 | 8.44E-01 | 9.90E-01 | 2.00E-01 | 9.41E-01 |
The upper half of the table reports the number of common targets between the groups indicated in the corresponding row and column. The lower half reports the value of the probability that the distributions of the results of the two corresponding groups are statistically indistinguishable according to the Wilcoxon signed rank test. Shaded cells indicate probability values greater than or equal to 0.01. Server 293 (Lee-server) and Group 267 (KudlatyPred-Human) only predicted 9 and 18 of the “Human and server” targets, respectively, and therefore are not included in the table.
Table IV.
Statistical Comparisons Among the Top 20 Server Groups on all CASP8 TBM Targets
| 426 | 293 | 438 | 322 | 12 | 409 | 182 | 425 | 13 | 122 | 20 | 443 | 429 | 131 | 154 | 279 | 256 | 166 | 140 | 408 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 426 | 97 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 293 | 5.19E-01 | 97 | 97 | 97 | 97 | 97 | 97 | 97 | 97 | 97 | 97 | 96 | 97 | 97 | 97 | 97 | 97 | 97 | 97 | |
| 438 | 1.34E-05 | 6.70E-03 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 322 | 4.91E-07 | 4.92E-03 | 1.64E-01 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 12 | 1.33E-06 | 2.50E-02 | 1.45E-01 | 8.90E-01 | 154 | 154 | 154 | 154 | 154 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 409 | 3.27E-10 | 2.79E-03 | 2.09E-01 | 8.49E-01 | 5.80E-01 | 154 | 154 | 154 | 154 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 182 | 2.00E-10 | 4.31E-04 | 8.26E-02 | 4.71E-01 | 8.56E-01 | 9.10E-01 | 154 | 154 | 154 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 425 | 2.09E-10 | 1.37E-04 | 3.41E-02 | 4.31E-01 | 6.07E-01 | 2.57E-01 | 9.28E-01 | 154 | 154 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 13 | 4.80E-09 | 9.60E-03 | 6.58E-02 | 3.07E-01 | 7.99E-01 | 2.46E-01 | 9.60E-01 | 9.73E-01 | 154 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 122 | 4.06E-09 | 9.55E-04 | 2.35E-02 | 9.93E-02 | 2.12E-02 | 8.06E-02 | 2.26E-01 | 4.86E-01 | 5.76E-01 | 154 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 20 | 1.10E-09 | 1.11E-03 | 5.21E-02 | 1.93E-01 | 4.39E-01 | 3.03E-01 | 9.50E-01 | 6.36E-01 | 1.88E-01 | 6.86E-01 | 154 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 443 | 2.65E-10 | 5.84E-03 | 4.12E-02 | 8.39E-02 | 7.51E-01 | 4.94E-02 | 5.90E-01 | 8.72E-01 | 2.46E-01 | 6.77E-01 | 7.10E-01 | 151 | 154 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 429 | 5.15E-13 | 8.00E-06 | 8.35E-04 | 1.79E-03 | 3.04E-02 | 1.56E-03 | 1.69E-02 | 1.89E-01 | 1.15E-01 | 6.16E-01 | 6.69E-02 | 3.67E-01 | 151 | 151 | 151 | 151 | 151 | 151 | 151 | |
| 131 | 9.70E-12 | 3.30E-04 | 3.35E-03 | 1.99E-02 | 2.87E-01 | 9.43E-03 | 1.07E-01 | 1.84E-01 | 7.43E-02 | 5.60E-01 | 1.22E-01 | 2.12E-01 | 9.25E-01 | 154 | 153 | 154 | 154 | 154 | 154 | |
| 154 | 5.28E-11 | 4.65E-05 | 7.70E-04 | 4.42E-02 | 2.51E-01 | 1.12E-01 | 2.13E-01 | 3.06E-01 | 2.54E-01 | 8.73E-01 | 4.41E-01 | 3.68E-01 | 4.11E-01 | 9.21E-01 | 153 | 154 | 154 | 154 | 154 | |
| 279 | 1.69E-13 | 6.35E-07 | 5.57E-04 | 5.69E-02 | 2.17E-01 | 1.62E-02 | 9.02E-02 | 3.82E-01 | 2.55E-01 | 8.60E-01 | 1.23E-01 | 1.29E-01 | 6.45E-01 | 8.94E-01 | 7.67E-01 | 153 | 153 | 153 | 153 | |
| 256 | 3.11E-12 | 1.02E-05 | 1.61E-04 | 6.99E-03 | 6.73E-02 | 2.82E-03 | 4.65E-02 | 1.28E-01 | 9.27E-02 | 3.29E-01 | 3.39E-02 | 1.50E-01 | 8.21E-01 | 7.54E-01 | 6.76E-01 | 7.05E-01 | 154 | 154 | 154 | |
| 166 | 2.22E-15 | 2.13E-08 | 1.91E-07 | 8.52E-06 | 1.09E-03 | 2.87E-05 | 8.32E-05 | 3.86E-03 | 1.18E-03 | 1.58E-02 | 7.10E-03 | 9.43E-03 | 5.13E-01 | 6.30E-02 | 3.07E-02 | 3.75E-02 | 7.00E-02 | 154 | 154 | |
| 140 | 1.36E-12 | 1.61E-05 | 1.27E-04 | 2.32E-02 | 5.15E-02 | 5.11E-02 | 7.86E-02 | 7.53E-02 | 1.40E-02 | 2.50E-01 | 8.52E-02 | 8.46E-02 | 8.60E-01 | 3.57E-01 | 2.58E-01 | 4.83E-01 | 4.59E-01 | 9.97E-02 | 154 | |
| 408 | 0.00E+00 | 1.28E-06 | 7.98E-04 | 3.51E-03 | 1.38E-02 | 3.55E-03 | 4.26E-03 | 6.63E-02 | 1.66E-02 | 1.62E-01 | 3.65E-02 | 2.39E-02 | 9.10E-01 | 3.45E-01 | 1.84E-01 | 6.57E-01 | 4.74E-01 | 2.03E-01 | 6.67E-01 |
The upper half of the table reports the number of common targets between the groups indicated in the corresponding row and column. The lower half shows the value of the probability that the distributions of the results of the two corresponding groups are statistically indistinguishable according to the paired Wilcoxon signed rank test. Shaded cells indicate probability values greater than or equal to 0.01.
The overall conclusions of the automatic evaluation of the first model for each human and server group can be summarized as follows.
Several groups (283 IBT_LT, 489 DBAKER, 71 Zhang, 426 Zhang-Server, 57 TASSER, 434 fams-ace2, 196 ZicoFullSTP, 46 SAM-T08-human, 299 Zico, 453 MULTICOM, 371 GeneSilico, 138 ZicoFullSTPFullData, 379 McGuffin, 282 3DShot1) performed well on the subset of “Human and server” targets and are statistically indistinguishable. Among the top predictors, only group 426 (Zhang-server) has officially registered as a server, although it is entirely possible that some of the other “human” groups used a completely automatic procedure.
When servers are compared to each other, group 426 (Zhang-server) is by far the best performing one. It is statistically indistinguishable from group 293 (Lee-server) but the latter group submitted predictions only on 97 out of 154 possible TBM domains. The next three best performing servers are 438 Raptor, 322 Phyre_de_novo, and 12 HHpred5, which compare less favorably with human predictors on the “Human” target subset. This can reflect a genuine better performance of human groups, but it could also be due to a different performance of the servers for the biased subset of human targets that are not randomly selected.22
DISCUSSION
CASP has been providing the assessors with the results of the automatic evaluation carried out by the Prediction Center at UC Davis for quite some time now. The procedure has been extensively tested and sufficiently standardized to be recommended for future CASPs, and is described in detail here. We also show here the results of the application of the procedure to the CASP8 data.
Deriving overall conclusions from the data provided is the duty and the privilege of the assessors and therefore the ranking provided here should be regarded as a starting point for the subsequent analysis of the outcome of the experiment.
The results of comparing server groups on all targets show that Zhang-server outperforms the rest of the completely automatic methods. It is the only fully automatic method that appears in the list of the 20 best performing CASP8 predictor groups.† The results obtained on the subset of “Human and Server” target subset are not particularly informative on the quality of the different methods, since most of them are statistically indistinguishable. This can be due to one of two reasons (or a combination of them): either the number of “Human and server” targets is not sufficiently high for deriving conclusions or most methods are genuinely very similar. The choice of selecting a subset of targets for nonserver predictors originated by the understandable difficulty of human groups in handling a large number of predictions in a short period of time. On the other hand, it is a fact that, at least for homology based models, most groups tend to rely on the same methodology using state-of-the-art sequence similarity search tools (such as HMMs or profile–profile methods) and well performing programs such as Modeller23 for building the final set of atomic coordinates.
We strongly encourage the prediction community to take advantage of the FORCASP forum for discussing these issues before the next experiment starts. This is important to ensure that the CASP effort in setting up the experiment, in standardizing the effective and reliable comparative measures of success described here and in discussing their shortcoming will foster further advances in the protein structure prediction field.
Acknowledgments
Grant sponsor: The US National Library of Medicine (NIH/NLM); Grant number: LM-07085; Grant sponsor: KAUST; Grant number: KUK-I1-012-43; Grant sponsor: EMBO; Grant sponsor: Italbionet (MIUR).
Abbreviations
- CM
comparative modeling
- FR
fold recognition
- RMSD
root mean square deviation
- TBM
template-based modeling
Footnotes
This article is dedicated to the memory of our friend and colleague Angel Ortiz.
The authors state no conflict of interest.
Results for other evaluation measures for each model are also reported in the CASP web site.
The Lee-server group submitted too few predictions on human/server targets and was not considered in the analysis.
REFERENCES
- 1.Kryshtafovych A, Prlic A, Dmytriv Z, Daniluk P, Milostan M, Eyrich V, Hubbard T, Fidelis K. New tools and expanded data analysis capabilities at the Protein Structure Prediction Center. Proteins. 2007;69(Suppl 8):19–26. doi: 10.1002/prot.21653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zemla A, Venclovas C, Moult J, Fidelis K. Processing and analysis of CASP3 protein structure predictions. Proteins. 1999;(Suppl 3):22–29. doi: 10.1002/(sici)1097-0134(1999)37:3+<22::aid-prot5>3.3.co;2-n. [DOI] [PubMed] [Google Scholar]
- 3.Venclovas C, Zemla A, Fidelis K, Moult J. Criteria for evaluating protein structures derived from comparative modeling. Proteins. 1997;(Suppl 1):7–13. doi: 10.1002/(sici)1097-0134(1997)1+<7::aid-prot3>3.3.co;2-c. [DOI] [PubMed] [Google Scholar]
- 4.Mosimann S, Meleshko R, James MN. A critical assessment of comparative molecular modeling of tertiary structures of proteins. Proteins. 1995;23:301–317. doi: 10.1002/prot.340230305. [DOI] [PubMed] [Google Scholar]
- 5.Zemla A. Venclovas, Moult J, Fidelis K. Processing and evaluation of predictions in CASP4. Proteins. 2001;(Suppl 5):13–21. doi: 10.1002/prot.10052. [DOI] [PubMed] [Google Scholar]
- 6.Moult J, Fidelis K, Zemla A, Hubbard T. Critical assessment of methods of protein structure prediction (CASP): round IV. Proteins. 2001;(Suppl 5):2–7. [PubMed] [Google Scholar]
- 7.Tramontano A, Leplae R, Morea V. Analysis and assessment of comparative modeling predictions in CASP4. Proteins. 2001;(Suppl 5):22–38. doi: 10.1002/prot.10015. [DOI] [PubMed] [Google Scholar]
- 8.Zemla A. LGA: a method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tress M, Ezkurdia I, Grana O, Lopez G, Valencia A. Assessment of predictions submitted for the CASP6 comparative modeling category. Proteins. 2005;61(Suppl 7):27–45. doi: 10.1002/prot.20720. [DOI] [PubMed] [Google Scholar]
- 10.Read RJ, Chavali G. Assessment of CASP7 predictions in the high accuracy template-based modeling category. Proteins. 2007;69(Suppl 8):27–37. doi: 10.1002/prot.21662. [DOI] [PubMed] [Google Scholar]
- 11.Siew N, Elofsson A, Rychlewski L, Fischer D. MaxSub: an automated measure for the assessment of protein structure prediction quality. Bioinformatics. 2000;16:776–785. doi: 10.1093/bioinformatics/16.9.776. [DOI] [PubMed] [Google Scholar]
- 12.Zhang Y, Skolnick J. Scoring function for automated assessment of protein structure template quality. Proteins. 2004;57:702–710. doi: 10.1002/prot.20264. [DOI] [PubMed] [Google Scholar]
- 13.Ortiz AR, Strauss CE, Olmea O. MAMMOTH (matching molecular models obtained from theory): an automated method for model comparison. Protein Sci. 2002;11:2606–2621. doi: 10.1110/ps.0215902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kryshtafovych A, Milostan M, Szajkowski L, Daniluk P, Fidelis K. CASP6 data processing and automatic evaluation at the protein structure prediction center. Proteins. 2005;61(Suppl 7):19–23. doi: 10.1002/prot.20718. [DOI] [PubMed] [Google Scholar]
- 15.Wang G, Jin Y, Dunbrack RL., Jr Assessment of fold recognition predictions in CASP6. Proteins. 2005;61(Suppl 7):46–66. doi: 10.1002/prot.20721. [DOI] [PubMed] [Google Scholar]
- 16.Tramontano A, Morea V. Assessment of homology-based predictions in CASP5. Proteins. 2003;53(Suppl 6):352–368. doi: 10.1002/prot.10543. [DOI] [PubMed] [Google Scholar]
- 17.Kopp J, Bordoli L, Battey JN, Kiefer F, Schwede T. Assessment of CASP7 predictions for template-based modeling targets. Proteins. 2007;69(Suppl 8):38–56. doi: 10.1002/prot.21753. [DOI] [PubMed] [Google Scholar]
- 18.Kinch LN, Wrabl JO, Krishna SS, Majumdar I, Sadreyev RI, Qi Y, Pei J, Cheng H, Grishin NV. CASP5 assessment of fold recognition target predictions. Proteins. 2003;53(Suppl 6):395–409. doi: 10.1002/prot.10557. [DOI] [PubMed] [Google Scholar]
- 19.Tress ML, Ezkurdia I, Richardson JS. Target domain definition and classification in CASP8. Proteins. 2009;77(Suppl 9):10–17. doi: 10.1002/prot.22497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Shapiro SS, Wilk MB. An analysis of variance test for normality (complete samples). Biometrika. 1965;52:591–611. [Google Scholar]
- 21.Keedy DA, Williams CJ, Headd JJ, Arendall WB, III, Chen VB, Kapral GJ, Gillespie RA, Zemla A, Richardson DC, Richardson JS. The other 90% of the protein: Assessment beyond the C-alphas for CASP8 template-based models. Proteins. 2009;77(Suppl 9):29–49. doi: 10.1002/prot.22551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kryshtafovych A, Krysko O, Daniluk P, Dmytriv Z, Fidelis K. Protein Structure Prediction Center in CASP8. Proteins. 2009;77(Suppl 9):5–9. doi: 10.1002/prot.22517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sali A, Blundell TL. Comparative protein modelling by satisfaction of spatial restraints. J Mol Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]