Skip to main content
PMC home page
HHS Author Manuscripts logoLink to HHS Author Manuscripts
. Author manuscript; available in PMC: 2015 Sep 30.
Published in final edited form as: Ann Occup Hyg. 2014 Nov 25;59(3):373–381. doi: 10.1093/annhyg/meu095

Protection Factor for N95 Filtering Facepiece Respirators Exposed to Laboratory Aerosols Containing Different Concentrations of Nanoparticles

Samy Rengasamy 1,*, Gary Walbert 1, William Newcomb 1, Christopher Coffey 1, James Terrence Wassell 1, Jonathan Szalajda 1
PMCID: PMC4589166  NIHMSID: NIHMS708806  PMID: 25429023

Abstract

A previous study used a PortaCount Plus to measure the ratio of particle concentrations outside (Cout) to inside (Cin) of filtering facepiece respirators (FFRs) worn by test subjects and calculated the total inward leakage (TIL) (Cin/Cout) to evaluate the reproducibility of the TIL test method between two different National Institute for Occupational Safety and Health laboratories (Laboratories 1 and 2) at the Pittsburgh Campus. The purpose of this study is to utilize the originally obtained PortaCount Cout/Cin ratio as a measure of protection factor (PF) and evaluate the influence of particle distribution and filter efficiency. PFs were obtained for five N95 model FFRs worn by 35 subjects for three donnings (5 models × 35 subjects × 3 donnings) for a total of 525 tests in each laboratory. The geometric mean of PFs, geometric standard deviation (GSD), and the 5th percentile values for the five N95 FFR models were calculated for the two laboratories. Filter efficiency was obtained by measuring the penetration for four models (A, B, C, and D) against Laboratory 2 aerosol using two condensation particle counters. Particle size distribution, measured using a Scanning Mobility Particle Sizer, showed a mean count median diameter (CMD) of 82 nm in Laboratory 1 and 131 nm in Laboratory 2. The smaller CMD showed relatively higher concentration of nanoparticles in Laboratory 1 than in Laboratory 2. Results showed that the PFs and 5th percentile values for two models (B and E) were larger than other three models (A, C, and D) in both laboratories. The PFs and 5th percentile values of models B and E in Laboratory 1 with a count median diameter (CMD) of 82 nm were smaller than in Laboratory 2 with a CMD of 131 nm, indicating an association between particle size distribution and PF. The three lower efficiency models (A, C, and D) showed lower PF values than the higher efficiency model B showing the influence of filter efficiency on PF value. Overall, the data show that particle size distribution and filter efficiency influence the PFs and 5th percentile values. The PFs and 5th percentile values decreased with increasing nanoparticle concentration (from CMD of 131 to 82 nm) indicating lower PFs for aerosol distribution within nanoparticle size range (<100 nm). Further studies on the relationship between particle size distribution and PF are needed to better understand the respiratory protection against nanoparticles.

Keywords: count median diameter (CMD), filter penetration, N95 filtering facepiece respirators, particle size distribution, protection factor (PF)

INTRODUCTION

Engineered nanoparticles are materials deliberately synthesized for specialized applications because of their unique physical and chemical properties. The concentration of nanoparticles released in some work-places is unlikely to pose substantial risk (Liao et al., 2009; Lee et al., 2011). However, some studies have reported the presence of high concentration of engineered nanoparticles in a variety of workplaces (Bello et al., 2009; Heitbrink et al., 2009; Peters et al., 2009; Brouwer, 2010; Methner et al., 2010; O'Shaughnessy, 2013). Nanoparticle exposure has been shown to produce pathophysiological changes in pulmonary and systemic functions indicating potential health risks to workers (Seaton et al., 2010; Shvedova et al., 2009). The possibility of worker exposure to nanoparticles from various sources is present in some workplaces. Inhalation is the most common route of nanoparticle entry in living beings. This suggests that respiratory protection against nanoparticles is an important aspect of workers safety and health.

The Occupational Safety and Health Administration (OSHA) defines the assigned protection factor (APF) as the workplace level of respiratory protection that a respirator or class of respirators is expected to provide to employees when the employer implements a continuing, effective respiratory protection program (Federal Register, 1998). Historically, 95% of users achieve the protection factor (PF) value assigned to the different types of respirator classes. Based on this, Lenhart and Campbell selected the 5th percentile method for determining the APF of a respirator (Lenhart and Campbell, 1984). An APF of 10 has been assigned to half-mask respirators including N95 filtering facepiece respirators (FFRs) (OSHA, 2006). A similar PF, called the workplace protection factor (WPF) is described as the protection provided in a real workplace, under the conditions of that workplace, by a properly selected, fit tested and functioning respirator while it is correctly worn and used (AIHA, 2002).

The WPF for different types of respirators in a variety of workplaces has been described (Nelson et al., 2001; Zhuang et al., 2003; Bidwell and Janssen, 2004; Janssen et al., 2007; Cho et al., 2010). In general, the contaminant particle diameter was >1 μm in many workplaces. Janssen et al. evaluated the performance of an FFR in a steel foundry and showed that the GM of the WPF was 119 with a lower 5th percentile value of 19 (Janssen et al., 2007). Similarly, an N95 FFR showed a GM for WPFs of 233 with a 5th percentile value of 24 in a concrete manufacturing plant (Bidwell and Janssen, 2004). Another study on elastomeric half-facepiece respirators with P100 filters reported a GM for WPFs of 920 with a GSD of 17.8 in a steel foundry (Zhuang et al., 2003). Recently, Cho et al have measured WPFs for N95 FFRs and elastomeric half-facepiece respirators on an agricultural farm and showed 5th percentile WPFs >10 (Cho et al., 2010). The 5th percentile WPF estimates in the above studies were generally larger than the expected APF value of 10, suggesting that half-facepiece respirators provided the expected protection levels in those workplaces.

A surrogate measurement of the WPF called simulated workplace protection factor (SWPF) in a variety of different laboratory settings has been reported (Cohen et al., 2001; Coffey et al., 2004; Lawrence et al., 2006; Hauge et al., 2012; Caretti et al., 2013). In one study, 18 N95 FFRs were tested by subjects performing a set of six exercises in a laboratory and the SWPF was measured using a PortaCount Plus (Coffey et al., 2004). In that study, many models had 5th percentile SWPF values of <10. Subsequently, the SWPFs for 15 models of N95 elastomeric respirators, 15 N95 model FFRs, and six models of surgical masks were reported (Lawrence et al., 2006). For elastomeric respirators and FFRs, the GM of SWPF values were 35.5 and 20.5, with 5th percentile values of 7.3 and 3.3, respectively. These results suggested that the OSHA-assigned APFs may overestimate their measured APF. A recent study, however, showed somewhat larger SWPF for an N95 FFR donned on subjects performing simulated tasks in three health care scenarios (Hauge et al., 2012). Two PortaCount with N95-Companion instruments measured the upstream and downstream concentrations and a real-time SWPF was obtained. The GM SWPF values for eight subjects ranged from 172 to 1073 (GSD 1.7–3.5).

Similarly, PF for N95 FFRs worn by subjects was measured as a ratio of particle concentration outside to inside the respirator in a controlled test chamber, using an Electrical Low Pressure Impactor (ELPI) (Lee et al., 2008). The ELPI measures the particle concentration of different aerodynamic diameter size particles. The PF values were lower for ~78 nm size range particles than for the other size particles, and increased with increasing particle sizes up to 1260 nm. Results showed PFs of <10 for about 29% of FFRs tested in that study. PF was also obtained using a manikin head form for respirators using water-based condensation particle counters (Brochot et al., 2012). PF was measured at two conditions (sealed and unsealed) on a Sheffield head form at constant and cyclic flow conditions using two different NaCl aerosols centered at 13 and 50 nm. The PF was greater for both types of aerosols at sealed condition. With major leaks, the PFs were lower than at sealed condition and showed no particle size dependency. The controversial results obtained in the above studies suggest that further studies are needed to better understand respiratory protection against nanoparticles.

Recently, a PortaCount Plus was used to measure the ratio of particle concentration outside (Cout) to inside (Cin) of filtering facepiece respirators (FFRs) worn by test subjects. The Cout/Cin ratio was used to calculate the total inward leakage [total inward leakage (TIL) = Cin/Cout] to evaluate the reproducibility of the TIL test method between two different National Institute for Occupational Safety and Health (NIOSH) laboratories (Laboratories 1 and 2) at the Pittsburgh Campus (Rengasamy et al., 2014). A good agreement (≥83%) of the TIL test data between the two laboratories was obtained. Particle size distribution showed a mean count median diameter (CMD) of 82 nm in Laboratory 1 compared to 131 nm in Laboratory 2, which indicated relatively higher concentration of nanoparticles in Laboratory 1.

In this study, the originally measured PortaCount Cout/Cin ratios were considered as PFs, and the influence of particle size distribution and filter penetration was evaluated. The purposes of this study are to: (i) calculate the GM of PFs and their 5th percentile values for the five N95 FFR models tested on 35 subjects exposed to aerosols of Laboratory 1 (CMD 82 nm) and Laboratory 2 (CMD of 131 nm), (ii) compare both the PFs and the 5th percentile values in the two laboratories for the five FFR models, (iii) evaluate the influence of particle size distribution and filter penetration on PF and 5th percentile value.

MATERIALS AND METHODS

This study uses the data collected in a previous study (Rengasamy et al., 2014). In that study, the Cout/Cin ratios for respirators were measured, and then converted to Cin/Cout ratios (TIL) to evaluate the reproducibility of the TIL test method between two laboratories. This article, however, has used the originally measured Cout/Cin ratios. Brief details of that study are described below. For more details, the methods used in that study are available in the above article.

Respirator selection

Five N95 FFR models were tested in the study. The manufacturers and models in parentheses are: 3M (Model 8000), 3M (Model 8511), 3M (Model 9210), Kimberly-Clark (Model 170/174), and Sperian–Willson (Model SAF-T-FIT) which were labeled randomly as A, B, C, D, and E.

Laboratory (ambient) aerosol specifications

A particle generator (TSI Model 8026) was employed, as needed, to supplement laboratory particle concentration levels with NaCl aerosol to maintain an ambient aerosol concentration between 0.01 to 5 × 105 particles/cm3 required for the PortaCount measurement. Ambient aerosol concentration (particles/cm3) in Laboratory 1 ranged between 1310 and 8740 (average 3010) and in Laboratory 2 ranged between 1370 and 10 100 (average 5410).

Test subjects

Thirty five subjects were tested for PF measurement with each of the five FFR models in both test laboratories. The NIOSH bivariate panel was used for placement of test subjects in specific face length by face width cells (Zhuang et al., 2008). The bivariate panel has ten cells and covers face length from 98.5 to 138.5 mm and face width from 120.5 to 158.5 mm. The small, medium and large face size categories achieved the highest geometric mean (GM) fit factors in the small, medium, and large respirator sizes, respectively. The results from the above study indicated that good fitting can be achieved by selection of proper size respirators for the facial dimensions. This study was approved by the NIOSH Human Subject Review Board and all subjects gave written consent to participate.

PF measurement

A PortaCount® Pro+ (Model 8038, TSI, Inc. Shoreview, MN), with the N95-Companion mode turned off, was used to measure the ambient and in-mask particle concentrations to obtain the PF. The accuracy of the PortaCount measurement is ±10% as specified by the manufacturer. Subjects were randomly chosen to start the test in either Laboratory 1 or Laboratory 2, and then completed the test in other laboratory on the same day. Different test operators administered the testing in each of the two laboratories and were blinded to the test results of the subjects in the other laboratory. Subjects performed the eight exercises described in the standard OSHA fit test protocol (OSHA, 1998b). These eight exercises were performed in the following order: (i) normal breathing, (ii) deep breathing, (iii) turn head side to side, (iv) move head up and down, (v) speak out loud (recitation of the ‘rainbow’ passage), (vi) reach for floor and ceiling, (vii) grimace, and (viii) normal breathing. The duration of time for each exercise is about a minute for a total of 8 min for the test. At the end of the test, the subject removed the FFR, redonned the same FFR, and repeated the test two more times consecutively with a 5-min break between the tests.

The PortaCount calculates the PF for each individual exercise (PFi),

PFi=Ambient concentrationIn-mask concentration

and then obtains the harmonic mean PF for seven exercises excepting the grimace as shown below with ‘n’ representing the number of exercises.

PF=n(∑i=1n1PFi)−1

Two similarly calibrated PortaCounts were used to measure the PF in the two test laboratories. Test data, including test subject and respirator identifiers were recorded by the FitPro Fit Test software (TSI, Inc.) and accessed after the test for analysis. Test data was also recorded manually for immediate review by project personnel and verification.

Laboratory aerosol size distribution measurement

Two Scanning Mobility Particle Sizers (SMPS, TSI, Inc.) with a long differential mobility analyzer (Model 3081) were used to measure the size distribution of particles in the 10–700 nm size range in the two laboratories. The SMPS was programmed to scan the particle size distribution for 135 s, three times, every hour from 8:00 AM to 4:00 PM Monday through Friday. From the SMPS scans, the average CMD of the laboratory aerosol was obtained. No specific attempt was made to maintain the aerosol size distributions different in the two laboratories. Laboratory 1 and Laboratory 2 are located in two different buildings with additional laboratories, where experiments not related to the work described in the article, were also performed. Particles generated by other processes in the two buildings could have contributed to the particle size distributions in the two laboratories.

Laboratory aerosol penetration

Only four N95 respirator models (A, B, C, and D) were tested because model E was not available during the initial part of the study. Instantaneous penetration for FFRs was measured using two ultrafine condensation particle counters (UCPCs) against aerosols in the test Laboratory 2 (Rengasamy et al., 2014). Figure 1 shows the schematic of the test set up used for filter penetration. Five FFR samples from each model were tested in the morning (8:30– 9:30 AM), stored and then tested in the afternoon (2:30–3:30 PM). Briefly, Laboratory 2 aerosol was drawn through a sealed respirator inside the test box at two different constant test flow rates of 30 and 85 l min−1. The particle number concentration upstream and downstream of the respirator was measured simultaneously after 1 min equilibration time. Percentage penetration was obtained from the ratio of the aerosol concentration downstream to upstream and multiplying by 100. From the penetration values, the filter efficiencies for the four models were assessed.

Figure 1.

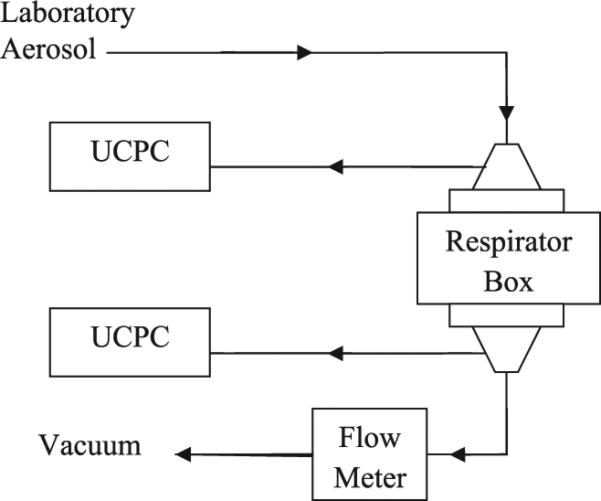
Figure 1

Open in a new tab

Schematic of the filtration test set up used for measuring laboratory aerosol filter penetration.

DATA ANALYSIS

Thirty-five subjects tested five N95 model FFRs three times (35 subjects × 5 FFR models × 3 donnings) to give a total number of 525 PF tests in each laboratory. The 5th percentile PF value was calculated using the formula GM/GSD1.645. Statistical significance tests were based on a mixed effects analysis of variance (with ‘subject’ as a random effect) using specific contrasts for hypothesis testing. R software was used for this analysis (R Core Team, 2013) with the ‘nlme’ package (Pinheiro et al., 2013).

Laboratory 2 aerosol size distribution data and penetration data were analyzed using the SigmaPlot® version 11 (Aspire Software International, Ashburn, VA, USA) computer program. The CMD values measured in the two laboratories were analyzed by a two sided t-test (Shapiro–Wilk). Average penetration values and 95% confidence intervals were calculated for each model. A one way analysis of variance on Ranks was conducted to evaluate the significance of penetration results among the four respirator models at 30 and 85 l min−1 flow rates.

RESULTS

Table 1 shows the GM of PF and GSD for the different N95 model FFRs. The GM of PF values for models B and E were significantly (P ≤ 0.05) larger than the other models in both laboratories. The GM of PFs for both B and E in Laboratory 1 were significantly (P ≤ 0.05) smaller than in Laboratory 2. The other three models showed marginal differences between the two laboratories. The 5th percentile PF values were ≥10 for all models, excepting model A, in the two laboratories. The 5th percentile values were larger for models B and E than for the other models in both laboratories. Models B and E showed slightly smaller 5th percentile PFs in Laboratory 1 than in Laboratory 2.

Table 1.

GM, GSD, and 5th percentile of PF values for the five N95 models tested in the two laboratories

N95 model Total number of tests PF
Laboratory 1
 Laboratory 2
GM GSD 5th percentile GM GSD 5th percentile
A 105 29.09 1.93 9.86 32.28 2.06 9.83
Ba 105 115.05 2.36 28.02 156.37b 2.54 33.74
C 105 44.12 1.80 16.78 43.28 1.58 20.39
D 105 39.07 1.43 21.69 36.43 1.52 18.29
Ea 105 92.05 2.07 27.81 111.15b 2.18 30.94
Open in a new tab
a

Significantly different from other models.

b

Significantly different from Laboratory 1 for this model.

Particle distribution was measured on all PF test days (27 days in Laboratory 1 and 32 days in Laboratory 2). The mean CMD was 82 ± 19 nm in Laboratory 1, which was significantly (P ≤ 0.05) lower than the CMD of 131 ± 23 nm in Laboratory 2. The difference in the size distribution is supported by the CMD values of <100 nm in Laboratory 1 on 93% of PF test days compared with 18% of test days in Laboratory 2. The CMD value represents 50% of particles above and below that size. The particle size distribution with CMD values of 82 nm in Laboratory 1, and 131 nm in Laboratory 2 indicates the presence of relatively higher concentration of nanoparticles in Laboratory 1.

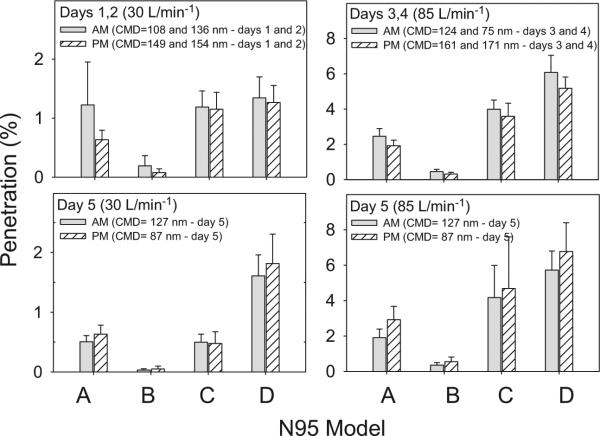
Filter penetration for four models (A, B, C, and D) was measured on 5 days only in Laboratory 2. The CMD values on Days 1–4 (108, 136, 124, and 75 nm, respectively) were smaller in the morning than in the afternoon (149, 154, 161, and 171 nm, respectively). In contrast, the CMD value on Day 5 was larger in the morning than in the afternoon (127 versus 87 nm, respectively).

Filter penetration was measured at 30 l min−1 on 2 days (Days 1 and 2), and at 85 l min−1 on 2 days (Days 3 and 4). Average penetrations at 30 l min−1 (Days 1 and 2) as well as at 85 l min−1 (Days 3 and 4) were calculated to explain the results better. Figure 2 shows the average penetration values for the four N95 FFR models at 30 l min−1 (left panel) and at 85 l min−1 (right panel). Penetration was relatively larger in the morning than in the afternoon at 30 and 85 l min−1 for all four N95 FFR models. The penetration values on Day 5 were not combined with the penetrations on other days, because of the opposite trend in penetration in the morning and afternoon at both flow rates (bottom panels). Penetration was relatively smaller in the morning than in the afternoon at both flow rates for all four N95 FFR models. Penetrations in the morning and afternoon were not statistically different on all 5 days. Model B showed significantly (P ≤ 0.05) lower penetration values than models A, C, and D at the above test conditions and was considered as a relatively higher efficiency model. Penetration values were larger when the CMD values were smaller and vice versa for all 5 days, showing an association between penetration and particle size distribution.

Figure 2.

Figure 2

Open in a new tab

Filter penetration in the morning (AM) and in the afternoon (PM) for four N95 FFR models (A, B, C, and D) against ambient Laboratory 2 aerosol. The CMD was smaller in the morning than in the afternoon on Days 1–4 and showed a reverse trend on Day 5. Top panels show the average penetration values on Days 1 and 2 at 30 l min−1 (top left) and on Days 3 and 4 at 85 l min−1 (top right). Bottom panels show the penetration values at 30 and 85 l min−1 on Day 5.

DISCUSSION

Data from this study showed an association between PF and particle size distribution. Two models (B and E) tested in the study showed that the GM of PFs in Laboratory 1 was significantly (P ≤ 0.05) smaller than in Laboratory 2, while the other three models showed only marginal or no effect. Parallel data on particle distribution showed that the CMD values in Laboratory 1 was <100 nm on 93% of test days compared with 18% in Laboratory 2. The mean CMD (for all PF test days) of 82 nm in Laboratory 1 was significantly (P ≤ 0.05) smaller than 131 nm in Laboratory 2. In the case of models B and E, the increase in the GM of PFs from Laboratory 1 to Laboratory 2 showed an association with the increase in mean CMD value.

The relationship between particle size and PF obtained in our study is corroborated by the findings in previous studies (Lee et al., 2008; Cho et al., 2010). The PF values for eight different particle size ranges between 40 to 1200 nm were measured for N95 FFRs worn by human subjects (Lee et al., 2008). PF values were lowest for 78–130 nm aerodynamic diameter particles and increased with increasing particle sizes up to 1200 nm. The ELPI measures particle numbers of different aerodynamic diameter size particles as opposed to the particle numbers based on electrical mobility diameters by the SMPS. Larger size particles also showed an increase in the 5th percentile WPFs from 16 to 223 for N95 FFRs with increasing particle diameters from 0.7 to 10 μm using an optical particle counter (OPC) (HHPC-6, Hach Company, Loveland, Co) (Cho et al., 2010). The similarity between the PortaCount measured PFs obtained in this study, and the PFs by the ELPI (Lee et al., 2008) and the WPFs by the OPC (Cho et al., 2010) using different technologies demonstrates the consistency of particle size dependency of PFs or WPFs.

Some studies have described a lack of correlation between particle size and WPF values (Bidwell and Janssen, 2004; Janssen et al., 2007; Janssen and McCullough, 2010). The particle size distribution showed approximately ~5 μm MMAD in the above workplaces. The absence of a correlation between particle size and WPF can be explained by the TIL (inverse function of respiratory protection) measured for respirators. Faceseal leakage and filter penetration that contribute to TIL were measured for N95 FFRs worn by human subjects as well as using a manikin head form (Grinshpun et al., 2009). Results showed that filter penetration as well as the faceseal leakage peaked at ~100 nm (aerodynamic diameter) and then decreased with increasing particle sizes. The results are supported by the decrease in the TIL measured with increasing particle sizes from 20 nm up to 800 nm size particles using a breathing manikin head form (Rengasamy and Eimer, 2012). The above results indicate that TIL values would be much smaller for larger size (~5 μm) particles and would be similar among larger size (e.g. between ~5 μm and ~10 μm) particles. As a result, particles of larger size ranges may not show a strong correlation with WPF.

Moreover, the measurement of Cin for larger size particles in a workplace with fewer numbers of larger size (~5 μm) particles may produce inconsistent Cout/Cin ratio. This may be a potential source for the lack of correlation between particle size and WPF in studies with mass-based particle concentration measurement, because the loss of a single large particle could underestimate Cin and may result in an overestimation of the WPF value (Janssen and Bidwell, 2007; Janssen et al., 2007). In contrast, a recent study estimated the WPF values for an N95 elastomeric respirator (ER) and an N95 FFR and showed a consistent increase in WPF values with increasing particle sizes from 0.7 to 10 μm using an OPC in an agricultural farm (Cho et al., 2010). Taken together, results from the above studies suggest that contaminant particle size distribution and concentration in the workplace, accuracy of Cin measurement, test equipment and methodologies are important criteria to obtain a strong correlation between particle size and WPF.

The results obtained in the study raises a question why only models B and E showed significantly (P < 0.05) higher GM PFs than the other three models in both laboratories. The results agree with the SWPF values obtained previously (Lawrence et al., 2006). In that study, SWPFs and 5th percentile values were obtained for 15 N95 FFR models (Lawrence et al., 2006). Three models showed relatively larger SWPFs and 5th percentile values than the other 12 models without fit testing. Interestingly, the two N95 models that gave higher GM of PF values in our study were found to be among the three models that showed higher SWPF values in the above study. The reason for the difference in PF (or SWPF) between respirator models has not been well studied. A difference in filter efficiency between respirator models can produce the above results. Of the four models tested, the filter efficiency of model B was relatively higher (lower filter penetration values) than models A, C, and D. The higher efficiency model had larger PF values in both laboratories than the lower efficiency models indicating a direct relationship between filter efficiency and PFs. This assumption is supported by the TIL measured for four N95 model FFRs using a breathing manikin head form at different artificial leaks in a controlled environmental chamber (Rengasamy and Eimer, 2012). Smaller TIL values were obtained for two relatively higher efficiency N95 FFRs at similar leak sizes indicating larger PFs. This clarification is consistent with the larger PF value for the higher efficiency model B than the smaller PF values for the three lower efficiency models.

The impact of particle size distribution on PFs can be explained by the filter penetration measured in Laboratory 2. Filter penetration measured in the morning and afternoon on 5 days showed larger penetration values for laboratory aerosol with a smaller CMD values and vice versa (Fig. 2). All four models showed smaller penetration values in the morning for Days 1–4, when the CMD values were smaller (108, 136, 124, and 75 nm, respectively) compared to the larger CMD values in the afternoon (149, 154, 161, and 171 nm, respectively). This is consistent with the higher penetration values obtained in the afternoon than in the morning on Day 5, because the CMD was 127 nm in the morning compared to 87 nm in the after-noon. The results show that aerosols with CMD values closer to ~50 nm, the MPPS for N95 model FFRs, would produce larger filter penetration than the aerosols with CMD values away from the MPPS. Higher filter penetration is expected to produce smaller PFs and vice versa, assuming that subjects had similar fit of FFRs in both laboratories. As expected, Laboratory 1 aerosol with a mean CMD 82 nm produced smaller PFs for the two FFR models than for Laboratory 2 aerosol with mean CMD 131 nm. The results agree with the theoretical considerations of particle filtration with respect to particle size distribution (Huang et al., 2013).

The limitations of the study include that subjects tested only five N95 models. Additional models need to be tested to get consistent information on the 5th percentile values for N95 FFRs. This study was done in two laboratories with aerosol distribution closer to each other (CMD values 82 and 131 nm, respectively). PF tests against aerosols with CMD values closer to ~50 nm size as well as away from that value such as >300 nm would be important to recognize the significance of PF values for nanoparticles and larger size particles. Further studies are underway in our laboratory to address the respiratory protection against nanoparticles.

CONCLUSIONS

The PFs and 5th percentile PFs for two N95 FFR models were smaller in Laboratory 1 for aerosol with a mean CMD of 82 nm than in Laboratory 2 with a CMD of 131 nm indicating an association between particle size distribution and PF values. The smaller CMD (CMD 82 nm) value in Laboratory 1 shows the distribution of relatively higher concentration of nanoparticles than in Laboratory 2 (CMD 131 nm). The results indicate that smaller PFs and 5th percentile values can be expected for particle size distributions within the nanoparticle size range (<100 nm). Filter efficiency was directly related to PF obtained in both laboratories. Further studies on PF for environments with particles <100 nm sizes are needed to evaluate the respiratory protection against nanoparticles.

ACKNOWLEDGEMENTS

The authors acknowledge NIOSH colleagues including Raymond Roberge, William Monaghan, and Emanuele Cauda for their useful suggestions and critical review of the manuscript.

FUNDING

National Institute for Occupational Safety and Health.

Footnotes

DISCLAIMER

Mention of commercial product or trade name does not constitute endorsement by the National Institute for Occupational Safety and Health. The findings and conclusions of this report are those of the authors and do not necessarily represent the views of the National Institute for Occupational Safety and Health.

The authors declare there are no conflicts of interest in relation to this article.

REFERENCES

  1. AIHA Respirator performance terminology [Letter to the editor] 2002;63:132. [Google Scholar]
  2. Bello D, Wardle BL, Yamamoto N, et al. Exposure to nanoscale particles and fibers during machining of hybrid advanced composites containing carbon nanotubes. J Nanopart Res. 2009;11:231–249. [Google Scholar]
  3. Bidwell JO, Janssen LL. Workplace performance of an N95 respirator in a concrete block manufacturing plant. J Int Soc Resp Prot. 2004;21:94–102. [Google Scholar]
  4. Brochot C, Michielsen N, Chazelet S, et al. Measurement of protection factor of respiratory protective devices toward nanoparticles. Ann Occup Hyg. 2012;56:595–605. doi: 10.1093/annhyg/mes032. [DOI] [PubMed] [Google Scholar]
  5. Brouwer D. Exposure to manufactured nanoparticles in different workplaces. Toxicology. 2010;269:120–27. doi: 10.1016/j.tox.2009.11.017. [DOI] [PubMed] [Google Scholar]
  6. Caretti DM, Baker DJ, Coyne KM. Simulated workplace protection evaluation of a dual cavity respirator concept. J Int Soc Resp Prot. 2013;30:79–94. [Google Scholar]
  7. Cho KJ, Reponen T, McKay R, et al. Large particle penetration through N95 respirator filters and facepiece leaks with cyclic flow. Ann Occup Hyg. 2010;54:68–77. doi: 10.1093/annhyg/mep062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Coffey CC, Lawrence RB, Campbell DL, et al. Fitting characteristics of eighteen N95 filtering-facepiece respirators. J Occup Environ Hyg. 2004;1:262–71. doi: 10.1080/15459620490433799. [DOI] [PubMed] [Google Scholar]
  9. Cohen HJ, Hecker LH, Mattheis DK, et al. Simulated workplace protection factor study of powered air-purifying and supplied air respirators. Am Ind Hyg Assoc J. 2001;62:595–604. doi: 10.1080/15298660108984658. [DOI] [PubMed] [Google Scholar]
  10. Federal Register . Respiratory Protection. Vol. 63. Code of Federal Regulations 29 Part 1910.134. Occupational Safety and Health Administration; Washington, DC: 1998. pp. 1150–1300. [Google Scholar]
  11. Grinshpun SA, Haruta H, Eninger RM, et al. Performance of an N95 filtering facepiece particulate respirator and a surgical mask during human breathing: two pathways for particle penetration. J Occup Environ Hyg. 2009;6:593–603. doi: 10.1080/15459620903120086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Hauge J, Roe M, Brosseau LM, et al. Real-time fit of a respirator during simulated health care tasks. J Occup Environ Hyg. 2012;9:563–571. doi: 10.1080/15459624.2012.711699. [DOI] [PubMed] [Google Scholar]
  13. Heitbrink WA, Evans DE, Ku BK, et al. Relationships among particle number, surface area, and respirable mass concentrations in automotive engine manufacturing. J Occup Environ Hyg. 2009;6:19–31. doi: 10.1080/15459620802530096. [DOI] [PubMed] [Google Scholar]
  14. Huang SH, Chen CW, Kuo Y-M, et al. Factors affecting filter penetration and quality factor of particulate respirators. Aerosol Air Quality Res. 2013;13:162–71. [Google Scholar]
  15. Janssen L, Bidwell J. Performance of a full facepiece, air-purifying respirator against lead aerosols in a workplace environment. J Occup Environ Hyg. 2007;4:123–8. doi: 10.1080/15459620601128845. [DOI] [PubMed] [Google Scholar]
  16. Janssen L, McCullough NV. Elastomeric, half-facepiece, air-purifying respirator performance in a lead battery plant. J Occup Environ Hyg. 2010;7:46–53. doi: 10.1080/15459620903373537. [DOI] [PubMed] [Google Scholar]
  17. Janssen LL, Nelson TJ, Cuta KT. Workplace protection factors for an N95 filtering facepiece respirator. J Occup Environ Hyg. 2007;4:698–707. doi: 10.1080/15459620701517764. [DOI] [PubMed] [Google Scholar]
  18. Lawrence RB, Duling MG, Calvert CA, et al. Comparison of performance of three different types of respiratory protection devices. J Occup Environ Hyg. 2006;3:465–74. doi: 10.1080/15459620600829211. [DOI] [PubMed] [Google Scholar]
  19. Lee JH, Kwon M, Ji JH, et al. Exposure assessment of workplaces manufacturing nanosized TiO2 and silver. Inhal Toxicol. 2011;23:226–36. doi: 10.3109/08958378.2011.562567. [DOI] [PubMed] [Google Scholar]
  20. Lee SA, Grinshpun SA, Reponen T. Respiratory performance offered by N95 respirators and surgical masks: human subject evaluation with NaCl aerosol representing bacterial and viral particle size range. Ann Occup Hyg. 2008;52:177–85. doi: 10.1093/annhyg/men005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lenhart SW, Campbell DL. Assigned protection factors for two respirator types based upon workplace performance testing. Ann Occup Hyg. 1984;28:173–82. doi: 10.1093/annhyg/28.2.173. [DOI] [PubMed] [Google Scholar]
  22. Liao CM, Chiang YH, Chio CP. Assessing the airborne titanium dioxide nanoparticle-related exposure hazard at workplace. J Hazard Mater. 2009;162:57–65. doi: 10.1016/j.jhazmat.2008.05.020. [DOI] [PubMed] [Google Scholar]
  23. Methner M, Hodson L, Dames A, et al. Nanoparticle Emission Assessment Technique (NEAT) for the identification and measurement of potential inhalation exposure to engineered nanomaterials–Part B: Results from 12 field studies. J Occup Environ Hyg. 2010;7:163–76. doi: 10.1080/15459620903508066. [DOI] [PubMed] [Google Scholar]
  24. Nelson TJ, Wheeler TH, Mustard TS. Workplace protection factors–supplied air hood. Am Ind Hyg Assoc J. 2001;62:96–9. doi: 10.1080/15298660108984615. [DOI] [PubMed] [Google Scholar]
  25. O'Shaughnessy PT. Occupational health risk to nano-particulate exposure. Environ Sci Process Impacts. 2013;15:49–62. doi: 10.1039/c2em30631j. [DOI] [PubMed] [Google Scholar]
  26. OSHA Assigned Protection Factors: Final rule. 2006 29 CFR Parts 1910, 1915, 1926 71:50121–192. http://www.osha.gov/pls/oshaweb/owadisp.show_document?_table=FEDERAL_REGISTER&p_id=18846.
  27. Peters TM, Elzey S, Johnson R, et al. Airborne monitoring to distinguish engineered nanomaterials from incidental particles for environmental health and safety. J Occup Environ Hyg. 2009;6:73–81. doi: 10.1080/15459620802590058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Pinheiro J, Bates D, DebRoy S, Sarkar D, Team RDC. nlme: linear and nonlinear mixed effects models. R package version 3. 2013:1–108. [Google Scholar]
  29. R Core Team . R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2013. ISBN 3-900051-07-0, URL http://www.R-project.org/) [Google Scholar]
  30. Rengasamy S, Eimer BC. Nanoparticle penetration through filter media and leakage through face seal interface of N95 filtering facepiece respirators. Ann Occup Hyg. 2012;56:568–80. doi: 10.1093/annhyg/mer122. [DOI] [PubMed] [Google Scholar]
  31. Rengasamy S, Walbert G, Newcomb W, et al. Total inward leakage measurement of particulates for N95 filtering facepiece respirators - A comparison study. Ann Occup Hyg. 2014;58:206–16. doi: 10.1093/annhyg/met054. [DOI] [PubMed] [Google Scholar]
  32. Seaton A, Tran L, Aitken R, et al. Nanoparticles, human health hazard and regulation. J Royal Soc Interface. 2010;7(Suppl. 1):S119–29. doi: 10.1098/rsif.2009.0252.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Shvedova AA, Kisin ER, Porter D, et al. Mechanisms of pulmonary toxicity and medical applications of carbon nano-tubes: Two faces of Janus? Pharmacol Ther. 2009;121:192–204. doi: 10.1016/j.pharmthera.2008.10.009. [DOI] [PubMed] [Google Scholar]
  34. Zhuang Z, Coffey CC, Jensen PA, et al. Correlation between quantitative fit factors and workplace protection factors measured in actual workplace environments at a steel foundry. Am Ind Hyg Assoc J. 2003;64:730–738. doi: 10.1202/475.1. [DOI] [PubMed] [Google Scholar]
  35. Zhuang Z, Groce D, Ahlers HW, et al. Correlation between respirator fit and respirator fit test panel cells by respirator size. J Occup Environ Hyg. 2008;64:617–628. doi: 10.1080/15459620802293810. [DOI] [PubMed] [Google Scholar]

RESOURCES