Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Oct 1.
Published in final edited form as: Med Eng Phys. 2014 Jul 4;36(10):1225–1232. doi: 10.1016/j.medengphy.2014.06.010

Inter-Scanner Differences in In Vivo QCT Measurements of the Density and Strength of the Proximal Femur Remain After Correction with Anthropomorphic Standardization Phantoms

R Dana Carpenter 1, Isra Saeed 2, Serena Bonaretti 2, Carole Schreck 2, Joyce H Keyak 3, Timothy Streeper 2, Tamara B Harris 4, Thomas F Lang 2
PMCID: PMC4589175  NIHMSID: NIHMS608850  PMID: 25001172

Abstract

In multicenter studies and longitudinal studies that use two or more different quantitative computed tomography (QCT) imaging systems, anthropomorphic standardization phantoms (ASPs) are used to correct inter-scanner differences and allow pooling of data. In this study, in vivo imaging of 20 women on two imaging systems was used to evaluate inter-scanner differences in hip integral BMD (iBMD), trabecular BMD (tBMD), cortical BMD (cBMD), femoral neck yield moment (Mt) and yield force (Fy), and finite-element derived strength of the femur under stance (FEstance) and fall (FEfall) loading. Six different ASPs were used to derive inter-scanner correction equations. Significant (p < 0.05) inter-scanner differences were detected in all measurements except My and FEfall, and no ASP-based correction was able to reduce inter-scanner variability to corresponding levels of intra-scanner precision. Inter-scanner variability was considerably higher than intra-scanner precision, even in cases where the mean inter-scanner difference was statistically insignificant. A significant (p < 0.01) effect of body size on inter-scanner differences in BMD was detected, demonstrating a need to address the effects of body size on QCT measurements. The results of this study show that significant inter-scanner differences in QCT-based measurements of BMD and bone strength can remain even when using an ASP.

Introduction

Quantitative computed tomography (QCT) is a valuable tool for measuring the bone mineral status, geometry, and strength of the proximal femur in multicenter studies and longitudinal studies [1–10]. One of the challenges confronting investigators in multicenter and longitudinal QCT studies is accounting for any inherent differences in QCT-derived bone mineral density (BMD) and bone strength parameters that may exist between different imaging systems. At least two different QCT imaging systems are often used for data collection in studies using two or more imaging centers. The use of multiple imaging systems may affect the ability of investigators to pool data and/or to compare measurements made at different time points, even when a standard bone mineral reference phantom is used for calibration of bone mineral concentration. During the course of a longitudinal study, hardware changes and software upgrades can result in the use of different imaging systems for performing measurements on the same individual at different time points.

Anthropomorphic standardization phantoms (ASPs), which mimic human anatomy and the x-ray attenuation of different tissues, have been used to assess inter-scanner differences and to provide cross-calibration relationships between different QCT and dual-energy x-ray absorptiometry (DXA) imaging systems [11–15]. During QCT imaging these phantoms are scanned atop the standard bone mineral reference phantom (Figure 1) in each imaging system, and the images are used to derive correction relationships between the known and measured values of volumetric BMD in regions of the ASP. These relationships can then be used to adjust the BMD of each voxel in the image prior to summing voxels for BMD measurements, computing biomechanical properties of bone sections, and performing finite element analysis of whole bone strength.

Figure 1.

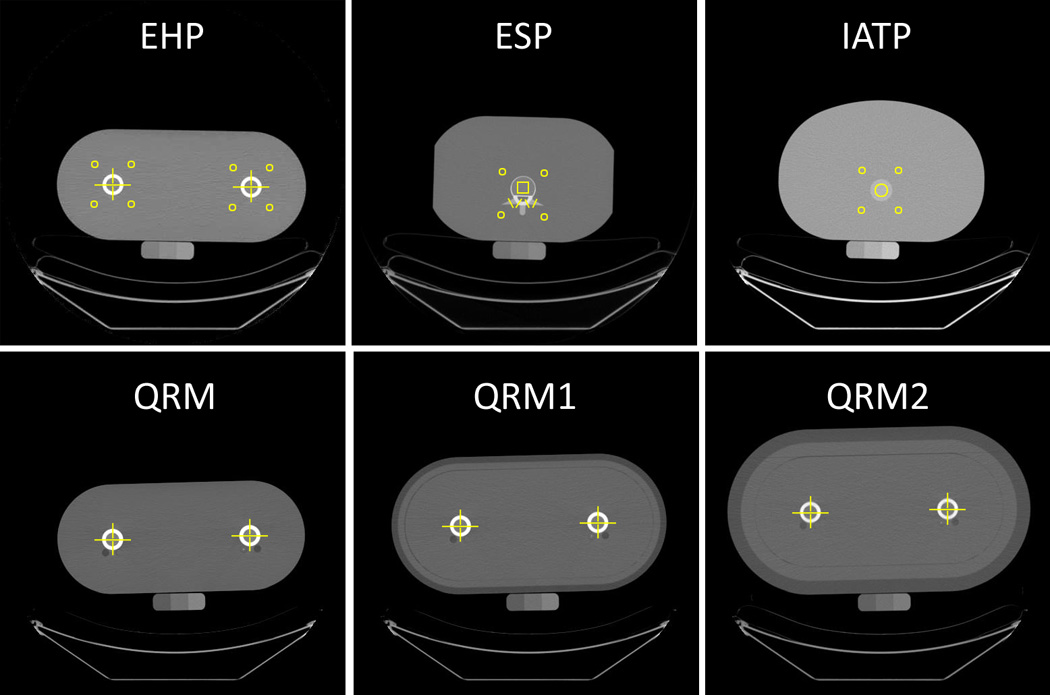
Figure 1

Open in a new tab

Quantitative computed tomography images of the ASPs used in the study. All standardization phantoms were scanned atop the three-chamber solid calcium hydroxyapatite bone mineral reference phantom. Yellow squares and circles bound the ROIs used for BMD measurements in simulated soft tissue and vertebral trabecular bone. Yellow lines indicate the profiles used for BMD measurements in simulated femoral cortices, femoral trabecular bone, vertebral arches, and transverse processes.

Given the increasing use of QCT measurements in multicenter and longitudinal studies, it is important to quantify the differences between measurements made on multiple imaging systems and to determine how effectively standardization phantoms can correct for those differences. Therefore the primary aims of this study were to 1.) determine whether inter-scanner differences in BMD and strength of the proximal femur exist even when using a standard bone mineral reference phantom, and 2.) quantify the ability of six different ASPs to reduce any observed differences in in vivo QCT measurements of the density, structure, and strength of the proximal femur obtained using two different CT imaging systems. We also sought to determine whether patient body size had an effect on any inter-scanner differences.

Methods

Subjects

Twenty women aged 60–69 years were recruited from the San Francisco Bay Area community, and all gave their informed consent to participate in the study. Subjects were excluded if they had undergone total hip arthroplasty, if they had any metal implants or rods in the thigh area, and if they had undergone spinal surgery in the area of the L4 vertebra. Overall subject characteristics are provided in Table 1. All study procedures were approved by the Committee on Human Research at the University of California, San Francisco.

Table 1.

Characteristics of the 20 female subjects

Characteristic Mean ± Standard Deviation
Age (years) 64 ± 3
Height (cm) 165.6 ± 10.5
Weight (kg) 70.0 ± 15.0
Body Mass Index (kg/m2) 25.5 ± 4.4
Open in a new tab

In Vivo Imaging and Analysis

Two different clinical CT imaging systems were used in the study: scanner A, a 64-slice GE Discovery VCT (GE Healthcare, Waukesha, WI, USA), and scanner B, a 16-slice Siemens Hi-Res Biograph (Siemens AG, Erlangen, Germany). For each of the 20 subjects in the study, a region extending from approximately 5 cm superior to the acetabulum to approximately 5 cm distal to the lesser trochanter was imaged on both scanner A and scanner B during the same day. The imaging parameters on the two scanners were adjusted to be as similar as possible within the confines of the two different types of hardware, software, and user interface offered by the different manufacturers (Table 2). A three-chamber, solid calcium hydroxyapatite reference phantom (Image Analysis, Inc., Columbia, KY, USA) was placed within the padding of the scanner bed and was included in the field of view of all images.

Table 2.

Imaging parameters used for both in vivo and ASP imaging

Imaging Parameter Scanner A
(GE Discovery VCT)		 Scanner B
(Siemens Hi-Res Biograph)
Voltage (kVp) 120 120
Tube current (mA) 150 105
Exposure time (ms) 500 1000
Field of View (mm) 500 500
Slice thickness 2.5 3.0
Table[CD1] height (mm) 179 149
Open in a new tab

The trabecular BMD (tBMD), cortical BMD (cBMD), and integral BMD (iBMD = volumetric BMD of entire proximal femur region of interest) of the left proximal femur were computed using previously-described methods [8, 16]. Briefly, the mineral concentration of each voxel in a given image was determined using the reference phantom values for each axial slice. Each image was then digitally rotated and reformatted to obtain slices along the femoral neck axis. The proximal femur was segmented from the surrounding soft tissue using a threshold-driven region growing algorithm, and the integral proximal femur region of interest (ROI) containing the femoral neck and intertrochanteric zone was automatically generated. A trabecular bone ROI was defined by eroding a layer of eight exterior voxels from the periphery of the integral ROI, and a cortical bone ROI was defined by applying a threshold to include all bone voxels that were located outside the trabecular ROI and had a BMD greater than 350 mg/cm3. The BMD of each ROI was then computed by summing the BMD of all voxels and dividing by the volume of the ROI.

The compressive strength and bending strength of the left femoral neck were computed at the location of the minimum femoral neck cross-sectional area (minCSA) using engineering composite beam analysis [17, 18]. To obtain these two strength parameters, the BMD value of each voxel in the minCSA section of the femoral neck was first converted to Young’s modulus (material stiffness) [11, 19, 20]. The amount of compressive force (Fy) and the average bending moment (My, taken over 360 different bending directions) that would cause bone in the femoral neck to reach a yield strain of 0.85% [21] was then computed.

The strength of the whole proximal femur in both stance and fall loading scenarios was computed using voxel-based finite element (FE) analysis [7, 22, 23]. To create subject-specific FE models, the entire left proximal femur was segmented from the surrounding soft tissue using a semiautomatic contouring program. A linear model was used to determine the force (FEfall) that would induce fracture in a fall impacting the posterolateral aspect of the greater trochanter [24], and a nonlinear model was used to determine the force (FEstance) that would induce fracture in a single-leg stance loading direction [22].

For analysis of the effects of body size on any potential inter-scanner differences observed in measured BMD and femoral strength parameters, the cross-sectional area of each subject’s body (CSAbody) was measured at the level of the center of the femoral heads. The external contour of each subject’s skin was manually traced in ImageJ, and the total area enclosed by the contour was computed.

Obtaining and Applying BMD Correction Equations Using ASPs

Images of four different ASPs in a total of six different configurations were used to adjust bone mineral density values obtained on the two scanners. The European hip phantom (EHP, Quality Assurance in Radiology and Medicine (QRM), Moehrendorf, Germany), European spine phantom (ESP, QRM, Moehrendorf, Germany), Image Analysis torso phantom (IATP, Image Analysis, Inc., Columbia, KY, USA), and the QRM Hip Phantom (QRM, Moehrendorf, Germany) with no outer tissue ring (QRM), with a 2-cm-thick ring simulating soft tissue and fat (QRMR1), and with a 4-cm-thick ring simulating soft tissue and fat (QRMR2) were used. Each ASP contained at least two different anatomical regions of nominal equivalent mineral concentration (Table 3). For the ESP, which contains three different vertebral inserts with varying density values, the middle insert was used. Images of each phantom were obtained on both scanner A and scanner B using the same image settings as the in vivo images. For determining intra-scanner precision values for ASP measurements, pairs of images of each ASP were obtained on the same day using scanner B. For these scan pairs, the ASP was removed from the scanner after the first scan and then replaced on the scanner bed for the second scan.

Table 3.

Nominal BMD values specified by the manufacturers and mean values ± standard deviation measured on the two CT scanners for each anatomical region in the ASPs. Intra-scanner precision values (standard deviation of repeat measurements reported in terms of mg/cm3) are listed for repeat measurements obtained on scanner B[CD2].

BMD (mg/cm3)
Phantom Region Nominal Scanner A Scanner B Intra-Scanner
Precision
EHP Soft tissue 0 15.0 ± 7.5 1.2 ± 2.9 0.38
Cortical bone 800 870.3 ± 21.6 802.6 ± 52.0 0.03
Soft tissue 0 0.3 ± 1.9 −4.0 ± 0.8 0.14
Trabecular bone 100 109.6 ± 11.5 99.8 ± 13.7 0.72
ESP Vertebral arch 800 766.5 ± 21.2 747.8 ± 10.1 5.49
Transverse processes 400 383.4 ± 16.5 381.3 ± 8.8 3.83
IATP Soft tissue 0 −1.7 ± 0.9 −2.3 ± 1.4 0.04
Trabecular bone 100 99.5 ± 16.3 93.6 ± 16.2 0.22
QRM Cortical bone 816 830.1 ± 26.8 790.6 ± 69.1 0.67
Trabecular bone 102 122.8 ± 7.8 107.4 ± 6.8 1.27
QRM1 Cortical bone 816 808.7 ± 38.7 787.5 ± 80.3 4.65
Trabecular bone 102 126.5 ± 11.4 108.2 ± 6.6 1.08
QRM2 Cortical bone 816 797.6 ± 37.9 761.9 ± 80.0 2.09
Trabecular bone 102 118.5 ± 11.8 114.0 ± 12.7 2.32
Open in a new tab

Each voxel in each ASP image was calibrated to solid hydroxyapatite mineral concentration based on the bone mineral reference phantom. A linear regression relationship between mean Hounsfield units and the known hydroxyapatite concentration in each phantom chamber was used to perform the calibration. A set of circular and square regions (for soft-tissue equivalent measurements and vertebral body trabecular bone measurements, respectively) and 3-voxel-wide linear profiles (for hip cortical bone, hip trabecular bone, vertebral arches, and transverse processes) were then manually drawn on each image using ImageJ (National Institutes of Health, Bethesda, MD), and the corresponding BMD values were recorded (Figure 1). For all circular and square regions, all voxels contained within each region were used to compute the corresponding mean BMD value. The BMD values in the trabecular cores of all three vertebral inserts in the ESP were used for generating correction equations. For cortical bone measurements in the EHP and QRM hip phantoms, the four peak BMD values along each profile were recorded, providing a total of 16 cortical BMD measurements per image, which were then averaged (Figure 2a). For trabecular bone measurements in the QRM hip phantoms, 10 BMD values from the central region of each profile were recorded, providing a total of 40 trabecular BMD measurements per image, which were then averaged (Figure 2a). The mean of the 16 hip cortical BMD values and the mean of the 40 hip trabecular BMD values were then used to determine the BMD correction equations. For measurements of the BMD of the vertebral arches and transverse processes in the ESP, the three central values in the peak along the profile through each arch (6 total measurements per vertebral insert) and the four central values in the peak along the profile through each transverse process (8 total measurements per vertebral insert) were recorded (Figures 2b and 2c). The mean arch value and mean transverse process value were then computed for each of the three vertebral inserts. The intra-scanner precision of each ASP measurement was calculated as the standard deviation of repeat measurements made on the pairs of images obtained on scanner B [25].

Figure 2.

Figure 2

Open in a new tab

Profiles used to obtain BMD measurements in ASPs. a.) For hip phantom cortices, the two peak values in each side of the cortex were averaged to obtain the profile’s cortical BMD. For QRM trabecular bone cores, the ten central values were averaged to obtain the profile’s trabecular BMD. b.) For transverse processes, the four central values of the peak were averaged to obtain the profile’s BMD. c.) for vertebral arches, the three central values of the peak were average to obtain the profile’s BMD.

The final BMD correction equations for each phantom on each CT scanner were determined by performing linear regression between the measured BMD values and the nominal, manufacturer-specified values for each analyzed anatomical region. The slope (m) and intercept (b) of each regression equation provided a phantom- and scanner-specific correction equation of the form

  • BMDcorrected = m·BMDmeasured + b,

where BMDmeasured is the BMD measured for any voxel or region of interest in the image and BMDcorrected is the corrected BMD value corresponding to a specific combination of ASP and scanner.

Corrections were applied to the regions of interest in all in vivo images on a voxel-by-voxel basis. Following image calibration based on the reference phantom, the BMD of each voxel was corrected using the each of the six different correction equations (one corresponding to each ASP) for the scanner on which the image was obtained. Paired t-tests were used to detect inter-scanner differences in iBMD, tBMD, cBMD, Fy, My, FEfall, and FEstance. Inter-scanner differences in each BMD and femoral strength parameter were quantified for uncorrected and corrected images by computing the coefficient of variation (CV) for repeat measurements in each of the 20 female volunteers [25]. Inter-scanner differences were also compared to the previously-determined intra-scanner CV (or measurement precision) values for hip BMD [26], femoral neck strength [27], and FE-based strength (unpublished data). Linear regression between CSAbody and relative percent inter-scanner difference in each measured parameter was performed to determine whether body size contributed to the differences and whether ASP-based BMD correction would help to decrease such an effect.

Results

Uncorrected measurements of BMD in all ROIs and profiles demonstrated a systematic difference between scanner A and scanner B, with every BMD value measured with scanner B lower than the corresponding value measured with scanner A (Table 3). Intra-scanner precision values for ASP bone regions ranged from 0.03 mg/cm3 to 5.49 mg/cm3, or 0.004% to 2.3% of the corresponding nominal BMD values (Table 3). Linear correction equations for adjusting the BMD using each of the ASPs had a slope relatively close to 1.0 (range 0.935–1.051), and the intercepts for scanner A’s correction equation were larger in magnitude than those for scanner B for five of the six phantoms (scanner B’s intercept was slightly larger for the IATP correction) (Table 4).

Table 4.

Correction equations for adjusting BMD on a voxel-by-voxel basis in the in vivo images of the proximal femur

BMDcorrected = m·BMDmeasured + b
Scanner A Scanner B
Phantom m b m b
EHP 0.935 −13.985 0.998 −1.228
ESP 1.028 −4.768 1.047 0.994
IATP 0.988 1.696 1.043 2.402
QRM 1.006 −19.886 1.021 3.833
QRM1 1.041 −26.832 1.025 7.816
QRM2 1.045 −18.806 1.051 0.259
Open in a new tab

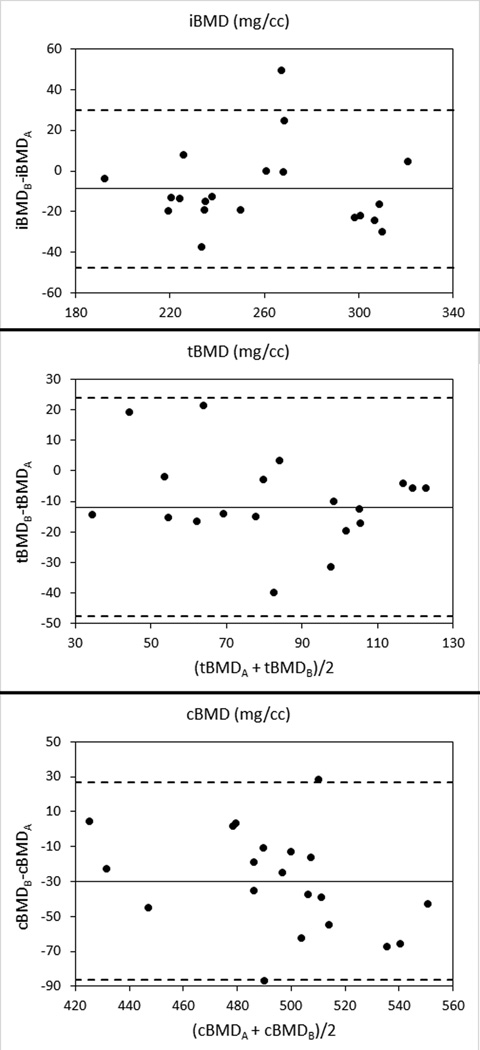
For the in vivo images of 20 women, the uncorrected inter-scanner CV was larger in all cases than the previously-determined intra-scanner precision (Figures 3 and 4, Table 5). The uncorrected inter-scanner difference was significant for all total femur BMD values (iBMD: p < 0.05; tBMD: p < 0.01; cBMD: p < 0.001), Fy (p < 0.01), and FEstance (p < 0.001). None of the correction equations eliminated the inter-scanner difference for all measured parameters, but the IATP correction eliminated all significant differences except that for tBMD. The difference in tBMD was not eliminated by using any of the ASPs. In some cases (e.g. FEfall), the BMD correction equation increased the inter-scanner CV and led to significant differences that did not appear when using uncorrected images.

Figure 3.

Figure 3

Open in a new tab

Bland-Altman plots for inter-scanner differences in volumetric BMD measurements in 20 women. Solid lines indicate the mean inter-scanner difference, and dashed lines indicate 95% confidence intervals (mean ± 1.96 standard deviations).

Figure 4.

Figure 4

Open in a new tab

Bland-Altman plots for inter-scanner differences in femoral neck sectional properties and finite element-based strength of the proximal femur in 20 women. Solid lines indicate the mean inter-scanner difference, and dashed lines indicate 95% confidence intervals (mean ± 1.96 standard deviations).

Table 5.

Inter-scanner coefficients of variation (CV) for uncorrected and corrected measurements in 20 women imaged on the two different scanners. Previously-measured intra-scanner CV values for repeat measurements on a single scanner are provided for comparison.

Parameter Intra-scanner
CV (%)		 Uncorrected

Inter-scanner
CV (%)		 Corrected Inter-scanner CV (%)
EHP ESP IATP QRM QRM1 QRM2
iBMD 1.1 4.7 a 4.9 c 4.1 4.4 3.9 b 3.9 b 3.4
tBMD 0.7 11.3 c 6.3 b 6.9 c 7.9 c 10.4 c 17.1 c 6.6 b
cBMD 1.4 3.8 c 2.0 3.2 b 2.5 2.9 c 3.9 c 3.4 c
Fy 6.6 15.5 b 13.4 a 14.0 12.6 13.1 13.5 13.2
My 3.9 15.7 17.1 a 15.7 15.6 16.2 17.1 15.8
FEfall 6.4 7.3 14.1 c 7.7 7.6 16.0 c 19.6 c 12.5 c
FEstance 1.6 9.2 c 7.4 b 6.5 a 5.9 6.9 a 7.4 b 5.9
Open in a new tab

Inter-scanner differences detected with paired t-tests:

a

p < 0.05,

b

p < 0.01,

c

p < 0.001

Body size (as measured by CSAbody) explained a significant portion of the variance in percent inter-scanner difference in uncorrected iBMD (r2 = 0.33; p < 0.01), cBMD (r2 = 0.35; p < 0.01), and FEfall (r2 = 0.25; p < 0.05). None of the inter-scanner correction equations eliminated the dependence of these differences on body size.

Discussion

The results of this study demonstrate that significant differences in BMD and femoral strength estimates can occur when using multiple QCT imaging systems in a single study, even when a bone mineral reference phantom is used. Furthermore, the use of ASPs to derive linear inter-scanner correction equations did not reduce inter-scanner differences to their corresponding intra-scanner precision values. However, in many cases, the correction equations did help to reduce inter-scanner differences to the point that they were not statistically significant (p ≥ 0.05). Of the BMD and strength measures evaluated in this study, only the inter-scanner difference in tBMD was not able to be corrected.

Of the six different phantoms evaluated in this study, the IATP reduced the most (six out of seven) inter-scanner differences to the point that they were not statistically significant. Only the difference in tBMD remained after applying the IATP correction. This result is somewhat surprising, as the IATP is the most geometrically simple phantom tested, covers the smallest range in equivalent hydroxyapatite concentration (0 – 100 mg/cm3), and is designed to simulate the torso, not the hip region. The QRM2 phantom, which is intended to simulate the hip region, provided the best correction of the inter-scanner difference in iBMD (CV = 3.4%) but increased the inter-scanner CV for FEfall from 7.3% to 12.5%. It should be noted that the FEfall models used a linear failure detection process, in which a standard force was applied to the femoral head, and the resulting stress distribution was scaled linearly until failure was detected. This technique may have made the fall models more sensitive to variations in local BMD values than the FEstance models, which used a nonlinear, iterative approach to predicting failure.

The inter-scanner effects leading to the differences measured in this study arose from a variety of sources, including differences in bone geometry, the location of the bone in the scanner field of view, patient body habitus, and the computational steps (e.g. raising density to a power) needed to calculate the different strength parameters. The aims of this study were to quantify the total inter-scanner effect that arises due to these factors and to determine whether ASP-based corrections can help to reduce the observed differences. The results suggest that the choice of which ASP to use in a multi-site or multi-scanner study should be made based on the specific anatomical site and parameter of interest in a given study.

Closer examination of the slopes and intercepts of the linear correction equations (Table 4) can help to explain the ways in which the use of different ASPs affects BMD values. The higher the measured BMD value, the more important the slope becomes, and the less important the intercept becomes. For example, for a tBMD of 100 mg/cm3 measured on scanner A, the correction equation for the QRM1 ASP (BMDcorrected = 1,041·BMDmeasured − 26.832) would provide a corrected value of 77 mg/cm3. For the same 100 mg/cm3 value measured on scanner B, the QRM1 ASP correction equation (BMDcorrected = 1.025·BMDmeasured + 7.816) would yield a corrected value of 110 mg/cm3. The majority of the change in both of these cases is due to the relatively large intercept values for the QRM1 ASP, and the corrected values for the two scanners are shifted in opposite directions from their measured values. On the other hand, for a cBMD of 1000 mg/cm3 measured on both scanners, using the QRM1 correction would yield a corrected value of 1014 mg/cm3 for scanner A and a corrected value of 1032 mg/cm3 for scanner B. In this case, both measured values were increased by the correction equation due to the relatively large measured values being multiplied by the slopes of the correction equations. As shown by this example, the slope of the correction equation is the key to correcting relatively high cBMD values, while the intercept affects tBMD to a greater extent.

While each ASP was able to reduce at least one inter-scanner difference to a statistically insignificant level, the inter-scanner CV values nearly always remained quite high (corrected CVs ranged from 2.0% to 19.6%) compared to the previously-determined intra-scanner precision values (range of 0.7% to 6.6%), even in cases where the correction reduced the mean difference between scanners to statistically insignificant levels. It should be noted that the intra-scanner precision is based on a total of four measurements (two instances of sampling the reference phantom and two instances of sampling each subject’s femur), while the corrected inter-scanner precision is based on a total of six measurements (two instances of sampling the reference phantom, two instances of sampling the ASP, and two instances of sampling each subject’s femur). Therefore the precision values after correction include two additional sources of error.

The CV reported in this study provides a measure of the absolute value of the difference expected between a pair of images obtained on scanner A and scanner B. On the other hand, paired t-tests were used to detect significant inter-scanner differences between the mean values of measured parameters. Since both positive and negative differences can occur between scanners, the mean values for a given parameter in all 20 women can be relatively similar, but the corresponding CV can remain relatively high. For example, the mean ± standard deviation of ESP-corrected My was 11.57 ± 2.80 N·m when measured on scanner A and 11.59 ± 2.90 N·m when measured on scanner B. The mean values on the two scanners were nearly identical (relative percent difference of 0.2%). However, the inter-scanner CV for the ESP-corrected My was 15.7%. Thus, the CV indicates that any pair of My values obtained on the two scanners will likely be quite different, no matter if the value is higher on scanner A or scanner B. Relying only on the mean values can “hide” inter-scanner differences. This finding has important implications for designing longitudinal studies that utilize multiple scanners to obtain images of the same subject at different time points, because the high levels of inter-scanner variability may decrease statistical power and require longer follow-up times in order to confidently measure temporal changes in QCT-based measurements. The inter-scanner variability may be a smaller cause of concern for cross-sectional studies that aim to combine data obtained on different scanners, because the results of the current study suggests that differences in mean values can be sufficiently corrected using an appropriate ASP.

It is notable that body size had an effect on the relative percent inter-scanner difference in iBMD, cBMD, and FEfall and that none of the linear correction equations eliminated this body size dependence. As shown by the measurements obtained with the three different QRM hip phantoms (Table 3), increased body size produced a trend of decreasing cBMD, likely due to increased beam hardening as more material was added within the scanner field of view. The tissue rings used to modify the size of the QRM hip phantom also offer the ability to make body-size specific inter-scanner corrections. However, the relatively small number of human subjects used in this study did not justify breaking the cohort into smaller groups. An additional set of studies with a larger number of subjects that can be grouped according to body size may help to further characterize the effect of body size on inter-scanner differences.

This study had some limitations that should be considered when interpreting and applying the results. First, only two imaging systems were used, due to radiation dose considerations. Therefore, the results and correction equations reported here are applicable only to those two specific systems (64-slice GE Discovery VCT and 16-slice Siemens Hi-Res Biograph). Any study utilizing two or more imaging systems should consider using methods similar to those used in this study to determine the correction equations specific to the scanners used. Second, only linear corrections were used in this study. For all phantoms except the ESP, a linear fit was the only feasible choice, because each of the other phantoms only contained two regions of nominal hydroxyapatite concentration. It is possible that higher-order correction equations based on phantoms with three or more nominal mineral concentrations could provide a more effective means of correcting inter-scanner differences. Third, while the imaging settings on the two different imaging systems were adjusted to be as similar as possible, it was not possible to obtain images with an identical combination of voltage, current, and slice thickness (Table 2). Therefore some of the differences observed in the study could stem from the different settings. Fourth, except for the IATP, all other ASPs were obtained from different manufacturers than the bone mineral reference phantom used for BMD calibration. Differences in formulations of equivalent water and mineral made by different manufacturers may have led to additional observed shifts in observed BMD and bone strength. Future parametric studies may help to quantify the contribution of each independent source of error (e.g. slice thickness, patient positioning, phantoms from multiple manufacturers, etc.) to the cumulative error measured in this study.

Together, the existence of all of these sources of error led to the main question being asked in this study: how can we be sure that measurements obtained on different imaging systems, many of which have different values of imaging parameters available to the user, are comparable? The results of this study suggest that uncorrected QCT-based measurements originating from different imaging systems may in fact not be comparable and that the use of an ASP to reduce inter-scanner differences is not always effective. Future studies using ASP designs (including the QRM hip phantom and others) that account for body size and that mimic the beam hardening effects of the structures in the relevant region of interest may help to improve inter-scanner correction strategies for QCT-based studies.

This study provided quantitative measurements of inter-scanner differences in QCT-based measurements of the BMD and strength of the proximal femur. As mentioned previously, the different choices of scanning parameters offered by different makes and models of CT imaging systems is one source. Each manufacturer also uses different x-ray sources, filters, and image reconstruction and correction algorithms, all of which contribute to the observed differences between scanners. A previous study by Birnbaum et al. [28] evaluated inter-scanner differences among five different multi-slice systems using an ASP, and they found significant inter-scanner variability in attenuation values for nine different simulated soft tissues. Modifying the convolution kernel used to reconstruct the images had different effects on tissue attenuation, depending on the specific combination of scanner and kernel. Our results show that similar inter-scanner differences occur in mineralized tissues and that ASP-based, linear correction equations can reduce some, but not all, of these differences.

In summary, inter-scanner differences in QCT-based measurements of the strength and density of the proximal femur remain even after correction using ASPs. This finding is of particular concern for longitudinal studies in which at least two different imaging systems are used to obtain images of the same subject at different time points. For cross-sectional studies that compare mean values of QCT measurements, ASP-based corrections can successfully reduce inter-scanner differences to statistically insignificant levels. We also found that body size can affect relative differences between scanners, but additional work is needed to better characterize this body size effect. These results can help to guide investigators in planning QCT studies, and they also suggest a need for improved ASPs for performing inter-scanner corrections.

Acknowledgements

This study was funded by the National Institute on Aging contract HHSN311200800243P and was supported in part by the Intramural Research Program of the National Institute on Aging. All procedures were authorized by the UCSF Committee on Human Research, Authorization Number 10-04697.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of Interest

None

References

  • 1.Black DM, Bouxsein ML, Marshall LM, Cummings SR, Lang TF, Cauley JA, et al. Proximal femoral structure and the prediction of hip fracture in men: a large prospective study using QCT. J Bone Miner Res. 2008;23:1326–1333. doi: 10.1359/JBMR.080316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Borggrefe J, Graeff C, Nickelsen TN, Marin F, Gluer CC. Quantitative computed tomographic assessment of the effects of 24 months of teriparatide treatment on 3D femoral neck bone distribution, geometry, and bone strength: results from the EUROFORS study. J Bone Miner Res. 2010;25:472–481. doi: 10.1359/jbmr.090820. [DOI] [PubMed] [Google Scholar]
  • 3.Bousson V, Adams J, Engelke K, Aout M, Cohen-Solal M, Bergot C, et al. In vivo discrimination of hip fracture with quantitative computed tomography: Results from the prospective european femur fracture study (EFFECT) J Bone Miner Res. 2010 doi: 10.1002/jbmr.270. [DOI] [PubMed] [Google Scholar]
  • 4.Carpenter RD, LeBlanc AD, Evans H, Sibonga JD, Lang TF. Long-term changes in the density and structure of the human hip and spine after long-duration spaceflight. Acta Astronautica. 2010;67:71–81. [Google Scholar]
  • 5.Engelke K, Fuerst T, Dasic G, Davies RY, Genant HK. Regional distribution of spine and hip QCT BMD responses after one year of once-monthly ibandronate in postmenopausal osteoporosis. Bone. 2010;46:1626–1632. doi: 10.1016/j.bone.2010.03.003. [DOI] [PubMed] [Google Scholar]
  • 6.Keaveny TM, Hoffmann PF, Singh M, Palermo L, Bilezikian JP, Greenspan SL, et al. Femoral bone strength and its relation to cortical and trabecular changes after treatment with PTH, alendronate, and their combination as assessed by finite element analysis of quantitative CT scans. J Bone Miner Res. 2008;23:1974–1982. doi: 10.1359/JBMR.080805. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Keyak JH, Koyama AK, LeBlanc A, Lu Y, Lang TF. Reduction in proximal femoral strength due to long-duration spaceflight. Bone. 2009;44:449–453. doi: 10.1016/j.bone.2008.11.014. [DOI] [PubMed] [Google Scholar]
  • 8.Lang TF, Sigurdsson S, Karlsdottir G, Oskarsdottir D, Sigmarsdottir A, Chengshi J, et al. Age-related loss of proximal femoral strength in elderly men and women: the Age Gene/Environment Susceptibility Study--Reykjavik. Bone. 2012;50:743–748. doi: 10.1016/j.bone.2011.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Lang TF, Leblanc AD, Evans HJ, Lu Y. Adaptation of the proximal femur to skeletal reloading after long-duration spaceflight. J Bone Miner Res. 2006;21:1224–1230. doi: 10.1359/jbmr.060509. [DOI] [PubMed] [Google Scholar]
  • 10.Marshall LM, Lang TF, Lambert LC, Zmuda JM, Ensrud KE, Orwoll ES. Dimensions and volumetric BMD of the proximal femur and their relation to age among older U.S. men. J Bone Miner Res. 2006;21:1197–1206. doi: 10.1359/jbmr.060506. [DOI] [PubMed] [Google Scholar]
  • 11.Faulkner KG, Gluer CC, Grampp S, Genant HK. Cross-calibration of liquid and solid QCT calibration standards: corrections to the UCSF normative data. Osteoporos Int. 1993;3:36–42. doi: 10.1007/BF01623175. [DOI] [PubMed] [Google Scholar]
  • 12.Kalender WA. A phantom for standardization and quality control in spinal bone mineral measurements by QCT and DXA: design considerations and specifications. Med Phys. 1992;19:583–586. doi: 10.1118/1.596899. [DOI] [PubMed] [Google Scholar]
  • 13.McCollough CH, Kaufmann RB, Cameron BM, Katz DJ, Sheedy PF, 2nd, Peyser PA. Electron-beam CT: use of a calibration phantom to reduce variability in calcium quantitation. Radiology. 1995;196:159–165. doi: 10.1148/radiology.196.1.7784560. [DOI] [PubMed] [Google Scholar]
  • 14.Nelson JC, Kronmal RA, Carr JJ, McNitt-Gray MF, Wong ND, Loria CM, et al. Measuring coronary calcium on CT images adjusted for attenuation differences. Radiology. 2005;235:403–414. doi: 10.1148/radiol.2352040515. [DOI] [PubMed] [Google Scholar]
  • 15.Pearson J, Dequeker J, Henley M, Bright J, Reeve J, Kalender W, et al. European semi-anthropomorphic spine phantom for the calibration of bone densitometers: assessment of precision, stability and accuracy. The European Quantitation of Osteoporosis Study Group. Osteoporos Int. 1995;5:174–184. doi: 10.1007/BF02106097. [DOI] [PubMed] [Google Scholar]
  • 16.Lang TF, Keyak JH, Heitz MW, Augat P, Lu Y, Mathur A, et al. Volumetric quantitative computed tomography of the proximal femur: precision and relation to bone strength. Bone. 1997;21:101–108. doi: 10.1016/s8756-3282(97)00072-0. [DOI] [PubMed] [Google Scholar]
  • 17.Carpenter RD, Beaupre GS, Lang TF, Orwoll ES, Carter DR. New QCT analysis approach shows the importance of fall orientation on femoral neck strength. J Bone Miner Res. 2005;20:1533–1542. doi: 10.1359/JBMR.050510. [DOI] [PubMed] [Google Scholar]
  • 18.Carpenter RD, Sigurdsson S, Zhao S, Lu Y, Eiriksdottir G, Sigurdsson G, et al. Effects of age and sex on the strength and cortical thickness of the femoral neck. Bone. 2011 doi: 10.1016/j.bone.2010.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Lotz JC, Gerhart TN, Hayes WC. Mechanical properties of trabecular bone from the proximal femur: a quantitative CT study. J Comput Assist Tomogr. 1990;14:107–114. doi: 10.1097/00004728-199001000-00020. [DOI] [PubMed] [Google Scholar]
  • 20.Orr TE, Beaupre GS, Carter DR, Schurman DJ. Computer predictions of bone remodeling around porous-coated implants. J Arthroplasty. 1990;5:191–200. doi: 10.1016/s0883-5403(08)80074-5. [DOI] [PubMed] [Google Scholar]
  • 21.Morgan EF, Keaveny TM. Dependence of yield strain of human trabecular bone on anatomic site. J Biomech. 2001;34:569–577. doi: 10.1016/s0021-9290(01)00011-2. [DOI] [PubMed] [Google Scholar]
  • 22.Keyak JH, Kaneko TS, Tehranzadeh J, Skinner HB. Predicting proximal femoral strength using structural engineering models. Clin Orthop Relat Res. 2005:219–228. doi: 10.1097/01.blo.0000164400.37905.22. [DOI] [PubMed] [Google Scholar]
  • 23.Keyak JH, Rossi SA, Jones KA, Les CM, Skinner HB. Prediction of fracture location in the proximal femur using finite element models. Med Eng Phys. 2001;23:657–664. doi: 10.1016/s1350-4533(01)00094-7. [DOI] [PubMed] [Google Scholar]
  • 24.Keyak JH, Sigurdsson S, Karlsdottir G, Oskarsdottir D, Sigmarsdottir A, Zhao S, et al. Male-female differences in the association between incident hip fracture and proximal femoral strength: a finite element analysis study. Bone. 2011;48:1239–1245. doi: 10.1016/j.bone.2011.03.682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Gluer CC, Blake G, Lu Y, Blunt BA, Jergas M, Genant HK. Accurate assessment of precision errors: how to measure the reproducibility of bone densitometry techniques. Osteoporos Int. 1995;5:262–270. doi: 10.1007/BF01774016. [DOI] [PubMed] [Google Scholar]
  • 26.Li W, Sode M, Saeed I, Lang T. Automated registration of hip and spine for longitudinal QCT studies: Integration with 3D densitometric and structural analysis. Bone. 2006;38:273–279. doi: 10.1016/j.bone.2005.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Carpenter RD. Mechanical Engineering Department. Stanford, CA: Stanford University; 2006. Mechanobiology of bone cross-sectional development, adaptation, and strength. [Google Scholar]
  • 28.Birnbaum BA, Hindman N, Lee J, Babb JS. Multi-detector row CT attenuation measurements: assessment of intra- and interscanner variability with an anthropomorphic body CT phantom. Radiology. 2007;242:109–119. doi: 10.1148/radiol.2421052066. [DOI] [PubMed] [Google Scholar]

RESOURCES