Computational techniques for using insole pressure sensors to analyse three-dimensional joint kinetics

Abstract

This study evaluated the feasibility of using insole pressure sensors together with whole body dynamics to analyse joint kinetics while running. Local affine transformations of shoe kinematics were first used to track the position of insole sensors during locomotion. Centre of pressure estimates derived from the insoles were within 10 mm of forceplate measures through much of stance, while vertical force estimates were within 15% of peak forceplate recordings. Insole data were then coupled with a least squares whole body dynamic model to obtain shear force estimates that were comparable to forceplate records during running. We demonstrated that these techniques provide a viable approach for analysing joint kinetics when running on uninstrumented surfaces.

1. Introduction

Pressure-sensitive insoles are a powerful tool for assessing the load distribution on the feet during locomotion. For example, insole data can be used to identify high-pressure spots, to locate the local centre of pressure (COP) and to estimate the net vertical ground reaction force (vGRF) (Burnett et al. 2000; Chesnin et al. 2000; Kernozek and Zimmer 2000; Forner-Cordero et al. 2006; Putti et al. 2007). Such information has proven useful for designing orthotics, assessing the cause of pressure ulcers und investigating foot–floor contact models (Ahroni et al. 1998; Cavanagh and Owings 2006).

It is also appealing to consider the use of insole pressure data to assess joint kinetics during gait. Compared to fixed forceplates, insoles have the advantage of being usable outside of laboratory environments and can facilitate collection of data over multiple strides. However, insoles do not currently provide shear force measurements or the global position of the COP. As a result, it is not feasible to use insole data for segment-by-segment inverse dynamics analysis (Winter 1990), since that requires the full complement of ground reaction data to be available. An alternative is to consider the use of whole body dynamics analysis, which can accommodate missing ground reaction data (Kuo 1998; Remy and Thelen 2009; van den Bogert and Su 2008). For example, a least squares inverse dynamics (LSID) formulation was shown to provide reasonable estimates of joint torques, even when a partial set of ground reactions (e.g. vGRF, global COP) and noisy acceleration data was used (Kuo 1998; van den Bogert and Su 2008). Thus, a primary challenge of using insoles for kinetics analysis is in tracking the global COP and estimating the missing shear forces from the data that are available.

The first objective of this study was to develop and evaluate a tracking algorithm using motion capture markers affixed around the sole of a shoe to compute the global COP from insole data during locomotion. To achieve this, we developed a piece-wise affine mapping approach to estimate insole sensor positions from shoe marker kinematics recorded during locomotion. The second objective was to evaluate the accuracy of using insole pressure data together with a whole body dynamics analysis to estimate shear forces under the stance foot during running. We then used this information to compute three-dimensional joint moments about the hip, knee and ankle. The estimated global COP, shear forces and joint moments were then evaluated by direct comparison with measures derived from fixed forceplates. Reasonable accuracy is shown such that the proposed approach can facilitate the use of insoles to characterise lower extremity joint kinetics when running on uninstrumented surfaces.

2. Methods

2.1 Subjects

Eight volunteers participated in this study (four males/four females, 25.3 ± 3.5 years old, 68.8 ± 6.9 kg, 173.5 ± 5.5 cm). The University of Wisconsin Institutional Review Board approved the testing protocol, and all subjects provided informed consent.

2.2 Experimental protocol

Pressure-sensitive insoles (Novel Inc., Munich, Germany), with 99 sensors per insole (data collection rate of 100 Hz), were fitted into each subject’s shoes. An eight-camera motion capture system (Motion Analysis, Santa Rosa, CA, USA) was used to measure the three-dimensional positions (at 200 Hz) of 56 retro-reflective markers, with 18 markers located on anatomical landmarks and 10 markers (10 mm diameter) affixed to the sole of the shoe (Figure 1). At each frame in the trials, piece-wise natural cubic splines were fit through the 10 shoe markers, creating 100 virtual markers around the shoe (Figure 2). Ground reaction forces (data collection rate of 2000 Hz) were simultaneously recorded with the kinematics using three fixed, sequential forceplates (AMTI, Watertown, MA, USA).

Figure 1.

(a) Ten markers (10mm in diameter) were affixed around the periphery of each running shoe. (b) The insole reference frame was positioned at the most posterior aspect of insole, with the y-axis direction pointed towards the toe. The local position, r⃑_i, for each sensor was then defined as the centroid of the sensor in the insole reference frame.

Figure 2.

A piece-wise cubic spline was used to define 100 virtual markers around the periphery of the shoe. To ensure continuity of the cubic splines, the 10 motion capture markers were always labelled consistently. An initial standing calibration trial was used to determine the sensor positions that maximised agreement between the insole- and forceplate-measured COP trajectories.

Each subject performed an initial upright stance trial (15 s) in which he/she Stood on a fixed forceplate and voluntarily shifted his/her COP in the fore–aft and mediolateral directions. Three repeated trials of three walking speeds (slow, preferred, fast) and two running speeds (preferred, fast) were collected.

2.3 Insole sensor position calibration

The COP information from the forceplate was used to calibrate the locations of the insole sensors in the upright stance trial. To do this, we first defined a local, undeformed insole reference frame (Figure 1). The centroid of each sensor, r_i, in the insole reference frame was then found using a scaled drawing of the insole provided by Novel Inc. This information was used to express the local COP, ρ, as a function of the pressure recorded by each sensor, σ_i at a time frame k in the dataset

$$\rho (kT)=\frac{{\displaystyle \sum _{k=1}^N}{\sigma }_i(kT)r_i}{{\displaystyle \sum _{k=1}^N}{\sigma }_i(kT)},$$ (1)

where T is the interval between data samples, and where N is the number of samples. We assumed that the foot remained flat on the ground and relatively stationary throughout the upright stance trial, such that a simple rotation matrix, R, could be used to describe the orientation of the insole reference frame relative to the global reference frame during the upright trial.

$$\mathbf{R}=\left[\begin{array}{ccc}cos(\theta )& -sin(\theta )& 0\\ sin(\theta )& cos(\theta )& 0\\ 0& 0& 1\end{array}\right],$$ (2)

where θ is the axial rotation of the foot relative to a vertical axis, z. The COP could thus be transformed from the insole to a global reference frame and compared to the COP, p, recorded by the forceplates. We defined a cost function, J, as the sum of the squared differences in the COP as estimated by the insole and measured by the forceplate

$$J=\sum _{k=1}^N{\mid \mathbf{R}\rho (kT)+\mathbf{d}-p(kT)\mid }^2.$$ (3)

For each subject, numerical optimisation (fminsearch, Matlab, MathWorks, Inc., Natick, MA, USA) was used to determine the rotation angle θ and translation d (vector between origins of global and insole reference frames) that minimised J. These transformation parameters were then directly used to define the global positions of each insole sensor, $s_i^{\ast }$, in the upright stance calibration trial

$$s_{\mathrm{i}}^{\ast }=\mathbf{R}{r}_{\mathrm{i}}+\mathbf{d}.$$ (4)

2.4 Insole sensor tracking

Affine transformations were used to map sensor positions from the calibration trial to a frame of a motion trial. This transformation was computed separately for each sensor by using virtual markers (cubic spline interpolated) close to each sensor (Figure 3). The positions of the virtual markers closest to the sensor on the left and right sides were defined as vectors v₁ and v₂, respectively. The weighted average of the next two closest virtual markers on the left and right sides was defined as vector v₃. A normal vector to the plane defined by these three markers was first taken as

Figure 3.

A graphical depiction of the sensor-tracking algorithm is shown. Piece-wise cubic spline interpolation is used to define 100 virtual markers from the measured foot marker locations. Sensor positions in a calibration trial are first computed so as to maximise agreement between insole and forceplate COP trajectories. Sensor positions during locomotion are then resolved using four virtual markers in close proximity in the calibration trial: the closest markers to the sensor on the left and right sides define the vectors v₁ and v₂ respectively, and a weighted average of the next two closest markers define vector v₃. These three vectors are then located in the frame of a locomotion trial. An affine transformation is then used to describe the translation, rotation and scaling of these three vectors from the calibration trial to the current motion trial frame.

$$\mathbf{n}=({\mathbf{v}}_2-{\mathbf{v}}_1)\times ({\mathbf{v}}_3-{\mathbf{v}}_1).$$ (5)

After identifying the three closest markers for a sensor, we computed an affine transformation that mapped the vectors v₁, v₂, v₃ and n from their values in the upright stance (denoted by *) trial to their measured values at each frame in a motion trial

$${\mathbf{T}}_i(kT)\ast {\left[\begin{array}{cccc}{\mathbf{v}}_1^{\ast }& {\mathbf{v}}_2^{\ast }& {\mathbf{v}}_3^{\ast }& {\mathbf{v}}_1^{\ast }+{\mathbf{n}}^{\ast }\\ 1& 1& 1& 1\end{array}\right]}_{\text{calibration}}={\left[\begin{array}{cccc}{\mathbf{v}}_1& {\mathbf{v}}_2& {\mathbf{v}}_3& {\mathbf{v}}_1+\mathbf{n}\\ 1& 1& 1& 1\end{array}\right]}_{\text{frame}k}$$ (6)

where the transformation matrix T_i is defined as

$${\mathbf{T}}_i(kT)=\left[\begin{array}{cccc}& {\mathbf{A}}_i(kT)& & {\mathbf{d}}_i(kT)\\ 0& 0& 0& 1\end{array}\right],$$ (7)

where A_i accounts for both scaling and rotation and d_i accounts for translation. This transformation was then used to map the corresponding sensor’s calibration position, $s_i^{\ast }$, to its global position, s_i, at a frame k in a motion trial

$$s_i(kT)={\mathbf{A}}_i(kT)s_i^{\ast }+{\mathbf{d}}_i(kT).$$ (8)

Subsequently, the global COP was estimated from each of the sensor positions during the motion trials using the global position, s_i, and the pressure from each sensor.

$$p^{\prime }{(kT)}_{\text{insole}}=\frac{{\displaystyle \sum _{k=1}^N}{\sigma }_i(kT)s_i}{{\displaystyle \sum _{k=1}^N}{\sigma }_i(kT)}.$$ (9)

The measured sensor pressures were scaled by the sensor cross-sectional areas to get the force associated with each sensor along the sensor’s normal direction, n. The component projected onto the vertical axis (k) of this sensor force vector in the global reference frame provided an estimate of the net vGRF, ${\mathbf{F}}_z^{\prime }$, acting on the foot

$${\mathbf{F}}_z^{\prime }{(kT)}_{\text{insole}}=\sum _{k=1}^N{a}_i{\sigma }_i(kT)\mathbf{n}·\mathbf{k}.$$ (10)

To evaluate the accuracy of the tracking algorithm, the insole-derived estimates of the COP and vertical force were compared with measures obtained from a fixed forceplate during walking and running.

2.5 Linked segment dynamic model

We used a 19-segment, 31 degrees of freedom (DOF) linked-segment dynamic model to relate whole body kinematics to the net external forces acting on the body. The pelvis served as a six-DOF base segment in the model. The lower limbs included a three-DOF ball-and-socket hip, a single-DOF knee in which non-sagittal rotations and translations were specified functions of the knee flexion angle (Walker et al. 1988) and a two-DOF ankle which included the talocrural and subtalar joints (Delp et al. 1990). The upper body was attached to the pelvis by a three-DOF ball-and-socket low-back joint at the L3–L4 level. Upper extremities include three-DOF ball-and-socket shoulder joints and single-DOF joints for elbow flexion–extension and pronation–supination. The whole body dynamic model was created using SIMM (SIMM 4.0, Musculographics Inc., Motion Analysis Corporation, Santa Rosa, CA, USA), and dynamical equations of motion were implemented using SIMM/Pipeline (v. 3.0) and SDFast (Parametric Technology Corporation, Waltham, MA, USA). The whole body model was scaled to each subject based on segment lengths measured in an upright standing trial. Anthropometric properties were estimated using regression equations based on subject mass, height and segment lengths (de Leva 1996).

A global optimisation inverse kinematics routine was initially used to estimate generalised coordinates (q′) that optimally fit the measured marker positions (Lu and O’Connor 1999) at each frame in a trial. Generalised coordinates were subsequently low-pass filtered at 6 Hz and then numerically differentiated to provide estimates of generalised speeds (q̇′) and accelerations (q̈′).

2.6 Least squares forward dynamics

A least squares forward dynamics (LSFD) routine was used to compute shear forces that satisfied whole body dynamic constraints while remaining optimally consistent with kinematic measures and available ground reaction data (Remy and Thelen 2009). To do this, we first formulated a set of six overall equations of motion that expressed the instantaneous relationship between external forces (F), external moments (M) and accelerations (q̈) given the current generalised coordinates (q) and generalised speeds (q̇) of the model

$$\mathbf{A}(q)\left[\begin{array}{c}F\\ M\\ \ddot{q}\end{array}\right]=f(q,\stackrel{.}{q},\ddot{q}).$$ (11)

In Equation (11), the matrix A contains information on segmental mass and geometry, while f accounts for gravity, coriolis and centripetal effects. Direct substitution of kinematic measures (q′, q̇′, q̈′) and insole-derived ground reactions (F′, M′ = p′×F′) would not satisfy Equation (11) on account of missing shear force data and uncertainty in COP, vertical force and acceleration estimates. We thus introduced variations, δ, to the experimental measures

$$\left[\begin{array}{c}F\\ M\\ \ddot{q}\end{array}\right]=\left[\begin{array}{c}{F}^{\prime }\\ M^{\prime }\\ {\ddot{q}}^{\prime }\end{array}\right]+\left[\begin{array}{c}\delta F\\ \delta M\\ \delta \ddot{q}\end{array}\right].$$ (12)

Substitution of (12) into (11) results in

$$\mathbf{A}(q)\left[\begin{array}{c}\delta F\\ \delta M\\ \delta \ddot{q}\end{array}\right]=f(q,\stackrel{.}{q})-\mathbf{A}(q)\left[\begin{array}{c}{F}^{\prime }\\ M^{\prime }\\ {\ddot{q}}^{\prime }\end{array}\right],$$ (13)

which can be cast as a set of underdetermined linear equations of the form

$$\mathbf{A}\delta =b,$$ (14)

where $\delta (={[\begin{array}{ccc}\delta F& \delta M& \delta \ddot{q}\end{array}]}^{\mathrm{T}})$ is a set of variations to experimentally derived estimates of the ground reactions and accelerations that are needed to enforce dynamic consistency with the whole body dynamic model.

Equation (14) was solved using the Moore–Penrose matrix inverse, with a weighting matrix W to account for uncertainty in measured quantities

$$\delta =\mathbf{W}{(\mathbf{AW})}^{+}b.$$ (15)

In this study, we used a diagonal weighting matrix, W, and assumed standard deviations of 1ms⁻² for translational generalised accelerations, 1–2 rad s⁻² for rotational generalised accelerations, 5% of the vertical force and 10 mm for the COP. The unknown shear forces were given a large standard deviation (100% of the vertical force), since these quantities were not measured via the insoles. Computed accelerations were subsequently integrated forward to determine the simulated generalised coordinates and speeds over a trial, with numerical optimisation used to find initial conditions that minimised the discrepancy between simulated and measured marker trajectories. LSFD was only used to process the running trials in this study. It could also be used to process the single phase of walking, but cannot decompose the left and right limb components of the shear force during double support without adding in additional assumptions.

2.7 Joint moments

The equations of motion for the linked segment model take the form

$$\mathbf{M}(q)\ddot{q}=G(q)+C(q,\stackrel{.}{q})+\mathbf{R}(q)E+\mathit{\tau },$$ (16)

where M(q) represents the system mass matrix, G(q) the forces due to gravity, C(q, q̇) the forces due to centripetal and coriolis effects, R(q) a matrix that transforms the external forces and moments (E = [FM]^T) into generalised forces and the vector τ includes both the joint moments and the residual forces and moments acting between the ground and the pelvis. We solved Equation (16) for the generalised forces τ at each time step for two cases: (1) using the measured kinematics (q′, q̇′, q̈′) and force platform ground reaction forces and moments ( $E={[FM]}_{\text{forceplate}}^{\mathrm{T}}$) directly; and (2) using the optimally estimated kinematics (q, q̇, q̈) and ground reactions derived from the insole sensors ( $E={[\begin{array}{cc}{F}^{\prime }+\delta F& M^{\prime }+\delta M\end{array}]}_{\text{insoles}}^{\mathrm{T}}$). In the second case, the residual forces are ensured to be zero as a result of solving Equation (14).

3. Results

3.1 Insole tracking

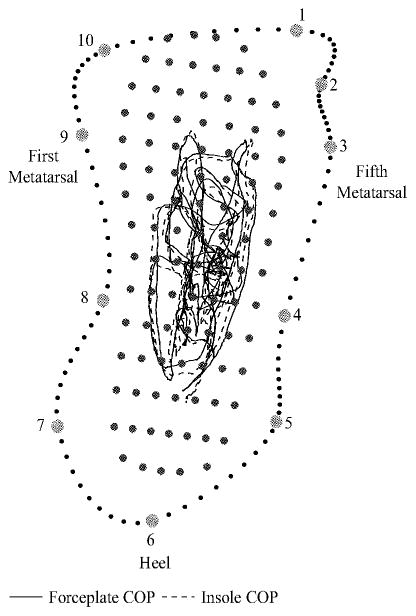
The insole tracking algorithm generated estimates for the vGRF and COP trajectories that were within one standard deviation of forceplate measures (Figure 4). Root mean square (RMS) differences in vGRF were < 14% of peak vertical force (~40–80N) for walking and < 10% of peak vertical force (80–130 N) for running (Table 1). Medio-lateral COP RMS errors during mid-stance (between 10 and 80% of stance phase) were <8 mm during walking and running (Table 2). Anterio-posterior COP errors were less than 12 mm between 10 and 80% of stance phase. The largest error in the estimated COP occurred during heel contact and prior to toe-off.

Figure 4.

The agreement between net vertical force and COP recorded by the insole and forceplate during the preferred walking trial (a) and running trial (b) for one subject. Good agreement in the COP is seen between the insole and forceplate data from 10 to 80% of the gait cycle. However, the insole COP tends to be anterior to the forceplate COP during heel contact and then posterior to the forceplate COP approaching toe-off (the last 20% of stance).

Table 1.

Mean RMS differences (± 1 SD) between the forceplate vGRF and insole vGRF.

	Speed (ms−1)	vGRF (N)			vGRF (% peak)
		0–10% stance	10–80% stance	80–100% stance	0–10% stance	10–80% stance	80–100% stance
Slow walk	1.0 (0.2)	65 (40)	40 (21)	87 (47)	9.2 (5.0)	7.0 (4.6)	13.3 (6.4)
Preferred walk	1.4 (0.1)	62 (37)	38 (12)	73 (41)	9.0 (5.2)	5.2 (1.9)	11.3 (7.4)
Fast walk	1.8 (0.2)	76 (46)	59 (28)	71 (34)	8.6 (4.3)	6.8 (3.2)	8.4 (4.3)
Preferred run	3.1 (0.5)	95 (65)	91 (36)	101 (64)	5.8 (3.5)	5.6 (2.2)	6.4 (4.1)
Fast run	5.0 (0.6)	127 (79)	92 (28)	109 (67)	7.5 (4.4)	5.4 (1.3)	6.8 (4.6)

Table 2.

Mean RMS differences (± 1 SD) between the forceplate and insole global position of the COP.

	Speed (ms−1)	AP COP (mm)			ML COP (mm)
		0–10% stance	10–80% stance	80–100% stance	0–10% stance	10–80% stance	80–100% stance
Slow walk	1.0 (0.2)	48.6 (12.3)	9.3 (3.9)	34.3 (11.7)	11.2 (3.8)	4.4 (2.5)	8.3 (4.0)
Preferred walk	1.4 (0.1)	57.0 (14.9)	8.6 (2.5)	43.5 (21.1)	15.0 (6.1)	7.3 (7.6)	7.2 (6.0)
Fast walk	1.8 (0.2)	57.0 (15.4)	11.6 (8.5)	38.0 (22.4)	12.1 (3.6)	5.3 (2.8)	8.3 (4.5)
Preferred run	3.1 (0.5)	62.7 (17.6)	10.1 (5.7)	42.8 (13.4)	17.5 (10.7)	5.7 (5.0)	6.3 (4.2)
Fast run	5.0 (0.6)	52.2 (25.2)	10.0 (5.4)	41.4 (9.2)	23.1 (8.2)	6.5 (4.2)	8.4 (4.3)

3.2 Least squares forward dynamics

Using the insole vGRF and COP estimates within the LSFD resulted in anterio-posterior shear force estimates that exhibited the characteristic braking and propulsion periods during stance (Figure 5). Average RMS errors for the anterior–posterior component were 52N (8% body weight, BW) and 70N (10% BW) for the preferred and fast running speeds, respectively. Average RMS errors for the medio-lateral force were 25N (4% BW) and 42N (6% BW) for these speeds, respectively (Table 3).

Figure 5.

The agreement between the forceplate-measured ground reactions and the computed-ground reactions using the least squares forward dynamics for the preferred running trials (note, only running was analysed with the LSFD approach because of the lack of double support phase). The solid lines represent all individual subject trials for the LSFD-computed GRFs, and the shaded region is the average over all subjects and trials for the forceplate GRFs mean (average of all trials and over all subjects) ± one standard deviation.

Table 3.

Mean RMS differences (± 1 SD) between the forceplate and computed ground reaction forces for the two running trials.

	Speed (ms−1)	Ground reactions (N)
		Anterio-posterior	Medio-lateral	Vertical
Preferred run	3.1 (0.5)	52.5 (25.6)	24.5 (14.5)	122.3 (63.3)
Fast run	5.0 (0.6)	70.3 (30.8)	41.7 (16.4)	135.6 (69.4)

The magnitude of the lower extremity joint moments estimated with the insoles was generally consistent with that computed using fixed forceplates (Figure 6 and Table 4). In particular, the hip adduction, hip internal rotation, knee flexion and ankle plantar flexion moments generally remained within one standard deviation of the forceplate-derived measures throughout stance. Greater discrepancy occurred in the hip extension moment in early stand, with the forceplate-derived values exhibiting an early peak that was not present in the moment trace derived from the insoles (Figure 6).

Figure 6.

Joint moment comparison for the preferred running trial. The solid lines represent the joint moments using the LSFD-computed ground reactions. The shaded region represents the mean ± one standard deviation of the joint moment (averaged over all subjects) computed from the forceplate GRF measures.

Table 4.

Mean RMS differences (± 1 SD) between the joint moments computed using the forceplate ground reactions and the joint moments computed using the insole data and LSFD approach.

	Speed (ms−1)	Hip flex/ext (Nm)	Hip abd/add (Nm)	Hip rot (Nm)	Knee flex/ext (Nm)	Ankle flex/ext (Nm)
Preferred run	3.1 (0.5)	36.5 (8.8)	16.8 (3.7)	6.9 (2.0)	20.1 (6.1)	9.0 (4.5)
Fast run	5.0 (0.6)	59.8 (12.9)	39.0 (9.2)	19.9 (7.8)	30.5 (9.5)	11.3 (3.8)

4. Discussion

We have demonstrated a novel approach for tracking the position of insole sensors and the global position of the COP during locomotion using affine transformations of motion capture data. This information was subsequently incorporated in a whole body dynamic model to estimate unmeasured shear forces and joint moments during running. Reasonable agreement was shown with data derived from fixed forceplate measures, thereby demonstrating the potential to analyse joint kinetics using pressure-sensitive insole data.

The use of an array of markers around the sole of the shoe allowed us to track the position of insole sensors during both walking and running. While we cannot independently verify the estimated sensor positions, the accuracy of the COP estimates derived from these data suggests that the sensor tracking was accurate. Indeed, our COP accuracy was comparable to measures made from insoles during upright standing (Forner-Cordero et al. 2006; Fong et al. 2008). Aside from doing joint kinetics analyses, a potential use of the sensor position data is to develop and validate foot–floor contact models, which are typically represented by an array of discrete visco-elastic units distributed across the sole of the foot (Gerritsen et al. 1995; Gilchrist and Winter 1996; Neptune et al. 2000; Anderson and Pandy 2001; Neptune et al. 2001). Stiffness and damping parameters of the discrete units are typically estimated from mechanical tests performed on the heel pad and/or sole of the shoe (De Clercq et al. 1994). However, such testing is difficult and time consuming to perform on a subject-specific basis; hence, generic contact model parameters are often assumed. The methodology developed for this study provides estimates of each sensor’s position and pressure, and thus could potentially be used to systematically estimate contact model parameters using data directly recorded during locomotion.

We have demonstrated that the insole data can be used within a whole body dynamics framework to estimate unmeasured shear forces at the foot–floor interface. Whole body dynamics analysis uses the redundant information present in kinematic and external force data to optimally estimate joint accelerations and unmeasured ground reactions. Either LSID (Kuo 1998; van den Bogert and Su 2008) or LSFD (Remy and Thelen 2009) approaches can be used to do this analysis. In a LSID approach, the generalised accelerations and ground reactions are optimally estimated while using the measured generalised speeds and positions in the system equations of motion (Equation (16)). A LSID approach is usually sufficient if one is only interested in estimating joint moments. In our formulation, LSID could be performed by solving the linear least squares problem (Equation (14)) and then substituting the estimated accelerations and ground reactions into the equations of motion (Equation (16)) to get the joint moments.

In this study, we elected to use LSFD which is more computationally demanding than LSID, but ensures dynamic consistency between the computed accelerations and the generalised speeds and positions over time (Remy and Thelen 2009). Thus, LSFD-derived kinematics can then be used as a starting point for conducting forward dynamic simulations of locomotion (Thelen and Anderson 2006). Forward simulations are beneficial if one is interested in analysing how joint moments (or muscles) contribute to movement or how movement will change as a result of a perturbation to the system (Chumanov et al. 2007; McLean et al. 2008). Joint moments computed using LSFD were comparable to joint moments obtained using traditional inverse dynamics analysis of running (Ferber et al. 2003; van den Bogert and Su 2008) with forceplate data (Figure 6, Table 4). A major discrepancy occurred in the sagittal hip moment during initial limb loading, with the forceplate-derived moment showing an early peak hip extensor moment that was not present in the data derived from the insoles (Figure 6). However, it has been previously shown that inconsistencies between filter cutoff frequencies used on kinematic and forceplate data can artificially induce a peak hip extensor moment during impact (Bisseling and Hof 2006). Hence, it is possible that the hip joint moment we computed through the LSFD approach may be close to the actual values.

Limitations do exist when using insoles for characterising biomechanical quantities. In particular, current insole pressure systems have substantially lower sample frequencies than forceplates. For example, the insoles used in this study have a maximum sample frequency of 100 Hz when two insoles are sampled. In addition, the insole only records the pressure between the foot and shoe, which can differ from the pressure between the shoe and floor. This likely contributes to the lower accuracy in the COP during heel contact and prior to toe-off (Figure 4). We demonstrated the tracking algorithm using 10 motion capture markers around the periphery of the shoe. Additional markers could easily be added, which may improve the position estimates of individual sensors (Figure 2).

The least squares dynamics approach can only provide an estimate of the net external shear force, and thus is unable to resolve the independent components arising from the two feet during the double support phase of walking. Others have used additional assumptions to address this issue (Pandy and Berme 1988; Davis and Cavanagh 1993). Finally, a diagonal weighting matrix was assumed for solving the linear least squares problem at each time step (Equation (15)). However, it is recognised that the various sources of measurement noise (e.g. marker kinematics) will propagate through the model in a manner that results in covariance between estimation variables (e.g. joint angular accelerations), van den Bogert and Su (2008) presented a Monte Carlo approach to numerically compute the estimation covariance matrix, which could be used for computing a non-diagonal weighting matrix (Equation (15)). Doing this could improve shear force estimates, but would likely require some tuning of measurement noise magnitudes to obtain reliable results (van den Bogert and Su 2008).

In conclusion, we have demonstrated a simple and accurate approach for coupling motion capture with insole pressure data to dynamically track the global pressure distribution on the feet during human locomotion. This information, in conjunction with a whole body dynamics analysis, can be used to analyse three-dimensional joint kinetics of running on uninstrumented surfaces.