EMRinger: Side-chain-directed model and map validation for 3D Electron Cryomicroscopy

Abstract

Advances in high resolution electron cryomicroscopy (cryo-EM) have been accompanied by the development of validation metrics to independently assess map quality and model geometry. EMRinger assesses the precise fitting of an atomic model into the map during refinement and shows how radiation damage alters scattering from negatively charged amino acids. EMRinger will be useful for monitoring progress in resolving and modeling high-resolution features in cryo-EM.

Recent computational and experimental developments in single particle electron cryomicroscopy (cryo-EM) now make it possible, in some cases, to build atomic models without any reference structures¹. Because these structures are otherwise inaccessible to X-ray crystallography or NMR², it is important to determine the reliability of the resulting atomic models, and in particular side chain placement, for their eventual use in directing detailed mechanistic studies or drug development³.

All-atom de novo cryo-EM models present several unique challenges for validation⁴. First, the Coulomb potential map itself must be validated by assessing the “gold standard” Fourier Shell Correlation (FSC) between two independently refined half maps⁵. Next the chemical reasonableness of the model is assessed using tools that are commonly applied in X-ray crystallography⁶. Similarly to crystallography, it is essential to balance the agreement to experimental data with the deviation from ideal geometry, while maintaining acceptable stereochemistry, Ramachandran statistics⁷, side chain rotamers⁸, and clash scores⁶.

The weighting between data and prior structural knowledge is key to the third step of model-to-map validation: determining whether the structure is accurately fitted, but not over-fitted, to the map⁹. Several cross validation schemes have been proposed recently^9–11 and can help to ensure that the model is not only reasonable, but also well fitted to the map. However, the tendency of simple correlation metrics to be dominated by low-resolution, high-signal features can render it difficult to assess the reliability of the highest resolution features of EM maps, such as side chain or ligand conformations^11,12. These problems can potentially be corrected by monitoring the correlation in Fourier space at high frequency⁹ or by using the real space correlation to band-pass filtered maps as a cross-validation target for refinement¹¹.

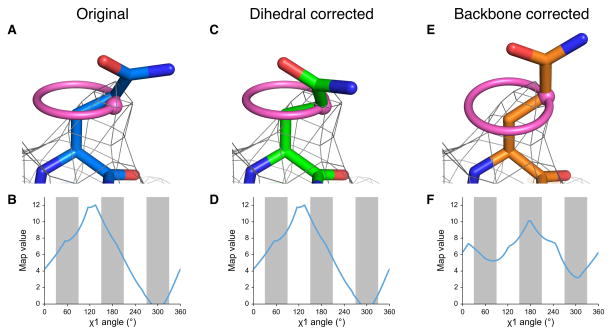
An alternative solution for assessing the reliability of high-resolution models is to examine statistical signatures of the weaker, high resolution, data. Here, we extend Ringer, an approach that detects unmodeled alternative conformations in electron density maps generated by high resolution X-ray crystallography^13,14, to directly reveal the side chain information content of EM maps. EMRinger interpolates the normalized value of the cryo-EM map at each potential position of the Cγ position around the χ¹ dihedral angle, assuming the currently modeled N, Cα, and Cβ atomic positions (Fig. 1a). We next plot the distribution of map values by dihedral angle (Fig. 1b), which reveals local information about both the map and correctness of the backbone of the atomic model. The peak in the distribution represents the most likely position of the Cγ atomof the side chain, even when it is not immediately obvious “by eye”. The position of Cγ is constrained to avoid “eclipsed” steric overlaps¹⁵, which is confirmed by high resolution X-ray structures^8,16. Therefore we expected that high quality EM maps with well fit backbone models would be enriched in density peaks near the rotameric χ¹ dihedral (N-Cα-Cβ-Cγ) angles of 60°, 180°, and 300° (−60°)¹⁷.

Figure 1.

EMRinger χ¹ map value sampling reports on backbone position and guides side-chain conformation. (a) The side chain of TrpV1 Gln 519 of Chain C (EMDB 5778, PDB 3J5P) is shown fitted, with a real space correlation coefficient (RSCC) of 0.590, to the potential map, shown at an isolevel of 10. (b) The EMRinger scan, reflected by the pink ring in a, for Gln 519 of Chain C reveals that the local map value peak (at 130°) occurs at a non-rotameric angle (white bars). This peak, shown as a pink dot in a, occurs 30° away from the modeled position. (c) The side chain can be rotated so that the χ¹ angle is at the map value peak (RSCC = 0.526). (d) The EMRinger results are unchanged as the sampling occurs relative to the backbone atoms, which have not moved. (e) Alternatively, the backbone position can be corrected with Rosetta refinement¹⁹ to place the model near a χ¹ map value peak a small reduction on the overall correlation of the residue to the map (RSCC = 0.442). (f) The peak at 175° is now in the rotameric region (grey bars).

However, there are several reasons, including noise in the map or an inaccurate model, why a side chain peak might occur at a non-rotameric angle. For example, residue Gln519 of TrpV1¹⁸ (PDB: 3J5P) is modeled in a rotameric position, but has a peak at a non-rotameric angle in a 3.27 Å resolution map (EMDB: 5778) (Fig. 1a,b). We observed singular peaks for most side chains in the TrpV1 map, which further suggests that noise is not the dominant reason why the peak occurs in a non-rotameric position. Alternatively, a peak in a non-rotameric position can indicate that the model is incorrect. If the N, Cα, and Cβ atoms are improperly positioned in the strong potential surrounding the backbone, EMRinger will measure the map values in the wrong locations. It is important to note that this occurs even the side chain is already modeled as rotameric. Changing the modeled side chain dihedral angle does not affect the result of EMRinger because the measurement relies only on the positions of the backbone and Cβ atoms (Fig. 1c,d). In contrast, a small backbone adjustment places the Cγ in the map value peak, while maintaining a rotameric side chain model, excellent stereochemistry, and a good map correlation (Fig. 1e,f).

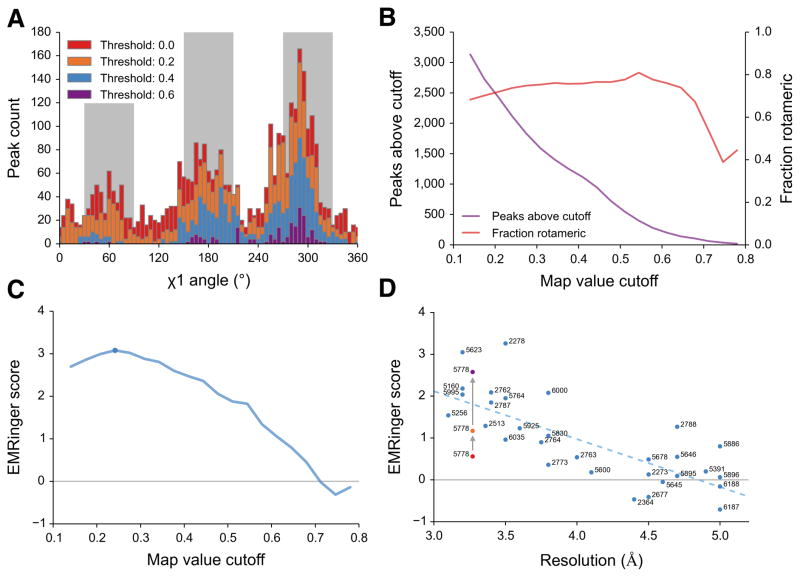
To test the quality of model to map fit, we quantified the enrichment of EMRinger peaks in rotameric regions (within 30° of 60°, 180°, or 300°) as a function of map value. We recorded the position and map value of the peak for each side chain χ¹ angle in the 3.2Å resolution 20S proteasome map (EMDB 5623, PDB 3J9I) and observed that the distribution becomes more sharply peaked as the map value cutoff increases (Fig. 2a and Supplementary Fig. 1a,b). At lower cutoffs, noise flattened the results, with less enrichment for peaks in rotameric regions. Although rotameric regions are sampled more at higher cutoffs, fewer residues had local map value peaks above these cutoffs, and noise from counting statistics dominated (Fig. 2b). To quantify the relationship between sample size and rotameric enrichment, we used the normal approximation to the binomial distribution to generate a model-length independent validation statistic: the EMRinger score (Fig. 2c and Supplementary Fig. 2). For the 20S proteasome, the EMRinger score was maximized at the 0.242 normalized map value cutoff and the signal was dominated by 1547 rotameric map value peaks, compared to 555 non-rotameric peaks (Supplementary Fig. 3). EMRinger scores are always calculated with a sampling angle of 5° to avoid inconsistent scoring, and are for the most part independent of grid spacing changes due to binning (Supplementary Fig. 4b–d).

Figure 2.

EMRinger reveals statistical enrichment at rotameric χ¹ angles in high resolution EM maps. (a) Histograms of EMRinger peaks for the T20S proteasome structure (EMDB 5623, PDB 3J9I) observed above multiple map value cutoffs. At high cutoffs, more residues are located in the rotameric regions (grey bars). As the cutoff lowers, relatively more peaks are added to the non-rotameric regions (white bars). (b) Scanning across map value cutoffs demonstrates the tradeoff between sampled peaks (left) and fraction of rotameric peaks (right) for the proteasome structure. (c) The EMRinger score balances the sample size and the rotameric enrichment and is maximized at a cutoff of 0.242 for the proteasome structure (blue circle). (d) EMRinger scores for maps deposited in the EMDB with atomic models demonstrate the relationship between model quality and resolution. A linear fit (R² = 0.549) highlights how refinement of TrpV1 improves from the deposited model (red, PDB 3j5p), the transmembrane domain of the deposited model (orange), and a model refined by Rosetta (green, PDB 3J9J) ¹⁹.

Next, we sampled a series of cryo-EM maps deposited in the EMDB, spanning a resolution range of 3–5 Å resolution, with atomic models built into the map density (Fig. 2d and Supplementary Table 1). Since a random distribution should produce an EMRinger score of 0, the trend line suggests that the χ¹ angle of side chains can be resolved at 4.5 Å resolution or better. We observed similar trends in decreasing EMRinger score as maps of the T20S proteasome were progressively low-pass filtered (Supplementary Fig. 4). A notable exception to the trend of increasing score with higher resolution is TrpV1¹⁸ (Fig. 2d), which had a low EMRinger score (0.56) despite high resolution map (3.27 Å). This de novo model was built manually and not subjected to either real- or reciprocal-space refinement. Upon exclusion of the poorly resolved ankyrin domain, the EMringer score increased to 1.17, as only the atoms modeled into the highest resolution data remain (Supplementary Fig. 1C and Supplementary Table 1). Further rebuilding and refinement using Rosetta iterative local rebuilding¹⁹ gradually improved the EMRinger score in most trials (Supplementary Fig. 6a). The best Rosetta trajectory improves the EMRinger score to 2.58, while the validation metrics for an independent reconstruction improved by a small margin (Table 1 and Supplementary Fig. 5 and 6b). In contrast to these existing measures, such as real-space correlation or FSC, the EMRinger score was sensitive to features at lower map values, amplifying improvements in the model that only show a minor impact in the agreement-to-density term used by Rosetta refinement (Table 1). These results demonstrate how small corrections of backbone position along secondary structures, introduced through independently-scored refinement procedures, can lead to improvements in EMRinger score and the accuracy of the resulting model (Supplementary Fig. 6c,d).

Table 1.

Statistics pre- and post-refinement. Cross correlation, FSC_mask, MolProbity scores and EMRinger score are calculated for the full unrefined TrpV1 model (EMDB 5778, PDB 3J5P), the transmembrane domain of the unrefined model, an intermediate model during refinement of the transmembrane region, and the final refined transmembrane region.

	Unrefined	Unrefined (Transmembrane Region)	Refinement Step 2 (Transmembrane Region)	Refinement Final (Transmembrane Region)
CC (3.27 Å Cutoff)	0.676	0.726	.715	0.728
CC (Training Map)	0.663	0.715	0.708	0.718
CC (Testing Map)	0.664	0.714	0.705	0.713
Integrated Model-Map FSC (15-3.4 Å)	0.473	0.553	0.513	0.526
All-atom Clashscore (MolProbity)	77.90	100.78	2.32	2.09
Modelled Rotamer Outliers (MolProbity)	26.6%	30.94%	0.35%	0%
EMringer Score	0.56	1.17	1.61	2.58

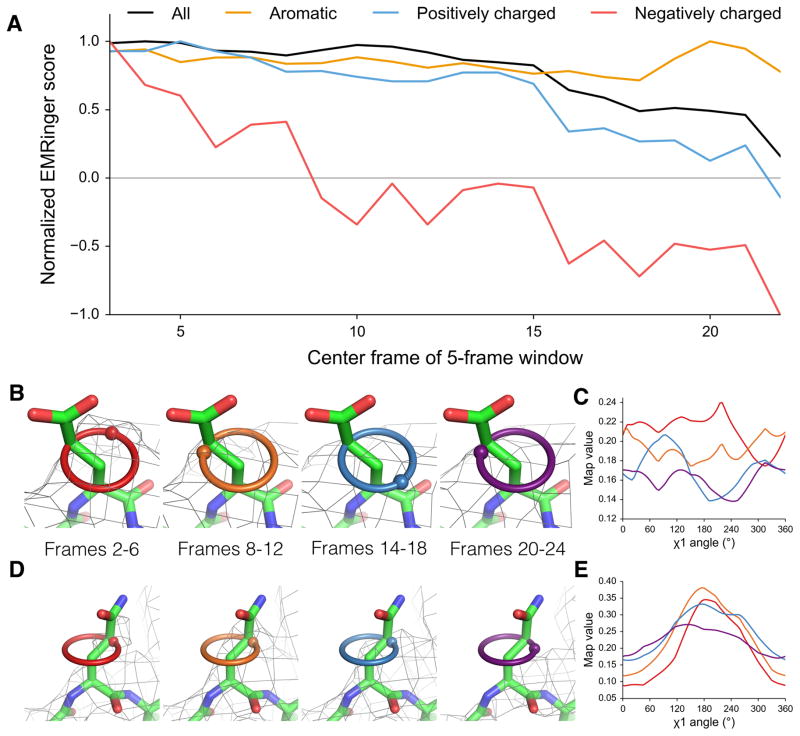
Recent motion corrected analyses have indicated that high-resolution information degrades as a function of total electron dose, likely as a result of radiation damage²⁰, and that the signal in the 5Å shell degrades rapidly in the second half of data collection²¹. In addition to these global metrics, previous work has hypothesized that differential radiation damage causes negatively charged glutamate and aspartate residues to have weaker density than neutral, but similarly shaped, glutamine and asparagine residues^20,22,23. To quantify the effect of radiation damage on the high resolution features of the map and to address whether effects vary by residue type, we used EMRinger for dose-fractionated maps of the T20S proteasome. The overall EMRinger score degrades as a function of dose, with a sharp loss of signal beginning around the 15th frame, corresponding to a total dose of ~18 e⁻/Ų (Fig. 3a). Amino acids with charged side chains generally lost signal more quickly as a function of dose than average, whereas aromatic residues were much more resistant to degradation (Fig. 3a).

Figure 3.

Acidic residues are differentially altered by radiation damage. (a) Normalized EMRinger scores are plotted for the T20S proteasome model (PDB: 3J9I) against maps calculated from 5 frames of data. Scores for the entire model (black), the aromatic residues (orange), and the positively charged residues (blue) slowly decrease as a function of dose. In contrast, negatively charged residues (red) experience a rapid drop and fall below a random score of 0. (b) Proteasome chain D residue Glu 99 shown in density (isolevel 0.18) for maps generated from frames 2–6 (red ring), 8–12 (orange ring), 14–18 (green ring), and 20–24 (blue ring), with spheres showing local map value peaks. (c) EMRinger plots for Glu 99 of Chain D corresponding to the maps in b show that peaks immediately flatten and eventually invert after high dose has accumulated. Colors correspond to the frames shown in b. (d) Proteasome chain 1 residue Gln 36 shown in density (isolevel 0.32) as in b. (e) EMRinger plots corresponding to the maps in d show a gradual loss of signal as a function of dose. Colors correspond to the frames shown in d.

Most notably, negatively charged side-chains lost signal much faster than positively charged side-chains, with EMRinger score dropping to zero by the map centered on the 8th frame. Since a map comprised only of noise (in the extreme of radiation damage) should result in a score of zero, differential damage is not sufficient to explain negative EMRinger scores observed in later frames. We observed that the initial map value peaks for some negatively charged residues inverted and became a local minimum in later frames (Fig. 3b,c). This behavior is in contrast to the flattening effect, where a peak slowly degrades into noise, seen generally for other residue types (Fig. 3d,e). The inversion of the peak may result from the electron scattering factors of negatively charged oxygen atoms, which are positive at high resolution but become negative at low resolution²⁴. The net effect of the negative scattering behavior could therefore result in an enrichment of peaks at non-rotameric positions and, consequently, a negative EMRinger score after substantial radiation damage has accumulated.

The dramatic advances in electron cryomicroscopy have created new challenges in building, refining, and validating atomic models. EMRinger extends and complements existing cryo-EM validation procedures at multiple levels. While current methods test conformational features independently of agreement with the map, the EMRinger tests these features by querying the model and map together. The EMRinger score reports specifically on statistical signatures in high-resolution data. To validate the model-to-map correctness of atomic models from cryo-EM, refinement should result in EM Ringer scores above 1.0 for well-refined structures with maps in the 3–4 Å range. EMRinger scores can be used in concert with cross validation procedures¹¹ and with other measures, such as gold-standard FSC-based resolution⁴ and Molprobity statistics⁶. EMRinger scores can quantify improvements in the resolvability of atomic features due to improvements to motion correction algorithms, to new data collection procedures that balance dose and radiation damage, and to classification of particles representing distinct biochemical states²⁵.

Additionally, the high sensitivity of EMRinger suggests a natural direction for model-building and refinement. At the resolutions commonly used for model building in EM, there are many closely related backbone conformations that can fit the map density with nearly equal agreement. Given a nearly finalized backbone position, side chains with non-rotameric peaks can be adjusted to fix the Cγ atom in the peak density. Subsequently, the backbone conformation and closure to adjacent residues can be optimized to maintain a rotameric side chain conformation, similar to the inverse rotamer approach used in some protein design applications²⁶. Similar approaches to quantifying statistical signatures in weakly resolved data may also prove helpful for modeling of non-amino-acid structures at lower resolutions, including glycans and nucleic acids^27,28.

Online Methods

Code availability

All scripts can be found at https://github.com/fraser-lab/EMRinger and can be run using Phenix/cctbx python (version numbers greater than 1894) or through an integrated graphical application (version numbers greater than 2067).

Map Values

We loaded CCP4 formatted maps using cctbx and used the map voxel values without normalization, sharpening, filtering, or other map manipulation. The wide range of normalization procedures used in constructing these maps explains the large differences in cutoff values used for different model-map pairs in our study. However, because EMRinger calculations are based on the relative values of a single map, we can compare EMRinger scores between maps without further normalization.

EMRinger Map Sampling and Analysis

EMRinger, as implemented in the Phenix software package²⁹, is an extension of the Ringer protocol developed previously^13,14. Ringer iteratively rotates side chain dihedral angles, interpolating the density at the terminal atom as it is rotated. We adapted EMRinger to work with real-space maps and to rotate the Cγ atom by increments of 5° around the χ¹ dihedral angle (starting at 0° relative to the amide nitrogen). EMRinger calculates and records the map value from a potential map at the position of the Cγ atom at each increment using the eight-point interpolation function supplied by Phenix. From this scan, EMRinger records the peak map value and the angle at which it is achieved. These peak map values and angles are used for all further tools in the EMRinger package. EMRinger is available as phenix.emringer in Phenix version dev-2016 or newer. Real space correlation coefficients were performed by the em_rscc.py script.

Global EMRinger Score Calculation

We sampled all non-γ-branched, non-proline amino acids with a non-H γ atom, and measured the percent of map value peaks that are within at most 30° of 60°, 180°, or 300° (which we classify as rotameric). With map values sampled every 5°, this leads to a total of 39 angle bins that are considered rotameric and 33 that are considered nonrotameric. The extra rotameric bins are due to cases that are exactly 30° away from the central angle of a bin, which are considered rotameric.

In order to separate the effects of peaks called from noise from peaks found in the density, we filtered peaks by a map value cutoff. If the map value of a peak is above this cutoff, it is interpreted to be likely to be signal and therefore reporting correctly on the backbone position. Map values below this cutoff are discarded. Rather than relying on a user-selected map value cutoff, EMRinger chooses a range of 20 cutoffs, sampling linearly from the average map value across all scanned residues to the maximum map value measured across all scanned residues, and calculates statistics about the distribution for each possible cutoff.

To determine the significance of this distribution, we calculated a Z-Score based on a normal approximation to the binomial distribution (Equation 1).

$$Z-{\mathit{score}}_{\mathit{threshold}}=\frac{\mathit{Number}\mathit{Rotameric}-\frac{39}{72}·\mathit{Number}\mathit{Above}\mathit{Threshold}}{\sqrt{\frac{39}{72}·\left(1-\frac{39}{72}\right)·\mathit{Number}\mathit{Above}\mathit{Threshold}}}$$ (1)

“Number Rotameric” is the number of peaks above the cutoff which had rotameric chi angles, and “Number Above Cutoff” is the total number of peaks above the cutoff. 39/72 is the distribution for the null hypothesis as predicted by the binomial distribution for 72 bins with 39 rotameric choices.

In order to compare Z-scores between models of different structures, the Z-score is rescaled to the “EMRinger Score” to account for the total number of amino acids in the model (Equation 2).

$$\mathit{EMRinger}{\mathit{Score}}_{\mathit{threshold}}=\frac{10·Z-{\mathit{score}}_{\mathit{threshold}}}{\sqrt{\mathit{Model}\mathit{Length}}}$$ (2)

“Z-score” is the output of equation 1. “Model Length” is the total number of amino acids in the model which were scanned by EMRinger regardless of cutoff: all non-γ-branched, non-proline amino acids with a modeled non-H γ atom.

EMRinger repeats these calculations across the range of map value cutoffs. The highest score calculated across this range of cutoffs is returned as the EMRinger score for the model-map pair. Because of this multiple testing and because of the correction to account for varying model length, the final EMRinger score should not be used as a Z-score for statistical purposes.

EMRinger score does not change when the model and map are multiplied (e.g. in the case of a polymer with high symmetry), so that the score is definitive and no issues arise of how many monomers should be included in the analysis. An EMRinger score of 1.0 sets an initial quality goal for a model refined against a map in the 3.2–3.5Å range, while very high quality models at high resolution generate scores above 2.0. Maps that are highly variable in resolution may have lower EMRinger Scores unless poorly resolved regions of the map are masked out and excluded from the model. Calculation of the EMRinger score is performed by the emringer_score.py script.

Rolling Window EMRinger Analysis

In order to quantify the local contributions to the EMRinger score, we perform EMRinger analysis on rolling 21-residue windows along the primary sequence of proteins. For each window, we calculated the fraction of residues whose peaks were rotameric. These values were plotted as a function of the window position and were compared between different models of a protein to distinguish regions of improved model quality. Rolling window EMRinger analysis is performed by the emringer_rolling.py script.

Refinement of TrpV1 with Rosetta Iterative Local Rebuilding

Refinement of TRPV1 used an iterative local rebuilding procedure to improve local backbone geometry as well as fit to the experimental density data (DiMaio et al, Nature Methods, In Press). Refinement began with the deposited PDB structure of TRPV1 (PDB 3J5P). The model was trimmed to the transmembrane region (residues 381–695), and bond angles and bond lengths were given ideal geometry. During local rebuilding, 5 cycles of backbone rebuilding were run; in each cycle, regions with poor fit to density or poor local geometry were automatically identified, and rebuilding focused on these regions. Each rebuilding cycle was followed by side chain rotamer optimization and all-atom refinement with a physically realistic force field. Following this protocol, 1000 independent trajectories were run, and the final model was selected by filtering on two criteria: first, the 800 most nonphysical models were eliminated by assessing each model against the Rosetta all-atom force field; second, fit-to-density was used to rank models and select the best model from these 200.

Table Statistics

The cross-correlation was calculated using Chimera’s “Fit in Map” tool across all contours and using a resolution cutoff for the calculated map. The integrated FSC was calculated between the model and an independent reconstruction over a masked region covering the protein only. The mask was truncated at 6 Å resolution, and we report the integrated FSC_mask over high-resolutions shells only (15 – ~3.4 Å). Molprobity statistics were calculated using the validate tool in Phenix nightly build 1894.

Radiation Damage Analysis

To identify the degradation of map signal with radiation damage, we used EMRinger with a single model across multiple dose-fractionated maps. Individual reconstructions were calculated based on each of the 24 frames of data collected using the alignments generated from the full reconstruction in Frealign ²¹. Five-frame averages were generated by performing voxel-by-voxel averaging between each of the five frames using the CCP4 ‘mapmask’ tool. For each five-frame averaged dose-fractionated map, the EMRinger Score is calculated for the full model. We additionally calculated EMRinger scores for subsets of the model comprised only of the aromatic, positively charged, or negatively charged residues, respectively, to compare the differential radiation damage effects for different amino acid classes.

In addition to calculating EMRinger scores, Radiation damage can lead to a negative scattering contribution near the true (rotameric) position in subsequent maps. Because the rotameric peak of the original map can therefore be lowered below the baseline, EMRinger will then identify a new peak at a different local maximum in the damaged map. This new local maximum is more likely to occur at non-rotameric angles because the original rotameric angle is now suppressed by negative scattering contributions in the damaged map. The results of the EMRinger analysis on dose-fractionated data suggest that reconstructions based on different doses may be required to maximize the resolvability of different sets of side chains, just as different degrees of sharpening are commonly used now during model building.

Residue-specific sampling is performed by the emringer_residue.py script.

Grid Spacing Adjustment

In order to change the grid spacing of maps to test the effect of grid spacing on EMRinger scores, real-space mas were first fourier transformed to structure factors using phenix.map_to_structure_factors. The maps were then transformed back into real space with specified grid spacing using phenix.mtz2map with variations in grid_resolution_factor to vary the grid spacing without affecting the resolution.