Estimating individual contribution from group-based structural correlation networks

Abstract

Coordinated variations in brain morphology (e.g., cortical thickness) across individuals have been widely used to infer large-scale population brain networks. These structural correlation networks (SCNs) have been shown to reflect synchronized maturational changes in connected brain regions. Further, evidence suggests that SCNs, to some extent, reflect both anatomical and functional connectivity and hence provide a complementary measure of brain connectivity in addition to diffusion weighted networks and resting-state functional networks. Although widely used to study between-group differences in network properties, SCNs are inferred only at the group-level using brain morphology data from a set of participants, thereby not providing any knowledge regarding how the observed differences in SCNs are associated with individual behavioral, cognitive and disorder states. In the present study, we introduce two novel distance-based approaches to extract information regarding individual differences from the group-level SCNs. We applied the proposed approaches to a moderately large dataset (n=100) consisting of individuals with fragile X syndrome (FXS; n=50) and age-matched typically developing individuals (TD; n=50). Additionally, we tested the stability of proposed approaches using permutation analysis. Lastly, to test the efficacy of our method, individual contributions extracted from the group-level SCNs were examined for associations with intelligence scores and genetic data. The extracted individual contributions were stable and were significantly related to both genetic and intelligence estimates, in both typically developing individuals and participants with FXS. We anticipate that the approaches developed in this work could be used as a putative biomarker for altered connectivity in individuals with neurodevelopmental disorders.

1. INTRODUCTION

Large-scale population brain networks can be constructed by examining coordinated variations in the brain morphometric data (Bassett et al., 2008; Bernhardt et al., 2011; Chen et al., 2011; Fan et al., 2011; Guye et al., 2010; He and Evans, 2010; Junfeng Sun, 2012; Lerch et al., 2006; Lv et al., 2010; Raj et al., 2010; Sanabria-Diaz et al., 2010; Wu et al., 2012; Zhou et al., 2011). These structural correlation networks (SCNs) have been shown to reflect synchronized maturational changes in brain regions (Alexander-Bloch et al., 2013a; 2013b). Further, evidence suggests that SCNs may reflect both anatomical and functional connectivity (Alexander-Bloch et al., 2013a), thereby providing a complementary measure of connectivity in addition to diffusion-weighted and resting-state functional networks. Previous studies have shown that alterations in SCNs were associated with aging (Wu et al., 2012), multiple sclerosis (He et al., 2009), Alzheimer’s disease (He et al., 2008), schizophrenia (Bassett et al., 2008), adult/pediatric cancers (Hosseini et al., 2012a; 2012b), reading difficulties (Hosseini et al., 2013), and epilepsy (Bernhardt et al., 2011).

While previous work has related individual functional connectivity with behavioral performance (van den Heuvel et al., 2009), very few studies have attempted to estimate individual differences in anatomical connectivity directly from the T1-weighted MR images. Recently, a series of innovative methods have been developed to derive information about single-subject anatomical connectivity from the respective subject’s T1-weighted MR images (Batalle et al., 2013; Raj et al., 2010; Tijms et al., 2012; Zhou et al., 2011). For example, Tijms et al (2012) have proposed a cube-based correlation approach to extract single-subject anatomical connectivity from the respective subject’s T1-weightet MR images. In this cube-based approach, the graph nodes were represented as small 3D cubes in the gray matter and the strength between nodes was computed by estimating intra-cortical similarities in the gray matter morphology (e.g., thickness measure). Similarly, in another study, individual anatomical connectivity was estimated from T1-weighted MR images using Gibbs probability models (Raj et al., 2010). These previous studies have demonstrated that the extracted individual networks from T1-weighted images show “small world” properties (Tijms et al., 2012) and can be used to improve classification between patient populations and healthy controls (Raj et al., 2010; Zhou et al., 2011). More recently, Batalle et al. (2013) applied the normalized cube-based correlation approach to extract individual networks in a pediatric population and demonstrated that the extracted gray matter connectivity at the individual level can be related to individual differences in behavioral functioning (Batalle et al., 2013).

Although innovative methods have already been proposed to derive information about single-subject anatomical connectivity from their T1-weighted images, it is unclear whether individual differences in anatomical connectivity can be directly extracted from the group-level SCN itself. Such extraction would allow for relating individual differences in behavior (and/or genetic measures) to the observed group-level differences in the SCN. Thus, to directly extract individual contribution towards anatomical connectivity from group-level SCNs, we introduce two distance-based approaches that can be used as putative biomarkers for altered connectivity in individuals with neurodevelopmental disorders. The first approach is based on the leave-one-out (LOO) strategy, where an individual’s contribution is estimated by leaving that individual out and re-estimating group-level SCN. Similar approaches have been used previously for cross-validation in machine-learning literature (Bishop, 2006). The second metric is designed for clinical populations, where the contribution of an individual with a disorder is extracted by adding his/her morphometric data to a set of control participants and by re-estimating changes in SCN due to such addition (henceforth referred to as Add-One-Patient (AOP) approach). The proposed approaches were applied to both global structural correlation matrices as well as to topological (or network) properties extracted from the SCNs.

We applied the proposed approaches to morphometric data from a moderately large group of participants with fragile X syndrome (FXS) and an age-matched group of typically developing participants (TD). Fragile X syndrome results from a trinucleotide CGG repeat expansion (locus Xq27.3), leading to hypermethylation of the fragile X mental retardation 1 gene (FMR1) promoter region and reduced levels of FMR1 protein (FMRP) (Verkerk et al., 1991). The percentage of FMRP is critical during neurodevelopment, as it is involved in regulating synaptic plasticity and dendritic pruning (Harlow et al., 2010). Reduced levels (or percentage) of FMRP has been associated with intellectual disability (Reiss and Dant, 2003), cognitive and behavioral impairments (Van der Molen et al., 2012), and high prevalence of autism symptomatology (Gabis et al., 2011). Further, FXS is linked with altered structural and functional brain connectivity (Haas et al., 2009; Hall et al., 2013; Wang et al., 2012).

Stability analysis was performed to examine the robustness of proposed approaches with increasing group size. Further, to assess the efficacy of these approaches, extracted individual contributions were tested for their association with intelligence scores in both FXS and TD groups and with percentage of FMRP in individuals with FXS. Additionally, we estimated how the morphometric properties of each cortical and subcortical region influences the extracted individual contributions towards group-level SCN. Estimating such regional influences, especially in patient populations, could provide confirmatory validity to our proposed approaches because FXS is widely associated with significant differences in regional morphometric properties (e.g., larger and abnormal shape of caudate nuclei volume) (Lightbody and Reiss, 2009; Peng et al., 2014).

2. MATERIALS AND METHODS

2.1 Participants

Fifty participants with a confirmed genetic diagnosis of FXS (30 females; mean age=17.61 years, S.D.=2.76) and an age-matched group of 50 typically developing (TD) participants (30 females; mean age=17.66 years, S.D.=2.65), all between the ages of 12 and 23 years were recruited. Diagnosis for individuals with FXS was confirmed using the Southern Blot DNA analysis (Kimball Genetics, Denver, CO). The two groups were matched for age (t(97)= 0.11, p=0.913), but the full scale IQ (Table 1; see section 2.2 for administration details) was significantly different between the two groups (t(96)= 13.55, p<0.0001). Typically developing participants were excluded for a history of any known genetic condition, premature birth, low birth weight, or any learning, developmental, psychiatric, neurological or medical disorder. All participants were free from MRI contraindications. Participants were recruited across the United States and Canada through advertisements, referrals, and word of mouth. Participants and/or their parents gave written informed consent and assent to participate in the study. The Stanford University’s Institutional Review Board approved all protocols.

Table 1.

Group-wise participant characteristics.

	Fragile X Syndrome (FXS)	Typically Developing (TD)
Number of participants	50 (30 females)	50 (30 females)
Age in years (S.D.)	17.53 (2.8)	17.66 (2.65)
Full Scale IQ (S.D.)	72.34 (19.8)	119.40 (14.4)
%FMRP (S.D.)	40.17 (26.9)	-
Mean Brain Volume (S.D.)	1258.884 (121.82)	1254.837 (100.15)
Mean Cortical Thickness (S.D.)	2.84 (0.142)	2.75 (0.114)
Subcortical Gray Volume (S.D.)	200.85 (17.8)	200.25 (17.7)

2.2 Intellectual functioning

General intellectual functioning (IQ) was assessed via the Wechsler Adult Intelligence Scale (WAIS-III) (Wechsler, 1997) or Wechsler Abbreviated Scale for Intelligence (WASI) (Wechsler, 1999) was used for participants 17 years and older and the Wechsler Intelligence Scale for Children (WISC-III) for participants younger than 17 years (Wechsler, 1991). For participants with FXS all IQ assessments were completed within 6 months of MRI imaging and for the TD group all IQs were assessed within 21 months of scanning. We used the full-scale intelligence quotient (FSIQ) as a measure of intellectual functioning for all participants. The mean FSIQ for participants with FXS was 72.63 (S.D.=19.93; Range=44–124) and for TD participants 119.56 (S.D.=13.96; Range=85–147).

2.3 Genetic assessments (quantification of FMR1 protein)

A mutation of the fragile X mental retardation 1 (FMR1) gene, associated with trinucleotide CGG repeat expansion, is considered to be the cause of FXS (Lightbody and Reiss, 2009). Typically developing individuals have around 29–30 CGG repeats in the FMR1 gene. When the size of repeat expands beyond 55, but is under 200, then the individual is considered to be a carrier of the fragile X pre-mutation. However, when the size of CGG repeats crosses the 200 mark, hypermethylation of the promoter region of gene is very likely to occur and result in transcriptional silencing of the FMR1 gene, which in turn limits the production of FMR1 protein (FMRP) (Bhakar et al., 2012; Lightbody and Reiss, 2009). This is referred to as the “full mutation”. Reduced levels of FMRP negatively impact brain development and function (Fung et al., 2012). Thus, the percentage of FMRP available in individuals with FXS provides a potential genetic biomarker of disease severity. We estimated FMRP percentage for each individual in the FXS group based on the percentage of peripheral lymphocytes containing FMRP as assessed by immunostaining techniques (Willemsen et al., 1997). The mean FMRP percentage for the FXS group was 40.89 (S.D.=26.79). In case of typically developing participants the FMRP percentage is assumed to be 100 and hence we did not assess FMRP percentage in this group.

2.4 Image acquisition and FreeSurfer data analysis

Anatomical T1-weighted images were acquired on General Electric 1.5 Tesla (Stanford University), in the coronal direction (repetition time = 35 milliseconds, echo time = 6 milliseconds, flip angle = 45°, slice thickness: 1.5 to 1.7 mm, in-plane resolution .9375 × .9375 mm, and acquisition matrix = 256 × 192 mm, 124 contiguous slices). We adjusted the slice thickness (range 1.5mm–1.7mm) across participants to insure coverage of the entire brain without increasing the number of slices. This approach was utilized as an increase in number of slices would have increased the scan time by an undesirable amount and could have resulted in “wraparound” and other unwanted image artifacts. Table 2 below provides information regarding the variation in slice thickness across participants in each group. As evident, a large proportion of the participants were scanned at 1.5mm slice thickness. A Chi-square test was used to assess if there was a systematic difference in slice thickness variation between groups. No significant differences were found between the groups (p=0.58).

Table 2.

Variation in slice thickness across participants in both groups (typically developing or TD and participants with FXS).

Slice Thickness (in mm)	Group		Total (n=100)
	TD (n=50)	FXS (n=50)
1.5	42	38	80
1.6	7	11	18
1.7	1	1	2

It is important to note that the data presented in this study were drawn from a larger longitudinal study (Bray et al., 2011). We selected scans from the longitudinal study using the following criterion – (a) appropriate age range, (b) met strict image quality requirements and (c) were free from artifacts induced by subject motion, blood flow or wraparound. Approximately 19% of scans in the larger study were unusable due to such artifacts.

The FreeSurfer toolkit (http://surfer.nmr.mgh.harvard.edu/) was used to parcellate the brain into 86 gray matter regions (68 cortical, 16 subcortical and 2 cerebellar regions). In this work, we used morphological measurement of thickness for cortical regions and of volume for subcortical regions and cerebellum. The technical details of these procedures are described previously (Dale et al., 1999; Fischl et al., 1999; Hosseini et al., 2013). Briefly, this processing analysis pipeline includes: (a) removal of non-brain tissue using a hybrid watershed/surface deformation procedure (Ségonne et al., 2004) ; (b) automated Talairach transformation; (c) segmentation of the subcortical white matter and deep gray matter volumetric structures (Fischl et al., 2004); (d) intensity normalization (Sled et al., 1998); (e) tessellation of the gray matter white matter boundary; (f) automated topology correction (Ségonne et al., 2007); and (g) surface deformation following intensity gradients to optimally place the gray/white (main) and gray/cerebrospinal fluid (pial) borders at the location where the greatest shift in intensity defines the transition to the other tissue class (Fischl and Dale, 2000).

Once the cortical models were complete, regional volumes were extracted by surface inflation (Fischl et al., 1999), registration to a spherical atlas which utilizes individual cortical folding patterns to match cortical geometry across participants (Fischl et al., 1999), and parcellation of the cerebral cortex into units based on gyral and sulcal structure (Desikan et al., 2006). The main and pial surfaces were visually inspected, and where needed, appropriate manual corrections were performed as per the Freesurfer Tutorial (http://surfer.nmr.mgh.harvard.edu/fswiki/FsTutorial). All raters who performed manual editing of FreeSurfer derived data were trained to achieve inter-rater reliability of ≥0.95 (intraclass correlation coefficient) with gold-standard datasets for all regions of interest. A similar approach has been used previously (Hosseini et al., 2013).

Cortical thicknesses, and cerebellar and subcortical volumes were corrected for mean cortical thickness, total cortical gray matter volume, and total subcortical gray matter volume, respectively, in addition to age, using linear regression (Hosseini et al., 2013). The residuals of these analyses were subsequently used for constructing structural correlation matrices. Normalizations by correcting global measures in this manner remove the individual differences in morphometric measures affected by overall brain size and are a prerequisite for construction of structural correlation networks (Bernhardt et al., 2011; Fan et al., 2011; Hosseini et al., 2012a).

2.5 Structural correlation matrix

Data from all the brain regions from a set of participants were used to construct morphology-based structural correlation networks. For each group, an <number of regions> x <number of regions> correlation matrix R was generated with each entry R_ij defined as the Pearson correlation coefficient between the extracted residuals of regions i and j. For later analyses, we used the structural correlation matrix R to represent weighted connectivity between regions.

2.6 Graph theory metrics

The network properties of structural correlation matrix were estimated using standard graph theory procedures, as implemented in the Brain Connectivity Toolbox (http://www.brain-connectivity-toolbox.net). Positive weighted structural correlation matrices were used to extract various graph theoretical properties. We restricted the analysis in this paper to two main network properties, i.e., integration and segregation (Rubinov and Sporns, 2010). For network integration, we estimated characteristic path length (L) of each network, which is defined as the average shortest path length between all pairs of nodes in the network. Given that our participant sample was in the developmental age range of late childhood to early adulthood, to assess the developmental changes in anatomical connectivity (especially, synaptic pruning (Gogtay et al., 2004)) we also included a measure of graph diameter (D). A graph’s diameter is usually defined in terms of maximal eccentricity of the graph, where eccentricity of each node is the maximal shortest path length between a node and any other node and the diameter is the maximum eccentricity of the whole graph/network (Hage and Harary, 1995). For network segregation, we estimated clustering coefficient (C) of each network, which is defined as the proportion of nearest neighbors of a node that are connected (Rubinov and Sporns, 2010).

2.7 Measures for individual contribution

Two novel distance-based approaches were proposed to extract individual contribution from the group-level SCNs. The proposed approaches were run separately on the global structural correlation matrices and the three graph theory based network properties. By extracting individual contribution from the overall structural correlation matrix itself, we were able to measure the impact of each individual on the overall configuration of the network, while by extracting individual contribution on graph theoretical properties we were able to measure the impact of each individual on specific network properties.

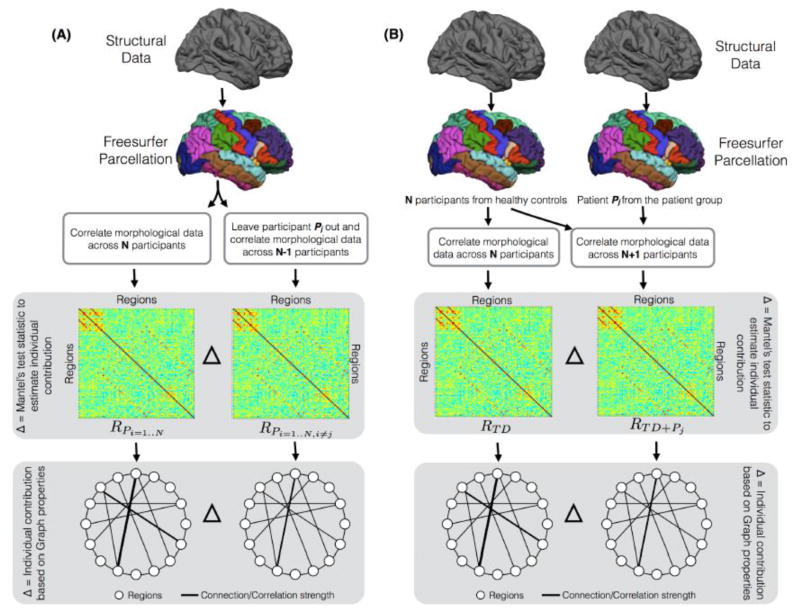
The first metric was based on the leave-one-out (LOO) approach, where within each of the groups (FXS and TD), each participant P_j was left out to estimate his/her individual contribution (Figure 1A). The contribution was estimated by finding similarity between the global structural correlation matrices before and after each participant was left out using the Mantel’s test statistic. Mantel’s test (Mantel, 1967) was designed to evaluate similarity between correlation matrices. Like the Pearson correlation (r) value, Mantel’s test statistic value also ranges from −1 (negative related) to 1 (positive related), where a value closer to 0 indicates null or no relationship. Mantel’s test statistic is based on a cross-product term:

$$z=\sum _{i=1}^n\sum _{j=1}^n{x}_{ij}{y}_{ij},$$ (1)

and is normalized as,

Figure 1.

The proposed approaches to extract individual contribution at the global level of structural correlation matrices and at the level of graph theory metrics. (A) Using the Leave-One-Out (LOO) approach, where within each group (FXS and TD), each participant P_j was left out to estimate his/her contribution. (B) Using the Add-One-Patient (AOP) approach, where the contribution of a patient participant is derived by computing the distance between a correlation matrix (or graph metric) derived from typically developing participants and a correlation matrix (or graph metric) derived from a new group that includes all typically developing participants and the patient P_j.

$$\mathit{Mantel}\mathit{Test}r(\mathit{X},\mathit{Y})=\frac{1}{n-1}\sum _{i=1}^n\sum _{j=1}^n\frac{x_{ij}-\overline{x}}{s_x}·\frac{y_{ij}-\overline{y}}{s_y},$$ (2)

where x and y are variables from X and Y correlation matrices, n is the number of elements in each matrix, and the s_x and s_y are standard deviations for X and Y correlation matrices. Thus, using the LOO approach, the contribution of participant P_j to the global structural correlation matrix (R) was quantified as,

$${IC}_{P_j}^{\mathit{LOO}}=1-\mathit{Mantel}\mathit{Test}r\left(R_{P_{i=\mathrm{1..}N}},R_{P_{i=\mathrm{1..}(N-1),i\ne j}}\right),$$ (3)

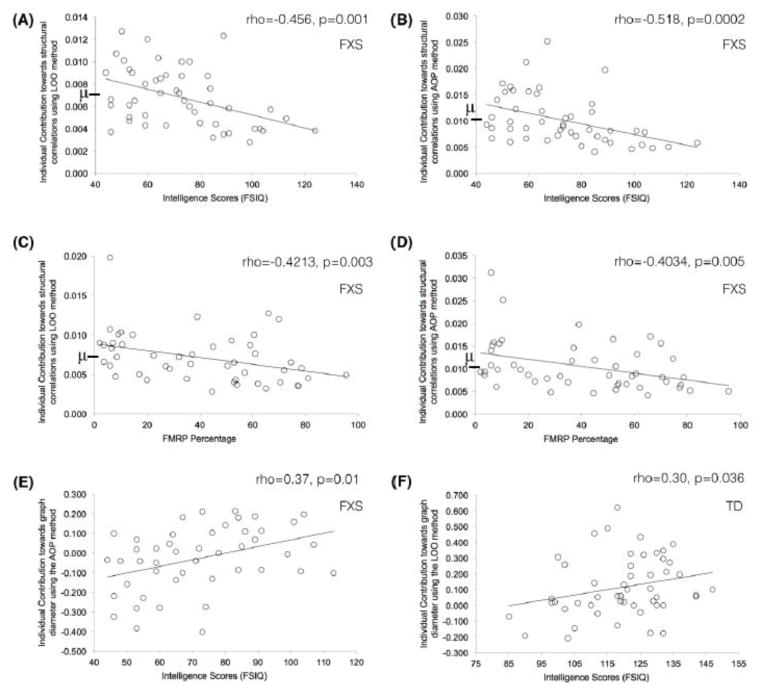
where N represents total number of participants in each group. It is noteworthy that a Mantel’s test value closer to 1 indicates high similarity between the two matrices and hence depicts low contribution from the participant P_j and vice versa. Thus, the individual contribution is defined as one minus the Mantel’s test statistic. Lastly, to determine the position of a participant’s individual contribution within group, we also report the mean group contribution in each plot (using the symbol μ and a bold line on the y-axis; Figure 2). This information can help estimate whether a given participant is contributing more or less towards structural correlations than the other participants in his/her group. Further, by comparing with average group contribution, we can also infer whether contributing more than group average leads to better (or worse) intellectual functioning and/or genetic scores.

Figure 2.

Relations observed between extracted contributions and behavioral/genetic measures. The symbol \mu and bold line on y-axis, in A–D, depicts group-mean of individual contribution and it is shown to provide information regarding position of each individual’s contribution with respect to the group mean. Full dataset was used for these correlations and Spearman rank correlation values (rho) are reported.

Using a similar LOO approach, the individual contribution to graph properties was estimated by leaving each participant P_j out; this was accomplished by subtracting the graph metrics calculated using all participants other than P_j from the graph metrics calculated using all participants including P_j (Figure 1A).

The second metric was specifically designed for clinical populations. In this metric, the contribution of patient P_j is derived by computing the distance between a correlation matrix derived from typically developing participants (R_TD) and a correlation matrix derived from a new group that includes all typically developing participants and the patient, P_j, i.e., R_TD+Pj (Figure 1B). Thus, using this add-one-patient (AOP) approach, the contribution of a participant with the disorder, P_j to the structural correlation matrix was quantified as,

$${IC}_{P_j}^{\mathit{AOP}}=1-\mathit{Mantel}\mathit{Test}r\left(R_{TD},R_{TD+P_j}\right),$$ (4)

From this perspective, a Mantel’s test value closer to 1 indicates high similarity between the two matrices and hence depicts low contribution from the participant P_j. As noted above, the individual contribution is defined as one minus the Mantel’s test statistic. Lastly, to determine the position of participant’s individual contribution in their group, we also report the mean group contribution in each plot (using the symbol μ and a bold line on the y-axis; Figure 2).

Using a similar AOP approach, adding a participant with disorder P_j from the FXS group to the age-matched TD group, the contribution of P_j to the three network properties was estimated, i.e., by subtracting graph metrics calculated using all TD participants and P_j from the graph metrics calculated using all TD participants only (Figure 1B).

2.8 Regional contribution to individual differences in the structural correlation matrix

To find the regions that contributed most to the individual differences in the correlation matrix for each group, we calculated column-wise absolute sum of the difference matrix for each of the two proposed approaches. Thus, regional contribution for participant P_j using the LOO approach was defined as,

$${\mathbf{RC}}_{P_j}^{\mathit{LOO}}=\sum _{\mathit{colwise}}\mid R_{P_{i=\mathrm{1..}N}}-R_{P_{i=\mathrm{1..}(N-1),i\ne j}}\mid ,$$ (5)

where RC represents a vector containing the regional contributions for each of the 86 regions. Similarly, for the AOP approach the regional contribution for participant P_j was defined as follows,

$${\mathbf{RC}}_{P_j}^{\mathit{AOP}}=\sum _{\mathit{colwise}}\mid R_{TD+P_j}-R_{TD}\mid$$ (6)

2.9 Relations between individual contribution and behavioral/genetic assessments

Spearman’s correlation (rho values) was used to assess relations between extracted individual contribution and behavioral measurements of intellectual functioning as well as genetic assessment of FMRP percentage. Alpha value of p=0.05 was used to find significant correlations. As pointed out in previous research (Wilcox and Muska, 2001), the presence of heteroscedasticity (unequal variability in predicted values across the range of values of a predictor) can make a correlation significant even though the variables are not truly correlated. Thus, to test whether the correlations between individual-contribution and assessments is merely due to heteroscedasticity, we employed robust correlations based on percentile bootstrap confidence intervals (Cyril R Pernet, 2012).

2.10 Stability analysis

One potential concern regarding the proposed approaches is that as the number of participants in a given group increases, the overall contribution of an individual participant (either left out or added to a control group) might decrease and potentially approach zero with particularly large datasets (N≫100). Thus, it is clear that with the increase in size of the base group (i.e., a group to which either the individual was left out or added to), the magnitude of individual contribution drops. It is not clear, however, how such a drop in individual contribution magnitude affects (if at all) the ability of individual contributions to relate with the behavioral and/or genetic assessments. To address this issue, several permutation analyses were run for both LOO and AOP approaches with different base group sizes (range: 3 to maximum group size). Thus, we extracted individual contributions of each participant (in both groups: FXS and TD) for different base group sizes, where base participants were selected using random selection with replacement from their respective groups. Further, this procedure was repeated 100 times to obtain stable estimates for each base group size. Altogether, this stability analysis was performed to examine variations in (a) individual contributions for a range of base group sizes and (b) correlation between individual contributions and behavioral/genetic measures for each base group size.

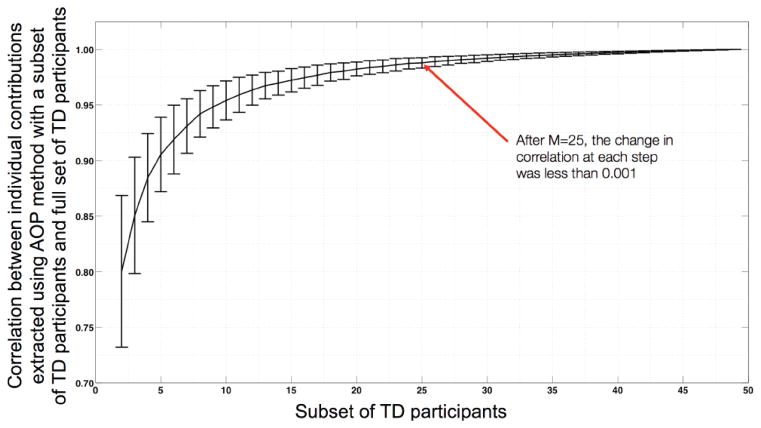
A second potential concern, specific to the AOP approach, is to examine how many TD participants are required to get stable estimates of individual contribution of participants with FXS. To perform such testing, we randomly selected M participants from the TD group, and calculated correlations between AOP-based individual contribution to the structural correlation matrix extracted from the original set (N=50) of TD participants and from different size subsets (M=2,3…50) of TD participants. To get stable estimates, the random selection and correlation procedure was repeated 1000 times for each subset size (M).

3. RESULTS

After extracting each participant’s contribution to overall connectivity (i.e., structural correlation matrix) and to individual network properties (i.e., using three graph theory metrics), we related these contributions with intelligence scores and genetic assessments (in FXS group only). We also examined the regional contribution to individual differences in both the LOO and AOP based approaches. Examining such relations and regional contributions provided us an opportunity to assess the criterion validity of the proposed approaches. Lastly, we present results from stability analyses that were performed to (a) examine robustness of proposed approaches as the number of participants increases (using FXS and TD data); and (b) estimate the number of control TD participants required to estimate stable AOP-based contribution for individuals with FXS.

3.1 Relations between individual contribution and intellectual functioning

For the FXS group, using both the LOO and AOP based approaches, we found significant correlations between intelligence scores and individual contribution to the structural correlation matrix as well as to the network properties. Specifically, using the LOO approach we found significant negative correlation between the individual contribution to the structural correlation matrix and intelligence scores (rho(48)=−0.4562, p=0.001; Figure 2A). Similarly, using the AOP approach we found significant negative correlation between the individual contribution to the structural correlation matrix and intelligence scores (rho(48)=−0.5, p=0.00016; Figure 2B). Altogether, using the mean group contribution across all participants in the FXS group (as shown by the dashed line in Figure 2A/B), it is evident that participants who contributed more than the group average towards global connectivity had lower intellectual functioning and vice versa.

Among the three network properties, individual contribution extracted using the AOP approach towards the graph diameter was also observed to positively relate with the intelligence scores (rho(48)=0.37, p=0.01; Figure 2E). Thus, suggesting that positive contribution towards graph diameter was associated with higher intellectual functioning in patients with FXS.

For the TD group, using the LOO approach, a significant positive relation was also observed between the individual contribution to the graph diameter and intelligence (rho(50)=0.30, p=0.036; Figure 2F). In line with the FXS group, positive contribution towards graph diameter was associated with higher intellectual functioning even in the TD group. No significant relation between contribution to the structural correlation matrix and intelligence scores was observed in the TD group.

3.2 Relations between individual contribution and genetic assessment

In addition to the intelligence scores, we also assessed the percentage of FMRP in the individuals with FXS. Using both the LOO and AOP based approaches, contribution to the structural correlation matrix negatively related to the FMRP percentage (rho(47)=−0.42, p=0.003 and rho(47)=−0.40, p=0.005, respectively for LOO and AOP approaches; Figure 2C and 2D). Altogether, using the mean contribution across all participants in the FXS group (as shown by the dashed line in Figure 2C/D), it is evident that participants who contributed more than the group average towards global connectivity had lower percentage of FMRP and vice versa.

3.3 Regional contribution to the estimated individual differences

To find which brain regions contributed most to the observed individual differences in structural correlation matrix, we calculated regional contributions for each of the two proposed approaches (using equations 5 and 6). The regional contributions using the LOO approach, within each group, is shown in Figure 3A. No single brain region stood out in contributing towards the individual differences. Using the AOP approach, however, the regional contributions of both left and right caudate nuclei towards individual differences in the FXS group were three standard deviations above the mean regional contributions across all regions (Figure 3B). This finding suggests that individual differences contributing to structural correlation in individuals with FXS was largely driven by abnormal morphometric properties of the caudate nuclei.

Figure 3.

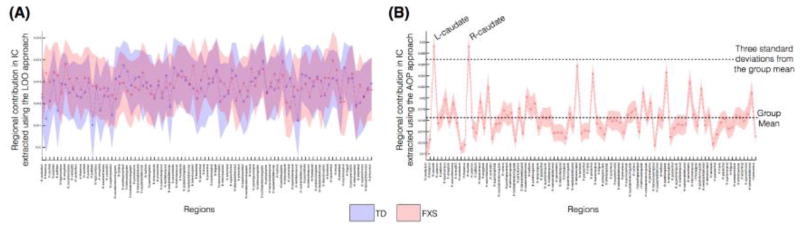
Regional contribution to individual differences in FXS and TD groups. (A) Using the LOO approach; and (B) using the AOP approach. Colored-band represents standard error of the mean for each group. The dashed lines in (B) indicate group mean and three standard deviations above the mean, to show that the influence of left and right caudate is prominent towards the extracted individual contribution using the AOP approach.

3.4 Stability analysis

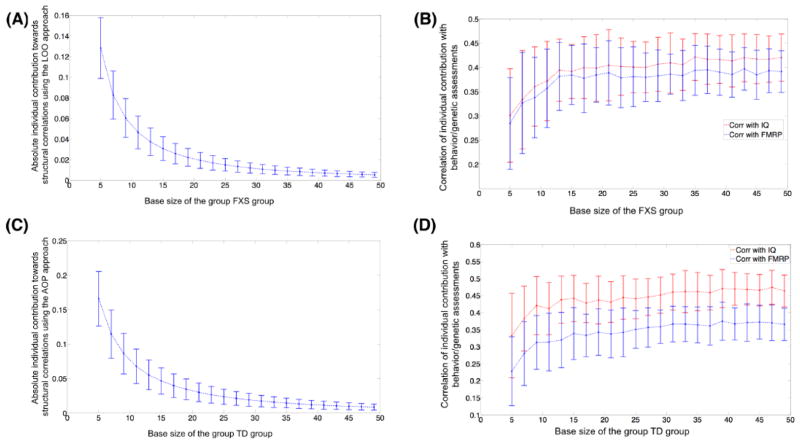
To examine the robustness of proposed approaches with increasing number of participants, permutation analysis was run with different group sizes. As expected, with increasing group size the individual contribution decreased for both approaches (Figure 4A and C). However, the correlation between intelligence/FMRP scores and individual contribution increased asymptotically with increase in group-size and stabilized around n=25–30 (Figure 4B and D). A similar pattern of reduction in magnitude of individual contribution and asymptotic increase in correlation between contribution and behavior was evident for both LOO and AOP based approaches for graph theoretical properties. In sum, for both patient and healthy groups, individual contribution extracted using our proposed approaches is associated with behavioral measures in a stable and robust fashion.

Figure 4.

Stability analysis to test the effect of increase in number of participants on the magnitude of individual contribution and on the correlation between individual contribution and behavioral/genetic measures. As evident, across groups, with increasing number of participants, the individual contribution exponentially decreases. However, the correlation between contribution and behavior/genetic scores asymptotically increases and stabilize around n=25–30. Similar pattern was evident for the network properties (e.g., diameter). Absolute value of individual contribution in used in A and C and the error bars represent standard error of the mean. Spearman rank correlation (rho) was used to estimated correlation between individual contribution and behavioral/genetic measures.

In another set of stability analyses, we estimated the required size of TD group for stable estimates of individual contribution extracted using the AOP approach. Using permutation analysis, we found that a group of twenty-five TD participants provide sufficiently stable estimates of AOP-based individual contribution (Figure 5).

Figure 5.

Number of TD participants required for stable estimation of individual contribution based on AOP approach for all participants in the FXS group. Graph was generated by randomly selecting subsets (of different size M) from TD participant pool. Repeating this random selection process 1000 times generated the error-bars on the graph. The error bars represent standard error of the mean. Y-axis depicts Spearman rank correlation (rho) values.

To test the stability of our proposed approaches with much larger datasets, we applied our methods to freely available data from the Human Connectome Project (HCP; site: http://www.humanconnectome.org). We used the HCP Q3 data release (N=226), which was processed using FreeSurfer version 5.2. Similar to our FXS and TD data, we used volumetric information for subcortical and thickness information for the cortical structures. To correlate individual contributions with intelligence, we used the behavioral performance score on progressive matrices test (Bilker et al., 2012), also provided by the HCP Q3 release. Supporting our observations for the FXS and TD data, results with the HCP data showed a consistent pattern, i.e., although the individual contribution towards group-level SCN reduces in amplitude with increasing group size, the correlation between individual contribution and behavioral assessment remains stable at larger group sizes (stable estimates were obtained for a group size of 25–30 participants and above; Supplementary Figure 3).

3.5 Heteroscedasticity analysis

To test whether the correlations between individual-contribution and clinical variables of interest is merely due to heteroscedasticity, we employed robust correlations based on percentile bootstrap confidence intervals (Cyril R Pernet, 2012). As shown in the Supplementary Figure 1 and Supplementary Table 1, all the observed correlations remain significance (p<0.05) after controlling for heteroscedasticity.

3.6 Effect of Sex on individual contribution and correlation to behavioral/genetic measures

In a separate set of analyses, we regressed out sex from the morphometric data (along with age and total cortical tissue thickness and subcortical volume) and reconstructed the structural correlation matrices (SCM). The individual contribution towards group-level SCN was then derived from the revised SCMs and was correlated with behavioral/genetic data in individuals with FXS and with TD participants. In the FXS group, the individual contribution was observed to be correlated with clinical assessments in the same manner as they were observed to be correlated without regressing out sex as a nuisance covariate (Supplementary Table 3). In the typically developing individuals, however, after regressing out sex the correlation between individual contribution to graph diameter and intelligence was not significant.

4. DISCUSSION

Comparing group-level SCNs provide crucial information regarding differences in structural connectivity between groups (Alexander-Bloch et al., 2013a). To estimate significant group-level differences in connectivity researchers bin individuals from both groups into pseudorandom sets and estimate the statistical significance using permutation statistics (Hosseini et al., 2012a). However, these observed group-level differences cannot be related to clinical assessments from individual participants in each group. Thus, our current work was motivated by the argument that relating observed differences in group-level connectivity and network properties to clinical assessments could provide better understanding of the underlying connectivity differences. We introduced two novel distance-based approaches to extract individual contributions to both overall connectivity and to network properties of segregation and integration. The efficacy of the proposed approaches was tested in two independent datasets. Additionally, the stability and robustness of proposed approaches was tested using permutation analysis.

One potential reason for the wide usage of SCNs lies in the fact that the required morphometric data can be extracted from T1-weighted images that are relatively straightforward to administer, acquire and aggregate, at a large-scale, across imaging centers and populations. Other neuroimaging modalities that provide information regarding anatomical connectivity, e.g., diffusion-weighted imaging (DWI), are generally characterized by longer scan durations, low signal-to-noise ratio, and higher susceptibility to head movement artifacts – making the investigation of anatomical connectivity harder especially in clinical populations. Thus, our proposed methods to extract individual differences from group-level SCNs could provide a relatively feasible and effective biomarker for altered neurodevelopmental brain connectivity.

To test the efficacy of the proposed approaches, we examined the relation between extracted individual contribution and intelligence scores in both groups. In the FXS group, we found that the individual contributions to both structural correlation matrix as well as network diameter were related to the intelligence scores. Using both the LOO and AOP approaches, the observed negative relations between the contributions to global structural correlations and the intelligence scores suggest that the participants with FXS who contribute higher than the group mean have lower intelligence scores. Previous research suggests that severe intellectual disabilities are frequently evident in individuals with FXS (Garber et al., 2008). Further, in a recent study, Hall et al. (2013) observed reduced resting-state functional connectivity in individuals with FXS as compared with age- and IQ-matched control participants, and within the FXS group reduced connectivity was linked with lower IQ scores (Hall et al., 2013). Although structural correlations complement resting-state connectivity, previous research also suggests a convergence in results from these approaches (Hosseini and Kesler, 2013). Thus, cautiously building upon previous work, the observed negative relation in our study suggests that higher alterations than the group mean in global anatomical connectivity, in individuals with FXS, are related to greater intellectual disability.

In addition to global structural correlations, individual contributions to the graph diameter were also related with intelligence scores in the FXS group, such that a positive contribution towards the graph diameter was associated with higher intellectual functioning in patients with FXS. Interestingly, using the LOO approach in the age-matched TD participants, a similar positive relation between individual contribution to graph diameter and intelligence scores was found. Graph diameter is a measure of network integration and represents the maximum distance between any two vertices (or regions) in the graph (Rubinov and Sporns, 2010). In the current paper, the distance between two regions is defined as the inverse of magnitude of correlation strength between the two regions. Thus, a graph with overall stronger correlation strength between regions would represent overall shorter distances between regions and hence shorter graph diameter and path length. Interestingly, shorter path length also indicates higher efficiency (in communicating signal from one vertex to another) of a graph and previous work investigating the neural correlates of intelligence in adults has suggested that both the integrity of connections (or white matter pathways) and the overall network efficiency are important (Deary et al., 2010; Li et al., 2009; van den Heuvel et al., 2009). Thus, it is unclear, why a positive contribution to graph diameter, and potentially reduced efficiency, is positively associated with intelligence in each of the two young cohorts (age range 12–23 years) studied here.

One plausible conjecture could be that previous work associating path length (and efficiency) with intelligence scores was limited to adults. Thus, it is unknown whether a similar relation would be observed in younger, still developing, populations, mainly due to the fact that the development of brain (and perhaps intelligence) involves a substantial amount of synaptic pruning (Gogtay et al., 2004; Luo and O’Leary, 2005; Paus, 2005; Paus et al., 2008). In a recent study, researchers observed that in individuals aged 10 to 21 years, cortical thickness in both left and right hemispheres decreases (speculated to be due to synaptic pruning) over time. Further, this decrease is positively related to intelligence (Schnack et al., 2014). Theoretically, pruning edges in a graph leads to increased diameter and eccentricity. Boersma et al. (2013), using EEG data, observed a similar increase in graph diameter and eccentricity with brain development (Boersma et al., 2013). Taking these results and theory into account, we speculate that the direct relation between a network’s graph diameter and intelligence for our young cohort is potentially in line with current knowledge of brain development and thereby provides putative criterion validity to the proposed approaches.

Although Leow and colleagues have recently examined the anatomical network properties in fragile X pre-mutation carriers (CGG repeat between 55 and 200) using DWI (Leow et al., 2014), it is unknown how the reduced percentage of FMRP in individuals with full mutation FXS (CGG repeats >200) affects anatomical connectivity and graph properties. In the present work, using both LOO and AOP approaches, we observed a significant negative relation between FMRP percentage and contribution to global structural correlations. Further, no relation was observed between individual contribution to the three graph properties and FMRP percentage, thereby suggesting that reduced FMRP affects anatomical connectivity at the global network configuration level.

In addition to relating individual contribution with behavioral and genetic measures, we also examined how every cortical and subcortical region influenced the contribution towards global structural correlations. Using the LOO approach, no single region or set of regions stood out as most contributory for either group. However, using the AOP approach, a clearly prominent influence was evident for bilateral caudate regions in individuals with FXS. Several previous studies, across different neuroimaging modalities, have shown abnormality in the size and/or shape of the caudate nucleus that are specific to individuals with FXS as compared to individuals with idiopathic developmental delay, autism and typical development (Gothelf et al., 2008; Hazlett et al., 2009; Hoeft et al., 2008; Peng et al., 2014). As the enlarged caudate in FXS is thought to be contributory to the cognitive as well as specific behavioral deficits associated with the syndrome (Lightbody and Reiss, 2009), its prominent influence towards individual contribution to global structural correlations provide conceptual support to the proposed AOP approach.

To test the robustness and stability of proposed metrics, two stability analyses were performed. Using permutation analyses, we observed that although the magnitude of individual contribution (across both LOO and AOP approaches) decreases with increasing number of participants, the relation between individual contribution and intelligence/genetic assessments increases asymptotically and stabilizes around base size of 25–30 participants. This finding suggests that the proposed approaches are robust and stable in predicting and relating to behavioral/genetic assessments. We also found that, on average, twenty-five control participants provide stable estimation of contribution for patients using the AOP approach.

To be consistent with the previous literature (He et al., 2006), thickness was used as the cortical morphological feature to construct structural correlation networks. For subcortical regions, volumetric information was utilized. Similar approaches of mixing thickness for cortical regions and volume for subcortical to construct structural correlation networks have been previously published (Hosseini et al., 2013). It is important to note that our proposed approaches should not be affected by the choice of morphometric measure. To confirm this assumption, using the same dataset, we constructed structural correlation networks using cortical and subcortical volumes and derived individual contribution using the proposed approaches. Similar, albeit weaker, relations were observed between individual contribution and behavioral/genetic metrics (Supplementary Figure 2 and Table 2).

Although widely used, structural correlation based connectivity models may not fully represent actual anatomical and/or functional connectivity. Recent studies have observed moderate to strong convergence between structural correlation based connectivity and anatomical/functional connectivity. For example, Gong et al. (2012) detected presence of axonal fiber bundles between cortical regions for which a structural correlation model had predicted strong connectivity (Gong et al., 2012). Similarly, Alexander-Bloch and colleagues (2013) showed that structural covariance in cortical thickness was related to the synchronized maturational change between distributed cortical regions and that the structural covariance networks were also associated with functional connectivity and network organization (Alexander-Bloch et al., 2013b). Based on the results of these and related studies, structural correlations are believed to at least partially depict actual anatomical/functional connectivity (Bernhardt et al., 2011; Cheverud, 1984; Wright et al., 1999; Zhang and Sejnowski, 2000).

Although the proposed approaches were successfully applied to both individuals with FXS as well as typically developing control participants, it is important to note that the relations observed between individual contribution and behavioral/genetic assessments in the FXS group could be inordinately influenced by the X-linked nature of the syndrome. That is, on the one hand we have males with FXS who have a full “dose” of the disorder (due to single X-chromosome), whereas females with FXS only have half of a “dose” and hence are intermediate between typically developing participants and full mutation males with respect to the brain anatomy and percentage of FMRP. Thus, the observed relations between individual contribution and clinical assessments could have been affected by the relatively larger variance associated with female participants with FXS. However, when we used sex as a covariate, the observed relations between individual contribution and behavioral/genetic measures were largely unaffected in individuals with FXS.

Although novel methods are proposed in this paper, one potential limitation of these methods is that they require a minimum number of participants (n=25–30) in order to extract stable individual differences. Further, no relations were observed between the extracted contribution and widely used graph theory metrics, i.e., characteristic path length and clustering coefficient. The cause for lack of such relations is unclear. However, one plausible explanation could be the young age group of our participants. Future research is required to apply the proposed approaches to adult patient populations. Additionally, our typically developing participant pool had an average IQ of about 119, which is more than one standard deviation above the norm value (100). Thus, this high IQ sample may not be representative of the population at large. Due to sampling with replacement, the correlation values reported in the stability analyses might be marginally inflated. However, this potential inflation would not affect the overall results regarding the robustness of our proposed approaches. Lastly, as Spearman’s rank correlation was used here to non-parametrically estimate statistical dependence between variables, it is important to point out that in ranked correlations the magnitude of difference between two values can not be interpreted. However, this issue does not limit our proposed approaches, as other correlations methods (e.g., Pearson) could instead be used where necessary.

Altogether, we proposed two approaches to estimate individual contribution to anatomical connectivity using group-based SCNs. We anticipate that the methods developed here could be used as a putative biomarker for altered neurodevelopment in clinical populations.