A Conceptual Framework for Improving Critical Care Patient Flow and Bed Use

Abstract

Rationale: High demand for intensive care unit (ICU) services and limited bed availability have prompted hospitals to address capacity planning challenges. Simulation modeling can examine ICU bed assignment policies, accounting for patient acuity, to reduce ICU admission delays.

Objectives: To provide a framework for data-driven modeling of ICU patient flow, identify key measurable outcomes, and present illustrative analysis demonstrating the impact of various bed allocation scenarios on outcomes.

Methods: A description of key inputs for constructing a queuing model was outlined, and an illustrative simulation model was developed to reflect current triage protocol within the medical ICU and step-down unit (SDU) at a single tertiary-care hospital. Patient acuity, arrival rate, and unit length of stay, consisting of a “service time” and “time to transfer,” were estimated from 12 months of retrospective data (n = 2,710 adult patients) for 36 ICU and 15 SDU staffed beds. Patient priority was based on acuity and whether the patient originated in the emergency department. The model simulated the following hypothetical scenarios: (1) varied ICU/SDU sizes, (2) reserved ICU beds as a triage strategy, (3) lower targets for time to transfer out of the ICU, and (4) ICU expansion by up to four beds. Outcomes included ICU admission wait times and unit occupancy.

Measurements and Main Results: With current bed allocation, simulated wait time averaged 1.13 (SD, 1.39) hours. Reallocating all SDU beds as ICU decreased overall wait times by 7.2% to 1.06 (SD, 1.39) hours and increased bed occupancy from 80 to 84%. Reserving the last available bed for acute patients reduced wait times for acute patients from 0.84 (SD, 1.12) to 0.31 (SD, 0.30) hours, but tripled subacute patients’ wait times from 1.39 (SD, 1.81) to 4.27 (SD, 5.44) hours. Setting transfer times to wards for all ICU/SDU patients to 1 hour decreased wait times for incoming ICU patients, comparable to building one to two additional ICU beds.

Conclusions: Hospital queuing and simulation modeling with empiric data inputs can evaluate how changes in ICU bed assignment could impact unit occupancy levels and patient wait times. Trade-offs associated with dedicating resources for acute patients versus expanding capacity for all patients can be examined.

Optimizing intensive care unit (ICU) use is fundamental to quality improvement efforts by critical care physicians. In certain hospitals, particularly large academic centers, demand for ICU beds may outstrip supply, evidenced by a 32% increase in emergency department (ED) length of stay for critically ill patients between 2001 and 2009 (1), despite increases in the number of ICU beds nationwide (2). Reduced ICU bed availability can adversely affect hospital-wide patient throughput, especially within the ED and postsurgical care areas, and increase mortality of critically ill patients due to prolonged wait times for ICU bed assignment (3, 4). Strategies to address capacity strain include unit expansion, revision of triage policies, and targeted efforts to reduce throughput delays (5–7). A step-down unit (SDU), or intermediate care-level unit, can relieve ICU congestion by caring for lower-acuity patients in alternative settings (8–11).

Balancing the opposing goals of minimizing admission wait time for critically ill patients and maximizing bed use should be tailored to individual hospitals’ priorities, patient population, and physical and financial constraints. Projected ICU use suggests that bed reconfiguration could help alleviate bed shortages (12). However, physically reconfiguring beds and observing the resulting impact on outcomes is time consuming, costly, and potentially catastrophic to patients, and therefore unwise to implement without clear evidence of its perceived benefit. Alternatively, a tailored computer simulation model can easily examine how different bed allocation or triage scenarios impact patient-centered outcomes. Simulation modeling and queuing theory are well-established methodologies used to improve hospital capacity planning (12–16). Prior studies have developed models to simulate varying hospital unit sizes, nurse or physician staffing levels, and different triage, discharge, and bed assignment policies to examine the impact on bed use, wait times, lengths of stay, readmissions, and mortality (17–22). Although many models capture patient flow through multidisciplinary ICUs (23), often with elective admissions (24), no studies included both an ICU and SDU with patients with different acuity levels within a single model.

This study’s aim is to present a framework for understanding and improving patient flow through the medical ICU and SDU, and to present illustrative analysis for a single hospital. We describe the model’s key assumptions, data analysis, and proposed outcomes. Our study offers insights for critical care physicians and hospital leaders aiming to better allocate limited ICU bed resources more effectively. Some of the results of the study have been previously reported in the form of abstracts (25, 26).

Methods

Before examining alternative bed allocation or triage strategies, a model of existing patient flow through a hospital unit, such as an ED or ICU, should be created. In general, queuing models must specify the arrival process, duration of service, and number of servers (e.g., beds, available staff); additional model components can be tailored for each specific setting. The main data requirements are patient-level throughput data and census or occupancy data for the specific hospital unit.

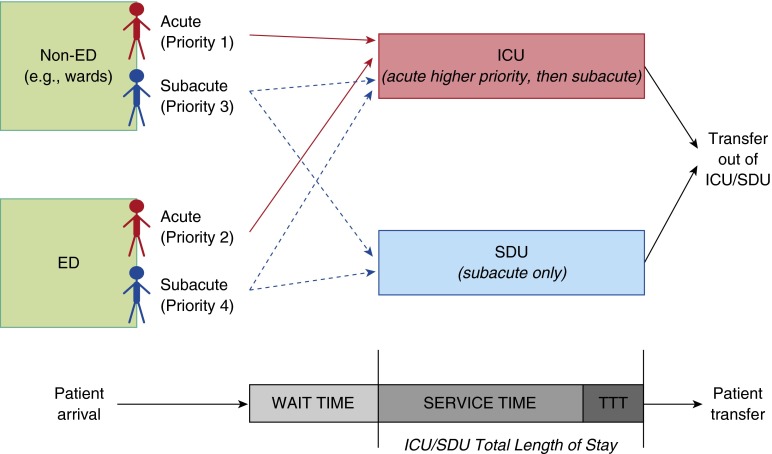
Within our ICU and SDU context, a queuing model includes five essential inputs: (1) number of beds for each unit, (2) patient type and priority level, (3) timing of patient arrival, (4) patient prioritization for admission, and (5) unit length of stay (Figure 1). To illustrate these elements and demonstrate queuing models’ analytic value, we present data and simulation results from a single institution’s medical ICU and SDU. Definitions and assumptions are given in Table 1. Full details on the methods used in model development can be found in the online supplement. Patient-level characteristics and hospital operations data (including locations and timestamps for admission and transfers) were collected for all patients admitted to the ICU and SDU (both of which primarily treat Medicine service patients, aged 18 years and older) over a 12-month period (June 2010 to June 2011). Data were collected via an automated query from Sunrise Clinical Manager and AllScripts (formerly Eclipsys) Sunrise Patient Flow and Bed Management database, with entry data for 20% of visits verified against written logs and chart documentation of Medical ICU/SDU admissions and discharges.

Figure 1.

This overview of the priority queuing model displays the two different bed types (intensive care unit [ICU], accepting all patient classes, and step-down unit [SDU], accepting only subacute classes 3–4) and the flow of patients entering and exiting the units. Patients of differing acuity classes (1–4) originate in either the emergency department [ED] or non-ED locations (e.g., medical wards). These patients are shown from arrival, through their ICU/SDU length of stay—which is composed of service time (interval from entrance to unit until request for transfer out of unit) and time to transfer (TTT; interval from request for transfer out of unit to physical exit from unit)—and then actual patient transfer.

Table 1.

Key definitions and model assumptions for a medical intensive care unit/step-down unit

Term	Definition	Assumptions
Bed types
ICU bed	ICU bed that can treat all acuity classes	Beds are identical and always staffed
SDU bed	SDU bed that can treat lower acuity patients	Beds are identical and always staffed
Patient characteristics
Acute	Those with a critical care–level diagnosis (27) or who require a critical care–level intervention (28)	Patients originating from non-ED locations are higher priority
Subacute	Those admitted directly to SDU or admitted to the ICU who do not either have a critical care–level diagnosis or receive a critical car–-level intervention	Patients originating from non-ED locations are higher priority
Short-stay	Those who stay less than 2 wk (acute patients) or 24 h (subacute patients)	Classification used to estimate service time distribution from past data
Long-stay	Those who stay longer than 2 wk (acute patients) or 24 h (subacute patients)	Classification used to estimate service time distribution from past data
Model inputs
Arrival rate	Number of patients per hour who require an ICU or SDU bed	Estimated from past data on patient throughput; calculated as the reciprocal of the average time between consecutive patient arrivals
Service time	Duration of time spent receiving care in the ICU or SDU	Estimated by fitting probability distributions to past data; can vary by acuity level and short or long stay
Time to transfer	Duration of time between request for transfer out of ICU or SDU and physical transfer to wards	Estimated using multivariate regression; can depend on concurrent patient census levels in the ICU/SDU and medical wards
Model outcomes
Wait time	Duration of time between ICU or SDU bed request and physical transfer out of unit	Shorter wait times are preferred; can be validated against past data
Bed occupancy	Number of bed-hours that are occupied divided by total available bed-hours	Higher occupancy is more profitable but results in lower bed availability

Definition of abbreviations: ICU = intensive care unit; SDU = step-down unit.

The institution’s Human Investigations Committee approved this medical record review study before initiation. All data were gathered retrospectively.

Number of Beds

We first identify the number of beds for the unit(s) under consideration. As many ICUs use SDUs to augment capacity, both units should be represented. Our illustrative analysis was for a tertiary, academic, and community hospital with a 51-bed ward composed of 36 medical ICU beds and 15 medical SDU beds. These two units received admissions and transfers from the hospital’s ED and inpatient Medicine wards, with a small fraction admitted from outside hospitals.

Patient Types

Admitted patients can be described in different ways, based on service (e.g., medicine, surgery), acuity, location of origin, diagnosis group, etc. In our setting, medicine service patients were categorized into one of four priority classes based on the observed triage policies (1 = acute non-ED, 2 = acute ED, 3 = subacute non-ED, and 4 = subacute ED), where 1 is the highest priority and 4 is lowest. This is a retrospective classification, which was not used clinically to triage patients at this institution but rather to model patient flow for this illustrative analysis. Acuity class was determined through detailed chart review (see Table E1 in the online supplement). Patients were assigned “subacute” status if they met the following criteria: (1) direct SDU admission, or (2) ICU admission for less than 24 hours, without a critical care–level diagnosis or receipt of a critical care–level intervention (27, 28). All other patients were designated as “acute” in severity, including those who expired within 24 hours of ICU admission. Although simplistic, this grouping allowed for straightforward comparisons when alternative strategies were later modeled.

Timing of Patient Arrivals

A patient “arrival” refers to the point when a physician requests ICU/SDU admission, before actual “service” (e.g., care within the unit) commences. The overall arrival rate can be estimated from patient-level timestamp data and is calculated as the reciprocal of the average time between consecutive patient arrivals. For each patient, ICU/SDU admission “wait time” is defined as the duration of time a patient spent in the ED or medical wards after a physician’s request for ICU/SDU admission, before physically entering the unit (Figure 1).

For our illustrative model, all patient admissions or transfers into the ICU or SDU were considered separate patient visits; readmissions to the hospital or ICU (i.e., “bounce-backs”) were included in the overall arrival rate. Patients treated in both the ICU and SDU appear as two separate observations in our dataset. ICU patients who “step down” to the SDU are modeled as exiting the ICU and immediately rearriving to the SDU.

ICU Triage Policy

The most complicated model component is the accurate representation of the ICU triage algorithm. Significant variation exists between institutions regarding admission criteria (29). Some hospitals consider acuity, diagnosis, and/or likelihood to benefit, whereas others use a “first-come, first-served” strategy.

The modeled medical ICU used a triage protocol incorporating the Society for Critical Care Medicine Guidelines for Admission, Discharge, and Triage for determining the acceptance and prompt transfer of critically ill patients (27). As part of hospital-wide throughput improvement efforts, minimizing ED length of stay was prioritized (30), prompting admission of intermediate-risk ED patients to the ICU if no SDU beds were available. Medicine ward patients with clinical deterioration requiring SDU or ICU transfer were prioritized over similar ED patients, as respiratory and nursing support were limited on the wards. Reflecting the institution’s current protocol, the simulation model permitted ICU beds to be used by acute or subacute patients, and SDU beds were used by subacute patients only.

Length of Stay

Although many studies measure ICU length of stay as a single value, in many hospitals, length of stay can consist of two discrete periods (31) (see Figure 1). On physical transfer to an ICU/SDU bed, “service time” commences and continues until a request to transfer out of the unit. The service time distribution within our model was fit to past data and differed based on priority class. Due to wide heterogeneity in ICU service times, we further classified patients as “long-stay” or “short-stay” to better fit empirical distributions. Acute patients were (1) short-stay, if service was less than 2 weeks; or (2) long-stay, if longer than 2 weeks, clinically reflecting patients requiring more extensive critical care resources (e.g., prolonged mechanical ventilation, chronic critical illness, etc.). Subacute patients were (1) short-stay, if service time was less than 24 hours; or (2) long-stay, if greater than 24 hours.

Immediately after service time ends, a second period denoted as “time to transfer” (TTT) begins while the patient remains in the ICU or SDU awaiting transfer to a medical ward bed. During this period, care by medical providers continues, although the patient has been deemed clinically ready for a lower level of care. Based on clinical experience, we hypothesized that TTT might be affected by census levels within the ICU/SDU and on the wards. We used multivariate regression analysis to examine this relationship and modeled TTT as the same for ICU-ward transfers and SDU-ward transfers (Table E2). The simulation model generated each patient’s TTT based on concurrent census levels, to capture the impact of ICU/SDU congestion on length of stay by accelerating TTT, as opposed to using fixed values from retrospective data.

Model Implementation

By sampling from the best-fitting empirical distributions, the simulation model randomly generated a set of variables for each hypothetical patient, including their priority class, arrival date and time, service time, and TTT. The model then assigned a particular bed based on availability and priority class. If no bed was immediately available, the patient queued until a bed was vacant. In our model, this process was performed for 2,000 patients, or approximately 6 months of ICU/SDU throughput, with calculation of several aggregate performance metrics.

The model implemented a priority queue, which assigned beds on a first-come, first-served basis, allowing for higher-acuity patients to “bump” those ahead in the queue. Once patients began their unit stay, a nonpreemptive policy was in effect (i.e., later patients could not displace existing patients in service). The bed assignment algorithm is detailed in the online supplement.

The model was validated by comparing model-simulated wait times for admission to those obtained from the retrospective cohort, by priority class, to ensure that the model closely represented patient flow through the ICU/SDU.

Simulated Bed Allocation Scenarios

In addition to simulating patient flow under the existing bed assignment policy, the model can be adjusted to explore different bed allocation strategies, which we illustrate with four broad policy or operational changes. First, we considered alternative partitions of the existing 51 staffed beds into separate ICU and SDU, ranging from 31 ICU + 20 SDU beds, up to 51 ICU + 0 SDU beds. Next, we considered a triage scenario holding constant the total bed number (36 ICU + 15 SDU) but with a cut-off policy that reserved the last unoccupied ICU bed for acute patients only. This was repeated for a scenario of two reserved beds. Third, unit expansion scenarios were simulated, where the 51-bed unit was enlarged by up to 4 additional ICU beds, with the SDU capacity remaining fixed at 15 beds. Finally, we simulated a hypothetical scenario (with 36 ICU + 15 SDU beds) where TTT was no longer census dependent but instead varied from a constant value of 6 hours down to 1 hour, to illustrate how improvements in transfer times could improve patient throughput.

Outcomes

Hospitals may wish to target various performance metrics as the outcome of interest. We identify two potential outcomes of consideration. Wait time for ICU/SDU admission by priority class is clinically relevant, as critically ill patients may deteriorate if care is delayed (32, 33). Second, average ICU/SDU bed occupancy levels—the proportion of time that beds are occupied—directly impacts profitability (34, 35). For each bed allocation scenario, we calculated each outcome across 10,000 simulation iterations.

Results

Patient Characteristics

Between June 2010 and June 2011, 3,165 patients were admitted to the ICU and 873 to the SDU. Among the ICU population, 14.4% were identified as subacute and alternatively could have been cared for in the SDU. Full patient characteristics and admission wait times were obtained for 2,710 patients. Service time, TTT, and corresponding census data were obtained for 1,694 patients (Table 2).

Table 2.

General patient characteristics, grouped by acuity class

Total	Acute (ICU only) (N = 2,099)	Subacute (SDU + ICU Subacute) (N = 611)
ED origin, n (%)	1166 (55.6)	186 (30.4)
Age, mean ± SD, yr	61.36 ± 17.93	61.86 ± 18.13
Men, n (%)	1,078 (51.4)	303 (49.6)
Insurance, n (%)
Medicare	1,176 (56.0)	340 (55.6)
Medicaid	464 (22.1)	143 (23.4)
Private	428 (20.4)	118 (19.3)
Self-pay/other	31 (1.5)	10 (1.6)
Admission wait times, median (IQR), h
	1.05 (0.63–1.78)	1.20 (0.75–2.14)
ED	1.23 (0.85–1.85)	1.23 (0.78–1.85)
Non-ED	0.79 (0.47–1.63)	1.18 (0.71–2.29)
ICU/SDU length of stay, median (IQR), h*
Total	51.73 (29.64–100.11)	24.93 (17.38–47.67)
Service time	39.73 (22.32–84.42)	15.92 (11.22–15.92)
Time to transfer	5.87 (2.98–14.01)	5.69 (3.23–11.62)
Hospital length of stay, median (IQR), d	8.01 (4.42–16.92)	6.20 (3.24–13.71)
In-hospital mortality, n (%)	329 (15.7)	56 (9.2)
Hospital readmission within 30 d, n (%)	471 (22.4)	137 (22.4)

Definition of abbreviations: ED = emergency department; ICU = intensive care unit; IQR = interquartile range; SDU = step-down unit.

^*ICU/SDU length of stay was captured for 1,694 patients (62.5%), 1,479 (87.3%) of whom were classified as acute and 215 (12.7%) as subacute.

The mean time between consecutive patient arrivals across all priority classes was 1.96 hours, resulting in an average arrival rate of 0.51 patients per hour, or approximately 12 patients per day (Figure E1). Approximately 58% of arrivals occurred between 7 a.m. and 7 p.m. Among acute patients, 98% stayed less than 2 weeks, with a mean service time of 52.3 hours (Table 3). A lognormal distribution best fit service time data for these patients. We similarly empirically fit distributions for other patient classes (Figure E2).

Table 3.

Service time distribution based on empiric data

	Acute Patients	Subacute Patients
Short-stay duration	≤2 wk	≤24 h
Proportion, %	98	27
Mean (SD), h	50.9 (53.3)	12.3 (6.5)
Median (IQR), h	33.7 (19.6–63.5)	13.3 (9.3–18.0)
Fit distribution	Lognormal	Uniform
Long-stay duration	>2 wk	>24 h
Proportion, %	2	73
Mean (SD), h	645.4 (387.3)	131.6 (112.7)
Median (IQR), h	499.3 (398.0–760.0)	90.2 (60.0–180.6)
Fit distribution	Exponential	Exponential

Definition of abbreviation: IQR = interquartile range.

Simulation Results: Existing Bed Allocation

Simulating the current structure of 36 ICU + 15 SDU beds resulted in a mean wait time for all patients of 1.13 hours (acute, 0.84 h; subacute, 1.39 h). Service time averaged 79.45 hours, and TTT averaged 3.73 hours. The simulated admission wait times by priority class were broadly similar to median values obtained from the retrospective cohort (Figure 2). Simulated service time and TTT values closely matched historical data (Figure E3).

Figure 2.

Mean wait times generated for each priority class within the simulation are represented as the colored bars. The historical data’s median wait times with associated interquartile ranges are displayed with the circle and error lines. (Median values selected for comparison due to highly skewed nature of the retrospective wait time distributions.) Overall, the model’s simulation output is similar to the median values seen in the empiric data, suggesting adequate calibration. The model generated longer average wait times for subacute emergency department (ED) patients (priority class 4) than seen in the empiric data, which may reflect a preference for bed assignment for patients with longer wait times.

Simulation Results: Alternative Policies

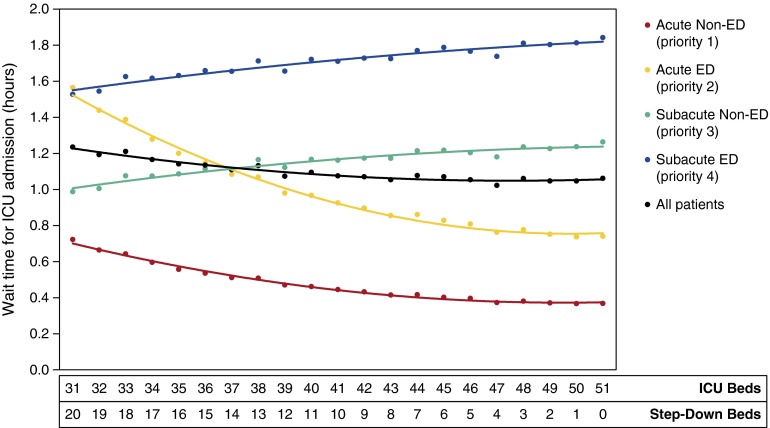
Reallocating SDU beds for ICU use—holding constant the total number of beds at 51—showed modest improvement in overall patient wait time as ICU size increased. With 31 ICU + 20 SDU beds, wait time averaged 1.23 hours; with 51 ICU beds, wait time decreased by 14% to 1.06 hours. However, the effect on individual priority classes differed substantially (Figure 3). Acute patients (priority 1–2) experienced a 52% reduction in wait time over this range in ICU bed allocation, whereas subacute patients (priority 3–4) suffered a 23% increase in wait time as fewer dedicated SDU beds were available. Detailed model results for each scenario are shown in Table 4.

Figure 3.

Average wait times for admission to the intensive care unit (ICU) or step-down unit (SDU) are shown for each scenario of ICU-SDU size (varying from 31 to 51 ICU beds, and 20 down to zero SDU beds). Wait times are grouped by priority class 1–4 and also in aggregate (black line). As the simulation was adjusted to have an increasing number of ICU beds reallocated from the SDU, wait times for all patients decreased on average but increased for subacute patients (priority class 3 and 4). ED = emergency department.

Table 4.

Results of simulated bed allocation scenarios

Bed Scenario	Wait Time (h)			Bed Occupancy (%)
	Overall	Acute	Subacute	Overall	ICU	SDU
Unit composition
51 ICU + 0 SDU	1.06 (1.04–1.09)	0.56 (0.54–0.58)	1.55 (1.52–1.59)	84.3 (84.3–84.4)	84.3 (84.3–84.4)	—
46 ICU + 5 SDU	1.05 (1.03–1.08)	0.60 (0.58–0.62)	1.48 (1.45–1.52)	84.3 (83.3–84.4)	83.1 (83.0–83.1)	95.7 (95.7–95.8)
41 ICU + 10 SDU	1.07 (1.05–1.10)	0.68 (0.67–0.70)	1.44 (1.40–1.47)	84.3 (84.2–84.3)	81.7 (81.7–81.8)	94.7 (94.7–94.7)
36 ICU + 15 SDU*	1.13 (1.11–1.16)	0.84 (0.82–0.86)	1.39 (1.35–1.42)	84.2 (84.1–84.2)	80.4 (80.4–80.5)	93.2 (93.2–93.2)
31 ICU + 20 SDU	1.23 (1.20–1.26)	1.14 (1.12–1.17)	1.26 (1.22–1.29)	84.0 (83.9–84.0)	79.6 (79.5–79.7)	90.7 (90.7–90.8)
Reserved acute beds
1 Reserved bed	2.23 (2.17–2.28)	0.31 (0.31–0.32)	4.27 (4.16–4.38)	84.7 (84.7–84.8)	80.8 (80.8–80.9)	94.0 (94.0–94.1)
2 Reserved beds	3.00 (2.93–3.07)	0.22 (0.21–0.22)	5.99 (5.85–6.12)	84.8 (84.7–84.8)	80.8 (80.7–80.8)	94.4 (94.4–94.4)
ICU bed expansion
37 ICU + 15 SDU	0.76 (0.74–0.78)	0.58 (0.56–0.59)	0.92 (0.89–0.94)	83.0 (82.9–83.0)	78.9 (78.8–79.0)	93.0 (93.0–93.0)
38 ICU + 15 SDU	0.50 (0.48–0.51)	0.39 (0.37–0.40)	0.59 (0.57–0.61)	82.0 (81.9–82.0)	77.7 (77.6–77.7)	92.9 (92.9–92.9)
39 ICU + 15 SDU	0.33 (0.32–0.34)	0.26 (0.25–0.27)	0.38 (0.37–0.40)	81.1 (81.1–81.2)	76.6 (76.6–76.7)	92.8 (92.8–92.8)
40 ICU + 15 SDU	0.21 (0.20–0.22)	0.17 (0.16–0.18)	0.24 (0.23–0.25)	80.5 (80.4–80.5)	75.9 (75.8–76.0)	92.7 (92.7–92.7)
Target TTT
1 h	0.69 (0.67–0.70)	0.51 (0.50–0.53)	0.83 (0.81–0.85)	73.5 (73.3–73.6)	65.5 (65.3–65.7)	92.7 (92.6–92.7)
2 h	0.85 (0.83–0.87)	0.64 (0.62–0.66)	1.03 (1.00–1.06)	74.7 (74.5–74.8)	67.1 (66.9–67.3)	92.9 (92.8–92.9)
3 h	1.06 (1.04–1.09)	0.79 (0.77–0.81)	1.30 (1.26–1.33)	75.5 (75.4–75.7)	68.2 (68.0–68.4)	93.1 (93.1–93.1)
4 h	1.28 (1.25–1.30)	0.94 (0.92–0.97)	1.56 (1.52–1.60)	76.6 (76.4–76.7)	69.6 (69.4–69.8)	93.3 (93.2–93.3)
5 h	1.57 (1.54–1.60)	1.16 (1.13–1.18)	1.93 (1.88–1.97)	77.6 (77.4–77.7)	70.9 (70.7–71.1)	93.5 (93.5–93.5)
6 h	1.96 (1.91–2.00)	1.44 (1.40–1.48)	2.40 (2.35–2.46)	78.6 (78.4–78.8)	72.3 (72.1–72.5)	93.7 (93.7–93.7)

Definition of abbreviations: ICU = intensive care unit; SDU = step-down unit; TTT = time to transfer.

Data presented as mean (95% confidence interval). Mean values are reported based on a simulation with 10,000 iterations; 95% confidence intervals are calculated assuming a “sample size” of 10,000. Wait time is time from ICU bed request to physical transfer. Bed occupancy is proportion of available bed-hours that are occupied by patients.

^*Existing number of ICU and SDU beds at this institution.

As more SDU beds were reallocated as ICU beds, average occupancy rates in both units increased. For example, ICU bed use increased from 80% (31 ICU + 20 SDU beds) to 84% (51 ICU beds), suggesting that ICU patients spent more time in a bed and less time waiting for admission.

Reserving the last available ICU bed for acute patients (assuming 36 ICU + 15 SDU beds) reduced wait times for these patients to 0.20 hours (priority 1) and 0.42 hours (priority 2), a 63% improvement. In contrast, wait times for subacute patients worsened to 4.27 hours (priority 3 and 4). With two reserved beds, wait times improved by a further 11% to 0.14 hours (priority 1) and 0.29 hours (priority 2), whereas wait times for subacute patients worsened by 40% (5.98 h for priorities 3 and 4).

The third simulation scenario considered a reduction in TTT for all patients and demonstrated linear improvements in bed occupancy rates and wait times. Reducing TTT from current levels to a target time of 1 hour for every patient led to a 46% improvement in wait times for bed assignment. This increased process throughput also freed up beds more quickly, reflected by the decrease in mean ICU bed occupancy from 80 to 66% with a 1-hour TTT target.

Finally, ICU bed expansion scenarios from one up to four extra beds substantially improved average wait times from 1.13 hours (status quo) to 0.76 hours (one additional bed) or 0.21 hours (four additional beds) for all patients. With this expansion, ICU bed occupancy modestly decreased from 79 to 76%, but SDU bed occupancy minimally changed (0.3% improvement).

Discussion

By presenting a conceptual framework and illustrative analysis for simulating patient flow through the ICU and SDU, this study demonstrated how queuing theory with data-driven inputs offers insights into improving ICU bed availability and admission wait time. Our empirically derived queuing model simulated ICU and SDU patient admissions and transfers, reliably replicated empiric wait times, and examined the effect of distinct bed allocation strategies and flexible triage policies on wait time and occupancy, tailored for a specific hospital.

The usefulness of queuing theory, a well-described analytical tool in operations management, has been documented in healthcare settings with practical applications for physicians and hospital leadership to better understand patient throughput and improve bed availability (36–38). Our model was informed by the current admission process at one institution but could be readily adapted to other locations with adjustments of empiric inputs and bed assignment algorithm. Similar to past ICU models maximizing potential health benefits or reserving unit beds for elective surgeries (14, 39, 40), we examined bed allocation strategies and flexible triage policies that can alleviate shortages during periods of high ICU demand. This model adds to the literature by incorporating both ICU and SDU bed types, using a priority bed assignment algorithm that paralleled actual clinical decision making and providing an excellent testing ground for system and practice changes.

The simulation results demonstrate some fundamental insights from queuing theory—which could apply across institutions—as well as some specific conclusions for our institution. Pooling beds, or eliminating different bed types, is a well-established queuing paradigm to reduce waiting, although of course effect size depends on the specific parameters of the hospital setting. In our setting, pooling the ICU and SDU into one unit may be preferred, when expansion of both units is not feasible due to physical or economic constraints. Reallocating SDU beds into one ICU unit (all 51 beds) improves bed use while reducing wait times, because it maximizes flexibility in permitting all beds to serve all patient types. In the original allocation (36 ICU + 15 SDU), it is possible for an acute patient to wait for ICU admission during high census, while an SDU bed is simultaneously unoccupied. When we eliminate SDU beds, pooling facilitates faster admission of acute patients.

There are potential shortcomings to pooling ICU/SDU beds, however. For instance, with a single pooled unit, staffing levels would likely change as the nursing-to-patient ratio is higher in an ICU than in an SDU, potentially increasing hospital costs. On the other hand, under the current system, subacute patients in the ICU use more nursing and specialist resources than clinically necessary, which is also costly (41–43). Before implementing such bed reconfigurations, a hospital could conduct a careful cost–benefit analysis to better measure these trade-offs. Flexible staffing models that better match patient type with needed resources (e.g., nursing and respiratory support) may generate further cost savings (44).

Our analyses highlighted another opportunity for improvement: reduction of TTT, an ineffective use of resources where patients occupy ICU beds while waiting for transfer to medical wards (31). We observed substantial improvements in admission wait times and overall bed availability with faster transfer times out of the ICU and SDU, regardless of unit sizing. For example, reducing TTT from current levels to 1 hour—which would involve centralized quality improvement effects affecting all patient flow from ED presentation to hospital discharge (30, 45)—generated improved wait times equivalent to building one to two additional ICU beds, a costly solution that would only temporarily relieve congestion without added patient benefit (46, 47). Moreover, reduced TTT was the only simulated scenario that achieved ICU bed occupancy levels below 70%, which is an increasingly important metric as the demand for ICU beds continues to grow. Nevertheless, reducing TTT would likely require operational changes, including additional transfer staff, greater coordination between the ICU and wards, and improved timeliness of hospital discharges, without increasing the risk of delays for ED patients awaiting admission to wards or early discharges for non-ICU patients (17, 18, 30).

Given the established link between delays in ICU admission and increased risk of mortality (3, 4), admission wait time is a clinically supported performance metric for our model (48). Although many hospitals focus on decreasing wait times for admission from the ED, critical care physicians and hospital administrators can evaluate additional performance metrics, such as ICU/SDU occupancy rates, before concluding that ICU expansion is needed (49, 50).

Strengths of our modeling approach are its use of empirical data over a 12-month period for two types of units (ICU and SDU) and an adaptive bed assignment algorithm that considers priority bed assignment to accommodate more critically ill patients earlier. The model also accounts for the “speed up” of TTT occurring during periods of higher ICU census, reflecting real-world observations of expedited patient transfer times when available ICU beds are limited.

Limitations of our model include the absence of a more granular severity of illness estimation in retrospective data. Although the acute/subacute and long/short-stay categorizations were based on chart documentation and published guidelines, there may be additional factors affecting acuity classification and admission priority. Although we aggregated subacute patients, these lower-risk patients admitted to the ICU may reflect a different clinical class than those admitted to the SDU (10, 51). We also had limited sample sizes for some patient subgroups, causing our distribution fitting for short-stay subacute patients to appear less precise than for other subgroups. Due to limited data on patient timestamps resulting from completely missing weeks of hospital operations reports, as well as only 9 months of ICU and medicine ward census data, our original sample size reflecting all admissions to the ICU/SDU over 1 year is reduced. However, we do not observe any systematic bias in the missing data. Historical census data were available for only four time points per day, which prevents us from examining how time-series trends in floor crowdedness affect ICU TTT. Future models could incorporate alternative staffing models, more granular measures of patient severity, and other triage policies similar to the bed reservation strategy in times of surge.

Using real-world patient-level data for a major academic U.S. hospital, we provided an illustrative framework to use queuing theory and simulation modeling to understand and improve ICU and SDU patient flow. We examined hypothetical unit resizing scenarios and measured the impact on admission wait times and bed occupancy rates. Before implementing large-scale bed reallocation plans or triage policies, such as switching SDU beds to ICU permanently or temporarily in times of ICU surge, such policies can be examined within simulation models such as ours, with adjustments made for local institutional policies and characteristics, to measure the resulting benefits and tradeoffs to patients and the health system as a whole. Small changes in bed assignment policies can have a significant effect on operational metrics, with potentially profound effects on patient health outcomes.