Spatial autocorrelation and congruence in the distribution of language and mammal richness: a reply to Cardillo et al. (2015)

Our paper on the relationship between the spatial distribution of language richness and mammal species richness recently argued that little congruence exists between the distribution of threatened languages and threatened mammals in New Guinea, despite high overlap between areas of high language richness and high mammal species richness across this island [1]. In reply to this, Cardillo et al. re-analysed the data at one of the spatial resolutions that we considered in our paper, claiming that the original analyses were statistically flawed [2]. In short, Cardillo et al. argue that the inclusion in our analyses of coastal pixels containing both land and sea, as well as a lack of consideration of spatial autocorrelation, has led us to wrongly derive conclusions about patterns of distribution in language and species richness.

We believe such conclusions are misleading for various reasons. First, the inclusion of coastal pixels in our analyses has no impact on the results reported. Re-running the analyses at the 50 km resolution without the inclusion of these mixed pixels, we show that the direction and significance of the Pearson correlation coefficients between language richness and mammal richness (r = 0.23, p = 0.004) and between threatened language richness and threatened mammal richness (r = −0.15, p = 0.03) both still hold. Although the correlation between threatened language richness and threatened mammal richness becomes non-significant when only coastal pixels are considered (r = −0.03, p = 0.75), we also show that both the direction and significance of the relationship between overall language richness and mammal richness still hold for analysis of coastal cells alone (r = 0.41, p < 0.001). Furthermore, a high number of languages, primarily in the recent Austronesian language radiation, show a narrow distribution along the northern coast of New Guinea [3] and are thus largely restricted to coastal pixels; excluding such an important component of New Guinea linguistic diversity from analysis may therefore be expected to bias conclusions about island-wide patterns and correlates of regional language richness.

Second, there is a fundamental difference between correlation and regression [4], which the authors fail to acknowledge. The use of regression implies a search for assumed causality, while the use of correlation simply looks for similarity (or dissimilarity) in patterns between associated variables. In this study, we did not expect a decrease in one index of richness to be the cause of a decrease (or increase) in the other, which is why we reported Pearson correlation coefficients and did not use linear models. Given that no causality was sought between mammal species richness and language richness, Pearson correlations were thus the most adequate option to explore the level of congruence in the spatial distribution of these indices.

Third, the assumptions made by Cardillo et al. that underpin the use of their simultaneous autoregressive error (SAR) approach to establish relationships between language richness and mammal species richness are actually invalid. Assuming that the authors log-transformed the variables while adding 1 (as a high number of pixels do not contain any threatened languages), simple Shapiro–Wilks normality tests show that their log-transformed response variables (namely, log(language richness) and log(threatened language richness)) are zero-inflated, displaying consistent and significant deviation from a normal distribution (all p < 0.001 at the 50 km resolution). Failure to secure a normal distribution for the variable to be predicted under the assumption of normally distributed errors is not the only issue; transformation of count data to continuous data further violates the assumptions of response variable distribution, with such transformed data known to perform poorly (especially if mean counts are low and dispersion high) [5].

Fourth, Cardillo et al. do not state how they accounted for spatial autocorrelation in their SAR modelling approach. This process is indeed very subjective; nearest neighbourhoods and spatial weights matrices can be defined in a number of ways [6,7], and there is no current standard ‘rule’ as to which approach is best. However, the choice of nearest-neighbour structure and spatial weights matrices can have a huge influence over the subsequent outcomes of SAR models [8]. We attempted to reproduce the findings reported by Cardillo et al. using inverse distance nearest neighbours estimation via variogram inspection with row-standardized spatial weights, combined with their subsequent SAR models. This approach produced the closest match to the reported Moran's I values and models in their table 1. There remained, however, differences between our values and the values Cardillo et al. reported, for example with our analyses producing much higher Moran's I values than the values reported for their analyses. In short, it has not been possible for us to reproduce their results, and our best attempt leaves us with significant spatial autocorrelation in the SAR model residuals based on Moran's I, with spatial autocorrelation present at similar low levels to those the authors claim must be accounted for in justification of the SAR modelling process they employ [2].

Table 1.

(a) Best (within a ΔAIC of 4) candidate models exploring language richness as a function of mean elevation, distance to the coast, latitude and mammal species richness at the 50 km spatial resolution, using a general linear model approach combined with a negative binomial distribution. (b) Best (within a ΔAIC of 4) candidate models exploring threatened language richness as a function of mean elevation, distance to the coast, latitude and threatened mammal species richness at the 50 km spatial resolution, using a general linear model approach combined with a negative binomial distribution.

model	AIC
(a)
language richness ∼ mammal richness × distance + elevation + latitude	1846.98
language richness ∼ mammal richness × distance + latitude	1848.05
(b)
threatened language richness ∼ distance × latitude + elevation	1055.84
threatened language richness ∼ elevation × latitude + distance	1056.98
threatened language richness ∼ elevation + distance + latitude	1057.46
threatened language richness ∼ distance × latitude + threatened mammal richness + elevation	1057.61
threatened language richness ∼ elevation × distance + latitude	1058.76
threatened language richness ∼ elevation × latitude + threatened mammal richness + distance	1058.95
threatened language richness ∼ threatened mammal richness + elevation + distance + latitude	1059.28
threatened language richness ∼ threatened mammal richness × latitude + elevation + distance	1059.62

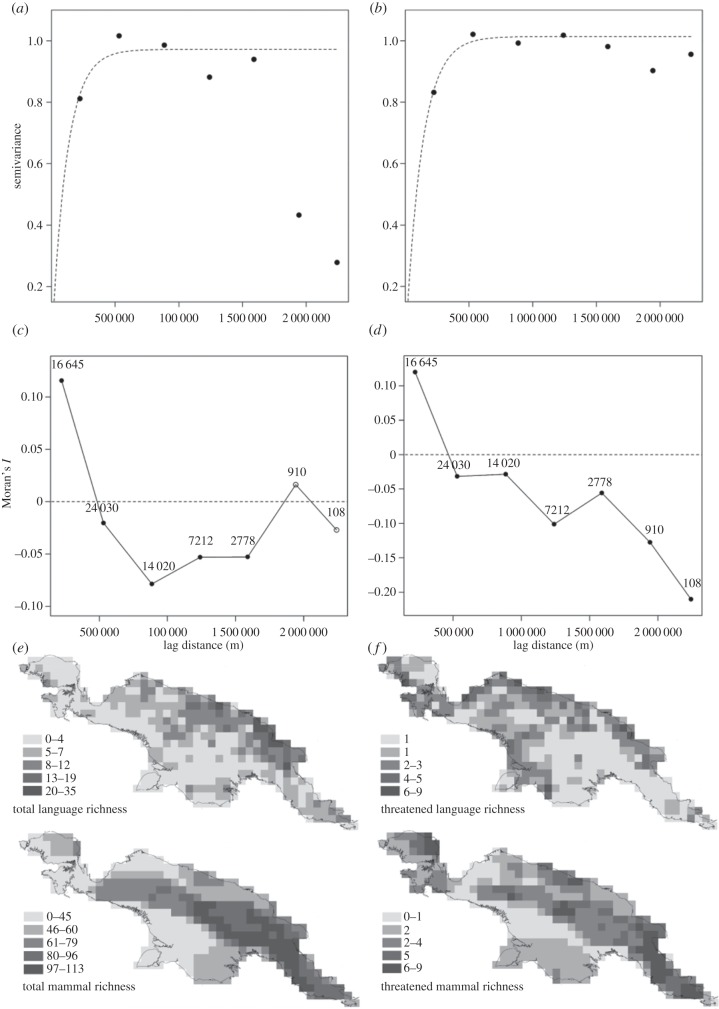
To check the validity of our original results, and to assess the potential for spatial autocorrelation to impact the level of significance in the relationships both between total language richness and mammal richness and between threatened language richness and threatened mammal richness, we decided to run new analyses. Because the response variables considered by Cardillo et al. cannot be considered to follow a Gaussian distribution, even post-transformation, we conducted general linear models with negative binomial error distributions and examined the relationships between total language richness and mammal richness and between threatened language richness and threatened mammal richness; we then calculated Moran's I on the residuals of these models. Using this approach, we show that total mammal richness positively and significantly influences language richness (estimate = 0.009 ± 0.001, p < 0.001), while threatened mammal richness negatively and significantly influences threatened language richness (estimate = −0.07 ± 0.003, p = 0.03). Examination of the spatial structure in the residuals of these models revealed the presence of positive spatial autocorrelation at very short distances (figure 1). We assessed the level of significance of the spatial autocorrelation in the residuals for these models via permutation tests [9]. These tests relied on calculating the smallest distance at which all grid cells were linked, and then building a row-standardized spatial weight matrix. While significant, the level of spatial autocorrelation in the model residuals was small: Moran's I = 0.07, p = 0.001 in both cases.

Figure 1.

Semivariograms and correlograms of spatial dependence in the residuals of general linear models (GLMs) between total language and mammal species richness (a,c,e) and threatened language and threatened mammal species richness (b,d,f) across New Guinea within seven equally spaced distance classes (the minimum number at which all classes contained more than 100 observations between pairs of residuals). Maps of total language and mammal species richness (e) and threatened language and mammal species richness (f) across New Guinea at the 50 km² grid considered in our analyses are also provided (increasing richness from paler to darker squares in richness bins selected according to natural breaks in the distribution of respective richness indices; see legends in (e) and (f)). The semivariograms (a) and (b) describe the similarity between pairs of model residuals according to Euclidean distance between them in space within the seven distance classes. Exponential variogram models (dashed line) have been approximated to model the spatial dependence of GLM model residuals for both relationships; the point of asymptote (or sill) depicts the distance at which spatial autocorrelation no longer exists in these residuals. The correlograms (c) and (d) describe the level and direction of spatial autocorrelation present in the GLM model residuals at each distance class (numbers of observations within each distance class is provided in the figure). Positive values of Moran's I denote positive spatial autocorrelation between model residuals, while negative values denote negative spatial autocorrelation. Filled circles indicate significant levels of spatial autocorrelation for given distance classes (Moran's I; R = 1000 permutation tests), while empty circles indicate non-significant levels of spatial autocorrelation.

We then modelled language richness as a function of elevation, distance to the coast, latitude and mammal species richness at the 50 km spatial resolution, again using a general linear model approach with a negative binomial error distribution. Using an Akaike information criterion (AIC) approach, results showed that total mammal richness was present as a significant predictor within all of the top candidate models (table 1a). Modelling threatened language richness instead of total language richness led to a different outcome; in this case, threatened mammal richness was present as a variable within four of the eight top models, and within only one model with ΔAIC < 2 (table 1b). In order to explore the influence of geographical factors on the spatial distribution of threatened language and mammal richness across New Guinea, we then used a general linear model approach combined with a negative binomial error distribution (or Poisson distribution, in the case of threatened mammal richness) to explore the respective influence of elevation, distance to the coast and latitude on these two response variables. In both cases, the best models (based on AIC weights) included all three predictor variables; whereas elevation and latitude had opposite effects on threatened language richness and threatened mammal richness (negative and positive, and positive and negative, respectively), distance to the coast negatively affected both threatened language richness and threatened mammal richness (table 2). Altogether, these results therefore confirm our previous conclusions, as there is positive congruence between total language richness and mammal richness, but spatial patterns of threatened language richness and threatened mammal richness appear to be driven by different processes.

Table 2.

The best-fitting general linear models (ΔAIC < 2) for threatened language richness and threatened mammal species richness (using negative binomial and Poisson error distributions respectively) according to the following geographical predictor variables: elevation, distance to the coast and latitude. (Coefficient estimates, standard errors (s.e.), and z- and p-values are provided. Variance inflation factors for all variables were less than or equal to 1.35.)

response variable	coefficient	estimate	s.e.	z-value	p-value
threatened language richness	intercept	1.52	0.14	10.76	<0.001
	elevation	−2.83 × 10−4	1.13 × 10−4	−2.49	0.01
	distance	−4.12 × 10−6	1.14 × 10−6	−3.62	<0.001
	latitude	0.18	0.02	7.52	<0.001
threatened mammal richness	intercept	0.76	0.11	6.81	<0.001
	elevation	1.85 × 10−4	1.31 × 10−5	1.41	0.16
	distance	−1.52 × 10−6	5.56 × 10−7	−2.74	0.01
	latitude	−0.01	0.02	−0.46	0.65
	elevation × latitude	−6.22 × 10−5	2.25 × 10−5	−2.76	0.01

Interestingly, consideration of spatial autocorrelation actually does not challenge our results. The Dutilleul's modified t-test considered by Cardillo et al. has been shown to remain prone to inflated type 1 error rates [10,11]. This test is moreover dramatically susceptible to the number of distance classes considered in the estimation of spatial autocorrelation and effective sample sizes, with a greater number of classes estimating greater spatial autocorrelation as well as a reduced effective sample size and degrees of freedom [12]. Running Dutilleul's modified t-tests on our dataset to reproduce Cardillo et al.'s findings reveals that the number of distance classes considered must have been based on Sturge's rule for bin width selection [13] (n = 17). However, given: (i) the low overall positive level of Moran's I found in the residuals of the relationships between language and mammal richness and between threatened language and threatened mammal richness (0.07), (ii) the significant negative autocorrelation in these residuals at greater distance classes (figure 1c,d), and (iii) the very small number of observations found within the greatest of 17 distance classes, we believe that consideration of such a large number of distance classes has probably resulted in overcorrection of the effective sample size. We thus ran further Dutilleul's modified t-tests for our data based on a reduced number of distance classes, defined: (i) as the minimum number at which all distance classes contained >100 observations (figure 1c,d; n = 7), and (ii) according to the distance threshold at which variation according to distance reached asymptote in visualized variograms of the residuals of the relationship between language richness and mammal richness and between threatened language richness and threatened mammal richness (600 km; figure 1a,b; n = 4). Results reveal the heavy dependence of this method on the allocation of distance classes, and assist in demonstrating the validity of the conclusions drawn in our original analyses. Modified t-tests for the correlation between total mammal richness and total language richness showed that while using seven equally spaced distance classes the correlation was non-significant (r = 0.28, p = 0.11), under selection via asymptote in visualized variograms the correlation was significant (r = 0.28, p = 0.04; n = 4 distance classes). However, under both distance class selection methods, the correlation between threatened mammal richness and threatened language richness remained non-significant (r = −0.11, p = 0.27 and 0.16, respectively).

In conclusion, the main message of our original study was that, although spatial congruence in language and mammal species richness exists across New Guinea, this pattern does not hold when looking at richness of threatened languages and species. This indicates that landscape-scale threats and associated conservation management requirements differ between these two components of biocultural diversity. The analyses presented by Cardillo et al. do not challenge our results, and the implications for regional maintenance of biocultural diversity are the same whether one considers our original analyses, the new analyses we present here, or even Cardillo et al.'s analyses. Whether there is either a significant negative correlation or no significant correlation between the spatial distribution of threatened languages and threatened mammal species, our original conclusions remain valid.