The spatial profiles and metabolic capabilities of microbial populations impact the growth of antibiotic-resistant mutants

Abstract

Antibiotic resistance adversely affects clinical and public health on a global scale. Using the opportunistic human pathogen Pseudomonas aeruginosa, we show that increasing the number density of bacteria, on agar containing aminoglycoside antibiotics, can non-monotonically impact the survival of antibiotic-resistant mutants. Notably, at high cell densities, mutant survival is inhibited. A wide range of bacterial species can inhibit antibiotic-resistant mutants. Inhibition results from the metabolic breakdown of amino acids, which results in alkaline by-products. The consequent increase in pH acts in conjunction with aminoglycosides to mediate inhibition. Our work raises the possibility that the manipulation of microbial population structure and nutrient environment in conjunction with existing antibiotics could provide therapeutic approaches to combat antibiotic resistance.

1. Introduction

Understanding how populations of antibiotic-susceptible bacteria give rise to resistant strains is essential to designing treatments that prevent or delay the development of antibiotic resistance [1]. Recent work has shown that heterogeneity in the spatial distribution of antibiotic in the environment can accelerate the evolution of genetically based antibiotic resistance [2–5]. However, the role of ecological changes resulting from the spatially structured microbial population itself remains to be explored. The spatial structure of a microbial population includes the density of cells, the combination of species and strains making up the population, and the spatial organization of cell types.

Most microbial communities consist of interacting, heterogeneous, multispecies populations [6,7]. The per-species spatial structure of microbial populations is a primary determinant of inter- and intraspecies interactions. The number density of cells is the simplest parameter characterizing spatial structure. Bacterial biofilms are high-density aggregates of bacteria that are embedded in an extracellular matrix and are often associated with phenotypic antibiotic resistance [8–12]. However, the impact of a microbial population's spatial distribution on the development of genotypic antibiotic resistance is unknown. Unlike biofilm-based phenotypic antibiotic resistance, genetically based antibiotic resistance can play a role in planktonic cells as well as in biofilms and has the potential to be inherited and spread to descendent populations.

Here, we show that, for spatially structured populations of bacteria with planktonic-like phenotype, increasing cell density can impair the survival of antibiotic-resistant mutants in the presence of aminoglycoside antibiotics. We term this negative impact ‘inhibition’. The antibiotic-resistant mutants in this study are strains of Pseudomonas aeruginosa, a common nosocomial pathogen that affects burned, wounded and ventilator-assisted patients, and also one of the leading proximate causes of death in patients with the genetic disorder cystic fibrosis (CF). We observe inhibition with two different aminoglycoside antibiotics: tobramycin, a frontline drug for treatment of P. aeruginosa infections, and gentamicin, used in the treatment of a wide range of Gram-negative bacterial infections [13,14]. Furthermore, we find that a wide range of microbial species can produce inhibition. Our results indicate that this is because the molecular agent of inhibition is a by-product of native bacterial metabolism of amino acids and that the mechanism of inhibition involves an alkaline change in the pH of the environment.

We use a diffusion-based analytical model to estimate the molecular weight (MW) of the agent of inhibition, which we find to be consistent with known alkaline by-products of metabolism. We also develop a model of inhibition in a well-mixed system, which considers microscopic, stochastic variation in cell density. This model quantitatively describes our observations and offers an explanation of the apparently contradictory observation that high-density mutant colonies are capable of growth in the presence of antibiotics.

Our work indicates that microbial population structure might be a target for, or a tool in, novel therapeutic approaches to combat antibiotic resistance, and that the lifetime of current antibiotics might be extended with the use of natural products as synergistic agents.

2. Material and methods

2.1. Bacterial strains and growth conditions

Pseudomonas aeruginosa PA14 was used as the wild-type (WT) strain (gift from Marvin Whiteley, UT Austin). WT overnight cultures, grown in antibiotic-free media, were plated on tobramycin 8 μg ml⁻¹ agar. Spontaneous antibiotic-resistant mutants grew colonies and were archived in 20–30% glycerol at −80°C. Upon subsequent plating, samples that showed mixed colony types were re-isolated.

To generate mutants in the presence of antibiotic, WT were passaged in twofold increasing tobramycin concentrations, starting at 0.3 μg ml⁻¹, for eight successive days. Samples were archived at −80°C daily.

Transposon-insertion mutants (electronic supplementary material, table S2) were obtained from the PA14 non-redundant transposon library [15]. P. aeruginosa strain PAO1, 17 clinical Pseudomonas isolates [16], Pseudomonas sandgrass isolate, P. fluorescens, methicillin-resistant Staphylococcus aureus Mu50 [17], Escherichia coli DH5α, Burkholderia cepacia and Δphz1/2 mutant [18] (gifts from Whiteley, UT Austin), Serratia marcescens (gift from Rasika Harshey, UT Austin) and Saccharomyces cerevisiae S288C (gift from Edward Marcotte, UT Austin).

All bacterial strains were grown in Luria–Bertani (LB) broth or on LB agar except where otherwise indicated [19]. Saccharomyces cerevisiae was grown in yeast–peptone–dextrose (YPD) broth or agar except where otherwise indicated [20]. Overnight cultures were shaken at 180 r.p.m. for 16–18 h at 37°C, except P. fluorescens and B. cepacia were grown at 30°C. When indicated, agar incorporated tobramycin (Indofine Chemical Company, NJ) or gentamicin (Fisher Scientific, NJ). Except when indicated otherwise, the concentrations used were 8 μg ml⁻¹.

2.2. Minimum inhibitory concentration

Minimum inhibitory concentration (MIC) was measured using broth microdilution [21].

2.3. Whole-genome sequencing

Except when stated otherwise, one spontaneous mutant strain was used for all experiments. This mutant strain was characterized using whole-genome sequencing (electronic supplementary material, text S1). Sequences were deposited in the National Center for Biotechnology Information Short-Read Archive http://www.ncbi.nlm.nih.gov/sra (accession no. SRP042054). Three single-nucleotide polymorphisms unique to the antibiotic-resistant mutant strain were identified (electronic supplementary material, table S3).

2.4. Experiments in spatially mixed systems

Cells (10⁶–10¹¹) in 3 ml of 0.6% LB agar were overlaid on tobramycin-containing agar (4 μg ml⁻¹). The number of cells was found from the optical density (OD₆₀₀) of the overnight cultures (Nanodrop 2000c, Thermo Scientific), using the conversion factor OD 1 is 0.8 × 10⁹ cells ml⁻¹. Plates were incubated at 37°C for 48 h and colonies were counted (ImageJ v. 1.47 [22]).

2.5. Disc diffusion assay for spatially structured systems

To form uniform lawns of antibiotic-resistant mutants on the surface of antibiotic agar, we used an overlay agar technique, approximately 10⁸ mutants, unless otherwise stated, were added to 3 ml of 0.6% (soft) LB agar and overlaid on antibiotic-containing LB agar.

For deposition onto discs, overnight cultures (32 ml) were centrifuged to form a pellet (4000 r.p.m., 20 min), washed three times by removing the supernatant and adding sterile media, and resuspended in 100 µl of fresh, sterile LB broth. From this, 10 µl (approx. 10⁹–10¹⁰ bacteria, approx. 10¹¹–10¹² yeast, unless otherwise stated) was deposited on sterile 7 mm diameter filter discs (Whatman) on the agar. We used the conversion factor OD 1 is 0.8 × 10⁹ cells ml⁻¹ for bacteria and 3 × 10⁷ cells ml⁻¹ for yeast. Plates were incubated at 37°C for 24–48 h, after which the width of inhibition (X) was measured.

2.6. Creating structured agar plates

To create agar with spatially structured composition, agar was poured and allowed to cool as usual. Then, cores of different diameters (7, 10 and 15 mm) were created with a sterile metal punch. Wells were filled with agar containing a different set of nutrients or antibiotic, and allowed to set. As soon as the cores set (within 10 min), filter discs were placed on the core and WT cells were deposited.

2.7. Using pH change to probe the nature of the released inhibitory factor

Bromthymol blue (BTB) was added to agar at a final concentration of 0.002%. Thirty-two millilitres of overnight microbial cultures was deposited as above. Plates were incubated at 37°C and observed every hour for an alkaline or acidic change around the filter discs. Images were taken immediately after deposition (for nutrient-free BTB agar) or 2 h after deposition (for LB–tobramycin BTB agar) or after overnight incubation (for antibiotic-resistant mutant lawns).

2.8. Testing the effect of different nutrient conditions of overnight growth media on inhibition

In LB and YPD, WT PA14, S. aureus and E. coli grew to a density of approximately 10⁹ cells ml⁻¹. In YPD, S. cerevisiae grew to a density of approximately 10⁸ cells ml⁻¹. S. cerevisiae grew poorly in LB medium, to a density of approximately 10⁷ cells ml⁻¹. The pH of the cell cultures and of the filter-sterilized supernatant was measured using pH indicator strips (Cardinal Health, IL).

Overnight cultures were centrifuged (4000 r.p.m., 20 min), washed three times, and resuspended in fresh, sterile LB or YPD broth (100 µl). Approximately 10⁹ cells were deposited on filter discs. Filter-sterilized supernatant from each culture condition and sterile, fresh LB and YPD broth were also deposited onto filter discs. Plates were incubated and pH change monitored as above.

2.9. Deposition of exogenous alkali compounds

Ten microlitres of ammonium hydroxide (NH₄OH; 14.8, 7.4, 4.9, 3.7, 2.9, 2.4 M), sodium hydroxide (NaOH; 1, 0.5, 0.33, 0.25, 0.2 M), sodium bicarbonate (NaHCO₃; 1, 0.5, 0.33, 0.25, 0.2 M) and 1 M ammonium chloride (NH₄Cl) were deposited on agar plates. Plates were incubated and pH change monitored as above. Ten microlitres of exogenous alkali compounds (2.1 M NH₄OH, 0.5 M NaOH and 0.5 M NaHCO₃) were also deposited on decreasing dilutions (10⁸–10⁵ cells) antibiotic-resistant mutant lawns overlaid on antibiotic-free LB agar.

2.10. Detection of ammonia and/or amine emission

An ion-selective electrode (Orion 920A, Thermo Scientific) was used to detect ammonia or amine emission. LB–tobramycin agar filled 20 ml sterile, narrow-necked glass vials almost filled to capacity. This reduced the headspace available between the upper meniscus of the agar and cap of the vial. Cells were deposited on the filter discs placed on the upper surface of the agar, and the vials were immediately capped. The electrode was calibrated using 0.1, 0.5, 1, 2.5 and 5 mg l⁻¹ concentrations of ammonium sulfate. While measuring ammonia levels for calibration and in the experiment vials, the electrode was held at a distance of 1 cm above the upper surface of the media (gaseous phase). All measurements were conducted at 37°C.

2.11. Modelling diffusion of the IF in a spatially structured system

The disc diffusion assay can be modelled using diffusion laws. In this system, a finite quantity of IF is released by cells at the disc and diffuses into a cylindrical agar volume with radius much larger than height. A system with this geometry has been solved with a non-closed form solution [23]. However, this solution has been shown numerically to be approximated by the solution of one-dimensional diffusion from a constant source [23]:

2.1

where [IF] is the concentration of IF as a function of distance from the disc x, time t, the initial concentration at the disc [IF]₀ and the diffusion coefficient D.

At the critical time T_c when zone size is set, the distance x = X defines the region in which the concentration of IF exceeds the critical concentration [IF]_c. Assuming the amount of IF produced is proportional to the number of cells on the disc gives equation (2.1). If the mutant overlay is pre-incubated for a set time h before the disc is placed, the zone size X is given by

where N₀ is the number of cells placed on the disc and N_c is the minimum number of cells on the disc required to produce a zone of inhibition. The diffusion coefficient of a molecule is inversely proportional to its radius. To first order, a molecule's volume and therefore its MW scales as the cube of its radius. Thus, for IF and a molecule A

2.12. Measurement of the critical incubation time T_c and the diffusion coefficient D of the IF

Increasing numbers of WT cells (10⁷–10¹¹ in 10 μl) were deposited on filter discs. A linear regression of (X²) as a function of ln(N₀), where X is the zone size and N₀ is the number of cells placed on the disc, was performed using R v2.15.2 (R Development Core Team, Vienna, Austria) [24].

In parallel, to measure critical time T_c, antibiotic-resistant mutants were overlaid onto antibiotic agar and then pre-incubated. At set increments of pre-incubation time, WT cells (approx. 10¹⁰) were placed on filter discs. To estimate the time after which no zone of inhibition would be formed, a linear regression of X² as a function of pre-incubation time was used to find the X² = 0 intercept. This is T_c. Corresponding experiments were performed for tobramycin as an MW calibrator.

2.13. Modelling the effect of small fluctuations in population density of antibiotic-resistant mutant survival in a spatially mixed system

We model the probability of mutant survival P in spatially mixed systems by

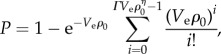where ρ₀ is the average cell density, V_e is an effective volume in which cells reduce antibiotic quantities per cell, and Γ and η are lumped parameters. The function P is defined for densities in which 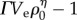is a positive integer n, such that ρ₀ must be equal to (n + 1/ΓV_e)^1/η. We linearly interpolate between values of ρ₀ which satisfy this condition to generate a continuous function 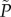. Model parameters were estimated using a nonlinear least-squares regression of the colony counts in replicate 1 (figure 1b; R v. 2.15.2 [24]). R² was calculated as the ratio of explained variance to total variance.

Figure 1.

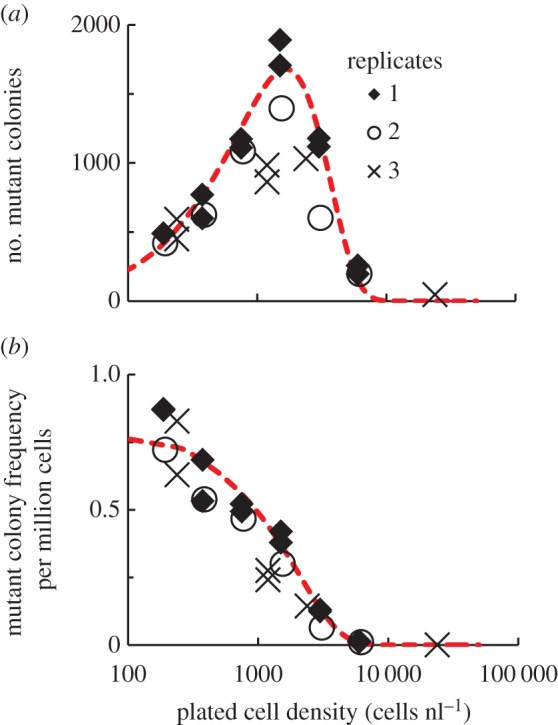
In a spatially mixed system, high cell densities negatively impact the survival of antibiotic-resistant mutants in the presence of antibiotic. Different cell densities from overnight PA14 cultures, containing WT cells and spontaneously generated antibiotic-resistant mutants, were plated on LB–tobramycin 4 μg ml⁻¹ agar. (a) The number of growing antibiotic-resistant mutant colonies varies non-monotonically with cell density. n = 3; independent biological replicates are indicated by diamonds, circles and multiplication symbols. (b) The fraction of the plated culture that grows into antibiotic-resistant colonies decreases monotonically with increasing cell density. n = 3. In (a), the red, dashed line shows our analytical model, derived using a Poisson distribution to describe random fluctuations in density, that describes the number of surviving antibiotic-resistant mutants as a function of cell density. This model was fitted to the colony number data from replicate 1. R² = 0.95. In (b), the red line shows the analytical model describing the frequency of mutant colonies as a function of cell density, using parameters determined from the previous fit. R² = 0.78. Model parameters: V_e = 0.004, η = 1.164, Γ = 0.370 nl^η−1 and μ = 1.10 × 10⁻⁶. (Online version in colour.)

2.14. Statistical tests

Correlation statistics and Student's t-tests were done in Microsoft Excel.

3. Results and discussion

3.1. In a spatially mixed system, increasing cell densities negatively impact the survival of antibiotic-resistant mutants

We grew P. aeruginosa PA14 cultures overnight and then plated portions of the resulting populations onto LB agar containing tobramycin at 4 µg ml⁻¹. This is approximately four times the MIC for WT PA14 cells (electronic supplementary material, table S1). The overnight cultures consisted of a mixture of WT PA14 cells and spontaneously generated antibiotic-resistant mutants (electronic supplementary material, table S1). We used each overnight culture to prepare multiple agar plates, varying the density of bacteria spread on the plate over four orders of magnitude. The number of antibiotic-resistant colonies that grow on antibiotic agar is the product of (A) the number of antibiotic-resistant mutants plated and (B) the probability that an antibiotic-resistant mutant will grow after plating. The first number, (A), will linearly increase as more of each culture is plated.

However, we find that the number of antibiotic-resistant colonies that grow depends non-monotonically on the initial density of the plated population. These data show a maximum, or ‘sweet spot’, for the number of plated mutants that survive antibiotic exposure and grow into colonies (figure 1a). The fraction of the plated culture that gives rise to mutant colonies, also known as the ‘mutation frequency’ [25], decreases monotonically with increasing cell density (figure 1b). Therefore, the probability of a mutant growing into a colony must also decrease with increasing cell density. Because there are orders of magnitude more WT than antibiotic-resistant mutant cells present in the initially plated cultures, we postulate that WT cells are inhibiting the antibiotic-resistant mutants.

3.2. In a spatially structured system, wild-type cells inhibit the growth of antibiotic-resistant mutants

For all further experiments, we used the same spontaneously generated mutant strain and tobramycin at 8 µg ml⁻¹, except when stated otherwise. (See electronic supplementary material for characterization of this mutant strain using whole-genome sequencing.) To investigate the role of WT cells in inhibition, we overlaid antibiotic-resistant mutants onto LB–tobramycin agar, placed filter-paper discs onto this background, and deposited WT PA14 cells onto the filter discs. This system offers a simplified model to examine inhibition in populations exhibiting macroscopic heterogeneity in cell density, and is inspired by the disc diffusion assay often used to evaluate antibiotic susceptibility [26]. After growth of the antibiotic-resistant mutant lawn, we observed circular zones of inhibition surrounding the filter discs (figure 2 and electronic supplementary material, figure S1). From these experiments, we conclude that, in the presence of antibiotic, WT PA14 cells inhibit antibiotic-resistant mutants.

Figure 2.

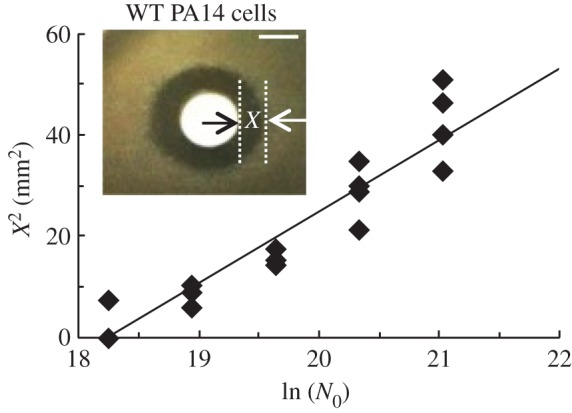
In a spatially structured system, WT PA14 cells inhibit the growth of antibiotic-resistant mutants. WT cells (approx. 10⁹–10¹⁰) were deposited on antibiotic-resistant mutant lawns on LB–tobramycin 8 μg ml⁻¹ agar. Inset: WT PA14 cells produce inhibition of antibiotic-resistant mutants (X = 4 mm). The width of inhibition X is measured from the edge of the filter disc to the edge of the inhibition zone. Scale bars, 5 mm. Increasing numbers of WT PA14 cells were deposited on antibiotic-resistant mutant lawns overlaid on LB–tobramycin 4 μg ml⁻¹ agar. The square of the width of inhibition (X²) varies linearly with the log of the number of WT cells deposited. R² = 0.87. n = 4. (Online version in colour.)

We also find that cell-to-cell contact or proximity, nutrient depletion, pyocins, quorum sensing and reactive oxygen species are not involved in inhibition, and that inhibition is caused by a diffusible factor that does not stick to glass and therefore may not be a protein (electronic supplementary material, figures S2–S7).

3.3. The inhibitory factor has a low-molecular weight

We model the disc diffusion assay, informed by previous studies modelling antibiotic diffusion [23,27]. Our model assumes

• (1) the IF is released by WT cells to a concentration [IF]₀ at the disc;

• (2) the IF diffuses out of the disc with a constant diffusion coefficient D;

• (3) a threshold concentration of IF, [IF]_th, is required to inhibit mutant cells; and

• (4) IF no longer causes inhibition after a critical time T_c of incubation.

Assumption (4) corresponds to an increase in the number of cells in the lawn that causes the per-cell concentration of IF to drop to subinhibitory levels [28,29]. This agrees with our finding that the size of the inhibition zone decreases with increasing initial lawn density (electronic supplementary material, figure S8a). The width of the inhibition zone is the distance between the edge of the disc and the edge of the inhibition zone, X (figure 2, inset). Our model approximates X² as

3.1

N₀ is the number of WT cells deposited on the disc, which we assume to be linearly proportional to the concentration of IF produced. F is a function independent of N₀. N_c is the minimal number of WT cells that produce measurable inhibition. The slope of X² as a function of ln(N₀) gives the diffusion coefficient D, if critical time T_c is known.

To vary N₀, we deposited increasing numbers of WT cells on antibiotic-resistant mutant lawns on tobramycin 4 µg ml⁻¹ agar and measured X. On a semi-log plot, X² varies linearly with ln(N₀), as predicted by the model (figure 2). To measure T_c, we pre-incubated the mutant lawn before depositing WT cells. X decreases with increasing pre-incubation times until X = 0 (electronic supplementary material, figure S8b). We measure T_c to be 110 ± 30 min and N_c to be of the order of a million cells.

By fitting the model to the data in figure 2, we estimate the diffusion coefficient D of the IF to be 4.5 ± 0.5 × 10⁻⁶ cm² s⁻¹. To calibrate the relationship between D and the MW of the IF, we performed the disc diffusion assay using varying concentrations of tobramycin (MW = 467.5 Da) deposited on filter discs on a WT lawn on antibiotic-free agar (electronic supplementary material, figure S9). We did two replicates of this experiment. Fitting these results gives a diffusion coefficient for tobramycin (averaged for the two replicates) of 1.2 ± 0.1 × 10⁻⁶ cm² s⁻¹. Using the Stokes–Einstein relation, we estimate that the IF has a MW of the order of 10 Da, indicating it is a small molecule.

We also performed the above experiments, twice, using a tobramycin concentration of 8 µg ml⁻¹ in the agar and find D of the IF (averaged for the two replicates) is 2.6 ± 0.3 × 10⁻⁶ cm² s⁻¹, so the MW of IF was again determined to be a few tens of Daltons (electronic supplementary material, figure S10). These results very nearly overlap with those taken at 4 µg ml⁻¹, and suggest that the size of the IF is near the lower limit of what we can measure using this approach.

3.4. The inhibitory factor is produced without antibiotic but causes inhibition only in the presence of antibiotic

When the agar does not contain antibiotic, inhibition does not occur (electronic supplementary material, figure S11). This could mean that antibiotic is required for production of the IF, the activity of the IF or both. To dissect this, we developed a set of complementary experiments, in which the filter disc was centred on top of a cylindrical core of agar with a different composition than that of the surrounding agar (electronic supplementary material, figure S12a).

When the core does not contain antibiotic, tobramycin must diffuse into the core from the surrounding agar before reaching the WT cells deposited on the filter disc. This introduces a delay before WT cells are exposed to tobramycin which increases with increasing core diameter. Because the timescale for diffusive transport over a distance L scales as L²/D, the core sizes we use correspond to delays in the range of tens of hours to reach the agar under the centre of the disc and up to 13 h to reach the agar under the edge of the disc. If exposure to tobramycin is required for IF production, this delay should act as a pre-incubation time and thereby decrease the size of the inhibition zones. On the contrary, we find no significant decrease in the size of the inhibition zones with increasing size of antibiotic-free cores (electronic supplementary material, figure S12b). These results show that antibiotic is not required for the production of IF.

To evaluate whether antibiotic is required for the activity of IF, we made cores of LB–tobramycin agar in antibiotic-free LB agar. With this geometry, we find no inhibition even at low lawn densities (electronic supplementary material, figure S12c). This confirms that antibiotic is required for the IF to cause inhibition.

Collectively, these results indicate that IF is likely a native product of WT PA14 cells that is produced without antibiotic but requires the presence of antibiotic to exert its inhibitory effect.

3.5. A wide range of bacterial species and a second aminoglycoside antibiotic, produce inhibition

We find that antibiotic-resistant cells deposited on antibiotic-resistant mutant lawns also produce inhibition (electronic supplementary material, figure S13). This is true both for the mutants we generated and for PA14 strains that have a gentamicin resistance cassette (aacC1) inserted into their genome [15]. These data indicate that growing cells also inhibit antibiotic-resistant mutants, and that mutants can inhibit their clonal siblings.

To determine whether IF is produced by organisms other than P. aeruginosa strain WT PA14, we evaluated a set of Gram-negative and Gram-positive bacteria as well as one strain of yeast. These organisms include known co-pathogens with P. aeruginosa as well as 17 clinical isolates of P. aeruginosa from CF patients [16]. All bacteria tested produce inhibition (table 1; electronic supplementary material, figures S14–S16 and table S2). However, the yeast Saccharomyces cerevisiae fails to produce inhibition. In the absence of antibiotic in the agar, no inhibition is observed with the bacterial strains. This is consistent with the idea that the inhibitory factors in these cases are the same as that produced by WT PA14 cells. Our results suggest that IF is produced by a wide range of bacterial species but not the yeast S. cerevisiae.

Table 1.

Microbial species/strains that produce inhibition.

species/strain	additional remarks
Pseudomonas strains
P. aeruginosa (WT PA14, WT PAO1)	laboratory strains
clinical P. aeruginosa strains (17)	cystic fibrosis isolates [16]
sandgrass isolate	uncharacterized environmental isolate
P. fluorescens	environmental isolate
Other microbial species
E. coli (DH5α, SM10)	laboratory strains
S. aureus (Mu50)	Gram-positive, methicillin- and vancomycin-resistant clinical isolate [17], co-pathogen with P. aeruginosa [30]
Serratia marcescens	Gram-negative, nosocomial human pathogen [31]
Burkholderia cepacia	Gram-negative, nosocomial co-pathogen with P. aeruginosa [32]

We tested five antibiotic-resistant mutant strains with different origins for susceptibility to inhibition. Three of these strains were spontaneously generated in antibiotic-free media and two evolved in the presence of increasing tobramycin concentrations. All show similar susceptibility to inhibition (electronic supplementary material, figure S13). Therefore, we infer that susceptibility to inhibition likely does not depend sensitively on the details of the mutation(s) conferring antibiotic resistance.

The tobramycin-resistant mutants that we generated are also resistant to another aminoglycoside, gentamicin (MIC = 9.7 µg ml⁻¹; electronic supplementary material, table S1). WT PA14 cells deposited on antibiotic-resistant mutant lawns on gentamicin agar also produce inhibition. This result demonstrates that inhibition occurs in the presence of two different aminoglycoside antibiotics (electronic supplementary material, figure S13).

3.6. Inhibition is observed when bacterial cells are deposited on media devoid of nutrients

It is striking that antibiotic-susceptible WT PA14 cells produce inhibition even though the antibiotic agar contains an inhibitory concentration of antibiotic, which should kill or inhibit WT PA14 cells shortly after plating. This suggests that IF production may not depend on utilization of nutrients from the agar. To test this, WT PA14 cells were deposited on ‘cores' of nutrient-free, tobramycin-containing agar (electronic supplementary material, figure S17a). To test for effects of diffusion from the surrounding LB agar into the cores, increasing core diameters were used. WT PA14 cells produce inhibition even when deposited on nutrient-free cores that is comparable to those seen with the ‘no core’ and ‘LB–tobramycin core’ controls (electronic supplementary material, figures S17b,c). These data indicate that the production of IF does not depend on the utilization of nutrients in the agar plate.

3.7. Alkaline metabolic products may play a role in inhibition

Because S. cerevisiae does not produce inhibition but all tested bacterial strains do, we infer that the nutritional substrate for microbial growth may be linked to the production of IF. All bacterial strains were grown in LB medium [19] but S. cerevisiae was grown in YPD medium. In LB medium, amino acids are the only significant source of carbon and bacteria grow by catabolism, which produces alkaline by-products [33,34]; overnight culture pH approximately 8. In contrast, S. cerevisiae grows in YPD medium using the sugar dextrose as a source of carbon [20]. Yeast's fermentation of sugar produces acidic by-products [35]; overnight culture pH approximately 6. To evaluate the relationship between pH and inhibition, we used agar plates that incorporated the pH indicator BTB. BTB has a pH range of 6–7.6, which permits detection of slight perturbations from neutral pH.

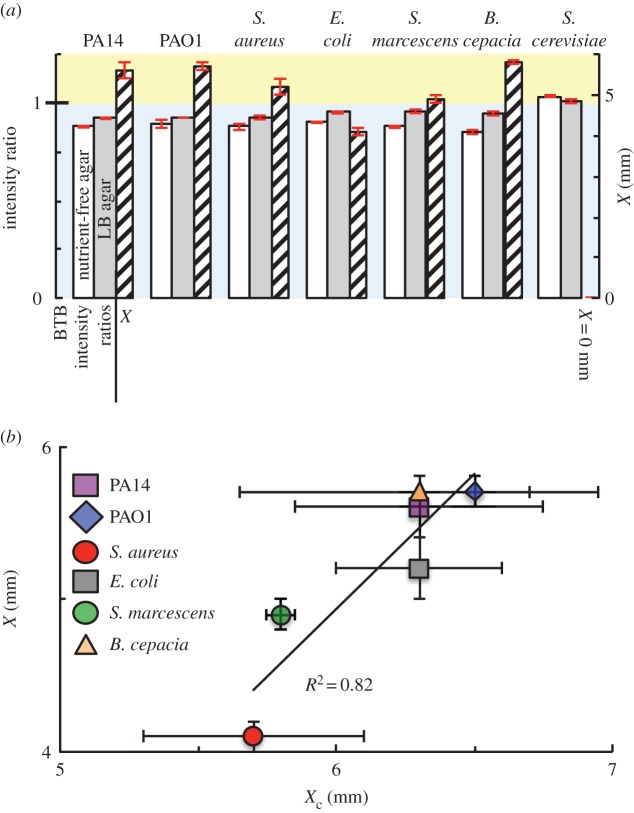
WT PA14 cells, WT PAO1 cells, S. aureus, E. coli, Serratia marcescens, Burkholderia cepacia, Pseudomonas sandgrass isolate, Pseudomonas PAO-JP2, Pseudomonas Δphz1/2 and S. cerevisiae were deposited on nutrient-free tobramycin agar and nutrient-containing LB–tobramycin agar containing BTB. To quantify changes in colour, images were split into red–green–blue channels and the red intensity profiles were analysed (electronic supplementary material, figure S18). We define intensity ratio as the intensity 2 mm from the disc edge divided by the intensity at a distance greater than 8 mm from the disc edge. With no colour change, the intensity ratio is expected to be approximately 1.

When deposited on nutrient-containing BTB agar, bacteria produce an alkaline change, with an intensity ratio less than 1 (figure 3a and electronic supplementary material, figure S19). Yeast produces a slightly acidic change or no change, with an intensity ratio greater than or equal to 1. The width of inhibition X and the width of the alkaline colour change X_c are correlated (figure 3b). These results agree with the idea that inhibition is caused by the alkaline bacterial by-products. Alkaline change on nutrient-free agar (electronic supplementary material, figure S20) is consistent with our finding that inhibition does not result from utilization of nutrients from the agar plate. Rather, metabolic by-products from cells in the overnight cultures continue to be released following deposition on the agar.

Figure 3.

Alkaline metabolic by-products from a wide range of bacterial species correlate with inhibition. (a) Different microbial strains were deposited on nutrient-free tobramycin BTB agar, on nutrient-containing LB–tobramycin BTB agar, and on antibiotic-resistant mutant lawns overlaid on LB–tobramycin agar. Images were taken immediately after deposition (for nutrient-free BTB agar), 2 h after deposition (for nutrient-containing LB BTB agar) or after overnight incubation (for antibiotic-resistant lawns on LB–tobramycin 8 μg ml⁻¹ agar). The width of inhibition (X) is shown as hatched bars. All bacterial strains produce inhibition of antibiotic-resistant mutant lawns, however, the yeast strain fails to produce inhibition. Error bars (in red) represent standard error of the mean; n = 3. (b) For different inhibiting strains, when the width of alkaline change (X_c, see electronic supplementary material, figure S18) is plotted as a function of the width of inhibition (X), a correlation is observed (R² = 0.82 from a linear fit, Pearson's correlation coefficient r = 0.9). Intensity profiles were used to measure the width of alkaline colour change (X_c), representing the distance from the edge of the disc to the edge of the alkaline colour change. For each replicate, X_c and X represent the average of four measurements made along two perpendicular axes. Error bars represent standard error of the mean; n = 2. (Online version in colour.)

3.8. The mechanism of inhibition is related to the alkaline pH change

To investigate a causative link between alkalinity and inhibition, we test exogenous alkaline solutions and find they produce both an alkaline change on BTB agar and inhibition of antibiotic-resistant mutants (figure 4 and electronic supplementary material, figures S21 and S22). We vary the concentration deposited and use linear regression to determine the relationship between concentration and X. From these, we extrapolate that deposition of 10 µl of 2.04 M NH₄OH, 1 M NaOH or 1 M NaHCO₃ produces inhibition of antibiotic-resistant mutants comparable to that seen with WT PA14 cells (electronic supplementary material, figures S21–S23). On antibiotic-free LB agar, zones of inhibition are either absent (with NH₄OH and NaHCO₃) or markedly reduced (with NaOH; electronic supplementary material, figure S24). Collectively, these results indicate that alkaline compounds can recreate the characteristics we have found for the IF.

Figure 4.

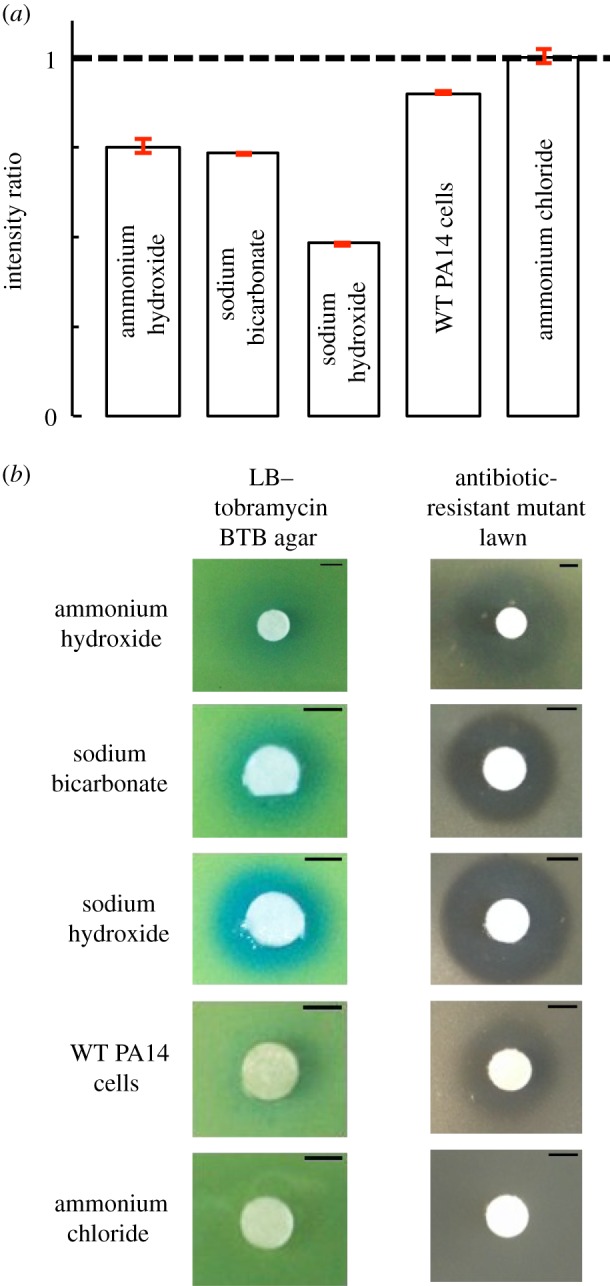
Exogenous alkaline solutions can recapitulate the phenomenon of inhibition. (a,b) Ten microlitres of exogenous compounds—2.4 M ammonium hydroxide (NH₄OH), 1 M sodium bicarbonate (NaHCO₃), 1 M sodium hydroxide (NaOH), WT PA14 cells and 1 M ammonium chloride (NH₄Cl)—were deposited on LB–tobramycin BTB agar and on antibiotic-resistant mutant lawns on LB–tobramycin agar. Images were taken 2 h after deposition (for LB–tobramycin BTB agar) or after overnight incubation (for LB–tobramycin agar with antibiotic-resistant mutant lawns). (a) BTB colour intensity ratios were determined as for figure 3, with the baseline grey value measured at a distance of more than 10 mm for NaOH, NaHCO₃ and NH₄Cl and WT PA14 cells, and more than 40 mm for NH₄OH. Intensity ratios less than 1 indicate an alkaline change, as produced by ammonium hydroxide, sodium hydroxide, sodium bicarbonate and WT PA14 cells. Ammonium chloride produces an intensity ratio approximately 1. Error bars (red) represent standard error of the mean; n = 2. (b) Representative images showing BTB colour change and presence or absence of inhibition produced by 2.4 M ammonium hydroxide (NH₄OH; X = 10 mm, X_c = 15 mm), 1 M sodium bicarbonate (NaHCO₃; X = 5 mm, X_c = 5.5 mm), 1 M sodium hydroxide (NaOH; X = 5 mm, X_c = 7.5 mm), WT PA14 cells (X = 5 mm, X_c = 6 mm) and 1 M ammonium chloride (NH₄Cl; X = 0 mm, X_c = 0 mm). Scale bar, 5 mm. (Online version in colour.)

Other researchers have shown that alkalinity significantly enhances the bactericidal activity of aminoglycosides [35,36]. At least two possible mechanisms have been suggested (i) enhanced active uptake of aminoglycosides [36–39]; (ii) more aminoglycosides in their non-ionized, more-bactericidal form [36]. Thus, we infer that the IF inhibits mutants by increasing pH.

We modify equation (3.1) to use a threshold pH rather than a threshold IF concentration as the determinant of cell survival, thus:

where pH_c is the pH above which cells die, k₀ is the IF production by one cell, and α and β are constants which account for the acid–base properties of the IF (electronic supplemental material). The N₀-dependent portion of this function is unchanged from equation (3.1). Therefore, pH-mediated inhibition does not change our MW measurements. Further, this model predicts a linear relationship between X² and the squared size of alkaline colour change (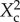), consistent with figure 3b.

3.9. Biogenic bases are plausible candidates for the inhibitory factor

The biogenic bases ammonia and amines are widespread by-products of bacterial catabolism of amino acids [33,34,40]. Ammonia has an MW of 17 Da, consistent with that of the IF. Microbially produced ammonia and amines can mediate long-range intercellular interactions and influence antibiotic resistance [41–46]. Gaseous ammonia, from bacterial supernatant, and trimethylamine, can decrease resistance to the aminoglycoside antibiotics kanamycin and spectinomycin [45,46].

We used an ion-selective electrode to measure ammonia and amine emission when bacteria and yeast were deposited onto filter discs on LB–tobramycin agar. WT PA14 produce an emission nearly five times that of S. cerevisiae (figure 5). In the disc diffusion assay, deposition of 1 M ammonium chloride (NH₄Cl) produces a slightly acidic change and no inhibition (figure 4). Thus, we find a correlation between alkaline change and inhibition, but no inhibitory effect by the ammonia molecule itself when the pH is acidic. Therefore, we attribute inhibition to an alkaline pH change that is mediated, in part or in whole, by biogenic ammonia and/or low-molecular-weight amines.

Figure 5.

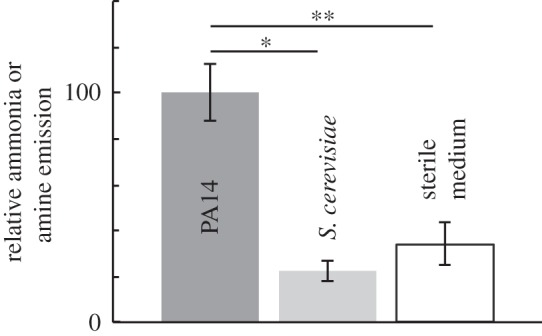
Production of ammonia or amines is associated with inhibition. Using an ion-selective electrode, ammonia or amine emission was measured following deposition of WT PA14 and S. cerevisiae cells on filter discs on LB–tobramycin agar in vials. Emission levels are normalized to the PA14 average. Significantly higher levels of ammonia or amine emission are detected following deposition of WT PA14 cells than following deposition of S. cerevisiae. Error bars represent standard error of the mean; n = 3. *p < 0.005 by two-tailed Student's t-test. **p < 0.02 by two-tailed Student's t-test.

3.10. Nutrient conditions provide a ‘switch’ to control inhibition

Microbes capable of using either amino acids or sugars as carbon sources should switch between producing inhibition and not producing inhibition depending on the carbon source available. S. aureus and E. coli can either catabolize amino acids or ferment glucose. P. aeruginosa is incapable of fermentation. S. cerevisiae ferments glucose. We grew each organism in two culture media—LB, which contains almost entirely amino acids as a carbon source, and YPD, which likewise contains copious amino acids but is also supplemented with the sugar dextrose. The pH of overnight cultures grown in LB was alkaline (pH = 9) for all bacterial strains and neutral (pH = 7) for the yeast strain. S. cerevisiae grew poorly in LB broth, so we pool cells from multiple cultures so that approximately the same number of cells were deposited onto filter discs in all cases. The pH of overnight cultures grown in YPD was alkaline (pH = 8) for WT PA14, and acidic for S. aureus, E. coli and S. cerevisiae (pH = 4, 4 and 5, respectively).

WT PA14, S. aureus and E. coli cultures grown in LB produce an alkaline colour change and inhibit antibiotic-resistant mutants (figure 6a; electronic supplementary material, figures S25a and S26). S. cerevisiae produces neither a pH colour change nor inhibition. When grown in YPD, WT PA14 cells produce an alkaline change and inhibition. However, S. aureus, E. coli and S. cerevisiae grown in YPD produce an acidic change and no inhibition (figure 6b; electronic supplementary material, figure S25b and S26). Culture supernatants and sterile LB and YPD media produce no pH colour change on nutrient-containing media and produce no inhibition (electronic supplementary material, figures S27–S29).

Figure 6.

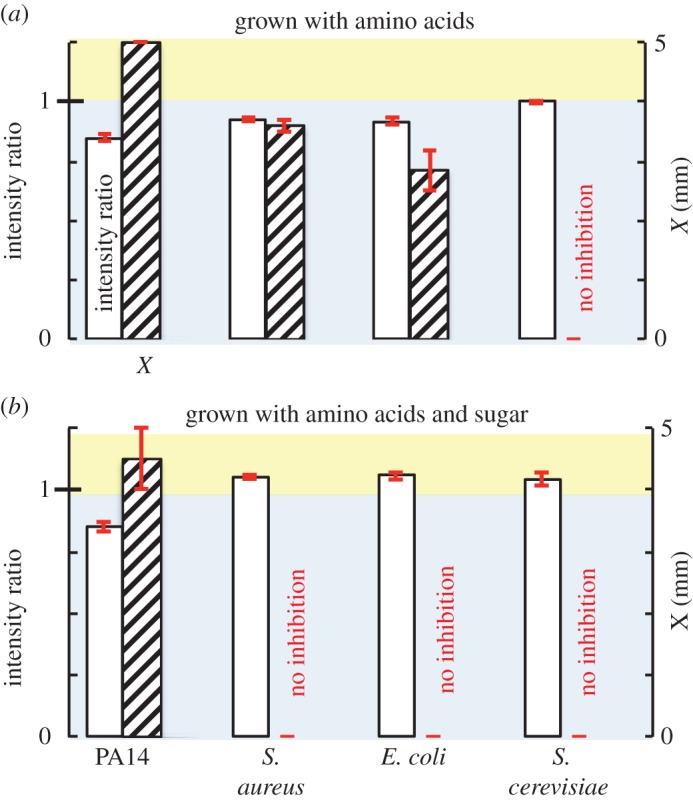
The carbon source used for growth can switch inhibition on or off. WT PA14, S. aureus, E. coli and S. cerevisiae were each grown in (a) LB medium, for which amino acids are the major carbon sources, and (b) YPD medium, which contains both amino acids and sugar as carbon sources. Following growth, cultures were deposited onto LB–tobramycin BTB agar and onto antibiotic-resistant mutant lawns on LB–tobramycin agar. (a) When grown on amino acids, the first three organisms produce both a BTB intensity ratio less than 1 and a zone of inhibition. The yeast S. cerevisiae produces no change in pH and no inhibition. (b) When grown in the presence of sugars, S. aureus, E. coli and S. cerevisiae ferment sugars and thereby produce an acidic change and no inhibition. WT PA14 catabolizes amino acids, causing an alkaline change and inhibition. Sterile LB and YPD media, and filter-sterilized culture supernatants, produce no BTB colour change and no inhibition (electronic supplementary material, figures S28 and S29). (Online version in colour.)

From this, we conclude that microbial metabolism and the nutrient environment can provide a switch to control inhibition.

3.11. Spatial fluctuations in population density influence the survival of antibiotic-resistant mutants in spatially mixed populations

In the spatially mixed system, mutant survival probability approaches zero with increasing cell density. Similarly, in disc diffusion assays, inhibition zone size increases with increasing density of deposited cells. Therefore, it seems paradoxical that mutant cells are able to grow into high-density colonies on the plate without inhibiting themselves. To resolve this paradox, we examine the effect of spatial fluctuations in initial population density on the survival of resistant mutants.

It is often found that the molar amount of an inhibitory substance per cell is a more accurate determinant of cell survival during exposure than the concentration, and therefore, higher-density populations of bacteria can survive higher concentrations of antibiotics than lower-density populations [8,9]. In a well-mixed, homogeneous system with a constant antibiotic concentration [AB], increasing cell density decreases the moles of antibiotic per cell, {AB}, thereby enhancing the resistance of cells to a given [AB]. However, we have postulated that the IF released by cells modulates antibiotic resistance by changing pH. Moreover, physically realistic spatial distributions of cells will have random fluctuations in cell density. Together, these two observations may lead to non-trivial probabilities of cell survival as a function of the average cell density.

We assume a uniform [AB] throughout the plate. {AB} in a small effective volume V_e containing N cells is thus [AB]V_e/N. If {AB} is less than a critical value {AB}_th, mutant cells in V_e will grow. Because the number of WT cells is much greater than the number of antibiotic-resistant mutants and the volumes in question are small, we assume that no more than one mutant will be in V_e and that it will survive if N_WT + 1 > ([AB]V_e)/({AB}_th), where N_WT is the number of WT in V_e.

We model random deposition of bacteria as a Poisson process. The Poisson cumulative distribution function gives the probability that the number of WT in V_e will be greater than N_WT as 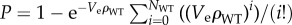ρ_WT is the average density of WT on the plate. Because ρ_WT ≈ ρ₀, where ρ₀ is the total cell density on the plate, we approximate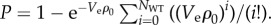

Previous studies at constant cell density have found an approximately exponential relationship between the MIC to aminoglycoside antibiotics and the pH [47]. We assume a similar exponential form for {AB}_th = A × 10^−b×pH + {AB}_min, where A and b are scaling constants, and {AB}_min is the minimum value of {AB}_th. We approximate the pH resulting from the release of IF as pH = α + βlog₁₀[IF], where α and β are constants describing the acid–base properties of the IF, and [IF] is the concentration of IF on the plate (electronic supplementary material). Assuming {AB}_min is small compared to {AB}_th, the condition for mutant survival can be approximated as N > ([AB][IF]^bβ V_e)/(A × 10^−αb). If [IF] = k₀ρ₀, where k₀ is a production constant and ρ₀ is the initial cell density, the probability of mutant survival becomes

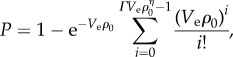3.2

where 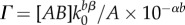and η = bβ. Γ is a lumped parameter which accounts for the alkalinity of the IF and a strain's production of IF and degree of antibiotic resistance; η accounts for the sensitivity of the antibiotic resistance to changes in pH; V_e accounts for the spatial extent over which surrounding cells can lower the {AB} to which a mutant is exposed. P is discrete with respect to ρ₀, and a continuous function 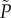can be approximated from it using linear interpolation.

The function 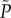gives the fraction of plated antibiotic-resistant mutants that will grow to form colonies and as a function of the initial density of cells. The fraction of the plated culture that grows into antibiotic-resistant colonies, M, is thus described by 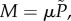where μ is the true proportion of mutants in the population. Similarly, the number of colonies formed, C, is given by 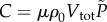, where V_tot is the total volume of the plated cell suspension.

We fit this model to our experimental data. A wide range of values of Γ, V_e, η and µ result in trends consistent with our measurements in figure 1 (electronic supplementary material, figure S30). We can estimate physically reasonable values of V_e by examining how an individual cell might impact its surrounding antibiotic concentration. By modelling a cell as an antibiotic sink, we estimate the lowest reasonable V_e value to be 0.004 nl, corresponding to 1000 times the volume of a cell, or a sphere of radius 10 µm (electronic supplementary material). With a V_e of 0.004 nl, values of η ranging from 0.90 to 2.5, Γ ranging from 8 × 10⁻⁶ to 4 nl^η−1 and μ ranging from 4 × 10⁻⁷ to 4 × 10⁻⁶, produce reasonable fits to our data, and the least-squares fit has an η of 1.186, Γ of 0.307 nl^η−1 and µ of 1.02 × 10⁻⁶ (R² = 0.92; figure 1). Additionally, V_e of 0.04, 0.4 and 4 nl, produce similar trends and fits (electronic supplementary material, figure S30 and S31). Overall, the wide range of parameter values that produce reasonable fits reflects a robustness of this model to changes in specific values, and indicates that fine-tuning of the parameters is not necessary to match the trends which we observe.

Guided by this model, we postulate that antibiotic-resistant mutants are able to grow into high-density colonies on antibiotic-containing agar because they are shielded from antibiotics by their WT neighbours. A mutant will grow into a colony if it is in a region with high local cell density that reduces the {AB} to which it is exposed below a threshold value. However, as the average cell density deposited on the plate increases, the resulting increase in [IF] on the plate lowers this threshold value by causing an increase in pH, so there is a net decrease in mutant survival probability with increasing average density. This interpretation implies that small initial fluctuations in density will be magnified as they control the subsequent growth of bacteria.

4. Conclusion

We have found that bacteria, regardless of their antibiotic susceptibility, can inhibit the survival and growth of antibiotic-resistant mutants in the presence of aminoglycosides. An alkaline by-product of amino acid catabolism, possibly ammonia or amines, mediates this inhibition. Further, these alkaline by-products likely mediate this effect by an increase in pH, which enhances the bactericidal effect of aminoglycosides. We find that microbial population structure, including cell density, spatial distribution and interspecies interactions, can impact the growth of pre-existing antibiotic-resistant mutations through this mechanism.

For a favourable mutation (i.e. one that confers a fitness advantage in the environment), the probability of fixation in a population increases with decreasing population size, which is a measure of the number of competitors [48,49]. Although our liquid cultures are grown without antibiotics, it is possible that the resistance-conferring mutation(s) conveys some other growth advantage in antibiotic-free liquid culture. In that case, the probability of the mutation fixing would depend on whether the mutation occurred early or late in culture growth. However, this possibility does not confound the results we present here, because in figure 1 the ratio of mutants to WT is the same within each experiment, because all the data points for each experiment are done for the same overnight culture suspension. Therefore, figure 1 measures the probability that a pre-existing mutant will grow into a colony, not the fixation of the mutants in a population.

Our finding, that increasing bacterial density can increase antibiotic susceptibility, is superficially in contrast to previous observations that in compact bacterial populations, such as in biofilms, the susceptibility against antibiotics is in fact decreased. However, it should be noted that bacteria in biofilms are in a different phenotypic state than that of the bacteria we plated from suspension onto agar. Most notably, biofilms are structured by embedding extracellular polymers, which can provide protection against aminoglycoside antibiotics. The bacteria in biofilm interiors also have limited access to growth substrates, which results in slowed growth and altered metabolic pathways that can protect against antibiotics.

Thus, the structure and the phenotypic state of the bacterial population needs to be considered when designing treatment strategies.

This can easily be seen in the case of CF, which is a genetic condition that renders the lung unusually susceptible to infection by P. aeruginosa and other pathogens. The CF lung contains an abundance of free amino acids [34,50,51]. In microbes sampled from CF lungs, the genes and pathways involved in amino acid catabolism are significantly upregulated [34,50]. In accordance, elevated ammonia levels have been found in CF sputum [34]. These observations would seem to suggest that the microbial population in the CF lung is well poised to inhibit each other in the presence of aerosolized tobramycin, which is commonly used in the treatment of CF.

However, CF results from a genetic defect in the CF transmembrane receptor, which causes decreased bicarbonate ion transport and acidification of CF airway fluids [52,53]. This would prevent inhibition. Inhaled bicarbonate therapy is a possible remediation for this and is already being studied as a therapy for CF because it may help restore the innate antimicrobial activity of airway surface fluids as well as facilitate the thinning and clearing of airway mucus [53,54]. Our results suggest a potential additional benefit for bicarbonate therapy in CF, where it could augment the activity of aminoglycosides and help curtail antibiotic resistance. Thus, optimizing therapeutic benefits of combining aminoglycosides with bicarbonate would require further work determining how the physiological environment of the host impacts microbial metabolism, pH changes and pharmacokinetics of base and aminoglycoside in the lung. Moreover, while early infections of the CF lung are transient and associated with a planktonic bacterial phenotype, decades-long chronic infections are associated with a biofilm phenotype. Because biofilms have phenotypic resistance to aminoglycosides, full realization of the potential benefits of the work we present here would require determination of the degree to which pH-mediated inhibition is active against clinical biofilm infections.

More broadly, our findings indicate that manipulating the nutritional and metabolic environment of the CF lung, chronic wounds or other sites of infection could potentially provide a set of management strategies that are complementary to and synergistic with conventional antibacterial therapies. Developing approaches that limiting the availability of sugars, and/or using anti-fungal therapy would promote amino acid catabolism and prevent microbe-caused acidification. Because the inhibition we characterize here results from highly conserved bacterial metabolic pathways, evolutionary escape is likely to be difficult. In addition, because the IF is produced by bacteria and will therefore be localized to infection sites, approaches to treatment that exploit the structure of microbial populations may reduce system-wide high concentrations of antibiotics and resultant toxicity to patients. This approach could both help to curtail the rise of antibiotic-resistant strains and also extend the usage of currently available antibiotics.

Funding statement

This work was supported by start-up funds to Dr Vernita Gordon at the Center for NonLinear Dynamics, Department of Physics, UT Austin, and by a gift to Dr Gordon from ExxonMobile. K.S.K. received a Graduate School Continuing Fellowship from UT Austin. N.R. received an undergraduate and summer research fellowship from UT Austin.