Rapid bursts and slow declines: on the possible evolutionary trajectories of enzymes

Abstract

The evolution of enzymes is often viewed as following a smooth and steady trajectory, from barely functional primordial catalysts to the highly active and specific enzymes that we observe today. In this review, we summarize experimental data that suggest a different reality. Modern examples, such as the emergence of enzymes that hydrolyse human-made pesticides, demonstrate that evolution can be extraordinarily rapid. Experiments to infer and resurrect ancient sequences suggest that some of the first organisms present on the Earth are likely to have possessed highly active enzymes. Reconciling these observations, we argue that rapid bursts of strong selection for increased catalytic efficiency are interspersed with much longer periods in which the catalytic power of an enzyme erodes, through neutral drift and selection for other properties such as cellular energy efficiency or regulation. Thus, many enzymes may have already passed their catalytic peaks.

1. Introduction

In this review, we will consider and update hypotheses for enzyme evolution. The textbook view is that primordial enzymes were poor catalysts, and that billions of years of natural selection have refined their activities until they have become the specialized, efficient enzymes we observe today [1]. This sedate increase in activity is illustrated in figure 1. This trajectory assumes that all enzymes are evolving towards ‘catalytic perfection’, which is reached when the catalytic efficiency of an enzyme is limited only by the rate of diffusion. There are a number of well-characterized perfect enzymes, the first of which to be identified was triosephosphate isomerase [2]. The catalytic efficiency of an enzyme is measured as a function of its turnover number, k_cat (the maximum number of reactions that can occur per enzyme active site per unit time; s⁻¹), and how well it binds its substrate (represented by the Michaelis constant, K_M, measured in M). An enzyme is considered to be a perfect catalyst if it has a k_cat/K_M of 10⁸–10⁹ s⁻¹ M⁻¹.

Figure 1.

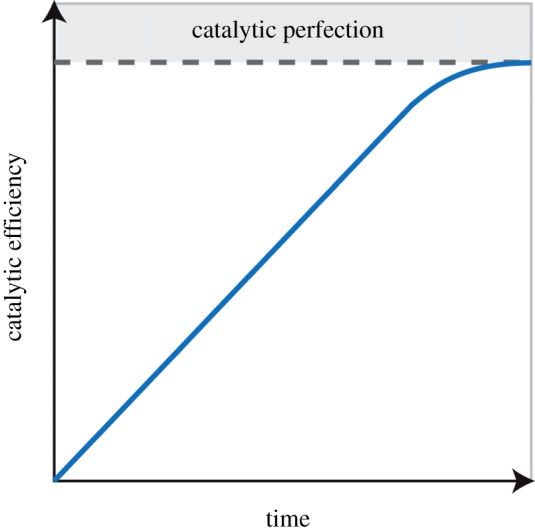
The simplest possible view of enzyme activity evolving over time.

If we assume that all enzymes are evolving to increase their efficiency towards catalytic perfection, then it follows that there were fewer perfect enzymes in the past and there will be more in the future. This conjecture is impossible to test directly (without the advent of a time machine); however, a technique that combines phylogenetics and biochemistry, ancestral sequence reconstruction (ASR), enables the resurrection of ancient enzymes. Surprisingly—and contrary to the trajectory shown in figure 1—many reconstructed ancestral enzymes show kinetic parameters that are superior to their extant descendants [3–9].

In an alternative model for enzyme evolution, we propose that many of the enzymes required for core metabolic processes evolved to peak catalytic performance very early in evolutionary history. We use the analogy of a weak link in metabolism: if a particular biochemical reaction becomes the single rate-limiting step for the growth and replication of a single-celled microorganism, then strong positive selection will be exerted upon the enzyme that catalyses this step. Such strong selection pressure can impart drastic improvements in a short period of time (discussed further below), yielding an evolved enzyme that is no longer the weak link in the metabolic network of the cell (figure 2a). Once that link is no longer the weakest, selection pressure shifts to another point (figure 2a). Moreover, the rapid accumulation of beneficial mutations by the enzyme under selection may make it more efficient than it needs to be in order to maintain flux through its metabolic pathway (figure 2b). In this ‘rapid burst’ scenario, we consider the enzyme to have overshot its activity threshold, which is defined here as the minimum activity required to maintain flux through a particular biochemical pathway without reducing cell growth. Once the catalytic efficiency of the enzyme is above its activity threshold, it is no longer subject to selection and its catalytic efficiency may begin to decrease (figure 2b), through either genetic drift or selection for other properties such as stability, regulation of metabolic flux or energy efficiency. Unlike the trajectory portrayed in figure 1, this model predicts that many extant enzymes have poorer activities than their ancient ancestors. Furthermore, it predicts that their activities will continue to decline into the future, as selection to retain or improve activity is only exerted when enzymes approach their activity threshold.

Figure 2.

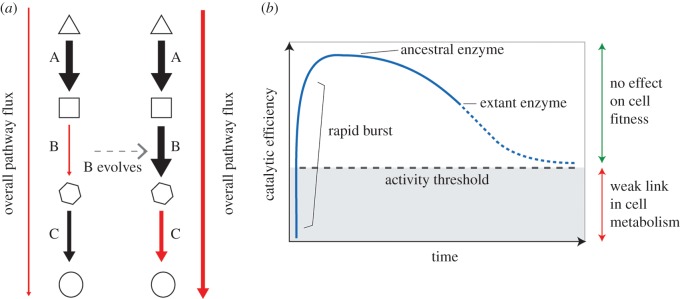
(a) Enzyme evolution via weak-link metabolism. The overall pathway flux on the left is dependent upon the rate of reaction B, which acts as the bottleneck for the whole pathway and, in a hypothetical single-celled organism, sets the rate for cell growth and division. Selection acts to improve the activity of enzyme B and increase the flux through this step. Step C becomes the bottleneck of the pathway and the new target of selection. (b) A hypothetical trajectory for enzyme evolution over time.

Here, we will consider activity thresholds largely in terms of catalytic efficiency (k_cat/K_M). This measure is not without its limitations—two enzymes with different k_cat and K_M values can have the same k_cat/K_M [10]. Furthermore, and intuitively, the activity threshold of an enzyme will be contingent upon myriad factors that act over different timescales. Enzymes that catalyse reactions in high-flux metabolic pathways (i.e. those for which the cell requires a lot of product) might be expected to have high activity thresholds and by the same logic, enzymes acting in low-flux pathways are predicted to have lower activity thresholds. A change in environment, such as the depletion of one carbon source or the introduction of another, will shift the relative fluxes through different pathways and thus transiently alter the activity thresholds in a given cell. Similarly, the different metabolic requirements at different growth phases, as well as throughout diurnal and seasonal cycles, will introduce different metabolic demands. While acknowledging these caveats and simplifying assumptions, we will argue here that the activity threshold concept is useful for inferring important trends and processes, occurring over evolutionary timescales of years to aeons.

In articulating the activity threshold concept, this review builds upon the pioneering work of Tony Dean and his co-workers [11]. While engineering the cofactor specificity of the Escherichia coli 3-isopropylmalate dehydrogenase (LeuB), his group found that mutations leading to significant reductions in catalytic efficiency had negligible effects on growth rates when the mutated enzymes replaced wild-type LeuB in vivo. However, the data formed a hyperbolic relationship: once catalytic activity was reduced below a certain point, there was an accompanying sharp reduction in organismal fitness. The relationship between enzyme kinetics and fitness was formalized mathematically for the LeuB system [11].

In the following sections, we critically appraise and modify the model of enzyme evolution that is presented in figure 2b. We review the experimental evidence for enzyme evolution in rapid bursts and for enzyme activities that exceed organismal activity thresholds. We also examine reconstructed enzymes before we conclude by dispelling the intuitive assumption that enzyme evolution is an inevitable climb towards a peak of catalytic perfection.

2. Punctuated equilibria in enzyme evolution

Our initial model (figure 2b) predicts that catalytic activities can rapidly increase by orders of magnitude when enzymes are under strong selection pressure as the weak (or missing) links in a metabolic network. It is rooted in two key concepts that were articulated in the mid-twentieth century. First, Horowitz [12] proposed that biochemical pathways evolved in reverse: when an essential metabolite obtained from the environment was exhausted, the cell had to evolve an enzyme to synthesize it from some precursor molecule. When this was in turn exhausted, a second enzyme was required to synthesize the precursor. This can be viewed as a procession of weak links in metabolic pathways, being rectified by rapid bursts of adaptive enzyme evolution under strong selection. Second, Eldredge & Gould [13] famously critiqued a purported ‘stately unfolding’ of the history of life (i.e. phyletic gradualism) by introducing the concept of punctuated equilibria in the evolution of new species. They asserted that gaps in the fossil record were not (entirely) owing to the failure of palaeontologists to find enough fossils, but instead provided evidence for ‘rapid evolutionary events punctuating a history of stasis’.

Is it possible that this model of punctuated equilibria also applies at the molecular level? Computer simulations both of evolution within a mixed population [14] and for the origin of enzymes within a hypothetical primordial metabolism [15] have yielded behaviours that mimic long periods of stasis punctuated with rapid bursts. Presumably, evolution of the very earliest biological catalysts must have necessitated a period of rapid rate enhancements. In the absence of a catalyst, many of the reactions that are essential for life take place on timescales of hours to millennia [16]. For example, the uncatalysed hydrolysis of a polysaccharide occurs approximately once every 5 million years [16]. For an enzyme to improve the rate of such a reaction so that it occurs on a biologically relevant timescale (typically >1 s⁻¹), the rate must be enhanced by as much as 10¹⁹- to 10²¹-fold. A recent and compelling case has been made for the importance of a ‘hot origin’ for enzyme evolution [17,18]. In this scenario, elevated temperatures in primordial environments would have lowered the kinetic barriers for converting substrates to products. At these temperatures, perhaps approaching 100°C, the first enzymes may only have needed to catalyse comparatively small rate enhancements in order to bring the relevant chemical transformations on to biological timescales. Not only that, but early enzymes which acted by reducing the enthalpy of activation (ΔH^‡), rather than enhancing the entropy of activation (TΔS^‡), would automatically produce increased rate enhancements when the environment cooled [17]. As an inevitable consequence of thermodynamics, this model is also valid regardless of the nature of the primordial cells or populations in which it may have been acting. Thus, the first rapid bursts of enzyme evolution towards greater catalytic efficiencies may have been inevitable by-products of life spreading into cooler environments.

Modern examples of punctuated equilibria in enzyme evolution have been characterized in bacteria that are adapting to the impact of humans on their environment. The phosphotriesterase enzyme from Pseudomonas diminuta catalyses the hydrolysis of a range of synthetic insecticides and chemical warfare agents, none of which were synthesized until the 1940s [19]. Remarkably, phosphotriesterase hydrolyses the insecticide parathion with an efficiency that approaches catalytic perfection (k_cat/K_M = 4 × 10⁷ s⁻¹ M⁻¹) [20]. The enzyme appears to have evolved from a lactonase ancestor with a very weak promiscuous phosphotriesterase activity (k_cat/K_M < 10 s⁻¹ M⁻¹), to near perfection, in approximately 50 years [21]. Similarly, Pseudomonas sp. strain ADP has evolved to use the herbicide atrazine, introduced into the environment in vast quantities beginning in 1958, as a novel carbon source [22–24]. An entire catabolic pathway has evolved to metabolize atrazine [25], co-opting three enzymes from the amidohydrolase family. The first enzyme in the pathway, atrazine chlorohydrolase [26], diverged from melamine deaminase, though it retains none of the original activity [27]. While it shares 98% sequence identity with the extant melamine dehydrogenase, it has adapted to the novel substrate and hydrolytically dechlorinates atrazine with a catalytic efficiency that is within the range of ‘average’ enzymes [28] at 1.5 × 10⁴ s⁻¹ M⁻¹ [25]. These examples demonstrate that enzyme evolution can be extraordinarily rapid, as shown in figure 2b.

Similarly rapid bursts of enzyme evolution can be observed in laboratory studies. A canonical example involved experimental evolution of a Salmonella enterica strain that was incapable of synthesizing the amino acid tryptophan, because the trpF gene (encoding the enzyme phosphoribosylanthranilate isomerase, PRAI) had been deleted. This strain was forced to evolve a compensatory function in an homologous enzyme from the histidine biosynthetic pathway—the N-(5′-phospho-l-ribosyl-formimino)-5-amino-1-(5′-phosphoribosyl)-4-imidazolecarboxamide (ProFAR) isomerase, encoded by hisA—in just 500 generations of laboratory evolution [29].

When suitably strong selection conditions arise, these examples indicate that enzymes can evolve to near catalytic perfection in periods of time that are remarkably short, in the context of the history of life.

3. Probing activity thresholds

Figure 2b illustrates the notion that rapid bursts of adaptive evolution might drive an enzyme to exceed its activity threshold by a considerable amount. It is certainly the case that single mutations can cause large increases in catalytic efficiency, and these may carry an enzyme well beyond its activity threshold in a single step. A classic early example was the site-directed mutagenesis of Thr51 to Pro in tyrosyl-tRNA synthetase, which increased k_cat/K_M by 25-fold [30]. However, an equally elegant ‘forward evolution’ laboratory experiment, evolving phosphotriesterase into an arylesterase, has recently been used to argue that a law of diminishing returns governs enzyme evolution [31]. That is, comparatively few mutations will confer large, beneficial effects on activity and these will be the first to achieve fixation in most evolving populations. The majority of beneficial mutations, on the other hand, will confer much smaller gains in activity and these may fix slowly—or not at all—in the population that is under selection [32]. In this model, the precise mutation that takes an evolving enzyme beyond its activity threshold (conferring sufficiently high activity that a different enzyme becomes the weak link in the metabolic network) is most likely to be of small effect, although factors such as population size and the magnitude of the overall improvement required to reach the activity threshold will also influence the likely evolutionary trajectory. If the law of diminishing returns is universal, then an enzyme is unlikely to exceed its activity threshold by more than a few percent before selection ceases to act on its kinetic parameters.

In contrast to the law of diminishing returns [31], there are numerous examples of experiments in which enzymes have been replaced by poorly functional alternates and yet cell growth has barely been compromised, if at all. Consistent with figure 2b, these suggest that enzymes can indeed exceed their activity thresholds, by several orders of magnitude. A classic early example was the identification and characterization of a cryptic β-galactosidase, Ebg, encoded within the genome of E. coli. The primary β-galactosidase, encoded by lacZ, enables growth on lactose as the sole carbon source and it has a k_cat/K_M of 1.2 × 10⁵ s⁻¹ M⁻¹ for the hydrolysis of lactose [33]. Constitutive expression of Ebg was insufficient to allow growth on lactose of E. coli from which the lacZ gene had been deleted (i.e. an E. coli ΔlacZ strain), implying that the activity threshold for this function was somewhat greater than the catalytic efficiency of Ebg (k_cat/K_M = 9.2 s⁻¹ M⁻¹; 13 500-fold worse than LacZ). A single point mutation in the α subunit (Asp92 → Asn) yielded an Ebg enzyme with a k_cat/K_M that was still 340-fold worse than LacZ (at 3.7 × 10² s⁻¹ M⁻¹), but vastly superior to the uncatalysed rate of one per 4.7 × 10⁶ years at 25°C [16]. The mutant Ebg enzyme now conferred a growth rate of 0.45 cell divisions per hour [34]. This compares favourably with the growth rates of other wild-type E. coli strains in minimal media [35,36]. The implication is that the activity threshold required for growth on lactose is somewhere close to 4 × 10² s⁻¹ M⁻¹, yet the LacZ enzyme exceeds this by at least two orders of magnitude.

A selection of similar rescue experiments is presented in table 1. Missing links have been created in metabolic pathways through gene deletion, and the enzymes that have been found to fill the gaps are often unexpected. As with the Ebg example, they have regularly displayed much poorer kinetics than the deleted specialist enzyme, and yet they are sufficient or almost so; that is, cellular growth rates are not reduced by anywhere close to the reduction in k_cat/K_M.

Table 1.

Selected enzyme ‘missing link’ studies performed in E. coli.

deleted enzyme (and its encoding gene)	kcat/KM (s−1 M−1)	rescuing enzyme	kcat/KM (s−1 M−1)	fold decrease in activity	decrease in cell growth	references
β-galactosidase (lacZ)	1.2 × 105	Ebg (D92N)	3.7 × 102	3.4 × 102	division rate of 0.45 h−1 in minimal medium	[33]
phosphoribosylanthranilate isomerase (trpF)	6.8 × 106	PurF (1–04)	0.3	2.3 × 107	30 h to form colonies instead of 12 h	[36]
phosphoserine phosphatase (serB)	8.7 × 104	Gph	1.6	5.4 × 104	colonies of 0.32 mm diameter after 72 h, instead of 1.2 mm	[37]
		HisB	7.6	1.1 × 104	colonies of 0.80 mm diameter after 72 h, instead of 1.2 mm
		YtjC	7.9	1.1 × 104	colonies of 0.52 mm diameter after 72 h, instead of 1.2 mm
glucokinase (glk)	5.4 × 106	YcfX	2.4 × 103	2.3 × 103	3–8 d to form colonies instead of overnight	[38]
		NanK	5.1 × 102	1.1 × 104	3–8 d to form colonies instead of overnight
		YajF	2.0 × 102	2.7 × 104	3–8 d to form colonies instead of overnight
N-acetylglutamyl-phosphate reductase (argC)	3.6 × 104	ProA (E383A)	4.6	7.8 × 103	growth to saturation in liquid medium took 45–70 h, instead of 24 h	[39]

As stated above, enzymes in low-flux pathways—such as tryptophan biosynthesis—might be predicted to have low activity thresholds. Together with cysteine, tryptophan is among the least abundant amino acids in the cell [40,41]. Therefore, this pathway can be sensitive for detecting enzymes with low activity; even very low levels can be sufficient to provide enough tryptophan to support growth. This was the case in a 2008 study [36], where over-expression of an enzyme from purine biosynthesis (glutamine phosphoribosylpyrophosphate amidotransferase; PurF) was able to rescue an E. coli ΔtrpF strain (lacking PRAI). The step remained the weak link in the cell because the growth rate was severely reduced (colony formation in 6 days instead of 1 day). However, a single round of random mutagenesis and selection yielded a PurF variant [PurF(1–04)] that enabled colony formation in only 30 h, compared with 12 h for the same strain expressing PRAI itself [36]. When PurF(1–04) was characterized in vitro, it was found to have remarkably poor catalytic efficiency that was barely above the rate of spontaneous hydrolysis of the labile substrate (k_cat/K_M = 0.3 s⁻¹ M⁻¹). This was over seven orders of magnitude worse than the catalytic efficiency of the enzyme it was replacing, PRAI (table 1).

A more recent study confirmed that PRAI has evolved to exceed its activity threshold by many orders of magnitude. Evran et al. [42] used a combination of site-directed mutagenesis and directed evolution to establish PRAI activity on the α-subunit of tryptophan synthase, TrpA. When expressed in an E. coli ΔtrpF strain, their three best TrpA variants each enabled colony formation at the same rate as the Thermotoga maritima PRAI (i.e. overnight incubation at 37°C). However, the catalytic efficiencies of these enzymes ranged from 27 s⁻¹ M⁻¹ to 235 s⁻¹ M⁻¹ [42]. Together, these two studies dramatically illustrate how marginal enzyme activities can be sufficient to give near-normal organismal fitness.

Serine is approximately fourfold more abundant in E. coli than tryptophan [40]; thus the flux through its biosynthetic pathway will be higher in nutrient-limiting conditions. Deletion of one of the enzymes in serine biosynthesis, phosphoserine phosphatase (SerB), can be rescued by over-expressing any one of three other phosphatases (Gph, HisB and YtjC) [43]. In vitro characterization of these enzymes and analysis of the growth rates that they enabled for E. coli ΔserB cells in the absence of exogenous serine [37] showed similar results to those described above: decreases in enzyme activity of more than 10⁴-fold were accompanied by much smaller decreases in growth (table 1).

Enzymes acting in a high-flux pathway such as glycolysis are expected to have high activity thresholds, owing to substantial demand for the products of the pathway. A pioneering study [38] identified three E. coli enzymes that could functionally replace the first enzyme in the glycolytic pathway, glucokinase. The catalytic efficiencies of these three enzymes—YcfX, NanK and YajF—ranged from 200 s⁻¹ M⁻¹ to 2400 s⁻¹ M⁻¹, and thus were higher than the examples that have been discussed from tryptophan and serine biosynthesis. Nevertheless, glucokinase itself is highly active so even these values represent reductions in activity of three to four orders of magnitude (table 1). Similar to the other examples, however, reductions in cell growth were only one order of magnitude (or less), demonstrating that many enzymes in a range of pathways have all evolved to exceed their current activity thresholds by surprisingly large amounts.

One caveat for all of the studies in E. coli described above, apart from the Ebg example, is that the rescuing enzymes were over-expressed from plasmid vectors. While there is an overall fitness cost to the cell that is associated with protein over-expression [35,44], this also provides a crude means to amplify weak activities to physiologically relevant levels [45]. Two of the studies [37,46] were continued to find mutations within (single copy) chromosomal genes that were sufficient to compensate for their respective missing links. In the case of compensating for the loss of SerB, a single point mutation in the chromosomal hisB gene (encoding the amino acid substitution Asp57 → Asn) was sufficient to allow colony formation within 2 days [37]. The catalytic efficiency of this mutated HisB protein was not reported; however, other variants identified through random mutagenesis of the plasmid-encoded version had k_cat/K_M values for the SerB reaction that were improved by only fourfold to 24-fold compared with HisB.

Similarly, Miller & Raines [46] selected for chromosomal mutations that enabled growth of their glucokinase-deficient strain of E. coli. Selection yielded a mutation in the promoter region of the yajF gene, which increased expression of the YajF protein by 94-fold. The revertant strain showed a similar growth rate (colony formation in 9 days) to that in which YajF over-expression was driven off a high copy number plasmid. YajF displayed a catalytic efficiency that was reduced by more than 10⁴-fold compared with glucokinase (table 1). These experiments demonstrated that over-expression could compensate for approximately 1% of this activity gap. However, the studies with chromosomal copies of Ebg, HisB and YajF all suggest that artificial over-expression is insufficient to compensate for the observed decreases in catalytic efficiency. The implication is that the metabolic enzymes β-galactosidase, phosphoserine phosphatase and glucokinase have all evolved beyond their expression level-adjusted activity thresholds by at least two orders of magnitude.

McLoughlin & Copley [39] conducted a similar test by using a chemical mutagen (N-methyl-N′-nitro-N-nitrosoguanidine) to introduce mutations directly into the chromosome of an E. coli strain that lacked the ability to synthesize arginine, owing to deletion of its argC gene. Selection on a growth medium without arginine yielded colonies in which the proA gene (encoding glutamylphosphate reductase) contained both a point mutation (encoding the substitution Glu383 → Ala) and a promoter mutation that led to a sixfold increase in ProA expression under the selection conditions. As with the other examples, the selected ProA variant displayed a substantial decrease in catalytic efficiency (k_cat/K_M = 4.6 s⁻¹ M⁻¹) compared with the ArgC enzyme that it was replacing (k_cat/K_M = 3.6 × 10⁴ s⁻¹ M⁻¹). This was accompanied by a much smaller reduction in cellular growth rate (table 1). Furthermore, ProA was under selection to retain its original function, as well as its new ArgC function. The Glu383 → Ala mutation reduced ProA activity by 2800-fold, from a catalytic efficiency of 3.3 × 10⁴ s⁻¹ M⁻¹ to 12 s⁻¹ M⁻¹. Thus the E. coli cell was now tolerating two poor (but essential) activities, catalysed by the same enzyme. Even when the sixfold over-expression of this enzyme is factored in, it is clear that wild-type E. coli harbours ArgC and ProA enzymes that are two to three orders of magnitude above their individual activity thresholds.

4. Whence excessively good enzymes?

The experiments described above demonstrate that many—and perhaps most—metabolic enzymes exceed their activity thresholds by several orders of magnitude. At first glance, this is counterintuitive, as there should be no selection to improve beyond the activity threshold. One possible resolution to this conundrum is that genetic drift incorporates mutations that are neutral with respect to organismal fitness but which continue to improve enzyme activity, even in the absence of selection. This has been observed in an experimental model of neutral drift, which used the TEM-1 β-lactamase enzyme [47]. However, the observed increases in catalytic efficiency were small (less than twofold). More generally, strongly beneficial mutations are rare compared with nearly neutral or slightly deleterious mutations [31,48–50]. The infrequency of these beneficial mutations, combined with an absence of selection (because the enzyme is already above its activity threshold), makes it extraordinarily unlikely that they would become fixed in an evolving population of cells.

A second, more plausible, explanation for enzymes exceeding their activity thresholds is that selection continues to act, albeit on properties other than catalytic efficiency—and that selection for these other properties is linked to improvements in k_cat/K_M. Rates of protein evolution have been associated with a large number of variables, in addition to their kinetic parameters, and the contribution of an enzyme to organismal fitness may be a function of many of these [51]. For example, it has been argued that selection acts to minimize the cost of producing misfolded proteins, therefore favouring sequences with increased robustness to errors of mistranslation [52]. This selection pressure increases with expression level, constraining sequence evolution. Thus, highly expressed proteins are predicted to evolve slowly. Highly constrained protein surfaces (such as those involved in protein-protein interactions) also dictate slow evolutionary rates amongst residues in the core of the protein [53]. It remains to be elucidated whether the contributions to protein evolutionary rates of expression level or constrained surfaces are correlated with effects on catalytic efficiency.

Recently, Tawfik [54] neatly summarized the potential trade-offs between catalytic efficiency and substrate selectivity. He observed that accuracy is a selectable trait, but that this may often arise through negative selection (i.e. mutations that disfavour the binding of incorrect substrates) rather than positive selection to increase reaction rates with the correct substrate. Nevertheless, mutations that improve transition state discrimination offer the potential for k_cat/K_M to increase, together with accuracy [54]. This has been observed for DNA polymerases [55]. Further, we note that those rare mutations that do improve transition state stabilization (i.e. ΔG^‡) will lead to exponential improvements in reaction rate, k, according to transition state theory:

The relationships between—and the potential for selection to act on—thermostability, protein dynamics, robustness to mutation and evolvability have also been investigated [51,56,57]. Many of these selectable determinants of protein evolutionary rates have been reviewed elsewhere [58,59]. Overall, however, experiments to investigate these properties have focused on retention of catalytic activity—so it remains uncertain whether selection for them could also drive significant improvements in k_cat/K_M.

Perhaps the most likely reason to keep selecting for ever more efficient enzymes, with k_cat/K_M values far exceeding experimentally determined activity thresholds, might be that this also enables selection to reduce enzyme expression levels. Flux through a given step in a metabolic pathway is proportional both to k_cat/K_M and to the enzyme concentration. Protein synthesis is by far the most expensive process in the cell energetically; it is estimated to account for 50–60% of the energy consumption in a rapidly dividing bacterium [60,61]. Thus, selection for highly efficient enzymes, expressed at low levels, is expected to maximize the energy efficiency of the cell (and therefore its fitness). Nevertheless, the examples described in the previous section suggest that many extant enzymes exceed their expression-adjusted activity thresholds.

Finally, it is naive to assume that activity thresholds have remained constant over time (figure 2b), as an organism adapts to myriad environmental challenges during the course of its evolutionary history. It is possible that any given extant enzyme exceeds its current activity threshold because the cellular demand for its function was greater in the past (figure 3a). In this scenario, a rapid burst of strong positive selection would have driven the evolution of an enzyme with a high catalytic efficiency. When the activity threshold was relaxed (for example, when an organism inhabited a new niche in which a nutrient became more abundant than it was previously), selection was also relaxed so that common but deleterious mutations were likely to cause a downward drift in k_cat/K_M (figure 3a). Alternatively, a relaxed activity threshold may also underpin a switch to selection for cellular energy efficiency (by optimizing expression level), regulatory mechanisms or thermostability. One implication of this scenario is that many contemporary enzymes—such as those listed in table 1—are likely to be evolving towards having lower activities in the future. Another implication is that many ancestral enzymes are likely to have had higher catalytic efficiencies than their extant descendants.

Figure 3.

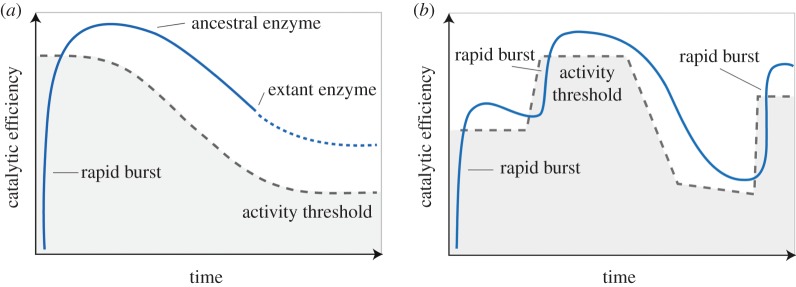
Alternative trajectories of enzyme evolution. (a) activity thresholds may change over time, relaxing selection pressure on the catalytic efficiency of an enzyme. (b) A more plausible trajectory: as the activity threshold changes over time, enzyme evolution alternates between rapid bursts of positive selection and downwards drift (or selection for traits other than k_cat/K_M).

Given the inordinate period over which selection has acted on evolving biological systems, the most plausible scenario is one in which the activity threshold of each metabolic enzyme has been varying over time (figure 3b). Any given enzyme might be expected to be interrupted from its downwards drift in activity when it suddenly becomes the weak link in metabolism (figure 2a). A key implication of this model is that enzymes from progressively older nodes along the same evolutionary trajectory are expected to show fluctuating catalytic efficiencies.

5. Insights from the reconstruction of ancient enzymes

Ancestral sequence reconstruction (ASR) provides us with a technique for testing the predictions made in figure 3. Combining phylogenetic and biochemical methods, it uses DNA and protein sequences from related organisms to infer a phylogenetic tree, and thus the sequences at given nodes on the tree. These ancestral gene sequences can then be synthesized, enabling the biochemical properties of the expressed proteins to be investigated. The ASR process and illustrative studies are comprehensively reviewed elsewhere [62–64]. Most previous ASR studies have been used to infer knowledge about ancestral life; some of the most ambitious projects have reconstructed proteins with predicted ages between 1 and 4 billion years old [3–6,65,66]. Ancient reconstructed proteins have been shown to possess increased temperature optima and thermostability [4,5,67–70] (confirming the importance of thermophily as an early life-history trait [17,18]), and, in some cases, broadened substrate range [9,69]. The field of ASR is still developing and there is debate over the optimal reconstruction methods [71]. Reconstructions represent a snapshot of a point deep in the history of an enzyme (millions to billions of years, with associated error) while we have used the previous sections to emphasize the importance of rapid bursts (on the order of decades). It follows that enzymes resurrected through ASR may not represent the most crucial points in evolution. Furthermore, it has been argued that the very first enzymes to emerge were hetero-oligomers of partially structured and/or partially functional subdomains [72,73], and it is not possible to infer these states using the phylogenetic information in modern sequences. Instead, alternative computational approaches have been taken in order to make inferences about the origins of protein folds [74,75]. Nevertheless, resurrected enzymes can provide evidence for the fluctuation of activity thresholds over time.

Core metabolic enzymes are highly conserved within, and often between, the three domains of life: Bacteria, Archaea and Eukarya. Phylogenetic evidence suggests that many of these enzymes were present in the last universal common ancestor of all life on the Earth, LUCA. Therefore, the initial rapid bursts of selective pressure acting upon weak links in metabolism, pushing individual enzymes beyond their activity threshold, would have occurred at the dawn of life.

Only a fraction of ASR studies have targeted metabolic enzymes and characterized the kinetic parameters of the resurrected enzymes (table 2). We review some of these studies here, in the light of our weak-link hypothesis for enzyme evolution. Consistent with our model, recent studies of thioredoxin, nucleoside diphosphate kinase (NDK), LeuB and uricase have all shown reconstructed enzymes with kinetic parameters superior to their extant descendants. Thioredoxins are small oxidoreductase enzymes that are ubiquitous in all three domains of life. Thioredoxins have been reconstructed from a range of very ancient nodes, including the last common ancestor of Bacteria (thought to have inhabited the Earth approx. 4.2 billion years ago), the last common ancestor of Archaea (approx. 4.1 billion years old) and the last common ancestor of Eukarya (approx. 1.6 billion years old) [3]. In each case, the reconstructed enzymes were found to exhibit catalytic efficiencies higher than extant thioredoxins. The most active enzyme was from the archaeal ancestor, while the enzymes from the bacterial and eukaryotic ancestors were each 150–200% more active than those from their extant descendants, E. coli and Homo sapiens (table 2). The reconstructed thioredoxins were also significantly more thermostable than the E. coli and H. sapiens enzymes [3]. Similarly, the NDK enzyme from the archaeal ancestor was recently reconstructed, using a variety of tree topologies and methods to assess the robustness of the ancestral sequence predictions [4]. The most robust ancestor, Arc5 (constructed using a tree that was reconciled with rRNA sequences), was both more thermostable and more active than its descendent, found in the species Archaeoglobus fulgidus (table 2). In contrast to a stately unfolding of enzyme evolution (figure 1), these data provide evidence that thioredoxins and NDKs had already undergone a rapid burst of evolution within a few hundred million years of the protein world originating.

Table 2.

Catalytic efficiencies of extant and ancestral enzymes.

enzyme (and substrate)	organism	age (years)	kcat/KM (s−1 M−1)	references
thioredoxin	E. coli	extant	2.5 × 105	[3]
	H. sapiens	extant	5.2 × 105
	ancestor of Eukarya	1.6 × 109	7.6 × 105
	ancestor of Archaea	4.1 × 109	8.2 × 106
	ancestor of Bacteria	4.2 × 109	4.7 × 105
nucleoside diphosphate kinase	A. fulgidus	extant	1.2 × 106	[4]
	archaeal ancestor Arc5	3.8 × 109	4.0 × 106
isopropylmalate dehydrogenase	B. subtilis	extant	7.5 × 104	[5,6]
	B. caldovelox	extant	4.8 × 104
	ancestor of Bacillus	9.5 × 108	2.1 × 105
	ancestor of Firmicutes	2.6 × 109	1.1 × 105
uricase	S. scrofa	extant	3.6 × 105	[7]
	ancestor of mammals	9.4 × 107	7.1 × 105
ribonuclease A	E. coli	extant	5.0 × 106	[76]
	artiodactyls	3.0 × 107	3.3 × 106
chymase	H. sapiens	extant	3.6 × 106	[8]
	ancestor of mammals	NRa	4.3 × 106
α-glycosidase (maltose)	L. elongisporus	extant	6.2	[9]
	yeast ancestor	1.2 × 108	13.0
α-glycosidase (maltotriose)	L. elongisporus	extant	1.7	[9]
	yeast ancestor	1.2 × 108	19.2
α-glycosidase (sucrose)	L. elongisporus	extant	11.0	[9]
	yeast ancestor	1.2 × 108	31.6
β-lactamase (benzylpenicillin)	E. cloacae	extant	2.6 × 107	[69]
	‘GPBCA’ ancestorb	1.5 × 109	7.0 × 106
	‘PNCA’ ancestorb	3.0 × 109	5.0 × 105
β-lactamase (cefotaxime)	E. cloacae	extant	2.6 × 103	[69]
	‘GPBCA’ ancestorb	1.5 × 109	3.7 × 104
	‘PNCA’ ancestorb	3.0 × 109	1.0 × 106
β-lactamase (ceftazidime)	E. cloacae	extant	6.5 × 102	[69]
	‘GPBCA’ ancestorb	1.5 × 109	5.0 × 103
	‘PNCA’ ancestorb	3.0 × 109	3.0 × 104

^aNR: not reported, although by analogy with [7] this ancestor is assumed to have an age of approximately 9.4 × 10⁷ years.

^bAbbreviations are as used in [69]. GPBCA, last common ancestor of Gammaproteobacteria; PNCA, last common ancestor of various Gram-positive and Gram-negative bacteria.

Two recent papers [5,6] have explored the evolutionary history of LeuB, a dehydrogenase from the conserved and ancient metabolic pathway of leucine biosynthesis. Reconstruction of enzymes from several nodes on the Bacillus tree has revealed a trend of fluctuating thermostability and thermoactivity over the past billion years of Bacillus evolution [5]. Of most relevance to our model (figure 3), the catalytic efficiencies also fluctuate, with the most ancient ancestor (of all Bacillus; 950 million years old) being the most active (table 2 and figure 4). This work was extended recently [6] to reconstruct the ancestor of all Firmicute LeuB enzymes (2.6 billion years old), which was found to have a k_cat/K_M that was intermediate between the more recent Bacillus ancestor and the extant enzymes that were studied (table 2 and figure 4). The emerging picture is one in which catalytic efficiency has risen and fallen over time, consistent with a rugged landscape of activity thresholds (figure 3b).

Figure 4.

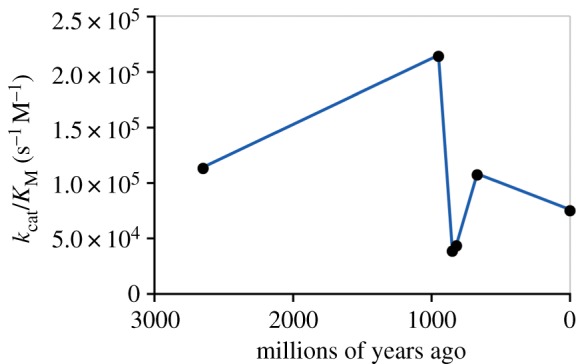
Fluctuating catalytic efficiencies over the evolutionary history of LeuB in the Firmicutes. Data are adapted from [5,6], with B. subtilis LeuB used as a representative of extant enzymes.

The recent reconstruction of uricase enzymes from the mammalian phylogenetic tree [7] was noteworthy because it explored a special case in which some extant homologues (from humans and other apes) have mutated to become completely non-functional. The authors mapped a steady decline in enzymatic activity since the last common ancestor of the mammals (94 million years ago); even an active extant enzyme from the pig, Sus scrofa, was approximately twofold less active than the ancestral mammalian uricase (table 2). Other pioneering studies of ancestral enzymes from similar historical time points include the reconstruction of an ancestral ribonuclease [76] and a chymase [8] (table 2).

Regardless of catalytic efficiency, it is generally assumed that ancient metabolic networks were populated by generalist, multi-tasking enzymes that were capable of catalysing multiple reactions on multiple substrates [77–79]. Two noteworthy recent ASR studies have found evidence for broadened specificity among ancestral enzymes. In the first, an ancestral yeast α-glycosidase was reconstructed from the sequences of extant enzymes that each exhibited specificity towards different combinations of di- and tri-saccharide substrates [9]. The common ancestor, estimated to be 119 million years old, was found to be a generalist with activity towards all nine of the substrates that were tested. In general, its kinetic parameters were inferior to those of extant specialist enzymes; however, they were superior to those of an extant generalist enzyme from Lodderomyces elongisporus (table 2). The ancestral α-glycosidase was a superior generalist enzyme.

The authors noted that the age of the ancestral α-glycosidase, 119 million years, coincided with the time at which flowering plants are predicted to have become widespread [80]. Ancestral yeasts were likely to have been colonizing new environments at that time, and there was likely strong selective pressure to be able to use a range of new carbon sources. The reconstructed enzyme thus represents a point at which there was likely to have been a rapid burst of adaptive evolution in the yeast α-glycosidase lineage. Reconstruction of an ancestral alcohol dehydrogenase also supports a readjustment of yeast metabolism to coincide with the rise of flowering plants [81].

Similar to the yeast α-glycosidase study, reconstruction of ancient bacterial β-lactamases (the enzymes responsible for hydrolysing β-lactam antibiotics) found that the reconstructed enzyme from a 3 billion year-old ancestor of Gram-negative and Gram-positive bacteria (‘PNCA’) possessed a much broader substrate specifity than its extant descendent, the TEM-1 β-lactamase from Enterobacter cloacae [69]. TEM-1 is a specialist, able to hydrolyse benzylpenicillin with a catalytic efficiency that is 10 000- and 40 000-fold greater than its activities toward cefotaxime and ceftazidime, respectively (table 2). In contrast, the PNCA enzyme is most active towards cefotaxime, and only twofold and 33-fold less active towards the other two antibiotics (table 2). An intermediate in the trajectory, from the 1.5 billion year-old ancestor of Gammaproteobacteria (‘GPBCA’), showed intermediate activities towards all three antibiotics (table 2), providing a snapshot of a generalist-to-specialist transition in the evolution of β-lactamases. The authors deliberately avoided sequences from clinical isolates of bacteria and thus described a fine example of what appears to be phyletic gradualism (figure 1), albeit by sampling at intervals of 500–1000 million years [69]. It would be fascinating to extend this work by reconstructing the enzymes that have evolved in an extremely rapid burst (figure 3) under the strong selection imparted by introducing β-lactam antibiotics into the clinic over the past 75 years.

6. Concluding remarks

It is tempting to envisage enzyme evolution as a sedate and near-constant accumulation of beneficial mutations that improve k_cat/K_M, until catalytic perfection is attained (figure 1). From our anthropocentric twenty-first century perspective, it is also difficult to appreciate the sheer depth of evolutionary time, or to imagine scenarios in which the catalytic efficiencies of core metabolic enzymes may diminish in the future. In this review, we have sought to summarize recent experimental data that highlight and reinforce these counterintuitive possibilities.

When strong selection is invoked, the catalytic efficiencies of enzymes in populations of evolving microorganisms can change by orders of magnitude in a matter of decades, or even years. This has been observed when synthetic pesticides or antibiotics are introduced into the environment and when bacterial populations have been subjected to experimental evolution [19,25,29]. Viewed through this lens, 4 billion years or so (since the origin of protein-based biology) is ample time for every core metabolic enzyme to have been the weak link in the metabolism of its host cell (figure 2a), and thus for every enzyme to have undergone a rapid burst of adaptive evolution. Indeed, it follows that organisms at the dawn of life are likely to have possessed highly active enzymes; reconstructions of very ancient enzymes such as ancestral thioredoxins [3], NDK [4] and LeuB [5,6] hint that this was the case.

Nevertheless, catalytically perfect enzymes are rare. Instead, the ‘average’ enzyme in central metabolism has a k_cat/K_M of approximately 10⁵ s⁻¹ M⁻¹ [28]. Not only that, but an accumulating body of experimental evidence (table 1) suggests that these imperfect enzymes are still orders of magnitude better than they need to be for their modern bacterial hosts. Synthesizing these data, we reasoned that the most plausible explanation is a long and rugged trajectory for enzyme evolution, in which rapid bursts of strong positive selection for k_cat/K_M are interspersed with much longer periods in which cellular energy efficiency, regulation and mildly deleterious mutations dominate evolution, eroding catalytic efficiency (figure 3b). This model is analogous to the notion of punctuated equilibria in the evolution of new species [13].

A corollary of our model is that many extant enzymes may have passed their catalytic peaks and are currently in a period during which their catalytic efficiencies are decreasing with time. Our model predicts that this will reverse at some point in the future, when the k_cat/K_M decreases to below its activity threshold (either via deleterious mutation, or by a change in environment that alters the activity threshold itself). This is purposely simplistic; selection also acts on properties other than catalytic efficiency. A catalytically inferior enzyme may provide a selective advantage to the cell if, for example, it allows for more nuanced regulation of flux through the relevant pathway.

The burgeoning field of ASR has provided valuable evidence that some enzymes were more active in the ancient past (table 2). However, the experiments reviewed herein also serve to highlight the difficulties in inferring past environments, past selection pressures and past activity thresholds. The non-falsifiable nature of ancestral reconstructions places them in the realm of just-so stories, rather than hypotheses, and doubts have been raised about the ability of ASR studies to reach justifiable conclusions [71]. Befitting an active field with enormous potential, these doubts have spurred methodological improvements such as the use of branch-heterogeneous models of sequence evolution [82] and species-aware gene trees [6].

With these caveats in mind, we hope that our pre-paradigmatic model highlights gaps in knowledge that could usefully be addressed. For example, it is comparatively uncommon to quantify differences between catalytic efficiency and activity threshold. More generally, many biochemists are averse to studying their enzyme in the context of organismal fitness, let alone population biology. Many evolutionary biologists are equally wary of enzyme kinetics and biophysics. Without doubt, a ‘functional synthesis’ [83] of approaches including enzymology, experimental evolution, ASR and evolutionary biology holds great promise for enriching our understanding of enzyme evolution.

Funding statement

Work in the authors' laboratories is supported by a grant from the Marsden Fund. M.S.N. was supported by the Maurice Wilkins Centre for Molecular Biodiscovery and an Otago Doctoral Scholarship. W.M.P. is the grateful recipient of a Rutherford Discovery Fellowship.