Abstract
Silk fibres from silkworm cocoons have lower strength than spider silk and have received less attention as a source of high-performance fibres. In this work, we have used an innovative procedure to eliminate the flaws gradually of a single fibre specimen by retesting the unbroken portion of the fibre, after each fracture test. This was done multiple times so that the final test may provide the intrinsic fibre strength. During each retest, the fibre specimen began to yield once the failure load of the preceding test was exceeded. For each fibre specimen, a composite curve was constructed from multiple tests. The composite curves and analysis show that strengths of mass-produced Muga and Eri cocoon silk fibres increased from 446 to 618 MPa and from 337 to 452 MPa, respectively. Similarly, their toughness increased from 84 to 136 MJ m−3 and from 61 to 104 MJ m−3, respectively. Composite plots produced significantly less inter-specimen variations compared to values from single tests. The fibres with reduced flaws as a result of retests in the tested section have a tensile strength and toughness comparable to naturally spun dragline spider silk with a reported strength of 574 MPa and toughness of 91–158 MJ m−3, which is used as a benchmark for developing high-performance fibres. This retesting approach is likely to provide useful insights into discrete flaw distributions and intrinsic mechanical properties of other fatigue-resistant materials.
Keywords: silk, retest, fatigue resistance, tensile properties, flaws
1. Introduction
The excellent mechanical properties of spider silk have received intense scrutiny over the years [1–3]. Transgenic and recombinant protein routes have been investigated to produce engineered spider silk fibres [4,5]. However, there are huge challenges of scalability, cost and fibre quality associated with such approaches to fibre production. Silkworm silks are mass-produced, but their mechanical properties are considered inferior to spider silk. However, fibres forcefully drawn from silkworms at the optimal spinning speed show much better strength and toughness than those obtained from their cocoons [6,7]. Such improved properties in fibres spun forcefully have been attributed to the higher order and orientation of molecules [8]. Another possible reason for the enhanced strength of forcefully drawn fibres compared to cocoon fibres is that the forcefully drawn fibres have fewer flaws, as indicated by microscopic images of ruptured fibres [9]. However, the contribution of the flaws to the reduced strength was not quantified. This work tries to develop a better understanding of the influence of spinning flaws on the mechanical properties of cocoon silk fibres and to estimate the intrinsic tensile properties of fibres without flaws.
The distribution of flaws in a silkworm silk fibre is expected to come from the spinning behaviour during the formation of the cocoon. The spun silk strand (bave), which contains two filaments, is laid continuously by a silkworm in a highly ordered manner due to its orchestrated movement [10]. We have observed that while silk gum anchors the already extruded strand to a surface during cocoon formation, the spatial movement of the spinning head exerts the drawing force to the newly extruded portion of the strand. There is acceleration and deceleration of the drawing motion particularly when the worm changes its direction [11]. As the drawing force plays an important role in fibre properties [12–14], it is postulated that flaws may be created, particularly at turning moments, reducing the strength of cocoon silk fibres [6,9].
To understand the influence of flaws on tensile properties, a testing regime is required that can isolate the effect of flaws from other factors responsible for tensile strength. We have determined the influence of flaws by testing the strength at various gauge lengths, as the probability of flaws (weak links) depends on the size of the specimen. In addition, we have also retested the unbroken portion of the fibre after each fracture test. It is expected that in the absence of significant fatigue and/or development of any major flaw during fracture, the unbroken section of the specimen should reach the same state when the maximum load of the previous test is reached. Following on, it should continue to bear load as it would have done without the flaw responsible for the previous failure. If this happens, a fibre can be retested a number of times to remove flaws one by one until the intrinsic strength of the flawless fibre is reached. This approach of retesting is used for the first time to validate the influence of flaws in fibres. It is supported by the ability of silk fibres to withstand repeated loading–unloading cycles without fatigue failure and to regain much of its original structure when allowed to recover [9,15,16].
This study was carried out on two mass-produced silkworm silk fibres, Muga and Eri, spun by Antheraea assamensis and Samia cynthia ricini silkworms, respectively. These two types of silk have similar macromolecular chemistry to spider silk. For example, the amino acid repeat sequences of (Ala)n of Muga and Eri silk fibroins form the β-sheets, which is also the case for spiders spidroins [17]. The difference lies in the length of (Ala)n segments. For instance, in Eri silk, n = 9–13 compared to n = 6 in spider silk [18]. However, these commercial cocoon fibres have relatively inferior mechanical properties compared to spider silk. Muga is the strongest while Eri is the weakest among the commercial silk fibres [19]. Moreover, the cocoon spinning behaviour of Eri silkworm is unique. Unlike other silk cocoons which have little floss (loose entangled fibres) at the outer cocoon surface and where a pupae is completely sealed without any opening in the cocoon, an Eri silkworm produces an open-mouthed cocoon with high floss. Therefore, these two silk fibre varieties are good candidates to study whether there are differences in the amount of flaws between them and how they influence their mechanical properties.
2. Experimental section
2.1. Materials
All silk cocoons were collected from silkworm rearing centres of northeast India. To retain the intrinsic properties of native silk fibres, the silk strand was manually gently reeled out without degumming. As there is less sericin in Muga silk, it was possible to separate the individual filaments from the twin strand. Single Muga fibre specimens were obtained from the first 5 m of reeled strand. For the Eri silk, a thin outer layer of cocoon shell was peeled out carefully for sampling, representing the initial part of the strand.
2.2. Tensile testing
Tensile tests were performed using a Favimat + ROBOT 2 (Textechno) fitted with a 265 cN load cell. Fibre specimens were mounted on the creels using 75 mg tension weights, and they were loaded into the instrument by the robot. The instrument was programmed to apply a pre-tension of 0.15 cN before recording load elongation data. Tests were conducted at 3, 25 and 60 mm gauge lengths. A 100 mm gauge length was also used for Muga fibres. Eri silk strand of this length could not be easily separated from the cocoon and hence maximum gauge length was restricted to 60 mm for this sample. Sixty specimens were tested for each sample. For all gauge lengths, the strain rate was maintained at 60% min−1. All samples were conditioned at 20°C ± 2°C and 60 ± 2% RH for 24 h prior to testing.
2.3. Tensile retesting
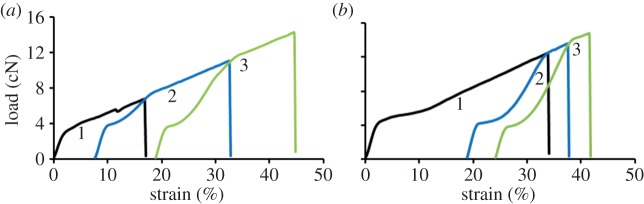
Twenty-five specimens were tested for tensile load–strain properties at 100 and 60 mm gauge lengths for Muga and Eri, respectively. The broken segments were stored in a dry state unless otherwise stated and allowed to relax for at least 2 h prior to subsequent retesting. In each retest, only the portion of the fibre that had been strained in the previous tests was used. Retests were performed at 60, 25 and 10 mm spans for Muga and 25 and 10 mm for Eri. Experiments were conducted on the dry samples after conditioning at 20°C ± 2°C and 60 ± 2% RH for 24 h. Only a small number of specimens broke early (less than 10% of samples) during retesting before the breaking load of the previous test was reached. Those specimens were then used again for the subsequent tests until the last retest was performed. Figure 1 shows the methodology used to compute the final load–strain plot from repeated tensile tests on a single specimen.
Figure 1.
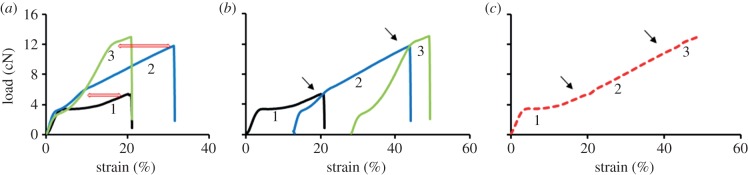
Development of a composite load–strain plot from three tests of a single Muga silk fibre specimen. (Online version in colour.)
As shown in figure 1a, when the breaking load of the initial test 1 was reached in the first retest (blue plot, test 2), the slope of the plot changed. Similarly, the slope of the test 3 plot (green plot) shifted when it reached the test 2 failure load. We shifted the starting position of the test 2 and test 3 plots in the strain axis as shown in figure 1b to generate the stress–strain plot that the fibre would have achieved without the flaws that caused failure in tests 1 and 2. Finally, using a retest plot analysis program for the data written in Matlab, we have obtained the red dotted plot combining the retests as shown in figure 1c, which represents the composite plot of the specimen. In the program, the individual curves were first analysed to find the maximum force. A smoothing spline was then fitted to the data up to the maximum force in the curve. A composite curve was then assembled. Firstly, data that were between the maximum force obtained in the initial test and the maximum force in the first retest was selected (the portion between the arrows in figure 1b,c). A strain correction factor was calculated by subtracting the strain at maximum load in the previous test. This correction factor was then added to all strains in the reduced dataset and the data then appended to the data of the initial test. This was then repeated with each dataset from each subsequent retest to produce a composite load–strain plot. Finally, the composite plot was fitted with a smoothing spline and the total work of fracture under the curve estimated.
Based on the images of fibres after fracture, we did not see any evidence of necking in the magnified images of fractured samples. The lack of evidence of necking post-fracture does not prove that the fibres are strained uniformly along their length. However, we have used this as a model assumption. Thus, the strain history of the retested fractions was the same as that of the entire section tested previously, and therefore the method of retesting could be used to develop the composite plots.
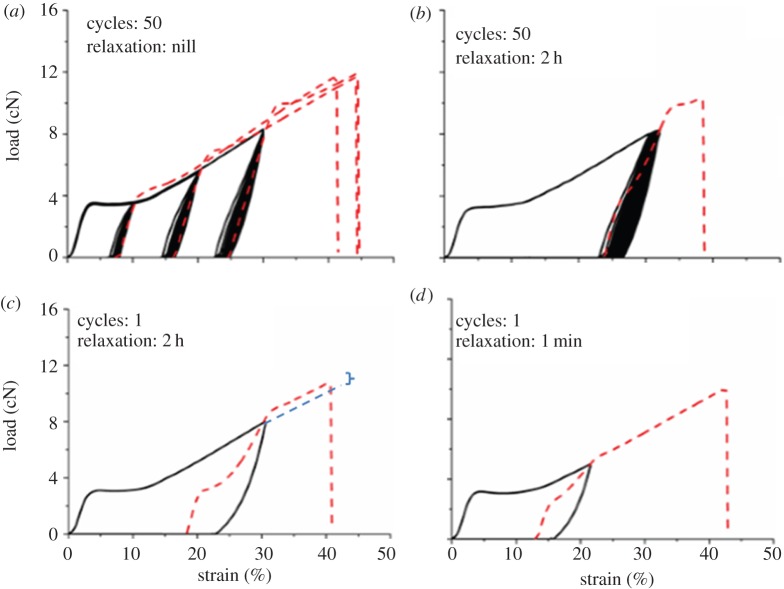
2.4. Cyclic tensile testing
To understand the hysteresis and fatigue behaviour, cyclic tests were performed. Pre-tension and strain rate were the same as for the tensile tests. A specimen was strained to reach either (i) a fixed strain ranging from 10 to 30% or (ii) a fixed load ranging from 4 to 8 cN. After the set-point was reached, the jaw was reversed to reach 0 cN load to complete the cycle. Either 1 or 50 cycles were performed and after completing the cycles, the specimen was either strained to break without relaxation or after 1 min or 2 h relaxation at 0% strain. Each experiment was repeated three times.
2.5. Cross section and fracture analysis
To measure the cross section of the silk fibres, about 50 fibre sections each 10 mm long were cut either from various parts of the 5 m long Muga filament or from the thin outer cocoon layer of Eri cocoon shell used for tensile tests. For both samples, the sections selected for mounting were adjacent to those used for tensile testing. For each sample, a bundle of fibres was mounted in a mould under light tension to remove the crimps and orient the fibres and then impregnated by a resin (Spurr replacement kit from TAAB Laboratories), followed by curing at 60°C for 24 h. Embedded fibres were sliced perpendicular to the fibre axis by an ultratrim diamond knife in an ultra-microtome (Cut 5062, SLEE). The cross sections were imaged by Zeiss SUPRA 55 VP at 2 kV accelerated voltage and 5–6 mm working distance after gold sputter coating. The cross-sectional area of at least 25 embedded fibres was determined using the ImageJ software. For fracture analysis, broken tips of selected fibres from the tensile tests and retests were also imaged.
3. Results and discussion
3.1. Fibre cross-sectional area
Figure 2 shows the SEM images of the cross section bundles for Muga and Eri. The mean ± s.d. of the measured cross-sectional areas were 240.7 ± 27.9 µm2 and 157.9 ± 23.9 µm2 for the Muga and Eri fibres, respectively. Both Muga and Eri have some variation in size and cross-sectional area, with the Eri fibres having the largest variability. The coefficient of variation of the cross-sectional area of Muga and Eri silk fibres were 11.6% and 15.2%, respectively.
Figure 2.
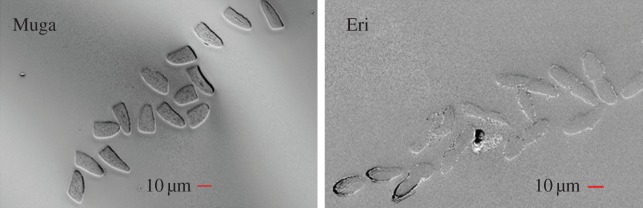
Cross sections of single filament (Muga) and bave (Eri). (Online version in colour.)
3.2. Tensile single tests and retests
Figures 3 and 4 show complete single fibre tensile stress–strain plots of a few representative specimens along with the ultimate strength and breaking strain of the remaining specimens, for the Muga and Eri samples, respectively. A 60 mm gauge length was used for these tests. Stress was calculated from the breaking load and the average cross-sectional area calculated from the SEM images (figure 2). It is clear from figure 3 that for Muga, the individual stress–strain plots nearly overlap each other, while the endpoints are tightly distributed along the common plot indicating only a small variation of size and structure between specimens. The Muga test specimens were harvested from a 5 m long reeled silk strand which is expected to be uniform in thickness and microstructure [19]. An Eri strand could not be reeled continuously and the specimens were collected from a thin layer of the cocoon shell, resulting in a wider dispersion in stress–strain profiles (figure 4) compared to Muga fibres (figure 3), which is consistent with the higher coefficient of variation in the cross-sectional area of Eri silk. The small dispersion seen in stress–strain profiles is expected to be proportional to the variations in cross-sectional area. However, owing to other possible fine structural variations between specimens such dispersions may not necessarily be attributed to variation in cross sections alone. There was a wide dispersion of breaking stress and strain for both silk varieties, indicating the dominance of flaws in initiating fractures in weak specimens, even though in the case of the Muga fibres there was a tight distribution of stress–strain profiles. A major flaw in a specimen can prematurely fail under a smaller load and thus the full strength of the remaining portion of the fibre is not used. Hence flaw-dominated failure will significantly reduce fibre breaking strain in addition to fracture strength.
Figure 3.
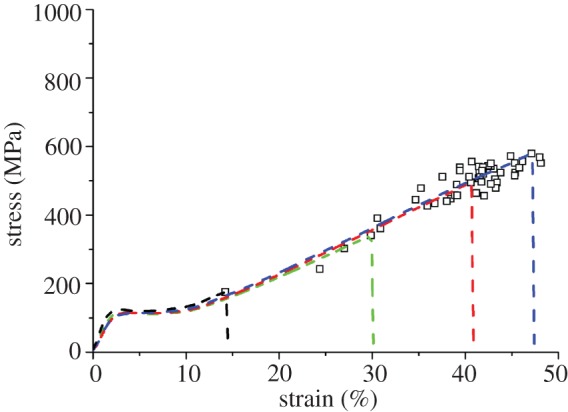
Stress–strain plots of selected specimens of Muga silk along with failure points of the rest of the specimens tested at 60 mm gauge length. (Online version in colour.)
Figure 4.
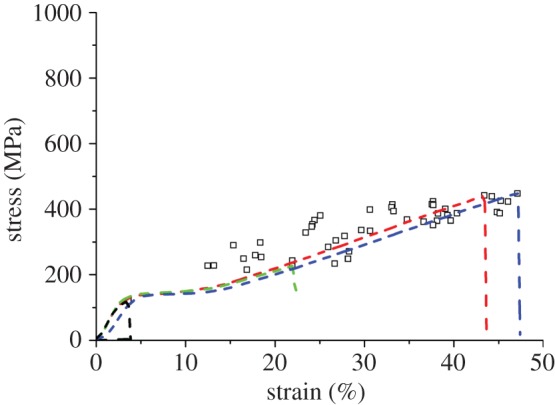
Stress–strain plots of selected specimens of Eri silk along with failure points of rest of the specimens tested at 60 mm gauge length. (Online version in colour.)
We found significant effects of gauge length on both breaking stress and strain confirming the strong influence of the weak link effect in both silk varieties (table 1). Weibull theory is an appropriate tool to estimate the weak link effect and to compute the intrinsic strength of materials. However, in natural fibres its application to predict intrinsic strength is complicated by the diameter variation within and between fibres. Calculations must be modified to predict strength at different gauge lengths if the fibre cross section varies along or between fibres [20]. However, Muga and Eri silk fibres are flat ribbon shaped and it is difficult to experimentally measure within fibre diameter variation in the short specimens used for tensile testing. Moreover, the Weibull statistics cannot be used to predict breaking strain and fracture toughness. Hence to estimate fibre strength without flaws, we used a new approach of retesting the unbroken portion of the fibre after each fracture test. The test methodology is described in the experimental method. Results from two Eri fibre specimens are shown in figure 5. It shows that although there was a significant difference in strength between the two fibre specimens in the initial test, after retests (test-2 and test-3) the difference in strength was significantly reduced. The breaking strength in test 1 was 5.6 cN (figure 5a) and 12.5 cN (figure 5b) but increased to 14.2 cN (figure 5a) and 14.8 cN (figure 5b), respectively in the final retests. The mean and standard deviation of fracture strength, strain and work (energy to break) from retesting are shown in table 1. Strain and work data are not considered in the case of 3 mm gauge length tests as any minor misalignment of the specimen between the jaws can produce a large error in the calculated strain. In the case of retests, strain and work calculations have been carried out only at the end of multiple retests and hence data after each retest are not shown.
Table 1.
Tensile properties at different gauge length from single tests and retests (mean ± s.d.).
| Muga |
Eri |
|||||
|---|---|---|---|---|---|---|
| strength (MPa) | strain (%) | work (MJ m−3) | strength (MPa) | strain (%) | work (MJ m−3) | |
| 100 | 446 ± 76 | 33 ± 5 | 84 ± 22 | |||
| 60 | 497 ± 68 | 39 ± 6 | 105 ± 23 | 337 ± 76 | 28 ± 10 | 61 ± 27 |
| 25 | 535 ± 69 | 41 ± 6 | 117 ± 28 | 362 ± 75 | 33 ± 9 | 74 ± 28 |
| 10 | 565 ± 76 | 45 ± 7 | 149 ± 42 | 399 ± 82 | 41 ± 10 | 101 ± 34 |
| 3 | 594 ± 44 | 408 ± 82 | ||||
| 100-60 | 537 ± 45 | |||||
| 100-60-25 | 559 ± 66 | |||||
| 100-60-25-10 | 618 ± 34 | 43 ± 2 | 136 ± 9 | |||
| 60-25 | 411 ± 53 | |||||
| 60-25-10 | 452 ± 32 | 41 ± 5 | 104 ± 13 | |||
Figure 5.
Retests of Eri silk. (Online version in colour.)
It is to be noted from figure 1 that a retested plot differs from the previous test plot to the breaking point and continues the original curves smoothly afterwards with an increased modulus in all subsequent tests. The increase in modulus after each subsequent loading above yield followed by recovery was reported earlier [21]. This change in the initial portion of the stress–strain curve is due to some changes in the fine structure of fibre. However, as the initial portion is not used in the construction of the composite plot, it does not influence the shape of the final plot, and therefore, the method can be used for estimating the strength of the fibre after eliminating flaws by repeated testing.
3.3. Intrinsic strength and distribution of flaws
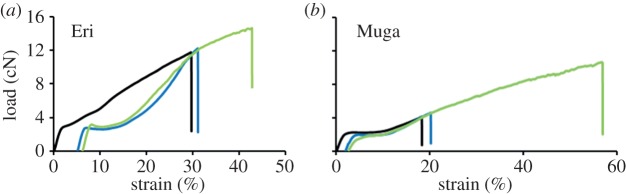
Composite plots of all Muga and Eri specimens after retesting are presented in figure 6. The distribution of the breaking points is much narrower than the single tests shown in figures 3 and 4, which are also reflected by the standard deviation values in table 1. All flaws could not be removed as only a limited number of retests could be performed. It is expected that increasing the number of retests further from the three used in this study and normalization of breaking load based on the actual initial cross section of each specimen, instead of the average of all specimens used in this work, would further improve the computation of the intrinsic tensile properties. Retesting had to be performed using shorter spans in all successive retests. Thus, there was a combined effect of gauge length and retesting on the results. As the gauge length was reduced, the maximum stress increased and distribution narrowed. However, it is evident from the cumulative distribution plots in figure 7 and data from table 1 that the retested specimen contained fewer flaws compared to single tests at any gauge length. For example, the breaking stress of retested Muga and Eri specimens at 10 mm was on average higher and had a narrower distribution compared with single tests performed at 10 mm as well as at 3 mm. Similarly on retesting, Muga at 60 mm and Eri at 25 mm produced higher average breaking stresses compared with single tests at the respective gauge lengths. We compared those results of single and retests at same gauge length using descriptive statistics at 95% confidence intervals using Excel and found statistically significant differences between the means. The distributions after retests were also significantly narrowed compared to single tests. The cumulative distribution plots therefore confirm that repeated tests removed flaws from the fibres, and the improvement in strength was not only due to a reduction in the gauge length in tensile testing.
Figure 6.
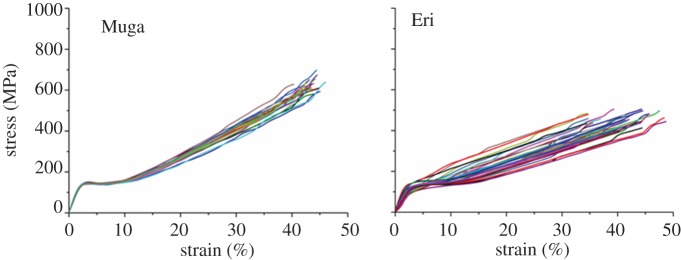
Composite stress–strain plots of all specimens after retests. (Online version in colour.)
Figure 7.
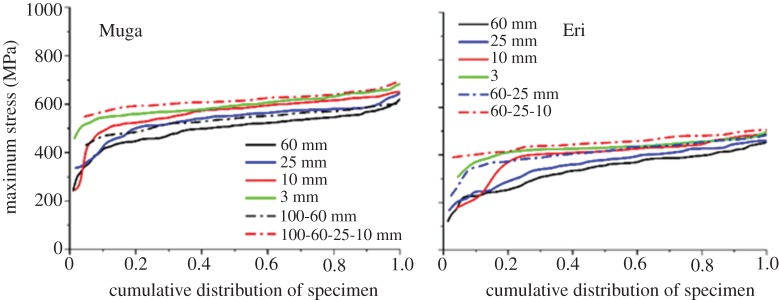
Cumulative distribution plots of maximum stress points for single tests at different gauge lengths and after retests. (Online version in colour.)
Figure 8 shows short sections of silk strand unravelled from cocoons. The movement and frequency of the change of direction of the silkworm during spinning can be determined from the crimp patterns as the filaments were pulled out very gently without affecting their crimp patterns and stress–strain properties. For tests at 3 mm gauge length, fibre specimens were harvested equally from both straight and crimped portions, while specimens tested at 25, 60 and 100 mm gauge lengths contained more than one reversing section. The breaking stress gradually increased as gauge length decreased, but there was no abrupt increase at 3 mm (table 1 and figure 7). Moreover, despite testing straight and crimped portions equally, there was no segregation of breaking stress into two groups in the data obtained at 3 mm gauge (figure 7), as would be expected if flaws were concentrated mostly in the reversing section. Breaking stress measurements at different gauge lengths indicate that the weak-link effect is more pronounced in Eri silk. When the gauge length was reduced from 60 to 10 mm, the breaking stress increased by 18.4% and 34% for single and retests, respectively. In contrast, for Muga, the corresponding increases were 13.6% and 24.3%. A higher number of flaws could be a reason for the lower strength of Eri silk compared with Muga, although it should be noted that even after retesting twice, the strength of the Eri fibres was still lower than the Muga fibres. The higher number of flaws in Eri could be from increased small-scale drawing stress fluctuations as a result of the irregular movement of the spinning head of the Eri silkworm during cocoon formation. The irregular motion of Eri silkworms produces open-mouthed, loose-structured cocoons with high floss compared with other varieties of silk [22].
Figure 8.

Images of silk strands unwound from the cocoons. (Online version in colour.)
3.4. Validating retesting by cyclic fatigue loading tests
The retest analysis assumes that the maximum load in the final test is not influenced by the loading history. This assumption was verified using cyclic fatigue loading tests. After the cyclic phase, the specimen was strained to break either with or without relaxation. As shown for Muga silk in figure 9, the load–strain trajectory did not change substantially when number of cycles was low and cycling was performed at lower load but still above the yield. The final load–strain curve crossed through the upper end of the cyclic loop and then plastically yielded to approximately follow the projected path that it would have had without the cyclic loading phase. Such behaviour has also been reported for other types of silk fibres [15,23]. As shown in figure 9a–c, there are small gaps between the final paths and the projected paths and one of these is shown with a dashed blue line in figure 9c. The gap depends on the viscoelastic response of the material. It increases when, (i) the maximum load used for cycling increases, (ii) less time is allowed for relaxation, and (iii) the number of cycles increases. There was only a small gap in the one-cycle-2 h relaxation-strain to break test (figure 9c) even though the fibre was unloaded from 8 cN, which is about 70% of the average breaking load. High fatigue resistance and small viscoelastic effect indicate quite small structural change in the fibre despite cyclically loading the sample to a load at which some specimens have already failed (figure 3). When the cycling was done at 4 cN, even after a very small relaxation time of 1 min, the final plot followed the projected path without any gap (figure 9d). The results suggest that despite some small loss of viscoelastic energy at high load, the one-cycle-relaxation-pull to break test effectively represents the case of retesting a broken fibre. We therefore expected that a retest plot would follow the projected plot of the previous test after reaching the previous point of failure. We subsequently confirmed that behaviour in retesting experiments as showed in figure 1. It was reported that for silk that recovery time more than 3 min was sufficient, and there was negligible effects on further increasing relaxation time on recovery behaviour [21]. Hence our 2 h relaxation time was sufficient for this work. The retesting approach however will be limited to testing fibres in which fatigue failure and structural changes during loading are very small.
Figure 9.
Cyclic tests of Muga silk (solid line) followed by straining up to break (dashed line) with or without relaxation. (Online version in colour.)
The fatigue resistance of Muga and Eri silk fibres is attributed to their structural recovery during the time-dependent relaxation after application of large load. The yielding pattern in the strain range of 3–10% reappears even after extensive loading. For example, after the 50-cycles-2 h relaxation test, a small yield was still evident (figure 9b), and it was quite prominent after one cycle with 1 min relaxation (figure 9d) as well as 2 h relaxations (figure 9c). This behaviour is similar to the formation of a plateau when similar strain was applied to spider silk followed by relaxation using a water vapour treatment [24]. Our study suggests that changes in the structure are metastable and substantial recovery including the reappearance of the initial yield at the same position could be seen. However, the increase in modulus and shorter yield plateau without any change in yield position on retests suggest that part of the structural change that happened during the previous test was not recovered during relaxation.
To facilitate more relaxation by breaking any strong hydrogen bonds formed during straining, we immersed the broken specimens in water for 2 h and allowed them to relax followed by dry conditioning and tensile testing prior to each retest. All other experimental protocols used for retests were the same as that of dry retests. Water treatment increased shrinkage and during retests the sharp yielding and a strong plateau similar to test 1 were evident (figure 10). Moreover, the small deflection in the composite plot at the positions of fracture of individual tests (figures 1, 5 and 6) disappeared after water treatment (figure 10). As such deflections in composite plots are very small in tests conducted after relaxation in a dry state, we do not anticipate a significance difference between tensile data of retested samples after wet and dry relaxation. In this work, we performed wet relaxation for a limited number of samples only, and therefore, average tensile test data of wet relaxation tests are not presented separately. However, further studies may be conducted in the future using wet relaxation to further improve recovery of structure and further reduce errors raised from such small deflections in the composite plots.
Figure 10.
Initial tests (test 1: black) and data from retesting after relaxation in water after test 1 (test 2: blue) and after test 2 (test 3: green). (Online version in colour.)
As these silk varieties do not have proline [25,26], there is no supercontraction similar to spider silk and the disorientation of molecules during relaxation after application of load is thought to be entropy driven. The influence of water on the structure and mechanical properties of silk is well known [27]. Wet relaxation is affected by free volume in the silk fibre that allows water to penetrate into the fibre [28]. Relaxation overcomes the weak hydrogen bonds that are responsible for holding the molecular chains in their elongated conformations [2]. The entropy-based elasticity of the amorphous domain of silk fibroin in the dry state has been demonstrated [29]. There are differences of opinion about the changes in microstructure of silk fibres on application of load. Some studied showed no changes in crystallinity and orientation while others suggested a decrease in crystallinity [30–33]. There is also no consensus on the change in amorphous domains during straining [21]. Hence the mechanisms of recovery of structure during the relaxation phase between the tests and retests and the relative importance of ordered and less ordered phases warrant further investigation. However, the capacity of the silk fibres to recover most of the original structure during relaxation even after application of large stress confirmed the validity of the retesting procedure for determining their intrinsic mechanical properties.
3.5. Fracture analysis
Broken pieces of strong and weak specimens from tensile tests were collected and their fracture surfaces were analysed to investigate fracture mechanisms and the role of flaws in fracture. Fracture tips of some strong and weak specimens are presented in figure 11a–c and figure 11d,e, respectively. The breaking stress and strain of the respective specimens are also given in the images. The fracture surface of a strong Muga specimen (figure 11a) contains the v-notch (arrow) which is typical of a ductile fracture [34]. It also has a granular surface running nearly perpendicular across the fibre axis indicating that the specimen failed catastrophically. Occasionally along with catastrophic granular fractures, there can be splits at the fracture surface as shown in the fracture tip of a strong Muga fibre after two retests (figure 11b). The catastrophic fracture mode of a strong Eri fibre is presented in figure 11c. There was no evidence of catastrophic failure with granular flat surface in any weak specimen and all weak specimens failed only as a result of multiple splits (figure 11d,e). In the process of split propagation, micro and nano fibrils are sometimes pulled out as shown for a weak Eri fibre in figure 11d. It is known that fibres that have fibrillar architecture can fail due to defibrillation if the cracks from defibrillation do not travel parallel to the fibre axis [34]. The splitting and crack propagation is assumed to be triggered by flaws in inter-fibril packing and such flaws may be caused by spinning defects. In figure 11e, an example is shown where splits in Muga fibre travelled at a shallow angle to the fibre axis, which resulted in fibre fracture and poor strength. We presume that major flaws of packing microfibrils, their distribution and orientation are important causes for silk fibre failure under a low load. In the absence of such flaws, all fibrils break almost simultaneously in a plane perpendicular to the fibre axis. There are micrometre-size holes in the granulated fracture surface in strong specimens (figure 11a–c) but neither the images nor the failure stress indicate that such pores had any major role in failure. We observed that irrespective of the fracture mode, a portion of a specimen 1–2 mm away from the fracture tip remained intact and hence retested portion did not have any influence from the splits and cracks present in the fractured tips.
Figure 11.
(a) Images of fracture tips of fibres after tensile tests; (a) a strong Muga fibre specimen after single fracture test, (b) strong Muga fibre specimen after retests, (c) strong Eri fibre specimen, (d) weak Muga fibre specimen and (e) weak Eri fibre specimen. (Online version in colour.)
3.6. Comparison with dragline spider silk
Repeated pull to fracture tests have helped us to estimate the strength of fibres with reduced flaws. It is reported that by forcefully altering the spinning behaviour, both spider as well as silkworm silk fibre properties can be changed significantly [6,7,9,13]. Apart from changing the orientation of molecules via a controlled drawing rate, forceful spinning is also expected to reduce spinning flaws. For spider silk forcefully spun under controlled conditions, excellent strength above 1 GPa and toughness of about 200 MJ m−3 could be obtained [3,35,36]. In contrast, the naturally spun dragline spider fibres were found to have an average breaking stress of 574 MPa based on 20 mm gauge length tests [37]. Our single fibre tests at 25 mm found average breaking stresses of 535 ± 69 MPa and 362 ± 75 MPa for Muga and Eri fibres, respectively (table 1). These values increased to 559 ± 66 MPa and 411 ± 52 MPa after retests at 25 mm and further to 618 ± 34 MPa and 452 ± 32 MPa at 10 mm. In addition, the breaking strain of more than 30% in most testing conditions makes these cocoon fibres very tough. At 25 mm span, the toughness for Muga and Eri was 117 ± 28 and 74 ± 28 MJ m−3, respectively. After retests at 10 mm, it increased to 136 ± 9 MJ m−3 and 104 ± 12 MJ m−3, which compare well with values of 91–158 MJ m−3 reported for naturally spun spider dragline fibres tested at 25 mm gauge [38]. The inferior toughness of Eri is attributed to the higher number of flaws in the fibre, some of which were not removed during retests. The relatively poor strength of Eri compared to Muga may be also accounted for by the difference in the primary amino acid sequence and protein microstructure, but these factors have not been investigated. However, the toughness values of Eri silk recorded in this work are still higher than the values of 57–75 MJ m−3 reported for naturally and forcefully spun mulberry silk obtained from B. mori silkworms [13,39].
As the test conditions, such as strain rate, influences the tensile results, it is difficult to directly compare the current data with the data reported elsewhere. However, intrinsic tensile properties of cocoon silk fibres particularly that of Muga silk estimated through the retest procedure, appears to be comparable to naturally spun spider dragline silk fibres. Based on studies of the influence of fibre diameter on mechanical properties, the high strength of spider fibre is attributed also to its fineness [3]. Finer fibres have a lower chance of having a large flaw and should therefore have higher breaking stress than coarser fibres [40]. The average cross-sectional area of the Eri and Muga fibres used in this study was 10–20 times that of spider silk. Hence if fibres as fine as naturally spun spider silk are spun from such silk protein with no significant presence of spinning flaws, their mechanical properties are expected to be much greater than cocoon fibres. However, designing a system to spin fine fibres without major flaws from silkworm silk proteins will remain a major challenge.
4. Conclusion
We have demonstrated that mass-produced cocoon silk fibres have excellent fatigue resistance based on cyclic loading performed at 70% of their average breaking load. Multiple tests and retests on the same specimen showed that the stress–strain profile can be computed from individual tests. Such computed plots demonstrated significantly higher strength, strain at break and toughness and lower inter-specimen variations compared with single tests at the same gauge length. The fibres with reduced flaws in the tested section had tensile strength and toughness comparable to naturally spun dragline spider silk fibres. Being mass-produced for textile applications, proteins from the fibres tested here can be an excellent feedstock for developing natural high-performance fibres. The approach of measuring intrinsic tensile properties by retesting has also been shown to provide insights into intrinsic tensile properties of other fatigue-resistant materials.
Data accessibility
The full set of experimental data is available at the Dryad repository.
Funding statement
The authors acknowledge the support from the Australian Research Council (DP120100139) and Deakin University Central Research Grant for this work.
Authors' contributions
R.R. performed the experimental measurements of silk strength and took the fracture surface images. J.K. performed the cross-sectional analysis. W.B., R.R. and X.W. developed the experimental plan. W.B. developed the retest analysis method and wrote the program in Matlab to analyse the data to assemble the composite curves. All authors reviewed the manuscript.
Conflict of interests
We have no competing interests.
References
- 1.Holland C, Terry AE, Porter D, Vollrath F. 2006. Comparing the rheology of native spider and silkworm spinning dope. Nat. Mater. 5, 870–874. ( 10.1038/nmat1762) [DOI] [PubMed] [Google Scholar]
- 2.Liu Y, Shao Z, Vollrath F. 2005. Relationships between supercontraction and mechanical properties of spider silk. Nat. Mater. 4, 901–905. ( 10.1038/nmat1534) [DOI] [PubMed] [Google Scholar]
- 3.Porter D, Guan J, Vollrath F. 2013. Spider silk: super material or thin fibre? Adv. Mater. 25, 1275–1279. ( 10.1002/adma.201204158) [DOI] [PubMed] [Google Scholar]
- 4.Scheibel T. 2004. Spider silks: recombinant synthesis, assembly, spinning, and engineering of synthetic proteins. Microb. Cell Factories 3, 1–14. ( 10.1186/1475-2859-3-14) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Teulé F, Miao Y-G, Sohn B-H, Kim Y-S, Hull JJ, Fraser MJ, Lewis RV, Jarvis DL. 2012. Silkworms transformed with chimeric silkworm/spider silk genes spin composite silk fibers with improved mechanical properties. Proc. Natl Acad. Sci. USA 109, 923–928. ( 10.1073/pnas.1109420109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shao Z, Vollrath F. 2002. Materials: surprising strength of silkworm silk. Nature 418, 741 ( 10.1038/418741a) [DOI] [PubMed] [Google Scholar]
- 7.Zhang Y, Yang H, Shao H, Hu X. 2010. Antheraea pernyi silk fiber: a potential resource for artificially biospinning spider dragline silk. J. Biomed. Biotechnol. 2010, 1–8. ( 10.1155/2010/683962) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Khan MMR, Morikawa H, Gotoh Y, Miura M, Ming Z, Sato Y, Iwasa M. 2008. Structural characteristics and properties of Bombyx mori silk fiber obtained by different artificial forcibly silking speeds. Int. J. Biol. Macromol. 42, 264–270. ( 10.1016/j.ijbiomac.2007.12.001) [DOI] [PubMed] [Google Scholar]
- 9.Fu C, Porter D, Chen X, Vollrath F, Shao Z. 2011. Understanding the mechanical properties of Antheraea pernyi silk—from primary structure to condensed structure of the protein. Adv. Funct. Mater. 21, 729–737. ( 10.1002/adfm.201001046) [DOI] [Google Scholar]
- 10.Zhang J, Kaur J, Rajkhowa R, Li JL, Liu XY, Wang XG. 2013. Mechanical properties and structure of silkworm cocoons: a comparative study of Bombyx mori, Antheraea assamensis, Antheraea pernyi and Antheraea mylitta silkworm cocoons. Mater. Sci. Eng. C 33, 3206–3213. ( 10.1016/j.msec.2013.03.051) [DOI] [PubMed] [Google Scholar]
- 11.Miura M, Pan ZJ, Aoyama S, Morikawa H, Mochizuki S. 1998. Analysis of the silkworm's shape distribution and serial shape changes in the course of spinning. J. Sericult. Sci. Jpn 67, 51–56. [Google Scholar]
- 12.Pérez-Rigueiro J, Elices M, Plaza G, Real JI, Guinea GV. 2005. The effect of spinning forces on spider silk properties. J. Exp. Biol. 208, 2633–2639. ( 10.1242/jeb.01701) [DOI] [PubMed] [Google Scholar]
- 13.Mortimer B, Holland C, Vollrath F. 2013. Forced reeling of Bombyx mori silk: separating behavior and processing conditions. Biomacromolecules 14, 3653–3659. ( 10.1021/bm401013k) [DOI] [PubMed] [Google Scholar]
- 14.Blamires SJ, Wu C-L, Blackledge TA, Tso I-M. 2012. Post-secretion processing influences spider silk performance. J. R. Soc. Interface 9, 2479–2487. ( 10.1098/rsif.2012.0277) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liu Y, Shao Z, Vollrath F. 2008. Elasticity of spider silks. Biomacromolecules 9, 1782–1786. ( 10.1021/bm7014174) [DOI] [PubMed] [Google Scholar]
- 16.Shao Z, Vollrath F. 1999. The effect of solvents on the contraction and mechanical properties of spider silk. Polymer 40, 1799–1806. ( 10.1016/S0032-3861(98)00266-3) [DOI] [Google Scholar]
- 17.Asakura T, Ito T, Okudaira M, Kameda T. 1999. Structure of alanine and glycine residues of Samia cynthia ricini silk fibers studied with solid-state 15N and 13C NMR. Macromolecules 32, 4940–4946. ( 10.1021/ma990442z) [DOI] [Google Scholar]
- 18.Asakura T, Nakazawa Y. 2004. Structure and structural changes of the silk fibroin from Samia cynthia ricini using nuclear magnetic resonance spectroscopy. Macromol. Biosci. 4, 175–185. ( 10.1002/mabi.200300098) [DOI] [PubMed] [Google Scholar]
- 19.Rajkhowa R, Gupta VB, Kothari VK. 2000. Tensile stress–strain and recovery behavior of Indian silk fibers and their structural dependence. J. Appl. Polym. Sci. 77, 2418–2429. () [DOI] [Google Scholar]
- 20.Zhang Y, Wang X, Pan N, Postle R. 2002. Weibull analysis of the tensile behavior of fibers with geometrical irregularities. J. Mater. Sci. 37, 1401–1406. ( 10.1023/A:1014580814803) [DOI] [Google Scholar]
- 21.Guan J, Porter D, Vollrath F. 2012. Silks cope with stress by tuning their mechanical properties under load. Polymer 53, 2717–2726. ( 10.1016/j.polymer.2012.04.017) [DOI] [Google Scholar]
- 22.Horrocks NPC, Vollrath F, Dicko C. 2013. The silkmoth cocoon as humidity trap and waterproof barrier. Comp. Biochem. Physiol. Part A: Mol. Integr. Physiol. 164, 645–652. ( 10.1016/j.cbpa.2013.01.023) [DOI] [PubMed] [Google Scholar]
- 23.Pérez-Rigueiro J, Viney C, Llorca J, Elices M. 1998. Silkworm silk as an engineering material. J. Appl. Polym. Sci. 70, 2439–2447. () [DOI] [Google Scholar]
- 24.Guan J, Vollrath F, Porter D. 2011. Two mechanisms for supercontraction in Nephila spider dragline silk. Biomacromolecules 12, 4030–4035. ( 10.1021/bm201032v) [DOI] [PubMed] [Google Scholar]
- 25.Lefevre T, Rousseau M-E, Pezolet M. 2007. Protein secondary structure and orientation in silk as revealed by Raman spectromicroscopy. Biophys. J. 92, 2885–2895. ( 10.1529/biophysj.106.100339) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sen K, Babu M. 2004. Studies on Indian silk. I. Macrocharacterization and analysis of amino acid composition. J. Appl. Polym. Sci. 92, 1080–1097. ( 10.1002/app.13609) [DOI] [Google Scholar]
- 27.Cheng Y, Koh L-D, Li D, Ji B, Han M-Y, Zhang Y-W. 2014. On the strength of β-sheet crystallites of Bombyx mori silk fibroin. J. R. Soc. Interface 11, 20140305 ( 10.1098/rsif.2014.0305) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Cranford SW. 2013. Increasing silk fibre strength through heterogeneity of bundled fibrils. J. R. Soc. Interface 10, 20130148 ( 10.1098/rsif.2013.0148) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Seydel T, et al. 2007. Silkworm silk under tensile strain investigated by synchrotron X-ray diffraction and neutron spectroscopy. Macromolecules 40, 1035–1042. ( 10.1021/ma0624189) [DOI] [Google Scholar]
- 30.Grubb DT, Jelinski LW. 1997. Fiber morphology of spider silk: the effects of tensile deformation. Macromolecules 30, 2860–2867. ( 10.1021/ma961293c) [DOI] [Google Scholar]
- 31.Glišović A, Vehoff T, Davies RJ, Salditt T. 2008. Strain dependent structural changes of spider dragline silk. Macromolecules 41, 390–398. ( 10.1021/ma070528p) [DOI] [Google Scholar]
- 32.Du N, Yang Z, Liu XY, Li Y, Xu HY. 2010. Structural origin of the strain-hardening of spider silk. Adv. Funct. Mater. 21, 772–778. ( 10.1002/adfm.201001397) [DOI] [Google Scholar]
- 33.Ling S, Qi Z, Knight DP, Huang Y, Huang L, Zhou H, Shao Z, Chen X. 2013. Insight into the structure of single Antheraea pernyi silkworm fibers using synchrotron FTIR microspectroscopy. Biomacromolecules 14, 1885–1892. ( 10.1021/bm400267m) [DOI] [PubMed] [Google Scholar]
- 34.Hearle JWS, Lomas B, Cooks WD. 1998. Atlas of fibre fracture and damage to textiles, 2nd edn Cambridge, UK: Woodhead. [Google Scholar]
- 35.Vollrath F, Madsen B, Shao Z. 2001. The effect of spinning conditions on the mechanics of a spider's dragline silk. Proc. R. Soc. Lond. B 268, 2339–2346. ( 10.1098/rspb.2001.1590) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Madsen B, Shao ZZ, Vollrath F. 1999. Variability in the mechanical properties of spider silks on three levels: interspecific, intraspecific and intraindividual. Int. J. Biol. Macromol. 24, 301–306. ( 10.1016/S0141-8130(98)00094-4) [DOI] [PubMed] [Google Scholar]
- 37.Garrido MA, Elices M, Viney C, Pérez-Rigueiro J. 2002. The variability and interdependence of spider drag line tensile properties. Polymer 43, 4495–4502. ( 10.1016/S0032-3861(02)00254-9) [DOI] [PubMed] [Google Scholar]
- 38.Denny M. 1976. The physical properties of spider's silk and their role in the design of orb-webs. J. Exp. Biol. 65, 483–506. [Google Scholar]
- 39.Zhou G, Shao Z, Knight DP, Yan J, Chen X. 2009. Silk fibers extruded artificially from aqueous solutions of regenerated Bombyx mori silk fibroin are tougher than their natural counterparts. Adv. Mater. 21, 366–370. ( 10.1002/adma.200800582) [DOI] [Google Scholar]
- 40.Wilson DM. 1997. Statistical tensile strength of Nextel™ 610 and Nextel™ 720 fibres. J. Mater. Sci. 32, 2535–2542. ( 10.1023/A:1018538030985) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The full set of experimental data is available at the Dryad repository.