Abstract
Morphology serves as a ubiquitous proxy in macroevolutionary studies to identify potential adaptive processes and patterns. Inferences of functional significance of phenotypes or their evolution are overwhelmingly based on data from living taxa. Yet, correspondence between form and function has been tested in only a few model species, and those linkages are highly complex. The lack of explicit methodologies to integrate form and function analyses within a deep-time and phylogenetic context weakens inferences of adaptive morphological evolution, by invoking but not testing form–function linkages. Here, we provide a novel approach to test mechanical properties at reconstructed ancestral nodes/taxa and the strength and direction of evolutionary pathways in feeding biomechanics, in a case study of carnivorous mammals. Using biomechanical profile comparisons that provide functional signals for the separation of feeding morphologies, we demonstrate, using experimental optimization criteria on estimation of strength and direction of functional changes on a phylogeny, that convergence in mechanical properties and degree of evolutionary optimization can be decoupled. This integrative approach is broadly applicable to other clades, by using quantitative data and model-based tests to evaluate interpretations of function from morphology and functional explanations for observed macroevolutionary pathways.
Keywords: geometric morphometrics analysis, finite-element analysis, response surface methodology, theoretical morphology, ancestral state reconstruction, Carnivora
1. Introduction
Organisms interact with their biotic and abiotic environments through their phenotypic characteristics, and phenotypic evolution in turn is mediated by the selection on genotypes. Palaeobiological studies of phenotypic evolution contribute critical and unique data to reconstruction of phylogenies and provide the deep-time context for evolution. Of particular interest to evolutionary biologists working within a deep-time context is how the record of organismal morphology can provide information about the tempo and mode of morphological adaptations, phenotypic features that enhance survival and reproduction for organisms in their interaction with the environment. However, complex trade-offs in the evolutionary optimization/transformation of those phenotypic traits may also influence subsequent rates of phenotypic change [1]. Dietary specialization is an important category of adaptations that has been viewed as central to understanding organismal evolution, because the incorporation of food energy for growth and reproduction is critical to survival [2].
Accurate identification of adaptations is contingent upon understanding the macroevolutionary and environmental context in which potentially adaptive traits arise [3]. Despite the critical importance of a deep-time perspective for understanding (and even identifying) potential adaptations, the limitation of the fossil record to mostly morphological remains prevents the direct application of modern biological toolkits for studying species behaviour, physiology, genetics and ecology to research on extinct taxa. Specifically, our knowledge of morphological macroevolutionary adaptations comes mostly from applying phylogenetic comparative methods to test form–function linkage among living taxa within a given clade. After discovering correlations between phenotypic and biomechanical characteristics, we then apply that form–function correlation or linkage to the study of fossils. However, besides the fact that redundancy is widespread in form–function linkages (e.g. many different morphological forms provide similar functions; the ‘many-to-one’ form–function mapping relationship) [4], the number of extant species for which specific form–function linkages are known constitutes a tiny fraction of the existing taxonomic diversity and morphological disparity found among organisms. A framework for directly evaluating functional implications of macroevolutionary changes in organismal form and their hypothesized ancestral morphologies, as well as the strength and direction of evolutionary pathways of transformation in putative adaptive features, therefore is much needed.
Recent developments in analyses of both form and function have permitted each aspect of organismal evolution to be addressed in increasingly measurable terms and allow the establishment of more quantitative links between the two [5–7]. Phylomorphospaces are now commonly employed to study macroevolutionary trends in morphological changes, and for functional morphological analysis, by correlation of morphology to biomechanical proxies such as those based on beam theory [8–10]. Explorations of theoretical morphology and theoretical morphospace in vertebrates have only just begun to take shape after decades of progress in research on invertebrates [11–15]. Yet, direct assessment of variations in assumed form–function linkages has seldom been conducted in any palaeobiological studies (but see [16]), and no study has yet combined all of these research approaches to test the validity of presumed evolutionary form–function linkages.
In this study, we present a new methodology to directly test form–function linkage integrating both modern taxa and deep-time morphological records from fossils. This new approach uses both terminal and reconstructed ancestral morphologies with a combination of quantitative analyses of form (geometric morphometrics, GMM) and mechanical properties (finite-element analysis, FEA). We also apply a method for determining strength and direction of functional changes along evolutionary pathways, using a form–function optimization criterion based on a design of experiment (DOE) protocol originally developed in the experimental statistics discipline.
As a case study, we sampled living and extinct species of carnivorous mammals in Carnivoramorpha, the clade including all living Carnivora (dogs, cats, seals, bears, etc.) and their extinct stem- and near-relatives within the Ferae, which includes Carnivora, the more inclusive clade Carnivoramorpha, and the extinct order Creodonta [17–20]. We analysed skulls of different feeding morphologies by quantifying shape differences using GMM analysis and conducted biomechanical simulations using FEA. We estimated the mechanical properties of terminal species and reconstructed ancestral forms based on two parameters hypothesized to be important factors in the evolution of feeding specializations: bite force (BF) production (represented by mechanical efficiency, ME, the ratio between output and input forces) and skull strength (represented by total skull strain energy, SE, a measure of skull stiffness). We then applied protocols from experimental statistics known as response surface methodology (RSM) to assess optimal directions of change in a GMM phylomorphospace of these two functional parameters at reconstructed ancestral nodes (figure 1). RSM is commonly used in chemical experiments and industry product development where optimal mixtures of multiple input variables are desired in order to maximize one or more parameters (e.g. costs of raw materials versus a desired property in the final product).
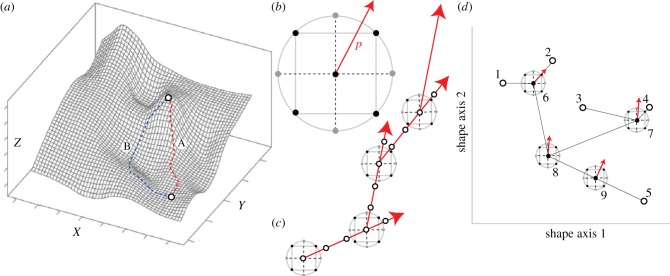
Figure 1.
Macroevolutionary application of RSM and paths of steepest ascent/descent. (a) A hypothetical functional landscape, showing the paths taken by the steepest ascent (path A) versus a non-optimal route (path B) to a local optimum in Z-value (measured performance or function) relative to the input factors X and Y (adapted from [21]). (b) The central composite design (CCD) approach of RSM, with a basic box or square structure (black points, the approach used in this study) and a crossed star structure (grey points), applicable for two-factor systems. A polynomial model is fitted to experiments conducted at each of the black and grey points, and a path of steepest ascent/descent (p) is calculated. (c) An example of iterative experiments informed by paths of steepest ascent/descent, showing a series of CCD experiments conducted at the peak of the projected steepest path in the preceding experiment. The paths lead progressively closer to the optimal solution. (d) How RSM can be applied in a macroevolutionary, functional morphological context. A hypothetical phylomorphospace of five terminal nodes (nos. 1–5) and four internal nodes (nos. 6–9). Thin lines connecting nodes represent approximate evolutionary pathways, and CCD experiments at internal nodes show the path of steepest ascent/descent (arrows) at that node. (Online version in colour.)
Given known trade-offs in the two biomechanical parameters among carnivore feeding morphologies, in which ME increases and SE decreases are associated with partially opposing changes in skull shape [22], we tested the hypotheses that: (1) ME and SE are not simultaneously optimized along the evolutionary pathways analysed [21], (2) hypercarnivores (meat specialists) evolved along morphological pathways of more optimal increases in ME for hunting large-bodied prey compared with dietary generalists, because of the larger force required to both kill and process the large prey that are necessary to satisfy their energetic demands [23], whereas (3) in the context of the ME–SE trade-off, strength should be just as important as, or more so than, ME in generalists. We expect generalists to have evolved along morphological pathways of either no optimization in ME or SE, or possibly a more optimal increase in overall SE to accommodate variable stresses produced by the different masticatory strategies required to process a broader range of food items and material properties, but which may not necessarily require high forces, compared with the feeding style of hypercarnivores.
1.1. Response surface methodology as an optimality criterion
The iterative process by which improvements in material yield, quality, etc. are guided by DOE analyses in industrial, engineering and chemical experiments shares several conceptual commonalities with hypothesis testing in functional morphology analyses in biology. In biological research, evolutionary changes in morphological characteristics are often interpreted as having selective advantages in some functional sense, e.g. in feeding, locomotion or reproduction [24]. For instance, when the descendant of an ancestor–descendant pair of species exhibits novel characteristics that appear to represent morphological specialization for a specific task (a form–function relationship), one hypothesis could be that the new characteristics permit more optimized performance relative to the ancestral condition. An exemplar case would be changes in the mechanical advantage of the feeding apparatus in jawed vertebrates: a longer in-lever arm for jaw-closing muscles relative to a given out-lever arm to the bite position translates into increased BF given the same magnitude of muscle input. In this case, one null hypothesis for the proposed adaptation for higher BF would be that the evolution of craniodental morphology tends to increase mechanical advantage from the ancestral to the descendant species.
Applying an RSM approach to testing a null hypothesis that, in measuring change in BF output from ancestor to descendant, it will reflect an optimal increase in mechanical advantage, involve running experiments on theoretical morphologies. This can be done using a factorial design, with the centre point as the ancestral morphology, and surrounding test points generated using theoretical morphology techniques (figure 1). Input factors for RSM tests would be morphological or shape measurements (e.g. skull depth, width and length; areas of muscle attachment; or multi-variate shape variables), and the response measurements then should be the resulting ME (as estimated using biomechanical first principles, or using a modelling approach) or some other functional parameter. After fitting a polynomial model to predict ME using morphological parameters, a path of steepest ascent (or descent, if the attribute is to be minimized instead of maximized) is calculated to indicate the direction of optimal change in morphology to achieve maximal improvement in function. The direction of actual evolutionary change in morphology from the ancestral to the descendant condition then can be compared with this path, and differences between them used to evaluate how closely the actual evolutionary pattern followed a theoretically optimal one predicted by RSM (figure 1d). As with all previous work on theoretical morphology approaches to studying macroevolution, the isolation of key morphological and functional factors is necessary, but at the same time represents simplifications of highly complex and integrative biological systems that may constrain the breadth of interpretations possible [12].
2. Material and methods
In this case study, we sampled five species from different living carnivoran families that covered a range of body sizes and dietary preferences: the hypercarnivorous caniform grey wolf (Canis lupus) and feliform leopard (Panthera pardus), the vertebrate/insect-feeding caniform striped skunk (Mephitis mephitis) and feliform Asian mongoose (Herpestes javanicus), and the omnivorous caniform raccoon (Procyon lotor), with the last three taxa all considered to be ‘generalist’ feeders (table 1). In addition, we analysed the extinct stem carnivoramorphan Oodectes herpestoides, which is a Palaeogene species represented by a nearly complete, undistorted skull suitable for the shape and functional analyses conducted in this study [18]. Lastly, we included the Palaeogene small hyaenodontid Thinocyon velox as a representative near relative or out-group for inferring ancestral states for the Carnivoramorpha/Carnivora. The goal was to apply a novel methodology to a case study of carnivorous mammals, thus our sampling is illustrative but not comprehensive.
Table 1.
Terminal Ferae species used for ancestral state reconstructions. Body mass and diet information adapted from [25,26]. Daggers indicate extinct species.
| family | species | body mass range (kg) | diet | feeding morphology |
|---|---|---|---|---|
| Mephitidae | M. mephitis | 0.7–6.3 | rodents, birds and insects | generalist |
| Procyonidae | P. lotor | 1.8–10.4 | wide range | generalist |
| Canidae | C. lupus | 23–80 | large mammals | hypercarnivore |
| Felidae | P. pardus | 17–65 | large mammals | hypercarnivore |
| Herpestidae | H. javanicus | 0.43–0.65 | 19–37% vertebrates, 63–70% non-vertebrates | generalist |
| ‘stem Carnivoramorpha’ | †O. herpestoides | n.a. | n.a. | generalista |
| Hyaenodontidae | †T. velox | n.a. | n.a. | hypercarnivorea |
aBased on [22].
2.1. Geometric morphometrics
All specimens were CT-scanned in the American Museum of Natural History Microscopy and Imaging Facility, New York, NY, using a GE v|tome|x high-resolution X-ray micro-CT scanner. Scanning parameters included a voltage of 150–170 kV, tube current of 55–180 mA and voxel size of 37–136 μm. Segmentation and three-dimensional reconstruction of the skull CT data were conducted in Mimics v. 16 (Materialise, Leuven, Belgium). The three-dimensional surfaces were exported as stereolithography files and imported into Landmark editor [27] for landmark digitization. A total of 126 three-dimensional landmarks, including 38 fixed landmarks distributed throughout the skull and 88 semi-landmarks on surfaces representing areas of attachment for the temporalis and masseter muscle groups, were digitized for each skull (electronic supplementary material, figure S1). The digitized three-dimensional landmark dataset was imported into MorphoJ [28], in which superimposition was conducted using generalized Procrustes analysis, and a covariance matrix generated [28]. Principal components analyses (PCAs) were conducted using the residuals of a regression analysis between landmark shape variables and log centroid size to remove the effect of size on shape variation. A phylogenetic tree based on those of Spaulding & Flynn [17] and Wesley-Hunt & Flynn [18] was imported into MorphoJ, and a phylomorphospace (phylogeny mapped onto a plot of PC scores) then was generated using unweighted squared-change parsimony (uSCP) estimation of ancestral nodes in the shape space based on the tree topology (also in MorphoJ).
We did not use branch length information in our phylogeny because reliable published estimates are not yet available for all of the nodal ages and internode branch lengths in our pilot study sample. However, to assess potential differences in the resulting internal node models, we conducted a sensitivity test to examine the effect of some branch lengths on the morphology of our ancestral state reconstructions, using unpublished nodal calibration data (JJ Flynn et al. 2015). Comparison of ancestral state reconstructions at internal nodes (see RSM methods below) indicates that most differ by less than an average 1.73% between uniform versus calibrated branch length reconstructions (electronic supplementary material, table S1). This difference is less than half of the average 3.86% difference found between nodal reconstructions within each branch length method (electronic supplementary material, table S2). The morphospace also appears visually similar between ultrametric and uniform branch length trees (electronic supplementary material, figure S3). Therefore, we concluded that there was minimal difference between and potential impact of different branch length methods (uniform versus calibrated) for biomechanical simulations conducted in this study.
Hypothetical landmark coordinate datasets, representing internal (ancestral) node reconstructions in the phylomorphospace, were obtained by back-transforming the PC scores at the locations of each of the internal nodes. The transformation was applied to the PC coefficient matrix [29] using a custom script written by the authors (Z.J.T.) in the R programming language (electronic supplementary material, appendix A). Only PC1 and PC2 scores were used because the basic box design implemented permits only two factors (figure 1). Reconstructed ancestral skull shapes were generated by morphing from the three-dimensional surface model of O. herpestoides, the most basal of the carnivoramorphan species examined, in Landmark editor, similar to the procedure used by Stayton [30]. The benefit of analysing ancestral skull shapes that were generated using the O. herpestoides base model is the ability to compare across homologous tooth positions in subsequent biomechanical analyses. The morphed skulls representing the estimated shapes at the nodes then were used as centre points in a factorial design experiment (figure 1b). In all cases, we used the box design (a total of five theoretical reconstructed models at each internal node), which was adequate to produce fitted first-order polynomial equations.
2.2. Finite-element analysis
All of the actual ancestral node, and the additional theoretical three-dimensional skull shapes required by the box design, were imported as stereolithography files into Mimics, and remeshed to standardize the quality and numbers of triangle elements that were distorted during the morphing process. All surfaces then were meshed with four-noded tetrahedral (‘tet4’) elements in Strand7 FEA software v. 2.4.6 (Strand7 Pty Ltd, Sydney, Australia). All models were scaled to the same total bone volume (electronic supplementary material, table S3). Therefore, all reported values are relative magnitudes used for comparisons within this suite of analyses, so are not to be interpreted in absolute terms [31]. Jaw-closing muscle attachment areas for the temporalis, masseter and pterygoid groups were highlighted in the theoretical reconstructed models according to analogous anatomical positions in actual species models, which are based on published literature [32,33]. Evenly distributed forces over the surface plates of the muscle attachment areas then were assigned to the attachment areas using the BoneLoad program written by Grosse et al. [31]. Input force percentages for all models were made proportional to estimated physiological cross-section area (in mm2), using the dry skull method [34]; the estimated areas were multiplied by 0.3 N, the maximum tension produced by a single mammalian muscle fibre [35,36]. This adjustment allowed the models to be used in future studies, when muscle fibre size and density data become available for extant species, and can be directly incorporated into the current models. This approach to estimating muscle input force generates BF results in finite-element (FE) models that are similar to those obtained using the dry skull estimate [37].
The skull models were constrained at the temporomandibular joints to allow rotation around the axis along the two joints, and single fixed nodes were placed at the crown tip of each tooth for calculating reaction forces. The skulls were assigned a homogeneous set of isotropic material properties based on mammalian cortical bone measurements from previous studies: an elastic modulus of 20 GPa and Poisson's ratio of 0.3 were used [38,39]. Teeth were not modelled as a separate material because our main interest was to obtain broad comparative patterns in ME and SE, but we recognize the importance of analyses that consider boundaries between different materials as complementary to, and informative for, our analyses of overall skull mechanical properties.
All FE analyses were linear and static. The responses measured from the FEA are BF (in newtons, later converted to ME by dividing BF by input muscle force) and skull SE (in units of microstrain) [31]. Bite positions tested ranged from the canine to the last cheek tooth and varied for the actual species models because of different dental formulae among them; all theoretical reconstructed models included bite simulations from the canine to the third molar (for a total of seven tooth loci). All models created are included in the electronic supplementary material, appendix B.
2.3. Response surface methodology
The theoretical reconstructed models from GMM analyses were set up and analysed with FE analyses using the same protocol applied to terminal species models above. We constructed four theoretical models around each ancestral node model by setting PC1–PC2 scores from the PCA in the GMM analyses to deviate from the ancestral node location in a square pattern (figure 1). The distance of deviation from the ancestral node was arbitrarily set at 0.01 units in both PC1 and PC2 (note that, because each PC axis explained a different proportion of total skull shape variation, a deviation of 0.01 translated to differing degrees of morphological change in PC1 versus PC2, analogous to coded factors in DOE methods); therefore, the four corners of the square experimental design had deviations from the ancestral node of (+0.01,+0.01), (+0.01,−0.01), (−0.01,+0.01) and (−0.01,−0.01) in PC1 and PC2 values, respectively. All models were scaled to have identical FE model volume in order to standardize the amount of material (i.e. bone) present in the models, and the shape of the skulls and muscle attachment surface areas were allowed to vary. We chose this scaling method based on the logic that the homogeneous cortical bone modelling approach used in this study is suitable for studying evolutionary shape modifications of an energetically expensive biomaterial, which might be expected to be minimized or kept constant under functional changes in shape instead of volume.
ME and SE values from FEA (electronic supplementary material, table S4) were fitted to first-order polynomial equations using the DOE Response Surface functions in Minitab statistical software (Minitab Inc., State College, PA, USA). A linear model was fitted to experimental data at each node, and the paths of steepest ascent in ME (for hypothesized maximum force production efficiency increase) and steepest descent in SE (for hypothesized minimum amount of energy absorbed by the skull) were calculated (electronic supplementary material, figure S4). The data from the response surface analyses then were graphed onto the phylomorphospace. All response surface analyses were conducted on the shape dataset with all landmarks treated as fixed. Using this approach also allowed a straightforward process of back-transforming any combination of PC scores into original x, y, z coordinates. The assessment of similarity in directions of actual and optimal evolutionary pathways was done using one-tailed t-tests of circular means of ME and SE values from all seven tooth loci of the theoretical reconstructed model FEA, against the branching direction provided by the GMM phylomorphospace. The t-tests were done using the Matlab toolbox CircStat [40].
3. Results
3.1. Geometric morphometrics
The two-dimensional morphospace generated from PCA of superimposed three-dimensional landmarks and semi-landmarks encompasses 75.31% of the variation in the skull shape dataset (PC1: 45.29%, PC2: 30.02%). Feliform species tend to have more negative PC2 scores, whereas caniforms tend to have more positive PC2 scores (figure 2). Canis lupus, representing the most basal crown group species, has a very positive PC1 score, similar to both the stem carnivoramorphan Oodectes and the out-group Thinocyon.
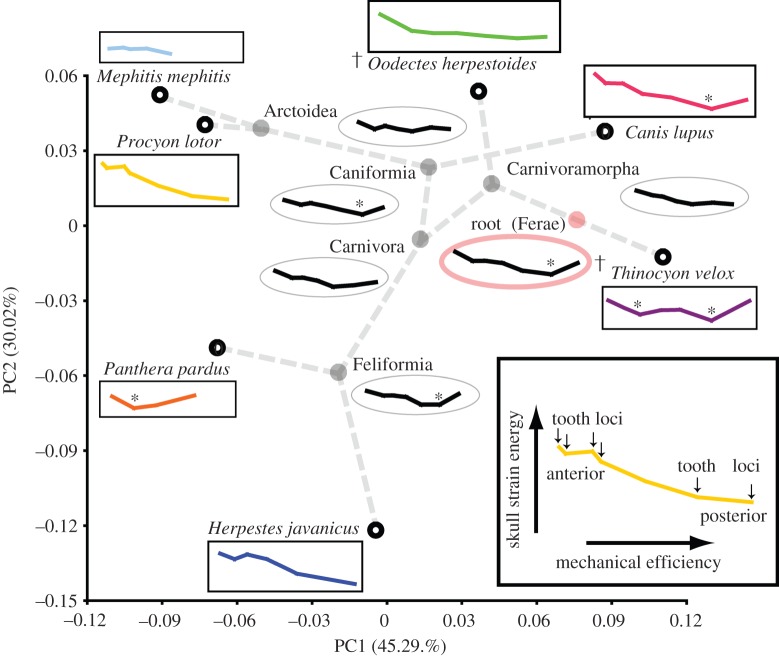
Figure 2.
Macroevolutionary changes in biting capability in a carnivore phylomorphospace. ME and skull SE curves for model simulations at terminal (rectangular boxes) and internal nodes (ovals). Profiles with inflection points associated with hypercarnivory are indicated by asterisks. Daggers indicate extinct species. Colours in the online version correspond to species data shown in the electronic supplementary material, figures S2 and S7. (Online version in colour.)
Mapping of a phylogeny onto this PCA morphospace produced six reconstructed ancestral nodes using uSCP. Nodes representing the root, Carnivoramorpha, Carnivora and Caniformia are in close proximity to each other. Ancestral node PC scores were back-transformed into three-dimensional skull models and exhibited intermediate shapes to the terminal species, as consistent with the intermediate positions of the internal nodes (electronic supplementary material, figure S1).
3.2. Finite-element analyses
Analyses of terminal species models returned a grouping of caniform species versus feliform species plus Thinocyon, as reported by Tseng & Flynn [22]. Feliforms plus Thinocyon show the lowest adjusted SE levels, followed by caniforms. Oodectes showed the highest SE values, but also exhibits a range of ME shifted towards a range of 15–30% compared with 10–25% for all of the other species sampled (electronic supplementary material, figure S2).
A total of four models around each node were used to form a box design, with corners that are 0.01 units in each direction from the centre, in the PC1–PC2 morphospace. Six internal nodes were analysed (plus a model at the origin of the morphospace for verification), resulting in a total of 30 theoretical reconstructed models (five for each of six internal nodes analysed) and 420 individual bite simulation analyses (seven tooth positions on each side of the tooth row simulated for left and right sides of all 30 models). The number of tet4 elements in the various models ranged from 962 806 to 1 569 897 (electronic supplementary material, table S3). Regression analyses between the number of tetrahedral FEs in each theoretical reconstructed model and the estimated muscle surface area (MSA) measured from the model indicated R2 values of 0.1–18.0%, suggesting that most variability in the data is not explained by linear relationships (electronic supplementary material, figures S5 and S6). Regressions between the residuals of the tet4 quantity-MSA (to remove size effects) and the outcomes of FEA (ME and SE) also showed similarly low R2 values between FE quantities and biomechanical attributes used for subsequent functional interpretations. Therefore, we conclude that the differences in quantities of FEs in each of the theoretical reconstructed models did not linearly bias the resulting biomechanical attributes measured from FEA.
Biting simulations of theoretical reconstructed models using FEA are summarized using whole-dentition biomechanical profiles [9]: ME–SE profiles for theoretical reconstructed models at internal nodes tend to be less extreme in the range of both ME and SE values than the terminal taxa (figure 2). The root (Ferae), Caniformia and Feliformia node theoretical reconstructed models all possess inflection points in the biomechanical profile, similar to those observed in the extant hypercarnivores (Panthera and Canis), whereas other internal nodes have declining profiles that more closely resemble extant vertebrate–insect (Mephitis and Herpestes) and omnivore (Procyon) feeders (figure 2).
To examine overall distributions of forces being conducted through the skull models, we visualized stress (or force per unit area) levels using heat maps of von Mises stress values (electronic supplementary material, figure S7). Von Mises stress distribution provides information about anatomical regions most likely to fail under a ductile mode of deformation [41]. The visualizations show that the zygomatic arches represent the weakest regions in all actual species and the theoretical reconstructed models tested. The more basal theoretical reconstructed node models also tend to exhibit more concentrated stress in the frontal region than the more crown-ward theoretical reconstructed models. Lastly, Canis and Procyon exhibit the most concentrated area of stress in the frontal and nasal regions of the skull under similar simulated biting scenarios compared with all other terminal species sampled (electronic supplementary material, figure S7).
3.3. Response surface methodology
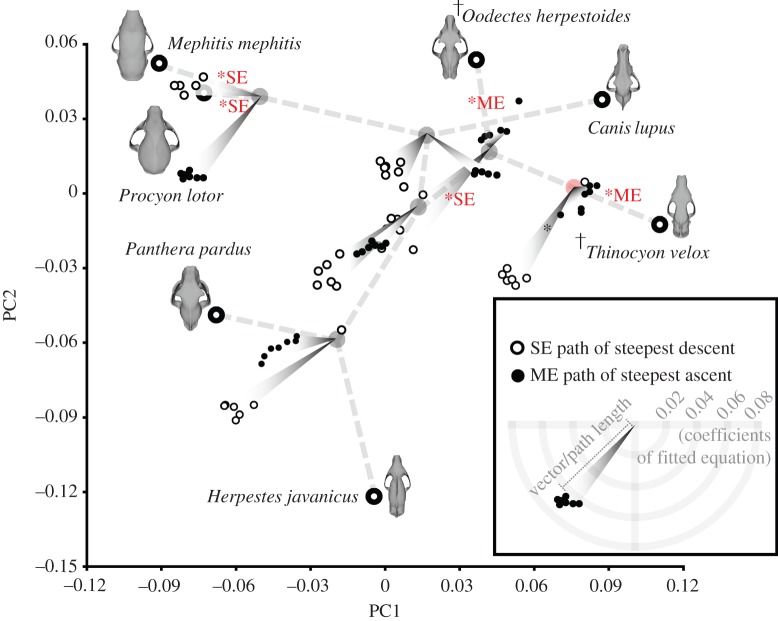
The fitted linear equations for both ME and SE values from hypothetical reconstructed models were used to generate paths of steepest ascent (for ME, showing optimal increase in force production) and descent (for SE, showing optimal decrease in SE absorbed by the skull, and corresponding increase in skull stiffness). Coefficients of changes along PC1 and PC2 axes ranged from 0.02 to 0.078 (figure 3; electronic supplementary material, figure S4). Optimal path directions for SE decreases tend to be steeper (i.e. the vectors representing coefficients are longer) than those for ME (figure 3; electronic supplementary material, figure S4). The variation in the direction of steepest decrease at an internal node, across the canine to third molar (M3) tooth loci, can be as high as approximately 124° between vectors of extreme values at each node (figure 3: variation indicated by shaded triangles). The range of angles decreased from the basal nodes to the more crown-ward nodes.
Figure 3.
Paths of steepest ascent for ME and descent for SE at each internal (ancestral) node, based on experimental results from hypothetical models using RSM. Longer path lengths indicate larger changes in attribute relative to change in PC1–PC2 values. Steepest paths of ME and SE change are shown for all tooth loci in the hypothetical models (from canine to M3). Path distances from each internal node are not in absolute units of the PC axes; they are enlarged to show trends, and only represent relative magnitudes of change and not in units of PC1–PC2 scores. Evolutionary pathways that are not statistically different from the reconstructed paths of steepest change are indicated by an asterisk, followed by the attribute that is optimized. Daggers indicate extinct species. For additional details of the RSM results, see the electronic supplementary material, figure S4. (Online version in colour.)
There are five cases in which the uSCP reconstructed evolutionary path from ancestral nodes is statistically indistinguishable from the steepest paths of ME increase or SE decrease calculated by RSM: the paths from (1) root node to T. velox, with ME increase; (2) Carnivoramorpha node to O. herpestoides, with ME increase; (3) Carnivoramorpha node to the Carnivora node, with SE decrease; (4) Arctoidea node to P. lotor with SE decrease; and (5) Arctoidea node to M. mephitis with SE decrease (figure 3). All other branches are different (p < 0.05) in one-tailed tests of mean angle with optimized paths of either ME increase or SE decrease (electronic supplementary material, table S5).
Optimal increases in ME per unit of skull shape change in the PC1–PC2 morphospace for branches leading to Oodectes and Thinocyon are much flatter in slope (i.e. the paths are closer to their respective internal nodes) than the BF increases per unit of skull shape change in Panthera. The ME increase is largest per unit of skull shape change at the Arctoidea node (figure 3). Skull SE decrease is largest at the root, Carnivora and Feliformia nodes, but none of the actual evolutionary pathways leading from these nodes fall in the optimal path direction (figure 3).
4. Discussion
To test several hypotheses about optimality in the evolutionary pathways of carnivoran feeding systems, we applied a new, integrative method that combines GMM, FEA and RSM to study ME and skull SE evolution in a sample of hypercarnivore and generalist (vertebrate–insect feeders and omnivore) carnivoran species. The results show that: (1) none of the evolutionary pathways analysed are optimized simultaneously in both ME and SE (figure 3; electronic supplementary material, table S5); (2) the two extant hypercarnivores C. lupus and P. pardus did not evolve along pathways of optimal increase in ME; and (3) the three carnivoran generalists in our sample evolved either along optimal pathways in SE decrease or along pathways that are optimized in neither ME nor SE. Therefore, the first and third hypotheses posed in this study were not rejected by the data in these tests.
The adaptational hypothesis that hypercarnivores evolved along morphological pathways of optimal increase in ME is not supported by the results. The morphospace is clearly dominated by phylogenetic structure, but both Canis and Panthera nevertheless show more pronounced inflected ME–SE profiles (see discussion below) relative to their theoretical reconstructed ancestral models, indicating evolutionary increases in skull stiffness. Thus, non-optimal ME evolution cannot be adequately explained as simply due to phylogenetic history. In a study of bone-cracking carnivoran species, Tseng [21] found that skull shapes of extant and fossil bone-crackers are less than optimal in their ME–SE ratios within a range of theoretically possible shapes, even though those species are likely to have been selected for high ME required to break through very hard materials such as bone. Therefore, functional requirements on craniodental morphology other than ME and SE may impose constraints that produced the observed patterns in our analyses, and a broader context examining additional functional parameters (e.g. for both sensory and feeding tasks) in the skull may be required to identify causes for limitations to ME optimization in these hypercarnivores.
Caniform and feliform species are at opposite ends of the PC2 axis within the phylomorphospace, and there is no clustering of predefined feeding morphologies across the two clades. Instead, hypercarnivore and generalist morphologies across these clades can be definitively identified using the shape of the ME–SE profiles. However, in spite of being able to recognize feeding morphologies across clades, the two taxa with optimal ME increase in their evolutionary pathways (Oodectes and Thinocyon) do not both belong to the same ecomorph categories based on form–function linkage among the species models—although Thinocyon is categorized as a hypercarnivore, as would be predicted for ME optimization, Oodectes instead is categorized as a generalist (table 1 [22]). This result indicates that evolutionary pathways that trend in the optimal direction of ME increase can be found in different feeding morphologies, and do not necessarily distinguish otherwise mechanically distinctive hypercarnivores from dietary generalist terminal taxa. Therefore, shared mechanical properties along evolutionary pathways can be decoupled from, or at least not tightly associated with, form–function linkages observed in extant terminal species, despite them being well-defined feeding morphologies.
Despite clear influence of phylogenetic structure in carnivore skull shape, and the decoupled results between species models and evolutionary pathways, functional signals are still recovered from the biomechanical analyses of ancestral node reconstructions. The hypercarnivore feeding morphologies (Panthera, Canis and Thinocyon) all show more pronounced inflections (having a clear low point in SE in biting simulations across tooth loci) in their biomechanical profiles than their respective ancestral node models (figure 2). An inflection in the biomechanical profile suggests that the biting mechanics of the skull does not simply follow a trend of decreasing SE and increasing ME as expected from first principles of lever mechanics; instead, a tooth locus exists at a position within the tooth row that produces BF at the lowest value of SE estimated across all biting positions. This inflection point thus represents a tooth location where bites can be produced most efficiently relative to minimizing SE (which is a measure of the work done by muscle forces in deforming the skull, with lower values indicating stiffer skulls that are better at conducting muscle force to output BF). In Canis and Thinocyon, a longer (relatively higher ME at posterior tooth loci) and deeper (relatively lower SE at inflection points) profile characterizes their specialization for higher ME and relatively stiffer skull response at key tooth loci in the lower carnassial (shearing) teeth.
A hypercarnivorous ancestral model, with a profile of inflection points at posterior tooth loci, evolved into a profile with an inflection point that is situated at a more anterior tooth locus in Panthera, indicating emphasis for ME and skull stiffness at anterior tooth loci in that felid predator (figure 2). These findings are consistent with observed phenotypic and behavioural differences between the bone-crushing posterior teeth of C. lupus and the hold-and-kill anterior dentition of P. pardus [25,42]. The results thus indicate that ancestor–descendant changes in ME and SE and the shape of the overall biomechanical profiles are both more informative for identifying hypercarnivorous specializations in the current dataset and analyses than is the strength of evolutionary increase in ME per se. A broader taxonomic sample is being assembled to further test this observation across larger datasets.
For dietary generalists, the evolutionary pathways leading from Caniformia to Mephitis and Procyon and from Feliformia to Herpestes are both represented by disappearance of inflection points in the biomechanical profiles, as well as shifts towards a typical generalist profile of gradually decreasing SE with increasing ME across tooth loci (figure 2). Arctoid skull shape evolved in a direction of optimal increases in skull strength, supporting the third hypothesis of generalists evolving greater skull strength for a broad diet. The evolutionary path from Feliformia towards Herpestes is optimal neither in ME nor in SE, but is still consistent with the hypothesis of generalists not emphasizing ME. Closer to the base of the tree, the ancestral node FEA indicates that the root (the Ferae clade) was a hypercarnivorous ancestor with a clear inflection in the biomechanical profile, whereas Carnivoramorpha and Carnivora ancestors were more omnivorous and lacked that inflection. Subsequently, Caniformia and Feliformia independently evolved more hypercarnivorous ancestral biomechanical profiles for those two main clades of carnivorans, and within Caniformia the Arctoidea reversed to a more generalist biomechanical profile (figure 2); this result could be a function of taxon sampling in our case study, because no hypercarnivores were sampled from within Arctoidea.
It is noteworthy that the reconstructed path of steepest descent in SE at all nodes tends to point in the same general direction (towards the left of the phylomorphospace, a region representing skulls with a relatively shorter and deeper face and cranial vault) and indicates the presence of a single locally optimal direction for skull strength evolution (figure 3). On the other hand, paths of steepest ascent in ME do not uniformly point in one direction, suggesting that there may be multiple optimal peaks. Evidence of selection of multiple peaks for biomechanical performance in ME of biting has been demonstrated in bats [43], and our findings suggest that it could have occurred in carnivoramorphans as well.
These new model-based and empirical results lead to several additional testable hypotheses for future research: (1) Is the overwhelming phylogenetic structure separating caniform and feliform skull shape still reflected in biomechanical attributes, when additional species are added? (2) Is the conclusion that feeding morphologies can be inferred from the ME–SE profiles (by examining only the relative shape of the profile for ME range and presence/absence of inflection points at tooth loci) supported when additional feeding morphologies (e.g. omnivorous ursids, bone-cracking hyaenids, frugivorous Nandinia, etc.) are analysed? (3) Whether the conclusion that caniforms and feliforms are convergently more hypercarnivorous than their common carnivoran or carnivoramorphan ancestor is supported by broader sampling in the crown clade, at the base of the tree, and with additional out-group ecomorphs? Future improvements in this combined FEA–GMM–RSM approach would also involve quantification of the effects of varying branch lengths to estimates of ancestral states [44] and examination of the effects of different ancestral state reconstruction methods for other continuous characters that are correlated to biomechanical properties.
An important point regarding the ancestral FE models used in this study is that the current method of morphing the most basal species in the dataset into all internal node models may be problematic if large ranges of morphological differences are present (for example, in a larger taxonomic dataset). One way to produce better estimates of ancestral shapes through morphing may be to use several iterations of averages of morphed shapes (by applying the morphing operation at each node using both descendant shapes, then averaging the two morphed shapes) among sister species from the tip to the base of the phylogeny. Using such an approach would make internal node models more closely resemble morphological characteristics of their descendant species/clades. Of course, such an iterative morphing process would be too time intensive to do by hand for larger datasets, and therefore a script or program could be developed to facilitate the testing of different morphing algorithms.
4.1. Limitations of the response surface methodology approach
An important, existing limitation of the range of theoretical morphological studies in the literature is the low number of functional traits or phenotypic parameters that often are distilled from observed organismal diversity for use in theoretical studies. The key factors studied typically represent but a fraction of the complexity of the biological structures themselves, and thus also those of the history of selection on them [12]. Simplification of a complex phenomenon renders the elucidation of broad functional mechanisms for the generation of morphological disparity difficult; however, models of functional evolution are nevertheless useful in permitting the relative importance of different factors to be assessed in silico. A second issue is that the robustness of conclusions derived from studies using RSM partially depends on the performance variables used, and therefore the reliability of those variables has an effect on RSM results. Estimates of skull stress and strain using FEA have not been widely validated [45], and much future work is needed in obtaining species-specific validation to more confidently use FEA results in theoretical reconstructed models to test form–function linkage hypotheses. Even so, in a purely comparative context, especially one employing theoretical morphology, it is the general patterns that are used for interpretation, not the absolute magnitudes of a given biomechanical property.
Other issues such as the number of material properties, input force estimation method and inherent variability in the calculations of FEA solutions all contribute to the downstream uncertainty in RSM results [46–48]. The FEA protocol used in this study involved two-dimensional estimation of muscle input force and simplified homogeneous material property models; further testing should be done using both three-dimensional muscle estimation and multiple-property models as well as experimentally derived data when those become available. Incorporation of additional replicates of the same RSM experimental design (i.e. building and analysing the same theoretical sampling points multiple times) is an additional way to account for uncertainty in FEA outputs. Lastly, the uSCP and phylomorphospace methods currently available all reconstruct evolutionary pathways as straight lines between nodes. The assumption that morphology will evolve exactly along this line is oversimplified; an improvement in this method would be to incorporate degrees of uncertainty into reconstruction of evolutionary pathways. Along the same lines, improved ways to account for uncertainty in the estimation of optimal directions of change (through larger RSM designs with more experimental replicates) and incorporating differential ‘penalties' for deviation of evolutionary pathways from steeper versus flatter optimal pathways are both aspects of the approach to be further developed. Having a range of possible evolutionary pathways and a more sophisticated optimality metric between any two nodes would permit more robust statistical tests to be conducted between samples of evolutionary pathways and samples of theoretical optimal pathways, and may be the best approach to testing hypotheses of evolutionary optimality. New statistical tests incorporating all of the above aspects of the methodology also would be worthy of further study and development.
5. Conclusion
To test several hypotheses about the optimality of two key biomechanical attributes in the evolution of carnivore feeding morphologies, we developed and implemented an integrative method using GMM, FEA and RSM that can be applied to a broad range of phenotypic characteristics, and, in principle, genotypic information as well. Such a model-based approach can be appropriate as long as the traits of interest that contribute to hypothesized functions can be altered (either in silico or in vivo) to generate theoretical forms. Combined with FEA–GMM and comparative methods to identify and account for phylogenetic signals in functional morphology, it can be a powerful addition to the phylogenetic comparative toolset. Process optimization using RSM is already a valuable method in an array of biological disciplines, such as biotechnology for synthesizing biological compounds with desired properties and performance, and with the wide spectrum of phylomorphospaces already available in the literature, the potential for this new approach to gain wider use in palaeobiology and functional morphology is clear. Topics such as biomechanical analyses of ancestral state reconstructions and tests of strength and direction of adaptive evolutionary pathways using RSM can be applied both to existing datasets and to future studies of evolutionary form–function linkage using phylomorphospaces. Continual improvements in each of the methodologies incorporated into this integrative approach, as well as further research into how these various techniques should be best combined to test macroevolutionary hypotheses, will further advance our understanding of complex form–function linkages in biology.
Supplementary Material
Acknowledgements
M. Hill and H. Towbin assisted with CT-scanning at the AMNH Microscopy and Imaging Facility. The Editor and six anonymous reviewers provided a plethora of constructive comments that greatly improved the context and structure of this paper, but any shortcomings remain our own.
Funding
This research was funded by NSF DEB-1257572 to J.J.F. and Z.J.T., and an AMNH Frick Postdoctoral Fellowship (to Z.J.T.).
References
- 1.Holzman R, Collar DC, Price SA, Hulsey CD, Thomson RC, Wainwright PC. 2012. Biomechanical trade-offs bias rates of evolution in the feeding apparatus of fishes. Proc. R. Soc. B 279, 1287–1292. ( 10.1098/rspb.2011.1838) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ferry-Graham LA, Bolnick DI, Wainwright PC. 2002. Using functional morphology to examine the ecology and evolution for specialisation. Integr. Comp. Biol. 42, 265–277. ( 10.1093/icb/42.2.265) [DOI] [PubMed] [Google Scholar]
- 3.Gould SJ, Lewontin RC. 1979. The spandrels of San Marco and the Panglossian paradigm: a critique of the adaptationist programme. Proc. R. Soc. Lond. B 205, 581–598. ( 10.1098/rspb.1979.0086) [DOI] [PubMed] [Google Scholar]
- 4.Wainwright PC. 2007. Functional versus morphological diversity in macroevolution. Annu. Rev. Ecol. Evol. Syst. 38, 381–401. ( 10.1146/annurev.ecolsys.38.091206.095706) [DOI] [Google Scholar]
- 5.Adams DC, Rohlf FJ, Slice DE. 2013. A field comes of age: geometric morphometrics in the 21st century. Hystrix 24, 7–14. ( 10.4404/hystrix-24.1-6283) [DOI] [Google Scholar]
- 6.Rayfield EJ. 2007. Finite element analysis and understanding the biomechanics and evolution of living and fossil organisms. Annu. Rev. Earth Planet. Sci. 35, 541–576. ( 10.1146/annurev.earth.35.031306.140104) [DOI] [Google Scholar]
- 7.O'Higgins P, Cobb SN, Fitton LC, Groning F, Phillips R, Liu J, Fagan MJ. 2011. Combining geometric morphometrics and functional simulation: an emerging toolkit for virtual functional analyses. J. Anat. 218, 3–15. ( 10.1111/j.1469-7580.2010.01301.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sakamoto M, Lloyd GT, Benton MJ. 2010. Phylogenetically structured variance in felid bite force: the role of phylogent in the evolution of biting performance. J. Evol. Biol. 23, 463–478. ( 10.1111/j.1420-9101.2009.01922.x) [DOI] [PubMed] [Google Scholar]
- 9.Sakamoto M. 2010. Jaw biomechanics and the evolution of biting performance in theropod dinosaurs. Proc. R. Soc. B 277, 3327–3333. ( 10.1098/rspb.2010.0794) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Figueirido B, Serrano-Alarcon FJ, Slater GJ, Palmqvist P. 2010. Shape at the cross-roads: homoplasy and history in the evolution of the carnivoran skull towards herbivory. J. Evol. Biol. 23, 2579–2594. ( 10.1111/j.1420-9101.2010.02117.x) [DOI] [PubMed] [Google Scholar]
- 11.Rasskin-Gutman D, Buscalioni AD. 2001. Theoretical morphology of the Archosaur (Reptilia: Diapsida) pelvic girdle. Paleobiology 27, 59–78. () [DOI] [Google Scholar]
- 12.McGhee GR., Jr 1999. Theoretical morphology: the concept and its applications, p. 316 New York, NY: Columbia University Press. [Google Scholar]
- 13.Figueirido B, MacLeod N, Krieger J, Di Renzi M, Perez-Claros JA, Palmqvist P. 2011. Constraint and adaptation in the evolution of carnivoran skull shape. Paleobiology 37, 490–518. ( 10.1666/09062.1) [DOI] [Google Scholar]
- 14.Raup DM. 1966. Geometric analysis of shell coiling: general problems. J. Palaeontol. 40, 1178–1190. [Google Scholar]
- 15.Raup DM. 1967. Geometric analysis of shell coiling: coiling in ammonoids. J. Palaeontol. 41, 43–65. [Google Scholar]
- 16.Young MT, Brusatte SL, Ruta M, De Andrade MB. 2010. The evolution of Metriorhynchoidea (mesoeucrocodylia, thalattosuchia): an integrated approach using geometric morphometrics, analysis of disparity, and biomechanics. Zool. J. Linn. Soc. 158, 801–859. ( 10.1111/j.1096-3642.2009.00571.x) [DOI] [Google Scholar]
- 17.Spaulding M, Flynn JJ. 2012. Phylogeny of the Carnivoramorpha: the impact of postcranial characters. J. Syst. Palaeontol. 10, 653–677. ( 10.1080/14772019.2011.630681) [DOI] [Google Scholar]
- 18.Wesley-Hunt GD, Flynn JJ. 2005. Phylogeny of the Carnivora: basal relationships among the carnivoramorphans, and assessment of the position of ‘Miacoidea’ relative to Carnivora. J. Syst. Palaeontol. 3, 1–28. ( 10.1017/S1477201904001518) [DOI] [Google Scholar]
- 19.Flynn JJ, Finarelli JA, Spaulding M. 2010. Phylogeny of the Carnivora and Carnivoramorpha, and the use of the fossil record to enhance understanding of evolutionary transformations. In Carnivoran evolution: new views on phylogeny, form, and function (eds Goswami A, Friscia A.), pp. 25–63. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 20.Flynn JJ, Finarelli JA, Zehr S, Hsu J, Nedbal M. 2005. Molecular phylogeny of the Carnivora (Mammalia): assessing the impact of increased sampling on resolving enigmatic relationships. System. Biol. 54, 317–337. ( 10.1080/10635150590923326) [DOI] [PubMed] [Google Scholar]
- 21.Tseng ZJ. 2013. Testing adaptive hypotheses of convergence with functional landscapes: a case study of bone-cracking hypercarnivores. PLoS ONE 8, e65305 ( 10.1371/journal.pone.0065305) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tseng ZJ, Flynn JJ. 2015. Are cranial biomechanical simulation data linked to known diets in extant taxa? A method for applying diet-biomechanics linkage models to infer feeding capability of extinct species. PLoS ONE 10, e0124020 ( 10.1371/journal.pone.0124020) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Carbone C, Mace GM, Roberts SC, Macdonald DW. 1999. Energetic constraints on the diet of terrestrial carnivores. Nature 402, 286–288. ( 10.1038/46266) [DOI] [PubMed] [Google Scholar]
- 24.Lauder GV. 1995. On the inference of function from structure. In Functional morphology in vertebrate paleontology (ed. Thomason JJ.), pp. 9–18. New York, NY: Cambridge University Press. [Google Scholar]
- 25.Ewer RF. 1973. The carnivores. Ithaca, IL: Cornell University Press. [Google Scholar]
- 26.Van Valkenburgh B. 1989. Carnivore dental adaptations and diet: a study of trophic diversity within guilds. In Carnivore behavior, ecology, and evolution (ed. Gittleman JL.), pp. 410–436. New York, NY: Cornell University Press. [Google Scholar]
- 27.Wiley DF, et al. 2005. Evolutionary morphing. IEEE Visual. 5, 431–438. ( 10.1109/VISUAL.2005.1532826) [DOI] [Google Scholar]
- 28.Klingenberg CP. 2011. MorphoJ: an integrated software package for geometric morphometrics. Mol. Ecol. Resour. 11, 353–357. [DOI] [PubMed] [Google Scholar]
- 29.Stayton CT. 2011. Biomechanics on the half shell: functional performance influences patterns of morphological variation in the emydid turtle carapace. Zoology 114, 213–223. ( 10.1016/j.zool.2011.03.002) [DOI] [PubMed] [Google Scholar]
- 30.Stayton CT. 2009. Application of thin-plate spline transformations to finite element models, or, how to turn a bog turtle into a spotted turtle to analyse both. Evolution 63, 1348–1355. ( 10.1111/j.1558-5646.2009.00655.x) [DOI] [PubMed] [Google Scholar]
- 31.Grosse I, Dumont ER, Coletta C, Tolleson A. 2007. Techniques for modeling muscle-induced forces in finite element models of skeletal structures. Anat. Rec. 290, 1069–1088. ( 10.1002/ar.20568) [DOI] [PubMed] [Google Scholar]
- 32.Schumacher GH. 1961. Funktionelle morphologie der Kaumuskulatur, p. 262 Jena, Germany: VEB Gustav Fischer Verlag. [Google Scholar]
- 33.Turnbull WD. 1970. Mammalian masticatory apparatus. Fieldiana Geol. 18, 149–356. [Google Scholar]
- 34.Thomason JJ. 1991. Cranial strength in relation to estimate biting forces in some mammals. Can. J. Zool. 69, 2326–2333. ( 10.1139/z91-327) [DOI] [Google Scholar]
- 35.Pollock CM, Shadwick RE. 1994. Allometry of muscle, tendon, and elastic energy of storage capacity in mammals. Am. J. Physiol. Regul. Integr. Comp. Physiol. 266, 1022–1031. [DOI] [PubMed] [Google Scholar]
- 36.Bennett MB, Taylor GC. 1995. Scaling of elastic strain energy in kangaroos and the benefits of being big. Nature 378, 56–59. ( 10.1038/378056a0) [DOI] [PubMed] [Google Scholar]
- 37.Figueirido B, Tseng ZJ, Serrano-Alarcon FJ, Martin-Serra A, Pastor JF. 2014. Three-dimensional computer simulations of feeding behaviour in red and giant pandas relate skull biomechanics with dietary niche partitioning. Biol. Lett. 10, 20140196 ( 10.1098/rsbl.2014.0196) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tseng ZJ. 2009. Cranial function in a late Miocene Dinocrocuta gigantea (Mammalia: Carnivora) revealed by comparative finite element analysis. Biol. J. Linn. Soc. 96, 51–67. ( 10.1111/j.1095-8312.2008.01095.x) [DOI] [Google Scholar]
- 39.Tseng ZJ, McNitt-Gray J, Flashner H, Wang X, Enciso R. 2011. Model sensitivity and use of the comparative finite element method in mammalian jaw mechanics: mandible performance in the gray wolf. PLoS ONE 6, e0019171 ( 10.1371/journal.pone.0019171) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Berens P. 2009. CircStat: a MATLAB toolbox for circular statistics. J. Stat. Softw. 31, 1–21. [Google Scholar]
- 41.Nalla RK, Kinney JH, Ritchie RO. 2003. Mechanistic failure criteria for the failure of human cortical bone. Nat. Mater. 2, 164–168. ( 10.1038/nmat832) [DOI] [PubMed] [Google Scholar]
- 42.Werdelin L. 1996. Carnivoran ecomorphology: a phylogenetic perspective. In Carnivore behavior, ecology, and evolution (ed. Gittleman JL.), ch. 17, pp. 582–624. New York, NY: Cornell University Press. [Google Scholar]
- 43.Dumont ER, Samadevam K, Grosse I, Warsi OM, Baird B, Davalos LM. 2014. Selection for mechanical advantage underlies multiple cranial optima in New World leaf-nosed bats. Evolution 68, 1436–1449. ( 10.1111/evo.12358) [DOI] [PubMed] [Google Scholar]
- 44.Finarelli JA, Flynn JJ. 2006. Ancestral state reconstructions of body size in the Caniformia (Carnivora, Mammalia): the effects of incorporating data from the fossil record. Syst. Biol. 55, 301–313. ( 10.1080/10635150500541698) [DOI] [PubMed] [Google Scholar]
- 45.Bright JA, Rayfield EJ. 2011. Sensitivity and ex vivo validation of finite element models of the domestic pig cranium. J. Anat. 219, 456–471. ( 10.1111/j.1469-7580.2011.01408.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bright JA, Rayfield EJ. 2011. The response of cranial biomechanical finite element models to variations in mesh density. Anat. Rec. 294, 610–620. ( 10.1002/ar.21358) [DOI] [PubMed] [Google Scholar]
- 47.Davis JL, Santana SE, Dumont ER, Grosse I. 2010. Predicting bite force in mammals: two-dimensional versus three-dimensional lever models. J. Exp. Biol. 213, 1844–1851. ( 10.1242/jeb.041129) [DOI] [PubMed] [Google Scholar]
- 48.Tseng ZJ, Flynn JJ. 2015. Convergence analysis of a finite element skull model of Herpestes javanicus (Carnivora, Mammalia): implications for robust comparative inferences of biomechanical function. J. Theor. Biol. 365, 112–148. ( 10.1016/j.jtbi.2014.10.002) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.