Abstract
The cerebral vascular network has evolved in such a way so as to minimize transport time and energy expenditure. This is accomplished by a subtle combination of the optimal arrangement of arteries, arterioles and capillaries and the transport mechanisms of convection and diffusion. Elucidating the interaction between cerebral vascular architectonics and the latter physical mechanisms can catalyse progress in treating cerebral pathologies such as stroke, brain tumours, dementia and targeted drug delivery. Here, we show that brain microvascular organization is predicated on commensurate intracapillary oxygen convection and parenchymal diffusion times. Cross-species grey matter results for the rat, cat, rabbit and human reveal very good correlation between the cerebral capillary and tissue mean axial oxygen convective and diffusion time intervals. These findings agree with the constructal principle.
Keywords: diffusion and convection time, mammalian vascular architecture, optimal, oxygen
1. Introduction
In addition to being the ultimate organ of life, the brain is one of the most metabolically active body systems. With an encephalization quotient of 7, indicating that the human brain is seven times larger in relation to our expected brain-to-body weight ratio, the modern human is the most encephalized species. Constituting 2% of the total body mass, with one quadrillion (1015) synapses, the adult human brain consumes about 25% of the resting body oxygen. Mainly due to the dense synaptic connections, oxygen utilization in the cerebral cortex is three- to fivefold that of white matter [1].
Cross-species in vitro and in vivo cortical oxygen uptake data suggest an inversely proportional correlation between oxygen utilization and brain (or body) weight. Unlike other body tissues, the random orientation of cerebral capillaries is a unique feature of the brain. Despite scientific advances such as scanning electron microscopy of corrosion casts, which permits the study of the morphology of the vascular bed with exquisite detail [2], currently no geometric principle coherently explains patterns in cerebral microvascular architectonics.
The idea of linking structure and fitness in physiological systems is not new in physiology. More than two centuries after the pioneering work of Young [3], the principles governing the architecture of the mammalian bronchial tree and vascular networks remain perplexing [4]. The first principle, stemming from evolution through the optimal arrangement of the constituent vascular elements in combination with the physical mechanisms, a transport network must have evolved in such a way so as to minimize the cost of delivering and removing vital substances (consult Murray's principle of minimum work [5]). The second is the space-filling vascular system ingrained in cellular tissue which provides every cell in the organism with the essential elements. Although applicable to a large part of the branching vasculature of the mammalian circulatory system, Murray's law and the arteriolar terminal vascular architectonics do not completely explain how cerebral perfusion and the removal of waste products are optimally attained, or what the guiding underlying physical principles are.
Much of the emphasis on deciphering the vascular branching patterns of biological organisms has been directed towards the respiratory system. A recurring question which attracted sustained attention focused on the physical parameters that govern microvascular architecture and substrate delivery [6,7]. The principles of optimal vessel diameter for the design of minimum mass branching or vascular conduits has also been studied in terms of fluid engineering distribution systems [8]. Yancopoulos et al. [9] examined the vascular growth factors that foster blood vessel development. In vitro and in vivo advances in vascular morphogenesis have also been the subject of extensive research efforts [10]. A recent study by Secomb et al. [11] attempted the question of the evolution of vascular patterning, in the rat mesentery, as guided by stochastic sprouting angiogenesis, structural adaptation and vessel generation by pruning. In an attempt to derive discernible trends of the microvasculature networks of the brain, other researchers have applied computer algorithms to ink-injected human brain sections [12].
Furthermore, mapping cerebral oxygen distribution with sufficient spatial resolution remains elusive. Expounding the interaction between the physical and physiological mechanisms and brain organization can potentially treat cerebral pathologies such as stroke, small vessel disease, dementia and targeted brain therapeutics. By virtue of being the most complex body organ, the brain merits special attention if we are to realize substantial progress in understanding its underlying organizational principles. One of the prominent questions to tackle is tied to the acute vulnerability of the mammalian brain to oxygen deprivation. In clarifying the characteristics of the preceding conundrum, we subsequently examine cerebral oxygen delivery by considering the interplay between microvascular network organization and tissue oxygen uptake.
2. Cerebral vasculature and oxygen transport
2.1. Brain oxygenation and vascular network
Regardless of the immense biological importance of oxygen, the terrestrial mammalian brain appears capable of storing diminutive glycogen and oxygen reserves [13]. Although it remains debatable whether aerobic or anaerobic metabolism accompanies the early stages of brain activation [14], one can say with certainty that brain homeostasis requires a continuous blood supply to sustain vital biological functions. This coupled with its high metabolic demands render the brain highly susceptible to anoxaemia. An interruption of 6 s in the human brain oxygen supply results in loss of consciousness while irreversible neuronal damage ensues within minutes. During evolution, the human brain has grown from 400 cm3 in the hominid, some 2.75 Ma, to its present volume of 1400 cm3 [15]. In light of the low cerebral oxygen inventory and given that brain anoxia under physiological conditions is seldom an issue, the determinants of cerebral vascular organization, to be addressed here, appear intriguing. From a biological perspective, systems optimization points to a highly sophisticated and robust transport network.
Maintenance of the physiological level of cerebral oxygenation is accomplished by a dense and intricate vascular network [16] and a combination of convective and diffusive transport. Convection administers oxygen delivery while diffusion governs oxygen extraction. Convection is responsible for transporting oxygen, bound to haemoglobin in the erythrocytes, through bulk blood flow. Free and facilitated diffusion transfer oxygen from microvessels to the mitochondria of brain cells. Oxygen efflux takes place at the arteriolar and capillary bed where the surface area reaches its maximum and diffusion distance shrinks to its minimum.
The subject of cerebral oxygen perfusion is quite involved constituting one of the perplexities of the brain. In particular, cerebral blood flow and transvascular exchange of oxygen does not manifest itself in a distinctly identifiable section of the vascular bed [17]. Rather oxygen in the mammalian brain escapes from the vascular network through small diameter vessels which comprise metarterioles, capillaries and post-capillary venules. However, depending on the physical conditions (e.g. cerebral neuronal activity, haemoglobin saturation and blood velocity), capillaries make-up the prime exchange medium or zone with a proportionally greater oxygen loss compared with other compartments [18]. Hence, we have opted to focus on capillary oxygen efflux recognizing also the premise that partial oxygen pressure (pO2) in the capillary bed is higher than that of the ensuing venules [19,20]. Elevated haemoglobin saturation levels [21] and the disproportionately large surface area [22] of the cerebral capillary compartment play a pivotal role in oxygen tissue delivery.
In the cerebral vasculature, convection is effective for transporting haematocytes over long distances ranging from millimetres to metres. Diffusion accounts for the random molecular motion along a concentration gradient. Diffusion is also a metabolically ‘free’ transport mechanism whose efficacy diminishes drastically with spatial extent in excess of tens of micrometres.
Diffusion is further divided into free and facilitated diffusion. While in the capillary, a concentration differential drives free diffusion, oxygen flux in the cerebral tissue is believed to be amplified by neuroglobin [23]. Henceforth, the term diffusion refers to the collective effect of the free and facilitated mechanisms, accounted for in the oxygen diffusivities. We shall show that convection and free and facilitated diffusion collectively minimize the pumping energy, (overall) transport cost, and time of the supply of oxygen to every point of the organ, necessary to sustain life.
2.2. Convection and diffusion times
Here, we propose a unifying principle exhibited by several other systems in nature, biology and technology, which coalesces the requirements of minimum work and maximum coverage. When the transport realm is sufficiently large, the transport mechanisms of diffusion and channelling bathe the volume faster, with less resistance, than diffusion alone. This combination is most effective when the tissue diffusion time matches the capillary convection time. Thus, maximum effectiveness is achieved when the time to flow slowly over a shorter distance (diffusion) equals the time to flow fast over a larger distance (channel).
This behaviour has been derived from the constructal principle (CP) [24,25] and has been shown to predict many phenomena of patterned flow in nature. The tendency of the non-equilibrium system to adapt its configuration in time such that it flows more easily as a whole is the CP: for a finite-size flow system to persist in time, its configuration must evolve such that it provides greater and greater access to its currents [26].
2.3. Convection and diffusion times predicted by the constructal principle
Consider the following model of longitudinal convection along a tube of length L and diameter D, continued by diffusion across the tissue of thickness x. The volume fraction occupied by the wall tissue in the total volume is fixed; therefore, the ratio x/D is a constant and the total volume scales as
| 2.1 |
The shape of the flow composite (D/L) can vary and is dictated by the CP of generation of flow configuration for greater flow access. The simplest flow model is based on a fluid with Poiseuille flow along the tube and Darcy flow across the wall tissue. The pressure gradient which drives the longitudinal flow is
| 2.2 |
where 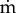 and ν are the total mass flow rate and the kinematic viscosity. The radial pressure difference which drives the same fluid through the wall tissue is of order
and ν are the total mass flow rate and the kinematic viscosity. The radial pressure difference which drives the same fluid through the wall tissue is of order
| 2.3 |
where K is the Darcy permeability defined by
| 2.4 |
where v is the volume averaged radial velocity and μ is the viscosity, or ρv. Henceforth, the word radial refers to an equivalent distance normal to the axial direction.
The global flow resistance of the composite is
| 2.5 |
This varies with both L and D subject to the volume constraint relationship (2.1). It is minimal when the shape of the construct is
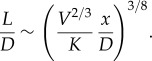 |
2.6 |
In this configuration, the longitudinal and radial pressure differences are in balance
| 2.7 |
Note that the times of the longitudinal and radial flow are also in balance. The longitudinal time is tx ∼ (L/U), where 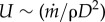 and
and 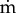 is given by equation (2.2). The radial time is tr ∼ (x/v), for which v is given by equation (2.4). Dividing tx by tr and using equations (2.6) and (2.7), we arrive at
is given by equation (2.2). The radial time is tr ∼ (x/v), for which v is given by equation (2.4). Dividing tx by tr and using equations (2.6) and (2.7), we arrive at
| 2.8 |
The configuration of flow access morphs in such a way that the time to travel long and fast (tx) matches the time to travel short and slow (tr). Bejan & Lorente [25] list many applications of the CP. Subsequently, we demonstrate that this principle holds for the mammalian brain as well.
2.4. Data and calculations
We compiled data on the erythrocyte, plasma and cerebral tissue oxygen diffusion coefficients, blood velocity, capillary supply region, capillary length and diameter for four mammals. Oxygen diffusivity values were predominantly acquired via microelectodes [27] or estimated from other sources. Blood velocity values were retrieved using intravital microfilming [28] and two-photon laser scanning microscopy [29], or interpolation. Data on the capillary and tissue were extracted from histological [30] and stereological methods [31], and corrosion casts.
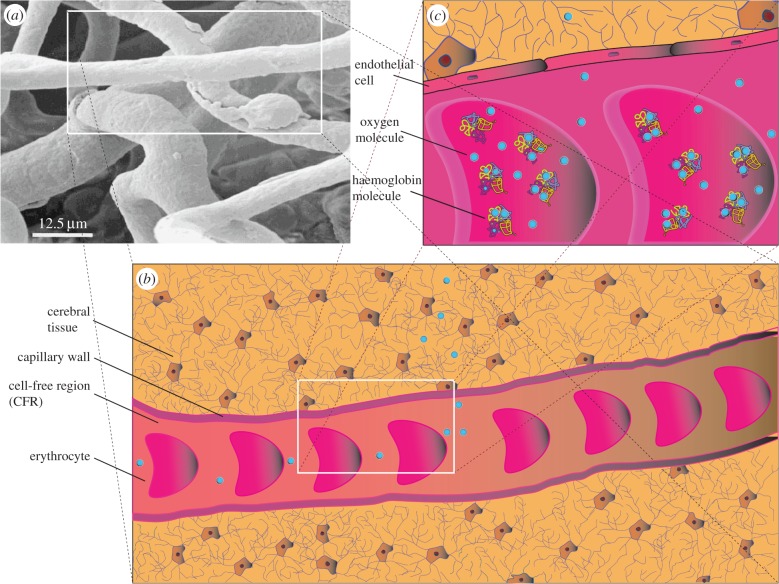
To calculate the convection and diffusion times of oxygen, we considered a Kroghian cylinder consisting of a constant diameter capillary with unidirectional blood flow feeding a volume of cerebral tissue peripheral to the vessel. As depicted in figure 1, red blood cells (RBCs), suspended in plasma, traverse the capillary surrounded by an outermost cell-free region (CFR). A ratio of erythrocyte to CFR thickness 1 : 7 was maintained for all calculations. The convective time (tconv) for intracapillary oxygen transport was calculated from
| 2.9 |
where zcap is the capillary half-length (0.5 Lcap) and vblood is the blood velocity (table 1). The calculation was based on a straight capillary with erythrocytes moving at a steady and constant unidirectional velocity. Notably, the straight line geometry, inspired by the top-left inset in figure 1, is frequently encountered in certain parts of the cortex [16]. Glass tube experiments reveal that erythrocytes have been observed to travel in bundled configurations [33].
Figure 1.
Erythrocyte to cerebral tissue oxygen transport. Top-left inset (a) depicts a corrosion cast of human cortical capillary vessels (adapted from [2]). The geometry of the framed straight capillary, measuring about 50 μm in length and 12 μm in diameter, is mapped on the bottom cartoon (b), which portrays oxygen efflux from erythrocytes moving from left to right, suspended in plasma, to tissue cells. Top right (c) magnification illustrates oxygen dissociating from haemoglobin molecules, encapsulated in erythrocytes, into the plasma. Once in the plasma, free oxygen molecules cross the endothelial cell wall junctions to be transported, by free and facilitated diffusion, to tissue cells to fuel aerobic and, possibly, anaerobic glycolysis. Bottom and top-right inserts are not to scale. (Online version in colour.)
Table 1.
Rat, cat, rabbit and human sample mean capillary diameter 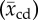 and half-length
and half-length 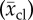 and their respective sample standard deviation (scd) and (scl).
and their respective sample standard deviation (scd) and (scl).
| species (popular) name | capillary diameter 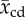 (μm) (μm) |
capillary diameter scd (×10−6) | capillary half-length 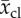 (μm) (μm) |
capillary half-length scl (×10−6) |
|---|---|---|---|---|
| rat | 4.57 | 1.22 | 57 | 0 |
| cat | 5.2 | 0.59 | 52 | 2.83 |
| rabbit | 9.3 | 4.42 | 70a | 0 |
| human | 6.22 | 1.56 | 100 | 0 |
Transcapillary and tissue oxygen diffusion times were determined from tables 1–3 using
| 2.10 |
for i = RBC, CFR and tissue regions, where oxygen diffusivity and diffusion distance are denoted by DO2,i and λO2,i , respectively. The diffusion time (tDiff, i) is the sum of the erythrocytic oxygen diffusion and oxyhaemoglobin desaturation times and the oxygen CFR and parenchymal diffusion times. Due to the large uncertainties in the haemoglobin dissociation time to be added to the erythrocyte diffusion time, calculated from (2.10), the latter effects were not taken into account. The small magnitude of desaturation time though, relative to the total diffusion duration, indicates that their influence will be minimal. Facilitated diffusion effects due to the presence of neuroglobin [23] in the cerebral tissue are included in the tissue oxygen diffusion coefficient, DO2, Tiss. Convective and diffusive transport times determined herein stem from steady-state cerebral oxygen consumption. By definition, steady-state oxygen utilization does not vary as a function of time. Oxygen consumption emanates from averaging the basal and activated cerebral metabolic rate of oxygen utilization (CMRO2). As overall brain oxygen utilization per unit mass for most mammals is 3.72 × 10−5 mmol(O2) ml s−1 [34–37], we consider that the species we investigate, namely, the rat, the cat, the rabbit and man, exhibit this CMRO2 value.
Table 2.
Rat, cat, rabbit and human sample mean capillary supply region 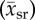 and blood velocity
and blood velocity 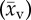 and their sample standard deviation (ssr) and (sv), respectively.
and their sample standard deviation (ssr) and (sv), respectively.
| species (popular) name | capillary supply region 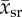 (μm) (μm) |
capillary supply region ssr (×10−6) | blood velocitya
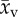 (mm s−1) (mm s−1) |
blood velocity sv (×10−4) |
|---|---|---|---|---|
| rat | 19.2 | 5.13 | 0.71 | 1.57 |
| cat | 15.3 | 6.66 | 0.71b | 1.57c |
| rabbit | 19.5 | 3.03 | 0.71b | 1.57c |
| human | 24.7 | 6.19 | 0.73 | 3.08 |
aBlood was assumed to travel at a constant velocity.
bSample mean blood velocity values were adapted from the rat (blood velocity) findings.
cBlood velocity sample standard deviations were based on the nearest size mammal, i.e. the rat.
Table 3.
Rat, cat, rabbit and human sample mean RBC 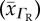 , CFR
, CFR 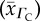 and tissue
and tissue 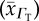 O2 diffusivities and their respective sample standard deviation
O2 diffusivities and their respective sample standard deviation 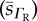 ,
, 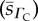 and
and 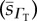 . (A zero sample standard deviation value indicates the existence of a single oxygen diffusivity value, e.g. in the case of the arat RBC O2 diffusivity). CFR stands for cell-free region.
. (A zero sample standard deviation value indicates the existence of a single oxygen diffusivity value, e.g. in the case of the arat RBC O2 diffusivity). CFR stands for cell-free region.
| species (popular) name | RBC O2 diffusivity 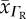 (10−6 cm2 s−1) (10−6 cm2 s−1) |
RBC O2 diffusivity s.d. 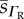 (×10−6) (×10−6) |
CFR O2 diffusivity 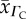 (10−5 cm2 s−1) (10−5 cm2 s−1) |
CFR O2 diffusivity 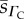 (×10−6) (×10−6) |
tissue O2 diffusivity 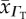 (10−5 cm2 s−1) (10−5 cm2 s−1) |
tissue O2 diffusivity 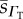 (×10−6) (×10−6) |
|---|---|---|---|---|---|---|
| rat | 8.0 | 0a | 2.4 | 0 | 1.55 | 2.19 |
| cat | 7.0 | 0 | 1.6 | 0 | 1.54 | 0 |
| rabbit | 9.5 | 0 | 2.18 | 0 | 1.75 | 2.12 |
| human | 7.4 | 2.63 | 2.11 | 4.89 | 1.65 | 0.71 |
Bootstrapping was used to broaden the scope of our investigation in light of the limited data available, used to determine the convection and diffusion times, we have managed to retrieve from various sources. The Monte Carlo simulations, which derive from a pseudorandom number generator, with normally distributed values, served exactly this need. Even though the Monte Carlo results are not truly random, they are practical to use, due to their reliability and computational efficiency [38]. A Monte Carlo technique was used to populate an adequately large dataset (n = 104) for the purpose of estimating the mean sample diffusion time (tDiff) from (2.10). The mean sample convection time (tConv) was obtained from (2.9). To ensure that the Monte Carlo estimators retained their consistency and unbiasedness, a data pool of n = 104 was used. Furthermore, to expand the data pool for the cat and rabbit erythrocyte velocities, we used the sample mean velocity 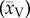 and sample standard deviation (sv) values of the rat—the neighbouring size mammal.
and sample standard deviation (sv) values of the rat—the neighbouring size mammal.
3. Results
Cross-species results of the arterial terminal level oxygen delivery and uptake of the rat, cat, rabbit and human demonstrate very good correlation between the cerebral capillary and tissue mean axial oxygen convective 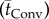 and diffusion
and diffusion 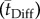 times (figure 2). This finding is commensurate with the convection–diffusion time predicted by the CP. The physical significance of balancing the diffusive and convective times is the maximization of access of the transport of oxygen throughout the three-dimensional vascular network ingrained in the volume. This time relation is another name for the microvascular architecture, i.e. the allocation of capillary channels to interstitial elemental volumes.
times (figure 2). This finding is commensurate with the convection–diffusion time predicted by the CP. The physical significance of balancing the diffusive and convective times is the maximization of access of the transport of oxygen throughout the three-dimensional vascular network ingrained in the volume. This time relation is another name for the microvascular architecture, i.e. the allocation of capillary channels to interstitial elemental volumes.
Figure 2.
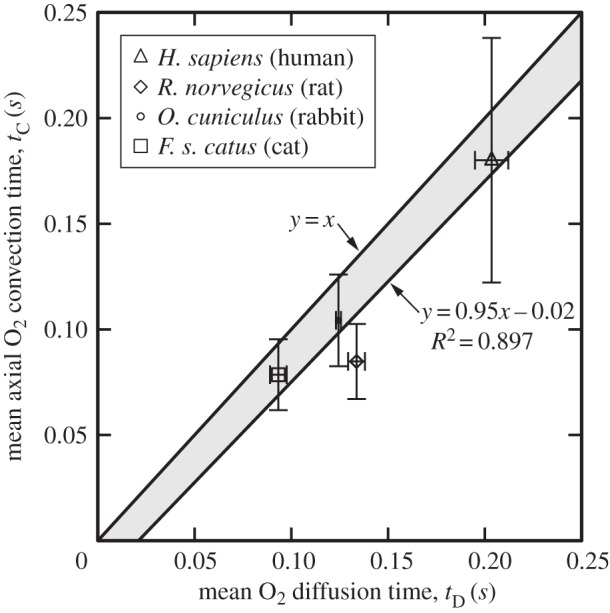
Mean oxygen convection and diffusion times for Rattus norvegicus, Felis silvestris catus, Oryctolagus cuniculus and Homo Sapiens. Mean arterial capillary level diffusion and convection times were evaluated from Monte Carlo calculations. Least-squares fit of the mean convective and diffusive times yielded a straight line with equation y = 0.95x − 0.02 and R = 0.897 which demonstrates strong agreement with line y = x. Standard deviation error bars were used.
As depicted in figure 2, the convective time standard deviation error bars for the cat, rabbit and human cross the line (y = x) on which diffusive and convective times are exactly equal. Least-squares regression of the species convection and diffusion times produced a straight line with equation y = 0.95x − 0.02 and R = 0.897 (figure 2), which is almost identical to y = x. With the rat being the only exception, the cat, human and rabbit mean transport times reside above line y = 0.95x − 0.02 and close to y = x (lightly shaded region, figure 2). Conspicuously, the human species with the biggest dataset and fastest RBC velocities (0.3–1.2 mm s−1) exhibits the highest standard deviation in axial convective time among all species.
By contrast, the dispersion in oxygen diffusivity coefficients is very small. The effectiveness of convection and diffusion is dominated by RBC (and blood) velocity and inter-capillary spacing, respectively. Variations in RBC velocity data arise from flow irregularities due to erythrocytic motion, in the capillaries, and the accuracy of the measurements acquired by the RBC probing technique (e.g. intravital video microscopy). As partially shown in the top-left inset in figure 1a, the random orientation of cerebral capillaries and the heterogeneous geometry of cerebral tissue [16] surrounding them explain the reported variability in the inter-capillary spacing values. There is evidence to suggest that cerebral capillary diameter decreases with decreasing size of the species [31]. With the exception of the rabbit, our data show that the rat, cat and man obey this trend.
4. Discussion
Apart from the conjecture that cerebral microcirculation has evolved in such a way so as to provide better flow access at minimum cost, no formal theoretical formulation of the distribution of the microvascular bed existed to date. Our attempt to elucidate the basic mechanism that guided microvessel branching in a manner that supplies every cell of the brain in an optimal way is therefore of fundamental interest. Supported by the findings presented herein, we postulate that the evolutionary biological mechanisms which originally laid the arterial exchange vessels could be driven (and constrained) by the primary transport mechanisms of convection and diffusion. Thus, the balancing of convection and diffusion functions to optimize access to the transport of oxygen in a timely fashion.
The mean convective and diffusive transport for the rat, cat, rabbit and human demonstrate very good correlation between the two mechanisms (figure 2). Commensurate diffusive and convective times, in line with CP, facilitate energy efficient oxygen delivery (convection) and uptake (diffusion). As the most widely studied species, man, presents us with the largest dataset of parameters used to determine the corresponding mean convective and mean diffusion times. Because of this, the human species affects the equation of the fitted line in an analogously dominant manner. Regardless, even when each species dataset is examined in isolation, independently of the rest, their mean convective and diffusive times almost coincide (i.e. y = x). Extracting a common pattern between all mammalian species not only broadens the scope of the investigation but can also yield a scaling relationship.
Collectively, the interaction and the physical limitations of convection and diffusion are perceived to play a pivotal role in laying the blueprint of the vascular bed. Our results shed light on microvascular architectonics, whose eventual geometric characterization, including vascular tortuosity, holds great potential in the treatment of cerebral pathologies such as stroke, brain tumours, atrophy and dementia.
Ultimately, these results reveal that the evolution of the cerebral microvasculature followed a path aiming at the optimization of oxygen delivery time and energy expenditure. Thus, they possibly explain the very low tolerance of the brain to perfusion interruption: the system followed an evolutionary path aimed at an optimized oxygen supply and not an oxygen reserve.
Acknowledgements
C.H. was financially supported by the Alexander Onassis foundation. This work benefited from discussions with M. Michalopoulou and K. Moyle. Y.V. acknowledges support, contributions and insight for the latest phases of this work from VPH-DARE@IT (FP7-ICT-2011–9–601055), a collaborative Research Project funded under the Co-operation specific programme of the Seventh Framework Programme of the European Union for research, technological development and demonstration activities.
Dedication
This paper is dedicated to the memory of Mrs Panagiota Ventikou, who suffered a perfusion/oxygenation-related acute cerebrovascular incident and sadly passed away while the manuscript was under final review.
References
- 1.Siesjö BK. 1978. Brain energy metabolism. Bath, UK: John Wiley. [Google Scholar]
- 2.De La Torre FR, Baeza RA, Barris SJ. 1998. Morphological characteristics and distribution pattern of the arterial vessels in human cerebral cortex: a scanning electron microscope study. Anat. Rec. 251, 87–96. () [DOI] [PubMed] [Google Scholar]
- 3.Young T. 1809. On the functions of the heart and arteries. Phil. Trans. R. Soc. 99, 1–31. ( 10.1098/rstl.1809.0001). [DOI] [Google Scholar]
- 4.West GB, Brown JH, Enquist BJ. 1997. A general model for the origin of allometric scaling laws in biology. Science 276, 122–126. ( 10.1126/science.276.5309.122) [DOI] [PubMed] [Google Scholar]
- 5.Murray CD. 1926. The physiological principle of minimum work: I and II. Proc. Natl Acad. Sci. USA 12, 207–214, 299–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.LaBarbera M. 1990. Principles of design of fluid transport systems in zoology. Science 249, 992–1000. ( 10.1126/science.2396104) [DOI] [PubMed] [Google Scholar]
- 7.Lubashevsky IA, Gafiychuk VV.2013. Analysis of the optimality principles responsible for vascular network architectonics. (http://arxiv.org/abs/adap-org/9909003. )
- 8.Williams HR, Trask RS, Weaver PM, Bond IP. 2008. Minimum mass vascular networks in multifunctional materials. J. R. Soc. Interface 5, 55–65. ( 10.1098/rsif.2007.1022) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yancopoulos GD, Davis S, Gale NW, Rudge JS, Wiegand SJ, Holash J. 2000. Vascular-specific growth factors and blood vessel formation. Nature. 407, 242–248. ( 10.1038/35025215) [DOI] [PubMed] [Google Scholar]
- 10.Ribatti D. 2015. Vascular morphogenesis: methods and protocols. New York, NY: Humana Press. [Google Scholar]
- 11.Secomb TW, Alberding JP, Hsu R, Dewhirst MW, Pries AR. 2013. Angiogenesis: an adaptive dynamic biological patterning problem. PLoS Comput. Biol. 9, e1002983 ( 10.1371/journal.pcbi.1002983) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cassot F, Lauwers F, Fouard C, Prohaska S, Lauwers-Cances V. 2006. A novel three-dimensional computer-assisted method for a quantitative study of microvascular networks of the human cerebral cortex. Microcirculation 13, 1–18. ( 10.1080/10739680500383407) [DOI] [PubMed] [Google Scholar]
- 13.Clarke DD, Sokoloff L. 1994. Circulation and energy metabolism of the brain. In Basic neurochemistry: molecular, cellular and medical aspects (eds Siegel GJ, Agranoff BW, Albers RW, Molinoff RB.), p. 645 New York, NY: Raven Press. [Google Scholar]
- 14.Fujita H, Kuwabara H, Reutens DC, Gjedde A. 1999. Oxygen consumption of cerebral cortex fails to increase during continued vibrotactile stimulation. J. Cereb. Blood Flow Metab. 19, 266–271. ( 10.1097/00004647-199903000-00004) [DOI] [PubMed] [Google Scholar]
- 15.Falk D, Redmond JC, Guyer J, Conroy GC, Recheis W, Weber GW, Seidler H. 2000. Early hominid brain evolution: a new look at old endocasts. J. Hum. Evol. 38, 695–717. ( 10.1006/jhev.1999.0378) [DOI] [PubMed] [Google Scholar]
- 16.Duvernoy HM, Delon S, Vannson JL. 1981. Cortical blood vessels of the human brain. Brain Res. Bull. 7, 519–579. ( 10.1016/0361-9230(81)90007-1) [DOI] [PubMed] [Google Scholar]
- 17.Reinhart K, Eyrich K. 1989. Clinical aspects of O2 transport and tissue oxygenation. Berlin, Germany: Springer. [Google Scholar]
- 18.Tuma RF, Durán WN, Ley K. 2008. Handbook of physiology: microcirculation, 2nd edn Boston, MA: Elsevier/Academic Press. [Google Scholar]
- 19.Hall JE, Guyton AC. 2011. Guyton and Hall textbook of medical physiology. Philadelphia, PA: Saunders Elsevier. [Google Scholar]
- 20.Widmaier EP, Raff H, Strang KT. 2014. Vander‘s human physiology: the mechanisms of body function, 13th edn Boston, MA: McGraw-Hill. [Google Scholar]
- 21.Hadjistassou CK, Ventikos Y. 2009. On the physiology of the blood oxygenation level dependent fMRI effect: a computational study. PhD thesis, University of Oxford, Oxford, UK. [Google Scholar]
- 22.Brady ST, Siegel GJ, Albers RW, Price DL. 2012. Basic neurochemistry: principles of molecular, cellular, and medical neurobiology. Amsterdam, The Netherlands: Elsevier Academic Press. [Google Scholar]
- 23.Burmester T, Weich B, Reinhardt S, Hankein T. 2000. A vertebrate globin expressed in the brain. Nature 407, 520–523. ( 10.1038/35035093) [DOI] [PubMed] [Google Scholar]
- 24.Bejan A. 2000. Shape and structure, from engineering to nature. New York, NY: Cambridge University Press. [Google Scholar]
- 25.Bejan A, Lorente S. 2006. Constructal theory of generation of configuration in nature and engineering. J. Appl. Phys. 100, 41 301–41 327. ( 10.1063/1.2221896) [DOI] [Google Scholar]
- 26.Bejan A, Lorente S. 2010. The constructal law of design and evolution in nature. Phil. Trans. R. Soc. B 365, 1335–1347. ( 10.1098/rstb.2009.0302) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ganfield RA, Nair P, Whalen WJ. 1970. Mass transfer, storage, and utilization of O2 in cat cerebral cortex. Am. J. Physiol. 219, 814–821. [DOI] [PubMed] [Google Scholar]
- 28.Kalinina MK, Levkovich YI, Ivanov KP, Trusova VK. 1976. Blood flow rate in capillaries of cerebral cortex (according to data of microcinematography). Dok Akad Nauk SSSR 226, 230–233. [PubMed] [Google Scholar]
- 29.Kleinfeld D, Mitra PP, Helmchen F, Denk W. 1998. Fluctuations and stimulus induced changes in blood flow observed in individual capillaries in layers 2 through 4 of rat neocortex. Proc. Natl Acad. Sci. USA 95, 15 741–15 746. ( 10.1073/pnas.95.26.15741) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hunziker O, Frey H, Schulz U. 1974. Morphometric investigations of capillaries in brain cortex of cat. Brain Res. 65, 1–11. ( 10.1016/0006-8993(74)90332-1) [DOI] [PubMed] [Google Scholar]
- 31.Pawlik G, Rackl A, Bing RJ. 1981. Quantitative capillary topography and blood flow in the cerebral cortex of cats: an in-vivo microscopic study. Brain Res. 208, 35–58. ( 10.1016/0006-8993(81)90619-3) [DOI] [PubMed] [Google Scholar]
- 32.Fenton BM, Zweifach BW. 1981. Microcirculatory model relating geometrical variation to changes in pressure and flow rate. Ann. Biomed. Eng. 9, 303–321. ( 10.1007/BF02364653) [DOI] [Google Scholar]
- 33.Secomb TW. 2003. Mechanics of red blood cells and blood flow in narrow tubes. In Modeling and simulation of capsules and biological cells (ed. Pozrikidis C.), pp. 163–191. Boca Raton, FL: Chapman and Hall/CRC. [Google Scholar]
- 34.Baish JW. 1994. Formulation of a statistical model of heat transfer in perfused tissue. J. Biomech. Eng. 116, 521–527. ( 10.1115/1.2895804) [DOI] [PubMed] [Google Scholar]
- 35.Baish JW, Ayyaswamy PS, Foster KR. 1986. Heat transport mechanisms in vascular tissues: a model comparison. J. Biomech. Eng. 108, 324–331. ( 10.1115/1.3138623) [DOI] [PubMed] [Google Scholar]
- 36.Charny CK, Levin RL. 1989. Bioheat transfer in a branching countercurrent network during hyperthermia. J. Biomech. Eng. 111, 263–270. ( 10.1115/1.3168377) [DOI] [PubMed] [Google Scholar]
- 37.Peattie RA. 2013. Transport phenomena in biomedical engineering: principles and practices. Boca Raton, FL: CRC Press. [Google Scholar]
- 38.Rubinstein RY. 2008. Simulation and the Monte Carlo method, 2nd edn Hoboken, NJ: John Wiley. [Google Scholar]