Abstract
A disturbance in the integration of information during mental processing has been implicated in schizophrenia, possibly due to faulty communication within and between brain regions. Graph theoretic measures allow quantification of functional brain networks. Functional networks are derived from correlations between time courses of brain regions. Group differences between SZ and control groups have been reported for functional network properties, but the potential of such measures to classify individual cases has been little explored. We tested whether the network measure of betweenness centrality could classify persons with schizophrenia and normal controls. Functional networks were constructed for 19 schizophrenic patients and 29 non-psychiatric controls based on resting state functional MRI scans. The betweenness centrality of each node, or fraction of shortest-paths that pass through it, was calculated in order to characterize the centrality of the different regions. The nodes with high betweenness centrality agreed well with hub nodes reported in previous studies of structural and functional networks. Using a linear support vector machine algorithm, the schizophrenia group was differentiated from non-psychiatric controls using the ten nodes with highest betweenness centrality. The classification accuracy was around 80%, and stable against connectivity thresholding. Better performance was achieved when using the ranks as feature space as opposed to the actual values of betweenness centrality. Overall, our findings suggest that changes in functional hubs are associated with schizophrenia, reflecting a variation of the underlying functional network and neuronal communications. In addition, a specific network property, betweenness centrality, can classify persons with SZ with a high level of accuracy.
INTRODUCTION
Schizophrenia (SZ) is a severe psychiatric brain disorder that affects about 1% of the population (Harrison, 1999; Insel, 2010; Ripke et al., 2013; Tandon et al., 2008). Symptoms of SZ suggest brain disturbances which affect many systems, and include hallucinations, delusions, disorganized thinking, loss of motivation, cognitive impairment and blunted emotional expression. While the etiology of schizophrenia remains poorly understood, it has been hypothesized that pathological connectivity among brain regions results in the loss of the functional integration and neural plasticity required for adaptive behavior (Andreasen et al., 1996; Friston, 1998; Stephan et al 2006).
In the last decade, the disconnectivity hypothesis of SZ has been examined using MRI measures of functional connectivity. The majority of these studies focused on the “default mode” network (DMN) (Raichle et al., 2001; Raichle and Snyder, 2007), and found abnormalities in schizophrenia in various aspects including altered amplitude, temporal frequency, and spatial extent/location. (Garrity et al., 2007; Ongür et al., 2010; Pomarol-Clotet et al., 2008; Zhou et al., 2008a). For instance, from resting-state fMRI data, DMN spatial extent was found to be significantly greater in the dorsal anterior cingulate cortex (Ongür et al., 2010). In an auditory oddball task, aberrant “default mode” functional connectivity was reported in the frontal, anterior cingulate, and parahippocampal gyri (Garrity et al., 2007). Besides DMN, investigation of other networks also revealed altered functional connectivity between brain regions (Liang et al., 2006; Zhou et al., 2008a; Zhou et al., 2008b). For instance, decreased functional connectivity among insula, prefrontal lobe and temporal lobe was observed along with increased connectivity from many cerebral cortical regions towards cerebellum (Liang et al., 2006).
The introduction of graph theoretical approaches applied to the brain has allowed quantitative analysis of local and global network properties derived from functional and structural brain imaging (Bullmore and Sporns, 2009; Lynall et al., 2010; Sporns, 2010; Supekar et al., 2008; van den Heuvel et al., 2013). This approach therefore is well suited for characterizing possible network alterations in schizophrenia. Methodologically, functional connectivity matrices (also referred to as a functional network) are usually derived from resting state fMRI data. In those, the strength of functional connections is usually characterized by the correlation of time courses between brain regions (Biswal et al., 1995). Brain network analyses have revealed a disruption of the functional and structural network structure in schizophrenia (Liu et al., 2008; Rubinov and Bullmore, 2013) including decreased clustering and small-worldness, and reduced presence of high-degree hubs. In addition, local differences of reduced degree and clustering were found in medial parietal, premotor and cingulate, and right orbitofrontal cortical nodes (Lynall et al., 2010). In another study applying independent component analysis (ICA) on resting state fMRI data, significantly lower clustering coefficient and lower small-world connectivity were also found for the network of independent components in schizophrenia patients (Anderson and Cohen, 2013). Abnormal rich club organization was also found for schizophrenia, which is potentially associated with altered functional brain dynamics.
Functional connectivity has usually been compared between groups of patients and control subjects (Lynall et al., 2010; Pettersson-Yeo et al., 2011). It is unclear whether network alterations have sufficient sensitivity and specificity to SZ to allow classification of individual subjects as affected or not. Supervised machine learning techniques may permit a much better degree of classification accuracy than convention statistical approaches, such as discriminant analysis. Previous studies have reported the potential of combining network features and machine learning for classification. For instance, a support vector machine classifier was able to differentiate older adults from younger adults based on resting state functional connectivity (Meier et al., 2012). In another study using a small set of edges showing high discriminative power, an unsupervised-learning classifier was also successful in discriminating schizophrenic patients from healthy controls with a high accuracy (Shen et al., 2010). Using a similar feature extraction approach, multiclass pattern analysis on functional connectivity also discriminated schizophrenic patients and their healthy siblings with a modest accuracy rate (Yu et al., 2013). In another study classifying schizophrenia patients based on functional network connectivity, the correlations between various ICA components were computed to be used as features and worked well for several linear and non-linear classification methods that are commonly used (Arbabshirani et al., 2013). Despite good classification performance in these previous works, the feature selection for classification was usually based on the strength of functional connectivity rather than network characteristics. There is only one study to our knowledge using network measures of clustering coefficient and small-worldness to classify schizophrenia (Anderson and Cohen, 2013), which yielded a classification accuracy of 65%.
Accuracy may be affected by the types of network measures utilized, and the criteria for quantifying connections. Functional connectivity networks have both positive and negative values as a result of pairwise correlations of time-series. The interpretation of negative connections is not yet completely understood, despite efforts to jointly analyze negative and positive connections (Deco et al., 2014; Goñi et al., 2014; Rubinov and Sporns, 2011). While thresholding the network is a plausible approach, it has been noted that most network metrics are very sensitive to doing so (Rubinov and Sporns, 2010). For instance, nodal degree or total degree decreases when a high percentage of connections are dropped. The clustering coefficient, small-worldness, global efficiency also changes accordingly. For this reason, we tested nodal betweenness centrality of the resting state functional networks, which turned out to be relatively unaffected by thresholding to compare the schizophrenic subjects (SZ) and non-psychiatric controls (NC).
Betweenness centrality (BC) is a network centrality measure that quantifies the influence of a node in connecting other nodes in a network (Freeman, 1977). It represents the fraction of all shortest paths in the network that pass through a given node (Rubinov and Sporns, 2010). The nodes with the highest BC are usually known as highly central or hubs (Buckner et al., 2009)(although other definitions of centrality exist). Previous studies have reported a reduction of betweenness centrality for frontal hubs in structural networks of schizophrenia patients (van den Heuvel et al., 2010). Because abnormal topological organizations of structural and functional brain networks have been reported for schizophrenia (van den Heuvel et al., 2013; Zhang et al., 2012), we hypothesized that there is a change of the nodal betweenness centrality in the magnitude and order (rank) that could be strongly associated with SZ and hence a key feature for our machine learning approach. Furthermore, the differences in BC are likely to be more substantial for the hubs (Rubinov and Bullmore, 2013). In order to better assess these changes, a collective analysis of an extensive set of nodes is desirable.
Based on this rationale, we employed a linear support vector machine (SVM) algorithm using nodal betweenness centrality as the feature space. The aim of this study was to test whether SVM could differentiate schizophrenia based on prior information of BC for a set of SZ and NC subjects. SVM is an unsupervised machine learning algorithm that has been widely used in classification and regression analysis. It has been successfully applied in neuroscience for multivoxel pattern analysis and differentiating different brain states (Cox and Savoy, 2003). By selecting highly discriminative feature set from all functional connectivity between 116 brain regions, SVM was able to discriminate schizophrenia from non-psychiatric controls with a high accuracy (Shen et al., 2010).
The purpose of this study was to classify SZ from non-psychiatric controls by applying support vector machine to betweenness centrality measures of the functional network. We also compared the performance of using different features derived from betweenness centrality. Because of large variability of functional connectivity (Wang et al., 2011), we expect that the rank of BC for a subset of nodes might be the best choice to distinguish schizophrenia from normal subjects.
METHODS
Subjects
27 SZs (8 female, mean age 36.7 ± 9.9 years) and 36 NCs (7 male, mean age 29.3 ± 6.5 years) were recruited and completed the study protocol. The subjects were provided verbal written informed consent. The study was approved by Institutional Review Board of Indiana University. Eight SZ subjects and 7 NC subjects were excluded from this study due to excessive head motion. Subjects used in the classification analysis included 19 SZs (6 female, 33.1± 10.9 years) and 29 NCs (15 female, mean age 28.1 ± 8.4 years). Diagnosis of schizophrenia was based on the Structured Clinical Interview for the DSM-IV Axis I Disorders (SCID-I) (First et al., 1995) and medical chart review. The SCID-I for non-psychiatric controls was used to determine that there was no history of Axis I disorders in the NCs. Current drug or alcohol abuse or dependence or a loss of consciousness lasting more than 5 minutes were exclusionary criteria for all participants. All subjects passed a urine screening for illicit substances at the time of the scan.
MRI data acquisition
Subjects were scanned on a Siemens TIM Trio 3 T MRI scanner using a 32-channel head coil. The high resolution (1 mm3) anatomical scan was performed in the sagittal plane with an MP-RAGE sequence with the following parameters: matrix = 256×256, FOV = 256×256 mm, TE/TR = 2.67/1800 ms, TI = 900 ms. A total of 200 volumes of resting state fMRI data were acquired with EPI sequences for 8 minutes and 20 seconds with the following parameters: TR/TE = 2500/30 ms, FOV = 220 mm, 128×128 matrix, oblique plane with slice thickness = 3.6 mm, number of slices = 36, iPAT factor = 2. During the resting state fMRI scan, the subjects were at rest with eyes closed and instructed not to think of anything in particular.
Head motion characterization
All functional data were motion corrected in FSL (http://fsl.fmrib.ox.ac.uk/). We computed the mean relative translational motion and rotational motion between consecutive volumes from the output of motion correction. The mean translational or mean rotation was computed as
where N is the number of volumes and a, b, c are the three degree of freedom for translational motion or rotational motion. A subject was excluded from the analysis if more than half volumes exceed 0.5 mm of absolute translational motion or 1 degree of rotational motion relative to the mid time point.
Characterization of the functional network
In conjunction with the anatomical image, the functional images were parcellated using a parcellation scheme recently proposed by Shen et al. (Shen et al., 2013). This parcellation divides the cerebral cortex into 278 ROIs, and was derived from resting state functional data of the healthy subjects by maximizing functional homogeneity within each ROI. After regressing out head motion, white matter and the CSF time signal, and band-pass filtering between 0.01–0.10 Hz, time courses were extracted from 278 brain ROIs and averaged. The functional network was computed from the pairwise Pearson correlation coefficients, giving rise to a square symmetric matrix (278×278). The resulting functional connectivity matrix has both positive and negative edges. Since the meaning of negative edges is not clear and negative edges prevent the assessment of several network features, a threshold was applied to the network to obtain a sparse network that has only positive connectivity measures. We tested a number of thresholds from 10% to 45% in a 5% increment, which kept a certain percentage of the total number of edges. We did not go beyond 45% threshold as negative edges started to arise for some subjects. As a result, the number of edges (or functional connectivity values that remained after the threshold procedure) stayed the same for all subjects, but the actual edge weights varied across subjects.
Betweenness centrality (BC)
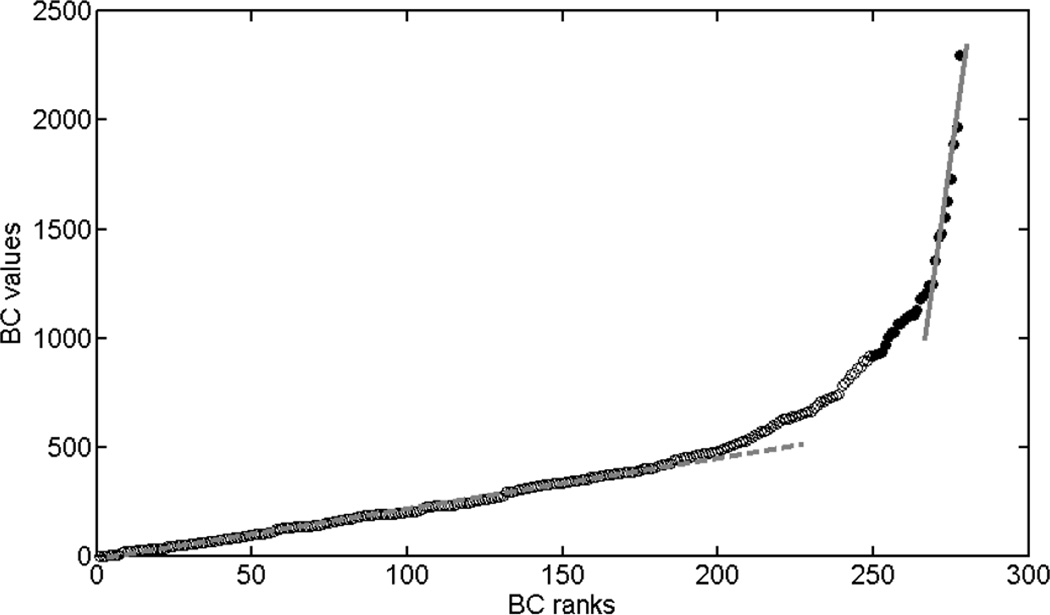
BC is a centrality measure defined as the fraction of all shortest paths in the network that pass through a given node (Freeman, 1977). It was computed using the Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/)(Rubinov and Sporns, 2010). Each node has a BC index; we used BC information of all nodes (which can be noisy) as well as a small set of selected nodes with high betweenness centrality. For the latter approach, we combined the networks of all the subjects to obtain an average pooled network and thresholded it by retaining only 30% of the edges with highest weights. Then the BC of each node of this mean network was computed. The nodes were then ordered based on their centrality from low to high. To determine how many nodes should be chosen for comparing the two groups, the BC values were plotted against the ranks (ranking BC from low to high). As shown in Fig. 1, there are two regimes showing linear relation between BC values and ranks and a transition zone. The first linear regime comprises BC ranks from 1 to 200 and follows a small slope; the second linear regime comprises BC ranks from 269 to 278, and has a much greater slope. We selected the nodes within regime 2 as it has the largest BC difference between nodes, and therefore less sensitive to confounds and noise. This selection resulted into ten nodes with highest BC, which were called hubs throughout this manuscript. Note that they are not necessarily hubs in terms of degree (Lynall et al., 2010; Rubinov and Sporns, 2010) or in terms of other existent centrality measurements (Zuo et al., 2012).
Figure 1.
Betweenness centrality as a function of ranks. The graph clearly shows two zones where BC values increases linearly with ranks. Zone 1 is approximately from rank 1 – 200; zone 2 is from rank 269–278. The top 10% nodes with highest BC are marked with solid circles.
Support Vector Machine
For the particular case of supervised two-class classification, SVM starts with the selection of some features as the basis for classification. These features form a high dimensional space. The next step is the classifier training. Linear SVM uses some models to find an optimal solution of a hyperplane that separates the classes and maximizes their margins. SVM can then be applied on a new vector in the feature space to predict which class it is associated with. Linear SVM analysis was performed on the nodal betweenness centrality data using the Matlab toolbox from LIBSVM that is freely available online (http://www.csie.ntu.edu.tw/~cjlin/libsvm/). The computed BC is susceptible to the variability of the constructed functional network and the effectiveness of the SVM may also suffer from large inter-subject variability. Therefore, we compared four different feature spaces: BC values of all nodes, BC values of selected hubs, BC ranks of all nodes and BC ranks of selected hubs. We adopted the ‘leave-one-out scheme’ to evaluate the accuracy rate of differentiating schizophrenia from non-psychiatric controls. For each NC or SZ subject, we used the remaining subjects (NC and SZ) as a training set, calculating the SVM parameters and applying new SVM model on the separated subject to predict if it belongs to SZ or NC group. An overall prediction rate was obtained by averaging the prediction accuracy (0 for wrong and 1 for correct) of each subject. For different methods, the regularization parameter was adjusted to obtain the highest prediction accuracy rate. As a control, two approaches were employed to test SVM in different conditions. First, we tested whether the hub nodes were differentially relevant for classification. We used different sets of nodes other than the hub nodes in SVM while keeping the same number of features. Second, we tested if there is a true difference in SZ and NC. Hence, we mixed all the subjects in the training set (mislabeling) and later performed SVM in the exact same way.
RESULTS
Betweenness centrality of each node was calculated for the average functional network. We reordered nodes based on their BC values. Figure 1 shows the BC values as a function of their ranks. The top ten nodes (solid dots) with highest betweenness centrality were considered as hubs. Because these nodes have the largest span of BC values as compared to any other ten nodes with continuous ranks, they were used for classifying the two groups.
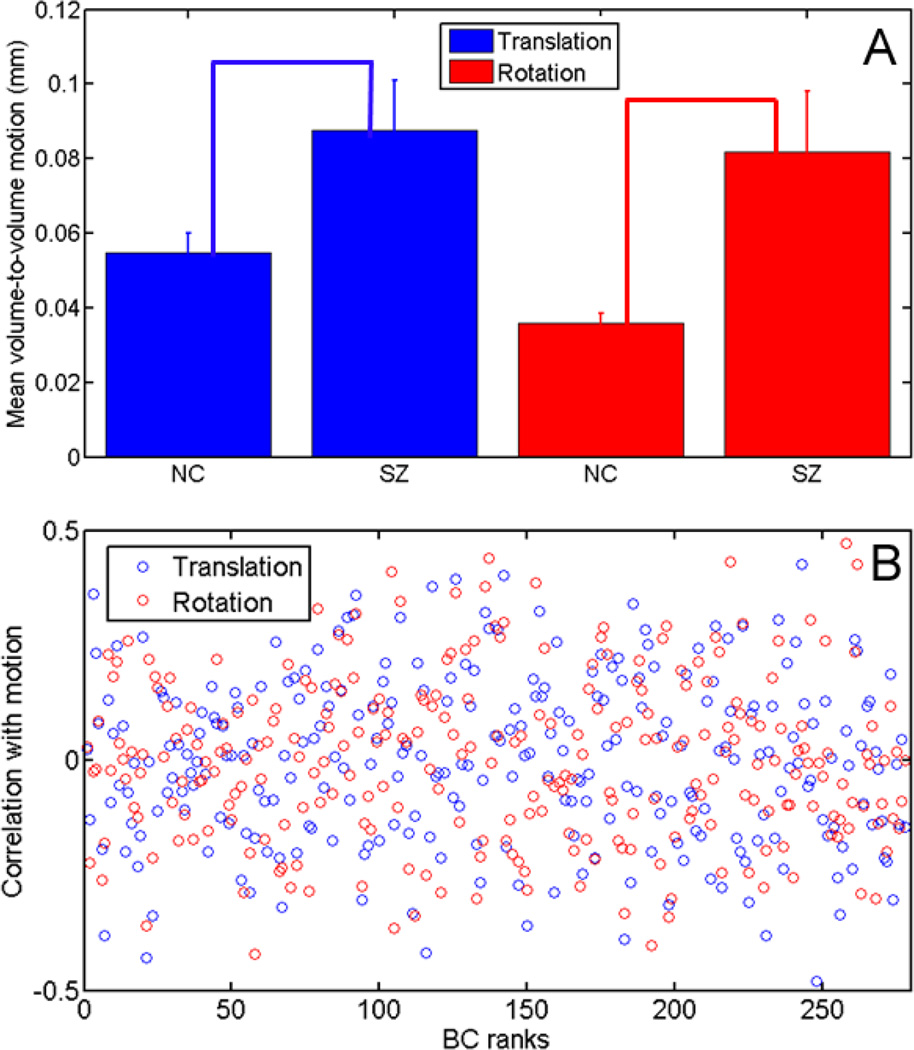
Before performing the SVM analysis, head motion was analyzed based on motion correction output to investigate if there was any correlation between the head motion and nodal BC values. Figure 2A compares both mean translational (blue) and rotational (red) motions between the SZ and NC groups. Error bars denote standard errors within each group. The SZ group had more motion than the non-psychiatric controls. The two sample t-test shows a significant difference for rotation (p = 0.001) and translation (p = 0.01). The variation of the motion is also larger for the schizophrenia subjects. The correlation coefficients between translational/rotational head motion and nodal BC values for all NC subjects are shown in Fig. 2B. The nodes are sorted based on their BC ranks of the average functional network of all subjects. The correlation coefficients fluctuate in the range of −0.5 to 0.5, with values 0.0003±0.1844 for translational motion and 0.0043±0.1897 for rotational motion. It can be seen that the level of fluctuation between nodes stays similar in the whole BC range and there is no apparent correlation between the correlation coefficients and BC rank (−0.05 for translational motion, −0.04 for rotational motion). Thus, while head motion was significantly different between NC and SZ groups, it did not yield significant effect on nodal betweenness centrality, and therefore will not affect our BC based SVM analysis.
Figure 2.
Comparison of both mean translational (blue) and rotational (red) motions between the SZ and NC groups (A); standard errors of motion within each group are indicated by the error bars. Correlation coefficients between motion parameters and BC values are shown in (B).
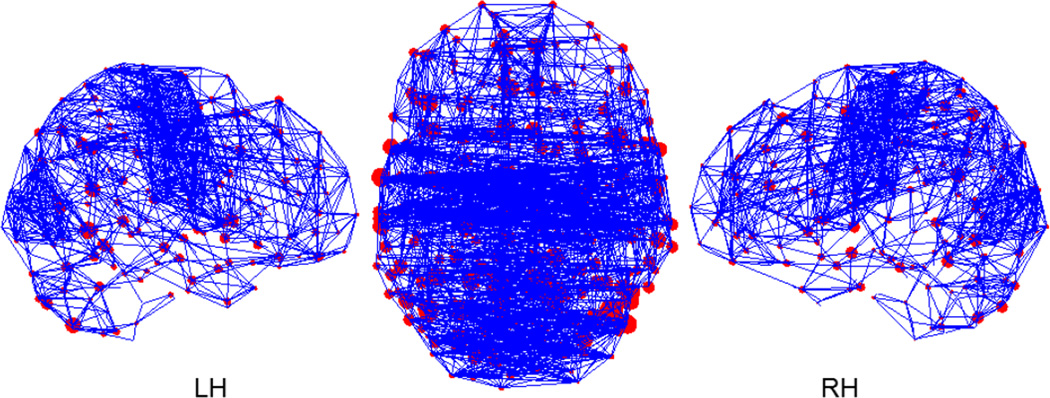
The thresholded average functional network obtained is shown in Figure 3 as graphs. The position of the nodes represents the center of mass of the actual location of ROIs in the parcellation projected on one plane (coronal or sagittal). The size of the node is proportional to the square root of its BC value. Only 5% of all the edges were retained for better viewing. Even with this threshold, the network is connected as a whole component. In other words, there are no isolated nodes or sub-networks. The nodes with high BC values are widely distributed over the brain. There are many intra-hemispheric connections (as shown in the sagittal views) as well as a significant number of inter-hemisphere connections, especially in the parietal and occipital lobes. It should be noted that the nodes with higher betweenness centrality do not necessarily have higher degree.
Figure 3.
Mean functional networks with 5% edges retained. The location of the nodes represents the coordinates of parcellated regions in MNI template. The size of the nodes is proportional to the square root of their BC values.
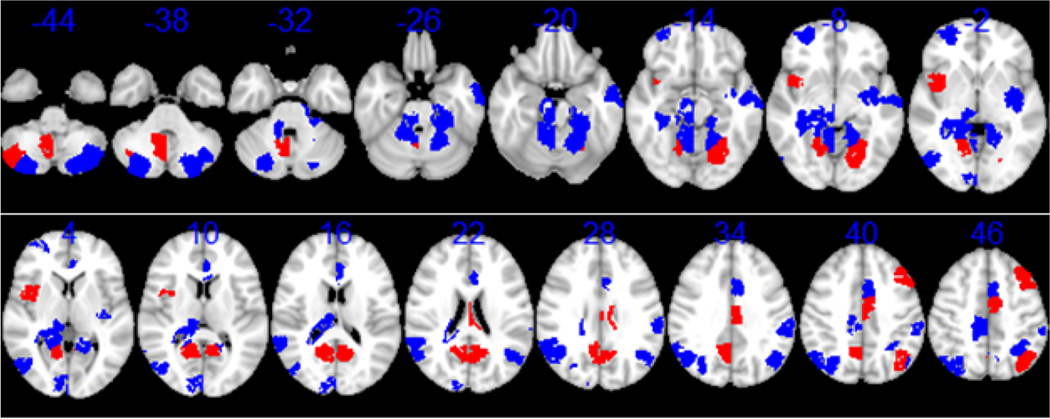
Besides the hubs, nodes with high betweenness centrality could also be key components in brain functional connectivity. Hence, we examined their physical location in the brain for the top 10% of nodes with highest centrality and the result is shown in Figure 4. The limbic system occupies a large portion of the nodes, including the cingulate gyrus, hippocampal formation, and amygdala. In this picture some core components of the default mode network can be seen in the frontal, parietal and posterior cingulate area (Buckner et al., 2008). The location of the ten hub nodes are highlighted in red, including lingual gyrus, posterior cingulate, cerebellum posterior lobule, insula, cingulate gyrus, precuneus, superior parietal lobe, fusiform gyrus, and middle frontal gyrus. Their MNI coordinates are listed in Table 1.
Figure 4.
Top 10% nodes with highest betweenness centrality displayed on the MNI template. The Z coordinates in mm are shown on top of corresponding slices. Ten nodes with highest betweenness centrality used for SVM analysis are colored in red, all others are colored in blue.
Table 1.
Corresponding brain regions, MNI coordinates and Talairach coordinates [x y z] of the ten nodes with highest betweenness centrality on the mean network with 30% threshold.
| Brain Region | MNI coordinate | Talairach coordinate |
|---|---|---|
| Middle Frontal Gyrus | [52 150 119] | [−40 24 41] |
| Fusiform Gyrus | [67 61 63] | [−25 64 −5] |
| Superior Parietal Lobe | [52 62 121] | [−40 −61 47] |
| Precuneus | [97 70 106] | [5 −54 33] |
| Cingulate Gyrus | [85 120 122] | [−7 −5 45] |
| Insula | [132 134 73] | [40 7 0] |
| Cerebellum Posterior Lobule | [130 61 24] | [38 −66 −38] |
| Posterior Cingulate | [103 70 87] | [11 −55 16] |
| Posterior Cingulate | [82 69 93] | [−10 −55 21] |
| Lingual Gyrus | [105 68 68] | [13 −57 −1] |
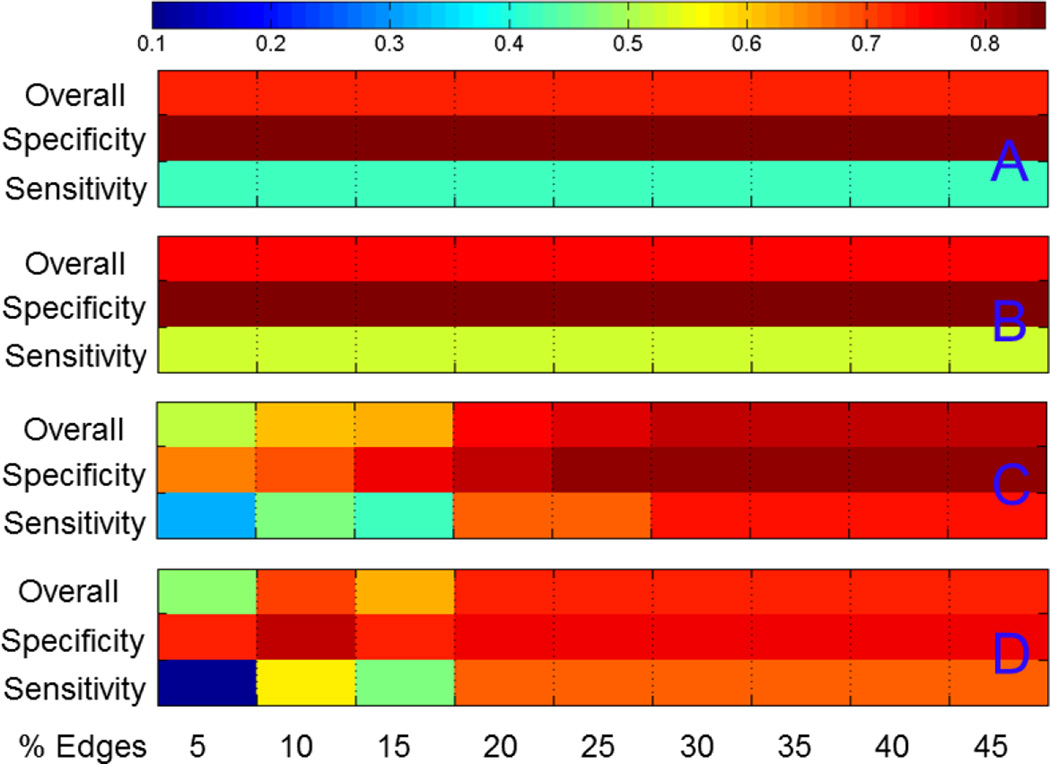
Prediction accuracies of support vector machine analysis using different methods at 20% threshold are shown in Table 2. Although all methods achieve relatively high overall accuracy rates above 70% and high accuracy rate for NC (specificity), the specific accuracy on schizophrenic subjects (sensitivity) is lower than 60% when betweenness centrality of all the nodes were included in the analysis. If only taking the ten hub nodes, using ranks of betweenness centrality rather than the actual values gave rise to slightly higher prediction rate. Figure 5 compares prediction accuracies of SVM analysis at different threshold. Fig. 5A is the result using BC ranks of all nodes; Fig. 5B is the result of using BC values of all nodes; Fig. 5C and 5D are the results for BC ranks and BC values of the ten hub nodes. Because there are more NC subjects, the prediction accuracy is always higher for NC. The classification accuracy stays the same for all thresholds if all nodes are used. With only hub nodes, the performance of the classifier is very stable for a thresholding range between 30% to 45%, with a sensitivity of 74% and a specificity of 83% by using BC ranks for SVM, and a sensitivity of 68% and a specificity of 76% by using BC values for SVM. Poor performance was found for thresholds lower than 20%. Comparing Fig. A and B, there is an advantage of using BC ranks over BC values, and the edge of advantage of using BC ranks almost held for all thresholds.
Table 2.
Classification accuracy rate for different SVM feature spaces, with 30% edges remaining. Based on BC, four sets of nodes were evaluated, namely centrality of all nodes, centrality of top ten nodes, rank of centrality of all nodes, and rank of centrality of top ten nodes.
| Centrality, all nodes |
Centrality, top ten hubs |
Rank of centrality, all nodes |
Rank of centrality, top ten hubs |
|
|---|---|---|---|---|
| Overall accuracy | 73% | 73% | 75% | 79% |
| Specifity | 93% | 76% | 90% | 83% |
| Sensitivity | 42% | 68% | 53% | 74% |
Figure 5.
Classification accuracy using ranks of betweenness centrality of all nodes (A); values of betweenness centrality of all nodes (B); ranks of betweenness centrality of top ten hub nodes (C); and values of betweenness centrality of top ten hub nodes (D).
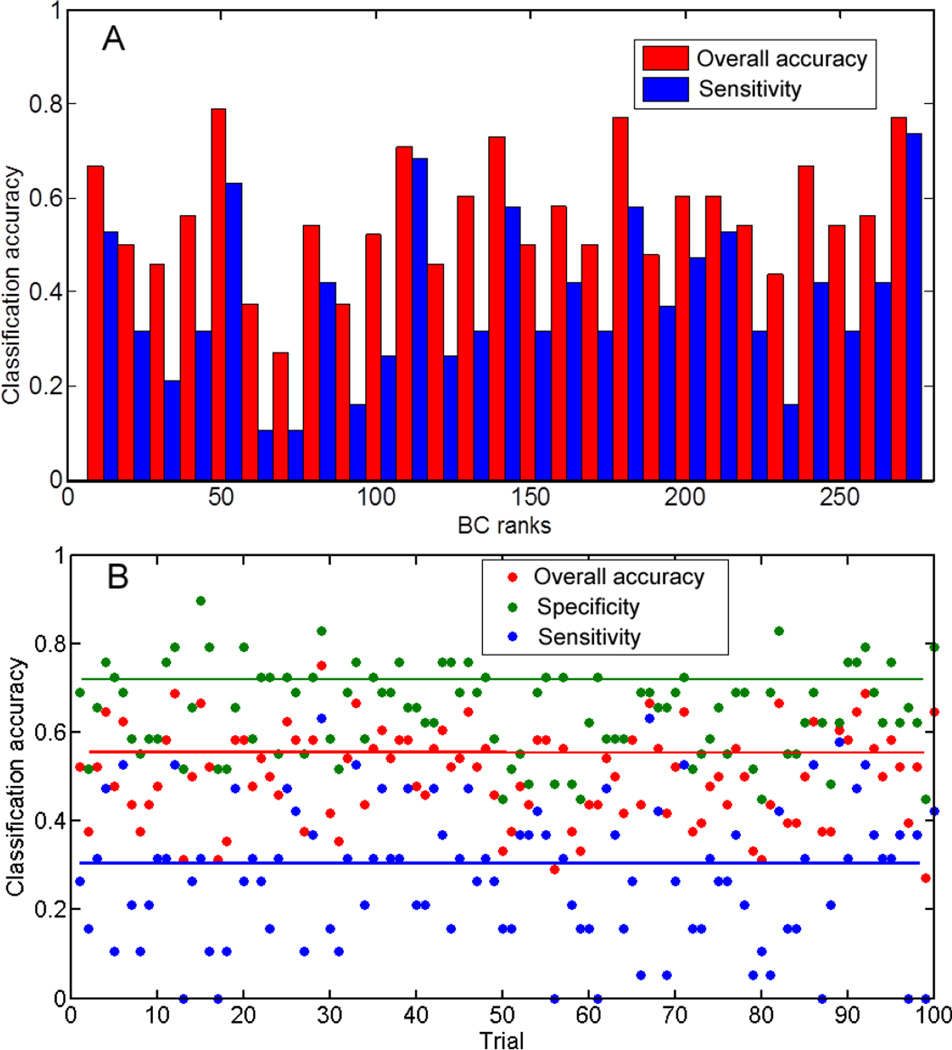
As a control, we performed SVM by using alternative methods. Fig. 6A shows the prediction rates as we chose every 10 nodes with continuous ranks of betweenness centrality starting from lowest to highest. Although many node sets give rise to high overall accuracy rate, only three achieve accuracy rates above 0.6 in predicting SZ. Fig. 6B is the result of randomizing NC and SZ subjects prior to SVM classification. For 100 trials, the performance varies, with an average classification accuracy of 0.56, and a sensitivity of 0.30.
Figure 6.
(A) shows classification accuracy using different sets of nodes in SVM while keeping the same number of features. The figure shows the prediction rates as we choose every 10 nodes with order of betweenness centrality starting from 9. Although many node sets give rise to high overall accuracy rate, only three sets achieve accuracy rates above 0.6 in predicting SZ. (B) shows the classification accuracy for 100 trials by randomly mixing SZ and NC subjects and performing SVM classification while still using the original labeling. The classification accuracy dramatically drops.
DISCUSSION
We showed that by using a small fraction of nodes with highest betweenness centrality, a classifier based on support vector machines can predict whether a subject belongs to the schizophrenia or healthy-control group with a reasonably high accuracy around 80%. The classification accuracy is very close or superior to previous results in classifying schizophrenia patients (Anderson and Cohen, 2013; Arbabshirani et al., 2013; Shen et al., 2010) as shown in Table 3. The prediction rate, however, goes down significantly for most other nodes. If putting the nodes in the order of BC values and dividing them into subsets with equal size of 10 nodes, only three sets achieve accuracy rates above 0.6 in predicting SZ. Our results suggest that alterations in the properties of the hub nodes may be a key network feature in schizophrenia, and support a disconnection model of the disorder.
Table 3.
Summary of reported sensitivity and specificity in classifying schizophrenia patients based on resting state functional connectivity.
| Number of subjects | specificity | sensitivity | |
|---|---|---|---|
| Shen et al. (2010) | Patients:32 Controls: 20 |
75% | 93.75% |
| Yu et al. (2013) | Patients: 24 Healthy siblings: 25 Controls: 22 |
87% | 66.7% |
| *Arbabshirani et al., (2013) | Patients:28 Controls: 28 |
100% | 67% |
| Anderson and Cohen (2013) | Patients:74 Controls: 72 |
65% | |
| Our work | Patients:19 Controls: 29 |
83% | 74% |
: many classification algorithms were tested in the paper, the result here is for linear SVM with reduced set of features (27 features), which is not the best compared to other nonlinear algorithms.
With higher classification accuracy than clustering coefficient and small-worldness, the power of classification using ranks of BC indicates a dramatic change of betweenness centrality order for the hubs in schizophrenia. This implies a reorganization of network topology, which has been reported by previous analysis on the functional and structural network (Rubinov and Bullmore, 2013; van den Heuvel et al., 2013). For the top ten nodes with highest centrality on the average functional network, some regions such as nodes at posterior cingulate and superior parietal lobe belong to the default brain network. Other regions such as nodes at precuneus, posterior cingulate, and lingual gyrus have been identified as hubs from the structural brain network (Nijhuis et al., 2013). In a latest review of schizophrenia and abnormal brain network hubs by Rubinov and Bullmore (Rubinov and Bullmore, 2013), they summarized nine network analyses of schizophrenia that showed alteration of hubs in SZ patients. In general, both studies of structural and functional network analysis identified hubs in frontal, temporal and parietal association areas, and insular area. This agrees well with our findings of those nodes having high betweenness centrality (Fig. 4). The six structural network analyses reported an overall reduction of hub nodes for schizophrenia. In three studies on functional networks using degree centrality, increased hubs were reported in some areas mixed with a decrease of hubs in other areas, which is also in line with our findings of BC value changes in the disorder. Figure 5 shows higher classification power with only ten hub nodes, indicating some of the hub nodes play an important role in distinguishing schizophrenia from normal controls. Including all nodes in the SVM analysis becomes destructive due to increasing noise. Despite that, the results depicted in figure 5 do not rule out topological reorganization of other nodes. Figure 6A shows that BC ranks of some other nodes may also have some classification ability but not as good as the hubs.
Most of the hub nodes that distinguish schizophrenia from non-psychiatric controls were believed to show relevance in schizophrenia by many other studies. As key nodes in the default-mode network, posterior cingulate and precuneus, along with cingulate gyrus, showed different activation levels between non-psychiatric controls and schizophrenia patients in an auditory oddball task (Garrity et al., 2007). Many deficits observed in schizophrenia are associated with insula functions including the processing of both visual and auditory emotional information, pain, and neuronal representations of the self (Wylie and Tregellas, 2010). Disruption of large-scale brain networks modulated by anterior insula was found in schizophrenia (Moran et al., 2013). Gray matter volume reduction was reported for middle frontal gyrus (Kikinis et al., 2010), accompanied by abnormality of white matter tracts connecting middle frontal gyrus to inferior frontal gyrus and striatum (Quan et al., 2013). In a quantitative meta-analysis of resting state functional MRI and positron emission tomography data, hyperactivation in bilateral lingual gyrus was found in schizophrenic patients (Kühn and Gallinat, 2013). Impaired eyeblink conditioning has suggested impaired functioning of the cerebellum in schizophrenia (Bolbecker et al., 2013). All these studies investigated brain deficits and abnormalities in schizophrenia from different perspectives; together they have formed a comprehensive picture which is now partly unveiled by network-based classification.
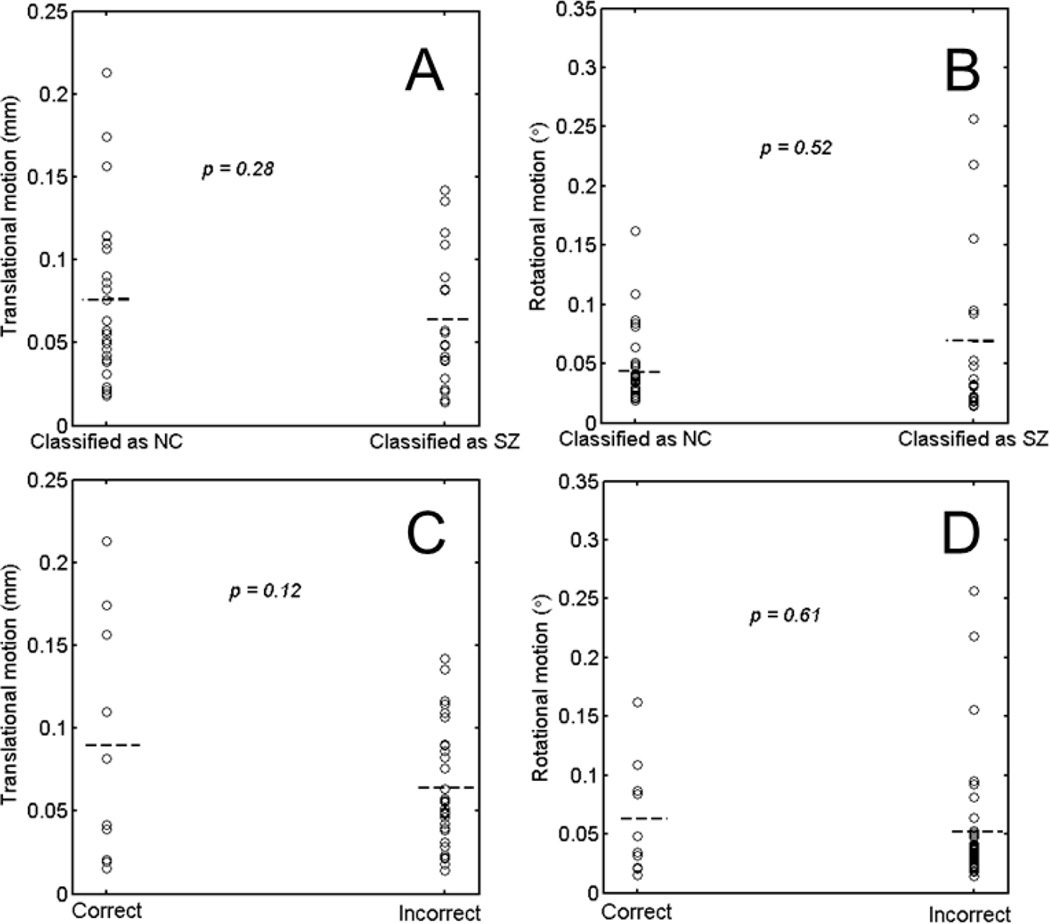
A challenge of using functional connectivity networks for classifying schizophrenia is the high variability that they present (Wang et al., 2011). One source of such high variability comes from the subject head movements (Van Dijk et al., 2012). Head motion can introduce spurious correlation while decreasing the true correlation. More importantly, the patients and non-psychiatric controls may have different levels of head motion, which imposes systematic biases in the constructed functional network. Figure 2 shows that the motion behavior is different between the two groups. It is a natural concern that motion may play a role in the classification. There are two possible effects of motion, one is a bias of classification toward non-psychiatric control or SZ patients; the other is overall low prediction rate. To test the bias due to motion, we compared the motion of those classified as a non-psychiatric control and the motion of those classified as SZ. Figure 7A and 7B show the results and p-values of two-sample t-tests for translational and rotational motion. There is no apparent suggestion that motion biased the classification toward SZ or NC. In addition, motion is a global effect. If motion significantly biased the classification, we should obtain high prediction accuracy for any ten nodes, which is not the case, as shown in Fig. 6A. To test the second effect, we compared the magnitude of motion with the classification performance for all the subjects at threshold of 30%. Figure 7C and 7D display the motion parameters and prediction performance of all subjects. The head motion showed larger variance and slightly higher mean values for wrong prediction, suggesting a trend that larger motion lead to wrong prediction, but no statistical difference on the performance was found.
Figure 7.
Motion effects on the SVM classification. (A) and (B) compare translational motion and rotational motion on those classified as NC and those classified as SZ. (C) and (D) compare translational motion and rotational motion on those classified correctly and those classified incorrectly. Results were from the network with threshold of 0.30.
The other source of variability is the intrinsic dynamics of functional connectivity (Chang and Glover, 2010). It was suggested that a minimum scan time of around 13 minutes is needed to account for the intrinsic variability (Birn et al., 2013). However, this condition was not met in our study due to difficulty to keep subjects alert for very long time. The high variability imposes some constraints on the choice of network metrics for classifying schizophrenia. Betweenness centrality stands out as a good feature for SVM for a number of reasons. First, a nice feature of betweenness centrality is that it is quite insensitive to thresholding. This is not surprising. The reason is that most of the shortest-paths heavily rely on the edges with highest weights (in our case in those edges with highest functional connectivity), and hence the impact of removing the edges with lowest weights should be minor. In fact, there is little difference for BC between threshold 20% and 45%. That is why the classification accuracy is constant for different thresholds when all nodes are used. This feature makes the classification more robust. Second, the top ten BC values have a much larger slope than others, making them or the order even more robust against noise and other variability. That is why using only the top ten nodes resulted in higher prediction accuracy. Third, performance can be further improved by using the rank of BC rather than BC itself. This is not surprising because the rank is less susceptible to inter-subject variability due to motion effects or intrinsic neuronal dynamics. The absolute value of BC is influenced by the actual values of correlation; the rank of BC, however, is a relative measure, and therefore less affected by any global effect of noise.
In summary, our results show that the nodes with high betweenness centrality in the functional connectivity network can be used to classify schizophrenia and non-psychiatric controls with a linear support vector machine algorithm. The prediction accuracy can be as high as 79% in overall and 74% for detecting schizophrenia by simply using the ranks of BC of these nodes, better than SVM method using clustering coefficient and small-worldness. The nodes with high BC values coincide well with previously reported regions showing abnormalities in schizophrenia. Because betweenness centrality is purely a network measure that characterizes the influence of a node in the connection to other nodes, our results suggest schizophrenia is associated with abnormality of brain networks and the hub nodes plays most important roles in the network abnormality.
ACKNOWLEDGEMENTS
This work was supported by the National Institute of Mental Health (R01 MH074983 and R01 2MH074983 to WPH).
Role of fundings
WPH and BFO were senior NIMH investigators. Funders had no role in the design, analysis, or interpretation of this study.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interests
All other authors declare that they have no conflicts of interest.
Contributions
HC did the data analysis, interpreted the analyses, carried out the literature review, and wrote the first draft of the manuscript. Author WPH, BFO, SN, and AB designed the study and reviewed the results. Author JSK, AB, and JH recruited the subjects and collected the data. Author SN, JG, BFO and AP interpreted the results and drafted the manuscript.
REFERENCE
- Anderson A, Cohen M. Decreased small-world functional network connectivity and clustering across resting state networks in schizophrenia: an fMRI classification tutorial. Front Hum Neurosci. 2013;7 doi: 10.3389/fnhum.2013.00520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arbabshirani M, Kiehl K, Pearlson G, Calhoun V. Classification of schizophrenia patients based on resting-state functional network connectivity. Front Neurosci. 2013;7 doi: 10.3389/fnins.2013.00133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn R, Molloy E, Patriat R, Parker T, Meier T, Kirk G, Nair V, Meyerand M, Prabhakaran V. The effect of scan length on the reliability of resting-state fMRI connectivity estimates. Nat Neurosci. 2013;83:550–558. doi: 10.1016/j.neuroimage.2013.05.099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin F, Haughton V, Hyde J. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Bolbecker A, Kent J, Petersen I, Klaunig M, Forsyth J, Howell J, Westfall D, O'Donnell B, Hetrick W. Impaired Cerebellar-Dependent Eyeblink Conditioning in First-Degree Relatives of Individuals With Schizophrenia. Schizophr Bull. 2013 doi: 10.1093/schbul/sbt112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner R, Sepulcre J, Talukdar T, Krienen F, Liu H, Hedden T, Andrews-Hanna J, Sperling R, Johnson K. Cortical Hubs Revealed by Intrinsic Functional Connectivity: Mapping, Assessment of Stability, and Relation to Alzheimer’s Disease. J. Neurosci. 2009;29:1860–1873. doi: 10.1523/JNEUROSCI.5062-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Andrews-Hanna JR, Schacter DL. The Brain's Default Network: Anatomy, Function, and Relevance to Disease. Annals of the New York Academy of Sciences. 2008 doi: 10.1196/annals.1440.011. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Chang C, Glover GH. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. NeuroImage. 2010;50:81–98. doi: 10.1016/j.neuroimage.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DD, Savoy RL. Functional magnetic resonance imaging (fMRI) “brain reading”: detecting and classifying distributed patterns of fMRI activity in human visual cortex. Neuroimage. 2003;19:261–270. doi: 10.1016/s1053-8119(03)00049-1. [DOI] [PubMed] [Google Scholar]
- Deco G, McIntosh A, Shen K, Hutchison R, Menon R, Everling S, Hagmann P, Jirsa V. Identification of Optimal Structural Connectivity Using Functional Connectivity and Neural Modeling. J. Neurosci. 2014;34:7910–7916. doi: 10.1523/JNEUROSCI.4423-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman L. A set of measures of centrality based on betweenness. Sociometry. 1977;40:35–41. [Google Scholar]
- Garrity A, Pearlson G, McKiernan K, Lloyd D, Kiehl K, Calhoun V. Aberrant “Default Mode” Functional Connectivity in Schizophrenia. Am J Psychiatry. 2007;164:450–457. doi: 10.1176/ajp.2007.164.3.450. [DOI] [PubMed] [Google Scholar]
- Goñi J, van den Heuvel M, Avena-Koenigsberger A, Velez de Mendizabal NR, Griffa A, Hagmann P, Corominas-Murtra B, Thiran JP, Sporns O. Resting-brain functional connectivity predicted by analytic measures of network communication. Proc. Natl. Acad. Sci. U.S.A. 2014;111:833–838. doi: 10.1073/pnas.1315529111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison P. The neuropathology of schizophrenia. A critical review of the data and their interpretation. Brain. 1999;122:593–624. doi: 10.1093/brain/122.4.593. [DOI] [PubMed] [Google Scholar]
- Insel T. Rethinking schizophrenia. Nature. 2010;468:187–193. doi: 10.1038/nature09552. [DOI] [PubMed] [Google Scholar]
- Kikinis Z, Fallon J, Niznikiewicz M, Nestor P, Davidson C, Bobrow L, Pelavin P, Fischl B, Yendiki A, McCarley R, Kikinis R, Kubicki M, Shenton M. Gray matter volume reduction in rostral middle frontal gyrus in patients with chronic schizophrenia. Schizophr Res. 2010;123:153–159. doi: 10.1016/j.schres.2010.07.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kühn S, Gallinat J. Resting-State Brain Activity in Schizophrenia and Major Depression: A Quantitative Meta-Analysis. Schizophr Bull. 2013;39:358–365. doi: 10.1093/schbul/sbr151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang M, Zhou Y, Jiang T, Liu Z, Tian L, Liu H, Hao Y. Widespread functional disconnectivity in schizophrenia with resting-state functional magnetic resonance imaging. Neuroreport. 2006;17:209–213. doi: 10.1097/01.wnr.0000198434.06518.b8. [DOI] [PubMed] [Google Scholar]
- Liu Y, Liang M, Zhou Y, He Y, Hao Y, Song M, Yu C, Liu H, Liu Z, Jiang T. Disrupted small-world networks in schizophrenia. Brain. 2008;131:945–961. doi: 10.1093/brain/awn018. [DOI] [PubMed] [Google Scholar]
- Lynall M, Bassett D, Kerwin R, McKenna P, Kitzbichler M, Muller U, Bullmore E. Functional Connectivity and Brain Networks in Schizophrenia. J. Neurosci. 2010;30:9477–9487. doi: 10.1523/JNEUROSCI.0333-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meier T, Desphande A, Vergun S, Nair V, Song J, Biswal B, Meyerand M, Birn R, Prabhakaran V. Support vector machine classification and characterization of age-related reorganization of functional brain networks. Neuroimage. 2012;60:601–613. doi: 10.1016/j.neuroimage.2011.12.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran L, Tagamets M, Sampath H, O'Donnell A, Stein E, Kochunov P, Hong L. Disruption of Anterior Insula Modulation of Large-Scale Brain Networks in Schizophrenia. Biol. Psychiatry. 2013;74:467–474. doi: 10.1016/j.biopsych.2013.02.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nijhuis E, van Walsum A, Norris D. Topographic Hub Maps of the Human Structural Neocortical Network. PLoS ONE. 2013;8:e65511. doi: 10.1371/journal.pone.0065511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ongür D, Lundy M, Greenhouse I, Shinn A, Menon V, Cohen B, Renshaw P. Default mode network abnormalities in bipolar disorder and schizophrenia. Psychiatry Res. 2010;183:59–68. doi: 10.1016/j.pscychresns.2010.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersson-Yeo W, Allen P, Benetti S, McGuire P, Mechelli A. Dysconnectivity in schizophrenia: Where are we now? Neurosci Biobehav Rev. 2011;35:1110–1124. doi: 10.1016/j.neubiorev.2010.11.004. [DOI] [PubMed] [Google Scholar]
- Pomarol-Clotet E, Salvador R, Sarró S, Gomar J, Vila F, Martínez A, Guerrero A, Ortiz-Gil J, Sans-Sansa B, Capdevila A, Cebamanos J, McKenna P. Failure to deactivate in the prefrontal cortex in schizophrenia: dysfunction of the default mode network? Psychol Med. 2008;38:1185–1193. doi: 10.1017/S0033291708003565. [DOI] [PubMed] [Google Scholar]
- Quan M, Lee S, Kubicki M, Kikinis Z, Rathi Y, Seidman L, Mesholam-Gately R, Goldstein J, McCarley R, Shenton M, Levitt J. White matter tract abnormalities between rostral middle frontal gyrus, inferior frontal gyrus and striatum in first-episode schizophrenia. Schizophr Res. 2013;145:1–10. doi: 10.1016/j.schres.2012.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL. A default mode of brain function. Proc Natl Acad Sci U S A. 2001;98:676–682. doi: 10.1073/pnas.98.2.676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raichle ME, Snyder AZ. A default mode of brain function: a brief history of an evolving idea. Neuroimage. 2007;37:1083–1090. doi: 10.1016/j.neuroimage.2007.02.041. discussion 1097–1089. [DOI] [PubMed] [Google Scholar]
- Ripke S, O'Dushlaine C, Chambert K, et al. Genome-wide association analysis identifies 13 new risk loci for schizophrenia. Nat. Genet. 2013;45:1150–1159. doi: 10.1038/ng.2742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Bullmore E. Schizophrenia and abnormal brain network hubs. Dialogues Clin Neurosci. 2013;15:339–349. doi: 10.31887/DCNS.2013.15.3/mrubinov. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Rubinov M, Sporns O. Weight-conserving characterization of complex functional brain networks. NeuroImage. 2011;56:2068–2079. doi: 10.1016/j.neuroimage.2011.03.069. [DOI] [PubMed] [Google Scholar]
- Shen H, Wang L, Liu Y, Hu D. Discriminative analysis of resting-state functional connectivity patterns of schizophrenia using low dimensional embedding of fMRI. Neuroimage. 2010;49:3110–3121. doi: 10.1016/j.neuroimage.2009.11.011. [DOI] [PubMed] [Google Scholar]
- Shen X, Tokoglu F, Papademetris X, Constable R. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. Neuroimage. 2013;82:403–415. doi: 10.1016/j.neuroimage.2013.05.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O. Network of the Brain. Cambridge, Massachusetts: The MIT Press; 2010. [Google Scholar]
- Supekar K, Menon V, Rubin D, Musen M, Greicius M. Network Analysis of Intrinsic Functional Brain Connectivity in Alzheimer’s Disease. PLoS Biol. 2008;4:e1000100. doi: 10.1371/journal.pcbi.1000100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tandon R, Keshavan M, Nasrallah H. Schizophrenia, “Just the Facts” What we know in 2008. 2. Epidemiology and etiology. Schizophr Res. 2008;102:1–18. doi: 10.1016/j.schres.2008.04.011. [DOI] [PubMed] [Google Scholar]
- van den Heuvel M, Sporns O, Collin G, Scheewe T, Mandl R, Cahn W, Goñi J, Hulshoff Pol H, Kahn R. Abnormal Rich Club Organization and Functional Brain Dynamics in Schizophrenia. JAMA Psychiatry. 2013;70:783–792. doi: 10.1001/jamapsychiatry.2013.1328. [DOI] [PubMed] [Google Scholar]
- van den Heuvel MP, Mandl RC, Stam CJ, Kahn RS, Hulshoff Pol HE. Aberrant frontal and temporal complex network structure in schizophrenia: a graph theoretical analysis. J. Neurosci. 2010;30:15915–15926. doi: 10.1523/JNEUROSCI.2874-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk K, Sabuncu M, Buckner R. The influence of head motion on intrinsic functional connectivity MRI. NeuroImage. 2012;59:431–438. doi: 10.1016/j.neuroimage.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J-H, Zuo X-N, Gohel S, Milham MP, Biswal BB, He Y. Graph Theoretical Analysis of Functional Brain Networks: Test-Retest Evaluation on Short- and Long-Term Resting-State Functional MRI Data. PLoS One. 2011;6:e21976. doi: 10.1371/journal.pone.0021976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie K, Tregellas J. The role of the insula in schizophrenia. Schizophr Res. 2010;123:93–104. doi: 10.1016/j.schres.2010.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y, Shen H, Zhang H, Zeng L, Xue Z, Hu D. Functional connectivity-based signatures of schizophrenia revealed by multiclass pattern analysis of resting-state fMRI from schizophrenic patients and their healthy siblings. Biomed Eng Online. 2013;12 doi: 10.1186/1475-925X-12-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Lin L, Lin C, Zhou Y, Chou K, Lo C, Su T, Jiang T. Abnormal topological organization of structural brain networks in schizophrenia. Schizophr Res. 2012;141:109–118. doi: 10.1016/j.schres.2012.08.021. [DOI] [PubMed] [Google Scholar]
- Zhou Y, Liang M, Tian L, Wang K, Hao Y, Liu H, Liu Z, Jiang T. Functional disintegration in paranoid schizophrenia using resting-state fMRI. Schizophr Res. 2008a;97:194–205. doi: 10.1016/j.schres.2007.05.029. [DOI] [PubMed] [Google Scholar]
- Zhou Y, Shu N, Liu Y, Song M, Hao Y, Liu H, Yu C, Liu Z, Jiang T. Altered resting-state functional connectivity and anatomical connectivity of hippocampus in schizophrenia. Schizophr Res. 2008b;100:120–132. doi: 10.1016/j.schres.2007.11.039. [DOI] [PubMed] [Google Scholar]
- Zuo X, Ehmke R, Mennes M, Imperati D, Castellanos F, Sporns O, Milham M. Network centrality in the human functional connectome. Cerebral Cortex. 2012;22:1862–1875. doi: 10.1093/cercor/bhr269. [DOI] [PubMed] [Google Scholar]