Abstract
Experimental data for density, viscosity, refractive index and surface tension of four phosphonium-based ionic liquids were measured in the temperature range between (288.15 and 353.15) K and at atmospheric pressure. The ionic liquids considered include tri(isobutyl) methylphosphonium tosylate, [Pi(444)1][Tos], tri(butyl)methylphosphonium methylsulfate, [P4441][CH3SO4], tri(butyl)ethylphosphonium diethylphosphate, [P4442][(C2H5O)2PO2], and tetraoctylphosphonium bromide, [P8888][Br]. Additionally, derivative properties, such as the isobaric thermal expansion coefficient, the surface thermodynamic properties and the critical temperatures for the investigated ionic liquids were also estimated and are presented and discussed. Group contribution methods were evaluated and fitted to the density, viscosity and refractive index experimental data.
Keywords: Phosphonium, ionic liquids, density, viscosity, refractive index, surface tension
1. Introduction
In recent years, ionic liquids (ILs) appeared as effective replacement solvents for many volatile organic compounds (VOCs), and thus contributed to the promotion and enlargement of more sustainable chemistry and technological processes. ILs are composed of large organic cations and organic or inorganic anions that cannot easily form an ordered crystal and thus remain liquid at or near room temperature. The academic and industrial interest, on these molten salts, results from their outstanding properties, such as negligible volatility, non-flammability, wide liquid electrochemical window, large liquidus temperature range, thermal stability, and the ability to dissolve a wide range of organic, inorganic and polymeric compounds [1–8], but mostly derived from the possibility of synthesizing an IL with a set of target properties suitable for a specific process or application. This ability to tune the ILs properties, through the combination or functionalization of cations and anions, lead to the designation of ‘designer solvents’. Moreover, these outstanding characteristics make ILs suitable candidates for a large number of applications, viz. as extractants, lubricants, thermal fluids, ionogels, plasticizers, catalysts, capacitors, sensors, among others.[2,9–13]
For the accurate design, optimization, and operation of (industrial) processes and an efficient investigation of the ILs potential as designer solvents, the knowledge of their thermophysical properties, namely viscosity, density, and interfacial tension, is important. Furthermore, reliable thermophysical data is required for the application of models employed in the development of efficient industrial processes and equipment design. Due to the large number of ILs that can be synthesized, the measurement of the thermophysical properties for all of them stands impractical, even unviable. Therefore, the selection and investigation of systematic series of compounds, representative of the different families, can provide insights on the ILs structure-property relationships and thus, allow the development of adequate correlations, equations of state or other models for these properties.
Phosphonium-based ILs, thermally more stable (in basic and nucleophilic conditions due to the absence of acidic protons in their moieties) and less expensive than their equivalent imidazolium ILs, [14–16] are widely reported in the literature covering a large set of properties.[17–24] Fraser et al.[19] stated that phosphonium ILs clearly offer, in some cases, several advantages over other types of ILs, including, in specific cases and applications, higher thermal stability, lower viscosity, and higher stability in strongly basic or strongly reducing conditions. Frackowiak et al.[22] demonstrated that phosphonium ILs are potential compounds for application as super capacitors due to their enhanced electrochemical window. Tsunashima et al.[23] studied the applicability of phosphonium ILs as battery electrolytes; their studies revealed that through chemical tuning, the low-viscosity phosphonium ILs display excellent electrochemical and thermal stabilities. Furthermore, their extreme low melting temperatures are of great importance in separation processes. These characteristics offer better scope and have proved to be valuable for many specific applications, like in the purification of biomolecules in aqueous two-phase systems [25,26], in the separation of ethanol-water mixtures as entrainers able to break the system azeotrope [27,28], in the extraction of metals [29,30] and in CO2 capture and gas separation processes [31–33].
Despite the numerous advantages reported for phosphonium ILs, their applications will remain limited without further characterization of their thermophysical properties. Thus, the collection of novel experimental density, viscosity, refractive index and surface tension data measured in this work, as well as other retrieved from literature, allows to infer on specific structural effects of ILs, such the impact of the cation’s alkyl chain length, ramification and symmetry and on the anion type. Additionally, derivative properties, such as the isobaric thermal expansion coefficient, the surface thermodynamic properties and critical temperature were also determined. Group contribution methods [34,35] for the density, viscosity and refractive index were also applied and evaluated.
2. Materials and methods
2.1.Materials
Four ILs were studied in this work, namely tri(isobutyl)methylphosphonium tosylate [Pi(444)1][Tos], tri(butyl)methylphosphonium methylsulfate [P4441][CH3SO4], tri(butyl)ethylphosphonium diethylphosphate [P4442][(C2H5O)2PO2] and tetraoctylphosphonium bromide [P8888][Br]. The ILs chemical structures and corresponding designations are presented in Table 1. All the ILs were kindly offered by CYTEC Industries Inc. with mass fraction purities higher than 98%.
Table 1.
Ionic structure, compound description, CAS number, molecular weight, water content and mass fraction purity of the studied ILs.
| IL | Ionic structure |
|---|---|
| tri(isobutyl)methylphosphonium tosylate [Pi(444)1][Tos] (CAS: 374683-35-9; M = 388.5 g·mol−1; H2O wt % = 0.0842%; wt % = 98%) |

|
| tri(butyl)methylphosphonium methylsulfate [P4441][CH3SO4] (CAS: 69056-62-8; M = 328.5 g·mol−1; H2O wt % = 0.0783%; wt % = 98%) |

|
| tri(butyl)ethylphosphonium diethylphosphate [P4442][(C2H5O)2PO2] (CAS: 20445-94-7; M = 384.5 g·mol−1; H2O wt % = 0.0741%; wt % = 98%) |

|
| tetraoctylphosphonium bromide [P8888][Br] (CAS: 23906-97-0; M = 563.8 g·mol−1; H2O wt % = 0.0105%; wt % = 98%) |

|
The water content plays an important role in the IL properties, especially on the surface tension and viscosity [36,37], and significant deviations can be found due to small amounts of water. Therefore, in order to remove traces of water and volatile compounds, individual samples of each IL were dried at moderate temperature (≈ 323 K), vacuum (≈ 10−1 Pa) and under continuous stirring, for a minimum period of 48 h prior to the measurements. The purity of each IL was checked by 1H and 13C NMR to assure that no degradation occurred during the purification procedure and measurements. The final IL water content, after the drying step and immediately before the measurements, was determined with a Metrohm 831 Karl Fischer coulometer (using the Hydranal-Coulomat AG from Riedel-de Haën as analyte) and is reported in Table 1.
2.2.Experimental Section
2.2.1. Density and Viscosity
Density (ρ) and dynamic viscosity (η) measurements were carried out using an automated SVM3000 Anton Paar rotational Stabinger viscometer-densimeter in the (283.15 to 353.15) K temperature range and at atmospheric pressure (≈ 0.1 MPa). The density absolute uncertainty is ± 5 × 10−4 g·cm−3, the dynamic viscosity relative uncertainty ± 1% and the temperature relative uncertainty is ± 0.02 K. Further details about the equipment and methodologies can be found elsewhere.[38]
2.2.2. Refractive Index
Measurements of refractive indices (nD) were performed in the 589.3 nm wave length using an automated Abbemat 500 Anton Paar refractometer. Refractive index measurements were carried out in the (283.15 to 353.15) K temperature range and at atmospheric pressure. The Abbemat 500 Anton Paar refractometer uses reflected light to measure the refractive index, where the sample on the top of the measuring prism is irradiated from different angles by a light-emitting diode (LED). The maximum deviation in temperature is ± 0.05 K, and the maximum uncertainty in the refractive index measurements is ± 2·10−5 nD. The capability of the equipment to determine accurate refractive indices of ILs has been previously verified.[39–42]
2.2.3. Surface Tension
The surface tensions of each IL were determined through the analysis of the shape of a pendant drop using a Data physics contact angle system, OCA-20 (Data Physics Instruments GmbH, Germany). Pendant drops were created using a Hamilton DS 500/GT syringe connected to a Teflon coated needle placed inside an aluminium air chamber capable of maintaining the temperature within ± 0.1 K. The temperature was attained by circulating water in the double jacketed aluminium cell by means of a Julabo F-25 water bath. The temperature inside the aluminium chamber was measured with a Pt100 which is at a distance of approximately 2 cm of the drop. The surface tension measurements were performed in the (293 to 344) K temperature range and at atmospheric pressure. After reaching a specific temperature, the drop was formed and the measurements were carried out after a minimum period of 30 min to guarantee the thermal equilibrium. Silica gel was kept inside the air chamber to maintain a dry atmosphere. For the surface tension determination, at each temperature and for each IL, at least three drops were formed and analyzed. For each drop, an average of 100 images was additionally captured. The analysis of the drop shape was achieved with the software module SCA 20. The IL density data required to the surface tension determination were those determined in this work. The equipment was previously validated through the measurement of the surface tension of ultra-pure water, decane and dodecane, as well as with a large number of ILs.[43]
3. Results and discussions
3.1.Density
The density measurements were carried out at atmospheric pressure and in the (283.15 to 353.15) K temperature range for [Pi(444)1][Tos], [P4441][CH3SO4] and [P4442][(C2H5O)2PO2] and from (318.15 to 353.15) K for [P8888][Br]. The respective values of densities are reported in Table 2 and depicted in Figure 1. As commonly observed the phosphonium-based ILs density is generally lower than that of the imidazolium-based ones.[39,44–46] At a given temperature, the density of the studied ILs follows the order: [Pi(444)1][Tos] > [P4441][CH3SO4] > [P4442][(C2H5O)2PO2] > [P8888][Br]. Furthermore, both [P8888][Br] and [P444(16)][Br], [24] with the same number of methylene units at the caiton (same molecular weight), present similar densities.
Table 2.
Densities, ρ, molar volumes, Vm, viscosities, η, and refractive index, nD, of the studied ILs as a function of temperature and at atmospheric pressure.
| [Pi(444)1][Tos] | [P4441][CH3SO4] | [P4442][(C2H5O)2PO2] | [P8888][Br] | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||
| T /K | ρ /kg·m−3 | 106Vm /m3·mol−1 |
η/mPa·s | nD | ρ /kg·m−3 | 106Vm /m3·mol−1 |
η /mPa·s | nD | ρ /kg·m−3 | 106Vm /m3·mol−1 |
η /mPa·s | nD | ρ /kg·m−3 | 106Vm /m3·mol−1 |
η /mPa·s | nD |
| 283.15 | 1082.4 | 359.0 | 21829.0 | 1.52489 | 1076.5 | 305.1 | 6214.1 | 1.48038 | 1021.5 | 376.4 | 1018.4 | 1.47176 | ||||
| 288.15 | 1079.3 | 360.0 | 11305.0 | 1.52338 | 1073.4 | 306.0 | 3840.1 | 1.47891 | 1018.0 | 377.7 | 669.5 | 1.46996 | ||||
| 293.15 | 1076.2 | 361.0 | 6231.9 | 1.52170 | 1070.3 | 306.9 | 2476.4 | 1.47742 | 1014.4 | 379.0 | 466.4 | 1.46809 | ||||
| 298.15 | 1073.2 | 362.0 | 3612.4 | 1.52030 | 1067.2 | 307.8 | 1629.2 | 1.47632 | 1010.9 | 380.3 | 316.8 | 1.46618 | ||||
| 303.15 | 1070.1 | 363.1 | 2199.9 | 1.51828 | 1064.1 | 308.7 | 1109.1 | 1.47427 | 1007.5 | 381.6 | 226.7 | 1.46474 | ||||
| 308.15 | 1067.0 | 364.1 | 1397.3 | 1.51635 | 1061.0 | 309.6 | 774.5 | 1.47232 | 1004.1 | 382.9 | 166.0 | 1.46308 | ||||
| 313.15 | 1064.0 | 365.2 | 917.9 | 1.51433 | 1057.9 | 310.5 | 555.0 | 1.47072 | 1000.7 | 384.2 | 124.7 | 1.46110 | ||||
| 318.15 | 1060.9 | 366.2 | 623.7 | 1.51233 | 1054.8 | 311.4 | 403.6 | 1.46912 | 997.6 | 385.4 | 94.6 | 1.45923 | 945.0 | 596.6 | 376.5 | 1.48262 |
| 323.15 | 1057.7 | 367.3 | 436.2 | 1.51055 | 1051.8 | 312.3 | 300.0 | 1.46758 | 994.3 | 386.7 | 73.4 | 1.45738 | 942.0 | 598.5 | 289.9 | 1.48092 |
| 328.15 | 1054.7 | 368.4 | 313.1 | 1.50872 | 1048.9 | 313.1 | 227.0 | 1.46603 | 990.9 | 388.0 | 57.9 | 1.45563 | 938.9 | 600.4 | 226.4 | 1.47916 |
| 333.15 | 1051.8 | 369.4 | 230.1 | 1.50698 | 1045.9 | 314.0 | 174.7 | 1.46457 | 987.6 | 389.3 | 46.4 | 1.45385 | 935.9 | 602.4 | 178.7 | 1.47699 |
| 338.15 | 1048.8 | 370.5 | 172.7 | 1.50537 | 1043.0 | 314.9 | 136.3 | 1.46318 | 984.3 | 390.6 | 37.5 | 1.45212 | 932.9 | 604.3 | 142.1 | 1.47523 |
| 343.15 | 1045.9 | 371.5 | 132.1 | 1.50391 | 1040.1 | 315.8 | 107.9 | 1.46185 | 980.9 | 392.0 | 30.8 | 1.45045 | 929.8 | 606.3 | 114.4 | 1.47354 |
| 348.15 | 1043.1 | 372.5 | 102.8 | 1.50252 | 1037.3 | 316.6 | 86.4 | 1.46067 | 977.6 | 393.3 | 25.6 | 1.44880 | 926.8 | 608.3 | 93.4 | 1.47195 |
| 353.15 | 1040.2 | 373.5 | 81.3 | 1.50124 | 1034.4 | 317.5 | 70.0 | 1.45965 | 974.3 | 394.6 | 21.6 | 1.447176 | 923.7 | 610.3 | 76.8 | 1.47035 |
Standard temperature uncertainty is u (T) = ±0.02 K and the combined expanded uncertainties, Uc, are Uc (ρ) = ±0.5 kg·m−3 ; Uc (η) = 0.1% ; Uc (nD) = 2 × 10−5 with an approximately 95% level of confidence.
Figure 1.
Density as a function of temperature (left) and relative deviations between the experimental data from this work and those available in the literature [14,18,20,47–51] (right). The solid lines represent the Gardas and Coutinho [34] group contribution method.
As depicted in Figure 2, the density decreases, for a common anion, with the cation alkyl chain length increase due to the lower density of the methylene groups. The anion, by other hand, imposes a greater effect on the IL density. With the increase of the anion molecular weight, and consequently the overall size and charge dispersion, there is an increase in the density, as depicted in Figure 2.
Figure 2.
Density as function of ionic liquids’ molecular weight, for tosylate- (308 K), methylsulfate- (298 K), 1-butyl-3-methylimidazolium (298 K) and trihexyl(tetradecyl)phosphonium-based ILs (323 K).[20,47,48,52–62] The lines are guides for the eyes.
Molar volumes, Vm, were calculated and are reported in Table 2 and depicted in Figure 3, as function of temperature. For the studied ILs, the molar volumes present a small temperature dependency and increase in the order: [P8888][Br] > [P4442][(C2H5O)2PO2] > [Pi(444)1][Tos] > [P4441][CH3SO4].
Figure 3.
Molar volumes as function of temperature for the studied ILs (left) and molar volume and density as function of ILs at 323.15 K (right).
The relative deviations between the density data measured in this work and those available in the literature [14,18,20,47–51] are displayed in Figure 1. Experimental data for the studied ILs are in good agreement with the available literature values, with absolute average relative deviations ranging from (0.02 to 1.19)%. The absolute average relative deviations towards [Pi(444)1][Tos] reported by Bradaric et al.[14], AlTuwaim et al.[18], Anthony et al.[50] and Domańska et al.[51] are 0.32%, 0.47% 0.31% and 0.57% respectively. The absolute average relative deviations towards the [P4441][CH3SO4] reported by Deive et al.[20] is 0.83%. Absolute relative deviations of 0.22%, 1.19% and 0.34% for [P4442][(C2H5O)2PO2] were found against the data of Deive et al.[20], Kilaru et al.[48] and Ficke et al.[47], respectively. The data from Kilaru et al.[48] present the higher deviations found, that seem to be related with the high amount of water present in the authors’ sample (1080 ppm). Absolute relative deviations towards [P8888][Br] was found to be 0.02% when compared to the data reported by Vaughan et al.[49].
Gardas and Coutinho [34] extended the Ye and Shreeve [63] approach to the estimation of IL densities for a wide range of temperatures, (288.15 to 353.15) K, pressures, (0.10 to 100) MPa, and ILs families according to the equation
| (1) |
where ρ is the density in kg·m−3, M the molecular weight in kg·mol−1, N the Avogadro constant, V the molecular volume in Å3, T the temperature in K and p the pressure in MPa. The universal coefficients a, b and c are 0.8005 ± 0.0002, 6.652·10−4 ± 0.007·10−4 K−1 and −5.919·10−4 ± 0.024·10−4 MPa−1, respectively, at a 95% confidence level.
The experimental density data were additionally used to extend the parameter table on the group contribution method previously proposed by Gardas and Coutinho [34]. Volumes for the [Pi(444)1]+ and [P1111]+ cations and [(C2H5O)2PO2]− and [CH3SO4]− anions were estimated based on density values taken from literature [20,47,48,52–60,62,64] and those reported in this work. With density data, for the anions investigated here, mainly available for the well characterized imidazolium family, the group contribution anionic volumes were determined using 240 experimental data points from six compounds. Despite the deviations found among different authors, a percentage absolute average deviations of 0.92% and 0.62% were obtained against data for [CH3SO4]− and [C2H5PO3]− anion-based ILs, respectively. Once the anions volume determined, that of the [P1111]+ cation was fitted against our experimental data and those of Deive et al.[20], Ficke et al.[47] and Kilaru et al.[48] with percentage absolute average deviation of 0.40%. The volumetric parameters for the anions [Tos]− and [Br]− were taken from previous works.[24,46] Both the estimated and literature values of cationic and anionic volumes are reported in Table 3. The proposed volumes provide a good description of the experimental density data, as shown in Figure 1, with an absolute relative average deviation of 0.16%, 0.20%, 0.046% and 0.52% for [Pi(444)1][Tos], [P4441][CH3SO4], [P4442][(C2H5O)2PO2] and [P8888][Br], respectively.
Table 3.
Ionic Volumes, V, determined using the Gardas and Coutinho Group Contribution Model [34] for the studied ILs.
Thermal Expansion Coefficient
The isobaric thermal expansion coefficients, αp, of the studied ILs, which reflect the ILs volumetric changes with temperature, were calculated from the fitting of the experimental data with the following equation,
| (2) |
where ρ is the density in kg·m−3, T the temperature in K, and p a fixed pressure.
The calculated thermal expansion coefficients for the pure liquids are listed Table 4 where it can be seen that the change in the ILs volume is small as the temperature increases which confirms the weak expansion ability of IL fluids.[65] The values obtained vary between 5.7 and 6.7 × 10−4 K−1 and are of the same order of magnitude, (5 to 7) × 10−4 K−1, of those reported for other ILs families, like ammonium-, sulfonium-, imidazolium-, pyridinium- and pyrrolidinium-based ILs.[39,41,42,65–69] The results also indicate that the alkyl side chain length presents a lower impact on the thermal expansion coefficient than that observed for the anion replacement.[39,46,65,69]
Table 4.
Coefficients of thermal expansion, αp, refractive indices, nD, isotropic polarizabilities, derived molar refractions, Rm, and free volumes, fm, surface entropy, Sγ, surface enthalpy, Hγ, and estimated critical temperatures using both Eötvös, Tc,Eot, [86] and Guggenheim, Tc,Gug, [87] empirical equations for the studied ILs.
| [Pi(444)1][Tos] | [P4441][CH3SO4] | [P4442][(C2H5O)2PO2] | [P8888][Br] | |
|---|---|---|---|---|
| 104·(αp ± σ) /K−1 | 5.706 ± 0.073 | 5.715 ± 0.073 | 6.726 ± 0.101 | 6.508 ± 0.052 |
| n D [#] | 1.51233 | 1.46912 | 1.45923 | 1.48262 |
| Polarizability[#] /bohr3 | 294.15 | 232.04 | 281.98 | 455.48 |
| Rm [#] /cm3·mol−1 | 109.95 | 86.74 | 105.40 | 170.26 |
| fm[#]/cm3·mol−1 | 256.28 | 224.65 | 279.99 | 426.31 |
| 105·(Sγ ± σ)/J·m−2·K−1 | 7.7 ± 0.31 | 6.4 ± 0.24 | 7.5 ± 0.27 | 5.7 ± 0.17 |
| 102·(Hγ ± σ) /J·m−2 | 6.1 ± 0.10 | 5.5 ± 0.06 | 8.5 ± 0.08 | 4.5 ± 0.05 |
| Tc,Eot /K | 891 ± 27 | 901 ± 3 | 792 ± 21 | 922 ± 22 |
| Tc,Gug /K | 892 ± 23 | 900 ± 3 | 796 ± 17 | 906 ± 17 |
at 318.15 K.
3.2.Viscosity
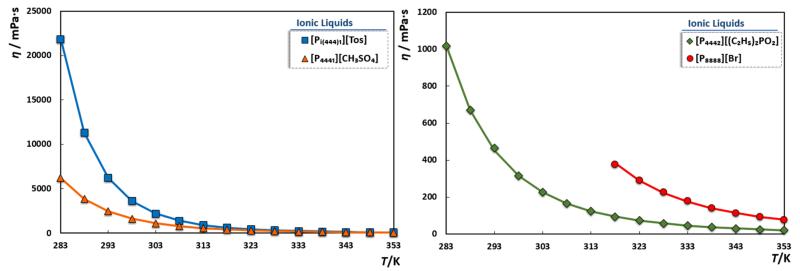
Viscosity is an important property for the design of industrial processes involving heat and/or mass transfer, dissolution or absorption of compounds in fluids; thereby, it stands as a key property on the selection of ILs suitable for a particular application. The experimental viscosity data for the studied ILs is reported in Table 2 and depicted in Figure 4.
Figure 4.
Viscosity data for the studied ILs. The solid lines represent the Vogel-Tammann-Fulcher (VTF) group contribution correlation.[35]
For the studied compounds, few viscosity data is available [18,20,70,71] in the literature. As depicted in Figure 5, viscosity data for [Pi(444)1][Tos] shows average relative deviations of −17.52% and 51.31% against Green et al.[71] and AlTuwaim et al.[18] data, respectively. Nonetheless, very high deviations of 166.6%, were obtained for [P4441][CH3SO4] when comparing the data from Deive et al.[20]. Experimental data for [P4442][(C2H5O)2PO2], on the other hand, present average relative deviation of 3.44%, 9.49% and −49.51% when compared to the data reported by Deive et al.[20], Ferguson et al.[70] and Green et al.[71], respectively. To the best of our knowledge no viscosity data are available for [P8888][Br]. When compared with experimental density data, larger differences are detected within viscosity values obtained by different authors. It is well known that viscosity is highly “sensitive” to the presence of impurities, namely to the adsorption of moisture during the experimental manipulation. Therefore, a purification step and a correct sample manipulation are of vital importance to achieve accurate viscosity data. While Green et al.[71] and AlTuwaim et al.[18] reported a purification procedure using vacuum for several days, Fergunson et al.[70] degassed the IL in a desiccator for 3 hours under low vacuum and Deive et al.[20] used the IL as received without further purification. Furthermore, most of the authors evaluated the ILs’ viscosity as a secondary measurement for calculations and, therefore, no special attention was given to its determination. In addition, while AlTuwaim et al.[18] and Deive et el.[20] report viscosity measurements using Anton Paar apparatuses, other authors do not mention the equipment and technique addopted. Thus, large discrepancies, in the viscosity values, are expected and observed among the different authors.
Figure 5.
Relative deviations between the experimental viscosity data of this work and those available in the literature.[18,20,70,71]
As commonly observed, viscosity markedly decreases with the temperature increase. The viscosity increases in the following order: [Pi(444)1][Tos] >> [P4441][CH3SO4] > [P8888][Br] > [P4442][(C2H5O)2PO2]. Similar to that observed previously for imidazolium- and piridinium-based ILs [41] the π–π interactions due to the presence of an aromatic ring, now at the ([Pi(444)1][Tos]) anion, leads to higher resistance to shear stress, to a more rigid IL structure and therefore to a bulkier distribution and higher viscosities.
The description of viscosities for the ILs studied was carried out using the group contribution method, based on the Vogel-Fulcher-Tammann (VFT) correlation,
| (3) |
where η is the dynamic viscosity in mPa·s, T is the temperature in K, and Aη,Bη and T0η are adjustable parameters estimated by fitting the equation to the experimental data. The fitted parameters are presented in Table 5. The fitting results are depicted in Figure 4 and present average absolute relative deviations of 0.16% for [Pi(444)1][Tos], 0.11% for [P4441][CH3SO4], 0.39% for [P4442][(C2H5O)2PO2] and 0.93% for [P8888][Br].
Table 5.
Vogel-Fulcher-Tammann (VFT) correlation parameters, Aη, Bη and T0η, for the studied ILs.
| IL | Aη | Bη /K | T0η /K |
|---|---|---|---|
| [Pi(444)1][Tos] | −3.15 | 1238 | 189 |
| [P4441][CH3SO4] | −3.75 | 1559 | 158 |
| [P4442][(C2H5O)2PO2] | −3.37 | 1199 | 167 |
| [P8888][Br] | −1.51 | 961 | 189 |
3.3.Refractive index
The refractive index specifies the dielectric response of a fluid to an electrical field induced by electromagnetic waves and is thus, an optical property of materials. The experimental refractive indices of the investigated ILs are shown in Figure 6 and reported in Table 2. The refractive indices were scanned upward and downward on temperature, with no hysteresis effects observed, and within the temperature range from (283.15 to 353.15) K. The refractive index decreases with the temperature increase. Furthermore, the refractive indices for the phosphonium-based ILs increase in the following sequence: [Pi(444)1][Tos] > [P8888][Br] > [P4441][CH3SO4] > [P4442][(C2H5O)2PO2].
Figure 6.
Refractive Index as a function of temperature (left) and relative deviations (right) between the experimental data from this work and those available in the literature.[18,20] The solid lines represent the Gardas and Coutinho [35] group contribution method.
The relative deviations between the data measured in this work and those reported in literature [18,20] are depicted in Figure 6. Experimental data for [Pi(444)1][Tos], [P4441][CH3SO4] and [P4442][(C2H5O)2PO2] are in good agreement with available literature values, with absolute relative average deviations ranging from (0.1 to 0.13)%. The absolute relative average deviations towards [Pi(444)1][Tos] reported by Altuwaim et al.[18] is 0.13%. Experimental data for [P4441][CH3SO4] and [P4442][(C2H5O)2PO2] present absolute average relative deviations of 0.12% and 0.1% when compared to the values reported by Deive et al.[20], respectively. To the best of our knowledge refractive indices for [P8888][Br] are here reported for the first time.
The refractive indices for the ILs studied were also fitted with the group contribution method proposed by Gardas and Coutinho [35], which results are depicted in Figure 6, and that follow a linear function of the form,
| (4) |
| (5) |
| (6) |
where ni is the number of groups of type i and k is the total number of different groups in the molecule. The estimated parameters ai,nD and bi,nD for the cations of the studied ILs are given in Table 6 along with the anionic volume previously reported.[35,46,72] The average absolute relative deviation between the experimental and the fitting data are 0.021% for [Pi(444)1][Tos] and [P4441][CH3SO4], 0.0079% for [P4442][(C2H5O)2PO2] and 0.0094% for [P8888][Br].
Table 6.
Group contribution parameters, ai,nD and bi,nD, determined using the Gardas and Coutinho group contribution method [35] for the refractive index.
The derived molar refractions, Rm, free volumes, fm, and polarizabilities were additionally determined as follows [73–75]:
| (7) |
| (8) |
| (9) |
where ni is the electronic polarizability, ε0 the vacuum permittivity, Rm the compound’s density, M the molecular weight and NA the Avogadro number. The obtained values for these properties are reported in Table 4.
Recently, on the premise that refractive indices are an indication of the dielectric response to an electrical field, induced by electromagnetic waves, and that refractive indices can be derived as the first order approximation response to electronic polarization within an instantaneous time scale, Seki et al.[76] evaluated the refractive indices of 17 ILs, as a function of temperature, against theoretical polarizabilities obtained through ab initio calculations. The authors proposed a correlation between the refractive index and the polarizability normalized in terms of the molecular volume. Following the work of Seki et al.[76] the correlation was previously verified against ammonium-, sulfonium-, phosphonium-, piperidinium- and pyridinium-based ILs experimental data and shown to provide an easy an accurate way to predict the refractive index or polarizabilities of ILs.[41,42,77] Here the phosphonium-based ILs were tested against the correlation and, once again, it was shown that it is able to describe, within the uncertainty of the correlation, this IL family refractive indices and/or polarizability, as depicted in Figure 7.
Figure 7.
Relationship between the refractive index and polarizability/molar volume for different ILs at 303.15 K. The unfilled triangles and the solid line represent the experimental data and the correlation of Seki et al.[76]. The unfilled squares and diamonds represent the experimental data reported in previous works.[41,42,77] The full symbols correspond to the ILs data determined in this work.
3.4.Surface tension
Experimental surface tension data measured for all the studied ILs are presented in Table 7 and depicted in Figure 8 as a function of temperature.
Table 7.
Surface tension, γ, for the studied ILs as a function of temperature and at atmospheric pressure.
| [Pi(444)1][Tos] | [P4441][CH3SO4] | [P4442][(C2H5O)2PO2] | [P8888][Br] | |
|---|---|---|---|---|
|
| ||||
| T /K | γ /mN·m−1 | γ /mN·m−1 | γ /mN·m−1 | γ /mN·m−1 |
| 293.2 | 38.1 | 35.5 | 31.4 | |
| 298.2 | 37.3 | 34.7 | 30.5 | |
| 303.2 | 36.6 | 34.1 | 29.8 | |
| 313.1 | 35.5 | 33.5 | 29.2 | |
| 318.1 | 27.4 | |||
| 323.1 | 35.0 | 32.9 | 28.5 | 27.1 |
| 333.1 | 34.3 | 32.2 | 27.5 | 26.6 |
| 343.1 | 38.1 | 35.5 | 31.4 | 26.0 |
Standard temperature uncertainty is u (T) = ±0.1 K and the surface tension expanded uncertainty is Uc (γ) = 0.1 mN·m−1, with an approximately 95% level of confidence.
Figure 8.
Surface tension data for the studied ILs as a function of temperature (left) and relative deviations between this work experimental surface tension data [18,48] and that available in the literature (right).
Using dynamic contact angle measurements, AlTuwaim et al.[18] reported surface tension data for [Pi(444)1][Tos] that presents average relative deviations of −14.4% to the data measured here. An average relative deviation of −8.90% was obtained for [P4442][(C2H5O)2PO2], using the Du Noüy ring method, reported by Kilaru et al.[48]. The deviations obtained seem to be associated to small traces of water, the technique employed and/or the sample purity.
From Figure 8, it can be seen that the surface tension of the studied ILs decreases linearly with temperature and follows the order: [Pi(444)1][Tos] > [P4441][CH3SO4] > [P4442][(C2H5O)2PO2] > [P8888][Br]. It can be observed that both the cation and anion significantly contribute to the surface tension of the IL at the air-liquid interface.[78,79] It is well established that the surface tension is related with the part of the molecule that is present at the interface and pointing towards the air phase. The moiety with the lower surface energy tends to accumulate at the interface. Typically these are alkyl chains oriented towards the gas phase. Santos et al.[80] showed that halide anion-based ILs may present a top layer formed entirely by the cation with the alkyl chains pointing towards the gas phase while the second layer is formed only by the halide. When the cation and anion have similar sizes and both present alkyl chains, as is the case for some of the compounds here studied, the cations and anions may occupy the same plane at the gas–liquid interface,[80] with the alkyl chains projecting towards the vapour phase and the anions and cation’s polar head groups forming a second layer. This structural behaviour allows one to picture the surface arrangement of the studied ILs and understand the surface tension values under the light of the intermolecular interactions strength playing an important role on the compactness and strength of the interface layer composed by the anion and cation’s head groups.
Surface Thermodynamic Properties
It is possible to derive the surface thermodynamic properties, viz. surface entropy and surface enthalpy, through the temperature dependence of the surface tension. The basic thermodynamic relationship applied to the surface of a homogeneous liquid is
| (10) |
where Hγ is surface enthalpy, Gγ is the Gibbs energy, T is the temperature (in K), and Sγ is the surface entropy. The surface entropy per unit area can be calculated according to the following equation [81,82],
| (11) |
while the surface enthalpy according to [81,82],
| (12) |
where γ stands for the surface tension and T for the temperature.
The values of the thermodynamic functions for all the ILs studied and the respective expanded uncertainties, derived from the slope of the curve γ = f(T) in combination with the law of propagation of uncertainties, are presented in Table 4.[83]
In agreement with the results previously reported for other ILs families, viz. imidazolium-, pyridinium-, pyrrolidinium- and piperidinium-based cations, [40,41,43,78,79,84], the investigated phosphonium ILs present lower surface enthalpies and entropies when compared with molecular organic compounds. These values reflect a high surface organization, as well as an inherent highly structured liquid phase in ionic liquids. These values of low surface entropies are an indication of a high surface organization as well as a highly structured liquid phase. Moreover, the results of similar surface entropy and surface enthalpy observed, for the different IL families, are an effect of similar dependency of the surface tension with the temperature.
Estimated critical temperatures
The critical temperature of fluids is one of the most relevant and significant thermophysical property frequently used in corresponding state correlations concerning equilibrium and transport properties.[85] However, owing to the intrinsic nature of ILs coupled with negligible vapor pressures and relatively low decomposition temperatures, the direct determination of the critical temperatures of ILs is not feasible. Rebelo et al.[1] proposed the use of the Eötvös [86] and Guggenheim [87] equations to estimate the hypothetical critical temperature of ILs, as described below,
| (13) |
| (14) |
where Tc is the critical temperature, M the molecular weight, ρ the density, and KEot and KGug are fitted parameters. Tc, KEot and KGug were determined by fitting Equations 13 and 14 to the experimental data. Both equations are based on the fact that the surface tension becomes null at the critical point and although an overestimation of the critical temperature is expected, since at the critical point the pressure becomes the critical pressure, these equations provide reasonable estimations.[85,88] The critical temperature values estimated from the surface tension data are summarized in Table 4. In agreement with the results obtained for other phosphonium-based ILs studied in a previous work [72] the compounds here reported also present significantly lower critical temperatures than imidazolium-, pyridinium-, piperidinium- or pyrrolidinium-based ILs.[41,43,84]
Conclusions
Experimental data on density, viscosity, refractive index, and surface tension for four phosphonium-based ionic liquids were measured in the temperature range between (283.15 and 353.15) K and at atmospheric pressure. Additionally, derivative properties, such as the isobaric thermal expansion coefficient, the surface thermodynamic properties and the critical temperatures for the investigated ionic liquids were also estimated and discussed.
In general, for a common anion the density decreases with the increase of the aliphatic moieties. The anion, nonetheless, imposes a greater effect on the IL density, with the anion molecular weight increase, and consequently the overall size and charge dispersion increase, leading to an increase on density. Moreover, the alkyl side chain increase presents a smaller impact on the thermal expansion coefficient than that observed for the anion replacement.
Similar to that observed previously for imidazolium- and piridinium-based ILs, the π–π interactions due to the presence of an aromatic ring ([Pi(444)1][Tos]) leads to higher resistance to shear stress, to a more rigid IL structure and therefore to a bulkier distribution and higher viscosities.
The investigated ILs present low surface enthalpy and entropies when compared with molecular organic compounds. These values reflect a high surface organization, as well as an inherent highly structured liquid phase. Furthermore, the low surface entropies are an indication of a high surface organization as well as a highly structured liquid phase.
The group contribution methods proposed by Gardas and Coutinho for density, viscosity and refractive index were evaluated and fitted to the experimental data, allowing to propose new parameters for the cations and/or anions investigated in this work.
Acknowledgements
This work was developed in the scope of the project CICECO-Aveiro Institute of Materials (Ref. FCT UID /CTM /50011/2013), financed by national funds through the FCT/MEC and when applicable co-financed by FEDER under the PT2020 Partnership Agreement. P.J.C. and A.B. also acknowledge FCT for their post-doctoral grants SFRH/BPD/82264/2011 and SFRH/BPD/77858/2011, respectively. M. G. Freire acknowledges the European Research Council (ERC) for the Starting Grant ERC-2013-StG-337753. The authors also acknowledge CYTEC Industries Inc. for kindly supplying the ionic liquids investigated in this work.
References
- [1].Rebelo LPN, Lopes J.N. Canongia, Esperança JMSS, Filipe E. J. Phys. Chem. B. 2005;109:6040–6043. doi: 10.1021/jp050430h. [DOI] [PubMed] [Google Scholar]
- [2].Seddon KR. J. Chem. Technol. Biotechnol. 1997;68:351–356. [Google Scholar]
- [3].Smiglak M, Reichert WM, Holbrey JD, Wilkes JS, Sun L, Thrasher JS, Kirichenko K, Singh S, Katritzky AR, Rogers RD. Chem. Commun. (Camb) 2006:2554–2556. doi: 10.1039/b602086k. [DOI] [PubMed] [Google Scholar]
- [4].Baranyai KJ, Deacon GB, MacFarlane DR, Pringle JM, Scott JL. Aust. J. Chem. 2004;57:145–147. [Google Scholar]
- [5].Matsumoto K, Hagiwara R, Ito Y. Electrochem. Solid-State Lett. 2004;7:L3. [Google Scholar]
- [6].Marsh KN, Boxall JA, Lichtenthaler R. Fluid Phase Equilib. 2004;219:93–98. [Google Scholar]
- [7].Earle MJ, Esperanca JMSS, Gilea MA, Canongia Lopes JN, Rebelo LPN, Magee JW, Seddon KR, Widegren JA. Nature. 2006;439:831–834. doi: 10.1038/nature04451. [DOI] [PubMed] [Google Scholar]
- [8].Wasserscheid P, Keim W. Angew. Chem. Int. Ed. Engl. 2000;39:3772–3789. doi: 10.1002/1521-3773(20001103)39:21<3772::aid-anie3772>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- [9].Earle MJ, Seddon KR. Pure Appl. Chem. 2000;72:1391–1398. [Google Scholar]
- [10].Rogers RD, Seddon KR. Science. 2003;302:792–793. doi: 10.1126/science.1090313. [DOI] [PubMed] [Google Scholar]
- [11].Wishart JF. Energy Environ. Sci. 2009;2:956–961. [Google Scholar]
- [12].MacFarlane DR, Seddon KR. Aust. J. Chem. 2006;60(1):3–5. [Google Scholar]
- [13].Rogers RD, Seddon KR. Ionic Liquids Iiib: Fundamentals, Progress, Challenges, And Opportunities; Transformations And Processes. American Chemical Society; 2005. [Google Scholar]
- [14].Bradaric CJ, Downard A, Kennedy C, Robertson AJ, Zhou Y. Green Chem. 2002;5:143–152. [Google Scholar]
- [15].Del Sesto RE, Corley C, Robertson A, Wilkes JS. J. Organomet. Chem. 2005;690:2536–2542. [Google Scholar]
- [16].Atefi F, Garcia MT, Singer RD, Scammells PJ. Green Chem. 2009;11:1595. [Google Scholar]
- [17].Adamová G, Gardas RL, Nieuwenhuyzen M, Puga AV, Rebelo LPN, Robertson AJ, Seddon KR. Dalt. Trans. 2012;41:8316. doi: 10.1039/c1dt10466g. [DOI] [PubMed] [Google Scholar]
- [18].Altuwaim MS, Alkhaldi KHAE, Al-Jimaz AS, Mohammad AA. J. Chem. Eng. Data. 2014;59:1955–1963. [Google Scholar]
- [19].Fraser KJ, MacFarlane DR. Aust. J. Chem. 2009;62:309. [Google Scholar]
- [20].Deive FJ, Rivas MA, Rodríguez A. J. Chem. Thermodyn. 2013;62:98–103. [Google Scholar]
- [21].Esperança JMSS, Guedes HJR, Blesic M, Rebelo LPN. J. Chem. Eng. Data. 2006;51:237–242. [Google Scholar]
- [22].Frackowiak E, Lota G, Pernak J. Appl. Phys. Lett. 2005;86:1–3. [Google Scholar]
- [23].Tsunashima K, Sugiya M. Electrochem. Commun. 2007;9:2353–2358. [Google Scholar]
- [24].Tomé LIN, Gardas RL, Carvalho PJ, Pastoriza-Gallego MJ, Piñeiro MM, Coutinho JAP. J. Chem. Eng. Data. 2011;56:2205–2217. [Google Scholar]
- [25].Louros CLS, Cláudio AFM, Neves CMSS, Freire MG, Marrucho IM, Pauly J, Coutinho JAP. Int. J. Mol. Sci. 2010;11:1777–1791. doi: 10.3390/ijms11041777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Cornmell RJ, Winder CL, Schuler S, Goodacre R, Stephens G. Green Chem. 2008;10:685. [Google Scholar]
- [27].Neves CMSS, Granjo JFO, Freire MG, Robertson A, Oliveira NMC, Coutinho JAP. Green Chem. 2011;13:1517–1526. [Google Scholar]
- [28].Carvalho PJ, Khan I, Morais A, Granjo JFO, Oliveira NMC, Santos LMNBF, Coutinho JAP. Fluid Phase Equilib. 2013;354:156–165. [Google Scholar]
- [29].Liu Y, Guo L, Zhu L, Sun X, Chen J. Chem. Eng. J. 2010;158:108–114. [Google Scholar]
- [30].Stojanovic A, Kogelnig D, Fischer L, Hann S, Galanski M, Groessl M, Krachler R, Keppler BK. Aust. J. Chem. 2010;63:511–524. [Google Scholar]
- [31].Carvalho PJ, Álvarez VH, Marrucho IM, Aznar M, Coutinho JAP. J. Supercrit. Fluids. 2010;52:258–265. [Google Scholar]
- [32].Ventura SPM, Pauly J, Daridon JL, Lopes da Silva JA, Marrucho IM, Dias AMA, Coutinho JAP. J. Chem. Thermodyn. 2008;40:1187–1192. [Google Scholar]
- [33].Kilaru PK, Scovazzo P. Ind. Eng. Chem. Res. 2008;47:910–919. [Google Scholar]
- [34].Gardas RL, Coutinho JAP. Fluid Phase Equilib. 2008;263:26–32. [Google Scholar]
- [35].Gardas RL, Coutinho JAP. AIChE J. 2009;55:1274–1290. [Google Scholar]
- [36].Jacquemin J, Husson P, Padua AAH, Majer V. Green Chem. 2006;8:172. [Google Scholar]
- [37].Grishina EP, Ramenskaya LM, Gruzdev MS, Kraeva OV. J. Mol. Liq. 2013;177:267–272. [Google Scholar]
- [38].Carvalho PJ, Regueira T, Santos LMNBF, Fernandez J, Coutinho JAP. J. Chem. Eng. Data. 2010;55:645–652. [Google Scholar]
- [39].Neves CMSS, Kurnia KA, Coutinho JAP, Marrucho IM, Lopes JNC, Freire MG, Rebelo LPN. J. Phys. Chem. B. 2013;117:10271–10283. doi: 10.1021/jp405913b. [DOI] [PubMed] [Google Scholar]
- [40].Almeida HFD, Passos H, Lopes-da-Silva JA, Fernandes AM, Freire MG, Coutinho JAP. J. Chem. Eng. Data. 2012;57:3005–3013. [Google Scholar]
- [41].Bhattacharjee A, Carvalho PJ, Coutinho JAP. Fluid Phase Equilib. 2014;375:80–88. doi: 10.1016/j.fluid.2014.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Bhattacharjee A, Luís A, Santos JH, Lopes-da-silva JA, Freire MG, Carvalho PJ, Coutinho JAP. Fluid Phase Equilib. 2014;381:36–45. doi: 10.1016/j.fluid.2014.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Almeida HFD, Teles ARR, Lopes-Da-Silva JA, Freire MG, Coutinho JAP. J. Chem. Thermodyn. 2012;54:49–54. [Google Scholar]
- [44].Gardas RL, Costa HF, Freire MG, Carvalho PJ, Marrucho IM, Fonseca IMA, Ferreira AGM, Coutinho JAP. J. Chem. Eng. Data. 2008;53:805–811. [Google Scholar]
- [45].Gardas RL, Freire MG, Carvalho PJ, Marrucho IM, Fonseca IMA, Ferreira AGM, Coutinho JAP. J. Chem. Eng. Data. 2007;52:1881–1888. [Google Scholar]
- [46].Freire MG, Teles ARR, Rocha MAA, Neves CMSS, Carvalho PJ, Evtuguin DV, Santos LMNBF, Coutinho JAP, Schröder B. J. Chem. Eng. Data. 2011;56:4813–4822. [Google Scholar]
- [47].Ficke LE, Novak RR, Brennecke JF. J. Chem. Eng. Data. 2010;55:4946–4950. [Google Scholar]
- [48].Kilaru P, Baker GA, Scovazzo P. J. Chem. Eng. Data. 2007;52:2306–2314. [Google Scholar]
- [49].Vaughan JW, Dreisinger D, Haggins J. ECS Trans. 2006;2:381–392. [Google Scholar]
- [50].Anthony JL, Anderson JL, Maginn EJ, Brennecke JF. J. Phys. Chem. B. 2005;109:6366–6374. doi: 10.1021/jp046404l. [DOI] [PubMed] [Google Scholar]
- [51].Domańska U, Paduszyński K. J. Chem. Thermodyn. 2010;42:707–711. [Google Scholar]
- [52].Matkowska D, Hofman T. J. Mol. Liq. 2012;165:161–167. [Google Scholar]
- [53].Soriano AN, Doma BT, Li M-H. J. Chem. Thermodyn. 2009;41:301–307. [Google Scholar]
- [54].Pereiro AB, Verdía P, Tojo E, Rodríguez A. J. Chem. Eng. Data. 2007;52:377–380. [Google Scholar]
- [55].Singh T, Kumar A. J. Solution Chem. 2009;38:1043–1053. [Google Scholar]
- [56].Beigi A.A. Miran, Abdouss M, Yousefi M, Pourmortazavi SM, Vahid A. J. Mol. Liq. 2013;177:361–368. [Google Scholar]
- [57].Costa AJL, Esperança JMSS, Marrucho IM, Rebelo LPN. J. Chem. Eng. Data. 2011;56:3433–3441. [Google Scholar]
- [58].Tomé LIN, Carvalho PJ, Freire MG, Marrucho IM, Fonseca IMA, Ferreira AGM, Coutinho JAP, Gardas RL. J. Chem. Eng. Data. 2008;53:1914–1921. [Google Scholar]
- [59].Matkowska D, Hofman T. J. Mol. Liq. 2013;177:301–305. [Google Scholar]
- [60].Wang JY, Zhao FY, Liu RJ, Hu YQ. J. Chem. Thermodyn. 2011;43:47–50. [Google Scholar]
- [61].Palgunadi J, Kang JE, Nguyen DQ, Kim JH, Min BK, Lee SD, Kim HSH. Thermochim. Acta. 2009;494:94–98. [Google Scholar]
- [62].Fernández A, García J, Torrecilla JS, Oliet M, Rodríguez F. J. Chem. Eng. Data. 2008;53:1518–1522. [Google Scholar]
- [63].Ye C, Shreeve JM. J. Phys. Chem. A. 2007;111:1456–1461. doi: 10.1021/jp066202k. [DOI] [PubMed] [Google Scholar]
- [64].Wang JY, Zhao FY, Liu YM, Wang XL, Hu YQ. Fluid Phase Equilib. 2011;305:114–120. [Google Scholar]
- [65].Gu Z, Brennecke JF. J. Chem. Eng. Data. 2002;47:339–345. [Google Scholar]
- [66].Pereiro AB, Deive FJ, Esperança JMSS, Rodríguez A. Fluid Phase Equilib. 2010;294:49–53. [Google Scholar]
- [67].Machanová K, Boisset A, Sedláková Z, Anouti M, Bendová M, Jacquemin J. J. Chem. Eng. Data. 2012;57:2227–2235. [Google Scholar]
- [68].Jacquemin J, Husson P, Mayer V, Cibulka I. J. Chem. Eng. Data. 2007;52:2204–2211. [Google Scholar]
- [69].Jacquemin J, Husson P, Majer V, Padua AAH, Gomes MFC. Green Chem. 2008;10:944–950. [Google Scholar]
- [70].Ferguson L, Scovazzo P. Ind. Eng. Chem. Res. 2007;46:1369–1374. [Google Scholar]
- [71].Green MD, Schreiner C, Long TE. J. Phys. Chem. A. 2011;115:13829–13835. doi: 10.1021/jp206138b. [DOI] [PubMed] [Google Scholar]
- [72].Almeida HFD, Lopes-Da-Silva JA, Freire MG, Coutinho JAP. J. Chem. Thermodyn. 2013;57:372–379. [Google Scholar]
- [73].Israelachvili JN. Intermolecular and Surface Forces. University, Academic Press; San Diego: 2011. [Google Scholar]
- [74].May EF. Measurement of the Thermodynamic Properties of Single Phases. IUPAC Experimental Thermodynamics, Volume VI. Elsevier; Amsterdam: 2003. [Google Scholar]
- [75].Brocos P, Piñeiro Á, Bravo R, Amigo A. Phys. Chem. Chem. Phys. 2003;5:550–557. [Google Scholar]
- [76].Seki S, Tsuzuki S, Hayamizu K, Umebayashi Y, Serizawa N, Takei K, Miyashiro H. J. Chem. Eng. Data. 2012;57:2211–2216. [Google Scholar]
- [77].Carvalho PJ, Ventura SPM, Batista MLS, Schröder B, Gonçalves F, Esperança J, Mutelet F, Coutinho JAP. J. Chem. Phys. 2014;140:064505. doi: 10.1063/1.4864182. [DOI] [PubMed] [Google Scholar]
- [78].Carvalho PJ, Freire MG, Marrucho IM, Queimada AJ, Coutinho JAP. J. Chem. Eng. Data. 2008;53:1346–1350. [Google Scholar]
- [79].Freire MG, Carvalho PJ, Fernandes AM, Marrucho IM, Queimada AJ, Coutinho JAP. J. Colloid. Interface Sci. 2007;314:621–30. doi: 10.1016/j.jcis.2007.06.003. [DOI] [PubMed] [Google Scholar]
- [80].Santos CS, Baldelli S. Chem. Soc. Rev. 2010;39:2136–45. doi: 10.1039/b921580h. [DOI] [PubMed] [Google Scholar]
- [81]. Adamson AW, Gast AP. Physical Chemistry of Surfaces. 6th ed. John Wiley: 1997. [Google Scholar]
- [82]. McNaught AD, Wilkinson A. Compendium of Chemical Therminology, IUPAC Recommendations. 2nd ed. Blackwell Science; Cambridge, UK: 1997. [Google Scholar]
- [83]. Miller JC, Miller JN. Statistics for Analytical Chemestry. 3rd ed. PTR Prentice Hall; Chichester: 1993. [Google Scholar]
- [84].Carvalho PJ, Neves CMSS, Coutinho JAP. J. Chem. Eng. Data. 2010;55:3807–3812. [Google Scholar]
- [85].Poling BE, Prausnitz JM, O’Connell JP. The Properties of Gases And Liquids. McGraw-Hill; New York: 2001. Fifth Edit. [Google Scholar]
- [86].Shereshefsky JL. J. Phys. Chem. 1931;35:1712–1720. [Google Scholar]
- [87].Guggenheim EA. J. Chem. Phys. 1945;13:253–261. [Google Scholar]
- [88]. Birdi KS. Handbook of Surface and Colloid Chemistry. 1st ed. CRC Press: 1997. [Google Scholar]