Modeling Localization of Amplitude-Panned Virtual Sources in Sagittal Planes

Abstract

Vector-base amplitude panning (VBAP) aims at creating virtual sound sources at arbitrary directions within multichannel sound reproduction systems. However, VBAP does not consistently produce listener-specific monaural spectral cues that are essential for localization of sound sources in sagittal planes, including the front-back and up-down dimensions. In order to better understand the limitations of VBAP, a functional model approximating human processing of spectro-spatial information was applied to assess accuracy in sagittal-plane localization of virtual sources created by means of VBAP. First, we evaluated VBAP applied on two loudspeakers in the median plane, and then we investigated the directional dependence of the localization accuracy in several three-dimensional loudspeaker arrangements designed in layers of constant elevation. The model predicted a strong dependence on listeners’ individual head-related transfer functions, on virtual source directions, and on loudspeaker arrangements. In general, the simulations showed a systematic degradation with increasing polar-angle span between neighboring loudspeakers. For the design of VBAP systems, predictions suggest that spans up to 40° polar angle yield a good trade-off between system complexity and localization accuracy. Special attention should be paid to the frontal region where listeners are most sensitive to deviating spectral cues.

0 INTRODUCTION

Vector-base amplitude panning (VBAP) is a method developed to create virtual sound sources at arbitrary directions by using a multichannel sound reproduction system [1]. VBAP determines loudspeaker gains by projecting the intended virtual source direction onto a basis formed by the directions of the most appropriate pair or triplet of neighboring loudspeakers. Within that pair or triplet, the loudspeaker signals are weighted in overall level. A problem of VBAP is associated with localization errors, that is, that virtual sources can be localized at directions deviating from the intended directions [2]. In this study we applied an auditory model in order to replicate [2] and investigate the limitations of VBAP with respect to sound localization.

We use the interaural-polar coordinate system shown in Fig. 1 to distinguish different aspects of sound localization. In the lateral-angle dimension (left-right), VBAP introduces interaural differences in level (ILD) and time (ITD) and thus, perceptually relevant localization cues [3]. In the polar-angle dimension, monaural spectral features at high frequencies cue sound localization [4]. This frequency dependence is, however, not captured in the broadband concept of VBAP and may cause localization errors.

Fig. 1.

Interaural-polar coordinate system with lateral angle, ϕ ∈ [−90°, 90°], and polar angle, θ ∈ [−90°, 270°).

Localization in the polar-angle dimension (i.e., in sagittal planes) is based on a monaural learning process in which spectral features, that are characteristic for the listener’s morphology, are related to certain directions [5]. Due to the monaural processing, the use of spectral features can be disrupted by spectral irregularities superimposed by the source spectrum [6]. The use of spectral features is limited to high frequencies (above around 0.7 kHz) because the spatial variance of head-related transfer functions (HRTFs) increases with frequency [7]. Sounds lasting only a few milliseconds can evoke an already strong polar-angle perception [8]. If sounds last longer, listeners can also use dynamic localization cues introduced by head rotations of 30° azimuth or wider in order to estimate the polar angle of the source [9]. However, if high frequencies are available, spectral cues dominate polar-angle perception [10]. In the present study we explicitly focus on monaural spectral localization cues and thus, consider the most strict condition of static broadband sounds and non-moving listeners.

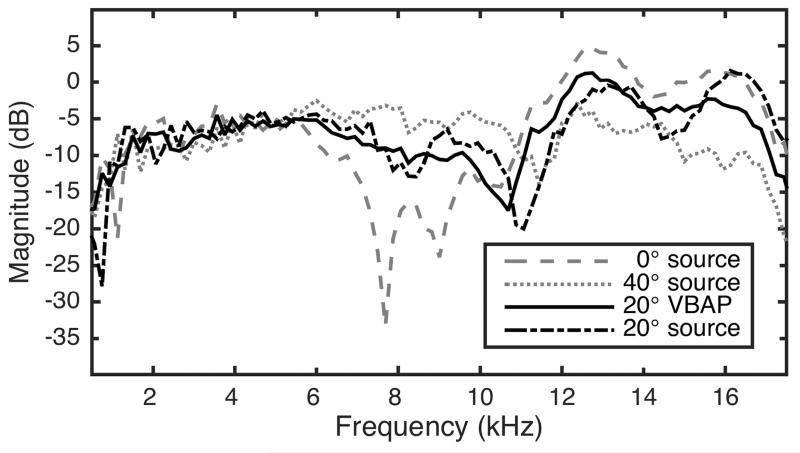
For a simple arrangement with two loudspeakers in the median plane, Fig. 2 illustrates the spectral mismatch between the HRTF of a targeted virtual-source direction and the corresponding spectrum obtained by VBAP. The loudspeakers were placed at polar angles of 0° and 40°, respectively, and the targeted direction was centered between the real sources, i.e., at 20°. The actual HRTF for 20° is shown for comparison. In this example, the spectrum obtained by VBAP is clearly different from the actual HRTF. Since HRTFs vary substantially across listeners [11], the spectral mismatch also varies from case to case. Psychoacoustic localization experiments showed that amplitude panning in the median plane might work for some unspecified listeners, but a derivation of a general rule holding for all listeners has not been achieved [2].

Fig. 2.

Example showing the spectral discrepancies obtained by VBAP. The targeted spectrum is the HRTF for 20° polar angle. The spectrum obtained by VBAP is the superposition of two HRTFs from directions 40° polar angle apart of each other with the targeted source direction centered in between.

In this study we aim at a more systematic and objective investigation of the limitations of VBAP by applying a model of sagittal-plane sound localization for human listeners [12]. This model has been extensively evaluated in previous studies [12, 13]. Our investigation was subdivided into two parts. In Sec. 2 we considered an arrangement with two loudspeakers placed in the median plane where binaural disparities are negligible and monaural spectral cues are mostly salient. With this reduced setup, accuracy in localization of virtual sources was investigated systematically as a function of panning angle and loudspeaker span. In Sec. 3 we simulated arrangements for sound reproduction systems consisting of various numbers of loudspeakers in the upper hemisphere and evaluated their spatial quality in terms of localization accuracy.

1 GENERAL METHODS

The sagittal-plane localization model aims at predicting the polar-angle response probability for a given target sound. Fig. 3 shows the template-based model structure. In stage 1 the filtering of the incoming sound by the torso, head, and pinna is represented by directional transfer functions (DTFs), that is, HRTFs with the direction-independent part removed [14]. Then the spectral analysis of the cochlea is approximated by a Gammatone filterbank in stage 2. It results in spectral magnitudes with center frequencies ranging from 0.7 to 18 kHz. Stage 3 differentiates the spectral magnitudes across frequency bands and sets negative gradients to zero. This positive spectral gradient extraction was inspired by neurophysiological findings from the dorsal cochlear nucleus in cats and was essential to accurately predict the effect of macroscopic spectral variations of the source spectrum on human localization performance [12]. The extracted positive spectral gradient profile is then compared with equivalently processed direction-specific template profiles in stage 4. The outcome of stage 4 is an internal distance metric as a function of the polar angle. In stage 5 these distances are mapped to similarity indices that are proportional to the predicted probability of the listener’s polar-angle response. The shape of the mapping curve is determined by a listener-specific sensitivity parameter that represents the listener-specific localization performance to a large degree [13]. In stage 6 monaural spatial information is combined binaurally whereby a binaural weighting function accounts for a dominant contribution of the ipsilateral ear [15]. After stage 7 emulates the response scatter induced by sensorimotor mapping (SMM), the combined similarity indices are normalized to a probability mass vector (PMV) in stage 8. The PMV provides all information necessary to calculate commonly used measures of localization performance. The implementation of the model is incorporated in the Auditory Modeling Toolbox (AMT) as the baumgartner2014 model [16]. Also, the simulations of the present study are provided in the AMT.

Fig. 3.

Structure of the sagittal-plane localization model used for simulations. Reproduced with permission from [12]. © 2014, Acoustical Society of America.

The predictive power of the model had been evaluated under several HRTF modifications and variations of the source spectrum [12]. For this evaluation, the SMM stage was important to mimic the listeners’ localization responses in a psychoacoustic task using a manual pointing device. Model-based investigations can benefit from the possibility to remove the usually considerably large task-induced scatter (17° in [12]), which might hide some perceptual details. For the following investigation, we did not use the SMM stage because we aimed at modeling the listeners’ perceptual accuracy without any task-induced modification. Predictions were performed for the 23 normal-hearing listeners (14 females, 9 males, between 19–46 years old) whose data were used also for the model evaluation in [12]. The following investigations were solely based on model predictions. Even though we already extensively evaluated the predictive power of the model for our pool of listeners, we also compared the obtained predictions with corresponding results from actual experiments described in previous studies.

Accuracy in localization of virtual sources was evaluated by means of the root mean square (RMS) of local (i.e., localized within the correct hemisphere) polar response errors, in the following called polar error. Note that the polar error measures both localization blur and bias. If not stated explicitly, simulated localization targets were stationary Gaussian white noise sources.

Amplitude panning was applied according to the VBAP method [1] briefly described as follows. Loudspeakers at neighboring directions, defined by Cartesian-coordinate vectors l_i of unity length, were combined to triplets, L = [l₁, l₂, l₃], forming bases in the three-dimensional (3D) space. In order to create a virtual source in the direction of the unity-length vector p, the basis with the smallest overall Euclidean distance between p and the basis vectors was selected and then, the amplitudes of the coherent loudspeaker signals were weighted according to the gains g = p^TL⁻¹/∥p^TL⁻¹∥. In case of a two-dimensional loudspeaker setup (all loudspeakers placed on a plane), only pairs of two loudspeaker positions were used to form the bases. Further, we define the panning angle as the polar-angle component of p and the panning ratio as the gain ratio, R = g₁/g₂, between two loudspeakers.

2 PANNING BETWEEN TWO LOUDSPEAKERS IN THE MEDIAN PLANE

2.1 Effect of Panning Angle

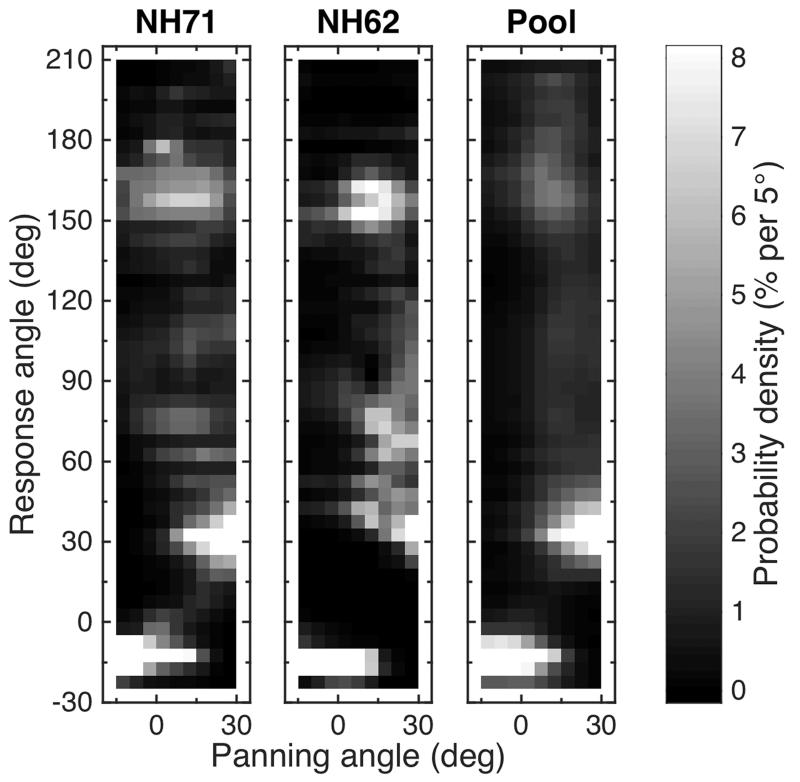
In this investigation we focused on the effect of the panning angle on the perceived polar angle and simulated the experiment I from [2]. In that study two loudspeakers were setup in the frontal median plane of the listener, one at a polar angle of −15° and the other one at 30°. For this setup, we simulated localization experiments for panning angles in steps of 5°. Fig. 4 shows the response predictions for two specific listeners and predictions pooled across all listeners. Each column in a panel shows the color-encoded PMV predicted for a target sound. In general, response probabilities were largest for panning angles close to a loudspeaker direction. Panning angles far from loudspeaker directions yielded smaller response probabilities. The model predicted that for those angles, virtual sources were localized quite likely at the loudspeaker directions or even at the back of the listener. Front-back reversals were often present in the case of listener NH62. Predictions for other listeners, like NH71, were more consistent with the VBAP principle.

Fig. 4.

Response predictions to sounds created by VBAP with two loudspeakers in the median plane positioned at polar angles of −15° and 30°, respectively. Predictions for two exemplary listeners and pooled across all listeners. Each column of a panel shows the predicted PMV of polar-angle responses to a certain sound. Note the inter-individual differences and the generally small probabilities at response angles not occupied by the loudspeakers.

In general, the model predictions were very listener-specific. We analyzed the across-listener variability in polar error and controlled for inter-individual differences in baseline accuracy. To this end, the increase in polar angle was calculated by subtracting the polar error predicted for a real source at the direction of the panning angle from the error predicted for the virtual source. Fig. 5 shows the listener-specific increases in polar error as functions of the panning angle. The increases in error ranged up to 50°, that is, even more than the angular span between the loudspeakers, while the variability across listeners was considerably large with up to 40° of error increase.

Fig. 5.

Listener-specific increases in polar error as a function of the panning angle. Increase in polar error defined as the difference between the polar error obtained by the VBAP source and the polar error obtained by the real source at the corresponding panning angle. Same loudspeaker arrangement as for Fig. 4. Note the large inter-individual differences and the increase in polar error being largest at panning angles centered between the loudspeakers, i.e., at panning ratios around R = 0 dB.

The large variability across listeners is consistent with the listeners’ experiences reported in [2]. For a quantitative comparison, we replicated the psychoacoustic experiments from [2] by means of model simulations. In that experiment the listeners were asked to adjust the panning between the two loudspeakers (at −15° and 30°) such that they hear a virtual source that coincides best with a reference source. Two reference sources were used at polar angles of 0° and 15°. Since all loudspeakers were visible, this most probably focused the spatial attention of the listeners to the range between −15° and 30° polar angle. Hence, we restricted the range of response PMVs to the same range. Response PMVs for various panning angles were interpolated to obtain a 1°-sampling of panning angles. In accordance with [2], simulated sound sources emitted pink Gaussian noise.

The model from [12] simulates localization experiments where listeners respond to a sound by pointing to the perceived direction. These directional responses are not necessarily related to the adjustments performed in [2]. We thus considered two adjustment strategies the listeners might have used in this task. According to the first strategy, called probability maximization (PM), listeners focused their attention to a very narrow angular range and adjusted the panning so that they would most likely respond in this range. For simulating the PM strategy, the panning angle with the largest response probability at the targeted direction was selected as the adjusted angle. The second strategy, called centroid matching (CM), was inspired by a listener’s experience described in [2], namely, that “he could adjust the direction of the center of gravity of the virtual source” (p. 758). For modeling the CM strategy, we selected the panning angle that yielded a centroid of localization responses closest to the reference source direction.

We predicted the adjusted panning angles according to the two different strategies for our pool of listeners and for both reference sources. We also retrieved the panning angles obtained by [2] from his Fig. 8. Our Fig. 6 shows the descriptive statistics of panning angles from [2] together with our simulation results. Pulkki observed a median panning angle that was about 5° higher than the reference source at 0°, and a median panning angle quite close to the reference source at 15°. Across-listener variability was at least 20° of panning angle for both reference sources, although 2 of 16 listeners were removed in [2], as they reported to perceive the sounds inside their head. For the reference source at 0°, the 5°-bias in the median panning angle found in [2] was well represented by both adjustment strategies; interquartile ranges and marginals (whiskers) were more similar to [2] for the CM than the PM strategy. For the reference source at 15°, predicted medians, interquartile ranges, and marginals were very close to the results from [2] for the PM strategy but too small for the CM strategy.

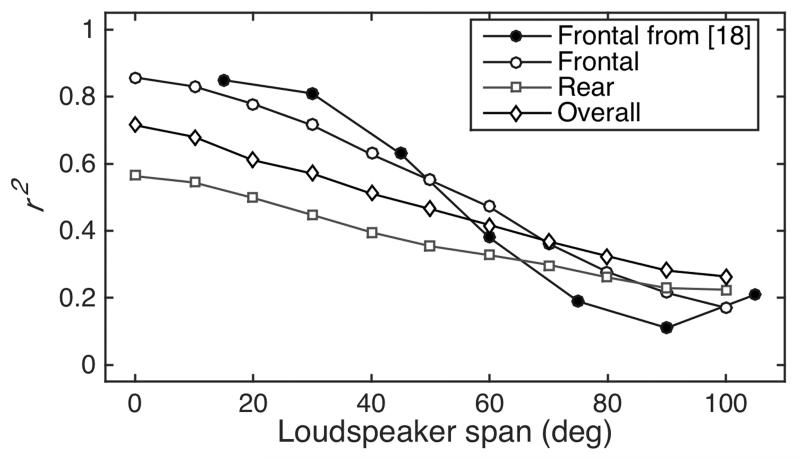
Fig. 8.

Effect of loudspeaker span in the median plane on coefficient of determination, r², for virtual source directions created by VBAP. Separate analysis for frontal, rear, and overall (frontal and rear) targets. Data pooled across listeners. Note the correspondence with the results obtained by [18].

Fig. 6.

Panning angles for the loudspeaker arrangement of Fig. 4 judged best for reference sources at polar angles of 0° or 15° in the median plane. Comparison between experimental results from [2] and simulated results based on various response strategies: PM, CM, and both mixed—see text for descriptions. Dotted horizontal line: polar angle of the reference source. Horizontal line within box: median; box: inter-quartile range (IQR); whisker: within quartile ±1.5 IQR; star: outlier. Note that the simulations predicted a bias similar to the results from [2] for the reference source at 0°.

In order to quantify the goodness of fit (GOF) between the actual and simulated results, we applied the following analysis. First we estimated a parametric representation of the actual results from [2]. To this end, we calculated the sample mean $\widehat{\mathrm{\mu }}$ and the variance $\widehat{\mathrm{\sigma }}$ for the two reference sources. Then we quantified the GOF between the actual and simulated results by means of p-values from one-sample Kolmogorov-Smirnov tests [17] performed with respect to the estimated normal distributions.

Table 1 lists the estimated means and standard deviations for the two different source angles together with the GOF for each simulation. The GOF was also evaluated for the results from [2] to show that the estimated normal distributions adequately represent these results. For the reference source at 0°, the p < .05 for the PM strategy indicates that our predictions represent those from [2] significantly different. For the reference source at 15°, predictions based on the CM strategy are significantly different.

Table 1.

Means and standard deviations of responded panning angles for the two reference sources (Ref.) together with corresponding GOFs evaluated for the actual results from [2] and predicted results based on various response strategies. Note the relatively large GOFs for the simulations based on mixed response strategies indicating a good correspondence between actual and predicted results.

			Goodness of fit
Ref.	$\widehat{\mathrm{\mu }}$	$\widehat{\mathrm{\sigma }}$	[2]	PM	CM	Mixed
0°	6.0°	5.1°	.77	.01	.42	.88
15°	15.6°	4.8°	.70	.37	.02	.84

Thus, we attempted to better represent the pool of listeners from [2] by assuming that listeners used either the PM or the CM strategy for the adjustment. To this end, we created a mixed strategy pool by assigning one of the two strategies to each of the listeners individually so that the sum of the two GOFs is maximum. This procedure assigned 12 listeners to the PM strategy and 11 listeners to the CM strategy. Both GOFs for the mixed strategies are larger than 0.8 and, thus, indicate a good correspondence between the simulated and actual results for both reference sources.

Note that the simulations based on mixed adjustment strategies were able to replicate the results obtained by [2] even though they were based on a different pool of listeners. In particular, the model was able to explain the 5°-bias in median panning angle for a reference source at 0°, which suggests that this bias is caused by a general acoustic property provided by human HRTFs. Furthermore, simulation of listeners’ individual adjustment strategies was required in order to explain the across-listener variability observed in [2]. A more detailed analysis targeted to find the reasons for listener-specific preferences in adjustment strategies is outside of the focus of this study.

2.2 Effect of Loudspeaker Span

The loudspeaker arrangement in our previous experiment yielded quite large polar errors, especially for panning angles around the center between the loudspeakers. Reduction of the span between the loudspeakers in the sagittal plane is expected to improve the accuracy in localization of virtual sources. For the analysis of the effect of loudspeaker span, we simulated two loudspeakers at R = 0 dB in the median plane and systematically varied the loudspeaker span within 90° in steps of 10°. For each listener and span we averaged the predicted polar errors across target polar angles that ranged from −25° to 205°.

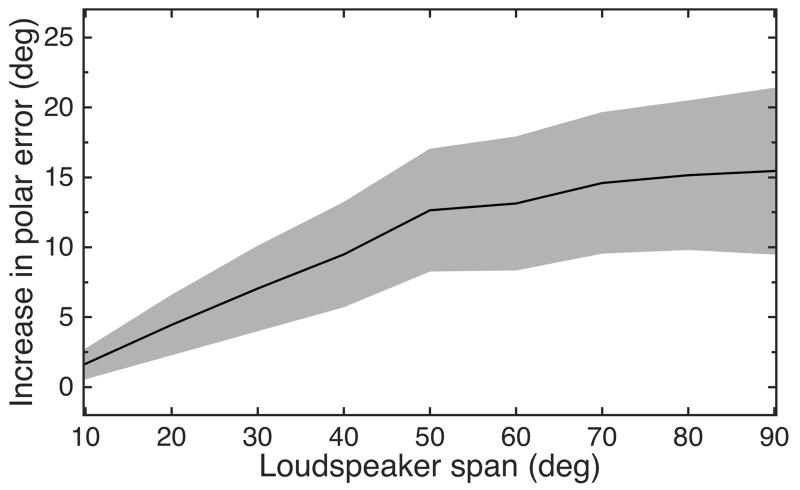
Fig. 7 shows the predicted increase in average polar errors as a function of the loudspeaker span. With increasing span the predicted errors increased consistently accompanied by a huge increase in across-listener variability. Compared to the results from Fig. 4, the predicted increases in polar error are much smaller. This is a consequence of including rear directions in the evaluation for which the localization accuracy is generally worse and leads to smaller differences between the baseline accuracy and the accuracy obtained by using VBAP.

Fig. 7.

Increase in polar error (defined as in Fig. 5) as a function of loudspeaker span in the median plane with panning ratio R = 0 dB. Black line with gray area indicates mean ±1 standard deviation across listeners. Note that the increase in polar error monotonically increases with loudspeaker span.

The predicted effect of the loudspeaker span was consistent with the findings from [18], i.e., the closer two sources are positioned in the median plane, the stronger the weighted average of the two positions is related to the perceived location. In order to directly compare our results with those from [18], we evaluated the correlation between panning angles and predicted response angles for the panning ratios tested in [18]: R ∈{ −13, −8, −3, 2, 7} dB. For each listener and panning ratio, predicted response angles were obtained by first applying the model to predict the response PMV and then generating 100 response angles by a random process following this PMV. Since listeners in [18] were tested only in the frontal part of the median plane, we evaluated the correlations for frontal target directions, while restricting the response range accordingly. For further comparison, we additionally analyzed predictions for rear as well as front and rear targets while restricting the response ranges accordingly.

Fig. 8 shows the predicted results together with those replotted from [18]. For all angular target ranges, the predicted coefficients decrease monotonically with increasing loudspeaker span. The results for the front show a strong quantitative correspondence with those from [18]. Compared to the front, rear sources were generally less accurately localized as indicated by the reference condition of 0° loudspeaker span, and consequently, panning angles at overall and rear directions also correlate less well with localization responses up to loudspeaker spans of about 70°. For the overall target range, our simulations show that for loudspeaker spans up to 40°, the VBAP principle can explain at least 50% of the localization variance in a linear regression model.

3 PANNING WITHIN MULTICHANNEL SYSTEMS

For multichannel sound reproduction systems that include elevated loudspeakers, plenty recommendations of specific loudspeaker arrangements exist. As shown in Sec. 2.2, the loudspeaker span strongly affects the accuracy in localization of elevated virtual sources. Thus, for a given number of loudspeakers, one can optimize the localization accuracy either for all possible directions or for preferred areas. In this section we analyzed the spatial distribution of predicted localization accuracy for some exemplary setups.

3.1 Selected Systems

We selected an exemplary set of six recommendations for 3D loudspeaker arrangements in the following denoted as systems A, … , F, which are sorted by decreasing the number of incorporated loudspeakers (Table 2). The loudspeaker directions of all systems are organized in layers with constant elevation. In addition to the horizontal layer at the ear level, system A has two elevated layers at 45° and 90° elevation, systems B, C, and D have one elevated layer at 45°, system E has elevated layers at 30° and 90° elevation, and system F has one elevated layer at 30°.

Table 2.

Loudspeaker directions of considered reproduction systems. Dots indicate occupied directions. Double dots indicate that corresponding directions to the right hand side (negative azimuth and lateral angle) are occupied as well. Ele.: elevation; Azi.: azimuth; Pol.: polar angle; Lat.: lateral angle.

Ele.	Azi.	Pol.	Lat.	A	B	C	D	E	F
0°	0°	0°	0°	•	•	•	•	•	•
	30°	0°	30°	• •			• •	• •	• •
	60°	0°	60°	• •	• •	• •	• •
	90°	0°	90°	• •	• •	• •
	115°	180°	65°				• •
	135°	180°	45°	• •	• •	• •		• •	• •
	180°	180°	0°	•			•
30°	30°	34°	26°					• •	• •
	135°	141°	38°					• •	• •
45°	0°	45°	0°	•
	45°	55°	30°	• •	• •	• •	• •
	90°	90°	45°	• •
	135°	125°	30°	• •	• •
	180°	135°	0°	•		•
90°	0°	90°	0°	•				•

System A represents the 22.2 Multichannel Sound System developed by the NHK Science & Technical Research Laboratories in Tokyo [19], in our present study investigated without the bottom layer consisting of three loudspeakers below ear level. Systems B and C represent the 11.2 and 10.2 Vertical Surround System (VSS), respectively, developed by Samsung [20]. System D represents a 10.2 surround sound system developed by the Integrated Media Systems Center at the University of Southern California (USC) [21]. Systems E and F represent the Auro-3D 10.1 and 9.1 listening format, respectively [22].

3.2 Methods and Results

Following the standard VBAP approach [1], the number of active loudspeakers depends on the desired direction of the virtual source and may vary between one, two or three speakers according to whether the desired source direction coincides with a loudspeaker direction, is located directly between two loudspeakers or lies within a triplet of loudspeakers, respectively. Since sagittal-plane localization is most important for sources in proximity of the median plane, we investigated only virtual sources within the range of ±45° lateral angle.

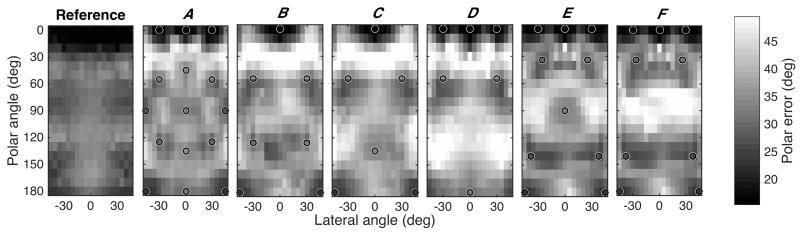
The model was used to predict polar errors as a function of the lateral and polar angle of a targeted virtual-source direction for the different arrangements and for a reference system containing loudspeakers at all considered directions. Fig. 9 shows the across-listener averages of the predicted polar errors. The simulation of the reference system shows that, in general, listeners perceive the location of sources in the front most accurately. In the various reproduction systems, polar errors tended to be smaller at directions close to loudspeakers (open circles), a relationship already observed in Sec. 2.1. Consequently, one would expect that the overall polar error increases with decreasing number of loudspeakers, but this relationship does not completely apply to all cases. System A with the largest number of loudspeakers resulted in a quite regular spatial coverage of accurately localized virtual-source directions. Systems B, C, and D covered generally less directions. Systems B and C showed only minor differences in the upper rear hemisphere, where system D yielded strong diffuseness. For systems E and F, which have a lower elevated layer and thus a smaller span to the horizontal layer, the model predicted very accurate localization of virtual sources targeted in the frontal region. This suggests that positioning the elevated layer at 30° is a good choice when synthesized auditory scenes are focused to the front, which might be frequent especially in the context of multimedia presentations. Note that 30° elevation at 30° azimuth corresponds to a polar angle of about 34°, whereas 45° elevation at 45° azimuth corresponds to a polar angle of about 55°, that is, a span for which larger errors are expected—see Sec. 2.2.

Fig. 9.

Predicted polar error as a function of the lateral and polar angle of a virtual source created by VBAP in various multichannel systems. System specifications are listed in Table 2. Open circles indicate loudspeaker directions. Reference shows polar error predicted for a real source placed at the virtual source directions investigated for systems A, … , F.

Table 3 summarizes the predicted degradation in localization accuracy in terms of the increase of errors relative to the reference and averaged across listeners. We distinguished between the mean degradation, Δe_mean, as indicator for the general system performance, and the maximum degradation, Δe_max, across directions as an estimate of the worst-case performance. The predicted degradations confirm our previous observations, namely, that systems with less loudspeakers and higher elevated layers yield virtual sources that provide poorer localization accuracy. Due to the lower elevation of the second layer, systems E and F provide the best trade-offs between number of loudspeakers and localization accuracy.

Table 3.

Predicted across-listener average of increase in polar errors as referred to a reference system containing loudspeakers at all considered directions. Distinction between mean (Δe_mean) and maximum (Δe_max) degradation across directions. N: Number of loudspeakers. Ele.: Elevation of second layer. Notice that this elevation has a larger effect on Δe_mean and Δe_max than N.

System	N	Ele.	Δ e mean	Δ e max
A	19	45°	6.7°	28.8°
B	11	45°	8.9°	38.6°
C	10	45°	10.0°	38.6°
D	10	45°	11.0°	31.3°
E	10	30°	6.4°	29.3°
F	9	30°	7.3°	29.3°

Our results are consistent with directional quality evaluations from [20]. In that study the overall spatial quality of system A was rated best, no quality differences between system B and C were reported, and system D was rated worse. Systems E and F were not tested in this study.

4 CONCLUSIONS

By using VBAP in multichannel sound reproduction systems, monaural spectral localization cues encoding different loudspeaker directions are superimposed with a frequency-independent weighting. This can lead to conflicting spectral cues that cause localization errors. We used a model in order to systematically investigate the limitations of VBAP with respect to localization in sagittal planes. Our simulations provide evidence for the following conclusions:

1. Virtual sources created by different loudspeaker arrangements and panning ratios are, on average across listeners, localized differently. Thus, findings for specific configurations cannot be generalized to other loudspeaker arrangements and panning ratios.

2. Within the same loudspeaker arrangement, listeners localize amplitude-panned virtual sources differently because of inter-individual differences in HRTFs. Generally, perceptual differences are largest for a panning ratio of 0 dB and increase with the polar-angle span between loudspeakers.

3. Loudspeaker spans below polar angles of 40° are required to obtain good localization accuracy, especially in the frontal region where listeners are most sensitive.

Biographies

THE AUTHORS

Robert Baumgartner

Robert Baumgartner is working as a research assistant at the Acoustics Research Institute (ARI) and is a Ph.D. candidate at the University of Music and Performing Arts Graz (KUG) since 2012. In 2012, he received his M.Sc. degree in electrical and audio engineering, a inter-university program at the University of Technology Graz (TUG) and the KUG. His master thesis was honored by the German Acoustic Association (DEGA) with a student award. His research interests include spatial hearing and spatial audio. Robert is a member of the DEGA, a member of the Association for Research in Otolaryngology (ARO), and the secretary of the Austrian section of the AES.

Piotr Majdak

Piotr Majdak, born in Opole, Poland, in 1974, studied electrical and audio engineering at the TUG and KUG, and received his M.Sc. degree in 2002. Since 2002, he has been working at the ARI and is involved in projects including binaural signal processing, localization of sounds, and cochlear implants. In 2008 he received his Ph.D. degree on lateralization of sounds based on interaural time differences in cochlear-implant listeners. He is member of the Acoustical Society of America, the ARO, the Austrian Acoustic Association, and the president of the Austrian section of the AES.