Cox Regression Models with Functional Covariates for Survival Data

Abstract

We extend the Cox proportional hazards model to cases when the exposure is a densely sampled functional process, measured at baseline. The fundamental idea is to combine penalized signal regression with methods developed for mixed effects proportional hazards models. The model is fit by maximizing the penalized partial likelihood, with smoothing parameters estimated by a likelihood-based criterion such as AIC or EPIC. The model may be extended to allow for multiple functional predictors, time varying coefficients, and missing or unequally-spaced data. Methods were inspired by and applied to a study of the association between time to death after hospital discharge and daily measures of disease severity collected in the intensive care unit, among survivors of acute respiratory distress syndrome.

1 Introduction

We introduce the proportional hazard functional regression model for data where the outcome is the possibly censored time to event and the exposure is a densely sampled functional process measured at baseline. The methodology was inspired by and applied to a study of the association between survival time after hospital discharge of survivors of acute respiratory distress syndrome (ARDS), and daily measures of organ failure during hospitalization.

The main innovation of our approach is to provide a fast and easy to use Cox model for functional regression based on modern developments in nonparametric smoothing, survival analysis methods and software, and functional data analytic concepts. More precisely, the method we propose has three important characteristics: 1) it employs penalized splines (Eilers and Marx, 1996; O'sullivan et al., 1986; Ruppert et al., 2003) to model the functional coefficient(s); 2) it treats the proportional hazards model that incorporates the functional parameter as a hazard rate with a mixed effects format on the log scale and uses modern survival data fitting techniques that incorporate nonparametric smoothing and frailty regression (Gray, 1992; Verweij and Van Houwelingen, 1993; Therneau and Grambsch, 1998); and 3) it estimates the amount of smoothing of the functional parameter using a likelihood-based information criterion such as AIC (Verweij and Houwelingen, 1994; Therneau et al., 2003), and thus avoids the use of principal component truncation, which may lead to highly unstable coefficient shapes.

Functional data regression is under intense methodological development (Marx and Eilers, 1999; Cardot et al., 1999, 2003; James, 2002; Müller and Stadtmüller, 2005; Cardot and Sarda, 2005; Ferraty and Vieu, 2006; Reiss and Ogden, 2007; Ramsay et al., 2009; James et al., 2009; Goldsmith et al., 2011; Harezlak and Randolph, 2011; Ferraty, 2011; McLean et al., 2012), though there are only a few modeling attempts in the case when outcome is time-to-event data. Probably the first paper to consider this topic was James (2002), who used a functional generalized linear model to model right-censored life expectancy, where censored outcomes are handled using the procedure of Schmee and Hahn (1979). The procedure has two steps: 1) use a truncated normal distribution to estimate the unobserved failure times; and 2) incorporate these estimates in standard least squares equations. The entire procedure is then iterated using the EM algorithm. This method for accounting for censored survival times is similar in spirit to the better known Buckley-James estimator (Buckley and James, 1979; Miller and Halpern, 1982). Müller and Zhang (2005) developed an alternative model for the mean remaining lifetime given a longitudinal covariate up to a given time, though their model does not allow for censored outcomes. Chiou and Müller (2009) incorporate the ideas of functional data analysis by modeling hazard rates as random functions, but they do not allow for functional predictors.

In parallel with these efforts in functional data analysis, important developments have been achieved by researchers in survival data analysis. Specifically, non-parametric smoothing approaches have been introduced to account for the possibly nonlinear effects of scalar covariates in a proportional hazards model. Therneau and Grambsch (1998) showed how to fit a model with a smooth covariate effect using penalized splines, and how this model was closely related to the more well-studied gaussian frailty model. Kneib and Fahrmeir (2007) developed an expanded mixed model that allows for non-parametric effects of scalar covariates, spatial effects, time-varying covariates, and frailties. Strasak et al. (2009) allowed for smooth effects of time-varying covariates. These techniques have now matured, are accompanied by high quality software (Belitz et al., 2013; Therneau, 2012, 2014), and continue to be developed. Our approach will take advantage of decades of development in survival data analysis, functional data analysis, and nonparametric smoothing. In particular, we will identify the most robust, easiest to use combination of approaches to achieve our goal: modeling survival data with nonparametric functional regression parameters.

Thus, we take advantage of these methods in order to model the e ect of a functional covariate on a (possibly censored) survival time, by including the functional covariate as a term in a Cox proportional hazards model (Cox, 1972). This approach has several advantages. First, the proportional hazards model is one of the most popular regression models ever, has been well-studied, and has a form that is familiar to a general audience. Second, the Cox model is widely considered to be the standard in regression for survival data due to its interpretability, applicability, and inferential flexibility. Third, it allows simple extensions of the fitting procedure to incorporate functional covariates. These properties allowed us to develop a model that is easy to implement and computationally efficient. Indeed, our software will be made publicly available as part of the pcox package in R (R Development Core Team, 2011), and fitting the model requires only one line of code.

We now briefly review some of the existing functional regression techniques that are relevant to this article. Scalar-on-function regression models the relationship between a scalar outcome and a functional covariate. Suppose that {Y_i} are a set of scalar outcomes, {X_i(t)} are functional covariates defined on the interval [0, 1], and {Z_i} non-functional covariates, where i ∈ {1, 2, …, N}. Then the generalized functional linear model that relates Y_i to Z_i and X_i(t) is $g\left({\mu }_i\right)=\alpha +{\mathbf{Z}}_i\gamma +{\int }_0^1{X}_i\left(t\right)\beta \left(t\right)dt$, where Y_i follows an exponential family distribution with mean μ_i, and g(·) is an appropriate link function (McCullagh and Nelder, 1989; James, 2002; Müller and Stadtmüller, 2005). The key feature of this model that differentiates it from a standard (non-functional) generalized linear model is the integral term, ${\int }_0^1{X}_i\left(t\right)\beta \left(t\right)dt$, which captures the contribution of the functional covariate X_i(t) towards g(μ_i). The integration essentially serves as a weighting mechanism for X_i(t), where the weights are given by the coefficient function β(t). Thus, we think of β(t) as the optimal weight function to express the contribution of X_i(t) towards g(μ_i).

In the next section, we propose an extension of the Cox proportional hazards model that incorporates a similar integral term for functional covariates, and describe how the parameters in such a model may be estimated. Section 3 describes a number of extensions to the model that allow for added flexibility. Section 4 assesses the performance of our model in a simulation study. In Section 5, we apply our model to our application of interest, and we conclude with a discussion of our findings in Section 6. Additional details regarding our software implementation using R's pcox package may be found in the supplemental material.

2 Cox Model with Functional Covariates

2.1 Proportional Hazards Model

Let T_i be the survival time for subject i, and C_i the corresponding censoring time. Assume that we observe only Y_i = min(T_i, C_i), and let δ_i = I(T_i ≤ C_i). We also assume that for each subject, we have a collection of covariates Z_i = {Z_i1, Z_i1, …, Z_ip}. The Cox proportional hazards model (Cox, 1972) for this data is given by log h_i(t; γ) = log h₀(t)+Z_iγ, where h_i(t; γ) is the hazard at time t given covariates Z_i and h₀(t) is a non-parametric baseline hazard function. The parameter vector exp(γ) is commonly referred to as the vector of hazard ratios, because it represents the multiplicative change in the hazard function for a one-unit increase in Z_i.

Suppose now that in addition to Z_i, we have also collected a functional covariate, $X_i\left(s\right)\in {\mathcal{L}}^2[0,1]$, for each subject. Without loss of generality, we assume that X_i(s) is centered by subtracting an estimator of the population mean function from the observed data. We propose the following functional proportional hazards model

$$\log h_i[t;\gamma ,\beta (\cdot \left)\right]=\log h_0\left(t\right)+{\mathit{Z}}_i\gamma +{\int }_0^1{X}_i\left(s\right)\beta \left(s\right)ds$$ (2.1)

The functional parameter, β(s), is slightly more difficult to interpret than its nonfunctional counterpart, γ. One interpretation is that the term exp $\left\{{\int }_0^1\beta \right(s\left)ds\right\}$ corresponds to the multiplicative increase in one's hazard of death if the entire covariate function, X_i(s), was shifted upwards by 1 unit (with Z_i held constant). In this context, one can refer to β(s) as a functional log hazard ratio. More generally, β(s) serves as a weight function for X_i(s) to obtain its overall contribution towards one's hazard of mortality. The model assumes proportional hazards; i.e., this contribution is the same over the entire domain t of the hazard function.

We note in particular the the domain of the functional predictor, s, is not the same as the time domain t over which the event is followed. We assume that X_i(s) is fully available at baseline, before the event can occur. If the functional predictor is measured concurrently with the event, then this predictor is a time-varying covariate. Alternative methods exist for this scenario, ranging from traditional approaches (Cox, 1972) to more modern developments in joint modeling of longitudinal and survival data (Tsiatis and Davidian, 2004; Ibrahim et al., 2010; Rizopoulos, 2012).

As proposed above, (2.1) is under-determined unless we make assumptions on the form of the functional coefficient β(s). We will take the common approach of approximating β(s) using a spline basis (Marx and Eilers, 1999; Cardot and Sarda, 2005; Ramsay and Silverman, 2005; Goldsmith et al., 2011). Let ϕ(s) = {ϕ₁(s), ϕ₂(s),…, ϕ_kb(s)} be a spline basis over the s-domain, so that $\beta \left(s\right)={\sum }_{k=1}^{k_b}{b}_k{\varphi }_k\left(s\right)$. Then (2.1) becomes

$$\begin{array}{cc}\hfill \log h_i(t;\gamma ,\mathit{b})& =\log h_0\left(t\right)+{\mathit{Z}}_i\gamma {\int }_0^1{X}_i\left(s\right)\varphi \left(s\right)\mathit{b}ds\hfill \\ \hfill & =\log h_0\left(t\right)+{\mathit{Z}}_i\gamma +c_i^{\prime }b\hfill \end{array}$$ (2.2)

where b = {b₁, b₂,…, b_Kb} and c_i is a vector of length K_b with k^th element ${\int }_0^1{X}_i\left(s\right){\varphi }_k\left(s\right)ds$. Note that this integral is based only on the covariate function and the (known) basis functions, and may be calculated using numerical integration.

As a choice of basis, we prefer penalized B-splines (Eilers and Marx, 1996), also known as P-splines. B-splines adapt flexibly to the data, have no boundary effects, and are fast to compute. In addition, by using a large number of knots and applying a roughness penalty, we prevent overfitting while eliminating the necessity to choose the number and precise location of the knots (O'sullivan et al., 1986; O'Sullivan, 1988). We have fit the model using other penalized bases, with minimal change to the estimated coefficient function.

2.2 Estimation via Penalized Partial Likelihood

For notational convenience, let θ = [γ b ] and ${\eta }_i\left(\theta \right)={\mathit{Z}}_i\gamma +c_i^{\prime }\mathit{b}$. Then the partial likelihood for this model is L^(p) (θ) = Π_i:δi=1 [exp{η_i(θ)}/Σ_j:Yj≥Yi exp{η_j(θ)}]. In order to ensure the smoothness of the coefficient function β(t), we will impose a penalty on the spline coefficients, b. Based on the above partial likelihood, we define the penalized partial log-likelihood (PPL) as

$${\ell }_{\lambda }^{\left(p\right)}\left(\theta \right)=\sum _{i:{\delta }_i=1}\left[{\eta }_i\left(\theta \right)-\log \left(\sum _{j:Y_j\ge Y_i}\exp \left\{{\eta }_j\right(\theta \left)\right\}\right)\right]-\lambda P\left(\mathit{b}\right)$$

where P(b) is an appropriate penalty term for the spline coefficients b, and λ is parameter that controls the smoothness of the resulting coefficient function.

The use of a penalized partial likelihood function in Cox models is not new. Gray (1992) introduced the function to allow for smooth effects of scalar covariates in a Cox model, and this method was extended and implemented in R by Therneau and Grambsch (1998). Verweij and Houwelingen (1994) and Therneau et al. (2003) exploited the well-known connection between mixed effects models and penalized splines to estimate frailty models via the penalized partial likelihood. Here, we follow a similar procedure to incorporate functional predictors into the Cox model.

We will assume that we can express the penalty term as $P\left(\mathit{b}\right)=\frac{1}{2}\lambda {\theta }^{\prime }\mathit{D}\theta$, where D is a symmetric, non-negative definite penalty matrix. Also, let ${\mathit{W}}_i=\left[\mathit{Z}\mathit{i}{c}_i^{\prime }\right]$ be the row of the design matrix corresponding to subject i, such that ${\eta }_i\left(\theta \right)={\mathit{W}}_i^{\prime }\theta$. Then for a given λ, the first and second derivatives (i.e., the gradient and hessian matrix) of ${\ell }_{\lambda }^{\left(p\right)}\left(\theta \right)$ may be easily computed. We can estimate the regression coefficients θ by maximizing the partial log-likelihood (for a given λ) using a Newton-Raphson procedure. In the results presented in Sections 4 and 5, we use a second-order difference penalty. This penalty is a discrete approximation to the integrated second derivative penalty, is computationally efficient, and is commonly used in P-splines (Eilers and Marx, 1996).

2.3 Optimization of the smoothing parameter

An essential step in the algorithm is the optimization of the smoothing parameter, λ. Unfortunately, typical optimization criteria, such as Allen's PRESS (cross-validated residual sum of squares) and Mallow's C_p, are not appropriate for Cox models. Verweij and Van Houwelingen (1993) proposed the cross-validated log likelihood (CVL) for the purpose of optimizing the smoothing parameter of a penalized partial likelihood. Let ${\widehat{\theta }}_{(-i)}^{\lambda }$ be the value of θ that maximizes ${\ell }_{\lambda ,(-i)}^{\left(p\right)}\left(\theta \right)$, the penalized partial log-likelihood when observation i is left out. Then the CVL for a given value of λ is given by $\text{CVL}\left\{\lambda \right\}={\sum }_{i=1}^n{\ell }_{\lambda ,i}^{\left(p\right)}\left\{{\widehat{\theta }}_{(-i)}^{\lambda }\right\}$, where ${\ell }_{\lambda ,i}^{\left(p\right)}(\cdot )={\ell }_{\lambda }^{\left(p\right)}(\cdot )-{\ell }_{\lambda ,(-i)}^{\left(p\right)}(\cdot )$ is the contribution of subject i to the penalized partial log-likelihood.

This expression is quite computationally intensive, as it requires calculating ${\ell }_{\lambda ,i}^{\left(p\right)}\left({\widehat{\theta }}_{(-1)}^{\lambda }\right)$ for each i. In practice, a computationally efficient alternative is the penalized version of the AIC, $\text{AIC}\left(\lambda \right)={\ell }_{\lambda ,i}^{\left(p\right)}\left({\widehat{\theta }}^{\lambda }\right)-e\left(\lambda \right)$, where $e\left(\lambda \right)=\mathrm{tr}\left[H_{\lambda }{\left({\widehat{\theta }}^{\lambda }\right)}^{-1}\mathit{H}\left({\widehat{\theta }}^{\lambda }\right)\right]$ is the effective dimension and H(·) is the unpenalized portion of the Hessian matrix. Although the AIC does not approximate the CVL directly, it is known that the changes in AIC or CVL from the null model are approximately equal, making the AIC a useful surrogate (Verweij and Houwelingen, 1994). pcox makes the AIC available, as well as two related criteria: the corrected AIC (AIC_c) of Hurvich et al. (1998), and the EPIC criterion of Shinohara et al. (2011). The AIC_c criterion has been recommended in cases with small n or large number of parameters to avoid overfitting (Burnham and Anderson, 2002), while the EPIC criterion corresponds to a likelihood ratio test at the α = 0.05 level for testing the significance of one additional parameter in two nested models. Practically, the three optimization methods offer three different levels of smoothness for the functional coefficient, with AIC resulting in the least smooth and EPIC the smoothest estimate.

2.4 Inference

There have been at least two proposals for the variance-covariance estimate of the parameter estimates in penalized partial likelihood models. Gray (1992) suggested using ${\mathit{V}}_1={\mathit{H}}_{\lambda }{\left({\widehat{\theta }}^{\lambda }\right)}^{-1}\mathcal{I}\left({\widehat{\theta }}^{\lambda }\right){\mathit{H}}_{\lambda }{\left({\widehat{\theta }}^{\lambda }\right)}^{-1}$. On the other hand, Verweij and Houwelingen (1994) use ${\mathit{V}}_2={\mathit{H}}_{\lambda }{\left({\widehat{\theta }}^{\lambda }\right)}^{-1}$, and refer to the square root of the diagonal elements of this matrix as “pseudo-standard errors”. Therneau et al. (2003) make both of these estimates available in their implementation, and we choose to take the same approach. For either choice of V, a pointwise 95% confidence interval for β(s₀) = ϕ(s₀)b may be constructed as $\widehat{\beta }\left(s_0\right)\pm 1.96\sqrt{\varphi \left(s_0\right){\mathit{V}}_{22}\varphi \left(s_0\right)}$, where V₂₂ is the lower-right K_b × K_b matrix of V.

Nonetheless, both proposals above for the variance-covariance matrix V are only valid when the smoothing parameter λ is fixed. When λ is optimized using one of the methods discussed in Section 2.3, these proposals may underestimate the true standard error. Thus, in addition to these two methods we propose to use a bootstrap of subjects (Crainiceanu et al., 2012a) to calculate the pointwise and joint confidence intervals for the model parameters. The performance of these four types of confidence intervals will be compared via simulation in Section 4.

3 Extensions

3.1 Additional penalized model covariates

An advantage of using penalized splines is that they are modular (Ruppert et al., 2003), making it very easy to extend Model (2.1) to include additional penalized terms. This makes the inclusion of additional functional predictors, smooth effects of scalar covariates, or frailty terms straightforward. Time-varying coeffcients for scalar covariates, X_iβ(t), may also be included by applying a penalized spline basis to the coeffcient function, allowing for non-proportional hazards (Zucker and Karr, 1990; Grambsch and Therneau, 1994). Each of these terms requires a corresponding penalty term in the penalized partial likelihood, with a separate smoothing parameter for each one. The pcox software package allows for each of these specialized terms in the model formula.

3.2 Full Likelihood Approach

An alternative estimation procedure may be employed by assuming a spline basis for the baseline hazard, and maximizing the penalized full data log likelihood (PFL). Such an approach was originally proposed by Cai et al. (2002) using a linear spline basis for the baseline hazard without any penalized covariates, and has been further extended to include penalized predictors including smooth covariate effects, spatial effects, and frailties by Kneib and Fahrmeir (2007); Strasak et al. (2009).

Since our model treats functional predictors as penalized regression terms, the PFL approach may be used to fit (2.2). Let ψ(t) = {ψ₁(t), ψ₂(t), …, ψ_K0(t)} be a spline basis over the time domain t, such that $\log h_0\left(t\right)=g_0\left(t\right)={\sum }_{k=1}^{K_0}{b}_{0k}{\psi }_k\left(t\right)$ is a spline approximation of the log baseline hazard, with spline coefficient b₀ = {b₀₁, b₀₂, …, b_0k0}.Then the PFL is

$${\ell }_{\lambda }^{\left(f\right)}\left(\theta \right)=\sum _{i=1}^n\left\{{\delta }_i{\eta }_i(T_i,\theta )-{\int }_0^{T_i}{e}^{{\eta }_i(u,\theta )}du\right\}-\frac{{\lambda }_0}{2}{\mathit{b}}_0^{\prime }{\mathit{D}}_0{\mathit{b}}_0-\frac{{\lambda }_1}{2}{\mathit{b}}^{\prime }Db$$

where ${\eta }_i(t,\theta )={\mathit{Z}}_i\gamma +{\mathit{b}}_0\psi \left(t\right)+c_i^{\prime }\mathit{b}$ and λ₀ and D₀ are the smoothing parameter and penalty matrix for the baseline hazard, respectively. The full likelihood approach has been shown to have advantages over the partial likelihood approach in cases where data is interval-censored (Cai and Betensky, 2003). However, in our application we do not have interval-censored data and we expect minimal benefit to using the PFL approach over the PPL approach. Due to the increased computational demand of using the PFL approach, we have chosen to use the PPL approach throughout this paper. The PFL approach will be offered in our software package.

3.3 Missing and unequally-spaced data

A common complication in functional regression occurs when the observed functional predictors are observed at widely spaced, unequal time intervals. This could occur for example when the functional predictor is measured at follow-up times that are not the same for each subject, or when there is substantial missingness in these observations. Goldsmith et al. (2011) showed how a functional principal components (FPCA) basis could be used to pre-smooth the observed data in a functional regression context, with minimal loss of information. We follow this approach in our modeling strategy. We perform FPCA by smoothing the empirical covariance matrix, as described in Staniswalis and Lee (1998) and Yao et al. (2003), and implemented using the fpca.sc() function in the R package refund (Crainiceanu et al., 2012b).

4 Simulation Study

4.1 Simulation design

In order to assess the performance of our model under a variety of conditions, we conducted an extensive simulation study. Of interest was our model's ability to accurately identify the coefficient function β(s). For simplicity, we consider only the scenario where there are no non-functional covariates Z, and only a single functional predictor X_i(s), of fixed domain. Let {s_j = j/100 : j = 0, 1, …, J = 100} be our grid of time points over the interval [0, 1]. For each subject i ∊ 0, …, N, we generate the survival time T_i and functional predictor X_i(s) based on the model h_i(t) = h₀(t) exp(η_i), where ${\eta }_i=\frac{1}{J}{\sum }_{j=1}^J{X}_i\left(s_j\right)\beta \left(s_j\right)$ and $X_i\left(s_j\right)=u_{i1}+u_{i2}{s}_j+{\sum }_{k=1}^{10}\left\{v_{ik1}\sin \right(2\pi k{s}_j)+v_{ik2}\cos (2\pi k10s_j\left)\right\}$. Here, h_i(t) is the hazard of T for subject i, h₀(t) is the baseline hazard, u_i1 ~ N(0, 25), u_i2 ~ N(0, 4), and v_ik1, v_ik2 ~ N(0, 1/k²). This model for simulating our functional predictors is based on the procedure employed by Goldsmith et al. (2011), which was in turn adapted from Müller and Stadtmüller (2005). We generated random survival times according to this proportional hazards model by following Bender et al. (2005). The baseline hazard was chosen to follow a Weibull distribution with shape parameter 0.75 and mean 600, where time is assumed measured in days. All subjects are censored at C_i = 730 days. These values were chosen to approximate the data that was used in our application. Based on the baseline hazard and censoring mechanism, we expect approximately 27% of subjects to be censored.

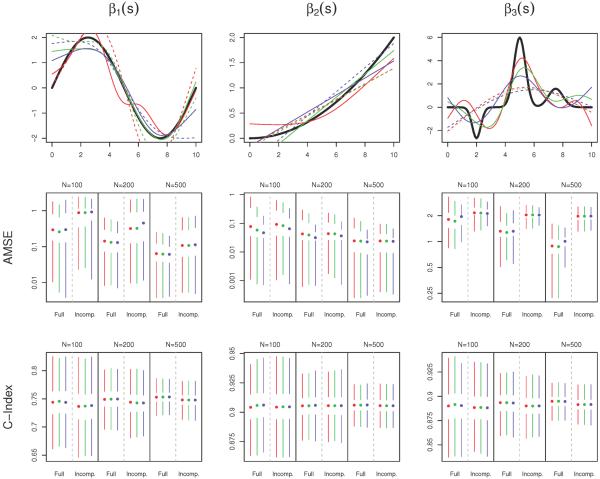
We apply three data-generating coefficient functions: ${\beta }_1\left(s\right)=2\sin \left(\frac{\pi s}{5}\right)$, β₂(s) = 2(s/10)², and β₃(s) = −2ϕ(s|2, 0.3) + 6ϕ(s|5, 0.4) + 2ϕ(s|7.5, 0.5), where ϕ(·|μ, σ) is the density of a normal distribution with mean μ and standard variance σ². The three coefficient functions appear in the top row of Figure 1.

Figure 1.

Simulation results. In all plots, color indicates the method for optimizing the smoothing parameter: red (AIC), green (AIC_c), or blue (EPIC). The top row displays the true coefficient functions (black), as well as the estimates with median AMSE when N = 200. The estimates based on the full data are given by the solid lines, and those based on the incomplete dataset are dashed. The second and third rows contain Tufte box plots of the distributions of AMSE and cross-validated concordance probability (C-Index) respectively, over the 1000 simulated datasets, stratified by sample size and missingness. The median value is indicated by a dot, the interquartile range by white space around the dot, and the smallest and largest non-outlying values by the endpoints of the colored bars. Outliers are defined to be data points more than 1.5 times the interquartile range from the nearest quartile. Lower AMSE and higher C-Index are indicative of better model performance.

We consider three different sample sizes, N ∈ {100, 200, 500} subjects. We are also interested in the amount of information that is lost when there is a large amount of missing data in the covariate measurements. In order to address this issue, we generate an “incomplete” version of the full covariate dataset as follows. First, for each subject we randomly select the number of measured values J_i as a random integer between 10 and 51, with equal probability. We then randomly select J_i of the J = 100 observations that are to be included in the incomplete dataset, again with equal probability. The result constitutes the observed, incomplete dataset. The incomplete coefficient functions are then smoothed using a functional principal components basis that retains enough principal components to explain 99% of the variability in the covariate functions.

For each combination of sample size, true coefficient function, and level of missingess (full vs. incomplete dataset), we generate R = 1000 simulated datasets and apply our model for Cox regression with a single functional predictor. The three versions each use a different criterion for selecting the smoothing parameter: AIC, AIC_c, or EPIC. In all cases, we use penalized B-splines to model the coefficient function (Marx and Eilers, 1999), using the difference penalty of Eilers and Marx (1996).

4.2 Evaluation criteria

The primary measure of model performance is its ability to estimate the true coefficient function. This is assessed by the average mean squared error (AMSE), defined as AMSE $\left(\widehat{\beta }\left(s\right)\right)=\frac{1}{J+1}{\sum }_{j=0}^J{\left\{\widehat{\beta }\left(s_j\right)-\beta \left(s_j\right)\right\}}^2$, where $\widehat{\beta }\left(s_j\right)$ is the estimated coefficient function at s = s_j and β(s_j) is the value of the true coefficient function at this location. A secondary measure of model performance is its predictive ability, which we measure with the cross-validated concordance probability, or C-Index (Harrell et al., 1996; van Houwelingen and Putter, 2012). The C-Index is the proportion of all pairs of observations for which the order of survival times are concordant with the model-based linear predictor; we use a 10-fold cross validated version of this statistic.

We also evaluated the coverage probability of four different pointwise 95% confidence intervals. The first two confidence intervals are formed using the two model-based estimates of the variance, as described in Section 2.4. The second two are bootstrap estimates based on 100 bootstrapped samples. One of these is a Wald-type confidence interval based on the bootstrap estimate of the variance, and the other is based on 2.5% and 97.5% quantiles of the bootstrap distribution of the estimates.

4.3 Simulation results

Box plots of the AMSE and cross-validated C-Index appear in Figure 1, along with the coefficient function estimates that had median AMSE for the scenario when N = 200. Overall, there is very little difference in the performance between the three optimization criteria. The EPIC criterion tends to have slightly better performance under β₂(s), as this coefficient function is very smooth and EPIC favors smoother estimates, but these gains are minimal.

β₃(s), with its sharp peaks and valleys, is by far the most difficult coefficient function to estimate, especially in the incomplete data case. Interestingly, despite its estimation resulting in the highest AMSE measurements, the models under this coefficient perform fairly well in terms of predictive ability, with median cross-validated C-indices near 90%. This observation reflects that this coefficient function's peaks, while difficult to estimate precisely, are relatively high in magnitude, which causes the model to “target” certain predictor functions as being more strongly or weakly associated with mortality. On the other hand, β₁(s) is relatively easy to estimate, but is much less strongly associated with survival. This result is due to the fact that the sine wave contains an equal amount of area that is positive and negative, causing subjects with relatively flat X_i(s) to not be clearly identified as either “high-risk” or “low-risk” for mortality. Only subjects who display a clear increasing or decreasing trajectory (high to low or low to high) in their predictor functions will be easily separable.

As expected, estimation of the coefficient functions is more difficult with low sample size and in the incomplete case, resulting in higher AMSE measurements. However, the model still seems to be useful in these cases. Interestingly, lower sample sizes and incomplete data do not seem to cause a very large drop in the C-Index measurements, indicating that these more challenging scenarios do not cause the model to lose much in terms of predictive ability. In order to assess whether differences in AMSE between the incomplete and full data scenarios were due the missing data in the incomplete case or the FPCA step that this data requires, we fit the same models to a version of the full data that was pre-smoothed by FPCA. The results (supplemental material) show very similar performance to those corresponding to the unsmoothed full dataset, indicating that it is the lack of information due to the missing data, and not the FPCA step, that causes the decreased model performance.

Coverage probabilities of the confidence intervals are shown in Table 1. The two model-based confidence intervals (V1 and V2) perform well in moderate-to-large sample size (N ≥ 200) with no missing data, for β₁(s) and β₂(s). However, when N is small or missing data is present, both tend to underestimate the variance of the estimates. This underestimation can be quite severe, with coverages as low as 25% in the most difficult scenarios. V1 tends to be more conservative than V2. The two bootstrap-based confidence intervals maintain coverage probabilities above 95%, except under β₃(s). However, in scenarios that are easier to estimate (full dataset, large N, and β₂(s)) these coverages seem to be overly conservative, especially B-V. Under β₃(s), which is the most difficult coefficient function to estimate, the bootstrap-based confidence intervals perform well when there is no missing data, but perform much more poorly on the incomplete datasets. Interestingly, this problem is exacerbated in larger sample sizes. We suspect that coverage may be improved by taking more than 100 bootstrap samples, which is what was chosen for these simulations. In all scenarios, coverage probabilities were highest when using the AIC criterion to optimize smoothness, and lowest with EPIC. These results are emphasized when examining plots of the pointwise coverage probability as a function of the domain s (supplemental material).

Table 1.

Mean coverage probability of each of the four pointwise 95% confidence intervals (averaged across s), under each scenario. VI and V2 are Wald-type confidence intervals based on the model-based estimates of the variance V₁ and V₂, defined in Section 2.4. B-V is a Wald-type confidence interval based on the variance of the bootstrap estimates, and B-Q is constructed from the 2.5% and 97.5% quantiles of the boostrap distribution.

N	Dataset	Opt. Method	β1(s)				β2(s)				β3(s)
			V1	V2	B-V	B-Q	V1	V2	B-V	B-Q	V1	V2	B-V	B-Q
100	Full	AIC	90	83	100	99	88	82	100	99	76	64	100	99
		AICC	87	81	100	98	86	82	100	98	70	58	99	95
		EPIC	68	63	96	94	82	80	100	96	56	46	93	86
	Inomplete	AIC	63	54	98	98	88	81	100	98	66	41	85	82
		AICC	60	52	98	98	87	80	100	98	64	40	85	81
		EPIC	50	44	96	96	84	79	100	97	55	36	82	77
200	Full	AIC	95	89	100	98	86	81	100	99	80	68	100	97
		AICC	95	88	100	98	86	81	100	98	76	64	99	95
		EPIC	89	80	97	94	79	76	100	96	61	50	86	82
	Inomplete	AIC	78	65	95	98	86	80	99	98	64	37	73	71
		AICC	76	64	95	98	85	79	100	98	63	36	72	70
		EPIC	65	56	91	96	78	75	100	97	53	33	69	67
500	Full	AIC	97	91	100	98	88	83	100	99	83	72	99	96
		AICC	97	92	100	98	88	82	100	99	82	71	99	95
		EPIC	95	87	98	94	79	75	99	96	63	51	80	81
	Inomplete	AIC	92	68	93	97	87	79	99	98	66	27	62	63
		AICC	92	68	93	97	87	79	99	98	66	27	61	63
		EPIC	88	65	90	96	80	74	98	96	56	25	59	60

5 Effect of SOFA Score on Post-ICU Mortality

5.1 Data description

The Improving Care of Acute Lung Injury Patients (ICAP) study (Needham et al., 2006) is a prospective cohort study that investigates the long-term outcomes of patients who suffer from acute lung injury/acute respiratory distress syndrome (ALI/ARDS). ALI/ARDS is a severe condition characterized by inflammation of the lung tissue. It can be triggered by a wide variety of causes, including pneumonia, sepsis, or trauma. Treatment consists of supported care, including mechanical ventilation in the intensive care unit (ICU), until the patient's condition stabilizes. Short-term mortality from ARDS can exceed 40% (Zambon and Vincent, 2008), and those that do survive are at increased risk for physical, cognitive, and emotional impairments, as well as death.

The ICAP study enrolled 520 subjects, with 237 (46%) dying in the ICU. We are concerned with long-term survival among the 283 survivors, once they are discharged from the hospital. Out of the 283 survivors, 16 subjects (5.7%) did not consent to follow-up, their mortality status was unknown after hospital discharge, and they were excluded from the analysis. Thus, our analysis is based on the remaining 267 subjects. All patients in the ICAP study who are discharged alive from the hospital and consented to follow-up were followed for up to two years from their date of enrollment in the study. If the subject died, mortality information was recorded to the nearest day, based on family report or publicly available records.

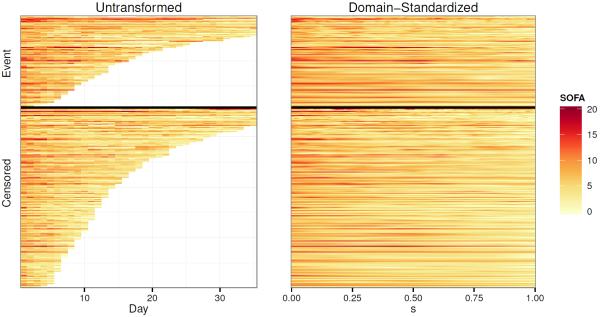
In the ICAP study, data recording starting upon enrollment in the study, and then daily thereafter during the patient's ICU stay. One measurement recorded daily during each subject's ICU stay is the Sequential Organ Failure Assessment (SOFA) score, which is a composite score of a patient's overall organ function status in the ICU. It consists of six physiological components (respiratory, cardiovascular, coagulation, liver, renal, and neurological), each measured on a scale of 0–4, with higher scores indicative of poorer organ function. The total SOFA score is the sum of these six subscores, ranging from 0–24. We consider each subject's history of measured SOFA scores, over time, to be a functional covariate, X_i(u), where u is the ICU day. These functions are depicted in the left panel of Figure 2 as a lasagna plot (Swihart et al., 2010).

Figure 2.

SOFA functions, before and after domain-standardization, depicted as lasagna plots. Each row corresponds to a subject, with color indicating the SOFA score at each time point. Subjects are ordered by domain width of the untransformed functions, U_i, within each outcome category (event vs. censored), in both plots.

5.2 Analysis plan

Our goal will be to estimate the association between post-hospital mortality and a patient's SOFA function. In addition to the SOFA function, our model also includes three non-functional covariates, which are meant to control for a subject's baseline risk of post-hospital mortality: age, gender, and Charlson co-morbidity index (Charlson et al., 1987). We consider “time zero”, the first day the subject is eligible for our event of interest, to be the day the subject is discharged from the hospital following ALI/ARDS, and subjects are censored at two years following their ALI diagnosis.

There are two features of the data that raise compilations in our analysis. The first complication occurs because some subjects are discharged from the ICU (due to an improvement in their condition) to a hospital ward, only to be readmitted to the ICU later during their hospitalization. Since SOFA measurements are only recorded in the ICU, these subjects will have gaps in their SOFA functions (indicated by gray space in Figure 2). Of the 267 subjects, 20 (7.5%) had gaps of this type, for a total of 4.4% of missing patient days. Based on clinical advice, we complete these gaps using a last observation carried forward (LOCF) imputation, though we test the sensitivity and sensibility of this approach by using alternative imputation approaches and by comparing to the complete case only analysis. As differences were found to be minimal, we present results for the LOCF imputation only.

The second, more significant complication is that each subject remains in the ICU for a different length of time, U_i. Since we use time as the domain of our functional covariate, this means that each function, X_i(u), will be measured over a different domain, [0, U_i]. The distribution of U_i up to 35 days can be seen in Figure 2, and overall ranges from as short as 2 days to as long as 157 days. Gellar et al. (2014) have proposed methods for accounting for this type of data in the context of classical functional regression using domain-dependent functional parameters. These approaches could be incorporated here, but we focus on a more traditional approach here to keep presentation simple. More precisely, we apply the subject-specific domain transformation s := g_i(u) = u/U_i to each function. This allows us to define new SOFA functions, ${\tilde{X}}_i\left(s\right)=X_i\left(s{U}_i\right)$, that are each defined over [0, 1]. The new SOFA functions defined over the s domain are a linearly compressed version of the original SOFA functions (Figure 2, right panel), and s, has the interpretation of being the proportion of the way through one's ICU stay that the measurement was taken. For example, ${\tilde{X}}_i\left(0.5\right)$ represents a subject's SOFA score half way through his ICU stay, and ${\tilde{X}}_i\left(1\right)$ is the SOFA score on the subject's last day in the ICU. We evaluate ${\tilde{X}}_i\left(s\right)$ at J = max_i(U_i) = 157 time points for each function.

Standardizing each subject's SOFA curve to a common domain may cause us to lose some potentially valuable information; specifically, we lose information regarding the original domain width, U_i. However, we note (Figure 3) that the average domain-standardized SOFA trajectory tends to be markably consistent across different strata of U_i. In particular, we do not observe any strong patterns in the functions across these strata, and U_i does not appear to affect the difference in curves between those who do and do not experience the event. These observations support our decision to standardize the SOFA functions to a common domain. In addition, since U_i itself could be a strong predictor of long-term mortality, we incorporate it into our model using a smooth effect on the log scale. The resulting model is

$$\log h_i(t;\gamma ,\beta (\cdot \left)\right)=\log h_0\left(t\right)+{\mathit{Z}}_i\gamma +{\int }_0^1{\tilde{X}}_i\left(s\right)\beta \left(s\right)ds+f\left\{\log \right(U_i\left)\right\}$$ (5.1)

where the the scalar covariates Z_i include subject age, gender, and Charlson Comorbidity Index. The Charlson Index (Charlson et al., 1987) is a commonly used measure of baseline health, with each existing clinical conditions assigned a score from 1–6 based on severity. In ICAP, total Charlson scores range from 0 to 15. A P-spline basis is used to approximate both the functional coefficient β(·) and the additive term f(·).

Figure 3.

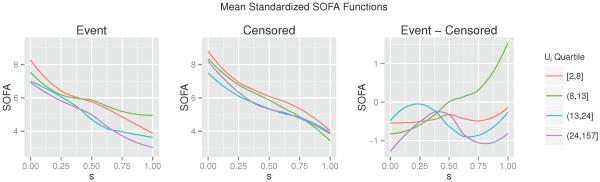
Mean domain-standardized SOFA functions, stratified by U_i and event status, as well as the difference in mean functions between those who did and did not experience the event. All curves are smoothed using a lowess smoother.

5.3 Results

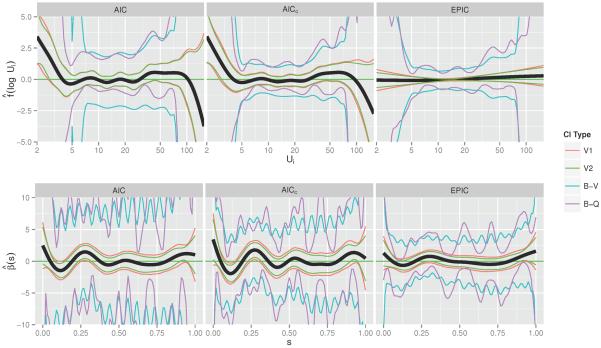
We plot the estimated additive function $\widehat{f}\left\{\log \right(U_i\left)\right\}$ and coefficient function $\widehat{\beta }\left(s\right)$ based on (5.1) in Figure 4, under each of the three optimization criteria. Overall, we see very little functional association between one's SOFA function and time to death after hospital discharge, as the 95% confidence interval covers the horizontal line β(s) = 0 throughout the entire domain s. This implies that the integral term of the model, ${\int }_0^1{\tilde{X}}_i\left(s\right)\beta \left(s\right)du$, will be close to zero for all subjects, so ${\tilde{X}}_i\left(s\right)$ offers little contribution towards one's hazard of death. There seems to be a positive association with length of stay for lengths of stay less than 5 days, but not for those greater than or equal to 5. On the other hand, two of the non-functional covariates, age and Charlson co-morbidity index, are highly associated with an increased hazard of death. According to the model optimized using AIC_c and the confidence interval calculated from the quantiles of the bootstrap distribution, we found that one's hazard of mortality increases by 5% (95% CI 4%–9%, p < 0.001) for every 1-year increase in age, and it increases by 12% (95% CI 6% – 36%, p = 0.001) for every 1-point increase in Charlson Index.

Figure 4.

Estimated associations between one's log hazard of mortality and their ICU length of stay (top row of figures) and the standardized SOFA functions (bottom row), under each of the three methods for optimizing λ. Pointwise 95% confidence intervals are formed by one of four methods. The first two (V1 and V2) are from model-based estimates of the variance. The second two are based on 10,000 bootstrapped samples of the dataset, one (B-V) which uses the pointwise bootstrap variance, and the other (B-Q) which uses the pointwise quantiles.

We see that the EPIC criterion imposes a stronger degree of smoothness in both $\widehat{f}(\cdot )$ and $\widehat{\beta }(\cdot )$ than the other two smoothing criteria, to the extent that very little functional signal can be detected for either estimate. The widely-varying bootstrap confidence intervals, especially for β(s), is likely due to a flat likelihood, without much information contributed by X_i(s). By imposing a higher degree of smoothness, the EPIC criterion results in more reasonable intervals.

In order to compare the three sets of estimates, we calculate the N-fold cross-validated C-Index for each one (Table 2, top 3 rows), as a measure of how well each model would predict mortality when applied to an independent dataset. The model fit with EPIC had the highest predictive ability. This observation reinforces the conclusion that there is not a very strong functional relationship between SOFA score in the ICU and long-term mortality among patients surviving their hospitalization, as EPIC favors estimates closer to the zero line.

Table 2.

Predictive ability of each model, measured by the N-fold cross-validated C-Index. All models are adjusted for the scalar covariates age, gender, and CCI, and they differ in the way they model the length of stay U_i and the SOFA function X_i(s), as well as the method for optimizing any smoothing parameters. M1–M4 refer to the mean SOFA scores in the regions [0,0.05], [0.05,0.2], [0.2,0.4], and [0.85,1] of the s-domain, respectively. S1–S3 refer to the slopes of a regression line through the SOFA scores in the regions [0,0.15], [0.15,0.3], and [0.3,0.45].

Ui	SOFA	λ-Opt	C-Index
P-Spline	Functional Effect	AIC	0.700
P-Spline	Functional Effect	AICC	0.714
P-Spline	Functional Effect	EPIC	0.715
Linear Spline	Functional Effect	AIC	0.702
Linear Spline	Functional Effect	AICC	0.730
Linear Spline	Functional Effect	EPIC	0.733
Linear Spline	Ml + M2 + M3 + M4		0.737
Linear Spline	Ml + M2 + M4		0.738
Linear Spline	Ml + M4		0.736
Linear Spline	Ml		0.735
Linear Spline	M4		0.739
Linear Spline	S1 + S2 + S3		0.729
Linear Spline	None		0.733
None	None		0.739

5.4 Follow-up Models

While often functional regression models are viewed as the final part of the inference, here we use them as exploratory tools. Indeed, a more careful examination of Figure 4 reveals some potentially important patterns; in this section we investigate those patterns further. First, we note that the plots for $\widehat{f}\left\{\log \right(\mathrm{LOS}\left)\right\}$ obtained using the AIC and AIC_c criteria indicate that the function may be appropriately modeled by a linear spline with one knot at 5 days. There is a visually striking effect after 100 days, as well, but as only three survivors had a length of stay longer than 100 days, we have decided to ignore it. Additionally, we note a number of regions over the s-domain of $\widehat{\beta }\left(s\right)$ with relatively large magnitude, even if the point-wise confidence intervals cover 0. These regions occur around s =0, 0.15, 0.3, and 1.

Using these observations as a guide, we fit a series of follow-up parametric models, and investigate their predictive ability via the N-fold cross-validated C-Index (Table 2). These models differed in their treatment of the functional predictor and the U_i variable. We also investigated whether or not incorporating the age covariate as a smooth term improved model fit, but in each case it did not so we only present results that treat age linearly. Interestingly, we have found that parameterizing the additive and functional effects resulted in superior predictive performance. In particular, we observed that removing the SOFA scores from the model completely resulted in a higher cross-validated C-Index than including them as functional effects; this seems to indicate that there is not a strong functional relationship between SOFA score and long-term mortality in this subset of patients.

The best-performing model included the scalar covariates Z_i, a linear spline for log(U_i), and the mean SOFA score over the region s ∈ [0.85, 1] (M4 in Table 2). The mean SOFA over s ∈ [0, 0.05] (M1) also shows a potentially important association. Investigating the effects in these regions further, Figure 5 depicts the Kaplan-Meier estimates of the survival curve, stratified by high vs. low values of M1 and M4. Based on these findings, we think that more exploration of functional approaches followed by aggressive thresholding of functional parameter estimates may actually lead to improved prediction and interpretation. This is likely to be the case in applications with a small to moderate number of subjects and weak functional effects.

Figure 5.

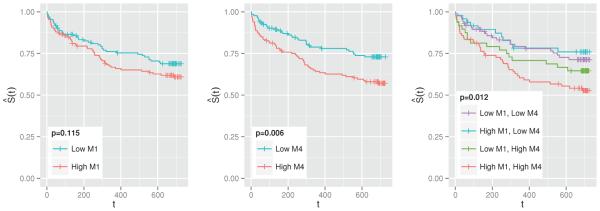
Kaplan-Meier estimates of the survival function, stratified by whether the subject has a higher or lower than median value of M1 (left), M4 (middle), and M1 and M4 (right). M1 is the mean SOFA score in the first 5% of one's ICU stay, whereas M4 is in the last 15%. p-values correspond to the log-rank test for the equivalence of the survival functions. “+” indicates censoring.

6 Discussion

We develop new methodology to account for functional covariates in a Cox proportional hazards model. We use a spline basis to approximate the functional coefficient, and estimation is accomplished by maximizing the penalized partial likelihood, with the degree of smoothness determined by optimizing one of three presented information criteria. The model is flexible and modular, in that it can be easily extended to incorporate a number of advances both in the fields of survival analysis and in functional data analysis. We have developed easy to use and computationally efficient software to implement this model.

We demonstrate through simulations that this model does a good job of estimating the true coefficient function even in cases with a moderate amount of missing data, except when the true coefficient function is especially complicated. Model-based estimates of the standard error resulted in pointwise confidence intervals that tended to be too narrow, and we therefore recommend bootstrap-based confidence intervals as a more conservative alternative.

We applied this model to estimate the functional association between SOFA score and post-hospital mortality among patients with ARDS. We found that this association is quite close to zero, throughout the domain of our functional predictor. Despite the null result, this observation is potentially quite clinically meaningful. It tells us that, among this patient population, one's survival after leaving the hospital does not appear to depend heavily on patterns of organ failure in the ICU, after accounting for age, gender, comorbidity status, and ICU length of stay. It was previously hypothesized by our collaborators that we may observe different patterns in mortality based on one's SOFA pattern. This analysis does not support that hypothesis.

Another possibility is that this model is mis-specified. Recall that we modified our original SOFA functions X(u) by collapsing them to $\tilde{X}\left(s\right)$. While this conveniently allowed us to avoid the problem of each function falling on a different domain, [0, U_i], it may have caused us to lose important information that was present in the original functions. A more appropriate model would allow for the coefficient function to change with U_i, resulting in a variable domain functional regression model with bivariate coefficient function β(u, U_i), similar to that proposed by Gellar et al. (2014). Another alternative is to allow for a time-varying effect of the SOFA functions, which would involve replacing the coefficient function β(s) in (5.1) with the bivariate coefficient function β(s, t). We do not explore these models in this paper, and leave them to future work.

Even though our analysis suggested a very weak functional relationship between SOFA and mortality, we were able to use our functional estimates to guide the design of simpler models that parameterize this association. These simpler models proved to demonstrate better predictive accuracy than the full functional approach, as measured by the cross-validated C-Index. This process shows the strength of functional regression techniques as an exploratory tool for understanding the relationship between a functional predictor and an outcome. In some cases the full functional model may be most appropriate, but more often than not this association may be simplified to a more parsimonious and interpretable relationship.