Abstract
As isothermal titration calorimetry (ITC) gains popularity for the characterization of enthalpies and equilibrium association constants of simple 1:1 biomolecular interactions, its use for more complex systems is growing. The method is increasingly used to study interactions in which a single binding partner (molecule “A”) interacts with multiple copies of a second partner (“B”); thus examinations of ABB and ABBB interactions are not uncommon. The structure of ITC data (commonly formatted as isotherms) has a strong bearing on the ability of the researcher to extract the necessary parameters from them. Usually, only 10-30 injections are recorded in a single ITC experiment. Even if replicates are performed, the data must support the extraction of up to twelve parameters from an ABBB system conducted in triplicate. Further, the refinement of some of the parameters is largely driven by only a subset of the data. The ability of ITC data to guide the deterministic estimation of these parameters may therefore be questioned. This work assesses the ability of both empirical and simulated ITC data of ABB and ABBB systems to support the simultaneous estimation of the desired thermodynamic parameters. The results demonstrate that multiphasic isotherms tend to (but do not always) support the estimation of multiple parameters. On the other hand, uniphasic data obtained from multi-site binding systems are more problematic. In all cases, a thorough exploration of how precisely the estimated parameters are specified by the data is justified.
Keywords: Isothermal titration calorimetry, treponemal lipoproteins, two-site binding, three-site binding, analytical ultracentrifugation, isotherm analysis
1. Introduction
Since the introduction of the modern power-compensating isothermal titration calorimeter in 1989 [1], the instrument has been widely and successfully used in a variety of fields. Such calorimeters have been used to study detergent micellization/demicellization [2], membrane partitioning and translocation of proteins and peptides [3], food science [4,5], pollutant catabolism [6], and enzyme kinetics [7,8]. Arguably, however, its widest use is to thermodynamically characterize the stoichiometric binding of two or more biomolecules in solution. Isothermal titration calorimetry (ITC) has been used to derive thermodynamic parameters for the interactions of small molecules, proteins, DNA, RNA, and all combinations of these biomolecules [9–15]. This solution method features label-free characterization and direct access to important thermodynamic parameters (e.g. enthalpy and free energy); its popularity is therefore straightforward to understand.
ITC is conceptually simple and has been extensively described elsewhere [8,10,14,16]; only the most pertinent details are recapitulated here. In a typical ITC experiment designed to study a biomolecular interaction, a molecule of interest is introduced into a metallic sample cell. A companion reference cell (often filled with water) is positioned close by, and sensors stationed between the cells detect any temperature difference between them. Each cell is equipped with a heating element, and a constant reference power is applied to the reference cell's heater. The sensor detects the growing temperature difference between the cells and actuates a feedback circuit that engages the sample-cell heater. The amount of power needed to maintain an equal temperature between the two cells comprises the signal in the experiment, which is monitored as a function of time, resulting in the “thermogram”. Addition of an interacting molecule into the sample cell via a rotating, motorized syringe assembly evolves or consumes heat, causing deflections from and recoveries to the baseline power in the thermogram. These peaks are usually integrated and evaluated as a function of injectant concentration (the “isotherm”).
Advances in instrumentation [17,18] and analysis [19–22] of ITC data have facilitated researchers’ abilities to quickly and accurately derive thermodynamic parameters for simple 1:1 biomolecular interactions. As a result, the method has been extended to study more complex interactions, featuring two [23–26] and three [20,27–29] distinct binding sites. While the cited efforts examined strongly featured isotherms or properly constrained analyses, other, more ambitious studies must contend with some countervailing facts. While a raw ITC thermogram may have thousands of data points, the isotherm derived therefrom typically only has between 20-50 data points. Furthermore, only a subset of these data points strongly bear on the parameter that is usually most desired by researchers, i.e. the equilibrium association constant (KA, sometimes termed KD, where KD = 1/KA). Indeed, this relative paucity of information on KA is one source of the recommendation that the unitless Wiseman c value (c = KA·M, where M is the molar concentration of reactant in the sample cell) be set to a value of above 40 [1,30]; this action ensures that the data are sufficiently informative to arrive at an accurate estimation of KA by fitting the data using least-squares methods.
An additional challenge for the analysis of multisite data is the availability of both microscopic and macroscopic (or “stepwise” [20]) binding models. To the author's knowledge, in popular ITC data-analysis software [19,31], only macroscopic analytic models are available for molecules having three or more binding sites. The distinction between macroscopic and microscopic multisite models may seem subtle, but it is important. In macroscopic/stepwise models, the sites are distinguished by the order in which they are occupied. Thus, if A represents a receptor with more than one binding site for a ligand B, the association constant KA(1) characterizes the binding of B to empty A, KA(2) describes the binding of B to the AB complex, etc. In a microscopic model, the sites are treated independently; thus B binding to a distinct site I on A would be characterized by , B binding to site II on A would be described by , and this constant is insensitive to whether site I is occupied by B or not. Both types of models are valid and have apt uses. For example, a trimeric peptide with three identical sites for an antibody [29] is an excellent example of a system that is best analyzed with a macroscopic model; the binding sites are identical, so building distinctions between into the model is artificial. However, one could imagine a three-domain protein with three unique binding sites for the same ligand. Such a system would best be analyzed using a microscopic model because the sites will very likely have distinct thermodynamic characteristics that the researcher will wish to determine. Although it is possible to interconvert microscopic and macroscopic association constants and enthalpies, these conversions are not straightforward, especially for the casual consumer of ITC data. Therefore, there is an impetus for the development of multisite microscopic binding models.
Given the analytic obstacles described above, a question naturally arises: does the limited information content in ITC data sets support the refinement of the several parameters needed to describe the microscopic thermodynamics of multiple-site binding systems? As a first effort in answering this question, a series of isotherms from an experimental system wherein a single protein has two independent binding sites for a partner was examined. In this system, the association constants and association enthalpies for the two binding sites were very different, resulting in feature-rich isotherms. Models and statistical tools available in the freeware analysis software SEDPHAT [19] were used to estimate fitting parameters and explore their errors. These analyses showed that, while the desired parameters may usually be reliably obtained from such data, some conditions may be encountered that limit their usefulness. Next, ITC data were simulated under a variety of conditions for two- and three-site microscopic binding models. Statistical analyses of these simulated data, coupled with the results from the real two-site data, suggest some general principles and caveats for the analysis of multi-site binding in ITC.
2. Methods
2.1 Protein preparation
Iron-free human lactoferrin (hLF) and Treponema pallidum Tp34 protein were prepared as previously described, as were mutants of Tp34 [26,32]. The proteins were dialyzed in the same vessel against ITC buffer, comprising 20 mM sodium phosphate pH 7.5, 100 mM NaCl, and 2 mM β-octylglucopyranoside. Proteins were stored at 4° C until needed for experimentation. The experimentally derived extinction coefficients [26] for the two proteins were used in conjunction with spectrophotometry to establish their respective concentrations.
2.2 Isothermal titration calorimetry
Titrations were carried out in a VP-ITC calorimeter (Malvern Instruments, Malvern, UK). A typical titration consisted of 32 8-μL injections of wild-type or mutant Tp34 (408 – 455 μM) into a stirred reaction cell of about 1.4 mL containing hLF (18.0 – 18.5 μM). The reference power was 10 μcal/s, and the stirring rate was 307 rpm. All titrations were performed in triplicate with identical concentrations and injection schedules.
2.3 Analytical ultracentrifugation
Before preparing the samples, they were dialyzed against ITC buffer (Section 2.1). To confirm the stoichiometry of the association between hLF and the H155A variant of Tp34 (H155A) [33,34], hLF alone (1.6 μM), H155A alone (16 μM), and a mixture of 16 μM H155A and 1.6 μM hLF were prepared. All preparations were incubated overnight at 4°C prior to the experiment. The experiments were carried out in a ProteomeLab XL-I analytical ultracentrifuge (Beckman-Coulter). The protein solutions (390 μL) were individually introduced into the sample chambers of two-sector, charcoal-filled Epon centerpieces that had been sandwiched between sapphire windows and placed in aluminum housings. An identical volume of ITC buffer was placed in the reference sectors, and the housings were fitted into an An50Ti rotor. The samples and rotor were then incubated in the instrument at the experimental temperature (20° C) for two hours before centrifugation at 50,000 rpm was commenced. The concentration profiles were monitored using absorbance optics tuned to 280 nm and interference optics. Centrifugation continued until all sedimenting species were apparently proximal to the centrifugal side of the sample sector.
3. Computation
3.1 Integration of thermograms
For empirically obtained ITC data, NITPIC version 1.1.0 [35,36] was used to integrate the thermograms. The data were serially integrated and placed (by NITPIC at the request of the user) into a single SEDPHAT configuration file for global analysis.
3.2 ITC data analysis
3.2.1 Parameter estimation for the hLF/Tp34 interaction
The integrated ITC data were analyzed using SEDPHAT version 12.01. The “A + B + B ↔ B + AB ↔ BA + B ↔ ABB with two non-symmetric sites, microscop K” model was used (A was defined as hLF and B was defined as Tp34 or one of its mutants). All three data sets for a respective hLF/Tp34 pair were imported into SEDPHAT and analyzed globally [19]. The microscopic association constants for the formation of the AB and BA complexes (the two binding sites on A are referred to as Site I and Site II, respectively, in the text; the equilibrium association constants are and , respectively) and heats of association for the formation of those complexes (ΔHI and ΔHII, respectively) were derived from the data. The refined parameters were , ΔHI, , (ΔHII/ΔHI) and fA, where the latter signifies the fraction of molecule A that is incompetent to bind to molecule B. No cooperativity was assumed. Also, a baseline heat was refined for each of the three data sets included in the global analysis (i.e. subtractions of control titrations of Tp34 into buffer were not performed or subtracted). Because NITPIC provides error estimates for all integrated data points, the SEDPHAT option to use these as weights in the fitting sessions was activated. Switching between the Simplex and Marquardt-Levenberg optimization routines was necessary to achieve the convergence of the parameter set. From this converged set of parameters, the best-fit reduced chi-squared, , was calculated by the program:
| (Eq. 1) |
where Ntot is the total number of data points over all experiments, we is the weight given to experiment e, Ne is the number of data points in experiment e, is data point f in experiment e, is the corresponding fitted point for point f in experiment e, and is the error in data acquisition for data point f in experiment e. In the case of ITC data, is the error estimation of the integrated heats provided by NITPIC. NITPIC provides the we terms based on the estimated noise in the integrated heats.
3.2.2 Error Intervals
To obtain 68.3% error intervals for a parameter, a strategy outlined by Bevington & Robinson [37] and Johnson [38] and implemented in SEDPHAT was used. The 68.3% error level was preferred in this study because it is similar to the “1-σ level” that is often quoted for parameter errors in biologically oriented reports. Briefly, (Section 3.2.1) was obtained and used to calculate , the critical chi-squared:
| (Eq. 2) |
where ν1 (the first degree of freedom) is the number of optimized parameters, ν2 (the second degree of freedom) is the number of data points minus the number of parameters, and the F factor is the upper quantile of the Fisher F distribution with the level of significance, first degree of freedom, and second degree of freedom as indicated in the parentheses [38]. When prompted after a fitting session, SEDPHAT automatically and systematically varies the value of the parameter of interest (Π). Π is set and held at a non-optimal value (e.g., a small decrement lower than the original), and the other fitted parameters are allowed to refine to new optima. This process is iterated until the test chi-squared that results from these new fitting sessions exceeds , at which point the lower end of the 68.3% error interval has been reached and is recorded as ΠL. The parameter is then returned to its optimum and varied in increments until is again reached; ΠU is recorded. Therefore (ΠL, ΠU) is the rigorously determined 68.3% error interval for Π. Thus, the error surface around the best solution is systematically sampled and evaluated. This one-dimensional view of the surface is called an “error surface projection” [35,39]. No special computations are required of the user to utilize this strategy; it is fully implemented in this version of SEDPHAT, and it usually only takes seconds to report an error interval for globally analyzed ITC data.
To provide a basis for comparison among the error intervals for different parameters, a “normalized parameter span” (EN) is here defined:
| (Eq. 3) |
where Πb is the optimized (“best”) value of parameter Π. The calculation of such spans has been deemed useful in the context of ITC data analysis [40]. It should be noted that, for the parameter Kd, SEDPHAT and other fitting approaches (e.g. [41]) refine the log(Kd). This approach has numerous advantages, such as strictly prohibiting negative Kd values. Examination of log(Kd) instead of Kd would result in much smaller values for EN; however, ultimately, the experimenter will desire to know how well Kd is determined. Therefore, the convention of determining EN for Kd as in Eq. 3 has been adopted in this paper.
3.3 AUC Multisignal SV analysis
The multisignal SV analytic strategy [33,34] was used to examine the stoichiometry of cosedimenting H155A and hLF. The analysis proceeded as outlined elsewhere [33]. In brief, the method usually requires three SV experiments monitored using at least 2 signals: (1) component A (hLF in this case) alone, (2) component B (H155A) alone, and (3) a mixture of the two. In the third experiment, one of the proteins (usually the smaller one; H155A in this case) should be included at a large molar excess over the other. This expedient forces all of the minority component into complexes by mass action, a prerequisite for the analysis. For experiment 1, the extinction information for components A determined by global analysis of the two signals; a known signal increment for one of the signals is inputted, and the increment for the other signal is refined. This procedure is repeated for component B (experiment 2). After these analyses, the Dnorm, which is a measure of spectral distinguishability [34], can be rigorously calculated. In this case Dnorm was 0.01, just above the nominal level of 0.065 [34]. The refined extinction information was input into a global analysis of a mixture of the two components, yielding component ck(s) distributions. The global analysis monitored sedimentation using two signals: absorbance at 280 nm and laser interferometry. Although the analysis converged on a good result as judged by the r.m.s.d.'s of the fits and the lack of systematicity in the residuals (not shown), integration of the ck(s) distributions, which should have yielded the known input concentrations of the components, instead revealed unacceptably high (ca. 10%) differences from the known input values, indicating a mass-defect error [34]. A mass-conservation constraint [42] was therefore introduced into the analysis, allowing at a maximum a 5% mass defect in either of the components.
Model testing in this experiment was performed as suggested before [33,43]. In these cases, a different formula than Eq. 2 was used to determine :
| (Eq. 4) |
with
| (Eq. 5) |
and
| (Eq. 6) |
where N tot is the total number of data points, and p is the total number of refined parameters. The confidence level of can be varied by changing the probability value in the Fisher term. For example, if the desired confidence was 90%, the corresponding value in the Fisher term would be changed to 0.1. The different equations used to determine (i.e. Eqs. 2 & 4) reflect differing goals; Eq. 2 is appropriate for exploring the error surface [38], but Eq. 4 has been deemed appropriate for discriminating the difference between models [43].
3.4 Simulation
3.4.1 ITC data simulation
Where possible, SEDPHAT's experimental simulation functions were used to generate simulated ITC data. These functions are described elsewhere in this issue [44]. All ITC data sets derived from SEDPHAT were generated in triplicate. The replicates had unique sets of random noise, but had the same concentrations and injection schedules. For multiple-concentration experiments (Section 4.1.6), the noise was varied according to the concentration of material the cell. Experience has shown that isotherm noise grows larger as the concentration of the material in the cell decreases. To mimic this situation, the isotherm describing the highest cell-content concentration (ch) was assigned a noise level (δh) of 0.1 kcal/mol, and the lower concentrations (cm and cl, respectively) were assigned noise at levels that scaled according to:
| (Eq. 7) |
where n stands in for m or l as needed. The three cell-content concentrations simulated in this study were 16 μM, 6 μM, and 1 μM.
SEDPHAT, nor any other software to the author's knowledge, however, does not have a model that defines the microscopic association constants for a molecule A containing three unique binding sites for a partner B. Therefore, an algorithm was written in Python v. 2.7.3 to obtain the concentrations of all possible components under a given pair of total concentrations of A (Atot) and B (Btot) and known microscopic association constants. Because each of the three binding sites on A is distinct, a nomenclature convention was adopted to distinguish them. Trivially, free A and free B were denoted as “A” and “B”, respectively. Each site on A was assigned a corresponding roman numeral (i.e. I, II, and III). Thus, the AB complex whose B component binds at site I on A was defined as ABI, etc. There are therefore nine possible components of this system: A, B, ABI, ABII, ABIII, ABIBII, ABIBIII, ABIIBIII, and ABIBIIBIII. Because dissociation constants were found to be more numerically stable, they were used in the calculations:
| (Eq. 8) |
| (Eq. 9) |
and
| (Eq. 10) |
where the italicized names of the complexes stand for their respective molar concentrations. The algorithm takes a numerical approach to finding the concentrations; it frames the problem of finding the nine concentrations as a least squares problem. The input to the function that is minimized is the set of concentration unknowns, and the output is the calculated dissociation constants. The minimization targets are the dissociation constants, and beginning guesses of the concentrations must be supplied. Appropriate concentration constraints are applied within the algorithm. This method works well for most concentration domains. However, in concentration ranges featuring significant depletion of one or more of the complexes, it becomes unstable, i.e. it converges to incorrectly low concentrations of the free constituents (A and B) and is extremely susceptible to small changes in the beginning guesses. To counter this problem, an evolutionary algorithm was employed. A set of 54 guesses is generated; four are known to produce good solutions in many cases, and the other fifty are randomly seeded within possible concentration space. The algorithm evaluates results given the guesses and scores them. The scores are derived from the KD residuals (termed “R”), which are based on the knowledge that, for the “global” equilibria expressed in Eqs. 8-10, there are sub-equilibria that must be fulfilled:
| (Eq. 11) |
| (Eq. 12) |
| (Eq. 13) |
where the lowercase letters represent the values of the respective component concentrations returned by the algorithm. One expects the R's to be vanishingly small in a correct solution; the success threshold was set such that all three R's should be less than 10−5 nM. This value was arrived at empirically; it tended to provide good, quick results while maintaining an acceptable level of accuracy. If the success condition is met, the algorithm exits and reports the results. If not, then the score (the total score S is the sum of the three R values) associated with the respective set of starting guesses are recorded. If no successful result was found after examining all 54 initial guess, the scores are rank-ordered, and the ten best are allowed to spawn five new guesses that are related to the parent guesses but feature small, random perturbations. One of the five guesses is “mutated” by circularly permuting the new guesses. This new generation is then re-evaluated as above. A maximum of 50 generations is allowed; if no solution is found, the algorithm returns spurious values. Because the cases shown below were chosen for well-behaved concentration domains, the correct solution is usually found in the first generation, and only rarely takes more than 10 generations to find. Future efforts will focus on improving the performance of the algorithm.
Once the concentrations of all components have been derived for a titration given a set of microscopic dissociation constants, the isotherm was generated. To accomplish this, the total heat of solution after a given injection s is:
| (Eq. 14) |
where V0 is the volume of the calorimeter's sample cell, and, when all indices are considered, the possible complex ABjB0 is meant to indicate the singly occupied ABj complex. Thus the heat change measured for this injection was
| (Eq. 15) |
Because the data were simulated as if generated in a VP-ITC calorimeter, appropriate concentration corrections for finite cell volume and displaced volume were applied as described elsewhere [19,31]. Finally, ITC data are traditionally normalized by the molar amount of injectant, and thus the ordinate of a standard ITC isotherm is termed q(s) = ΔQ(s)/z, where z is the molar amount of injectant. All data sets simulated using this method had 32 injections of 8 μL each. For single-concentration simulations, molecule A was always in the cell, and its concentration was 70 μM. The concentration of molecule B in the syringe was always 1.8 mM. Realistic noise was applied to the data by adding random samples of a normal distribution scaled by the desired noise level, 0.1 kcal/mol, to the generated heats of injection. For multiple-concentration simulations (see Section 4.2), the concentration pairs in the cell/syringe were 10/300 μM, 70/1,800 μM, and 190/4,500 μM. Noise was scaled according to cell concentration as described for two-site simulations (see Eq. 7, this Section).
3.4.2 Analysis and error intervals of simulated two-site data
The global analysis of the triplicate SEDPHAT-generated two-site ITC data was performed as in Section 3.2.1, but all data points were given an equal weight in the fitting sessions. The procedure to obtain error intervals from these data was as described in Section 3.2.2.
3.4.4 Fitting the three-site simulated data
After generating noisy data with a given set of parameters, the data were fitted by using a Marquardt-Levenberg least-squares algorithm to optimize the parameters KI, KII, KIII, ΔHI, ΔHII, and ΔHIII. All data points were weighted uniformly. The starting values of the parameters were always the simulated ones. The algorithm described in Section 3.4.1 was used by the Marquardt-Levenberg method to generate test isotherms with the test parameters to compare against the simulated data. This method always converged on an isotherm having a smaller rmsd than the starting isotherm (not shown).
3.4.5 Error intervals from the three-site simulated data
Error intervals for the parameters estimated from the optimized parameters obtained in Section 3.4.4 were calculated using a manual procedure similar to that outlined in Section 3.2.2. However, instead of , the sum of squared residuals (SSR) was used, where, given n injections,
| (Eq. 16) |
with the subscripts “o” and “f” representing the observed (simulated) and fitted data points, respectively. Thus the SSR for best-fit isotherm was termed SSRb, and the critical value for SSR was SSRc. The factor used to determine SSRc from SSRb is the quantity in brackets on the right-hand side of Eq. 1. The parameter of interest was fixed at a non-optimal value while all other parameters were allowed to refine. If the resulting test sum of squared residuals (SSRt) exceeded SSRc, then the limit was said to have been reached. If not, iterative parametric exploration was continued until SSRt was greater than SSRc.
3.5 Figure generation
Structure illustrations were generated in PyMol version 1.5.0.5 (Shrödinger LLC). ITC and SV illustrations were made using GUSSI version 1.0.8e (http://biophysics.swmed.edu/MBR/software.html).
4. Results
4.1 Two-site binding models
4.1.1 Biphasic wild-type Tp34:hLF data
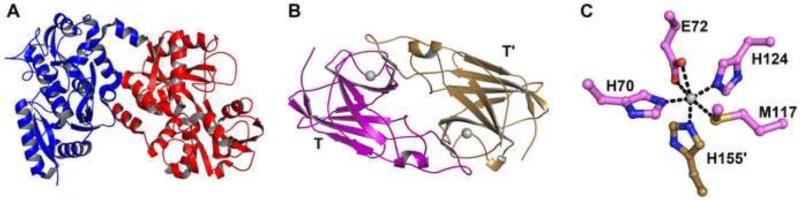
Both calorimetric [26] and hydrodynamic means [26,32,33] have demonstrated that the Treponema pallidum protein Tp34 interacts with the human mucosal iron-sequestering protein hLF in a 2:1 ratio. In determining the proper model to employ in the analyses of Tp34/hLF data, it is instructive to examine the respective crystal structures of the proteins (a co-crystal structure of the proteins has not been determined). Two similar but non-identical metal-binding lobes comprise the 76-kDa hLF protein [45]; each lobe binds to a single iron ion and has a mixed α/β structure resembling a bacterial periplasmic binding protein (Fig. 1A). The fold of Tp34 (Fig. 1B; its molar mass is ca. 20 kDa), which is far smaller than hLF, is dominated by an eight-stranded β-sandwich that is similar to the classic Ig-fold [26]. Both hLF and Tp34 are monomeric in solution in the absence of metal ions, but the presence of divalent cations of the transition metals induces the dimerization of Tp34 [26,32]. Because the current studies were performed in the absence of any added metal ions, it was assumed that only the monomeric forms of the proteins were present. Thus, the existence of two non-identical lobes on hLF implies that a binding model with two physically unique (or, in the parlance of SEDPHAT, “asymmetric”) binding sites for Tp34, with each having its own microscopic association constant, is the most appropriate choice. For the discussion below, the two binding sites are termed “Site I” and “Site II”, with all estimated parameters bearing the respective Roman numeral.
Figure 1. Structural aspects of hLF and Tp34.
(A) The crystal structure of hLF. Shown is a ribbons diagram of PDB deposition 1LFG [45]. The N-terminal lobe of the protein is colored blue, and the C-terminal lobe is colored red. (B) The Tp34 dimer. The proteinaceous asymmetric unit contents of PDB deposition 3PJN are shown, along with the two metal ions (gray spheres) commonly found at the dimer interface of Tp34. One monomer (T) is colored purple, the other (T′) tan. (C) A close-up view of the main metal-ion binding site in wild-type Tp34. In this site, one of the monomers (T) provides four amino-acid side chains to ligate the metal ion; the other monomer (T′) provides the fifth and final side chain (H155′). The carbon atoms are colored according to the origin of their respective monomer as defined in part B. Oxygen atoms are colored red, nitrogen atoms are blue, and the sulfur atom is colored yellow. The lone Zn2+ cation is colored gray. Black dashed lines indicate inner-sphere contacts between protein atoms and the cation.
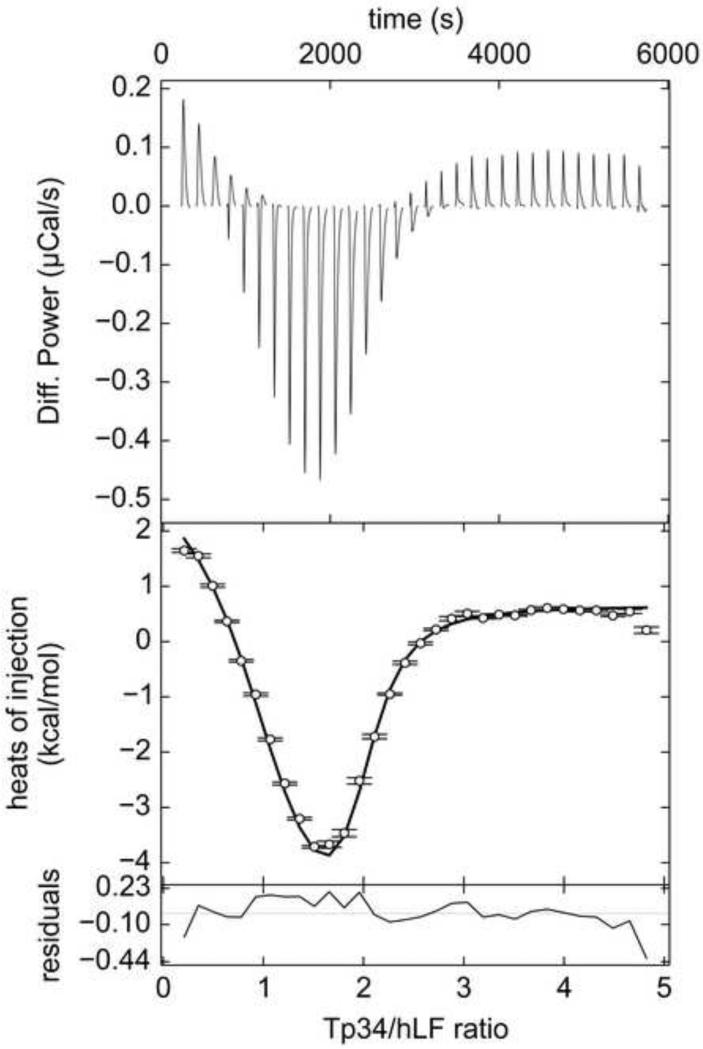
As shown in Figs. 2-4, the isotherms resulting from titrating Tp34 into hLF exhibit a visually obvious biphasic structure. The initial integrated heats of injection show a trend toward increasingly negative enthalpy, while later data trend positively until saturation is reached. This biphasic appearance is consistent with earlier calorimetric work with this system indicating two-site binding [26]. The asymmetric, two-binding-site model was globally applied to these isotherms (data were acquired in triplicate; see Section 2.2) with excellent results. The model clearly accounts for the biphasic structure of the data (Fig. 2; Table 1). Site I features ca. sevenfold tighter binding than Site II, and the two sites have very different enthalpies of binding. The refinement of a single, global parameter revealed that about 2.5% of the hLF was incompetent to bind to Tp34.
Figure 2. ITC data from wild-type Tp34 and hLF.
The top panel is the SVD-reconstructed isotherm from NITPIC [35]. The middle panel features the data (white circles) with error bars provided by NITPIC. The black line in this panel represents the fit with the best parameters from SEDPHAT. The bottom panel has the residuals represented as a black line. Here, 455 μM Tp34 was titrated into 18.5 μM hLF.
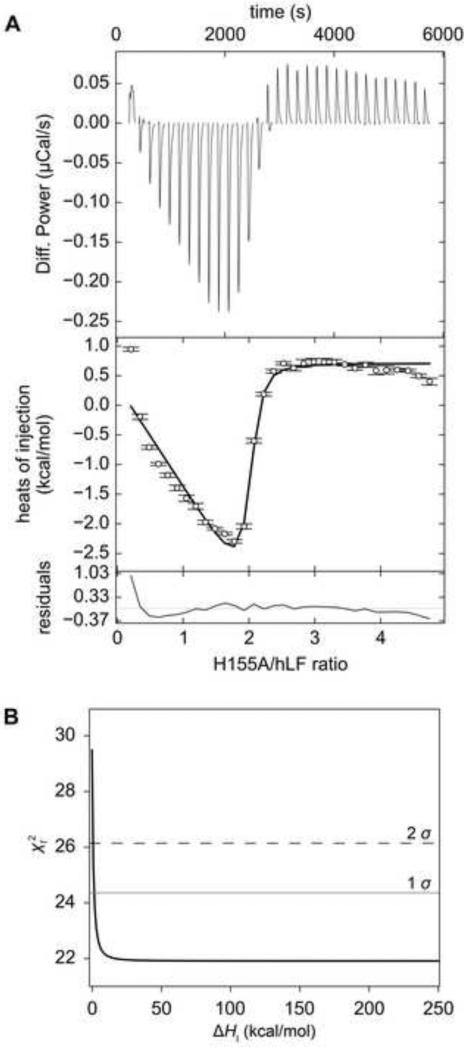
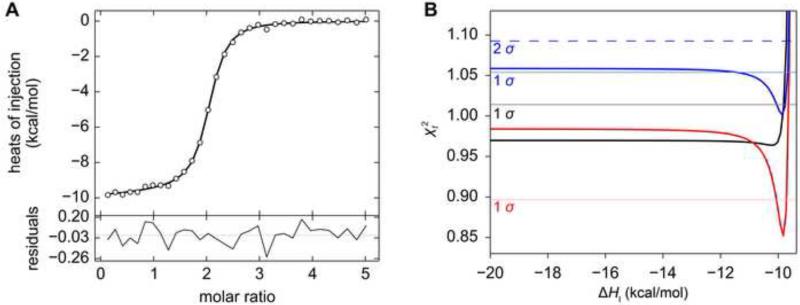
Figure 4. ITC data and the error surface of the fit from H155A.
(A) ITC data. See Fig. 2 for an explanation of line shades and symbols. (B) One-dimensional error-surface projection for the H155A ITC data. The value obtained by holding ΔHI at various values (the x-coordinate) is shown on the y-coordinate. The χ2 levels defining the 1 σ (68.3% confidence interval) and 2 σ (95% confidence interval) levels are shown as a gray or black dashed line, respectively. In this experiment, 445 μM Tp34 was titrated into 18.4 μM hLF.
Table 1.
Results of Tp34 and its mutants binding to hLF
| Tp34 Protein | Parameter | Best Estimate | 68.3% Error Interval | EN |
|---|---|---|---|---|
| WT | 6.99 | (6.82, 7.15) | ND | |
| ΔHI (kcal/mol) | 3.0 | (2.2, 4.4) | 0.73 | |
| −0.83 | (−0.98, −0.65) | ND | ||
| ΔHII/ΔHI | −2.8 | (−3.5, −2.2) | ND | |
| 100 | (70, 150) | 0.80 | ||
| 700 | (610, 770) | 0.23 | ||
| ΔHII (kcal/mol) | −8.3 | (−9.6, −7.6) | 0.24 | |
| E72A | 6.5 | (6.2, 6.7) | ND | |
| ΔHI (kcal/mol) | −1.6 | (−2.1, −0.3) | 1.12 | |
| −1.0 | (−1.3, −0.6) | ND | ||
| ΔHII/ΔHI | 4 | (3, 22) | ND | |
| 340 | (180, 650) | 1.38 | ||
| 3,300 | (2,300, 4,100) | 0.54 | ||
| ΔHII (kcal/mol) | −6.5 | (−7.5, −5.9) | 0.25 | |
| H155A unconstrained | 7.20 | (6.9, 7.7) | ND | |
| ΔHI (kcal/mol) | 199 | ND | ND | |
| −0.007 | (0.4, U)b | ND | ||
| ΔHII/ΔHI | −1.02 | ND | ND | |
| 60 | (20, 140) | 2.0 | ||
| 60 | (30, U) | ND | ||
| ΔHII (kcal/mol) | 203 | ND | ND | |
| H155A | 7.3 | (6.9, 7.7) | ND | |
| ΔHI (kcal/mol) | 10.0a | N/A | N/A | |
| −0.1 | (−0.4, −0.1) | ND | ||
| ΔHII/ΔHI | −1.4 | N/A | ND | |
| 50 | (20, 120) | 2.0 | ||
| 70 | (40, 90) | 0.71 | ||
| ΔHII (kcal/mol) | −14.0a | N/A | N/A | |
| H155A high-c/low-cc | 7.2 | (7.0, 7.5) | ND | |
| ΔHI (kcal/mol) | 198 | ND | ND | |
| −0.007 | (−0.3, 0.3) | ND | ||
| ΔHII/ΔHI | −1.0 | ND | ND | |
| 60 | (40, 100) | 1.0 | ||
| 60 | (40, 80) | 0.67 | ||
| ΔHII (kcal/mol) | −202 | ND | ND |
values were obtained while placing a constraint on ΔHI
A “U” means that the limit could not be found
The two c-values were 370 (empirical) and 70 (simulated), based on of the constrained fit.
ND—Not determined
N/A—Not applicable
Having established that the model can describe the data well, the next question to be addressed is: how well do the data specify the estimated parameters? In other words, what are the error bars? The method outlined in Section 3.2.2 was used to determine 68.3% confidence intervals for four of the global parameters: , ΔH, , and ΔHII / ΔHI. The derived KA values were converted to KD, and EN (Section 3.2.2) values were obtained from them, as they are more intuitive to interpret. They are shown in Table 1. was reasonably well specified, with an error interval of (70, 150) nM (EN = 0.80). The ΔHI error interval was similar in its relative magnitude: ((2.2, 4.4) kcal/mol, EN = 0.73). Although the EN is comparable for these two parameters, ΔH is usually better defined in ITC data. For comparison, the interval for Tp34 H70A binding to hLF (an interaction that exhibits only one binding site but similar magnitudes of integrated heats) yields an EN of 0.13 [36]. In retrospect, the lack of precision could have been guessed, given that the heat of binding at Site II obscured the heat of association at Site I. The interval for is well specified by the data ((610, 770) nM; EN = 0.23), and ΔHII has a similar interval to that of ΔHI, but an ΔN of 0.24.
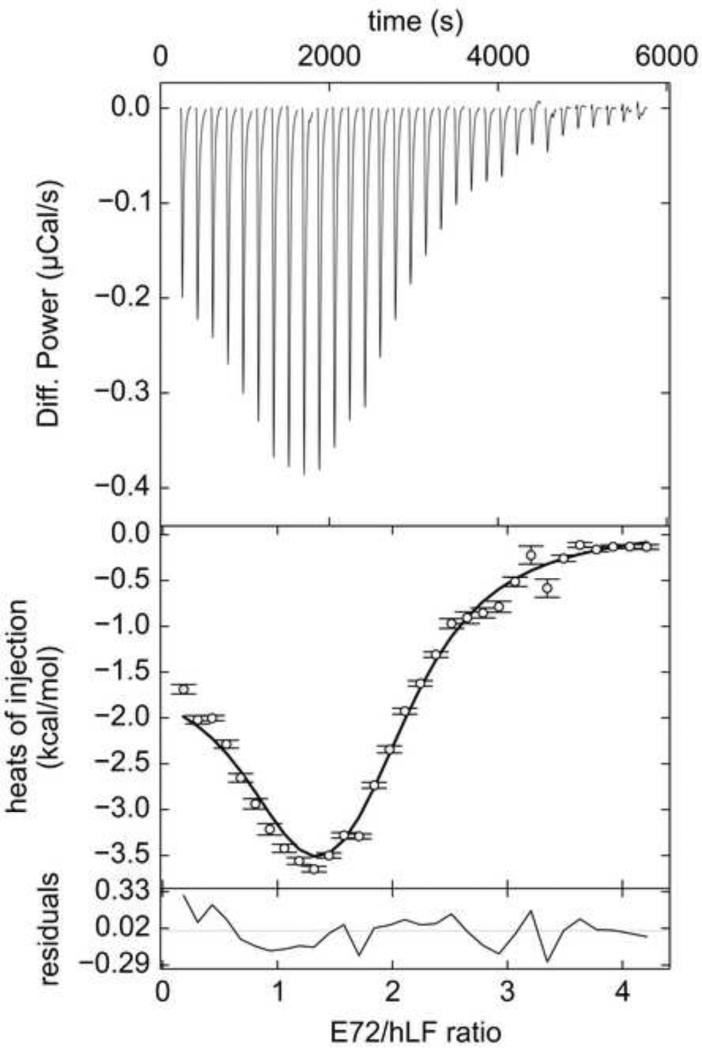
4.1.2 Biphasic data from the Tp34 mutant E72A binding to hLF
From the crystal structures of Tp34, its dimerization interface is known [26,32]. The residues H70, E72, M117, H124, and H155 all participate in a symmetry-related pair of metal-binding sites at this interface (Fig. 1C). Although no metal ion was included in the current ITC assays, it was of interest to study if mutations to these residues affected the hLF/Tp34 interaction. The convention is here adopted of referring to the mutant Tp34 by its amino-acid mutation designation, e.g. the Tp34 protein bearing a mutation of histidine 155 to alanine is designated “H155A”. “WT” is hereafter used to refer to the wild-type Tp34 protein.
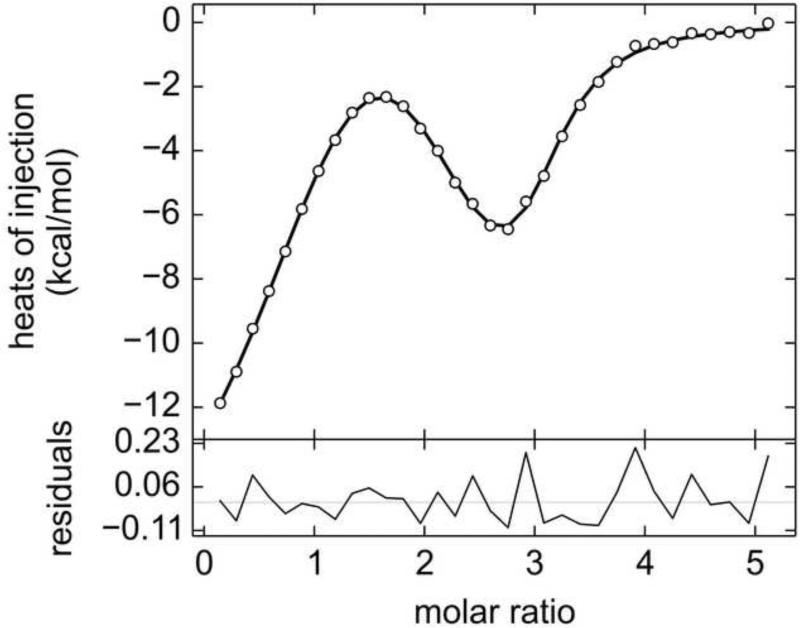
The first mutant studied was E72A. Tp34 bearing this mutation had an impaired ability to dimerize in the presence of divalent transition metal ions [32]. Clearly, the mutation of E72 does not eliminate the binding of Tp34 to hLF: titrating the mutant protein into hLF resulted in the characteristic biphasic thermograms (Fig. 3). Again, the asymmetric, two-site binding model describes the data well (Fig. 3, Table 1). However, the discriminatory power of the data appears to be diminished, inasmuch as the EN values for all refined parameters were higher (Table 1). This degradation of discrimination occurs despite the fact that the for the fit to the E72A data is better than that for the WT data (7.7 vs. 11.5). Therefore, even though the appearances of the E72A data sets are similar to those obtained from WT, they are inherently less informative.
Figure 3. ITC data from E72A and hLF.
Line shades and symbols are the same as in Fig. 2. In this experiment, 408 μM Tp34 was titrated into 18.0 μM hLF.
4.1.3 Biphasic H155A:hLF data
The final mutation of Tp34 considered in this study is H155A. H155 occupies a unique position in the metal-coordinating sites of a Tp34 dimer (Fig. 1C). If the two monomers in the dimer are designated “T” and “T′” (Fig. 1B), then at a given metal-binding site, all of the metal-coordinating residues are supplied by T, except for H155A, which is provided by T′ [26]. Like E72A, H155A has a severely impaired ability to dimerize in the presence of metal ions [32].
Similar to WT and E72A, the titration of H155A into hLF provides a robust, biphasic heat signal (Fig. 4A). Close scrutiny of the isotherms’ shapes demonstrates that the second phase is marked by an abrupt return of the integrated heats to their baseline values. The first attempts to fit these data to the two-site, asymmetric binding model succeeded, but resulted in nonsensical parameters for ΔHI and ΔHII (199 and -203 kcal/mol). The error limits for most fitted parameters could not be rationally determined (Table 1). For example, the error-surface projection for ΔHI was essentially flat except near to a value of 0, where it apparently approaches a singularity (Fig. 4B). Thus, for almost any fixed value of ΔHI, a set of parameters can be obtained that allow a fit of the data having a similar to that of the supposedly best fit. It was therefore clear that the ΔH values are not uniquely specified in these latter data sets, despite their evident biphasic nature. A macroscopic two-site model was also applied to these data to determine if they could be analyzed rationally. However, similar pathologies in determining parameters and error estimates were observed (not shown).
To counter the difficulty with the ill-defined values of ΔH, constraints were applied within SEDPHAT. Specifically, ΔHI was not allowed to vary outside the range of 0.0 to +10.0 kcal/mol. The lower limit was designed to allow the program to avoid the singularity, while the upper limit seemed reasonable inasmuch as it restricts ΔHI from increasing more than 3.3-fold from the WT value (Table 1). Because of the constraints, an error interval for ΔHI was not determined. Because ΔHII is determined as the ratio (ΔHII / ΔHI), the former is constrained defacto, and therefore its error interval was also not determined.
With the constraint in place, error intervals for the refined KA values could be determined (Table 1). was not as well specified as . A comparable EN value for was obtained even without the constraint in place (Table 1).
What information can therefore be gleaned from the H155A data? The results demonstrate that, if the constraint is trusted, the two KA values have been determined, albeit imprecisely. However, essentially no information is available on the ΔHI values, except for the qualitative conclusion that they must be nearly equal in magnitude and opposite in sign.
4.1.4 Can additional titrations save the H155A data?
The nonexistent resolution for ΔH in the H155A data sets raises the question of whether anything regarding the ITC experimental configuration could have been altered to avoid or ameliorate the difficulties. For example, it is possible that reversing the titration configuration, i.e. titrating hLF into H155A, could have provided more information on ΔHI and ΔHII in a global analysis with the already extant data.
To address this issue, ITC data were simulated using a utility in SEDPHAT [44]. The data were generated using parameters identical to those refined for H155A, and each data set was given a similar noise level. For these three data sets, the simulations were performed as if 93-103 μM of hLF were titrated into approximately 15 μM H155A. The resulting isotherms also display a distinct, biphasic appearance (not shown), but the region surrounding the second inflection point is less steep than in the empirically obtained titrations. However, despite the inclusion of 93 more data points and a roughly orthogonal view of the heat landscape of the interaction, the global analysis of the simulated data sets together with the empirical data sets offered no additional discrimination in the ΔH values. The phenomenon of parameters adjusting to allow an acceptable fit for almost any ΔHI value persisted.
Noting that the c value for the first binding site (i.e. ) is larger than recommended (> 40) [30], another promising approach to a deterministic refinement of the binding parameters might be to lower the concentration of hLF in the sample cell. Therefore, using the parameters of the constrained fit of H155A titrated into hLF, three data sets with c = 70 and with random, realistic noise were simulated and added to the global analysis of the high-c H155A ITC data. This strategy has the added benefit of exploring more than one c value in a global analysis, which has been shown to be beneficial [44,46]. Although this resulted in improvements in the EN values for the association constants (Table 1), the addition of the new, lower-c data could not resolve the ambiguity in the ΔH parameters. Notably, the improvement in the EN's appears to be entirely from adding 96 new data points, not from the addition of inherently more informative data (not shown). Evaluating the lower-c data alone does not ameliorate the poor behavior of the fitted parameters.
4.1.5 Hydrodynamic confirmation of the 2:1 binding model for H155A
Given the difficulties fitting the H155A data, a question arose: is the model of 2 H155A molecules binding to 1 hLF correct? Other models are conceptually possible. For example, a third, low-enthalpy binding site could be present. Alternatively, H155A binding could be coupled with the dimerization or multimerization of hLF.
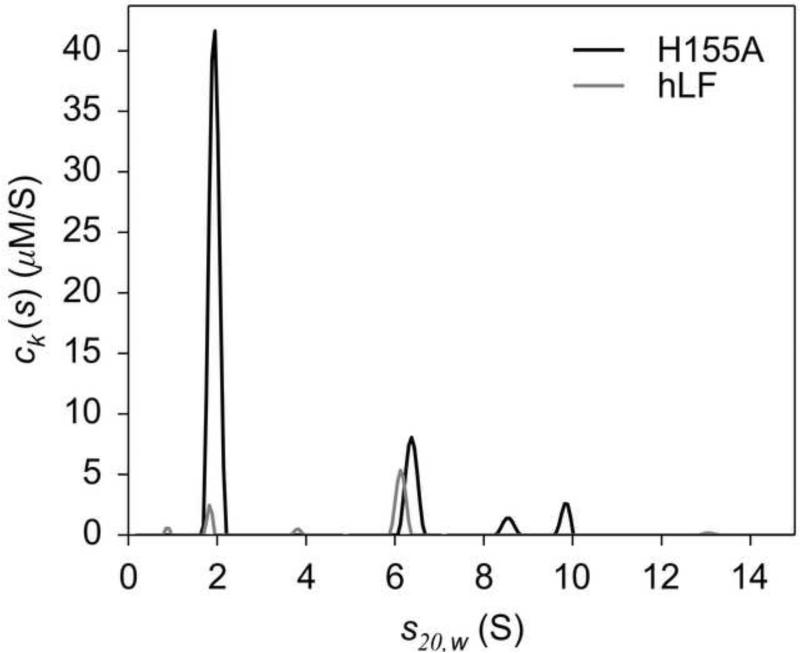
Hydrodynamic (i.e. AUC) experiments were conducted to answer this question. Specifically, the correctness of the model was addressed using mass-conservation multisignal sedimentation velocity (MC-MSSV) [42]. This method can reveal the stoichiometry of a cosedimenting complex. Amidst a ten-fold molar excess of H155A, hLF was sedimented, and a H155A:hLF complex peak was observed at an experimental s-value of 6.2 S in a c(s) distribution (Fig. 5). Unconstrained spectral decomposition of this peak demonstrated that both H155A and hLF were co-sedimenting at a molar ratio of 1.84:1. This result, coupled with the calculated molar mass of this species (128,000 Da) and the theoretical molar mass of a 2:1 complex of H155A and hLF (117,000 Da), suggested that the most probable stoichiometry of this complex is 2:1. Because of the spectral-discrimination difficulties encountered with these data (Section 3.3), a strategy was adopted to test this hypothesis. The best reduced χ2, (0.283582), was noted, and then two critical χ2 values were calculated (Section 3.3). They are called and , as they represent the reduced values that would define the 68% and 90% error intervals, respectively [33,43]. Having calculated these values (0.284353 and 0.285695, respectively), constraints on the molar ratio of the cosedimenting species at 6.2 S were put in place, and the resulting “test” χ2, , was monitored. With a 2:1 H155A to hLF ratio enforced, did not rise above . The model with this constraint in place was therefore statistically indistinguishable from the unconstrained model; i.e. the 2:1 constraint is entirely consistent with the SV data. However, when a 1:1 or 3:1 molar-ratio constraint was applied, , rose above (0.2881295 and 0.2859834, respectively), indicating that these latter models may be safely discarded. It was thus concluded that the 2:1 model is likely to be correct, and the inability to definitively parameterize the ITC data did not stem from an inappropriate model.
Figure 5. MC-MSSV results for the H155A:hLF interaction.
The ck(s) distributions for H155A and hLF are shown (shades are indicated by the legend). Integration of the peak at ~6.2 S results in [H155A] = 2.56 μM and [hLF] = 1.39 μM.
4.1.6 Simulated two-site uniphasic data
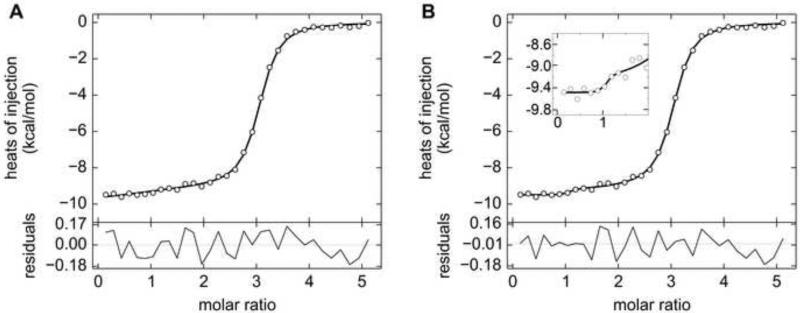
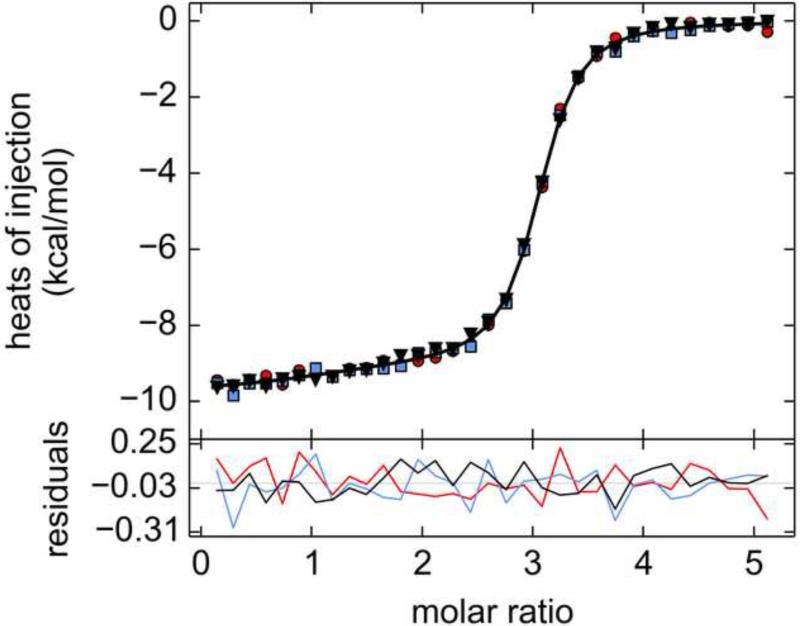
The mixed performance of the two-site models described in Sections 4.1.1 – 4.1.5, prompts the question of whether uniphasic ITC data could adequately guide the estimation of parameters using this microscopic-site model. Therefore, six uniphasic data sets were simulated using functions available in SEDPHAT [44]. All titrations were simulated as if they were acquired from triplicate (same concentrations, same injection schedules, different random noise) experiments in a VP-ITC calorimeter. The cell concentrations were between 15 and 18 μM. The same binding model (Section 3.2.1) was used as for the Tp34/hLF interaction. A realistic case was simulated in which the first binding site on molecule A had a four-fold stronger association than the second . The enthalpy of the site I was -10.0 kcal/mol, and the poorer binding at site II was entirely attributed to a less favorable enthalpy (ΔHII = -9.2 kcal/mol). As shown in Fig. 6A, these simulated data only have a single visually discernible transition at a molar ratio of 2:1 (injectant:cell contents). No heats of dilution were simulated or refined, and the same was true of incompetent fractions.
Figure 6. Simulated uniphasic two-site ITC data and related error-surface projections.
(A) Simulated ITC data (circles) and fit thereto (line). Residuals from the fitting session are shown as in Fig. 2. (B) One-dimensional error-surface projections. The overall presentation is similar to that described in Fig. 4B. Three error-surface projections from the simulated trials in Table 2 are shown. The black line and gray 1-σ limit are from Trial #1. The red line and pink limit are from Trial #4. The blue line, light blue 1-σ limit and blue (dashed) 2-σ limit are from Trial #6.
The performance of this model in estimating fit parameters was variable. On one hand, the fitting sessions arrived at reasonable estimates that were close to the simulated values (Table 2). However, in three out of the six trials (#1-#3), only one-sided error intervals for three out of the four refined parameters could be established. These results contrast sharply with those from the final three trials, wherein the parameters ΔHI, , and ΔHII are well-defined. Interestingly, the EN values of increased dramatically for these better-behaved trials (Table 2). Scrutiny of the parameters underlying the simulations reveals no strong correlations that explain these behaviors. The error surfaces for the parameter ΔHI are similarly shaped and asymmetric (Fig. 6B). Those with well-defined error 68.3% error intervals sometimes do not have boundaries that would circumscribe a 95% interval (Fig. 6B, blue trace). It appears that success in describing the error intervals in this case is dependent on favorable features in the experimental noise.
Table 2.
Two-site uniphasic simulations and resulting fitted parameters
| Parameters | Input values | Trial #1 | Trial #2 | Trial #3 | Trial #4 | Trial #5 | Trial #6 |
|---|---|---|---|---|---|---|---|
| 7.0 | 6.9 | 6.8 | 6.7 | 7.3 | 7.3 | 7.2 | |
| ΔHI (kcal/mol) | −10.0 | −10.2 (U)a | −10.2 (U) | −10.6 (U) | −9.7 (0.04) | −9.9 (0.06) | −9.9 (0.18) |
| −0.60206 | −0.4 | −0.4 | −0.2 | −0.9 | −0.9 | −0.8 | |
| ΔHII/ΔHI | 0.92 | 0.9 | 0.9 | 0.8 | 0.96 | 0.93 | 0.9 |
| 100 | 50 (1.46) | 140 (1.47) | 180 (1.12) | 50 (2.04) | 50 (2.16) | 60 (1.50) | |
| 400 | 330 (U) | 360 (U) | 320 (U) | 460 (0.22) | 420 (0.27) | 420 (.48) | |
| ΔHII (kcal/mol) | −9.2 | −9.0 (U) | −9.1 (U) | −8.6 (U) | −9.4 (0.04) | −8.8 (0.06) | −9.3 (0.19) |
numbers in parentheses are the respective EN values; U denotes that the error interval was unbounded
Another experimental strategy for such a system is, instead of globally analyzing exact replicates, to attempt the global analysis of three data sets obtained at three different cell concentrations [44,46]. Therefore, five sets of triplicate data sets were generated; within each replicate, three different concentrations of protein in the cell were allowed: approximately 1, 6, and 16 μM. The same general pattern was observed as in the uniform-concentration trials, in that some trials performed well, while others did not. In sum, rational limits on the ΔH parameters could not be found for 2 out of the 6 trials (Supplemental Table S1).
4.2 Simulated three-site ITC data
To examine more challenging systems, data from an asymmetric, three-site system were simulated (see Section 3.4.1). First, an isotherm that had easily discernible features in it was simulated. This test case comprised a molecule “A” that had three differing binding sites for the second molecule, “B”. Each binding site on A had a unique microscopic equilibrium dissociation constant (dissociation constants were more numerically stable than association constants; see Section 3.4.1) and a distinct ΔH (Table 3). With invariant B, these widely diverging parameters might seem unrealistic; however, there are instances in the literature of such strongly featured isotherms that have been fitted with three-site binding models [27,28]. Given the triphasic appearance of the isotherm, it was expected that fitting to this isotherm would yield well-defined parameter estimates. Realistic (0.1 kcal/mol) noise was included in this isotherm, and the isotherm was simulated as if it occurred in a VP-ITC calorimeter, with 32 8-μL injections of 1.8 mM B into 70 μM A in a 1.4 mL cell. On the other hand, some aspects of this simulation are not realistic; no incompetent fraction (nor “N” value) was simulated, and no attempt to refine this value was made. Also, no baseline offsets to compensate for heats of dilution were included or optimized. The simulation therefore represents a best-case scenario for these data, in that up to twelve parameters could have been refined, but only six (three KD's and three ΔH's) were applied.
Table 3.
Simulation parameters and fitting results for triphasic data
| Parameter | Simulated value | Refined value |
|---|---|---|
| 250 | 230 (0.44)a | |
| 1,000 | 900 (0.75) | |
| 4,000 | 4,000 (0.42) | |
| ΔHI (kcal/mol) | −20 | −20 (0.40) |
| ΔHII (kcal/mol) | 20 | 19 (0.48) |
| ΔHIII (kcal/mol) | −20 | −19 (0.58) |
Numbers in parentheses represent the respective EN value
As expected, the fitting of the parameters to this isotherm was well behaved. That is, the optimization session converged on parameters that resembled the input parameters (Table 3, Fig. 7). The next question to address, then, is how well to the data specify these parameters? The error intervals and EN values for this fit are acceptable, despite the fact that only 32 data points are available to drive the estimation of the six parameters. The quantity had the most variation in the error analysis, but all other parameters had EN values between 0.40 and 0.58.
Figure 7. Simulated triphasic three-site ITC data and fits.
Graphs and symbols are as described in legend to Fig. 6A. See Table 3 for parameters.
These encouraging results prompted a new simulation, one that should reflect a physically realistic but more computationally challenging situation. In this scenario, using the same three-site model with the same concentrations and injection schedule, the first binding site has a higher affinity than the other two, and the enthalpies are all negative and differ by a maximum of 1.5 kcal/mol (Table 4). The appearance of the isotherm is shown in Fig. 8A. It clearly has only one inflection point, and the singular feature that would lead an experimenter to suspect three binding sites is that saturation occurs near to a molar ratio of 3. This simulation is therefore the three-site equivalent of the uniphasic isotherms presented above (Section 4.1.6).
Table 4.
Input parameters and results of fitting for the uniphasic three-site model
| Parameters | Simulated | Trial #0a | Trial #1 | Trial #2 | Trial #3 | Trial #4 | Trial #5 |
|---|---|---|---|---|---|---|---|
| 250 | 1.3 | 37 | 130 | 110 | 770 | 230 | |
| 1,000 | 510 | 780 | 780 | 1,200 | 800 | 420 | |
| 1,100 | 1,800 | 1,500 | 1,300 | 1,200 | 860 | 1,800 | |
| ΔHI (kcal/mol) | −10.0 | −9.5 | −9.6 | −9.8 | −9.7 | −16.9 | −10.7 |
| ΔHII (kcal/mol) | −9.2 | −9.3 | −9.2 | −9.3 | −15.9 | −11.1 | −8.0 |
| ΔHIII (kcal/mol) | −8.5 | −8.8 | −8.8 | −8.6 | −2.2 | 0.4 | −9.1 |
this trial had only a single replicate. All others comprised three replicates.
Figure 8. Simulated uniphasic three-site ITC data with starting values and optimized values.
(A) Graphs and symbols are as described in the legend to Fig. 6A, except the line represents the results of the noiseless simulation, not the set of refined parameters (Table 4, “Simulated”). (B) Uniphasic ITC data after fitting. The graphs and symbols are as described in part A, except now the line represents the best-fit parameters (Table 4, Trial #0). The inset shows an expansion of the same graph near to a molar ratio of 1, where noise features were fitted by the optimization algorithm.
In this case, the optimization session did not yield realistic parameter estimates for the dissociation constants, despite the fact that the converged solution had a smaller r.m.s.d. than that of the isotherm yielded by the starting (exactly correct) guesses (see Trial #0 in Table 4). In particular, the dissociation constant of the first binding site refined to an estimate that was lower than the simulated value by a divisor of approximately 200. A close examination of the fit reveals the reason for this behavior. Although the data were simulated with random noise, there is a brief upward trend that occurs near to a molar ratio of 1. The fitting algorithm optimized the value of to fit this trait of the noise (Fig. 8B). In other isotherms using these parameters and random noise, the KD values in general were not well-specified by the data (not shown). As a result, no error intervals were attempted for this scenario.
Given the difficulties noted above, it was suspected that global analysis of multiple data sets with random noise might allow the parameter estimates to converge deterministically. The rationale behind this notion was that the fitting algorithm would be less apt to fit noise features that, by chance, had an artifactual trend at a critical position in the isotherm. Thus, the 32-injection data were simulated in triplicate, with unique, normally distributed noise added to each replicate, but using identical concentrations and titration schedules. This approach appeared promising, in that the refined estimated parameters gleaned from a global fitting session were not as far from the starting ones (see Table 4, Trial #1). Therefore, four more triplicate trials were generated and each set of three isotherms was separately fitted. Individual global fits to these triplicated data sets estimated KD's that were generally not close to the simulated values (Table 4; Fig. 9). It was therefore concluded that the information in these data do not warrant allowing all six parameters to refine simultaneously.
Figure 9. Simulated triplicate uniphasic three-site ITC data.
The red circles, blue squares, and black inverted triangles represent data from the three respective replicates used in this analysis. The black line represents the isotherm from the best globally optimized parameters. The data and the parameters are from Table 4, Trial #2. The residual lines in the lower graph are colored according to their respective replicate.
As with the two-site simulations (Section 4.1.6), the notion that the global analysis of three sets of multi-concentration could improve the behavior of the parameter refinement was tested. In this case, in-cell protein concentrations of 10, 70, and 190 μM were simulated and analyzed as above. The results are shown in Supplemental Table S2. As with the single-concentration data, the refinement of the parameters was generally ill-behaved.
The inability to rationally estimate parameters from these data suggested that constraints must be put in place. In an actual experimental setting, it is most likely that constraints could be set by determining the KD values of one or more of the binding sites on A. For example, perhaps A comprises three separable domains arranged in tandem; the experimenter could genetically separate them and express them individually, determining KD values from another method. These KD's could be set as fixed parameters in the global analysis discussed above, reducing the number of optimized parameters and perhaps allowing their definitive estimation.
To test this idea, one of the Trials above (#2) was selected for constrained fitting sessions. All possible combinations of fixing the KD's at their correct values were attempted. Most solutions did not converge on rational sets of parameters (Table 5), i.e. at least one of the parameters was far from the simulated value. This was even true in the case wherein all KD's were held constant at their known values, i.e. the ΔH values did not closely resemble the known, simulated values. The only set of constraints that yielded acceptable parameter estimates was that disallowing only the refinement of . However, attempts to calculate error intervals for this case did not yield intelligible bounds on the remaining estimated parameters (not shown).
Table 5.
Results of fixing parameters in the uniphasic three-site system
| Parameters | Subtrial 1 | Subtrial 2 | Subtrial #3 | Subtrial #4 | Subtrial #5 | Subtrial #6 |
|---|---|---|---|---|---|---|
| 250* | 130 | 130 | 250* | 120 | 250* | |
| 790 | 1,000* | 980 | 1,000* | 1,000* | 1,000* | |
| 1,200 | 1,100 | 1,100* | 1,000 | 1,100* | 1,100* | |
| ΔHI (kcal/mol) | −10.0 | −9.8 | −9.8 | −10.0 | −9.7 | −10.0 |
| ΔHII (kcal/mol) | −9.3 | −12.0 | −11.2 | −1,100 | −11.6 | −10.8 |
| ΔHIII (kcal/mol) | −8.3 | −5.9 | −6.7 | 1,100 | −6.4 | −6.9 |
Value was fixed in the analysis.
As a final attempt to obtain reasonable limits on the parameters for this three-site system, another scenario was simulated (Subtrial 7 of Table 5). In this case, it was assumed that and could be modeled as having fixed multiplicative relationships to , which was fitted:
| (Eq. 17) |
Likewise, the following fixed relationships were established between the fitted parameter ΔHI and the other ΔH's:
| (Eq. 18) |
This scenario is similar to the approach that was taken by Gustchina et al. in a recent study on a trimeric peptide that can bind three antibody molecules [29]: they globally analyzed uniphasic ITC data, along with AUC and fluorescence spectroscopy data, albeit with a macroscopic model. In that study, the latter two methods provided most of the information regarding the association constants. Also, only one K was refined (the others were assumed to be microscopically identical to the first), and the three ΔH's were constrained such that only one was refined, with the other two being constrained to be identical to the first. This final case described by Eqs. 17 & 18 behaved excellently; EN was 0.1 for , and 0.006 for ΔHI (Table 5).
5. Discussion
It has long been established that excellent estimates of the thermodynamic parameters from simple 1:1 biomolecular interactions can be obtained by ITC [1,16,47]. The work presented herein aimed to explore how well ITC data specify parameters from bimolecular interactions featuring more than 1 binding site on one of the components. Cautions regarding the overinterpretation of multisite ITC data have been issued before [8,20,27,29,48], but this work specifically focuses on microscopic binding models using both real and simulated data. While the scope of this report is not comprehensive, the results point to some important conclusions for researchers and consumers of ITC data.
5.1 Two-site binding models
Generally good results were obtained when fitting a two-site model to clearly biphasic, empirically obtained ITC data (Figs. 2-4, Table 1). Such data often provide the optimization algorithms ample information to arrive at a deterministic and precise estimation of the underlying thermodynamic parameters. In the examples shown in Sections 4.1.1 and 4.1.2, eight parameters have been fitted to the 93 available data points with good results, in that the derived parameters appear to be realistic and well-defined. This observation comports with a wealth of other two-site binding data [20,23–26] that show biphasic isotherms and apparently well-behaved fits.
However, the results with the H155A Tp34 protein (Figs. 4 & 5, Table 1) conclusively demonstrate that a biphasic isotherm does not always specify a unique solution to the equilibrium and mass action equations. The ΔH terms could vary to a large degree to compensate for many different combinations of parameters without significantly worsening the quality of the fit. This defect in these data allowed the estimated ΔH's to assume unphysical values when not constrained. Restricting the first enthalpy to be physically rational resulted in good fits, but ΔHI always assumed its maximum allowed value. The parameters derived from this constrained analysis must therefore be viewed with suspicion; they certainly allow only limited conclusions to be drawn about these data. This result was unexpected; the data appeared to be similar to that obtained with other hLF/Tp34 titrations (Figs. 2 & 3) and other two-site binding systems [23,25,26]. Some aspect of the underlying parameters must obscure the true nature of the binding events. Examination of the parameters shows that the two KA's are similar and the two ΔH's are of similar magnitudes but opposite signs. This combination of thermodynamic parameters proved to be pathologically ill-behaved when attempting to fit the data to a model. These difficulties might indicate that the model is incorrect; however, structural knowledge (Fig. 1) and MC-MSSV data (Fig. 5) confirmed the propriety of the two-site model with microscopic dissociation constants. Further, the simulations described in Section 4.1.4 suggest that varying the experimental conditions would not ameliorate these difficulties. Indeed, whatever actual parameters underlie the observed data, they appear to be ill-suited to discovery using ITC (Table 1).
Although fitting biphasic ITC data in two-site systems can be daunting, uniphasic ITC data present unique challenges when two distinct binding sites are present. In the simulations presented in Section 4.1.6 (Fig. 6, Table 2, Table S1), fluctuations in the noise features have a strong influence on the ability of the error-surface-projection method to find sensible error intervals. This occurred when attempting to refine only four parameters globally against 96 data points. Real data would have additional parameters (i.e. baselines, incompetent fractions) that likely would make fitting the data even more difficult.
5.2 Three-site binding models
The examination of the performance of three-site binding models was accomplished using simulated noisy data from a three-site model featuring microscopic dissociation constants and ΔH's (Section 3.4.1; Figs. 7-9; Tables 3-5). The general lesson gleaned from efforts to fit the simulated data was that three distinct phases of the isotherm allowed the optimization algorithm to arrive at accurate and acceptably precise parameter estimates. This conclusion comports with other results showing that triphasic ITC data could be reliably fitted, albeit with macroscopic or “sequential” models [27,28]. On the other hand, it is straightforward to imagine a three-site binding scenario that would yield monophasic ITC data (Figs. 8 & 9; Table 4). Attempts to fit such data can be susceptible to local, random variations in the data and generally do not appear to support the unrestrained refinement of six parameters. However, the final “Subtrial” using a highly constrained set of parameters (Table 5, Subtrial 7) revealed that if strict relationships between the dissociation constants and enthalpies can be assumed or discovered, a uniphasic isotherm is sufficient to reveal two parameters. This conclusion accords with the results of Gustchina et al. [29].
5.3 Monte Carlo methods of error estimation
It has been suggested [8,27] that Monte-Carlo methods be used to estimate error intervals for ITC data, and the method has been used extensively for the simulation of ITC data and their attendant errors [9,27]. In short, this procedure performs the experiment hundreds or thousands of times in silico, adding newly generated random noise around the best-fit line at the outset of each iteration. The simulated data are then subjected to the same optimization procedure as the experimental data. Statistics are compiled from the fitting results; for instance, the 68% error interval for ΔHI would look for the bounds defining the central 68% of values obtained for this parameter. This method should provide an excellent estimate of the influence of the noise structure on the refined parameter estimates. Such an analysis was carried out for H155A:hLF ITC data, but the resulting error intervals were essentially symmetric and small (e.g. EN for ΔHI = 0.06). The same procedure was attempted with the uniphasic two-site data, Trial #1, with similar results (e.g. EN for ΔHI = 0.006). Thus, the Monte-Carlo simulations fail to observe the pathologies in the error surfaces for the optimized parameters. Experience has shown this result to be generally true when Monte-Carlo error-estimation methods are applied to globally analyzed ITC data. Although this has not been thoroughly explored, it seems likely that, in the Monte-Carlo method, the least-squares methods efficiently find very similar solutions from many different constellations of simulated random noise. However, this method apparently does not effectively probe the parameter correlations that may be present in ITC data, such as those presented herein. Thus, the systematic error-surface projection method is preferred for most ITC data, and certainly for ITC data in which the underlying model contains more than one binding site.
5.4 Conclusions and best practices
Multisite models can be effectively used for the accurate and precise discernment of parameter estimates from multiphasic ITC data. However, the estimates thus derived are especially worthy of careful scrutiny. As a best practice, researchers should thoroughly examine error surfaces of the estimated parameters to investigate the precision with which the parameters have been estimated and to discover any parameter correlations that may be present. Even data with easily observed, multiple phases may not describe a unique set of parameters, and it is incumbent upon the investigator to unearth these faults, if present, and report them. Uniphasic ITC data are not generally well-suited to the refinement of multiple thermodynamic parameters; only under substantially constrained conditions can they reveal reliable values. Such constraints can be provided by global multimethod analysis [29]. Researchers should be realistic and forthright when reporting the results of fitting binding models to unconstrained uniphasic data, perhaps reporting the estimates as limits. Finally, when uniphasic data are observed, it may be worthwhile to simulate the system [44] to see if there are any unique heat features, perhaps at different concentrations [46], that can be exploited to constrain the analysis. This strategy can be especially useful when complex equilibria are suspected [44].
Supplementary Material
ITC is increasingly used to study complex biomolecular systems
Biphasic, empirical data often can be used to determine thermodynamic parameters
However, such data can also obscure the underlying parameters
Uniphasic data present significant difficulties when fitting to multisite models
Care must be exercised when fitting multisite models to ITC data
Acknowledgments
The author thanks Dr. Thomas Scheuermann for critically reading the manuscript. The author also thanks Drs. Ranjit Deka and Michael Norgard for supplying hLF, Tp34, and the Tp34 mutant proteins. A portion of this work was supported by NIH grant AI56305 (to Norgard).
Abbreviations
- AUC
analytical ultracentrifugation
- hLF
human lactoferrin
- Ig
immunoglobulin
- ITC
isothermal titration calorimetry
- MC-MSSV
mass-conservation multisignal sedimentation velocity
- MSSV
multisignal sedimentation velocity
- Tp34
the recombinant gene product of Treponema pallidum gene tp0971
- WT
wild-type
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Wiseman T, Williston S, Brandts JF, Lin LN. Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal. Biochem. 1989;179:131–137. doi: 10.1016/0003-2697(89)90213-3. [DOI] [PubMed] [Google Scholar]
- 2.Majhi PR, Blume A. Thermodynamic Characterization of Temperature-Induced Micellization and Demicellization of Detergents Studied by Differential Scanning Calorimetry. Langmuir. 2001;17:3844–3851. [Google Scholar]
- 3.Vargas C, Klingler J, Keller S. Membrane partitioning and translocation studied by isothermal titration calorimetry. Methods Mol. Biol. 2013;1033:253–270. doi: 10.1007/978-1-62703-487-6_16. [DOI] [PubMed] [Google Scholar]
- 4.Poncet-Legrand C, Gautier C, Cheynier V, Imberty A. Interactions between flavan-3-ols and poly(L-proline) studied by isothermal titration calorimetry : effect of the tannin. J. Agric. Food Chem. 2007;55:9235–9240. doi: 10.1021/jf071297o. [DOI] [PubMed] [Google Scholar]
- 5.Zheng Y, Dong L, Liu M, Chen A, Feng S, Wang B, et al. Effect of pH on the complexation of kaempferol-4′-glucoside with three β-cyclodextrin derivatives: isothermal titration calorimetry and spectroscopy study. J. Agric. Food Chem. 2014;62:244–250. doi: 10.1021/jf404320w. [DOI] [PubMed] [Google Scholar]
- 6.Mariana F, Buchholz F, Harms H, Yong Z, Yao J, Maskow T. Isothermal titration calorimetry - a new method for the quantification of microbial degradation of trace pollutants. J. Microbiol. Methods. 2010;82:42–48. doi: 10.1016/j.mimet.2010.03.024. [DOI] [PubMed] [Google Scholar]
- 7.Todd MJ, Gomez J. Enzyme kinetics determined using calorimetry: a general assay for enzyme activity? Anal. Biochem. 2001;296:179–87. doi: 10.1006/abio.2001.5218. [DOI] [PubMed] [Google Scholar]
- 8.Freyer MW, Lewis EA. Isothermal titration calorimetry: experimental design, data analysis, and probing macromolecule/ligand binding and kinetic interactions. Methods Cell Biol. 2008;84:79–113. doi: 10.1016/S0091-679X(07)84004-0. [DOI] [PubMed] [Google Scholar]
- 9.Tellinghuisen J. Statistical error in isothermal titration calorimetry: variance function estimation from generalized least squares. Anal. Biochem. 2005;343:106–15. doi: 10.1016/j.ab.2005.04.026. [DOI] [PubMed] [Google Scholar]
- 10.Velazquez-campoy A, Leavitt SA, Freire E. Characterization of protein-protein interactions by isothermal titration calorimetry. Methods Mol. Biol. 2004;261:35–54. doi: 10.1385/1-59259-762-9:035. [DOI] [PubMed] [Google Scholar]
- 11.Halvorsen K, Agris PF. Cross-platform comparison of nucleic acid hybridization: Toward quantitative reference standards. Anal. Biochem. 2014;465:127–133. doi: 10.1016/j.ab.2014.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Oda M, Nakamura H. Thermodynamic and kinetic analyses for understanding sequence-specific DNA recognition. Genes Cells. 2000;5:319–26. doi: 10.1046/j.1365-2443.2000.00335.x. [DOI] [PubMed] [Google Scholar]
- 13.Salim NN, Feig AL. Isothermal titration calorimetry of RNA. Methods. 2009;47:198–205. doi: 10.1016/j.ymeth.2008.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Buurma NJ, Haq I. Advances in the analysis of isothermal titration calorimetry data for ligand-DNA interactions. Methods. 2007;42:162–72. doi: 10.1016/j.ymeth.2007.01.010. [DOI] [PubMed] [Google Scholar]
- 15.Bishop GR, Ren J, Polander BC, Jeanfreau BD, Trent JO, Chaires JB. Energetic basis of molecular recognition in a DNA aptamer. Biophys. Chem. 2007;126:165–175. doi: 10.1016/j.bpc.2006.07.009. [DOI] [PubMed] [Google Scholar]
- 16.Pierce MM, Raman CS, Nall BT. Isothermal titration calorimetry of protein-protein interactions. Methods. 1999;19:213–21. doi: 10.1006/meth.1999.0852. [DOI] [PubMed] [Google Scholar]
- 17.Peters WB, Frasca V, Brown RK. Recent developments in isothermal titration calorimetry label free screening. Comb. Chem. High Throughput Screen. 2009;12:772–790. doi: 10.2174/138620709789104889. [DOI] [PubMed] [Google Scholar]
- 18.Demarse NA, Quinn CF, Eggett DL, Russell DJ, Hansen LD. Calibration of nanowatt isothermal titration calorimeters with overflow reaction vessels. Anal. Biochem. 2011;417:247–55. doi: 10.1016/j.ab.2011.06.014. [DOI] [PubMed] [Google Scholar]
- 19.Houtman JCD, Brown PH, Bowden B, Yamaguchi H, Appella E, Samelson LE, et al. Studying multisite binary and ternary protein interactions by global analysis of isothermal titration calorimetry data in SEDPHAT: application to adaptor protein complexes in cell signaling. Protein Sci. 2007;16:30–42. doi: 10.1110/ps.062558507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Freire E, Schön A, Velazquez-Campoy A. Isothermal titration calorimetry: general formalism using binding polynomials. Methods Enzymol. 2009;455:127–55. doi: 10.1016/S0076-6879(08)04205-5. [DOI] [PubMed] [Google Scholar]
- 21.Keeler C, Poon G, Kuo IY, Ehrlich BE, Hodsdon ME. An explicit formulation approach for the analysis of calcium binding to EF-hand proteins using isothermal titration calorimetry. Biophys. J. 2013;105:2843–53. doi: 10.1016/j.bpj.2013.11.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Krainer G, Broecker J, Vargas C, Keller S. Quantifying high-affinity binding of hydrophobic ligands by isothermal titration calorimetry. Anal. Biochem. 2012;84:10715–10722. doi: 10.1021/ac3025575. [DOI] [PubMed] [Google Scholar]
- 23.Buczek P, Horvath MP. Thermodynamic characterization of binding Oxytricha nova single strand telomere DNA with the alpha protein N-terminal domain. J. Mol. Biol. 2006;359:1217–1234. doi: 10.1016/j.jmb.2006.02.082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lin L-N, Mason AB, Woodworth RC, Brandts JF. Calorimetric studies of the binding of ferric ions to human serum transferrin. Biochemistry. 1993;32:9398–9406. doi: 10.1021/bi00087a019. [DOI] [PubMed] [Google Scholar]
- 25.Gorshkova I, Moore JL, McKenney KH, Schwarz FP. Thermodynamics of cyclic nucleotide binding to the cAMP receptor protein and its T127L mutant. J. Biol. Chem. 1995;270:21679–21683. doi: 10.1074/jbc.270.37.21679. [DOI] [PubMed] [Google Scholar]
- 26.Deka RK, Brautigam CA, Tomson FL, Lumpkins SB, Tomchick DR, Machius M, et al. Crystal structure of the Tp34 (TP0971) lipoprotein of Treponema pallidum: implications of its metal-bound state and affinity for human lactoferrin. J. Biol. Chem. 2007;282:5944–5958. doi: 10.1074/jbc.M610215200. [DOI] [PubMed] [Google Scholar]
- 27.Le VH, Buscaglia R, Chaires JB, Lewis EA. Modeling complex equilibria in isothermal titration calorimetry experiments: thermodynamic parameters estimation for a three-binding-site model. Anal. Biochem. 2013;434:233–241. doi: 10.1016/j.ab.2012.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Osawa M, Dace A, Tong KI, Valiveti A, Ikura M, Ames JB. Mg2+ and Ca2+ differentially regulate DNA binding and dimerization of DREAM. J. Biol. Chem. 2005;280:18008–14. doi: 10.1074/jbc.M500338200. [DOI] [PubMed] [Google Scholar]
- 29.Gustchina E, Li M, Ghirlando R, Schuck P, Louis JM, Pierson J, et al. Complexes of neutralizing and non-neutralizing affinity matured Fabs with a mimetic of the internal trimeric coiled-coil of HIV-1 gp41. PLoS One. 2013;8:e78187. doi: 10.1371/journal.pone.0078187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Broecker J, Vargas C, Keller S. Revisiting the optimal c value for isothermal titration calorimetry. Anal. Biochem. 2011;418:307–309. doi: 10.1016/j.ab.2011.07.027. [DOI] [PubMed] [Google Scholar]
- 31.MircroCal . ITC Data Analysis in Origin: Tutorial Guide, Version 7.0. MicroCal, LLC; Northampton, MA: 2004. [Google Scholar]
- 32.Brautigam CA, Deka RK, Ouyang Z, Machius M, Knutsen G, Tomchick DR, et al. Biophysical and bioinformatic analyses implicate the Treponema pallidum Tp34 lipoprotein (Tp0971) in transition metal homeostasis. J. Bacteriol. 2012;194:6771–6781. doi: 10.1128/JB.01494-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Padrick SB, Deka RK, Chuang JL, Wynn RM, Chuang DT, Norgard MV, et al. Determination of protein complex stoichiometry through multisignal sedimentation velocity experiments. Anal. Biochem. 2010;407:89–103. doi: 10.1016/j.ab.2010.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Padrick SB, Brautigam CA. Evaluating the stoichiometry of macromolecular complexes using multisignal sedimentation velocity. Methods. 2011;54:39–55. doi: 10.1016/j.ymeth.2011.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Keller S, Vargas C, Zhao H, Piszczek G, Brautigam CA, Schuck P. High-precision isothermal titration calorimetry with automated peak-shape analysis. Anal. Chem. 2012;84:5066–73. doi: 10.1021/ac3007522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Scheuermann TH, Brautigam CA. High-precision, automated integration of multiple isothermal titration calorimetric thermograms: new features of NITPIC. Methods. 2015 doi: 10.1016/j.ymeth.2014.11.024. this issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bevington PR, Robinson DK. Data reduction and error analysis for the physical sciences. 2nd ed. WCB/McGraw-Hill; Boston, MA: 1992. [Google Scholar]
- 38.Johnson ML. Why, when, and how biochemists shoule use least squares. Anal. Biochem. 1992;206:215–225. doi: 10.1016/0003-2697(92)90356-c. [DOI] [PubMed] [Google Scholar]
- 39.Coussens NP, Schuck P, Zhao H. Strategies for assessing proton linkage to bimolecular interactions by global analysis of isothermal titration calorimetry data. J. Chem. Thermodyn. 2012;52:95–107. doi: 10.1016/j.jct.2012.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tellinghuisen J. Statistical error in isothermal titration calorimetry. Methods Enzymol. 2004;383:245–282. doi: 10.1016/S0076-6879(04)83011-8. [DOI] [PubMed] [Google Scholar]
- 41.Attri AK, Minton AP. Composition gradient static light scattering: a new technique for rapid detection and quantitative characterization of reversible macromolecular hetero-associations in solution. Anal. Biochem. 2005;346:132–138. doi: 10.1016/j.ab.2005.08.013. [DOI] [PubMed] [Google Scholar]
- 42.Brautigam CA, Padrick SB, Schuck P. Multi-signal sedimentation velocity analysis with mass conservation for determining the stoichiometry of protein complexes. PLoS One. 2013;8:e62694. doi: 10.1371/journal.pone.0062694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Johnson ML, Straume M. Comments on the analysis of sedimentation equilibrium experiments. In: Schuster TM, Laue TM, editors. Mod. Anal. Ultracentrifugation Acquis. Interpret. Data Biol. Synth. Polym. Syst. Birkhäuser; Boston, MA: 1994. pp. 37–65. [Google Scholar]
- 44.Zhao H, Piszczek G, Schuck P. SEDPHAT- a platform for global ITC analysis and global multi-method analysis of molecular interactions. Methods. 2015 doi: 10.1016/j.ymeth.2014.11.012. this issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Haridas M, Anderson BF, Baker EN. Structure of human diferric lactoferrin refined at 2.2 A resolution. Acta Crystallogr. 1995;D51:629–646. doi: 10.1107/S0907444994013521. [DOI] [PubMed] [Google Scholar]
- 46.Freiburger LA, Auclair K, Mittermaier AK. Elucidating protein binding mechanisms by variable- c ITC. Chembiochem. 2009;10:2871–2873. doi: 10.1002/cbic.200900614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Leavitt S, Freire E. Direct measurement of protein binding energetics by isothermal titration calorimetry. Curr. Opin. Struct. Biol. 2001;11:560–6. doi: 10.1016/s0959-440x(00)00248-7. [DOI] [PubMed] [Google Scholar]
- 48.Zhao H, Schuck P. Global multi-method analysis of affinities and cooperativity in complex systems of macromolecular interactions. Anal. Chem. 2012;84:9513–9519. doi: 10.1021/ac302357w. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.