Regulation of Ribulose-1,5-bisphosphate Carboxylase/Oxygenase (Rubisco) Activase

Background: Rubisco activase (Rca) maintains carbon fixation, coordinates photosynthetic pathways, and regulates dark-light transitions.

Results: Positive cooperativity of ATP hydrolysis is afforded by ADP binding to oligomeric assemblies in the Rca-Mg-ATP-Mg state.

Conclusion: Magnesium-mediated allosteric regulation involves the coexistence of ATP- and ADP-bound states.

Significance: In dark-adapted chloroplasts, wasteful ATP hydrolysis may be prevented by low magnesium.

Abstract

In many photosynthetic organisms, tight-binding Rubisco inhibitors are released by the motor protein Rubisco activase (Rca). In higher plants, Rca plays a pivotal role in regulating CO₂ fixation. Here, the ATPase activity of 0.005 mm tobacco Rca was monitored under steady-state conditions, and global curve fitting was utilized to extract kinetic constants. The k_cat was best fit by 22.3 ± 4.9 min⁻¹, the K_m for ATP by 0.104 ± 0.024 mm, and the K_i for ADP by 0.037 ± 0.007 mm. Without ADP, the Hill coefficient for ATP hydrolysis was extracted to be 1.0 ± 0.1, indicating noncooperative behavior of homo-oligomeric Rca assemblies. However, the addition of ADP was shown to introduce positive cooperativity between two or more subunits (Hill coefficient 1.9 ± 0.2), allowing for regulation via the prevailing ATP/ADP ratio. ADP-mediated activation was not observed, although larger amounts led to competitive product inhibition of hydrolytic activity. The catalytic efficiency increased 8.4-fold upon cooperative binding of a second magnesium ion (Hill coefficient 2.5 ± 0.5), suggesting at least three conformational states (ATP-bound, ADP-bound, and empty) within assemblies containing an average of about six subunits. The addition of excess Rubisco (24:1, L8S8/Rca6) and crowding agents did not modify catalytic rates. However, high magnesium provided for thermal Rca stabilization. We propose that magnesium mediates the formation of closed hexameric toroids capable of high turnover rates and amenable to allosteric regulation. We suggest that in vivo, the Rca hydrolytic activity is tuned by fluctuating [Mg²⁺] in response to changes in available light.

Introduction

The primary carbon-fixing enzyme ribulose-1,5-bisphosphate carboxylase/oxygenase (Rubisco)² requires the synergistic action of Rubisco activase (Rca) to cope with a variety of inhibitory mechanisms. Some of these are regulatory by nature, such as nocturnal inhibition (1) or inhibition of decarbamylated Rubisco by its substrate ribulose 1,5-bisphosphate (RuBP) (2), whereas others appear to be intrinsic to turnover in an oxygenic atmosphere (3, 4). Regardless, the release of competitive inhibitors is substantially accelerated by the motor protein Rca, with subsequent degradation of some inhibitors by their specific phosphatases (5, 6). A comprehensive understanding of all co-regulatory mechanisms that enhance or diminish biological carbon fixation is critical in predictive modeling of net photosynthesis and biological pathway engineering to improve plant performance (7–9).

In higher plants, Rca plays a key role in modulating the overall level of carbon fixation, as well as the rate of photosynthetic induction under changing environmental conditions (10). With the aid of ATP hydrolysis, hexameric ring-like assemblies of Rca are thought to shift the conformational equilibrium of Rubisco to favor dissociation of dead-end inhibitors from the active sites. Within the chloroplast stroma, the light-dependent energy charge is thought to control Rca activity through the prevailing ATP/ADP ratio and redox status (10). Many plants express Rca in two isoforms. The longer α-isoform is distinguished from the shorter β-isoform by the presence of a 30-residue C-terminal extension that harbors two conserved redox-active cysteine residues regulated via the thioredoxin-f system (11). The Rca subunit concentration in the chloroplast stroma has been estimated to be ∼7 to ∼21 mg/ml (160–480 μm) (12), whereas the Rubisco holoenzyme concentration is ∼500 μm. These values suggest a ratio of approximately 1 Rca hexamer per 10 Rubisco holoenzymes, crowded together in an environment where ∼3% of all stromal proteins consist of Rca and ∼40% of Rubisco.

Multisubunit Assemblies of Rca

Rca is a member of the AAA⁺ superfamily of P-loop ATPases (13, 14). Frequently, proper assembly of AAA⁺ proteins requires nucleotide binding (15–18), and some members utilize their partner proteins as assembly scaffolds (19). Although AAA⁺ hexameric rings appear to be most common (18, 20–23), some exceptions to this rule are known (24–26). In general, higher plant Rca preparations are highly polydisperse in vitro. Recently, we have provided experimental evidence that in vitro the hexamer formation of cotton β-Rca is maximized around 30 μm subunit concentration (27), with close to 80% of protomers forming six-subunit assemblies in the presence of excess ATPγS and high magnesium ion concentrations (28). These data suggest that in the chloroplast stroma, Rca is always fully assembled to a hexameric or higher order form.

Recently, it has become clear that Rca proteins derived from different plant species show differences in their in vitro assembly mechanism. For example, the assembly of tobacco β-Rca was reported to be nucleotide-independent (29). In addition, a subunit concentration of 5 μm (0.2 mg/ml) or larger was shown to provide a weight-averaged sedimentation coefficient consistent with a hexamer (29). However, these experiments also demonstrated that tobacco β-Rca remained highly polydisperse over the entire concentration range tested (30). The stable formation of a hexameric species could only be demonstrated for the tobacco β-Rca-R294V mutant (31, 32). By negative stain electron microscopy, this mutant provided images of closed-ring hexamers in the presence of either ATP·Mg or ATPγS·Mg (32).

Some years ago, spinach α-Rca was shown to exhibit substantially elevated thermal stability in the presence of ATPγS·Mg (33). This complex was recently reported to form obligate hexameric species in vitro, in stark contrast to the shorter spinach β-Rca, which was reported to exhibit a high degree of size heterogeneity under identical conditions (29). Spinach β-Rca appeared to aggregate beyond the hexameric state, even in the presence of excess ATPγS·Mg (29). This behavior is more similar to that reported for other higher plant Rca proteins, such as creosote, tobacco, and Arabidopsis Rca (34, 35).

Structural Organization of Rca Subunits and Relationship to the AAA⁺ Superfamily

The 200–250-residue AAA⁺ module contains an ATP-binding cassette with an N-terminal domain harboring the Walker A and B motifs. The C-terminal domain is connected by a linker, such that a nucleotide-binding pocket is formed at the hinge region. Oligomerization allows a conserved Arg of the N-domain (“Arg finger”) to contact the ATP γ-phosphate bound to the adjacent subunit (36). In this way, conformational adjustments are likely communicated between subunits, in step with catalytic cycles of ATP binding, hydrolysis, and ADP release. If the system is loaded with a cognate macromolecule, mechanical work will lead to the structural remodeling of the target protein.

Currently, x-ray structures are available for bacterial Rca (37) and for higher plant Rca proteins from two different species. The 1.9 Å resolution creosote bush substrate recognition domain (38) consists of a helical bundle that forms the core of the AAA⁺ C-domain and an insertion that bears the specificity residues. The 2.9 Å resolution structures of the nucleotide-free AAA⁺ modules of tobacco (32) and Arabidopsis thaliana (39) Rca demonstrate a spiral arrangement of subunits in the crystal. Although in both structures, one turn consists of six protein chains, the tobacco structure exhibits a shorter pitch along the helical axis (32), whereas the Arabidopsis structure exhibits a tighter hinge-bending angle between the AAA⁺ N- and C-domains (39). This subtle movement is likely due to the trapping of a sulfate ion in the nucleotide-binding pocket. Structural information for the N- and C-terminal extensions of the AAA⁺ domain is not yet available.

Within the classic clade, many AAA⁺ proteins control protease activity, such as the bacterial proteins HslU, FtsH, ClpA, ClpX, and the archaeal proteasomal PAN ATPase. Most closely related to Rca are the ClpA D2 domain (15% sequence identity with the tobacco β-Rca AAA⁺ module), FtsH (14%), and ClpX (10%). For some of these proteins, x-ray structures of both spiral assemblies (40) and topologically closed 6-unit rings have been reported (41, 42). For a subset of these such as HslU, both 6-fold symmetric and asymmetric closed rings have been described (15, 43). Notably, 6-fold (41), 2-fold (42), and 3-fold (44) crystal symmetries were observed for FtsH. For all these systems, it remains unclear which of the available hexameric arrangements is most relevant to the catalytic cycle.

ATPase Activity and Rubisco Reactivation Models

Rca is capable of hydrolyzing ATP both in the presence and in the absence of Rubisco, and the addition of small amounts of Rubisco to the reaction mixture has been shown to have no effect on the hydrolytic rate (12, 32). Typically, published kinetic constants have been estimated using Rca subunit concentrations at or below 2.3 μm (0.10 mg/ml), with a recent report indicating 48 turnovers/s⁻¹ for tobacco β-Rca (30). At 2 μm Rca, turnover rates have been reported to range from 45 to 60 min⁻¹ in the presence of 2 and 2.5 mm ATP, respectively (32, 45). For other species, reported rates were 30.4 min⁻¹ for spinach β-Rca at 2 mm ATP (33), 17.4 min⁻¹ for cotton β-Rca at 4 mm ATP (46), and 23.9 and 32.6 min⁻¹ for Arabidopsis β-Rca at 2 and 4 mm ATP, respectively, measured by two different assay types (47). Utilizing fluorescence quenching of a protein-binding dye, K_d values of 0.57 and 5.9 μm were reported for ADP·Mg and ATP·Mg, respectively (45). A 4-min end point assay revealed loss of activity of Arabidopsis β-Rca in the presence of ADP. Apparently, the enzyme turned over 45.6 min⁻¹ in the presence of ATP alone, 25.2 min⁻¹ at a molar ratio of ADP/ATP equal to 1:3, and 7.8 min⁻¹ at a molar ratio of ADP/ATP equal to 1 (11). Similarly, the ATPase activity of spinach and cotton β-Rca was demonstrated to be 20% of maximum at an ADP/ATP equal to 1:3 (46). In the same work, the cotton β-Rca ATPase activity was measured as a function of Rca concentration up to 1.8 μm (0.080 mg/ml), indicating a relatively steady increase in hydrolytic rate up to 13 turnovers min⁻¹ (46).

Although several Rca-Rubisco binding geometries have been proposed (9, 32, 48), the actual mechanisms of recognition, interaction, and activation of Rubisco remain unknown. It is tempting to speculate that the sequestration of less ordered Rubisco segments by the central pore of Rca toroids plays a role, as demonstrated for a number of other AAA⁺ assemblies, such as FtsH (42), PAN (49), ClpX (50), Cdc48 (51), and ClpA/B (18). A mutational analysis of tobacco β-Rca pore loop residues has provided evidence consistent with a peptide binding or threading mechanism (32). Regardless, a significant difficulty in devising binding models is imposed by the poorly understood extent of Rca shape modification upon nucleotide hydrolysis. Although such structural adjustments would provide the mechanical force to open Rubisco active sites, the process itself may or may not involve direct interactions with these sites.

To date, key features of the Rca ATPase activity remain poorly understood, such as the allosteric control mechanisms of multisubunit assemblies thought to fine-tune hydrolytic activity. In work presented here, steady-state turnover kinetic methods were utilized to investigate the regulation of Rca ATPase activity by the available adenine pool, by magnesium binding, and by interactions with Rubisco. This work provides a significant step toward the quantitative description of ADP inhibition as product concentrations rise. We demonstrate subunit communication between at least three protomers, mediated by magnesium binding that augments catalytic activity 8–9-fold. We anticipate that steady-state kinetic data will form the foundation for the development of models for the reaction cycle in terms of stochastic, coordinated sequential switching or concerted conformational switching. Ultimately, the elucidation of the Rca ATPase mechanism is expected to help answer critical questions in bioenergetics, such as ATP consumption per Rubisco reactivation event.

Materials and Methods

Preparation of Cotton and Tobacco Short Form (β) Rca

Cotton β-Rca bearing a C-terminal Ala-Cys insert and tobacco Rca were cloned into the pET151/D-TOPO vector and transformed into Escherichia coli BL21*(DE3) (Invitrogen) as described previously (27). This procedure results in a construct bearing an N-terminal His₆ tag followed by a tobacco etch virus protease cleavage site. Liquid cultures were grown, and protein was purified essentially as described previously (35). Briefly, bacterial cells were grown in 3 liters of culture to A₆₀₀ ∼0.6, then induced by addition of isopropyl 1-thio-β-d-galactopyranoside, and grown at 25 °C and 180 rpm for 8 h. The cells were pelleted, stored at −80 °C, and lysed by sonication in the presence of 0.5 mm ADP. Purification entailed affinity chromatography using nickel-nitrilotriacetic acid resin in the presence of 0.5 mm ADP, cleavage of the His₆ tag with tobacco etch virus protease, followed by repurification over nickel-nitrilotriacetic acid. Protein fractions were concentrated and buffer-exchanged using a PD-10 column (GE Healthcare). The final buffer consisted of 25 mm HEPES, pH 8.0, 300 mm KCl, 10% glycerol, 1 mm DTT, with ADP added as required for the particular experiment, usually 2 mm ADP. Protein aliquots were frozen in liquid N₂ and stored at −80 °C. Apo-Rca was prepared by omitting ADP from all buffers used in purification and storage. Protein was quantitated utilizing the Bradford method with BSA as a standard.

Nucleotides

ADP (97% pure) was purchased from Alfa Aesar, and ultrapure ATP (≥99%) was purchased from Sigma or Alpha Aesar. The NADH assay was utilized to determine that ultrapure ATP (≥99% Sigma or Alpha Aesar) contained 0.36–0.42% ADP contamination.

NADH Activity Assay

The rate of ATP hydrolysis was measured by monitoring the rate of ADP release utilizing an enzyme-coupled continuous spectrophotometric assay. In this assay, the coupled actions of pyruvate kinase and lactate dehydrogenase provide for stoichiometric use of ADP to convert NADH to NAD⁺ (52). The reaction mixture contained 100 mm Tricine, pH 8.0, 20 mm KCl, 5 mm DTT, 5 mm MgCl₂, 2 mm phosphoenolpyruvate, 0.3 mm NADH, 4.8–8 units of pyruvate kinase, and 7.2–11.2 units of lactate dehydrogenase (Sigma). Upon addition of an aliquot of Rca to a cuvette containing assay mixture to provide a final volume of 1.0 ml, the A₃₄₀ was monitored for 60 s to obtain a stable signal. Subsequently, ATP was added, the contents were mixed manually with a cuvette mixer, and the reaction was monitored for 300 s. The extinction coefficient of NADH (6,220 m⁻¹ cm⁻¹) was used to calculate the rate of NADH loss.

EnzChek Phosphate Assay (MESG Assay)

The rate of inorganic phosphate release due to the ATPase activity of Rca was monitored by an enzyme-coupled spectrophotometric assay (53). In this assay, purine nucleoside phosphorylase (PNP) is utilized to catalyze the reaction of phosphate with the guanosine analog 2-amino-6-mercapto-7-methylpurine ribonucleoside (methylthioguanosine MESG, λ_max 330 nm), which generates the corresponding purine product 2-amino-6-mercapto-7-methylpurine (λ_max 360 nm) and ribose 1-phosphate. To assay inorganic phosphate production by Rca in a continuous fashion, the absorbance difference between the PNP reactant and product species was monitored at 360 nm. The assay is quantitative between 2 and 150 μm phosphate and between pH 6.5 and 8.5. The procedure was modified from the manufacturer's recommendations (Molecular Probes, Eugene, OR) by increasing the amount of PNP 3-fold and by addition of various buffer components, as described in detail below.

To prepare a 1 mm stock solution, MESG as provided by the manufacturer was solubilized in 20 ml of Nanopure water. To prepare PNP stock solution, the enzyme as provided by the manufacturer was solubilized in 500 μl of Nanopure water. An ATP stock solution was prepared fresh each day and consisted of 500 mm ATP (purity >99%, Sigma) in 100 mm HEPES, pH 8.0.

Preparation of the EnzCheck Standard Curve

To generate a phosphate standard curve, a standard curve working solution was prepared by combining 550 μl of 1 m HEPES, pH 8.0, 500 μl of 20× assay kit buffer (50 mm Tris, 1 mm MgCl₂, 0.1 mm sodium azide), 16 μl of 500 mm DTT, 80 μl of 500 mm MgCl₂, and 6.254 ml of Nanopure water (7.4 ml final volume). 740 μl of working solution were added to the sample and reference cuvettes, and the A₃₆₀ was set to 0. Subsequently, between 10 and 29 μl of nanopure water, 200 μl of MESG stock, and 30 μl of PNP stock (3 units) were added to the sample cuvette, and the time scan was started. After 60 s, either 1 μl of water blank or between 1 and 20 μl of 5 mm potassium phosphate were added (final 5-100 μm P_i), such that the combined addition of water and phosphate equaled 30 μl. The solution (1.0 ml total volume) was mixed using a manual cuvette mixer, and the A₃₆₀ was monitored for 300 s. For each scan, the maximum absorbance upon signal saturation was corrected by subtracting the absorbance observed prior to phosphate addition. The A₃₆₀ values were plotted as a function of phosphate concentration and fit to a straight line by linear regression.

EnzCheck Baseline Scan in the Absence of Rca and ATP

To collect blank runs and to assay for Rca activity, 7.00 ml of turnover working solution was prepared by combining 550 μl of 1 m HEPES, pH 8.0, 500 μl of 20× assay kit buffer, 16 μl of 500 mm DTT, and 5.934 ml of Nanopure water. To collect a blank absorbance time scan in the absence of both Rca and ATP, 700 μl of turnover working solution were added to each sample and reference cuvettes; the A₃₆₀ was autozeroed, 200 μl of MESG stock, 30 μl of PNP stock, 12 μl of 0.67 m MgCl₂ stock, and 50 μl of Rca buffer blank were added to the sample cuvette, and the time scan was started. After 60 s, 8 μl of HEPES, pH 8.0, were added, the solution was mixed, and the A₃₆₀ was monitored for 300 s. These conditions provide for a total Mg²⁺ concentration of 9.0 mm in a 1-ml final volume in the cuvette (1 mm Mg²⁺ contributed by the assay kit buffer).

EnzCheck Baseline Scan to Monitor Residual Phosphate

To control for residual phosphate present in the assay components, a baseline was collected in the presence of ATP but without Rca. As before, 700 μl of turnover working solution were added to each of the samples and reference cuvette; the A₃₆₀ was autozeroed, and 200 μl of MESG stock, 30 μl of PNP stock, 12 μl of 0.67 m MgCl₂ stock, and 50 μl of Rca buffer blank were added to the sample cuvette, and the time scan was started. After 60 s, 8 μl of 500 mm ATP stock was added to provide a final concentration of 4 mm ATP in a 1.00-ml volume. The solution was mixed with a manual cuvette mixer, and the A₃₆₀ was monitored for 300 s. For different experiments, the volumes of MgCl₂ and ATP stock solutions were adjusted as needed, while keeping the total volume of the 2 aliquots equal to 20 μl.

EnzCheck ATP Turnover Assays

To assay the ATPase activity of Rca, 700 μl of turnover working solution were added to the sample and reference cuvettes; the A₃₆₀ was autozeroed, and 200 μl of MESG stock, 30 μl of PNP stock, 12 μl of 0.67 m MgCl₂ stock, and 50 μl of Rca (4.50 mg/ml solubilized in 25 mm HEPES, pH 8.0, 300 mm KCl, 1 mm DTT, 10% glycerol) were added to the sample cuvette, and the time scan was started. After 60 s, 8 μl of ATP stock (500 mm) was added; the solution was mixed using a manual cuvette mixer, and the A₃₆₀ was monitored for 300 s.

To determine the initial velocity of Rca turnover, the turnover time scans were corrected by subtracting the baseline collected in the presence of ATP, and the slope of the steepest part of the resulting curve (15–20 s) was determined (usually 30–50 s after addition of ATP). Care was taken to ensure that the maximum absorbance value utilized to calculate the slope fell within the linear range of the standard curve. The slope was utilized to calculate the enzyme turnover velocity in terms of micromolar phosphate produced per s by means of the standard curve. This value was converted to turnover rates by normalizing with respect to Rca subunit concentration (5.0 μm). Each reaction was carried out in triplicate. The highest enzymatic turnover rate that can be quantitatively measured with this assay was shown to be equal to the production of 4.5 μm P_i/s.

According to the protocol described above, the final Rca concentration in the cuvette was 5.0 μm; the ATP concentration was 4.0 mm, and the total Mg²⁺ concentration was 9.00 mm. Once coordination of one magnesium ion to ATP was taken into account (K_d = 27.78 μm at pH 8.6 (54)), the residual, i.e. free Mg²⁺ concentration, was calculated to be 5.0 mm. In solution, coordination of a second magnesium ion to ATP occurs with a K_d value of 10.2 mm (54). Therefore, a small fraction of the Mg²⁺ concentration termed “free Mg²⁺” may be bound to the pool of ATP. This second equilibrium was not included in the calculations of free cation concentrations, because the protein-based second Mg²⁺-binding site may involve coordination to ATP as well.

The ATPase assays were repeated with ATP concentrations between 0 and 4 mm, and concomitant adjustment of total magnesium was based on the desired conditions. Initial velocities were converted to initial turnover rates k_o (min⁻¹), and computer-fitted to a steady-state turnover model using the programs Kaleidagraph^TM or Origin^TM (Equation 1). In the fitting procedure, n_H is the Hill coefficient, k_cat the maximal turnover rate upon substrate saturation, and K_m the Michaelis constant.

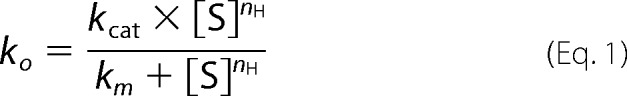EnzCheck ADP Inhibition Studies

The EnzCheck assay described above was adapted to measure initial rates of ATPase activity in the presence of varying concentrations of ADP, while keeping the “free” magnesium ion concentration constant at 5.0 mm. The magnesium ion concentration in the turnover working solutions was adjusted to give the desired final free Mg²⁺ concentration, as calculated from the dissociation constants K_{d (ATP-Mg)} = 27.78 μm (54) and K_{d (ADP-Mg)} = 240.96 μm (55) at pH 8.0. Rca stock solutions purified in the presence of 0.5 mm ADP were exchanged into buffers containing the appropriate amount of ADP by using a PD-10 column (GE Healthcare), such that dilution in the cuvette resulted in the desired final ADP concentration during turnover measurements. For example, 50 μl of Rca in buffer containing 1 mm ADP will result in 50 μm ADP upon 20-fold dilution in the cuvette. In all kinetic experiments presented here, the Rca concentration was kept constant at 5.0 μm. Nominal final ADP concentrations of 0, 18, 42, 60, 112, and 132 μm were utilized, with each concentration assayed in the presence of 0–4.0 mm ATP. The NADH assay was employed to demonstrate that ultrapure ATP (≥99% Sigma or Alpha Aesar) contained 0.36–0.42% ADP contamination. Therefore, for the nominally zero-ADP reactions, the ADP contamination resulted in about 4 μm ADP in reactions containing 1 mm ATP. For each ADP concentration, the normalized initial velocities were plotted as a function of substrate concentration. Global curve fitting to Equation 2 was carried out using the program Origin^TM. The fitting procedure involved fixing the K_m at a constant value, fitting the K_i for ADP inhibition globally, and fitting the k_cat and n_H values individually for each curve. Because the commercial ADP preparation utilized in this study contains some amount of phosphate, the maximum amount of ADP tolerated by the assay was shown to be about 140 μm.

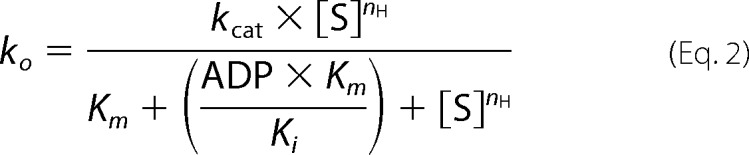EnzCheck Assays as a Function of Magnesium Concentration

Rca turnover data were determined at free Mg²⁺ concentrations of 1.0, 3.0, 4.0, 5.0, 6.5, 8.5, and 10 mm. As before, free Mg²⁺ was calculated using published dissociation constants K_{d (ATP-Mg)} = 27.78 μm (54) and K_{d (ADP-Mg)} = 240.96 μm (55) at pH 8.0. For each free Mg²⁺ concentration, ATP concentrations were varied between 0.05 and 4.0 mm, and the initial turnover rates were fit to Equation 1 to extract k_cat and K_m values. In these curve fits, a Hill coefficient n_H = 1.0 for ATP hydrolysis provided the best fit to the data. The catalytic efficiency k_cat/K_m was plotted against the free Mg²⁺ concentration and fitted to Equation 3, where A represents baseline activity of the ATP·Mg minimal substrate complex in the absence of free Mg²⁺; [Mg] represents the concentration of free magnesium ions, and n_H is the Hill coefficient.

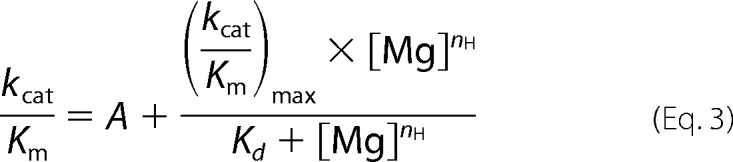In control reactions, the ionic strength difference between 1.5 and 6.5 mm MgCl₂ was accounted for by the addition of 15 mm KCl to reactions containing 1.5 mm MgCl₂. For these controls, a full Michaelis-Menten curve was generated.

EnzCheck Assay in the Presence of Crowding Agents

The effect of Ficoll as a crowding agent was tested using the standard cuvette assay described above. As described previously, a standard curve working solution was prepared to a final volume of 7.4 ml; however, 2.5 ml of 40% Ficoll 70 (w/v, Sigma) was added while reducing the water aliquot to 3.754 ml. In this way, the reaction mixture in the cuvette (1 ml) contained 10% Ficoll. Similarly, the turnover working solution for the Rca activity assays was prepared to a final volume of 7.00 ml as described previously; however, part of the water aliquot was replaced with 2.5 ml of 40% Ficoll 70 to provide for a final Ficoll concentration of 10% in the cuvette.

ATPase Assays in the Presence of Rubisco

Rubisco preparations isolated from tobacco leaves and flash-frozen in ammonium sulfate were a generous gift from Michael Salvucci (United States Department of Agriculture-ARS). On the day of the experiment, an ammonium sulfate pellet was thawed on ice and centrifuged for 10 min at 14,000 rpm, and the supernatant was discarded. The pellet was resuspended in 170 μl of 20 mm Tricine-NaOH, pH 8.0, and 0.2 mm EDTA buffer (inactivation buffer). A Sephadex G-50 column was equilibrated in the same buffer; excess buffer was removed, and Rubisco was loaded and the column centrifuged for 2 min at 400 × g. Rubisco preparations were subsequently concentrated using a centrifugal concentrator unit (Millipore, Amicon Ultracel 10K). Control reactions containing Rubisco buffer blanks were carried out by collecting the flow-through during the concentration step. Desalted Rubisco in the E-form was either used directly for experiments, or RuBP was added to 0.5 mm followed by a 2-h incubation period (4 °C) to generate the E·RuBP form.

EnzCheck Microplate Assays

For reactions in the presence of Rubisco, the EnzCheck assay was carried out in 200-μl volumes, using a Biotek Synergy HT microplate reader in combination with Corning NBS 96-well plates at 25 °C. The reduced volume was necessary to perform experiments in the presence of high Rubisco concentrations. The volumes of all solutions were adjusted accordingly, and experiments were carried out with and without 10% Ficoll.

Rubisco Reactivation Assays

The Rubisco reactivation activity of different Rca preparations was measured using a two-stage assay that employs coupling enzymes to determine the concentration of 3-phosphoglycerate (3-PGA) produced after 5 min of reactivation (56). Enolase from bakers' yeast and pyruvate kinase and lactic dehydrogenase from rabbit muscle (PK-LDH) were purchased from Sigma. Di-phosphoglycerate mutase preparations bearing a streptavidin tag (dPGM-streptavidin) and tobacco Rubisco preparations were a generous gift from Dr. Salvucci (United States Department of Agriculture-ARS).

For stage 1, stock solutions of tobacco Rubisco in the ECM form were prepared in 100 mm Tricine-NaOH, pH 8.0, 10 mm MgCl₂, and 10 mm NaHCO₃. Stock solutions of tobacco Rubisco in the ER form were prepared in 20 mm Tricine-NaOH, pH 8.0, 0.2 mm EDTA, 4 mm RuBP, and 5% PEG-3350. 1.25 μl of Rubisco stock was added to 0.5-ml Eppendorf tubes containing reaction buffer. The final volume of each reaction was 12.5 μl, and the final reaction mixture contained 1.84 μm (1.0 mg/ml) Rubisco holoenzyme, 5.0 μm (0.22 mg/ml) Rca, and 4.0 mm ATP. For reactions with the ECM form, the final buffer solution also contained 110 mm Tricine-NaOH, pH 8.0, 9.8 mm HEPES, pH 8.0, 21.6 mm KCl, 2.07 mm DTT, 0.72% glycerol, 9.72 mm MgCl₂, 10.7 mm NaHCO_3, 5 mm RuBP, and 5% PEG 3350. For reactions with the ER form, the final buffer solution also contained 102 mm Tricine-NaOH, pH 8.0, 9.8 mm HEPES, pH 8.0, 9 mm MgCl₂, 10.7 mm NaHCO_3, 21.6 mm KCl, 2.07 mm DTT, 0.72% glycerol, 0.02 mm EDTA, 5.4 mm RuBP, and 5.5% PEG-3350. Reactivation mixtures were allowed to incubate for 5 min at room temperature. The reactions were quenched by the addition of 37.5 μl of hot (95 °C) 100 mm Tricine-NaOH, pH 8, followed by 5 min of heating at 95 °C. Each reaction was vortexed briefly and centrifuged to remove the precipitate and then stored at −20 °C.

For stage 2, the 3-PGA content of each reaction was assayed in 96-well UltraCruz® UV plates, utilizing a BioTek (Synergy HT) plate reader. A four-enzyme assay mix was prepared consisting of 100 mm Tricine-NaOH, pH 8.0, 10 mm MgCl₂, 10 mm NaHCO₃, 20 mm KCl, 5 mm DTT, 0.5 mm NADH, 1.85 units of pyruvate kinase, 2.33 units of lactic dehydrogenase, 0.5 units of enolase, 0.5 units of diphosphoglycerate mutase, 0.2 mm 2,3-diphosphoglycerate, and 2 mm ADP. For control reactions carried out to ensure high activity of coupling enzymes, 177.8 μl of the four-enzyme assay mix was placed into each well; the temperature was equilibrated to 30 °C, and the initial A₃₄₀ value was recorded. 18.2 μl of water and 4 μl of 100 mm 3-PGA were added, and the solution was mixed. After 7 min of incubation, the final absorbance was recorded. To determine Rubisco activity by measuring the total amount of 3-PGA produced during the reactivation reaction, 177.8 μl of four-enzyme assay mix were placed into each well, followed by the addition of 7.2 μl of H₂O and equilibration at 30 °C. The initial absorbance was recorded; 15 μl of quenched Rubisco re-activation mix was added and incubated for 7 min, and the final absorbance was recorded. The difference in A₃₄₀ was utilized to calculate the amount of NADH oxidized (ϵ₃₄₀ = 6220 m⁻¹ cm⁻¹), which is equal to the total amount of 3-PGA present in the sample.

Thermofluor Stability Assays

The Thermofluor assay was carried out essentially as described (35). Data were collected using an Applied Biosystems ABI Prism 7900HT sequence detection system. Stability experiments were performed using a 384-well polypropylene TempPlate PCR plate covered with optically clear covers. Wells contained 20 μl of final volume with tobacco β-Rca at 0.21 mg/ml (∼5 μm), 25 mm HEPES, pH 8.0, 250 or 228.7 mm KCl, and 300× SYPRO Orange (prepared from a 5000× stock in DMSO with Nanopure water). Samples with the lower KCl concentration were controls for the ionic strength in the presence of MgCl₂. The above samples were prepared as two 1.1× premixes (high and low KCl), from which 18-μl aliquots were transferred into each well, followed by the addition of 2 μl of concentrated stocks at variable concentrations (e.g. ATPγS, MgCl₂, or both). Each individual condition was measured in triplicate. Thermal denaturation experiments, data collection, and analysis were performed as described previously (35).

Results

ATPase Activity of Tobacco β-Rca Provides a Michaelis Constant in the Mid-micromolar Range

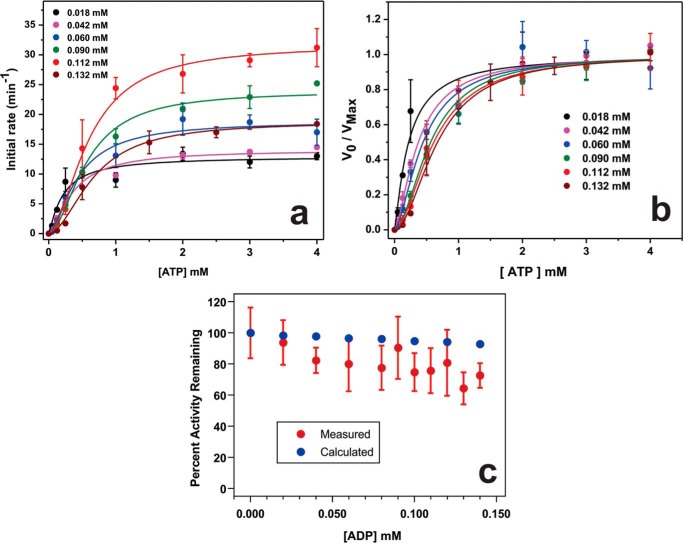
To examine the regulation of Rca turnover by the available ATP and ADP pools, a continuous enzyme-coupled ATPase assay was developed that monitors the kinetics of phosphate (P_i) release, while tolerating moderate amounts of ADP in the reaction (EnzCheck assay) (53). Near-homogeneous preparations of tobacco β-Rca were produced by bacterial expression, affinity purification, and enzymatic cleavage of the N-terminal His₆ tag (Fig. 1a). To generate apo-Rca, all purification procedures were carried out in the absence of nucleotide. Each protein preparation yielded at most 2 mg of Rca/liter of liquid culture, providing sufficient material to measure the initial velocity of 5.0 μm Rca with ATP concentrations ranging from 0 to 4 mm ATP (Fig. 1b). In this set of experiments, the free Mg²⁺ concentration, i.e. Mg²⁺ not coordinated to ATP, was kept constant at 5 mm. The concentration of free Mg²⁺ was calculated using K_{d (ATP-Mg)} = 27.78 μm, which describes Mg²⁺ coordination to the β- and γ-phosphoryl groups of ATP (54).

FIGURE 1.

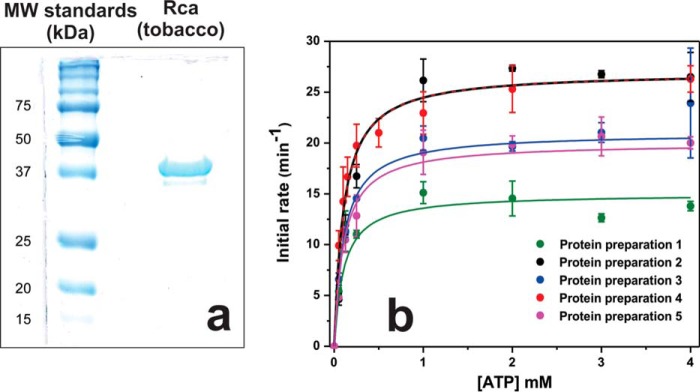
Tobacco Rca protein preparations and hydrolytic velocities. a, SDS-polyacrylamide gel documenting the purity of Rca expressed in E. coli and affinity-purified. b, Rca turnover in the absence of ADP. Initial velocities were monitored using 5 μm Rca, 5 mm free Mg²⁺, and 0–4 mm ATP by use of the EnzCheck assay. Data were computer-fitted to Equation 1 using the program Origin, with k_cat fitted individually for each data set, and K_m and n_H fitted globally for all five data sets, which were derived from five different protein preparations.

The initial velocities as a function of ATP were computer-fitted to a Michaelis-Menten-type steady-state turnover model with inclusion of cooperativity (see Equation 1). Five data sets generated from five different protein preparations provided independent evidence of rate saturation near 1 mm ATP (Fig. 1b). The extracted k_cat values varied from one protein pool to another, providing an average value of 22.3 ± 4.9 turnovers min⁻¹ per subunit (22% relative population standard deviation) for n = 5 independent determinations (Table 1). The observed range likely reflects the experimental errors associated with the Bradford and EnzCheck assays. Typical differences in independent Bradford concentration determinations were about 15%, and for independent EnzCheck assays, between 6 and 25% difference in measured rates was observed.

TABLE 1.

Catalytic parameters of tobacco apo-Rca derived from global curve fitting procedures

Experiments were carried out at 5 μm Rca and 5 mm free Mg²⁺. Data were fit to Equation 1 (k_cat fitted individually, and K_m and n_H fitted globally). Except for the average k_cat, indicated errors were estimated by the curve fitting algorithm.

Protein preparation	kcat	Km	nH
	min−1	mm
1	15.4 ± 0.6	0.104 ± 0.024	1.0 ± 0.1
2	27.1 ± 0.7
3	21.5 ± 0.6
4	27.1 ± 0.7
5	20.6 ± 0.6
Average ± S.D.	22.3 ± 4.9 (n = 5)

Regardless, individual fitting of the five Michaelis-Menten curves (Fig. 1b) provided essentially constant Michaelis constants K_m and Hill coefficients n_H. Therefore, global curve fitting procedures were applied to all five data sets using the program Origin, with the parameters K_m and n_H restrained to single values, while fitting k_cat individually for each data set (Fig. 1b). Using this procedure, the K_m value for ATP was extracted to be 104 ± 23 μm, and the Hill coefficient n_H was extracted to be 1.0 ± 0.1 (population standard deviation determined by the fitting algorithm) (Table 1). A Hill coefficient of unity implies a lack of allosteric interactions, providing the surprising result that ATP hydrolysis of oligomeric assemblies involves neither positive nor negative cooperativity under these conditions (5.0 μm apo-Rca with 5 mm free Mg²⁺). Using the NADH assay (52), no residual ADP was detected in apo-Rca preparations. However, trace amounts of ADP are introduced when adding ATP to initiate turnover, as indicated by our measurements of 4 μm ADP contamination in 1 mm ATP (28).

To validate the results described above, Michaelis-Menten curves were also generated using the NADH assay and then compared with the EnzCheck assay under identical conditions. In these experiments, tobacco β-Rca activity was monitored at a subunit concentration of 5.5 μm, while varying the ATP concentrations between 0.25 and 4.0 mm and keeping the total Mg²⁺ concentration constant at 5 mm. Using single data sets, extracted k_cat values were 20.2 ± 1.1 min⁻¹ for the EnzCheck assay and 15.3 ± 0.8 min⁻¹ for the NADH assay, whereas the extracted K_m values were 136 ± 50 and 122 ± 45 μm, respectively (Equation 1). The standard deviations provided here were estimated by the curve fitting algorithm. Because a better estimate of the true error is obtained by fitting multiple data sets as described above (Fig. 1b), it appears that the kinetic constants extracted from the two assays fall within experimental error of each other.

To examine whether the variations in hydrolytic k_cat values observed for different protein preparations (Fig. 1b) result in different Rubisco reactivation activities, three different Rca preparations were tested. At 4 mm ATP, 5 mm free magnesium, and 5 μm Rca, the hydrolytic turnover numbers were determined to be 27.5 ± 1.3, 19.7 ± 1.2, and 25.4 ± 2.2 min⁻¹. On the same day, 5 μm Rca from each preparation was incubated for 5 min with tobacco Rubisco in either the ER or the ECM form. Upon heat denaturation, the total amount of 3-PGA produced was measured spectrophotometrically using the coupling enzymes enolase, diphosphoglycerate mutase, pyruvate kinase, and lactic dehydrogenase (56). For each Rca preparation, percent Rca reactivation activity was calculated by comparing the amount of 3-PGA produced in reactions containing the ER form with that produced in reactions containing the ECM form. Overall, Rubisco reactivation activities appeared to follow the same trend as hydrolytic activities, with relative reactivation activities determined to be 88.4 ± 26.4, 72.5 ± 11.8, and 87.5 ± 18.7% for the three Rca preparations. However, the similarity of values and associated errors do not allow for a quantitative distinction of measured reactivation activities.

Surprisingly, cotton β-Rca was shown to turn over five to six times more slowly than tobacco β-Rca, with an estimated turnover rate of 3.8 ± 1.2 min⁻¹ (n = 6) under substrate-saturation conditions (28). In these preliminary experiments, we have estimated a K_m value for ATP hydrolysis of about 1.5 mm, suggesting substantially weaker substrate binding compared with tobacco β-Rca. Because the low hydrolytic rate of cotton β-Rca observed in our laboratory yielded relatively weak and noisy signals, mechanistic work on this variant was not pursued further.

ADP Provides Moderate Inhibition at Low ATP Concentrations

To investigate the regulation of Rca by the prevailing ATP/ADP ratio, the ATPase assays were repeated in the presence of various amounts of ADP, again utilizing 5 μm tobacco β-Rca and 5 mm free Mg²⁺. A series of Michaelis-Menten curves were generated varying ATP from 0 to 4 mm, with each curve generated in the presence of either 18, 42, 60, 90, 112, or 132 μm ADP in the reaction mixture (Fig. 2a). The maximum amount of ADP tolerated by the assay was found to be about 140 μm, as higher concentrations lead to poor signal-to-noise ratios due to residual P_i in commercial ADP preparations. Curve fitting of individual data sets to Equation 1 suggested that the apparent K_m value (K_m(app)) for ATP was increasing steadily with increasing ADP, in general agreement with competitive product inhibition (Table 2). This effect became particularly apparent when normalizing each curve with respect to its k_cat value, thereby illustrating the gradual shift of curves to higher [ATP] with increasing [ADP] (Fig. 2b). As determined previously, turnover numbers of different protein preparations varied substantially. Although a weak trend in k_cat could be discerned in the presence of ADP, the average k_cat value (20.1 ± 6.8 min⁻¹, n = 6, Table 2) cannot be distinguished from that determined in the absence of ADP (22.3 ± 4.9 min⁻¹, n = 5, Table 1). To examine whether k_cat changes as a function of ADP, Rca hydrolytic activity was measured with increasing ADP while keeping ATP and free Mg²⁺ constant (2 and 5 mm, respectively). The data were normalized with respect to the turnover rate observed at zero ADP, and the experiment was repeated three times with independently prepared protein preparations (Fig. 2c). The results clearly demonstrate that hydrolytic activity is not activated by micromolar amounts of ADP. The measured percent hydrolytic activity remaining with increasing ADP (Fig. 2c) follows closely the activity calculated using the kinetic constants extracted from our competitive inhibition model (see below and Table 3). Based on these data, we conclude that within the range tested, k_cat does not depend on ADP concentrations.

FIGURE 2.

Effect of ADP on Rca turnover. a, ADP ranging in concentration from 18 to 132 μm was added to tobacco Rca preparations prior to initial rate measurements as a function of ATP concentration. Curve fits to Equation 2 are shown. The inhibition constant K_i for ADP was fitted globally, whereas k_cat and n_H were fitted individually for each data set (Table 3). The K_m value was fixed to 104 μm (Table 1). (Each data set was also fitted individually to Equation 1, see Table 2.) b, data from a replotted upon normalization with respect to k_cat values. c, initial turnover velocities measured as a function of ADP concentration and normalized with respect to 0 ADP. Experiments were carried out at 2 mm ATP and 5 mm free magnesium ion concentration and utilizing three different protein preparations. At each ADP concentration, the average percent rate and its standard deviation were calculated for 3–6 individual rate determinations (red data points). For each ADP concentration, the expected percent activity remaining was calculated from the kinetic constants shown in Table 3 (blue data points).

TABLE 2.

Catalytic parameters of ADP-bound tobacco Rca derived from individual curve fitting procedures

Experiments were carried out at 5 μm Rca and 5 mm free Mg²⁺. The data sets were fit individually to Equation 1 for each ADP concentration, and the apparent catalytic efficiency k_cat/K_{m (app)} was calculated from the fitted parameters. Indicated errors were estimated by the curve fitting algorithm and propagated to estimate the error on the apparent catalytic efficiency.

[ADP]	nH	kcat	Km (app)	kcat/Km (app)
μm		min−1	mm	min−1 mm−1
18	1.2 ± 0.1	12.9 ± 0.6	0.152 ± 0.034	84.7 ± 19.3
42	1.5 ± 0.1	14.3 ± 0.3	0.272 ± 0.033	52.6 ± 6.5
60	1.6 ± 0.1	18.9 ± 0.7	0.274 ± 0.049	68.9 ± 12.6
90	1.8 ± 0.2	24.6 ± 0.5	0.440 ± 0.048	56.0 ± 6.2
112	1.8 ± 0.1	31.2 ± 1.0	0.359 ± 0.059	86.8 ± 14.5
132	1.9 ± 0.2	18.6 ± 0.6	0.428 ± 0.067	43.4 ± 6.8
Average ± S.D.		20.1 ± 6.8 (n = 6)

TABLE 3.

Catalytic parameters of ADP-bound tobacco Rca derived from global curve fitting procedures

Experiments were carried out at 5 μm Rca and 5 mm free Mg²⁺. The data sets were fit to Equation 2 with a fixed K_m value of 0.104 mm. The K_i value for ADP was fit globally, whereas k_cat and n_H values were fit individually for each ADP concentration. Indicated errors were estimated by the curve fitting algorithm.

[ADP]	Km	Ki	kcat	nH
μm	mm	mm	min−1
18	0.104 mm	0.037 ± 0.007	12.9 ± 0.5	1.2 ± 0.1
42			14.0 ± 0.5	1.5 ± 0.1
60			18.8 ± 0.6	1.6 ± 0.1
90			23.9 ± 0.6	1.8 ± 0.2
112			31.7 ± 0.8	1.8 ± 0.1
132			18.7 ± 0.8	1.9 ± 0.2

The ADP Inhibition Constant Is Estimated to be One-third of the K_m Value for ATP Hydrolysis

To extract precise kinetic constants, the five ADP-dependent Michaelis-Menten curves (Fig. 2a) were subjected to global curve fitting procedures, utilizing a steady-state turnover model with inclusion of competitive inhibition (Equation 2). Using the program Origin, the K_m value was fixed to 104 μm (Table 1), and the ADP inhibition constant K_i was fitted as a global parameter. At the same time, the k_cat and n_H values were fitted individually for each data set (Fig. 2a). In this way, the K_i value for ADP was extracted to be 37 ± 7.0 μm (Table 3), about one-third of the K_m value for ATP, raising the possibility of tighter product binding compared with substrate and reflecting previously reported thermal stability data (28).

ADP Is Essential for Positive Subunit Cooperativity

Surprisingly, the individual Michaelis-Menten curves adopted a distinctly sigmoidal shape with rising ADP concentrations (Fig. 2b), and curve fitting provided a consistently increasing Hill coefficient (Table 3). At zero ADP, n_H was best fit with a value of 1.0 ± 0.1 (Table 1), whereas at 132 μm ADP, the best-fitted n_H value was extracted to be 1.9 ± 0.2 (Table 3). These values indicate that at least two subunits interact with each other, providing for a net positively cooperative system. The highest ADP concentration accessible by this assay, 132 μm, equals 3–4 times the K_i value for ADP binding, suggesting that at this point ADP may occupy additional sites within Rca oligomers, thereby causing weak inhibition of ATP binding. At the same time, these observations provide evidence that in oligomeric Rca assemblies, a fraction of subunits must be occupied by ADP to achieve an allosterically regulated system.

Magnesium-mediated Activation of Rca Hydrolytic Activity

Although substantial magnesium-dependent enhancement of Rca hydrolytic activity was reported some years ago (57, 58), a detailed mechanistic description of this phenomenon has not yet been provided. In solution, ATP is known to tightly coordinate one magnesium ion, a feature that appears critical for Rca-mediated hydrolysis. Our data indicate that the complete absence of magnesium ions abolishes enzymatic turnover. Moreover, noncoordinated ATP appears to compete with ATP·Mg for binding to the active site, as the addition of 3 mm free ATP to 5 mm ATP·Mg results in decreased turnover rates. We conclude that the minimal Rca substrate consists of ATP·Mg. However, Rca hydrolytic activity increases substantially upon addition of Mg²⁺ in excess of that tightly coordinated to ATP (58), suggesting that a second protein-based magnesium-binding site may serve as co-activation site (57).

To examine activation by binding of a second Mg²⁺ ion, the ATP-dependent turnover rate of tobacco apo-Rca was determined as a function of free Mg²⁺ between 0.1 and 10 mm. A total of 10 Michaelis-Menten curves were generated by varying ATP between 0 and 4 mm for each curve, while keeping free Mg²⁺ at a constant value and measuring each data point in triplicate (Fig. 3a). Each curve was fit to Equation 1 to extract k_cat and K_m(app) values (Table 4). In all cases, a lack of cooperativity (n_H = 1) provided the best fit to the data, in full agreement with our observations described above in the absence of ADP. An examination of extracted k_cat values did not suggest a Mg²⁺-related trend (Table 4) and provided an average k_cat of 21.7 ± 3.0 min⁻¹ (n = 10), within error identical to the average values reported in Tables 1 and 2.

FIGURE 3.

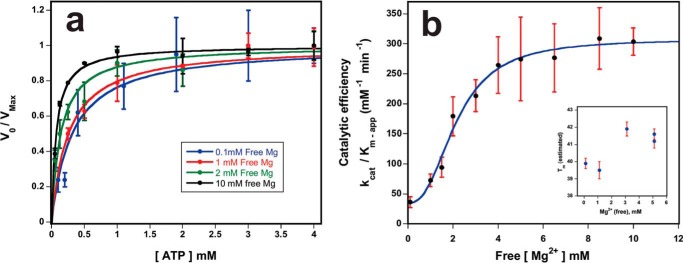
Effect of free Mg²⁺ on the catalytic efficiency of ATP hydrolysis by tobacco Rca. a, initial rates were monitored as a function of ATP concentration while varying the free magnesium ion concentration from 0.10 to 10 mm (Table 4). For clarity, four out of 10 curves are shown, each normalized with respect to the k_cat value. Each data point represents the average of three measurements. The data were fit to Equation 1 with n_H = 1. For each free [Mg²⁺], k_cat and apparent K_m values were extracted from the curve fits, and the catalytic efficiency k_cat/K_m(app) was calculated. b, catalytic efficiency as a function of free [Mg²⁺] was fit to Equation 3, and the K_d and n_H values for binding of the second magnesium ion were extracted. Inset, thermostability of tobacco Rca at low (0–1 mm) free [Mg²⁺] and high (3–5 mm) free [Mg²⁺], as measured by the Thermofluor assay.

TABLE 4.

Catalytic parameters of tobacco apo-Rca as a function of free magnesium ion concentration, derived from individual curve fitting procedures

Experiments were carried out at 5 μm Rca. The data sets were fit individually to Equation 1 for each ADP concentration, and the catalytic efficiency k_cat/K_{m (app)} was calculated from the fitted parameters. In all cases, the best fits were obtained with a Hill coefficient n_H = 1.0. Indicated errors are estimates provided by the curve fitting algorithm. NA, not applicable.

[Mg2+]free	kcat	Km (app)	kcat/Km (app)
mm	min−1	mm	min−1 mm−1
0.1	16.4 ± 1.1	0.453 ± 0.110	36.3 ± 9.2
1.0	23.5 ± 0.8	0.323 ± 0.046	72.8 ± 10.6
1.5	27.6 ± 1.1	0.292 ± 0.051	94.4 ± 16.6
2.0	21.3 ± 0.8	0.119 ± 0.021	179 ± 32
3.0	24.1 ± 0.5	0.113 ± 0.014	214 ± 27
4.0	20.9 ± 0.5	0.079 ± 0.014	264 ± 47
5.0	22.8 ± 0.6	0.083 ± 0.021	275 ± 70
6.5	19.1 ± 0.6	0.069 ± 0.014	277 ± 57
8.5	20.7 ± 0.5	0.067 ± 0.011	309 ± 51
10.0	20.7 ± 0.3	0.068 ± 0.005	304 ± 23
Average ± S.D.	21.7 ± 3.0 (n = 10)	NA	NA

In contrast, the extracted K_m(app) values followed a steady downward trend with increasing Mg²⁺ ions, with magnitudes decreasing from 453 ± 110 μm at 0.1 mm free Mg²⁺ to 69 ± 14 μm at 6.5 mm free magnesium (Table 4). These data provide evidence that ATP binds more tightly to the Rca active site, or is hydrolyzed more rapidly, when a total of two magnesium ions are coordinated to the Michaelis complex.

For each curve, the catalytic efficiency k_cat/K_m(app) was plotted as a function of the free Mg²⁺ concentration (Fig. 3b). Based on the observed saturation behavior, these data were fit to a steady-state model describing augmentation of base level activity upon binding of a second Mg²⁺ ion (Equation 3). Because of the distinctly sigmoidal shape of this curve, a Hill coefficient for magnesium-mediated activation (n_H-Mg) was included in the model. By curve fitting, the apparent K_d value for the second Mg²⁺-binding site was estimated to be 6.8 ± 2.6 mm. Based on the extracted Hill coefficient n_H-Mg = 2.5 ± 0.5, Mg²⁺ binding is judged to be a cooperative process that involves at least three Rca subunits. The catalytic efficiency is shown to increase 8.4-fold with rising free magnesium, a substantial elevation from a baseline value of 36.3 ± 9.2 min⁻¹/mm for ATP·Mg to a maximum of 309 ± 51 min⁻¹/mm for ATP·Mg·Mg (Table 4). Because of the allosteric behavior, the steepest increase is observed between 1 and 2 mm free Mg²⁺ with half-maximal efficiency at ∼1.5 mm free Mg²⁺ (Fig. 3b).

Control reactions carried out by adjusting the ionic strength with KCl rather than with MgCl₂ provided clear evidence that the increased catalytic efficiency at high [Mg²⁺] is due to an increase in divalent cation, rather than an increase in ionic strength. Similarly, control reactions were carried out in the presence of MnCl₂ rather than MgCl₂. In these reactions, 5 μm Rca and 0.5 mm ATP were combined with 5.5 mm total divalent cation. In the presence of Mg²⁺, the turnover rate was measured to be 8.3 ± 0.3 min⁻¹, whereas in the presence of Mn²⁺, the rate was measured to be only 0.26 ± 0.02 min⁻¹. The 32-fold drop in activity when replacing magnesium with manganese ions clearly indicates that catalytic activation is specific to magnesium coordination, rather than the result of a more general divalent cation effect.

Thermofluor assays indicate an ∼2 °C increase in the apparent mid-point for protein denaturation (T_{m (app)}), when free [Mg²⁺] is raised from 1.0 to 3.0 mm (Fig. 3b, inset). Therefore, magnesium-mediated activation appears to be accompanied by thermal stabilization of Rca assemblies, a feature that is consistent with the formation of topologically closed rings.

In combination, the observed positive subunit cooperativity and the reduced K_m value suggest that subunit-subunit interactions are mediated by a magnesium ion located in or near the active site bearing the minimal substrate ATP·Mg. Therefore, the second metal ion may not only coordinate ATP but also bridge molecular contacts between adjacent protein chains. This idea is further supported by previously published results from our laboratory on magnesium-mediated assembly of cotton β-Rca (28). We suggest that the fully activated Michaelis complex may be best represented by Rca·Mg·ATP·Mg, and may form upon light adaptation in the stroma.

Predicted Turnover Rates Provide Evidence for Incremental Regulation by the Prevalent ATP/ADP Ratio

In general, the regulation of Rca oligomeric assemblies may be afforded by a combination of product inhibition and subunit cooperativity. To examine Rca regulation by the available (i.e. unbound) nucleotide pool, the extracted kinetic constants were utilized to predict turnover velocities at nucleotide concentrations ranging from 0.1 to 5 mm (Equation 2). The Hill coefficient for ATP turnover was fixed at either 1.0, 2.0, or 4.0 (Fig. 4, a–c, respectively), and normalized velocities V₀/V_max were calculated using the constants K_m = 104 μm and K_i = 37 μm (Table 3), values determined in the presence of saturating magnesium (free [Mg²⁺] = 5 mm). As expected, activities increase with rising amounts of available nucleotide until saturation is observed. Because of the moderate degree of product inhibition (K_m ≈3K_i), slightly convex velocity curves are obtained in the absence of cooperative behavior (n_H = 1) (Fig. 4a). The introduction of cooperativity (n_H = 2 or 4) produces a sigmoidal shape that becomes more pronounced at higher n_H values (Fig. 4, b and c). Specifically, the simulated curves predict that with n_H = 2, Rca will operate between 10 and 80% capacity, if the available nucleotide pool equals 1 mm (Fig. 4b, blue curve). Under these conditions, about 70% of maximal ATPase activity would be achieved at high energy charge (ATP/ADP = 9:1) but only about 15% activity at low energy charge (ATP/ADP = 1:1). This example demonstrates the feasibility of substantial Rca down-regulation, if ADP were to accumulate in the stroma.

FIGURE 4.

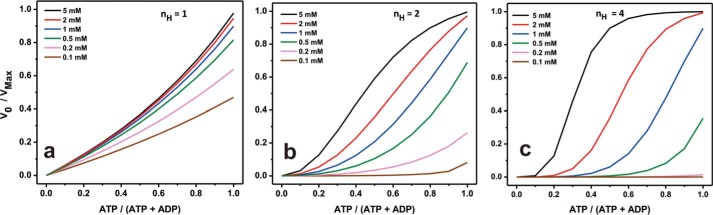
Simulations of predicted normalized velocities as a function of adenine nucleotide concentration. Calculations were carried out using Equation 2, while fixing the Hill coefficient n_H for ATP hydrolysis at either 1, 2, or 4, as indicated in a–c, respectively. The following parameters were utilized to calculate initial velocities (Table 3): k_cat = 22.3 min⁻¹, K_m = 104 μm, and K_i = 37 μm, values that were extracted in the presence of saturating magnesium (free [Mg²⁺] = 5 mm). All simulations were carried out keeping the available adenine nucleotide concentration (ATP + ADP) constant at either 0.1, 0.2, 0.5, 1, 2, or 5 mm. For each nucleotide concentration, Rca activity was calculated as a function of the mole fraction of adenosine triphosphate, i.e. [ATP]/([ATP + ADP]).

Neither Crowding Agents nor Elevated Concentrations of Rubisco Modulate Rca Hydrolytic Activity

To evaluate excluded volume effects due to macromolecular crowding, the ATPase activity of tobacco β-Rca was measured in the presence of 10% Ficoll-70, an inert carbohydrate polymer (59). At this concentration, the experimental volume fraction of Ficoll-70 has been estimated to be about 7%, a condition that was shown to provide a 5-fold increase in the enzymatic activity of phosphoglycerokinase (59). Therefore, the ATPase activity of tobacco β-Rca was analyzed with and without Ficoll using the EnzCheck assay. Kinetic data were collected in triplicate on 5 μm Rca, 4 mm ATP, and 5 mm free Mg²⁺. Surprisingly, we found that Ficoll-70 had no discernible effect on Rca hydrolytic activity. The average turnover rates ± Ficoll exhibited standard deviations of 11.4 and 5.0%, and differed from each other by only 12.4%, well within the estimated error of ∼22% for kinetic experiments (Table 1).

To examine the effect of high Rubisco concentrations on Rca hydrolytic activity, the ATPase assays were repeated in a microplate reader to reduce the reaction volume. Inactivated Rubisco isolated from tobacco leaves was added either in its E- or ER-form. The E-form was prepared by incubation with EDTA to decarbamylate active sites, and the ER-form was generated by subsequent addition of 500 μm RuBP. ATPase assays were performed with 5 μm Rca and Rubisco concentrations ranging from 1.4 to 20 μm. At the highest Rubisco concentrations tested, the molar ratio of Rubisco holoenzyme to Rca hexamer was 24 (Rubsico/Rca₆ = 24:1). Even under these conditions, the observed turnover rates remained essentially identical to the rates observed in the absence of Rubisco. To promote more highly associated states, the effect of 10% Ficoll-70 was tested in samples containing 20 μm Rubisco. However, as determined previously, no difference in hydrolytic rates could be discerned, as the average hydrolytic rates (n = 3) measured with and without Ficoll differed by only 1%.

Discussion

Hydrolytic Activity Appears to Vary Greatly among Higher Plant Rca Proteins

We have developed a continuous enzyme-linked ATPase assay based on the production of phosphate (53). This assay has opened the door to Rca enzyme kinetic studies that interrogate the effect of ADP in the reaction mixture. Traditionally, Rca ATPase activity has been measured by monitoring the production of ADP (52), an approach that limits mechanistic studies, because the ATP/ADP ratio cannot be adjusted in the reaction mixture. Utilizing both assay types, we have determined tobacco β-Rca and cotton β-Rca hydrolytic activities as a function of substrate concentration. We found that the k_cat value of tobacco Rca determined in this work, 22.3 ± 4.9 min⁻¹ (Table 1), is substantially lower than previously reported values, which range from 45 to 60 min⁻¹ (32, 45). In this work, Rca hydrolytic activity was determined at a subunit concentration of 5 μm, and in published works, the activity was measured utilizing 2 μm Rca or less. A spike in ATPase activity has been reported to occur at 1–2 μm subunit concentration, followed by a downward trend at somewhat higher concentrations (30).In support of this notion, preliminary data in our laboratory indicate a substantial reduction in turnover rate with increasing protein concentration.³ This effect, likely related to concentration-dependent assembly equilibria (29), fully accounts for the discrepancy observed between our turnover rates and those reported previously. Similarly, in our hands, cotton β-Rca turns over about 4-fold more slowly than previously reported (46), again suggesting that assembly equilibria may modulate hydrolytic activity.

Notably, we found that tobacco operates with a 5–6-fold higher k_cat value than cotton β-Rca. The existence of substantial activity variations among higher plant Rca proteins has been noted previously, although the physiological significance of these species-specific differences remains poorly understood (10). However, β-Rca is the only isoform expressed in tobacco, whereas cotton expresses both α- and β-isoforms of Rca. Some years ago, a direct comparison of ATP hydrolytic and Rubisco reactivation activities of cotton α- and β-Rca has demonstrated that ATPase activity follows the same trend as Rubisco reactivation activity (46). The authors reported that compared with cotton α-Rca, 2 μm cotton β-Rca exhibited substantially less ATPase and activase activity, whereas mixing of the two isoforms augmented turnover rates.

Tobacco β-Rca Assembly States

Because of its high activity, the mechanistic studies reported here were carried out on tobacco β-Rca at 5 μm subunit concentration, either in the apo-form (Fig. 1) or the ADP-bound form (Fig. 2), with ATP added to initiate hydrolytic turnover. Tobacco Rca is known to form heterogeneous mixtures under most conditions. However, the weight-averaged sedimentation coefficient was recently reported to be consistent with a hexameric state at concentrations of ∼0.2 mg/ml (∼5 μm) or higher, without any discernable differences as a function of nucleotide status (29). These data strongly suggest that hexamers are present in the reaction mixtures studied here, as all kinetic assays were carried out at 5 μm tobacco Rca. Although average particle sizes as a function of Rca concentration have been published (29), the microscopic assembly equilibria of tobacco Rca have not yet been determined. Therefore, the percent hexamer remains unknown, and our kinetic analysis of tobacco Rca can only be interpreted in terms of average turnover rates per subunit. In contrast to tobacco β-Rca, no more than 50% of cotton β-Rca appears to form hexamers at 5 μm concentration (28), underscoring the substantial species-specific differences not only in activity but also in assembly.

Previous reports have shown that the minimal oligomeric unit for ATP hydrolysis consists of about three subunits (30, 32). It is not surprising that the estimated stoichiometry for ATP hydrolysis is smaller than that for Rubisco reactivation, because in AAA⁺ proteins, active sites functional in hydrolysis are formed at the molecular interface of two subunits. However, Rubisco reactivation must couple ATP hydrolysis to mechanical work, a process that likely requires six-subunit rings to form the reactivation-competent state (32), lending biological relevance to the mechanistic interpretations presented here.

Allosteric Regulation Is a Function of ADP Binding

Using the steady-state approximation, we have obtained Hill coefficient n_H = 1.0 for ATP hydrolysis in the absence of ADP and n_H = 1.9 in the presence of 132 μm ADP (Tables 1 and 2). These values suggest that an ATP-bound Rca subunit cannot allosterically interact with a neighboring ATP-bound or empty subunit. Instead, such an interaction appears to require a partner subunit occupied by ADP, indicating that positive cooperativity involves at least two sites. We conclude that the presence of ADP is absolutely critical in facilitating functional communication between subunits (Fig. 2, a and b). However, we do not observe any activation of hydrolytic rate at micromolar ADP concentrations (Fig. 2c), although such an effect was recently reported for the distant homolog ClpX (60). In ClpX, ∼100 μm ADP is thought to set the homo-oligomeric ring into a catalytically activated conformational state, as evidenced by a moderate jump in ATPase activity.

The larger K_m value for ATP (104 μm) compared with the K_i value for ADP (37 μm) may imply that positive subunit cooperativity is a result of stronger ADP interaction with the active site compared with ATP. Although the K_d for ATP remains unknown, tighter ADP binding has been suggested based on relative thermostabilities (28). The relative K_m and K_i values (K_i/K_m = 0.36) suggest that the availability of excess ATP over ADP may be critical in accessing conformational states that promote hexameric ring closure (see below).

Light-dependent Magnesium Activation

In this work, we demonstrate that the apparent K_m value for ATP hydrolysis is reduced ∼6.6-fold in the presence of high Mg²⁺ concentrations (Table 4). This effect leads to a substantial regulation of ATP turnover rates as a function of available (unbound) magnesium ions, with half-maximal catalytic efficiency observed at about 2 mm free [Mg²⁺]. In previous works, we and others have demonstrated that excess magnesium ions increase the binding affinity of ATP (28, 35, 61). Recently, we have reported that magnesium concentrations in the low millimolar range promote cotton β-Rca assembly to hexameric states and disfavor the formation of larger supramolecular complexes (28). In line with this observation, we propose that cation binding involves both coordination to ATP in the active site of one protomer and coordination to several acidic residues located on the adjacent protomer (28). Although the Mg²⁺ dependence of tobacco Rca assembly has not yet been investigated, we demonstrate here that 5 μm tobacco Rca is stabilized by ∼2 °C when free [Mg²⁺] is raised above 2 mm (Fig. 3b, inset). An increase in thermal stability would be consistent with the formation of topologically closed toroidal rings from open hexameric assemblies. In combination, it appears plausible that the structural basis of Mg²⁺ activation consists of ring closure of six-subunit assemblies, whereas open ring-like hexamers may provide a template for supramolecular assembly (Fig. 5) (28).

FIGURE 5.

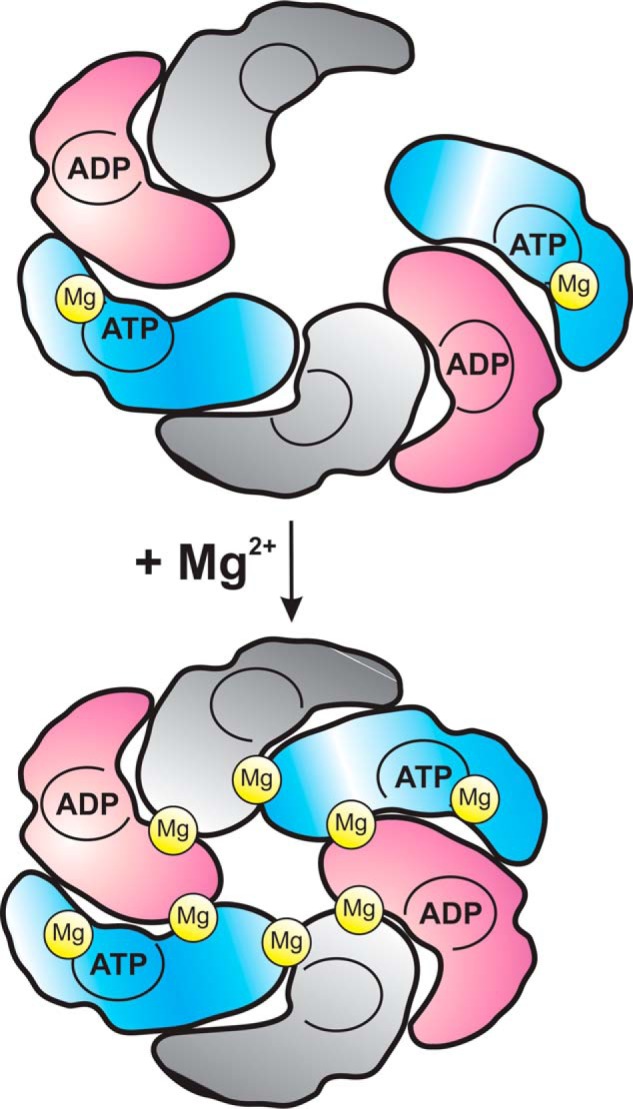
Hypothetical model for site asymmetry and magnesium activation in hexameric Rca assemblies. Based on the Hill coefficients presented in this work, hexameric Rca assemblies are proposed to operate with positive cooperativity of at least three protomers. One Rca₆ toroid may consist of sites occupied by ATP, of sites occupied by ADP, and of empty sites. The minimal substrate for hydrolysis is ATP·Mg, whereas the second Mg²⁺ ion serves as co-activator by mediating proper subunit-subunit contacts. The proposed mechanistic model involves an open ring-like assembly at low magnesium ion concentrations. When Mg²⁺ rises upon light exposure of the chloroplast, binding of the co-activator Mg²⁺ at a second site may lead to the formation of topologically closed hexameric toroids, with concomitant increase in catalytic efficiency by about 1 order of magnitude.

Magnesium ion concentrations are known to vary in the stroma as a function of proton pumping across the thylakoid membranes. In dark-kept intact chloroplasts, available [Mg²⁺] has been estimated to be 0.50 ± 0.53 mm, whereas a 10-min illumination period has provided an estimate of 1.95 ± 0.97 mm free [Mg²⁺] (62). As the pH of the stroma rises, [Mg²⁺] increases to provide electrostatic compensation, thereby up-regulating Rca hydrolytic activity to reactivate Rubisco for CO₂ fixation. This notion would provide a plausible answer to an as yet unresolved question of how uncontrolled Rca-mediated ATP hydrolysis is prevented in the stroma.

Different Classes of Sites May Promote Functionally Relevant Ring Asymmetry

In a toroidal assembly, communication across subunits may require coordinated conformational changes within the ring that exhibit substantial energy barriers. The low degree of subunit cooperativity observed in this work (n_H ≈2) supports pairwise binding of ATP, implying that three different classes of sites may co-exist in ring-like assemblies (Fig. 5). Substantial support for the existence of three classes of sites is provided by the Hill coefficient for magnesium activation of hydrolytic activity (n_{H (Mg)} = 2.5). This coefficient implies that at least three different classes of sites cooperate to achieve a high catalytic rate upon binding of a second Mg²⁺ ion. According to this model, the nucleotide occupation of sites may be coordinated with empty sites within the ring, in line with previously proposed models for ClpX and PAN, distant relatives of Rca among the classic clade AAA⁺ proteins. These proteins form monodisperse hexamers for which sub-stoichiometric ATP binding has been demonstrated (50, 63). In addition to empty sites, high and low affinity nucleotide-binding sites have been characterized, suggesting a sequential arrangement of tight-weak-empty-tight-weak-empty sites in hexameric toroids (64). Extracted Hill coefficients (n_H) indicate positive cooperativity between 2 or 3 sites, in support of a stochastic or coordinated cyclic pattern of hydrolysis (63, 64). The “symmetry mismatch” problem in this system (six AAA⁺ domains stacked onto the seven-subunit proteasome outer ring) has led to the idea that at any one time only two subunits associate with the partner protein. Similarly, the stoichiometric mismatch described for the six-subunit AAA⁺ rings formed by N-ethylmaleimide-sensitive factor interacting with its 4-fold symmetric partner protein has recently been attributed to asymmetric interaction geometries during the catalytic cycle (65).

The hinges forming the nucleotide binding pockets and connecting the AAA⁺ N- and C-domains are thought to adjust continuously during catalysis (64, 66). The general picture emerging from these studies suggests that the population of AAA⁺ conformational states is tightly coupled to the types of nucleotides bound in the active sites.

Predicted Catalytic Activities under Varying Environmental Conditions

In the chloroplast stroma, Rca activity is thought to be substantially modulated by the mole fraction of adenosine triphosphate, [ATP]/([ATP + ADP]), with the total pool of adenine nucleotides remaining constant at about 5 mm (10). The hydrolytic activities calculated using the constants determined here demonstrate that ATPase activity strongly depends on the adenine nucleotide pool (Fig. 4). Unfortunately, reliable estimates of unbound adenine nucleotide concentrations in the stroma are not readily available. Therefore, the expected levels of in vivo Rca hydrolytic activity remain difficult to delineate. Our calculations suggest that at high magnesium a free nucleotide pool of 1 mm may provide for appropriate biological regulation as a function of the available ATP/ADP ratio, covering a range from 90% under all-ATP conditions to 15% at low ATP (ATP/ADP = 1). Regardless, none of the predicted curves are steeply convex in appearance, indicating that tobacco β-Rca does not operate in a switch-like fashion at high magnesium concentrations (Fig. 4). Instead, incremental changes in the ATP/ADP ratio are predicted to provide for incremental changes in hydrolytic activity, supporting the idea that ATP turnover is highly tunable in this system.

Knowledge of the Hill coefficient under physiologically relevant conditions appears critical when analyzing “energy charge” curves in relation to product inhibition (Fig. 4, a–c). Although in this work we have measured Hill coefficients of 1.9 and 2.5, we cannot exclude the possibility that under different conditions the Rca assemblies will operate with a higher degree of positive cooperativity. For example, n_H was shown to vary between 2 and 4 for ClpX (50), supporting functional models that involve conformational switching in the four-nucleotide state (64). It is feasible that for tobacco Rca, the measured Hill coefficients appear depressed due to co-existing populations of oligomeric species with less than six subunits or due to coexisting populations of larger supramolecular assemblies that are less ATPase active. Regardless, the observed positive subunit cooperativity supports a process that involves pairwise switching in an either coordinated or stochastic fashion (n_H ≈2) but excludes a fully concerted process (n_H ≈6). We suggest that high ATP and high magnesium set ring-like assemblies into a Rubisco reactivation-competent state. Once the catalytic state has been reached, the occupation of a fraction of active sites with ADP may result in a cooperative system capable of high turnover rates in a steady-state fashion (Fig. 5). Based on our kinetic data, we estimate that each Rca subunit hydrolyzes about 10 ATP molecules within 30 s, followed by a sharp decrease in velocity. If a 30-s steady-state turnover of one hexamer were coupled to one Rubisco activation event, the entire process would require the hydrolysis of 60 ATP molecules.

Loading of Rca Assemblies with the Rubisco Substrate Does Not Modulate Turnover

In general, the ATP turnover rate of AAA⁺ proteins may be stimulated, dampened, or unaffected by the partner protein. Although literature reports have suggested that Rubisco does not affect ATP turnover, the Rubisco concentrations used in these assays were significantly lower than those of Rca, e.g. ∼1.5 μm Rubisco holoenzyme in combination with 4.7 μm Rca (32). Therefore, we have tested the effect of high Rubisco concentrations, up to 24 Rubisco holoenzymes per Rca hexamer, under conditions where ∼7% of the volume is occupied by a macromolecular carbohydrate-based crowding agent. In support of previous results, these conditions did not significantly alter Rca hydrolytic rates, confirming that the partner protein is not involved in the regulation of Rca ATPase activity. Under in vivo conditions, where excluded volume effects are estimated to be about 50%, Rca may not be able to fully engage with Rubisco until assemblies are activated by a rise in stromal magnesium in response to light.

Summary and Conclusions

In summary, our data support a mechanism in which Rca ring asymmetry plays a critical functional role. Our kinetic data, collected under conditions consistent with an average hexameric state, suggest a minimum of three different classes of sites. ATP hydrolysis appears to be activated substantially by the cooperative binding of a second Mg²⁺ ion. The mismatch in assembly stoichiometries of Rca and Rubisco may have functional relevance. For example, Rca hexameric assemblies exhibiting 2-fold symmetry could function by engaging only two or four subunits with Rubisco. We hope that the development of a mechanistic framework will serve as a starting point from which in vivo regulation of Rubisco activation can be understood.

Author Contributions

S. H., J. N. H., K. L., and M. T. H. acquired, analyzed, and interpreted the experimental data. R. M. W. developed the research strategy, directed the project, and wrote the manuscript. All authors reviewed the results and approved the final version of the manuscript.