GWAS with longitudinal phenotypes: performance of approximate procedures

Abstract

Analysis of genome-wide association studies with longitudinal data using standard procedures, such as linear mixed model (LMM) fitting, leads to discouragingly long computation times. There is a need to speed up the computations significantly. In our previous work (Sikorska et al: Fast linear mixed model computations for genome-wide association studies with longitudinal data. Stat Med 2012; 32.1: 165–180), we proposed the conditional two-step (CTS) approach as a fast method providing an approximation to the P-value for the longitudinal single-nucleotide polymorphism (SNP) effect. In the first step a reduced conditional LMM is fit, omitting all the SNP terms. In the second step, the estimated random slopes are regressed on SNPs. The CTS has been applied to the bone mineral density data from the Rotterdam Study and proved to work very well even in unbalanced situations. In another article (Sikorska et al: GWAS on your notebook: fast semi-parallel linear and logistic regression for genome-wide association studies. BMC Bioinformatics 2013; 14: 166), we suggested semi-parallel computations, greatly speeding up fitting many linear regressions. Combining CTS with fast linear regression reduces the computation time from several weeks to a few minutes on a single computer. Here, we explore further the properties of the CTS both analytically and by simulations. We investigate the performance of our proposal in comparison with a related but different approach, the two-step procedure. It is analytically shown that for the balanced case, under mild assumptions, the P-value provided by the CTS is the same as from the LMM. For unbalanced data and in realistic situations, simulations show that the CTS method does not inflate the type I error rate and implies only a minimal loss of power.

INTRODUCTION

In longitudinal studies, repeated measurements from the same participant are gathered over a period of time. Such studies have an important role in clinical and epidemiological research since they can relate changes in an individual to covariates. Longitudinal studies have been recently introduced in genome-wide association studies, where the goal is to find single-nucleotide polymorphisms (SNPs) that impact change in physical condition of individuals. Hundreds of diseases and traits have been investigated cross-sectionally, identifying thousands of significant SNPs. For several traits, it is relevant to explore their change over time. In this article, the evolution of bone mineral density (BMD) in elderly people participating in the Rotterdam Study¹ is taken as a guiding example.

Measurements taken from the same individual are correlated, which invalidates the basic assumption of a linear regression model. Therefore, dedicated statistical procedures are required. In practice, participants are often not examined at regular time points, they stop the study permanently (dropouts) or miss visits (intermittent missingness). The linear mixed model (LMM) is one of the popular approaches to analyze such irregularly measured responses. Fitting one LMM to thousands of individuals takes about a second. However, performing the LMM computations millions of times makes the whole-genome scans prohibitive in practice, especially with the growing amount of SNP data implied by the 1000 Genomes Project. Additionally, the model building process may require repetition of the whole analysis for different mean and/or covariance structures.

Mixed models have been intensively used in GWA studies involving related individuals, where the dependence structure needs to be properly modeled. This is also time consuming. Speeding up mixed models in this context is therefore also important and received quite some attention, see for example.^{2, 3} However, limited research has been devoted in this respect for longitudinal data.

It is expected that only a few SNPs correlate with the change of the trait over time. The longitudinal effect of a SNP is measured by the SNP × time interaction term in the mean structure of the model. Current GWAS are focused on identifying markers for which the P-value is lower than the threshold of 5 × 10⁻⁸. Sikorska et al⁴ explored several approximate procedures that identify the important SNPs in a fast manner. In particular, the authors proposed the conditional two-step (CTS) approach that is based on the conditional LMM (CLMM).⁵ They explored the properties of this method on longitudinal BMD data collected in the Rotterdam Study and compared their proposal with several other approaches. The CTS proved to be an excellent approximation to the LMM approach. The CTS approach is basically reducing the computations to fitting one LMM in the first step and in the second step a simple regression model, for each SNP at a time. Sikorska et al⁶ showed how to achieve huge speed ups in the second step via so called semi-parallel regression (SPR). Many SNPs are analyzed at the same time using big matrix operations, which replace time-consuming loops. In this way, a GWAS with simple linear regression is performed 50–60 times faster than with standard implementations. Solutions for efficient SNP data access have also been discussed in Sikorska et al.⁶ As a result, the combination of the CTS and the SPR makes an analysis of a GWAS with longitudinal data feasible even on a desktop computer, thereby considerably reducing demands on computing resources. Here, we further investigate the properties of the CTS approach, analytically as well as by simulations. In addition, we compare it with a related method, the two-step approach. Our goal is to explore the robustness of the two approximate methods for different data scenarios allowing us to draw general conclusions. Moreover, we discuss the speed gains achieved by applying jointly the CTS and the SPR. Our simulations lead us to the discussion on the practical aspects of the fast analysis of a longitudinal GWAS. Finally, in the Supplementary Material we provide R code useful for the implementation of the CTS approach.

MATERIALS AND METHODS

The development of fast approximate procedures was inspired by the data collected in the Rotterdam Study. In this prospective cohort study, the BMD of more than 5000 individuals, aged 55 or over, was measured at baseline and after approximately 2, 6 and 12 years. After an extensive whole-genome research on the cross-sectional BMD⁷ it was decided to explore genetic contributions to the change of BMD over time in elderly people. The BMD data from the Rotterdam Study are unbalanced and the missingness rates at the second, third and fourth recording times were 30, 50 and 70%, respectively. Due to the unbalanced structure of the data, the LMM was chosen for the analysis. Originally, the model was corrected for the age at entry to the study and the evolution of body weight. However, for ease of illustration, in this article we consider only time and SNP. Below, we indicate how additional covariates should be handled in practice. In the Supplementary Material, we provide simulations indicating that conclusions remain the same when other covariates are included into the model.

The linear mixed model

The LMM describing the vector y_i, which consists of n_i measurements taken on individual i over time, can be expressed as

where X_i and Z_i are n_i × p and n_i × q design matrices for fixed and random effects. The fixed effects model the overall population characteristic and are common to all individuals with the same X_i. The random effects describe the individual deviation from the average population evolution. Additionally ɛ_i represents a n_i × 1 vector of measurement errors. We adopt model (1) to our motivating example, describing the response BMD for an individual i at the occasion j as follows:

In model (2) the fixed effects are represented by SNP (s_i), time (t_ij) and their interaction (s_it_ij). We assume that the response evolves over time in a linear manner. The SNP variable can be represented by either an integer from {0,1,2} denoting the genotyped number of the reference allele or a continuous number between 0 and 2 describing the expected genotype count after imputation. The subject-specific part of the model consists of a random intercept (b_0i) and a random slope (b_1i). The first describes an individual deviation of the baseline BMD level from β₀. The latter characterizes the subject-specific fluctuation of the slope around β₂ + β₃s_i. Classically, it is assumed that the random effects have a bivariate normal distribution with mean 0 and covariance matrix

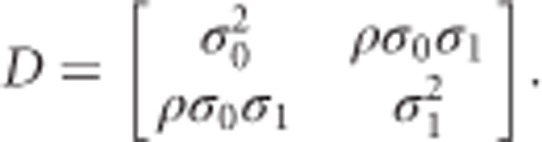Finally, ɛ_ij denotes a normally distributed measurement error with mean 0 and variance σ². It is assumed that the ɛ_ij is independent from b_i = (b_0i,b_1i)^T. From the above, it follows that the n_i-dimensional response y_i has covariance matrix given by 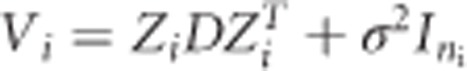, where Z_i is a n_i × 2 dimensional matrix with ones in the first column and t_ij in the second columns and 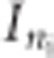is the identity matrix of size n_i. More information about the mixed model formulation can be found in Verbeke and Molenberghs.⁸

The fixed effects and the unknown variance components in (2) are commonly estimated iteratively using (restricted) maximum likelihood ((RE)ML). The parameter estimates (apart from the SNP terms) of model (2) for the BMD data applied to women are shown in Table 1. Our main interest lies however in the estimate of β₃ and more precisely in the P-value for testing H₀:β₃=0. In the Supplementary Material we show that when the data are balanced (t_ij = t_j and n_i = n), the ML estimate of β₃ is equal to:

Table 1. Estimates of the parameters in model (2) from the BMD data for women obtained from a LMM analysis of the Rotterdam Study (taken from Sikorska et al⁶).

Effect	Parameter	Estimate
Intercept	β0	0.970
Time effect	β2	−0.004
sd(b0)	σ0	0.110
sd(b1)	σ1	0.003
cor(b0, b1)	ρ	−0.140
sd(ɛ)	σ	0.040

where 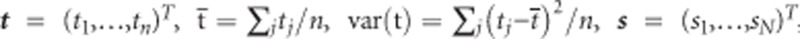, 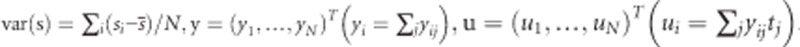. Assuming that the variance components are known, the variance of 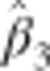is given by (see Supplementary Material):

In practice the unknown 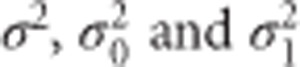are replaced by their (RE)ML estimates. The ratio 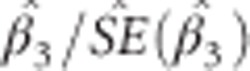gives the value of the t-statistic which determines p*, the P-value for the SNP × time effect.

The conditional linear mixed model

The CLMM has been suggested when baseline characteristics are not of interest or cannot be properly modeled. Verbeke et al⁵ and Verbeke and Fieuws⁹ showed that misspecification of the cross-sectional part of the model may lead to biased estimates of the longitudinal part. Such a misspecification happens, when, for example, an important cross-sectional SNP effect has been omitted from model (2). We are interested only in the longitudinal part of the model and therefore we aim for unbiasedly estimating the longitudinal part irrespective of estimating the cross-sectional part. Below we explain why that is particularly useful. The idea behind the CLMM is to map the time-stationary part of the model to zero. This is achieved by multiplying both sides of the model (1) by a full-rank n_i × (n_i −1) matrix 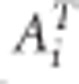such that 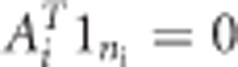and 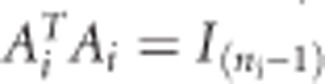, where 1_ni is a n_i-length vector of ones. In our case, the CLMM corresponding to (2) has the following form:

where 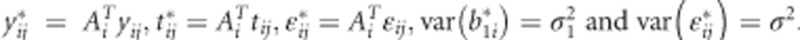. Matrix A_i can be easily found using properties of orthogonal polynomials. If the LMM is correctly specified, then the estimates from the LMM and the CLMM are the same in the balanced case.⁵ In the unbalanced case, empirical evidence suggests that they are similar.⁵ But other operational characteristics such as the type I error rate and the power of the CLMM versus the LMM have not yet been investigated, to our best knowledge. When the cross-sectional part of the LMM is wrong, the CLMM may prevent bias in estimation of the longitudinal effects. The data transformation is easily done in SAS, as shown in Verbeke et al⁵ or in R using the code provided in the Supplementary Material.

Approximate procedures

Fitting model (2) for one SNP takes around 4 s in the R package nlme¹⁰ and around 1 s in the package lme4.¹¹ In a GWAS millions of such models may need to be fitted that results in weeks or months of computations on a single computer. Below we show how a GWA analysis based on a mixed model can be reduced to fitting simple linear regression models to each SNP providing an approximate P-value for the hypothesis test H₀ : β₃ =0 for each SNP separately.

Two-step

The first step consists of fitting model (2) omitting the SNP effects, thus the following reduced model

All additional covariates (time-stationary and time-varying) should be also included in the reduced model. The variance-covariance matrix of the random effects for model (6) has changed to

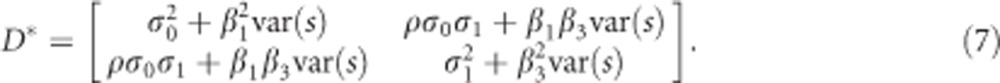More detailed derivation of the two-step (TS) approach can be found in the Supplementary Material. The second step of the TS approach involves regressing the estimated random slopes 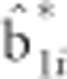on the omitted SNP using the following simple regression model:

We are interested in the relationship of the P-value from testing the hypothesis 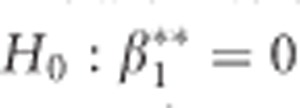with p*. It can be shown (see Supplementary Material) that the ML estimate of 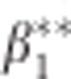in the balanced case has the form

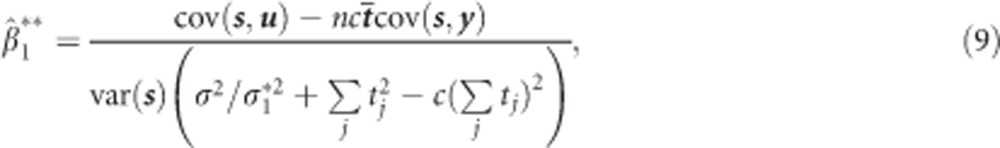where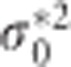 and 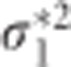are the diagonal elements of D* and 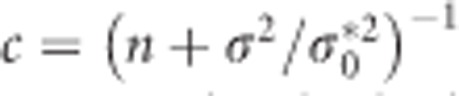. It can be shown using elementary algebraic manipulations that 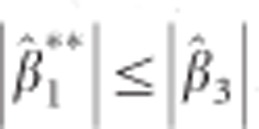. This illustrates the shrinkage effect of BLUP estimators, see for example.¹² We note that expression (9) is based on the assumption that the covariance part in D* is zero. If there is no cross-sectional effect of the SNP (β₁=0), then this implies that ρ must be zero. Now one can always turn the covariance of the original random intercept and slope into zero by choosing an appropriate translation of the time. That is, when t_ij is replaced by t_ij − a with a=−ρσ₀/σ₁ the covariance of the changed random effects becomes zero. However, such a change in origin drastically changes the other settings of the model, for example, the time variable does not start anymore from zero. Consequently, we cannot compare the transformed situation with the situation whereby the correlation is zero at the start. When β₁ is not zero, the covariance will be equal to β₁β₃var(s). However, its value will be relatively small, because of the very small SNP effects in a GWAS setting. To see how (3) and (9) are related, one takes σ² much smaller than 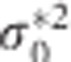and 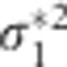. Then 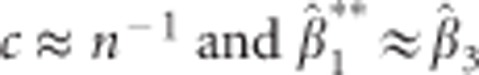. However, in many practical situations this assumption will not hold. For the standard error of 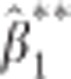no insightful expression could be obtained. Therefore, the relationship between p* and the P-value for 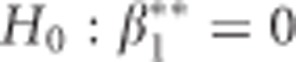remains unclear and needs to be evaluated numerically.

Conditional two-step

The CLMM corresponding to model (2) is given by (5). The transformed outcome 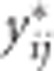is a function of only longitudinal effects including the effect of interest: SNP × time interaction. Following the rationale from the TS approach we build a reduced CLMM

with 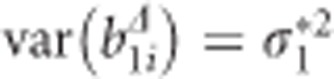and as in the two-step approach, 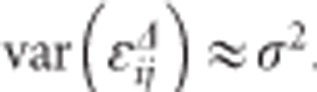. Note that all additional baseline covariates vanish from the CLMM through the data transformation. However, the transformed time-varying covariates remain in the reduced CLMM. The idea is now to regress the EBLUPs of 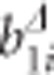on SNPs via the following simple regression model

The ML estimate for the SNP effect in model (11) and its variance are for the balanced case given by

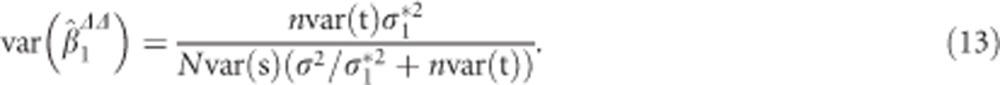It is easy to relate 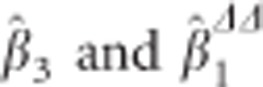by

Now the shrinkage effect of the BLUPs is immediately clear from the above relationship. For the Rotterdam Study, this shrinkage factor is about 0.32. The relationship between the t-statistics is given by:

where t_CTS and t_LMM are the t-statistics for the CTS approach and the LMM, respectively. Since also the variance of 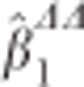is shrunken compared with that of 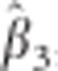, the t-statistic of the CTS approach is not necessarily smaller in absolute value. In GWAS, SNP effects are usually very small, which means that 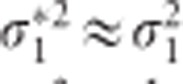. Consequently, t_CTS ≈ t_LMM, implying approximately the same P-values for the two methods. Note that we have compared the performance of the CTS with the LMM, while it is in fact an approximation to the CLMM. The LMM was chosen as comparator, because of its popularity. But, for reasons stated above we might have chosen also the CLMM to compare with, since for the balanced case t_CLMM = t_LMM.^{5, 9} While our analytical derivations lead to a clear relationship between p* and the P-value from the CTS approach, for the TS approach things are less clear. Unknown remains also the impact of cross-sectional SNP effect on the TS approach. Moreover, our derivations are limited to balanced data with known variance components, which rarely occurs in practice. Performance of the TS and the CTS approaches in more practical situations is addressed in a simulation study.

Simulation study

The settings in our simulation study are based on the characteristics of the BMD data. In particular, we assume that the data for 2000 individuals come from model (2) with the parameter values equal to those in Table 1. For the balanced scenario, we assumed that the measurements were taken for all individuals at baseline and after 2, 6 and 12 years without missing data. The SNP variable was taken as a random number with a uniform distribution on [0, 2]. We denote this setting as Scenario 1. Then, we considered modifications of that scenario whereby the values for ρ and σ₁² were changed. The scenarios are described in Tables 2 and 3. We ran an additional eight scenarios with σ =0.04 (inspired by value in Table 1) replaced by σ/2. But, since the results were quite the same we did not include these results here. In the unbalanced case, we assumed that times of measurements after baseline are slightly different between individuals. We used a jittering function that adds the times from the balanced case a random number between −0.8 and 0.8. Additionally we simulated a missing at random (MAR) dropout. The MAR mechanism assumes that the probability of missing observation depends on the observed outcome values but is independent from the unobserved values.¹³ More specifically, we assumed that the probability of dropping out from the study at time 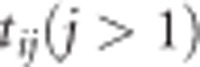depends on y_{ij −1} according to the following logistic model:

Table 2. Balanced case.

			P (type I error)			Max loss of power (%)		SDDIFF
Scenario	ρ	σ1	LMM	TS	CTS	TS	CTS	TS	CTS
1	−0.14	0.003	0.044	0.045	0.044	0.48	0	0.05	0.006
2	0	0.003	0.047	0.045	0.047	0.40	0	0.17	0.006
3	0	0.03	0.059	0.058	0.059	0.23	0	0.03	0.015
4	−0.5	0.003	0.063	0.052	0.063	31	0	0.66	0.007
5	−0.9	0.003	0.053	0.054	0.053	91	0	1.38	0.007
6	0.5	0.003	0.061	0.052	0.061	27	0	0.72	0.007
7	0.9	0.003	0.053	0.062	0.053	67	0	1.19	0.007
8	−0.9	0.03	0.056	0.056	0.056	0.5	0.21	0.12	0.015

Comparison of probability of type I error, loss of power with respect to LMM and precision measured by SD_DIFF of two-step and conditional two-step

Table 3. Unbalanced case.

			P (type I error)			Max loss of power (%)		SDDIFF
Scenario	ρ	σ1	LMM	TS	CTS	TS	CTS	TS	CTS
1	−0.14	0.003	0.053	0.056	0.053	5.50	0.20	0.26	0.15
2	0	0.003	0.029	0.036	0.033	1.20	1.10	0.2	0.11
3	0	0.03	0.066	0.067	0.066	0.31	0.03	0.08	0.07
4	−0.5	0.003	0.055	0.052	0.055	53.40	2.40	1.04	0.30
5	−0.9	0.003	0.055	0.058	0.052	94.30	11.00	1.51	0.49
6	0.5	0.003	0.054	0.050	0.052	43.90	0.67	0.9	0.11
7	0.9	0.003	0.052	0.043	0.058	84.00	4.30	1.29	0.25
8	−0.9	0.03	0.047	0.047	0.050	40.10	13.00	1.52	0.90

Comparison of probability of type I error, loss of power with respect to LMM and precision measured by SD_DIFF of two-step and conditional two-step

where p_ij is the probability of a missing y_ij. The values of α and β determine how important the dropout is and were chosen such that the dropout at the second measurements was about 30%, implying a dropout at the third and fourth occasions of around 50 and 70%, respectively. The simulation scenarios for the MAR case were chosen the same as for the balanced case (Tables 2 and 3). To evaluate the two approximate procedures several criteria were considered. Comparison is done mainly with the LMM, for reasons stated above. First is the probability of type I error. Preferably, we would like to have it around α=0.05 as for the LMM. Second, the power should be close to the power of the LMM. Due to very long computational times involved in the standard simulation-based power calculation for the LMM, we used a probit-model approach. Details about this fast approach to power calculation can be found in the Supplementary Material. We also evaluated the precision defined as the standard deviation of log₁₀(p_LMM)−log₁₀(p_A), where p_A is the P-value from the approximating method. We denote this measure as SD_DIFF. Finally, we are interested in the influence of β₁ on the approximations given by the TS approach. Two values for β₁ were chosen: 0.01 and 0.05. The first one is the estimate obtained in the cross-sectional GWA analysis for BMD data. All simulations were performed using the R software.¹⁴ The LMMs were fitted using the package lme4. In our experience, this package is faster and encounters less problems with convergence than the package nlme.

RESULTS

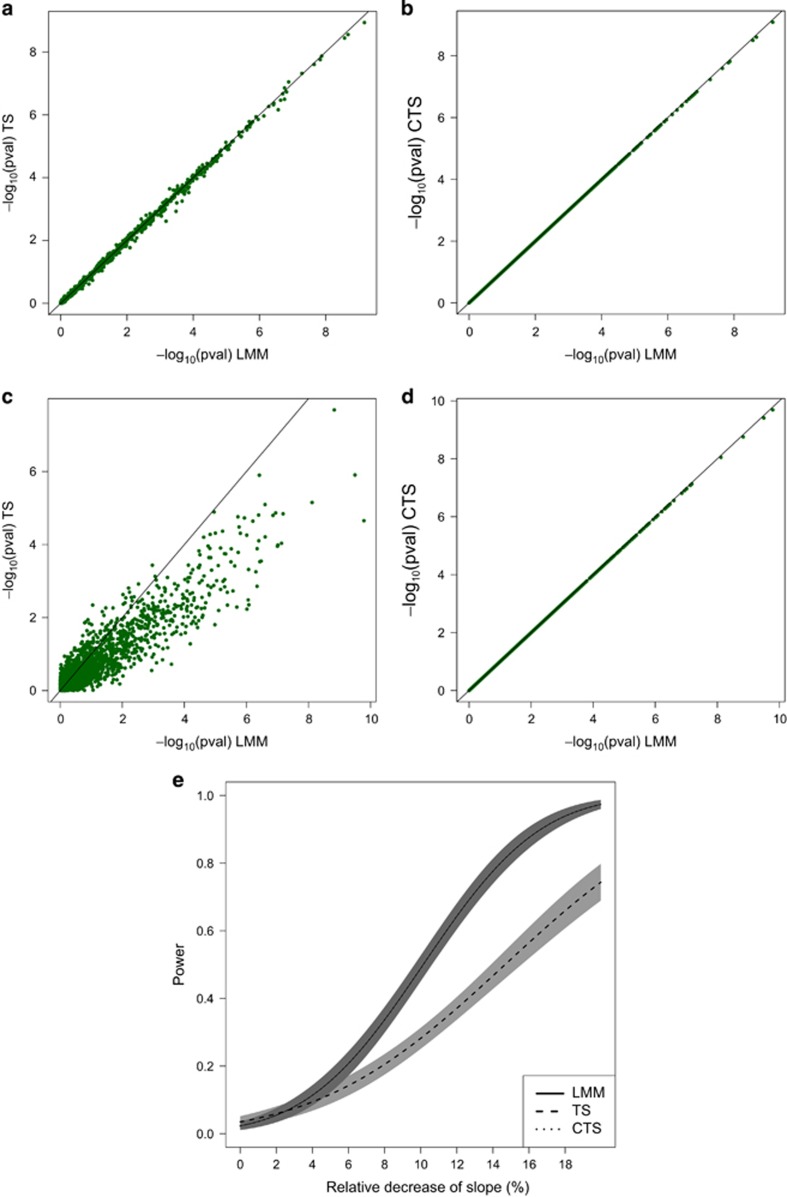
The results of the simulation study for the balanced case are summarized in Table 2. We observe a high impact of the correlation between random effects (ρ) on the performance of the TS approach. For the variance of the random slope like in the BMD data, the power of the TS decreased with about 31 and 91% for ρ equal to −0.5 and −0.9, respectively. When 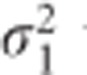was further increased, the TS procedure revealed only a minor loss of power (0.5%) even when the correlation ρ was set to −0.9 (Scenario 8, Table 2). A positive sign of the correlation affected slightly less the approximation. The CTS approach exhibits a stable behavior across all the scenarios, resulting in a similar type I error rate and power as LMM. The difference in performance between the TS and CTS approach is also illustrated in Figure 1. The minimal loss of power for CTS in Scenario 8 may be caused by a small difference between σ² and σ^*2 in case of larger β₃ simulated for that scenario. 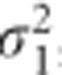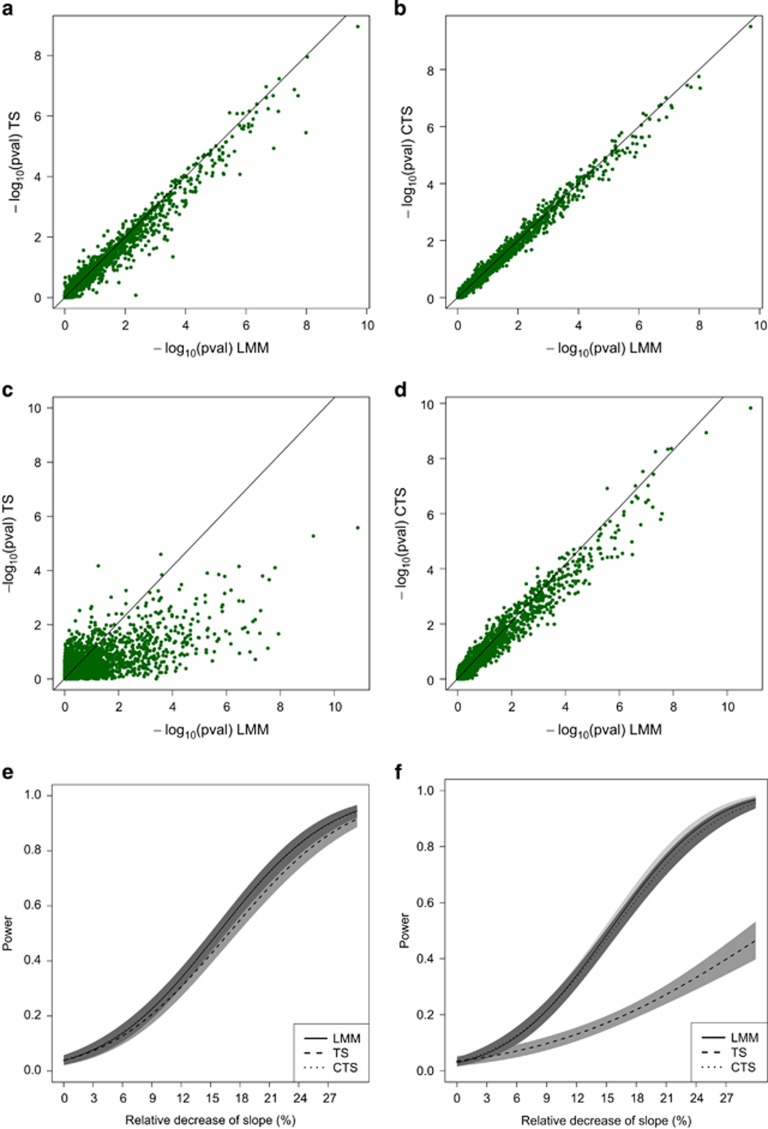When the data are unbalanced, both approximate methods are sensitive for the changes in ρ and , but the effect on the CTS approach is often minimal. The results from our simulations are shown in Table 3. We observed a loss of power for the TS and CTS approach when |ρ| increases. However, the TS approach was more affected by a large |ρ|. For ρ =−0.5, the CTS approach lost up to 2.4% of power while the TS approach was highly underpowered (max loss of 53%). As for 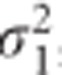(Scenario 8) improved the approximation for the TS approach, but did not reduce power loss for the CTS approach. For all scenarios, the type I error rates for the two approaches were similar to LMM. The performance of the approximations for the unbalanced case is illustrated in Figure 2.

Figure 1.

Balanced case, Scenarios 1 and 4. Panels (a) and (b) display the approximation of the P-values obtained in TS and CTS for Scenario 1. Panels (c) and (d) display the approximation for Scenario 4. Panel (e) shows the power curves for Scenario 4, together with 95% pointwise CI. The curves for LMM and CTS are overlapping. The x axis of the power plot represents the relative reduction of the slope per one unit increase in reference allele. In the plots displaying accuracy, results of simulations under the null and under alternative have been merged.

Figure 2.

MAR case, Scenarios 1 and 4. Panels (a) and (b) display the approximation of the P-values obtained in TS and CTS for Scenario 1. Panels (c) and (d) display the approximation for Scenario 4. Panels (e) and (f) show the power curves for Scenarios 1 and 4, together with 95% pointwise CI. The x axis of the power plot represents the relative reduction of the slope per one unit increase in reference allele. In the plots displaying accuracy, results of simulations under the null and under alternative have been merged.

Heteroscedasticity and robust standard errors

The variance of the estimated BLUPs from the LMM is given by

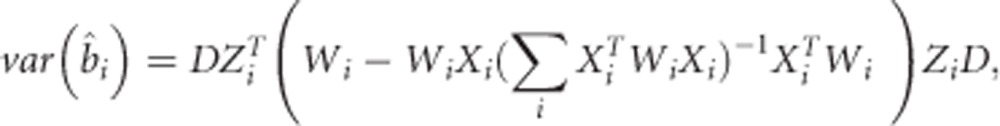where 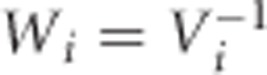.⁸ From this expression, we observe that the variation of the estimated individual slopes may be quite different between individuals, especially in case of unbalanced data, which could lead to heteroscedasticity in the second step of the TS procedures. Replacing the simple linear regressions by weighted linear regressions with weights obtained in the first step had, however, almost no impact on our simulation results. In general, one might of course prefer the weighted regressions solutions at the expense of a small extra computation time.

Influence of the cross-sectional SNP effect

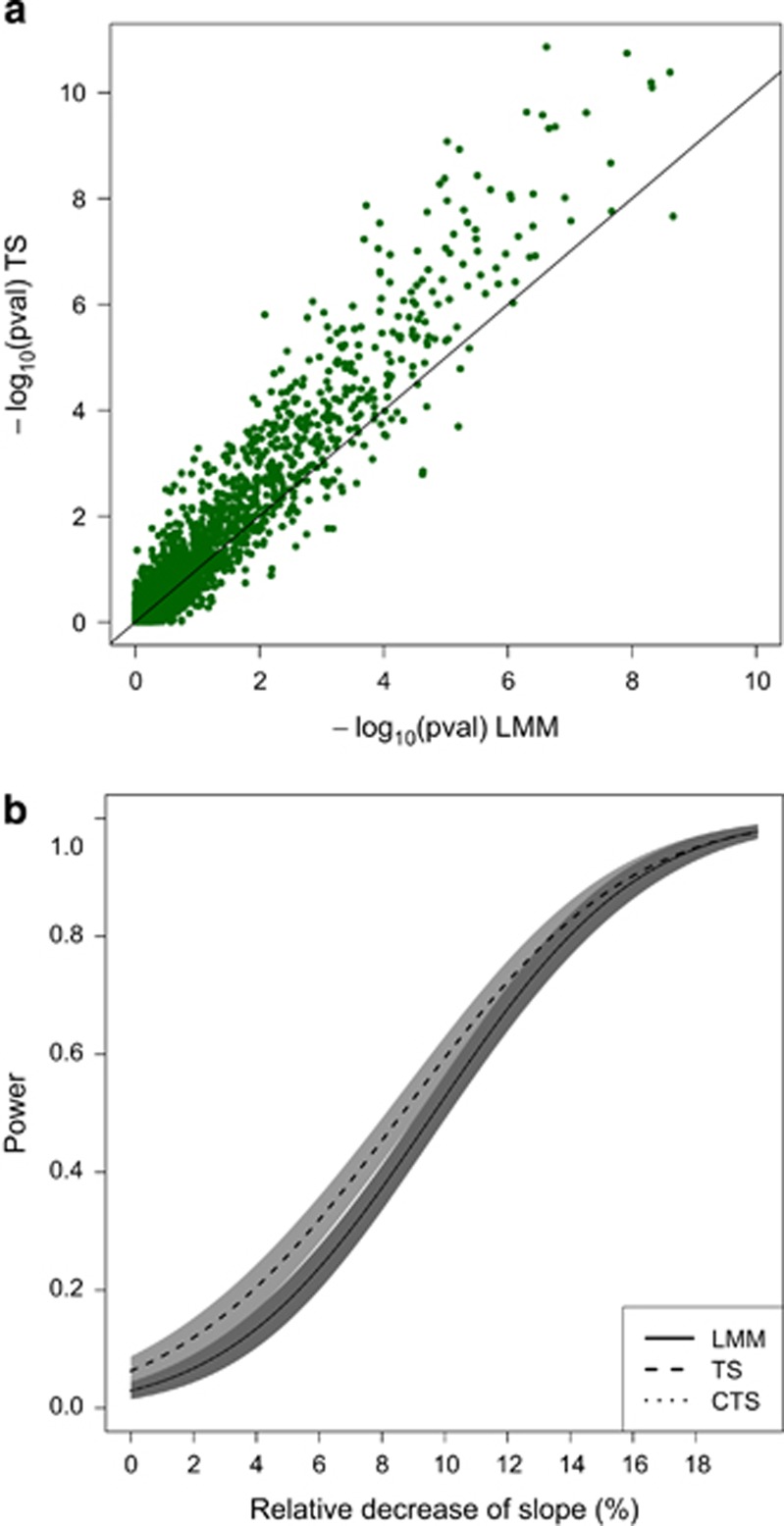
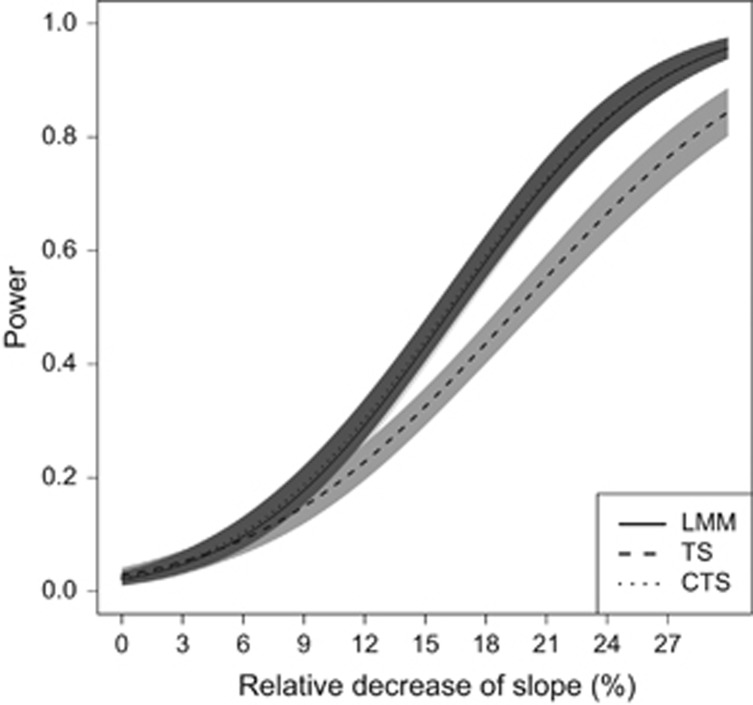
Our simulations showed a big impact of the cross-sectional SNP effect on the performance of TS. In the balanced case, when β₁ =0.01 only a minor power loss of the TS approach was observed (1%). However, for β₁ =0.05, the type I error rate was inflated to 0.10 compared with 0.038 for LMM and the CTS approach. The performance of the TS approach for that scenario is displayed in Figure 3. For the MAR case, a cross-sectional SNP effect of 0.01 led to a loss of power for the TS approach to even 17% (Figure 4). For β₁ =0.05, the type I error rate was inflated to 0.54. The performance of the TS approach worsened even more when the signs of the cross-sectional and longitudinal SNP effects were opposite.

Figure 3.

Balanced case, Scenario 1 with β₁=0.05. Panel (a) shows the approximation given by the two-step. Panel (b) shows the power curves (and 95% pointwise CI) for LMM, TS and CTS. The x axis of the power plot represents the relative reduction of the slope per one unit increase in reference allele. In the plot displaying accuracy, results of simulations under the null and under alternative have been merged.

Figure 4.

MAR case, Scenario 1 with β₁=0.01. Power curves (with 95% pointwise CI) for LMM, TS and CTS. The x axis of the power plot represents the relative reduction of the slope per one unit increase in reference allele.

Effect of distributional assumptions

We explored the performance of the approximate procedures in cases where the distributional assumptions of the LMM are not met. We considered MAR dropout and two modifications of Scenario 1. In the first modification, we simulated measurement error from the strongly asymmetric, exponential distribution with rate parameter equal to σ₁ to keep the same variance like in the BMD data. We next shifted this distribution such that the mean was equal to 0. In the second case, we applied the exponential distribution to the random effects, also keeping variances like those in the BMD data. For the exponentially distributed measurement error, the type I error rate was approximately 0.05 for all the methods and the maximum loss of power was equal to 7 and 1% for TS and CTS, respectively. Similarly, for the exponentially distributed random effects, the maximum loss of power for both TS approaches was only 1% with the type I error rate approximately 0.05. Note that in this case the random effects were simulated as independent.

Discussion of the simulation results

In the balanced case, the TS seriously suffers from lack of power in Scenarios 4–7, where small variability of the random slope is combined with a high correlation between the random effects. However, it is not the high correlation per se that causes the drop in power since one can always render the correlation zero. In fact, it is the complex interplay between σ, σ₀, σ₁, ρ and the values t₁,...,t_n that have an impact on the power. Our simulation study did not unravel this complex interplay, but had only the intention to show that some loss of power can be expected in some extreme situations.

The CTS approach provides an approximation to the slope obtained by the CLMM. Now, since the CLMM removes the effect of the cross-sectional part on the estimation of the slope, different results from those of the LMM should be expected. As mentioned above, the advantage of the CLMM is that it is less vulnerable to misspecification of the cross-sectional part. To appreciate the CTS as an approximation of the CLMM, we also compared the P-value obtained from the CTS and the CLMM. For this, we only deal with the unbalanced case of Scenario 5, where the greatest drop in power is seen. From Supplementary Figure 1, it is clear that the CTS perfectly approximates the P-value obtained in the CLMM, suggesting that its power loss with respect to LMM is implicitly related to the conditional model. We can safely conclude from the above simulation results that the CTS approach is superior to the TS approach, loosing basically no power in the balanced case compared with the LMM and showing a minimal power loss in the unbalanced case. The eventual loss in power is due to the loss of power with the CLMM, and this loss must be weighted against the advantage of the conditional approach that it is less vulnerable to model assumptions than the LMM. More details on that topic can be found in the Supplementary Material.

Practical aspects and computation times

Our simulation study clearly indicates that the CTS approach is the method of choice for the approximate computations in longitudinal GWAS. We illustrated that especially for unbalanced data (and we expect the readers to be mainly dealing with such data) this approach is more precise and reliable than the TS approach. In our experience, the CTS approach does not inflate the type I error and leads to only a minor loss of power, which depends on the data scenario. In practice, one can learn a lot about the data by fitting a LMM without a SNP. The variance component parameters will basically not change when the SNP is included in the model, as the effects in GWAS are very small. This provides useful information on the expected power loss when applying the CTS approach. Additionally, is it advisable to conduct a small simulation study, say for 100 SNPs, assessing the quality of approximations. After the approximate GWAS is performed, one will obviously confirm the findings by fitting the LMM to the most promising SNPs. Depending on the expected small power loss, a somewhat increased number of ‘the top' SNPs can be considered. The practical use of the CTS approach is also displayed in Supplementary Figure 2. We compared the pure computation times (without time spent on data access) using the 3.0.2 64-bit version of R software¹⁴ on a desktop computer with i5-3470, 3.20 GHz and 8 GB of RAM. Fitting one LMM (2) for 2000 individuals takes around 2 s using the package nlme and around 0.5 s using the package lme4, which would imply 23 and 6 days, respectively, for 1 M of SNPs. This computation time is linear in the sample size. Applying the two TS procedures we reduce the computations to fitting one LMM for all the SNPs and a simple linear regression for each SNP at a time. One should also note that the data transformation needed for CTS is performed within a minute. Using a standard procedure in R, function lm, fitting 1 million regressions takes around 1 h. Applying the SPR we can perform this analysis within 2 min. Finally, one should add the time spent on re-analyzing ‘the top' SNPs with the LMM, around 2 min for fitting 100 regression models. To summarize, we speed up the computations for 1 M of SNPs from 23 or 6 days to 5 min. Supplementary Figure 3 displays the time needed to perform the second step of the TS procedures and the speed up with respect to the LMM for different sample sizes and the number of repeated observations. Note that the computation time for the TS methods is essentially the same regardless the number of longitudinal observations. With 10 observations per individual the CTS approach is 50 000 times faster than the function lmer. This is partially due to the fact that values for a SNP, which are read from the files as N-dimensional vector do not need to be expanded to length N*n, which is an additional cost of the standard analysis in R functions. Another aspect of the analysis is SNP data access, which remains the same issue for any type of computations. Application of array-oriented binary files has been discussed in Sikorska et al⁶ showing that an additional 5 min is needed to access the data for 1 M of SNPs. As a result, we make the GWAS computations feasible on a single everyday computer.

DISCUSSION

We explored the performance of two approximate procedures for GWAS on longitudinal data in different scenarios. Our analytical investigations for the balanced case showed that the CTS approach provides an excellent approximation of the P-value for the SNP × time interaction term obtained from the LMM and the CLMM. This result was also confirmed in the simulation study. The performance of the TS approach is less straightforward, due to lack of insightful expression for the standard errors. For the balanced case, this method showed to be sensitive for the variance-covariance structure of the random effects. The same behavior was observed for the CTS approach with unbalanced data; however, the loss of power is always much lower than in the TS approach. One should note that in our simulations we considered extreme values for ρ. In practice, the correlation of −0.9 is improbable. We also indicated that it is not necessarily the correlation that drives the results, since this correlation can always be made zero. We additionally illustrated the possible danger in using the TS approach when a SNP is cross-sectionally important, leading to either strongly inflated type I error rate or considerable loss of power. In conclusion, the CTS approach provides, in virtually all practical situations, a very good approximation of the P-value for the SNP × time effect obtained from the CLMM. At the same time, it better protects the user against model misspecification than the LMM and the TS approach. We also validated performance of the CTS approach for low minor allele frequencies. The simulations indicated a good performance for MAF equal to 0.05 and even 0.01 (results not shown). In addition, it hugely reduces demands on computing resources. Finally, the TS approaches can be viewed as approaches that perform inference on the longitudinal fixed effects using longitudinal summary measures, namely the random slopes. In this paper, we focused on evaluating the importance of the SNPs separately, but it is clear that the CTS approach can be extended to cover mixed models with a non-linear evolution in time modeled either in a non-linear or in a smooth manner. Another interesting point is to explore performance of our method under more complicated missing data mechanism, such as MNAR. When the missing data process is MNAR, none of the likelihood approaches will do a perfect job. This also applies to our approach. Strictly speaking, the only thing that can be done is to apply a sensitivity analysis whereby a variety of missing data models are combined with the measurement model (here the mixed model). Finally we note that our approach assumes uncorrelated measurement errors. Thus, in principle correlated errors are not covered here. However, in Jacqmin-Gadda et al¹⁵ it is shown that the estimation of fixed effects is robust against violation of independence assumption as long as random intercept and slope are present in the mixed model. This is also confirmed in the Supplementary Figure 4. We believe that our approach therefore offers a wide range of possibly complex statistical procedures that are practically feasible with limited computational resources.

The authors declare no conflict of interest.