Gene Expression Evolves under a House-of-Cards Model of Stabilizing Selection

Abstract

Divergence in gene regulation is hypothesized to underlie much of phenotypic evolution, but the role of natural selection in shaping the molecular phenotype of gene expression continues to be debated. To resolve the mode of gene expression, evolution requires accessible theoretical predictions for the effect of selection over long timescales. Evolutionary quantitative genetic models of phenotypic evolution can provide such predictions, yet those predictions depend on the underlying hypotheses about the distributions of mutational and selective effects that are notoriously difficult to disentangle. Here, we draw on diverse genomic data sets including expression profiles of natural genetic variation and mutation accumulation lines, empirical estimates of genomic mutation rates, and inferences of genetic architecture to differentiate contrasting hypotheses for the roles of stabilizing selection and mutation in shaping natural expression variation. Our analysis suggests that gene expression evolves in a domain of phenotype space well fit by the House-of-Cards (HC) model. Although the strength of selection inferred is sensitive to the number of loci controlling gene expression, the model is not. The consistency of these results across evolutionary time from budding yeast through fruit fly implies that this model is general and that mutational effects on gene expression are relatively large. Empirical estimates of the genetic architecture of gene expression traits imply that selection provides modest constraints on gene expression levels for most genes, but that the potential for regulatory evolution is high. Our prediction using data from laboratory environments should encourage the collection of additional data sets allowing for more nuanced parameterizations of HC models for gene expression.

Introduction

Regulatory variation within and between species is thought to explain a large proportion of phenotypic diversity of life (Wilson et al. 1974; King and Wilson 1975; Hammer and Wilson 1987). In the past decades, gene expression microarrays and transcriptome sequencing have revealed remarkable natural variation in gene expression levels within populations as well as between species (Townsend et al. 2003; Gilad 2012). However, more than a decade after the first genome-wide assay of gene expression, we still lack an explicit evolutionary model for the processes governing the generation and elimination of the abundant gene expression variation within populations (Warnefors and Eyre-Walker 2012). Transcriptomic comparisons of humans and chimpanzees have been used to suggest that gene expression evolves neutrally (Khaitovich et al. 2005; Chaix et al. 2008). However, analyses of species divergence at longer timescales (Rifkin et al. 2003; Lemos et al. 2005) and contrasts of mutation accumulation assays with natural variation (Denver et al. 2005; Rifkin et al. 2005; Landry et al. 2007) provide strong evidence for the role of stabilizing selection in shaping gene expression variation and divergence for a large proportion of the genome in species from yeast to fruit flies to mammals. While reconciling these ideas and observations and revealing the diversity of ways that evolution shapes gene expression across ecological and demographic contexts will be the work of decades, framing research in this area in light of explicit theoretical models can help to more clearly illuminate the key unknowns. Here, we link a longstanding body of quantitative genetic theory with genomic data sets to illustrate the potential of new empirical sources of data combined with classical theory to guide future research.

Quantitative genetics theory predicts that populations attain an equilibrium of phenotypic variation when the contribution of new mutations to phenotypic variance is balanced by selection and drift. A class of models designed to quantify this equilibrium variation describe fitness as a unimodal function of the focal phenotype influenced by mutations drawn independently from a fixed distribution. Although a general result that applies across all parameter values has been challenging to obtain, three asymptotic models yield analytical expressions relating the standing genetic variance to the strength of selection and the frequency and distribution of mutational effects. In a neutral model, selection is assumed to be negligible and the equilibrium genetic variance derives from a balance between mutation and drift (Lynch and Hill 1986). Two additional models incorporating selection differ in how mutation and selection impact standing genetic variation. In the Gaussian model (Lande 1976), mutations are relatively frequent, are of small effect compared with standing genetic variation, and are countered by weak selection. In the House-of-Cards (HC) model (Kingman 1978; Turelli 1984; Burger et al. 1989), mutations are infrequent, their effects can exceed standing genetic variation, and selection is correspondingly stronger to maintain equilibrium levels of genetic variation.

Empirical data characterizing mutational input permit the evaluation of these longstanding evolutionary hypotheses against one another, in part because the variance in mutational effects should be much larger under an HC than under a Gaussian process of stabilizing selection. As a consequence of the direction and magnitude of mutational effects, some phenotypes could evolve neutrally, though for organismal level traits, phenotypic evolution under strict neutrality is thought to be relatively rare (Estes and Arnold 2007). To better characterize the effects of mutations, the rate at which mutation contributes new variation to a population each generation, or mutational variance (V_m), has been estimated using mutation accumulation experiments. For a number of organismal traits including Drosophila viability, bristle number, and alcohol dehydrogenase activity, Tribolium pupal weight, Daphnia life history, corn vegetative and reproductive traits, barley biomass and grain yield, and mouse skeletal traits, these experiments suggest that mutation supplies substantial mutational variation consistent with evolution in the HC domain (Lynch 1988; V_m/V_e = 10⁻⁴–10⁻²). Estimates of mutational variance for gene expression tend to be substantially smaller (Denver et al. 2005; Rifkin et al. 2005; Landry et al. 2007; V_m = 10⁻⁵–10⁻⁴). Furthermore, the strength of selection on expression level of single genes might be supposed to be substantially less, at least on average, than that imposed on organismal traits more proximal to fitness. Both observations raise the question of whether stabilizing selection on gene expression might be more consistent with a Gaussian or even a neutral model of phenotypic evolution. Identifying a theoretical model capable of capturing the patterns evident in natural populations for this fundamental molecular phenotype could have the potential to illuminate evolutionary principles at higher levels of biological organization.

As mutation accumulation experiments and measurements of genetic variance for gene expression become increasingly accessible for emerging model species (Pannebakker et al. 2008; Roles and Conner 2008; Molnar et al. 2011; Ness et al. 2012; Hall et al. 2013; Latta et al. 2013), one of the key empirical unknowns required for parameterizing theoretical models of stabilizing selection is the number of loci controlling gene expression levels. Because the availability of new variation in expression scales with the number of loci at which mutations can induce changes in expression, this parameter fundamentally influences inferences about the strength of selection. Despite its importance, the number of genes controlling gene expression has been challenging to characterize empirically. Studies identifying eQTLs have historically been underpowered to map loci with small effects, and are restricted to variants currently segregating in natural populations. More manipulative assays, like screens for the effects of gene deletions on gene expression, have been confined to analyses of nonessential genes in tractable model organisms. These methodological limits may yet be overcome (e.g., Bloom et al. 2013; Duveau et al. 2014), but for the moment, the level of selection can be inferred in relation to a range of likely values corresponding to the unknown genetic architectures.

Here we apply genomic measurements of mutational variance, the number of loci contributing to gene expression, population variation, and mutation rates to evaluate the appropriate model for gene expression evolution. We calculate the level of stabilizing selection according to the best-supported model to ascertain the possible strengths of stabilizing selection on gene expression, from nearly neutral to strong constraint. We then contrast our range of estimates for the strength of stabilizing selection on gene expression with estimates of stabilizing selection for other phenotypes as well as other sources of empirical data addressing the effect of expression change on fitness in order to confirm and more fully characterize the dynamics of gene expression evolution. We verify our inference by comparing the level of selection inferred across genes with other sources of empirical data addressing the effect of expression change on fitness, and contrast the observed patterns of evolution in this important molecular phenotype with other organismal traits.

Results

Theory

The neutral (N) approximation for genetic variance (V_g) predicts the magnitude of V_g as

$$V_g{}^{\text{N}}=2N_e{V}_m$$ (1)

where N_e is the effective population size and V_m is mutational variance (Lynch and Hill 1986). Because V_g, N_e, and V_m are each measurable, the neutral prediction of the genetic variance $V_g^{\text{N}}$ can be calculated from measured N_e and V_m and then compared with the empirical estimate of V_g. In contrast, the Gaussian (G; Lande 1976) and HC (Kingman 1978; Turelli 1984) models allow a role for stabilizing selection in constraining genetic variance, and thus feature a common parameter for selective variance V_s. As a metric of the breadth of the fitness landscape around the optimal phenotype that is inversely proportional to the strength of stabilizing selection (Johnson and Barton 2005), V_s is challenging to measure (Kingsolver et al. 2001; Rest et al. 2013). Theoretical and simulation work has demonstrated that these two models are accurate in different regions of mutation–selection parameter space (Turelli 1984; Bürger 2000), and has identified the domains of their accuracy. Thus, to establish which model applies, we calculate V_s for each model from its measurable parameters and check whether estimates of V_s based on the two models are consistent with their domains of accuracy. Accordingly, the original forms of the approximations can be solved for selective variance, V_s, to yield

$${V_s}^{\text{G}}=\frac{V_g{}^2}{2n{V}_m}$$ (2)

$$V_s{}^{\text{HC}}=\frac{V_g}{2n\mu }$$ (3)

where V_s is defined based on the magnitude of V_g, V_m, the number of loci contributing to expression variation (n), and the phenotypic mutation rate (μ). The Stochastic House-of-Cards (SHC) approximation (Turelli 1984) relaxes the assumption of infinite population size by incorporating effective population size (N_e). It can be solved for V_s using substitutions based on the definition of mutational variance, $V_m=2n\mu {\alpha }^2$, where α² is the variance in mutational effects, to yield

$$V_s{}^{\text{SHC}}=\frac{N_e{V}_g{V}_m}{2n\mu (2N_e{V}_m-V_g)}$$ (4)

Consistent with their differing assumptions about the relative importance of standing genetic variation and the variance in mutational effects, the G and HC estimates of V_s differ by a factor of $\frac{V_g}{2n{\alpha }^2}.$To differentiate between these stabilizing selection scenarios, the empirically measured values for the relevant parameters and the calculated value of V_s for each model can be contrasted with the boundary line between the domains in which the G and HC models apply, 20 μV_s = ${\alpha }^2$ (Turelli 1984), and the results based on V_s can be compared. Evolution characterized by frequent mutations of small effect under weak selective constraint lies in the G domain

$$\text{2}0\mu V_s>{\alpha }^2$$ (5)

and is well described by the Gaussian description of mutation–selection balance. Evolution characterized by rarer, more variable mutational effects under moderate selective constraint lies in the HC domain

$$\text{2}0\mu V_s<{\alpha }^2$$ (6)

and is well described by the HC class of models. We can empirically determine the consistency of data with this boundary using the HC, G, or a model-averaged approach to determine V_s.

Nearly neutral theory predicts that selection is most effective at large population sizes and that population dynamics become more similar to neutral drift as N_e or selection coefficients (s) decline; nearly neutral evolution is predicted to occur around $N_{e}s\approx 1$ (Ohta 1976; Ohta and Gillespie 1996). To estimate the typical selective effects of individual deleterious alleles s from the population level measure of selection V_s, we used Bürger’s (2000, p. 280) approximation of the average selective effect of a deleterious mutation in a population $\overline{s}=\frac{{\alpha }^2}{2V_s}$. To be consistent with a trait evolving under nearly neutral evolution, inferred .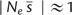

Analysis

Data on the budding yeast, Saccharomyces cerevisiae, yielded estimates and uncertainty distributions for the necessary parameters to analyze these models. We assembled gene-specific genetic variances among largely Italian vineyard-derived isolates for gene expression, mutational variances based on mutation accumulation lines, estimates of the number of loci n controlling gene expression encompassing two data sets capturing the effects of gene knockouts on expression levels, a global rate of mutations, μ, likely to influence gene expression based on the frequency of phenotype-altering mutations, and an effective population size based on wine yeast nucleotide diversity scaled by mutation rate for 3,412 genes (Materials and Methods and table 1). By sampling from the uncertainty distribution for each estimated parameter and calculating results through equations (1)–(4), our analysis generated uncertainty distributions for $V_g^{\text{N}}$, $V_s^{\text{G}}$, and $V_s^{\text{HC}}$.

Table 1.

Genome-Wide Summary of Parameter Estimates and Their Sources.

		Saccharomyces cerevisiae	Caenorhabditis elegans	Drosophila melanogaster (The Netherlandsa)	Drosophila melanogaster (Zimbabwe)
No. of Genes Analyzed		3,412	930	4,950	563
Vg	Median	0.101	0.050	0.097	0.088
	Interquartile range	0.073–0.145	0.031–0.90	0.054–0.147	0.052–0.158
	No. of individuals	9	5	8	8
	Ref.	Fay et al. (2004)	Denver et al. (2005)	Hutter et al. (2008)	Hutter et al. (2008)
Vm	Median	1.12 × 10−4	3.90 × 10−4	3.43 × 10−5
	Interquartile range	7.17 × 10−5–1.70 × 10−4	2.61 × 10−4–6.67 × 10−4	1.96 × 10−5–7.24 × 10−5
	No. of lines	4	4	12
	Ref.	Landry et al. (2007)	Denver et al. (2005)	Rifkin et al. (2005)
μ	Median	1.08 × 10−5
	Interquartile range	3.53 × 10−6–2.51 × 10−5
	Ref.	Kondrashov (2003)
Ne	Point estimate	1.06 × 106	1.75 × 104	2.6 × 106
	Ref.	Lynch et al. (2008); Elyashiv et al. (2010)	Denver et al. (2005)	Andolfatto et al. (2011)

^aDrosophila melanogaster V_g data from the Netherlands population are used for results reported in the main text. Further analyses are presented in the supplementary material, Supplementary Material online.

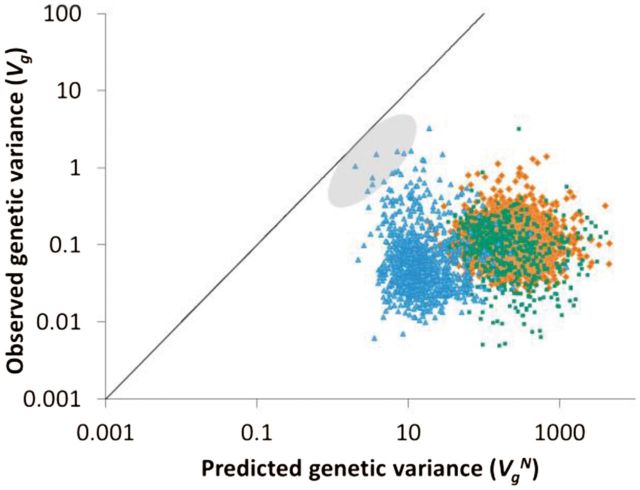
For all genes, estimates of $V_g^{\text{N}}$ were much larger than observed V_g (fig. 1), and estimates of $V_s^{\text{G}}$ and $V_s^{\text{HC}}$ differed substantially (supplementary table S2, Supplementary Material online). Estimates of the selective variance V_s for each gene individually exhibited considerable uncertainty. Nevertheless, both $V_s^{\text{G}}$ and $V_s^{\text{HC}}$, when sampled from their uncertainty with other parameters, yielded values that were consistent with equation (6), indicating that gene expression fell into the space described by HC models comprising stochastically large mutations and moderate selection. Although the Gaussian model could not be rejected for every gene, estimates of the variance of mutational effects (${\alpha }^2)$ and the joint effect of the phenotypic mutation rate and selection (μV_s) nearly all fell outside the regime that would support a Gaussian model (fig. 2a). Relaxing the infinite population size assumption of the HC model through the SHC approximation (eq. 4), which interpolates between HC stabilizing selection and neutral drift, produced outcomes nearly identical to HC (fig. 2a and supplementary fig. S1, Supplementary Material online). Whether the Gaussian model was rejected or not, the likeliest estimate for virtually all genes fell in the parameter space corresponding to HC conditions (99.5% of measured genes). Indeed, in no case could we reject the possibility that a yeast gene evolved under HC conditions. The number of loci controlling gene expression (n) does not impact model choice. This insensitivity is expected as a consequence of the term $\frac{1}{n}$ appearing on both sides of the inequality in the definitions of V_s and α².

Fig. 1.

Scatter plot of predicted genetic variance in gene expression based on a strictly neutral model versus observed genetic variance. The solid line represents the neutral prediction. Predicted and observed genetic variances are plotted for genes in Caenorhabditis elegans (blue triangles, 930 genes), Drosophila melanogaster (green boxes, 563 genes), and Saccharomyces cerevisiae (orange diamonds, 3,405 genes). Points plotted are the medians of the posterior distributions for each gene. Caenorhabditis elegans genes with confidence intervals that overlap neutrality are shaded in gray (seven genes for which P > 0.05).

Fig. 2.

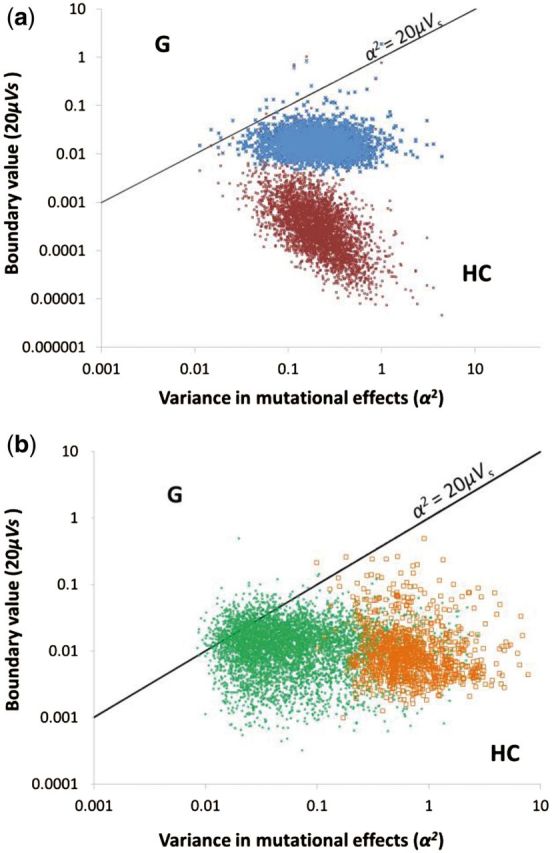
Scatter plot of the variance in mutational effects for gene expression (α²) by the product of mutation rate and the inverse strength of selection (20μV_s) for identifying the appropriate evolutionary model. The solid line represents the boundary between the domain of the Gaussian and HC models estimated by Turelli (1984). For each gene, the median of the uncertainty distribution for α², estimated as V_m/2nμ, is plotted on the x axis for n_KO1, and the median of the uncertainty distribution for the quantity 20μV_s is plotted on the y axis for (a) Saccharomyces cerevisiae genes using the Gaussian (open maroon squares), HC (blue circles), and SHC (dark blue crosses) approximation for V_s; and for (b) Drosophila melanogaster (green squares) and Caenorhabditis elegans (blue triangles) genes using the HC-Gaussian model-averaged estimate for V_s.

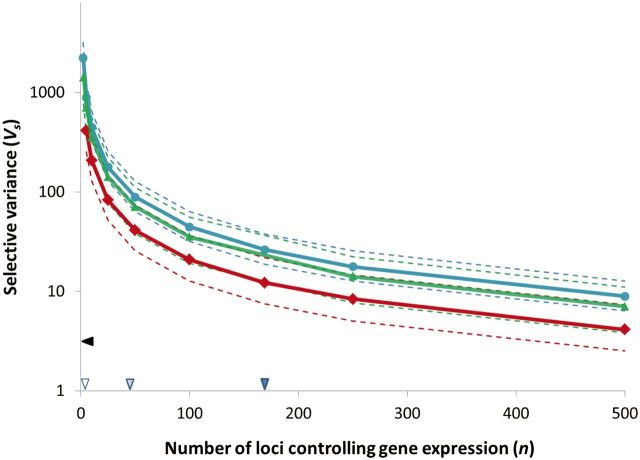
While evaluating the inequalities in equations (5) and (6) yielded support for the HC model for all n, the strength of selection inferred under the model depended on the choice of n (table 2). Taking the number of eQTLs detected as a proxy for the number of loci controlling gene expression to calculate $V_s^{\text{HC}}$ (hereafter V_s) yielded large values genome-wide, with a positive skew (median gene-specific V_s = 2.2 × 10³). Progressively larger values for n decreased the magnitude of V_s (fig. 3) with V_s estimated using mean values of n drawn from expression profiling of gene deletion mutants representing substantially stronger selection (KO₁: n = 48, median gene-specific V_s = 88.4; KO₂: n = 169, median gene-specific V_s = 26.2). Despite this uncertainty, V_s estimates for gene expression generally indicated weaker stabilizing selection than standardized selection gradients (γ) previously reported for morphological and phenological traits (Kingsolver and Diamond 2011) using the approximation $\frac{V_s}{V_p}=-\frac{1}{2\gamma }$ (Johnson and Barton 2005). This approach to detection of stabilizing selection in morphological and phenological traits relies on partial regressions of fitness on trait values that provided limited power to detect weak stabilizing selection (Kingsolver et al. 2001; see also Stinchcombe et al. 2008). If we limit our attention to the domain of n supported by empirical data, the magnitude of selection inferred on gene expression is weaker than reported estimates of selection on phenological and morphological traits (fig. 3, median $\frac{V_s}{V_p}=$3.1). We specified a normal distribution describing selection parameterized by the mean population expression and selective variance for all of our yeast genes. A logistic regression on “knockout values” based on the amount of this normal distribution that fell below zero predicted an independent, empirically determined data set on gene essentiality in rich media (Seringhaus et al. 2006; P < 0.001).

Table 2.

Parameter Estimates for the Number of Loci Controlling Gene Expression and their Sources..

Data Source		Saccharomyces cerevisiae	Caenorhabditis elegans	Drosophila melanogaster
eQTL	No. of genes analyzed	3,412	930	563
	Median n	2	1	1
	Interquartile range	1–3	1–1	1–3
	Ref.	Smith and Kruglyak (2008)	Vinuela et al. (2010)	Ruden et al. (2009)
KO1	No. of mutants analyzed	211	—	—
	Median n	48	—	—
	Interquartile range	24–96	—	—
	Ref.	Hughes et al. (2000)	—	—
KO2	No. of mutants analyzed	754	—	—
	Median n	169	—	—
	Ref.	Ho and Zhang (2014)	—	—

Fig. 3.

The influence of the number of loci controlling gene expression (n) on the genome-wide strength of selection. The median genome-wide V_s based on the HC model is plotted on the y axis based on values of n drawn from exponential distributions with means represented on the x axis for yeast genes (blue circles, 3,412 genes), fruit fly genes (green triangles, 4,950 genes), and nematode genes (red squares, 930 genes). Dotted lines represent the quartiles across all genes analyzed. Triangles on the x axis represent three empirical estimates for n (see table 2). The triangle on the y axis represents the median magnitude of stabilizing selection inferred on morphological and phenological traits for data reanalyzed from Kingsolver and Diamond (2011).

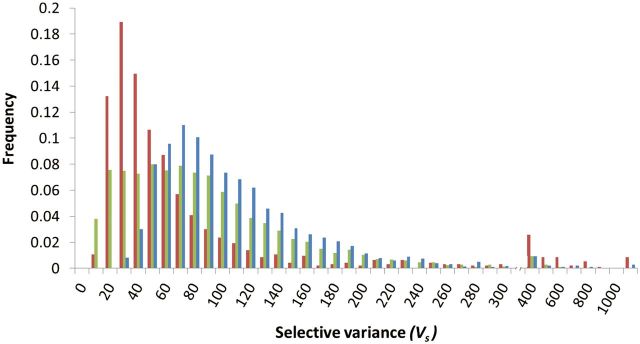
We also analyzed the neutral, Gaussian, and SHC models in two other model taxa, the fruit fly Drosophila melanogaster and the nematode Caenorhabditis elegans. As in yeast, $V_g^{\text{N}}$ was much greater than observed V_g for gene expression (fig. 1) in both European and African populations of fruit flies (Hutter et al. 2008) and in a cosmopolitan sample of nematodes (Denver et al. 2005). Using mutation accumulation expression data and a range of values for n to estimate α² and V_s values for each gene (fig. 3), the best estimates for gene expression in the fruit fly and nematode fell clearly within the domain of the HC model (e.g., with n_KO1 = 48, 99.7% of worm genes and 91.6% of fly genes; fig. 2b). Using $V_s^{\text{HC}}$ for V_s to evaluate the inequality 20μV_s < ${\alpha }^2$ yielded rejection of the Gaussian model for 88% of measured genes for nematodes and 30.2% for fruit fly (P < 0.05; a lower fruit fly V_m leads to estimates of ${\alpha }^2$ that are closer to 20μV_s; fig. 2b and supplementary table S1, Supplementary Material online). Using $V_s^{\text{G}}$ to evaluate the inequality was less conservative, rejecting the Gaussian model for 95% of nematode genes and 51% of fruit fly genes (P < 0.05). $V_s^{\text{HC}}$ and $V_s^{\text{SHC}}$ estimates were virtually identical for fruit fly genes. Typically, $V_{\text{s}}^{\text{SHC}}$ was greater than $V_s^{\text{HC}}$ for nematode genes, but resampling gene-specific or genome-wide uncertainty distributions for $V_s^{\text{HC}}$ and $V_s^{\text{SHC}}$ did not yield statistically significant differences between the two models. These two multicellular organisms yielded remarkably similar levels of selective constraints to yeast under the HC model, with many genes in the range of moderate selective constraint (e.g., with n_KO1 = 48, fly median $V_s^{\text{HC}}$ = 70.5, worm median $V_s^{\text{HC}}$ = 41; fig. 4). Repeating the Drosophila analysis for 260 genes in which estimates for the heritability of male gene expression permitted V_g to be distinguished from V_p (h² median = 0.19, range from 3.8 × 10⁻²¹ to 0.588; Wayne et al. 2007) strengthened the support for the HC model (20μV_s < ${\alpha }^2$ for 99.2% of tested genes), and substantially increased the strength of stabilizing selection inferred (e.g., with n_KO2 = 48, the median $V_s^{\text{HC}}$ = 1.3, and the interquartile range was 0.22–5.8).

Fig. 4.

The genome-wide frequency distributions of V_s based on the HC model. V_s values based on n estimated from differential expression in gene deletion strains (n_KO1 = 48) are binned and charted as bars for yeast (blue, 3,412 genes), fruit fly (green, 4,950 genes), and nematode (red, 930 genes).

Using an approximation for the average deleterious effect of a mutant allele for a population under stabilizing selection $\overline{s}=\frac{{\alpha }^2}{2V_s}$ (Bürger 2000, p. 280) facilitated further characterization of the level of selection in the context of population size. For yeast and fruit flies, few genes were consistent with nearly neutral evolution (based on the KO₁ gene deletion-derived values of V_s, yeast median |N_es| = 2.8 × 10⁴, 99.9% of genes significantly greater than 1 at P < 0.05; fruit fly median |N_es| = 1.1 × 10⁴, 99.9% of genes significantly greater than 1 at P < 0.05). Although the average population s values inferred for the nematode worm gene expression were intermediate between those of yeast and fruit flies, the smaller population size of this self-fertilizing species produced estimates consistent with nearly neutral evolution across most of the genome (median |N_es| = 1.3 × 10², 35% of genes significantly greater than 1 at P < 0.05).

Inferred levels of selection were robust to the choice of natural population. Recalculating V_s based only on the isolates collected from an Italian vineyard in two consecutive years demonstrated that results were robust to the inclusion of three non-Italian isolates (HC model linear regression: y = 0.96x + 78, R² = 0.93; supplementary fig. S2a, Supplementary Material online). Similarly, repeating the Drosophila analysis with an independent population of African flies illustrated that the genome-wide distribution of V_s values was robust to choice of fruit fly populations (supplementary fig. S2b, Supplementary Material online).

Discussion

We have demonstrated that the HC model best describes the patterns of genome-wide gene expression evolution observed across the model species S. cerevisiae, D. melanogaster, and C. elegans. The neutral model predicted a much larger V_g than was observed for all genes. Combining the distribution of mutational effects with the selective variance inferred under two different selective models provided support for the HC models over the Gaussian model, a result that was robust to contrasting estimates of the number of genes regulating gene expression. This support agrees with the functional observation that mutation of one or a few nucleotides can produce large changes in gene expression (Brown et al. 2008). The selection of the HC models, characterized by high mutational variance and moderate selective constraint, as best supported for gene expression phenotypes also agrees with analyses of mutational variance for several organismal phenotypes (Lynch 1988).

By providing a common theoretical framework, these quantitative genetic models allow comparisons across disparate species when parallel data sets are available. Using comparable sources of parameter values to identify V_s for a unicellular fungal microbe and two highly divergent multicellular animals revealed remarkably similar levels of selective constraint suggesting fundamental parallels in the action of natural selection on gene expression, filtered by the particulars of demography and life history. Examining estimated selection coefficients in the light of the relative population sizes suggested that even the weak selection inferred with n values based on eQTLs is nonetheless sufficiently strong to constrain population variation in gene expression for S. cerevisiae and D. melanogaster. The V_s values inferred for nematode C. elegans were on the same order of magnitude as the other two species, but were not as highly constrained, as would be expected if the species less efficiently removes deleterious variation, given its smaller effective population size and self-fertilizing life-history. For all three species, our use of empirical estimates of phenotypic variance (V_p) to approximate genetic variance (V_g) biases our estimate of V_s toward inferring weaker selection (greater V_s) than would be inferred from a known V_g. This bias is on the order of broad sense heritability as V_g = H²V_p (Lynch and Walsh 1997). The effect of this bias is conservative for our conclusion that the HC model applies better than the Gaussian model (20μV_s < ${\alpha }^2$), providing robust support for the HC model of stabilizing selection on the trait of gene expression.

The magnitude of stabilizing selection on gene expression inferred under the HC model was sensitive to the number of loci controlling gene expression variation, n, yielding relatively weak selection for n estimated from eQTLs to moderately strong stabilizing selection for n estimated from gene deletion studies. These estimates likely bound the true range of n: Underpowered eQTL studies frequently provide significant underestimates of n (Bloom et al. 2013), whereas the n derived from the effects of gene deletions on genome-wide gene expression might represent an overestimate of the number of genes in which variation arises by mutation in natural populations (Stern 2000). Support for the hypothesis that n is in the lower range we explored here for the majority of genes comes from explicit regulatory network models integrating diverse genomic data sets: The number of regulators represented by in-degree in these network models is another approximation of n. A recent predictive model in Drosophila using machine learning to integrate TF binding, sequence motif, chromatin modification, and expression data inferred a median genome-wide in-degree of 10 with a maximum of 188 (Marbach et al. 2012, Yang B, personal communication) Similarly, yeast network analysis has suggested that 93% of genes are regulated by 5 or fewer transcription factors (Guelzim et al. 2002). These results suggest that for the majority of the genome an appropriate effective value for n lies between n_eQTL and n_KO1, implying the strength of stabilizing selection centers around the lower end of the range estimated here. The HC and Gaussian models have been formulated under an assumption that all n regulators are interchangeable either in their rate of mutation or in their mutational effects. Improved information about the distribution of effect sizes on expression levels (Ho and Zhang 2014) and their frequency (Metzger et al. 2015) could make it possible to relax this assumption, exploring the influence of realistic variation in mutational effect size and frequencies. For example, mutations in cis and trans may occur at different frequencies or exhibit different magnitudes of effect (Gruber et al. 2012). Models capable of incorporating or accounting for a greater complexity of mutational frequency and effect (or even selective consequences, e.g., Coolon et al. 2014) could guide future hypotheses regarding the consequences of stabilizing selection on gene expression variation.

At the low end of the possible range of estimates of n, the predicted intensity of stabilizing selection on gene expression was sufficiently weak that one might ask if the level of selective constraint that we detect within populations contributes to meaningful changes in fitness. Several lines of evidence confirm that, at least for yeast, it does. In a previous analysis of the energetic cost of gene expression for yeast populations, Wagner (2007) identified a selective threshold, s = 1.47 × 10⁻⁷, below which he suggests that genetic drift dominates. The level of selection we estimate here for every yeast gene is stronger than that threshold. Thus, this independently established threshold supports our finding that even the weakest stabilizing selection detected in the yeast analysis could suffice to forestall large changes in gene expression and constrain the population distribution of expression variation when population sizes are sufficiently large. Accordingly, careful laboratory analyses manipulating expression levels have revealed impacts on fitness of even small changes in gene expression within yeast (Rest et al. 2013). Constraint on changes in gene expression is also evident even on longer time scales such as the divergence of species of Drosophila (Bedford and Hartl 2009). Furthermore, our observation that the inferred level of selection on zero expression in yeast significantly predicts the gene essentiality of the yeast knockout collection demonstrates that the selection detected here relates to the effect of fully abolishing expression.

Mutation–selection balance models such as the HC model miss some of the complexities that may be important in gene expression evolution. An analysis by Rockman et al. (2010) of population variation in C. elegans highlighted the role that genomic context can have in shaping expression variation: Inbreeding due to self-fertilization in this species reduces the rate of recombination, and these authors show that mutational pressure and frequency of recombination between linked sites are the most significant predictor of expression variation in this species. One implication of this finding is that models such as the Gaussian or HC model that neglect the role of genomic context may be most applicable to species with relatively high rates of recombination like yeast (Magwene et al. 2011) or fruit flies (Chan et al. 2012). Nonetheless, even with an estimate of population size that was highly conservative for this purpose, our analysis within these models did yield differences in the effectiveness of selective constraint in removing deleterious mutants between C. elegans and the other two species, consistent with the observed pattern of reduced recombination in the nematode. More complex models that incorporate the particularities of the life history and demography of the species under study would be of interest in extending the scope and accuracy of inferences of stabilizing selection within populations.

A key element for future estimates of stabilizing selection on gene expression will be the extension of models to incorporate interactions among genes. Covariances among traits are likely to be particularly important for expression phenotypes, which arise from interactions of transcription factors and other regulatory molecules with cis regulatory DNA (Harbison et al. 2004; Choi and Kim 2009). These interactions are challenging to characterize at a genome-wide scale due to the number of potential interactions, which goes up as the square of the number of genes. Covariances can arise in evolution as a consequence of correlated mutational effects as well as correlated selection on independent mutational effects (Walsh and Blows 2008). Disentangling the two requires assessing covariances among traits separately for new mutations and for segregating variants in natural populations. Fortunately, high throughput methods for identifying the frequency and identity of new mutations (Gruber et al. 2012; Duveau et al. 2014) as well as the source of segregating variation in natural populations (Ehrenreich et al. 2010; Taylor and Ehrenreich 2014) promise to accelerate the pace at which empirical data characterizing variation for gene–gene interactions become available (Mackay 2014). Investigations separating the influences of mutation from selection should also enable collection of more precise estimates of the rate at which mutations introduce phenotypic variation into a population (μ), as well as identify covariation between the number of genes affecting a trait and the magnitude of mutational effects on that trait. A model-based incorporation of interactions between genes into this evolutionary framework would strengthen our understanding of genome-wide gene expression evolution and enhance its realism (e.g., Innocenti and Chenoweth 2013). In particular, network output could be a more coherent unit of selection compared with individual gene expression (Harcombe et al. 2013).

Fully explaining the low selective constraint on gene expression estimated in these model organisms will also require greater consideration of the role of the environment in modulating selection on gene expression. Because gene expression is highly plastic to environmental variation, the degree of constraint detected will depend both on the strength of selection in the selective environment and on the correlation between population expression in the selective environment and in the environment in which expression was assayed. Laboratory environments, characterized by ideal conditions and enriched nutrition, are likely to be particularly permissive of variant expression, as illustrated by the survival of a large proportion of yeast gene knockout strains in this environment (Giaever et al. 2002). Moreover, correlations of gene expression among individuals within a population decrease in permissive environments (Hodgins-Davis et al. 2012). For these reasons, stabilizing selection on gene expression in natural environments might be considerably stronger than that measured here in artificial environments. Further resolution of the population genetics of stabilizing selection on gene expression requires studies that gather additional population variation and mutational accumulation data exploring gene expression across diverse environments. Incorporating a diversity of environments that are as close to natural as possible would provide further insight into the importance of mutation–selection balance in maintaining population genetic variation for gene expression.

The ascertainment of the appropriate model for population genetic variation in gene expression can facilitate efforts to appropriately parameterize gene expression evolution within populations and between species. Additionally, the estimates of the magnitude of the strength of stabilizing selection on genome-wide gene expression can facilitate diverse other molecular evolutionary studies ranging from the evolution of codon bias, transcription, and translation, to gene essentiality and gene duplication. Ultimately, comparisons to other modes of evolution including frequency-dependent selection or heterosis (Bulmer 1989) should be performed. Ideally, future studies should also map out the validity of the HC model across environments, identify how variation in ecological context influences the strength of selection on genome-wide gene expression, and fully characterize the strength of selection on expression across genes.

Materials and Methods

To estimate the magnitude of V_s under each model, each model parameter was estimated from empirical genomic data incorporating the full uncertainty inferred from available data, summarized in table 1. Uncertainty distributions for V_g and V_m were calculated from microarray data on mutation accumulation lines and population isolates of yeast (Fay et al. 2004; Landry et al. 2007), fruit flies (Rifkin et al. 2005; Hutter et al. 2008), and nematodes (Denver et al. 2005). Estimates of natural variation captured by V_g were derived from a population of yeast largely sampled from an Italian vineyard (Fay et al. 2004), European and African populations of fruit flies (Hutter et al. 2008), and a cosmopolitan sample of nematodes (Denver et al. 2005) and chosen so that the environment and developmental stage in which gene expression was assayed was matched as closely as possible to the mutation accumulation data available. Normalized fluorescence intensities were obtained from NCBI GEO, then analyzed using BAGEL (Townsend and Hartl 2002) to generate posteriors for relative gene expression level. We sampled from these posterior distributions for each genotype to create gene-specific uncertainty distributions for phenotypic (V_p) and mutational (V_m) variances. Because gene expression phenotypes in clonal cultures of S. cerevisiae exhibit extremely high heritabilities (median 84%; Brem et al. 2002), we approximated V_g with V_p for most of the analyses presented here. For Drosophila, the consequences of approximating V_g with V_p were assessed by calculating V_g for genes for which nonzero estimates of heritability were available for male gene expression (Wayne et al. 2007). Estimates of V_m were scaled by generations of mutation accumulation (yeast: 4,000; flies: 200; worms: 280). For yeast, a common genotype in the data sets (Fay et al. 2004; Landry et al. 2007) facilitated a common scaling of V_g and V_m; for worms, population and mutation accumulation data sets had already been compared within a single microarray study; for flies, each data set was scaled by the mean value of the population measured.

To establish the robustness of inferred levels of selection to the choice of natural population, two further analyses were carried out. First, to ensure that V_g was not artificially inflated by inclusion of a cosmopolitan sample of S. cerevisiae genotypes, yeast population data were reanalyzed excluding three lab and oak isolates to characterize the V_s values based only on isolates collected from an Italian vineyard in two consecutive years. Second, because the American D. melanogaster lab strain used to found the mutation accumulation lines was likely more closely related to European than African populations (Laurent et al. 2011), V_s values reported in the main text for D. melanogaster drew on V_g derived from a population of fruit flies collected in the Netherlands. However, an additional population of D. melanogaster collected from Zimbabwe provided an independent estimate of V_g (table 1; Hutter et al. 2008) and the analysis was repeated with this population.

Estimates of N_e were drawn from the literature for D. melanogaster and C. elegans (Cutter 2006; Andolfatto et al. 2011). S. cerevisiae N_e was derived by scaling measured nucleotide diversity (π) for wine yeast (Elyashiv et al. 2010) by the empirically measured nucleotide mutation rate (μ_nt, distinct from the phenotypic mutation rate μ of the models) (Lynch et al. 2008), using the classically defined relationship π = 4N_eμ_nt (Charlesworth 2009).

Empirical sources of data characterizing the number of loci controlling a given gene expression trait (table 2) include eQTL studies (Smith and Kruglyak 2008; Ruden et al. 2009; Vinuela et al. 2012) and gene expression profiling of the yeast gene knockout collection (Hughes et al. 2000). Because eQTL studies have limited power, we corrected for unobserved loci in yeast using the approach of Otto and Jones (2000), applying a genome-wide threshold for eQTL detection rather than a gene-specific threshold. Our uncertainty distribution was defined by the likelihood of each number of eQTL loci (eq. 7 of Otto and Jones 2000) over a domain of 1–30 loci (supplementary fig. S4, Supplementary Material online). Because eQTL studies likely underestimate the total number of genes contributing to gene expression variation, we also analyzed a second yeast data set to provide a maximum possible n for yeast gene expression that characterized the consequences of gene deletion on genome-wide gene expression (Hughes et al. 2000). The proportion of 211 diploid gene deletion strains that significantly changed gene expression (P < 0.01) was multiplied by the number of total genes in the yeast genome. These values were treated as point estimates of n and were used to recalculate V_s for those genes for which all data sources were available. A third estimate of n was drawn from the analysis of trait importance for gene expression by Ho and Zhang (2014). In this work, the authors perform a combined analysis of the effect of several experiments testing the effect of deletion of 754 different genes on genome-wide gene expression as measured in microarray experiments, identifying a 2-fold change in expression in 3.3% of the genome. The number of genes influencing gene expression could be extrapolated directly from the number of gene deletions captured by this survey to the total number of genes in the yeast genome. For all three empirical estimates, values for n were drawn from an exponential distribution whose mean was defined by the point estimates. To thoroughly explore the behavior of these models across the uncertainty of n, response of V_s estimates and model probabilities were calculated for exponential distributions with mean values up to a maximum of n = 500.

To parameterize a gamma uncertainty distribution for mutation rate μ, we used the method of moments on direct estimates of phenotypic mutation rate for 20 Mendelian disease-causing loci in humans (Kondrashov 2003), yielding a mean 4.7 × 10⁻⁴ and variance 0.22. Substituting a point estimate for μ drawn from mutational analysis of gene expression for the yeast gene TDH3 (Gruber et al. 2012) produced comparable results (supplementary fig. S3, Supplementary Material online).

Uncertainty distributions for selective variance based on the HC (Turelli 1984), SHC (Turelli 1984), and Gaussian approximations (Lande 1976) were calculated based on 10,000 independent draws from each parameter uncertainty distribution. Uncertainty distributions for both 20μV_s and ${\alpha }^2=\frac{V_m}{2n\mu }$ were calculated similarly, using the Gaussian, HC, SHC, and model-averaged estimates of V_s (supplementary material, Supplementary Material online). P values for the statistical significance of model rejection and for the model weights for the model-averaging were determined by the proportion of joint samples from these distributions that satisfied 20μV_s < ${\alpha }^2$.

The prediction of nearly neutral theory that $s\approx \frac{1}{N}$, where s is a selective coefficient and N is population size (Ohta and Gillespie 1996), was used to identify the consistency of the empirically estimated V_s values with the domain of nearly neutral evolution for all three species. To estimate s, we used Bürger’s (2000, p. 280) approximation that $s=\frac{{\alpha }^2}{2V_s}$ is the deleterious effect of an average mutant within a population, and calculated the uncertainty distribution for the quantity |N_es| based on 10,000 samples from parameter distributions for V_s and α². P values for the consistency of the quantity |N_es| with nearly neutral evolution were determined by the proportion of samples from the |N_es| distributions that were ≤ 1.

To test whether the degree of selective constraint predicted essentiality for each gene, we parameterized a normal distribution with the first central moment defined by the median of the uncertainty distribution for mean population expression level and the second central moment defined by the median of the posterior distribution for HC V_s. The cumulative density function of this distribution was evaluated at 0 as a hard selective bound on expression level, and used as a logistic predictor for independently gathered data on essentiality in rich media (Seringhaus et al. 2006). Diverse other genomic correlates, listed in the Supplementary Material online, did not show significant relationships with V_s.

Supplementary Material

Supplementary materials and methods, figures S1–S3, and tables S1 and S2, file, and references are available at Molecular Biology and Evolution online (http://www.mbe. oxfordjournals.org/).