Abstract
Population responses such as the auditory brainstem response (ABR) are commonly used for hearing screening, but the relationship between single-unit physiology and scalp-recorded population responses are not well understood. Computational models that integrate physiologically realistic models of single-unit auditory-nerve (AN), cochlear nucleus (CN) and inferior colliculus (IC) cells with models of broadband peripheral excitation can be used to simulate ABRs and thereby link detailed knowledge of animal physiology to human applications. Existing functional ABR models fail to capture the empirically observed 1.2–2 ms ABR wave-V latency-vs-intensity decrease that is thought to arise from level-dependent changes in cochlear excitation and firing synchrony across different tonotopic sections. This paper proposes an approach where level-dependent cochlear excitation patterns, which reflect human cochlear filter tuning parameters, drive AN fibers to yield realistic level-dependent properties of the ABR wave-V. The number of free model parameters is minimal, producing a model in which various sources of hearing-impairment can easily be simulated on an individualized and frequency-dependent basis. The model fits latency-vs-intensity functions observed in human ABRs and otoacoustic emissions while maintaining rate-level and threshold characteristics of single-unit AN fibers. The simulations help to reveal which tonotopic regions dominate ABR waveform peaks at different stimulus intensities.
NOMENCLATURE
- ABR
Auditory brainstem response
- AN
Auditory nerve
- BM
Basilar membrane
- CN
Cochlear nucleus
- CF
Characteristic frequency
- dB HL
dB hearing level
- dB peSPL
dB peak-equivalent sound-pressure level
- dB SL
dB sensation level
- dB SPL
dB sound-pressure level
- EFR
Envelope-following response
- FFR
Frequency-following response
- HiSR
High spontaneous rate
- IC
Inferior colliculus
- IHC
Inner hair cell
- LoSR
Low spontaneous rate
- MeSR
Medium spontaneous rate
- OAE
Otoacoustic emission
- OAEDS
Distortion-source OAE
- OAERS
Reflection-source OAE
- SFOAE
Stimulus-frequency OAE
- TBOAE
Tone-burst OAE
- SR
Spontaneous rate
Tuning associated with the equivalent-rectangular bandwidth
I. INTRODUCTION
The auditory brainstem response (ABR), envelope-following response (EFR), frequency-following response (FFR), and complex ABR (cABR) to speech stimuli are scalp-recorded responses originating from sub-cortical portions of the auditory nervous system. They have been used extensively for both clinical and basic neurophysiological investigation of auditory function (see Picton, 2011; Burkhard et al., 2007 for an overview). For instance, ABRs in response to transient stimuli are routinely used in early detection of neonatal hearing impairment, while recent work suggests that the relative magnitudes of ABR wave-I and wave-V may be sensitive to the presence of cochlear neuropathy and hyperacusis (Schaette and McAlpine, 2011; Gu et al., 2012; Hickox and Liberman, 2014). Further, EFRs in response to high-frequency modulations applied to noise or tonal carriers (>80 Hz) have been used to assess supra-threshold temporal coding in the brainstem when cochlear gain and mechanotransduction are intact (Purcell et al., 2004; Bharadwaj et al., 2014; Bharadwaj et al., 2015). Because hearing impairment is characterized by frequency-dependent anomalies in cochlear gain and de-afferentation, it is important to understand which tonotopic regions along the length of the cochlear partition contribute to population responses such as the ABR and the EFR and how their generation depends on stimulus characteristics.
Though a considerable body of literature describes the phenomenology of aggregate population responses like the ABR and the EFR, not much is known about their relationship to single neuron responses. Computational models are thus essential to bridge this gap and relate ABRs, EFRs, and FFRs to the known properties of single neurons in the auditory nerve (AN), cochlear nucleus (CN), and inferior colliculus (IC). Further, computational models can illuminate the relationships between the responses at these different nuclei, especially given that detailed experimental data comparing responses across regions in the same species are scarce.
Embedding single-unit models into population response models is not new, and has led to functional ABR models (Dau, 2003; Rønne et al., 2012) that use single-unit AN models to drive population responses in parallel auditory filterbanks (Zhang et al., 2001; Heinz et al., 2001; Zilany and Bruce, 2006; Zilany et al., 2009; Zilany et al., 2014; Ibrahim and Bruce, 2010). The single-unit AN simulations in these models are good at capturing rate-level and temporal envelope synchrony characteristics of AN fibers (Heinz et al., 2001; Zilany and Bruce, 2006; Zilany et al., 2009), justifying their use as preprocessors for population-response models. Unfortunately, existing functional ABR models do not adequately account for broadband phenomena over a range of sound levels. This weakness is important for a number of reasons.
-
(1)
The ABR wave-V latency decreases 1.2–2 ms for a stimulus level increase of 40 dB in normal-hearing listeners (Gorga et al., 1985; Dau, 2003; Elberling et al., 2010; Strelcyk et al., 2009). ABR wave-V latency for different stimulus intensities is determined by how cochlear excitation patterns sum across the partition at different sound levels and hence provides an important metric for evaluating level-dependent characteristics of peripheral auditory models. However, current functional ABR models underestimate how much ABR wave-V latency changes with increasing intensity (∼0.5 ms/40 dB; Dau, 2003; Rønne et al., 2012). Because ABR wave-V latency-vs-intensity characteristics show many similarities to how transient-evoked otoacoustic emission latency changes as a function of intensity (Neely et al., 1988; Rasetshwane et al., 2013), this model failure suggests that existing approaches do not capture all aspects of the level-dependence of broadband peripheral responses.
-
(2)
AN models are evaluated based on single-unit responses, such that free model parameters are fit to match data recorded at one characteristic frequency or at one sound level. This poses a problem when using such models as preprocessors for population responses because the AN models are not calibrated for broadband stimuli. A complete ABR model should produce reasonable single-unit responses while accounting for broadband population response characteristics; these two aspects of the model response should not be treated independently. However, in existing ABR models it is impossible to unravel whether broadband responses fail because they do not adequately capture how AN fiber thresholds vary across frequency, or whether basilar-membrane (BM) excitation patterns to broadband stimuli are misrepresented over a range of stimulus levels.
-
(3)
Existing functional ABR models typically do not include low-spontaneous rate (LoSR) AN fibers. In light of recent experimental evidence suggesting their importance for processing supra-threshold hearing and their vulnerability to noise-exposure (Kujawa and Liberman, 2009; Furman et al., 2013; Bharadwaj et al., 2014), incorporating LoSR responses into ABR and EFR models could provide a convenient method for testing the potential contributions of LoSR fibers to responses at supra-threshold intensities. It is possible that LoSR fibers may not contribute much to ABRs in quiet based on their small onset amplitudes (Taberner and Liberman, 2005; Buran et al., 2010) or to the compound action potential (Bourien et al., 2014). However, their modulation response properties (Joris and Yin, 1992) may make their contribution to EFRs in response to sounds at moderate to high stimulus levels relatively important (Bharadwaj et al., 2014; Bharadwaj et al., 2015). Additionally, LoSR fibers may contribute to ABR growth rates at supra-threshold levels, which are shallower for noise-exposed animals with normal hearing thresholds than for controls (Lin et al., 2011; Furman et al., 2013).
-
(4)
Last, existing functional ABR models use a phenomenological kernel-based transformation where the summed AN response (wave-I) is convolved with a unitary response to yield the scalp-recorded ABR wave-V (Dau, 2003; Rønne et al., 2012). Even though the approach has proven useful, it obscures how information is transformed by processing in the CN and IC, which sharpen onset responses (Delgutte et al., 1998; Nelson and Carney, 2004) and introduce modulation tuning (Frisina et al., 1990; Langner and Schreiner, 1988; Krishna and Semple, 2000).
The present paper introduces a functional model of human ABRs that includes level-dependent features of cochlear processing, in combination with single-unit models of AN fibers, CN, and IC neurons. The resulting model captures broadband characteristics of normal-hearing human ABR responses. Simulated broadband characteristics are validated using available human data on the level-dependence of both ABR wave-Vs and otoacoustic emissions (OAEs). The presented normal-hearing model includes parameters reflecting frequency-specific cochlear gain, making it easy to simulate different patterns of both hearing loss and (selective) cochlear neuropathy and to study how they impact peripheral auditory responses.
II. THE MODEL
Figure 1 gives an overview of the different processing stages of the model and shows the signal flow. Stimulus pressure passes through a first order low-pass (4 kHz) and second order high-pass (0.6 kHz) filter with pass-band gain characteristics (18 dB) matching those of human middle-ear transfer functions (Puria, 2003). The filtered stimulus pressure then enters a nonlinear transmission-line representation of the cochlear partition (Verhulst et al., 2012), after which BM velocity is translated into IHC bundle deflection using a transformation gain constant. At each CF, the IHC bundle deflection passes through a compressive nonlinear function (Zhang et al., 2001) and a second order low-pass filter with cutoff frequency of 1 kHz to account for the roll off in temporal fine-structure phase locking caused by IHC membrane sluggishness. The AN synapse model is based on the three-store diffusion model proposed by Westerman and Smith (1988), of which variations appear in several computational AN models (Zhang et al., 2001; Heinz et al., 2001; Zilany and Bruce 2006; Zilany et al., 2009; Zilany et al., 2014). The present model does not account for either refractoriness or the dependence of spiking probability on longer-term input history observed in recorded AN post-spike timing histograms; however, this study focuses on onset responses, where such effects are not critical. At each CF, instantaneous firing rates of AN fibers with different spontaneous firing rates are summed at the input to the CN model stage. The envelope-tuned behavior of bushy cells in the ventral CN and the IC is used to represent some of the key aspects of brainstem processing (Nelson and Carney, 2004). Outputs of the model consist of population responses obtained by summing responses of all represented CFs above 175 Hz, either just before the CN (i.e., ABR wave-I), just before the IC (i.e., ABR wave-III) and just after the IC (i.e., ABR wave-V). Additionally, the model generates reflection and distortion-source otoacoustic emissions (Verhulst et al., 2012), which are simulated by transforming the stapes pressure into ear-canal pressure (i.e., OAEs) using a first order band-pass (0.6–3 kHz) reverse human middle-ear filter (Puria, 2003).
FIG. 1.
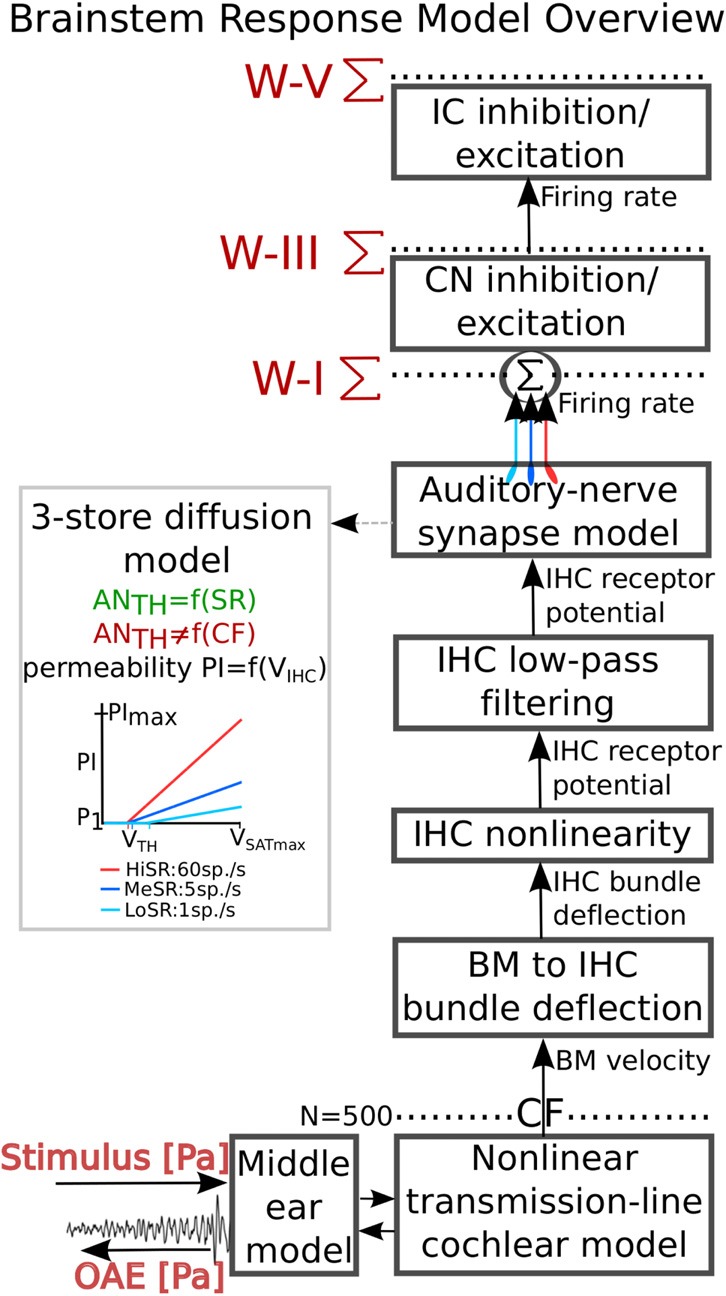
(Color online) Overview of the human auditory brainstem response model. Sound pressure enters a band-pass filter simulating the middle-ear forward transduction, after which cochlear transformation takes place by means of a time-domain nonlinear transmission-line model that discretized the cochlea in 1000 sections. OAEs are generated through a combination of cochlear reflection-sources and nonlinearities and travel back to the ear canal via a first order band-pass reverse middle-ear filter to form ear-canal OAE pressure. Simulated BM velocity from 500 CFs is translated into IHC bundle deflection using a gain transformation ratio, after which a logarithmic compressive IHC function is applied. IHC membrane properties are simulated using a second order low-pass filter with a cutoff frequency of 1 kHz. The AN synapse is modeled using a three-store diffusion model that allows for SR dependence of the fiber properties. Contributions from 19 AN fibers [70% HiSR (60 sp./s), 15% MeSR (5 sp./s), and 15% LoSR (1sp./s)] are added for each simulated CF before a functional model of the bushy cells in the CN and IC is applied. The inset illustrates how the AN fiber type influences the level-dependent properties of the immediate permeability of the three-store diffusion model and thereby the AN firing rate; properties that were kept CF-independent. ABR wave-V responses are simulated by summing up energy in all simulated CF channels above 175 Hz at the level of the IC. Wave-I and wave-III are obtained from summations just before and after CN processing (but after adding different SR contributions), respectively.
The middle-ear and cochlear model equations were computed in the time-domain using the differential equation solvers described by Altoè et al. (2014) at a sampling frequency of 100 kHz. Stimuli were initially generated in Matlab, which then called the cochlear model implementation in Python. Cochlear model simulations were done for 1000 logarithmically spaced CFs spanning the range of hearing (Greenwood, 1961). For half of these CFs, the simulated BM velocity and associated IHC bundle deflection was fed into the AN model (derived from C-code from Zhang et al., 2001; Zilany and Bruce, 2006; Zilany et al., 2009; Zilany et al., 2014; Ibhrahim and Bruce, 2010). The AN model was computed at a sampling frequency of 100 kHz for three AN fiber types differing in their SRs (1, 5, and 60 spikes/s or sp./s). The discrete SRs were chosen to represent the AN SR spiking histogram peaks for low, medium and high SR fibers (Liberman, 1978), based on the theoretical derivation that SR histograms of AN fibers can be explained by only few discrete SRs in combination with long-range dependence of spiking probability (Jackson and Carney, 2005). The resulting AN simulations were downsampled to 20 kHz, combined at each CF according to a ratio of AN fiber types representative of SR distributions in cat (Liberman, 1978), and fed into the CN and IC model (Nelson and Carney, 2004). The CN and IC modeling stages were implemented in Matlab. Population responses were generated, stored, and analyzed in Matlab at three levels of processing (waves-I, -III, and -V).
A. Basilar-membrane motion
Transmission-line models represent the cochlea as a set of coupled differential equations that describe the scalae pressure, BM displacement, and BM velocity for a large number of cochlear sections that span the cochlear place-frequency map (Greenwood, 1961; Table I). In section n of the current model, the shunt admittance of the BM and the series impedance of the fluids are given by the following frequency-domain equations (Zweig, 1991; Shera and Zweig, 1991):
| (1) |
| (2) |
where , with , and is the in vacuo resonant frequency of the cochlear section n. and represent the acoustic BM mass and the scalae fluid mass, respectively, at the basal-most section. The values of and are set by the parameter —which determines the number of wavelengths each traveling wave traverses before reaching its peak—through the relationship , with representing the space constant of the cochlear map (Zweig, 1991). The damping parameter , feedback strength , and dimensionless delay determine the location of the double pole of , and thus impact the gain and width of the cochlear filters. The input impedance of the model is resistive at angular frequencies much less than .
TABLE I.
Model parameters.
| ME and cochlear transformation | See also Table I of Verhulst et al. (2012) | Cochlear mechanics |
| = 4000 Hz | Cutoff frequency of the first order forward middle-ear filter (Puria, 2003) | |
| = 600 Hz | Cutoff frequency of the second order forward middle-ear filter (Puria, 2003) | |
| = 3000 Hz | Cutoff frequency of the first order reverse middle-ear filter (Puria, 2003) | |
| = 600 Hz | Cutoff frequency of the first order reverse middle-ear filter (Puria, 2003) | |
| Frequency-place distribution of characteristic frequencies along the position x along the basilar membrane (Greenwood, 1961) | ||
| [1/s] | Natural angular frequency at the base of the cochlea | |
| [Hz] | Characteristic frequency at the base of the cochlea | |
| [Hz] | Characteristic frequency at the apex of the cochlea | |
| [-] | Greenwood (1961) map exponent | |
| [-] | Zweig (1991) cochlear map parameter | |
| [-] | Number of traveling wave cycles before peak is reached | |
| vBM@NLTH = 4.3652 × 10−6 [m/s] | BM velocity threshold between linear and compressive BM behavior. The value corresponds to the v BM at CF to a 30-dB-SPL 1-kHz pure tone in a linear implementation of the model with a constant α* of 0.051. | |
| BMirr = 5% of [-] | Strength of BM irregularities giving rise to reflection-source OAEs | |
| C = 0.4 [dB/dB] | Compression slope of the cochlear nonlinearity | |
| Damping term that determines the location of (Shera, 2001) | ||
| Feedback term that determines the location of (Shera, 2001), was kept constant at 1.74 in Verhulst et al. (2012) | ||
| Feedback strength that determines the location of (Shera, 2001) | ||
| Parameter defined in footnote 8 of Shera (2001) | ||
| c = 120.9 | Parameter defined in footnote 8 of Shera (2001) | |
| BM to IHC bundle deflection | G = yBmax/vBMmax [s] | Transformation gain |
| yBmax = 200 × 10−9 [m] | Maximum IHC bundle deflection (Russell et al., 1986) | |
| vBMmax = 41 × 10−6 [m/s] | Maximum vBM in the cochlear model for a 100-dB SPL 1 kHz pure-tone | |
| Nonlinear IHC transformation | AIHC = 8 × 10−3 [-] | Scaling parameter in IHC model |
| BIHC = 12 × 106 [V/m] | Parameter in IHC model | |
| CIHC = 0.33 [-] | Exponent in IHC model | |
| DIHC = 200 × 10−9 [m] | Displacement offset in IHC model | |
| IHC low-pass filter | Fcut = 1 × 103 [Hz] | Cutoff frequency of the IHC low-pass filter |
| NFilter = 2 | Filter order | |
| Auditory nerve synapse | VTH, SR = 2 × 10−3 [V] | VIHC corresponding to a ∼40 dB shift in AN firing threshold for low SR vs high SR, according to VIHC-(VTH, SR/eSR) in Eq. (8) |
| VTH = 50 × 10−6 [V] | VIHC threshold below which the AN remains at SR for HiSR fibers. | |
| VSATmax = 1 × 10−3 [V] | VIHC yielding maximum PI. VSATmax determines the slope of the permeability function as a function of stimulus level in Eq. (8) and was determined iteratively such that for a HiSR fiber was in the same range as the implementation of Zilany et al. (2014). | |
| 0.1 < SR < 60 [sp./s] | AN spontaneous rate | |
| PTS = 1 + [6SR/(6 + SR)] [-] | Peak-to-steady-state ratio of rAN | |
| ASS,n = 150 + (CFn/100) | AN steady-state firing rate at saturation. CF-dependent fit to the range of AN fiber saturation rates found in Fig. 17 of Liberman (1978) | |
| = SR | Amplitude ratio between the and amplitudes of the rapid and short-term adaptation strength | |
| CG = 1 | Global Permeability, free parameter in the Westerman and Smith (1988) model | |
| τR = 2 × 10−3 [s] | Rapid AN time-constant (Zhang et al., 2001) | |
| τST = 60 × 10−3 [s] | Short-term AN time-constant (Zhang et al., 2001) | |
| Swave-I = 1.845 × 1014 | Scaling factor to yield a wave-I population response peak amplitude of 0.15 μV | |
| Cochlear nucleus | Swave-III = 93.8 × 10−6 | Scaling factor to yield a wave-III population response peak amplitude of 0.3 μV |
| DCN = 1 × 10−3 [s] | Disynaptic delay along inhibitory pathway (Oertel, 1983) | |
| SCN,INH = 0.6 [-] | Relative strength of inhibition vs excitation | |
| τex = 0.5 × 10−3 [s] | Exhibition time-constant (Oertel, 1983) | |
| τinh = 2 × 10−3 [s] | Inhibition time-constant (Oertel, 1983) | |
| Inferior colliculus | Swave-V = 90.9 × 10-6 | Scaling factor to yield an ABR peak-to-trough amplitude of 0.5 μV |
| DIC = 2 × 10−3 [s] | Synaptic delay along inhibitory pathway (Nelson and Carney, 2004) | |
| SIC,INH = 1.5 [-] | Relative strength of inhibition vs excitation |
Descriptions of the coupled set of equations describing BM pressure and velocity [] at each of the 1000 simulated cochlear sections were derived from Eqs. (1) and (2) and are provided in footnotes 1–3 of Verhulst et al. (2012). The set of coupled equations was solved in the time domain using a differential equation solver (Altoè et al., 2014) to yield time-domain values of BM velocity []. The frequency-domain model description in Eqs. (1) and (2) that was used as a basis for the simulated makes it easy to manipulate cochlear nonlinearity and auditory filter width in a controlled way, because both can be set by changing the double pole of the trajectory as a function of stimulus level (Shera, 2001; Verhulst et al., 2012) and CF. Whereas the previous model implementation used a “scaling-symmetric” approach in which the double-pole location was taken independent of n, so that the auditory filters all had constant tuning Q (Verhulst et al., 2012), the current implementation varies the value of based on the variation of human auditory filter tuning with CF. These values were calibrated using estimates (i.e., tuning derived from the equivalent-rectangular bandwidth) derived from stimulus-frequency OAEs (Shera et al., 2010) and human psychoacoustic forward-masking tuning curves (Oxenham and Shera, 2003).
The relationship between and double pole of was found by computing model solutions to a low-level 80 μs-click with iterated between 0.02 (maximally active, ) and 0.35 (passive; ) for each implementation (see also Fig. 1 in Verhulst et al., 2012). The power spectra of the BM responses at the 1-kHz CF locations for different were used to calculate where the equivalent rectangular bandwidth, corresponds to the area underneath the unity-normalized power spectrum of the BM impulse response at location . A power-law function describing the relationship between the simulated and values was used to implement CF-dependent tuning derived from human stimulus-frequency OAE group delays (Shera et al., 2010). Another power-law function, , was found to describe these otoacoustic tuning estimates well, and was adopted here to set for low stimulation levels (i.e., levels below those where nonlinear compression kicks in). For CFs > 5.2 kHz in the normal-hearing model, and values were set to 17 and 0.037, respectively, in order to keep the model solutions stable.
The above procedures determine of the auditory filters for low-level stimuli where the model behavior is linear. Compressive growth of BM level-functions was obtained by letting the values depend on the instantaneous amplitude of local BM motion. The details of the implementation are identical to those described in footnote 2 of Verhulst et al. (2012), with the exception that the model used here remains compressive at high levels (i.e., in contrast to the previous implementation, the value of does not necessarily approach a constant value at high stimulus levels). For BM velocities below the compression threshold = 4.3652 μm/s, the model behaves linearly with a constant whereas above this threshold, follows a hyperbolic trajectory dependent on the ratio |. The chosen parameters produce a BM compression slope of 0.4 dB/dB. This compression slope is somewhat higher than the values reported in animal studies from sensitive preparations (Robles and Ruggero, 2001), but falls within the range of those reported in human transient-evoked OAE growth studies (as summarized in Verhulst et al., 2011).
Even though changes with CF in the current implementation, the compression threshold () was held constant across CF. This yields simulated BM compression thresholds that depend on the filter gain strength at low stimulus levels (i.e., for high CFs where the gain is high, the nonlinearity “kicks in” at lower sound levels) and on how middle-ear transmission shapes the excitation pattern. These assumptions allow both loss of gain and loss of compression to be modeled using a single parameter. Using CF-independent values, simulated BM nonlinearity thresholds ranged between 25 and 40 dB sound pressure level (SPL) for frequencies between 0.5 and 4 kHz, and increased to 45 dB SPL for the 8 kHz pure-tone due to decreased middle-ear transmission at high frequencies. These values are close to previously reported average human compression thresholds of 40 dB (Johannesen and Lopez-Poveda, 2008) and demonstrate a frequency dependence that matches the 30 and 45 dB compression thresholds at 0.5 and 4 kHz (respectively) found using human distortion-product OAEs (Gorga et al., 2007).
B. IHC transduction stage
Modeling the mechanical coupling between BM and IHC bundle deflection is complicated by the fact that in vivo measurements are challenging in a system where mechanics of the fluid covering the OHCs between the reticular lamina and the tectorial membrane drive the IHC cilia (overview in Guinan, 2012). In the traditional view, shear motion between the reticular lamina and tectorial membrane causes the BM velocity to dominate the IHC responses at low CFs and the BM displacement/acceleration to dominate at high CFs (Freeman and Weiss, 1990a,b). IHC bundle deflection has been modeled by applying a high-pass filter with cutoff frequency around 500–900 Hz to the modeled BM displacement (Shamma et al., 1986) or a low-pass filter with cutoff frequency at 470 Hz to the modeled BM velocity at each CF (Sumner et al., 2002). Even though the order of the BM to IHC transduction filter is generally low, it can influence the relative contribution of different CF regions to the population response. For example, including a filter with a fixed low-pass filter cutoff frequency at each cochlear section reduces the relative contribution of the high-frequency single-unit IHC responses to the population response. In an alternative approach, a second-filter mechanism (where IHC velocity is modeled as a high-pass filter with a cutoff frequency proportional to the BM location) keeps the relative contributions of different CF channels unchanged while simulating the BM to IHC transduction stage (Allen, 1980). Because the form of the mechanical coupling between the BM vibration and IHC bundle deflection remains unclear, the transformation from instantaneous BM velocity to IHC bundle deflection is modeled using a constant gain, independent of CF,
| (3) |
The transformation gain G maps the maximal BM velocity represented in the model (i.e., max to a 100-dB 1 kHz pure tone) to the maximal IHC bundle displacement in the model (yBmax = 200 nm; in range of measurements by Russell et al., 1986). Consequently, there are neither CF-dependent gain reductions nor phase shifts in the IHC bundle displacement at low vs high CFs.
The IHC nonlinearity that describes the relation between IHC bundle deflection and IHC receptor potential is modeled as a compressive nonlinear function (Zhang et al., 2001) scaled to the input and output ranges of intracellular IHC recordings in mice (Russell et al., 1986):
| (4) |
with
| (5) |
The parameters are listed in Table I, and correspond to a dimensionless scaling parameter (), the IHC voltage per IHC bundle deflection ratio (), a compression exponent (), and bundle deflection offset (). Subscript indicates that is the IHC receptor potential before any IHC low-pass filtering. Figure 2(A) shows the shape of the compressive nonlinear IHC transduction adopted here. This nonlinearity was taken from Zhang et al. (2001), who motivate the use of this function over a standard Boltzmann function as providing a better fit to the AC/DC ratio of the IHC receptor potential.
FIG. 2.
Inner-hair-cell transduction. (A) Input−output characteristics of the logarithmic compressive function transforming IHC bundle deflection into IHC receptor current. (B) The IHC potentials' AC/DC ratio across frequency shows that the implemented second order low-pass filter yields IHC AC/DC ratios comparable to those reported in Palmer and Russell (1986; dashed), in range with other model implementations including the models of Zhang et al. (2001), Zilany et al. and that of Lopez-Poveda and Eustaquio-Martín (2006) (solid). The IHC bundle deflection at which the AC/DC ratio was calculated corresponded to that indicated by the gray filled symbol in panel A.
The receptor potential was obtained by passing through a second-order low-pass filter with a cutoff frequency of 1 kHz to model IHC membrane characteristics. This IHC low-pass filtering process is thought to account for the loss in the ability to phase-lock to the temporal fine structure of sound stimuli (Sellick and Russell, 1980; Russell and Sellick, 1983; Palmer and Russell, 1986) above the cutoff frequency of the IHC membrane filter. The present implementation differs from earlier ABR models in the order and cutoff frequency of the low-pass filter (second order 1-kHz filter here vs seventh order 3–3.9 kHz low-pass filter; Zhang et al., 2001; Zilany and Bruce, 2006; Zilany et al., 2009, Zilany et al., 2014; Rønne et al., 2012). The current implementation is closer to that of the first order filters adopted in Shamma et al. (1986); Sumner et al. (2002); and Jepsen et al. (2008).
The shape of the nonlinearity and the characteristics of the low-pass filter have important consequences for the AC/DC ratio of the IHC receptor potential and the AN phase-locking properties to temporal fine structure (Palmer and Russell, 1986). These effects are evident in Fig. 2(B), which shows the frequency dependence of the IHC AC/DC ratio for stimulus levels of 80 dB SPL in the data of Palmer and Russell (1986), alongside simulation results from the present as well as other models. It is clear that the implemented second order low-pass filter with 1-kHz cutoff leads to a shallower roll-off of the AC/DC ratio as a function of CF than does a seventh order filter (Zilany et al., 2014), but that the lower cutoff frequency (1 instead of 3 kHz) qualitatively improves the match of the response to the data of Palmer and Russell (1986). Filter description differences arise from fitting either the steepest part of the roll-off (Weiss and Rose, 1988; Zhang et al., 2001; Zilany et al., 2014) or where the curve starts bending (present model). Both approaches lead to a loss of AN synchrony to temporal fine structure at 4 kHz compared to 1 kHz.
C. AN-synapse
The majority of existing models of AN processing (Zhang et al., 2001; Heinz et al., 2001; Sumner et al., 2002; Sumner et al., 2003; Zilany and Bruce, 2006; Zilany et al., 2009; Zilany et al., 2014) based their implementations on the three-store diffusion model of the AN synapse by Westerman and Smith (1988) with characteristics similar to the earlier Meddis (1986) implementation (Zhang and Carney, 2005). The different model implementations are similar in that they describe instantaneous auditory-nerve firing rate as
| (6) |
where [i.e., in Meddis, 1986] equals the concentration of synaptic neurotransmitters in the immediate store, and where [i.e., in Meddis, 1986] determines the neurotransmitter vesicle release permeability to the immediate store. It is important to note that is the only parameter in the AN model that is stimulus-level dependent, through . Because the AN synapses depend on spontaneous rate (SR) in the current model, all equations of the three-store diffusion model (originally outlined in Westerman and Smith, 1988; Zhang and Carney, 2005) are implemented here (see the Appendix). Existing AN model implementations differ mainly in the description of the immediate permeability , which includes the treatment of the thresholds and SR-dependence of the AN fibers. In the present model, remains constant below the fibers' threshold , and increases linearly as a function of once the threshold is reached:
| (7) |
| (8) |
AN fiber thresholds were rendered SR dependent through the factor in Eq. (8), which yielded AN thresholds that are ∼40 dB higher for a LoSR fiber of 1 sp./s than for a HiSR fiber of 100 sp./s (in agreement with cat AN recordings in Liberman, 1978). Second, the slope of the permeability function, which determines how instantaneous AN firing depends on stimulus level, was set by the parameter , which determines the at which is maximal (see inset Fig. 1). This procedure can yield overall instantaneous AN firing rates that are higher than is realistic [determined by and the slope of ]. Though not included here, the addition of refractory effects would reduce the instantaneous spiking rates to more realistic values as measured using post-spike time histograms (Zilany et al., 2009; Zilany et al., 2014). The parameter , which determines the SR at threshold, was implemented similarly to previous models (Zhang et al., 2001; Heinz et al., 2001; Zilany and Bruce 2006; Zilany et al., 2009; Zilany et al., 2014):
| (9) |
where corresponds to the SR-dependent fibers' peak-to-steady-state ratio (Heinz, 2001; Zhang and Carney, 2005) and to the steady-state firing rate at saturation. was made frequency dependent to match the frequency dependence of cat HiSR AN fiber saturation in Liberman (1978). Last, the SR-dependence of the parameter was implemented using the original description in Westerman and Smith (1988) through
| (10) |
To qualitatively account for the slower recovery times of LoSR fibers than HiSR fibers to prior stimulation (Relkin and Doucet, 1991), , the ratio between the amplitudes of the rapid and short-term exponentials in the simulated instantaneous firing rate, was set to the fibers' SR [Eqs. (A9) and (10)]. Because the ratio does not influence the instantaneous firing rate amplitudes, but only affects the time constants of the decay for constant amplitude stimulation (Westerman and Smith, 1988), setting its value to SR yields slower recovery for LoSR fibers than for HiSR fibers, which could be important for capturing the onset responses of different fiber population types to repeated stimuli (Relkin and Doucet, 1991).
Because the present study focuses on onset-responses to tones, tone-bursts, and clicks, power-law adaptation was not included in the model. Power-law adaptation has been shown to account well for the fibers' response properties to sound offsets and intensity increments (Zilany et al., 2009, Zilany et al., 2014); if important, such adaptations could be incorporated into future implementations. The current model did not explicitly model either refractoriness (Zilany et al., 2009, Zilany et al., 2014) or the long-range dependence of spike timing (Jackson and Carney, 2005) visible in post-spike time histograms.
It is known that between 10 and 30 AN fibers synapse onto the average IHC, depending on species and cochlear location (Liberman et al., 1990; of these fibers, about 15%, 25%, and 60% constitute LoSR, MeSR, and HiSR fibers, respectively; Liberman, 1978). The normal-hearing model set to 19 fibers per IHC, of which three were LoSR (1 sp./s), three were MeSR (5 sp./s) and 13 were HiSR (60 sp./s) fibers. At each CF, this leads to the summed and normalized AN response ,
| (11) |
For each simulated cochlear section, was used as an input to the functional CN model. Cochlear neuropathy can be simulated by selectively removing different numbers and types of fibers while keeping in Eq. (11) fixed. Specific ratios of fibers can be set according to physiological studies (e.g., Kujawa and Liberman, 2009; Furman et al., 2013; Sergeyenko et al., 2013). is a scaling value that yields a realistic 0.15 μV wave-I peak amplitude for a normal-hearing model with 19 fibers at each CF.
D. Functional VCN and IC model
Unlike the unitary response approach described in earlier ABR models (Dau, 2003; Rønne et al., 2012), the present implementation adopts a functional inhibition/excitation model of the spherical bushy cells in the ventral cochlear nucleus (VCN) and inferior colliculus (IC) (Nelson and Carney, 2004). ABR wave-III and wave-V response generation is assumed to originate through the spherical bushy-cell pathway in the CN and IC. The model does not currently include other parallel pathways, such as those in the dorsal cochlear nucleus (DCN, Schaette and McAlpine, 2011) or lateral lemniscus, which likely contribute to the ABR (Voordecker et al., 1988; Melcher and Kiang, 1996; Ponton et al., 1996). These additional pathways were omitted based on arguments that waves beyond wave-I are absent in cat VCN lesion studies, and that spherical bushy cells are more common than globular bushy cells in humans (Melcher and Kiang, 1996). The model may not account for all of the neural sources that contribute to the ABR, but illustrates outcomes using the approach of capturing the functionality of the modulation-sensitive VCN and IC cells that likely dominate wave-III and wave-V responses, respectively (Melcher and Kiang, 1996).
The included functional CN and IC model was designed to account for the common band-pass shaped modulation transfer functions of chopper and onset neurons (Frisina et al., 1990), as well as sharp peaks in response to stimulus onsets in post-stimulus time histograms (Langner and Schreiner, 1988 and Fig. 11 of Nelson and Carney, 2004). Because the neurons with the strongest sensitivity to amplitude-modulation characteristics also have onset responses with sharp temporal precision (Frisina et al., 1990), modeling the amplitude-modulation properties of CN and IC neurons may automatically predict their precise onset responses. The inclusion of functional CN and IC models is also beneficial when simulating EFRs (Bharadwaj et al., 2014). Instantaneous firing rates at the CN and IC processing stages were computed using an established inhibition/excitation model (Nelson and Carney, 2004):
| (12) |
| (13) |
where , and are the time constants associated with excitation and inhibition, respectively. and are the synaptic delays associated with the CN and IC neurons (Table I), and and are parameters that scale the responses to yield wave-III and wave-V population response amplitudes in range with normal hearing human recordings (i.e., 0.3 μV and 0.5 μV, respectively; Table VIII-1 in Picton, 2011). The convolution [denoted by the operator * in Eqs. (12) and (13)] of the exponential functions and the instantaneous firing rate models the low-pass filter membrane properties of the bushy cells (Oertel, 1983).
Note that the integration properties of Eqs. (12) and (13) yield a spurious response at the onset of a new simulation where the input starts at a non-zero constant value [e.g., for firing at SR]. To differentiate this spurious response from that driven by true transient stimulation, it is advisable to run the model for a “burn-in” period of a few milliseconds before presenting a transient stimulus. For the transient stimuli adopted in this study, a minimum of 20 ms of silence was fed to the model before stimulus onset.
E. Simulation of population responses
Simulated population responses were obtained by summing the instantaneous firing rate across cochlear sections either at the level of the auditory nerve (yielding ABR wave-I), at the level of the CN (ABR wave-III), and at the level of the IC (ABR wave-V). The relationship between actual neural responses and the scalp-measured ABRs was assumed to be quasi-static (i.e., it was assumed there are no additional latencies introduced by tissue volume conduction), which is justified for responses below about 10 kHz where the brain/scull/scalp tissues are purely conductive (Hämäläinen et al., 1993). The dominant ABR waves-I, -III, and -V were simulated separately for each corresponding processing stage (i.e., AN, CN, and IC) because the functional model approach did not fit the relative latencies of the different waves beyond differences determined by the latencies introduced by the CN and IC models (Nelson and Carney, 2004). The model did not exhaustively account for the synaptic delays of all processing centers, which might affect the timing of different subcomponents of ABR waveforms recorded from the human scalp. For example, wave-II and -IV were not modeled here, even though their interaction with the other wave-generators might be important for the resulting ABR waveform-shape. However, the model does capture wave-I, -III, and -V peak amplitudes, which are robust in human recordings, allowing the systematic study of the roles of cochlear broadband and single-unit response properties in the generation and level-dependent effects of population responses. Only cochlear frequency channels above 175 Hz were included in the sum, in line with ABR measurements which show that contributions of the mid and high frequency tonotopic sections of the cochlea dominate ABRs (Don and Eggermont, 1978). In order to explore the full frequency range of the neural responses, the simulated ABR responses were not low-pass filtered, even though experimental studies often focus exclusively on low-frequency portions of the responses and filter ABRs with a low-pass cutoff frequency between 1.5 and 3 kHz.
To elucidate the mechanisms leading to level-dependent changes in ABR latency, ABR wave-V latency was not only calculated as the time between the onset of the stimulus and the peak of the ABR wave-V (Dau, 2003; Rønne et al., 2012), but also using a “forward latency” measure (Rasetshwane et al., 2013). Forward latency, , was introduced in experimental studies to isolate the cochlear contribution to ABR latency. Forward latency is calculated by subtracting neural and synaptic delays (assumed to be 5 ms in humans, Neely et al., 1988) from the measured ABR wave-V latency. In the present simulations, was obtained by subtracting the 3 ms conduction delays in CN and IC (i.e., DCN + DIC) from the simulated ABR wave-V latency.
F. Simulation of OAEs
The transmission-line model of the cochlea simulates distortion and reflection-source OAEs. These emission components can be isolated by manipulating the magnitude of the BM irregularities responsible for reflection-source OAE generation (Shera and Guinan, 1999). Similar to OAE recordings, the simulated ear-canal pressure in a model including BM irregularities consists of three components: (1) a stimulus component ( comprising the stimulus and the passive component of the response (governed by middle-ear and passive cochlear mechanics); (2) a reflection-source OAE component (); and (3) a distortion-source component () arising from cochlear nonlinearity. The relative amplitudes of the three components vary with stimulus level. was estimated by linearly rescaling the value of computed in the low-level linear regime (20 dB SPL) using simulations from a model with no micromechanical irregularities. This smooth, linear model simulated at low stimulus levels produces neither nor emissions. Using the resulting estimate of STIM, the total OAE () in the normal model was then computed as the difference
| (14) |
This method makes it possible to compute the OAE response without stimulus artifacts, which complicate human tone-burst OAE measurements. Experimental studies often use time truncation to separate the STIM component from the rest of the response (e.g., Neely et al., 1988; Rasetshwane et al., 2013). Tone-burst OAEs at frequency CFn were simulated for -ms long Hanning windowed pure-tones of 1, 2, and 4 kHz as inputs; the resulting outputs were compared to experimental recordings (Rasetshwane et al., 2013). In the experimental study (which used a Blackmann window, which is very similar albeit not identical to a Hanning window), was calculated using the energy-weighted group delay of the OAE waveform (Goldstein et al., 1971, Rasetshwane et al., 2013) after zero-padding the OAE waveform to a duration 0.5 ms longer than the stimulus duration (). Similarly, the simulated tone-burst emission OAEs were zero-padded before calculating the latency from the stimulus onset to the maximum of the waveform. The peak-to-peak latency method was used in the simulations because the energy-weighted group delay method in simulated, noise-free OAEs is dominated by low-amplitude long-latency OAE components that would be masked by measurement noise in actual recordings. For TBOAE recordings that show one dominant burst of energy in response to the evoking tone-burst, the energy-weighted group delay and the peak-to-peak method yield similar latencies.
III. RESULTS
The following sections discuss the ability of the model to simulate key level-dependent single-unit AN, CN, and IC properties. After that, it is shown how including OAE-derived human cochlear filter tuning parameters produces a model that naturally captures the frequency dependence of human cochlear tuning. Finally, the level-dependent properties of simulated ABRs and OAEs in response to broadband stimuli are compared to existing datasets as well as predictions from other functional ABR models in order to elucidate how the current model differs from previous, similar efforts.
A. Single-unit simulations
Figure 3 shows how single-unit simulations at the output of the AN, CN, and IC are affected by changes in stimulus intensity and modulation frequency. Figure 3(A) shows AN rate-level curves to 0.5 to 8 kHz 2-ms cosine ramped 120-ms long pure-tones for all three AN fiber types. Rate-level curves were calculated from the maximum instantaneous firing rate during the 60–80 ms window of the simulation to allow evaluation of the steady-state behavior of the responses. The maximum-instantaneous-rate measure approximates the energy underneath the instantaneous firing waveform irrespective of whether fine structure or envelope phase-locking is the dominant mechanism driving the response.
FIG. 3.

Single-unit properties of AN fibers and CN/IC neurons. (A) Steady-state AN rate-level functions calculated from the maximum of the instantaneous firing rate in the 60–80 ms window after tone onset for pure-tones between 0.5 and 8 kHz evaluated at CF. Results are shown for a HiSR (60 sp./s), MeSR (5 sp./s), and LoSR (1 sp./s) fiber. (B) Instantaneous firing rates in response to two 70-dB peSPL pure tones of 1 and 4 kHz separated by 50 ms silence, evaluated at the fibers' CF for a LoSR (1 sp./s) and HiSR (60 sp./s) AN fiber. (C) Onset responses of the AN responses depicted in B. (D) Second to first AN onset peak amplitude ratio in response to two 50-ms separated pure tones, showing that LoSR fibers recover slower than do HiSR fibers in this model. (E) Amplitude modulation gain to a 50-dB-SPL 4-kHz 100% sinusoidally amplitude-modulated tone of different modulation frequencies analyzed at CF. Modulation gain was computed from the spectrum of the recorded waveform at the modulation frequency and normalized by the maximum modulation across all tested CFs. The CN and IC processing stages show sharper band-pass filter characteristics than observed in the AN. (F) Modulation gain as a function of sound intensity for a fixed 100% modulation depth and 100 Hz modulation frequency. LoSR fibers contribute to the modulation-gain properties of the CN and IC processing stages at medium to high stimulus levels.
It is interesting to evaluate how AN firing rate varies with stimulus level for different types of AN fibers because the variation of simulated rate-level curves with AN fiber type and CF was not specifically calibrated in the current model. Instead, AN firing rates are a direct consequence of the values of the SR-dependent parameters and how the different AN fibers are driven by CF-dependent cochlear excitation. Comparing across panels in Fig. 3(A), LoSR fibers have higher firing thresholds than MeSR and HiSR fibers, irrespective of their CF. In accordance with experimental observations, simulated high-threshold (LoSR) AN fibers have larger saturation rates than do low threshold fibers (Sachs and Abbas, 1974; their Fig. 3). Across all CFs, the maximal difference in threshold between LoSR and HiSR fibers, given by the factor in Eq. (8), was 40 dB. The discharge rate at saturation for levels well above a fibers' threshold is frequency dependent and follows the shape of the parameter across CF (consistent with the frequency dependence reported in Fig. 17 of Liberman, 1978 for HiSR fibers).
Note that in physiologic responses, the steady-state firing rate is influenced by refractoriness in the nerve. As a result, the simulated is not expected to fit experimental data quantitatively (e.g., Liberman, 1978); refractoriness was not included here. In general, including a refractory period in the model will reduce steady-state firing rates; roughly approximated as , where equals the absolute refractory period (assumed 0.75 × 10–3 s), is the AN firing rate without refractoriness, and the firing rate with refractoriness (Vannucci and Teich, 1978). Thus, assuming = 0.75 × 10–3 s, the steady-state response rate in a model including refractoriness would equal around 140 sp./s for low CF responses, given that the rate computed from the current implementation of the model was 160 sp./s. This difference in saturation rates for models including and ignoring refractoriness is relatively small.
Figure 3(B) shows the instantaneous AN firing rate for both a LoSR and a HiSR fiber in response to two 70 dB-SPL 120-ms pure tones whose acoustic frequency is the CF, separated by a 50 ms gap. Whereas the 1 kHz responses phase lock to the fine structure of the stimulus, the 4 kHz responses show little phase locking, instead following only the onset−offset envelope of the stimulus. This demonstrates that the implemented second order 1 kHz IHC low-pass filter captures realistic AN phase-locking properties. Figure 3(C) zooms in on the onset response to the pure tone and shows that the onset peak latency of LoSR fibers occurred later than for HiSR fibers (1 ms at 1 kHz and 0.2 ms at 4 kHz), consistent with experimental data showing that first-spike latencies are greater for the LoSR fiber than for the HiSR fiber (Fig. 6 in Rhode and Smith, 1985; Fig. 6 in Bourien et al., 2014). In the model, the ratio of the onset-firing rate relative to the steady-state firing rate is greater for the HiSR fiber than for the LoSR fiber, also in line with experimental data (Taberner and Liberman, 2005; Buran et al., 2010). Further, the model qualitatively predicted that following a stimulus gap, LoSR fibers have a longer recovery time than do HiSR fibers (Relkin and Doucet, 1991). This aspect of the model response comes about because of the way in which the amplitude ratio [the rapid adaptation constant over the short-term adaptation constant, Eqs. (A9) and (A10)] depends on SR. Figure 3(D) shows that a 50-ms gap between the offset of one tone burst and the onset of a successive tone burst has a stronger effect on the LoSR fiber than on the HiSR fiber.
Figures 3(E) and 3(F) show single-unit AN, CN, and IC modulation tuning properties to 4-kHz 100% sinusoidal amplitude-modulated 50-dB-peSPL pure tones at CF. The modulation transfer function was calculated as the modulated firing rate of the single-unit response (see Joris et al., 2004 for a review) computed by normalizing the Fourier spectrum (in dB). by the maximum modulation strength; this is shown both as a function of modulation frequency [Fig. 3(E)] and as a function of stimulus level [Fig. 3(F)]. The cascading of the inhibitory and excitatory filtering in the “same-frequency” inhibition/excitation CN model [Eqs. (12) and (13); Nelson and Carney, 2004] resulted in modulation transfer function cutoff frequencies that are progressively lower from AN to CN to IC. Figure 3(E) shows that whereas modulation transfer functions are broader for AN fibers (i.e., inherited from cochlear filter bandwidth), the CN and IC functions have narrower band-pass characteristics, in agreement with gerbil data (i.e., Frisina et al., 1990; their Fig. 14 at 50 dB). Other studies confirm modulation band-pass behavior at higher stimulus levels; however, modulation frequency tuning can vary across units (Rhode and Greenberg, 1994; Langner and Schreiner, 1988; Krishna and Semple, 2000) and can be more low-pass in shape for lower stimulus presentation levels (Frisina et al., 1990). Second, Fig. 3(F) demonstrates that when multiple AN fibers types synapse onto each CN [Eq. (11)], amplitude modulation can be represented even at high stimulus levels, where LoSR AN fibers contribute more strongly to the overall modulation properties of the CN and IC response. The level-dependent operating ranges of amplitude-modulation sensitivity observed in the AN simulations in Fig. 3(F) qualitatively capture that LoSR auditory-nerve fibers have a dynamic range covering higher sound intensities than do HiSR fibers [see Fig. 8(C) in Joris and Yin, 1992].
B. Human cochlear filter tuning
The top panels in Fig. 4 illustrate how human stimulus-frequency (SF) OAE measurements can be used to determine the tuning parameter in the model through calibration of the double pole of [Eq. (1)]. First, was set to 0.051 for low stimulus levels at 1 kHz, a value determined to model realistic cochlear filters from the BM impulse response using the of 12.7 derived in Shera et al. (2002). The BM impulse response method considers the total energy in the power spectrum of the impulse response and calculates , where BW corresponds to the bandwidth of a normalized rectangular filter whose power is the same as that calculated from the spectrum of the BM impulse response. Using a value corresponding to a of 12.7, SFOAEs were derived from ear-canal pressure simulations to 2.5 ms onset ramped 10-dB-SPL 80-ms long pure tones with frequencies between 950 and 1050 Hz. For each frequency, SFOAEs were obtained by subtracting simulated ear-canal pressure in a model without BM irregularities (i.e., no ) from a model where BM irregularities were included (i.e., with ). The phase of the emission was determined from the Fourier spectrum [see Fig. 4(A)]. The slope of a quadratic fit through the measurement points yielded a slope of −0.0132 cycles/frequency, corresponding to a dimensionless SFOAE group delay () value of 13.2. Using (Shera et al., 2002), the dimensionless tuning value is 14.4 at 1 kHz, which is sharper than the target 12.7 value reported in human forward masking and SFOAE studies at 1 kHz (Shera et al., 2002). refers to the tuning ratio relating BM filter tuning to AN tuning curves. This parameter was set to 1.1 to match the derived tuning ratio of cat near 1 kHz and higher CFs (Fig. 9 in Shera et al., 2010). The simulated was sharper than reported in experimental SFOAE studies, while the calibrated using the equivalent rectangular bandwidth method of the local BM impulse response (i.e., the actual cochlear filter) did correspond to the target 12.7. This is likely due to a methodological difference. In the present model, the group-delay-based method (approximated using ), with the group-delay of a simulated BM impulse response, yields tuning values that are up to 1.3 times sharper than that of the calculated from the spectrum of the same BM impulse response. To precisely model human SFOAE tuning values in future implementations, the target values for local BM impulse responses should be set ∼0.74 times lower than those determined from the measured .
FIG. 4.
Frequency dependence of cochlear filter tuning. (A) The slope of the simulated SFOAE phase as a function of frequency provides an estimate of SFOAE group delay of 13.1, in line with values found for human SFOAE measurements. The discontinuities evident in the SFOAE phase are a computational artifact caused by the finite frequency resolution of the analysis. Using the 1.1 tuning ratio of cat describing the relationship between SFOAE tuning and cochlear filter tuning, can be computed from the SFOAE measure (i.e., black encircled white dot in panel C; Shera et al., 2010). (B). The relationship between cochlear filter shapes and the value of of is shown for BM impulse responses to an 80-μs-0-dB-peSPL click at 2 kHz CF simulated for different values. These simulations show that changing as a function of frequency or intensity can yield desired values at those CFs or intensities. (C) Simulated 's calculated from the SFOAE phase slope (), the spectra of BM impulse responses (BMIRs), and from iso-response AN tuning curves measured at CF to pure-tone stimulation of neighboring frequencies (criterion: 10% increment of SR). Simulations are compared to derived psychoacoustic iso-response (Eustaquio-Martín and Lopez-Poveda, 2011, ELP2011; Shera et al., 2010, SGO2010) and iso-level (Eustaquio-Martin and Lopez-Poveda, 2011; Glasberg and Moore, 1990, GM90) human cochlear filter tuning estimates along with tuning estimates derived from human SFOAE recordings (Shera et al., 2010; SGO2010).
Because filter tuning is determined by the value of the double pole of , both filter width and gain are altered when the pole value is changed (e.g., as a function of CF or level). Figure 4(B) illustrates how the value of of relates to the spectral filter shape, showing magnitude spectra of BM impulse responses at 2 kHz CF to an 80-μs click for fixed values of . Implementing level-dependence of filter tuning was achieved by first determining based on the desired -vs-frequency relationship at low stimulus levels (Shera et al., 2010). Then, was set to vary with intensity as a hyperbolic function with a compression slope of 0.4 dB/dB (see Verhulst et al., 2012 footnotes). With this fit, the corresponding filter shapes (determined by ) were less sharp, with their maxima moving basal-ward as stimulus intensity increased. The benefit of altering the of (as opposed to changing the stiffness or damping parameters in independently) is that BM impulse response zero-crossings are invariant with stimulus level (Shera, 2001). The implemented cochlear filters thus conform with the observation that BM impulse-response envelope shapes change drastically with stimulus level even though their zero-crossings are relatively constant (Recio et al., 1998; Recio and Rhode, 2000). Second, to model the loss of cochlear gain due to outer-hair-cell damage, can be increased to achieve a desired gain reduction; this change simultaneously results in elevated detection thresholds and wider cochlear filters, with no additional parameter changes [Fig. 4(B)].
Figure 4(C) shows the frequency dependence of cochlear filtering in the model using a range of filter tuning estimates matching human data. The metric was derived from the negative slope of the simulated SFOAE phase () for frequencies surrounding the center frequency of the tested filter (Shera et al., 2002). As discussed above, the simulated in Fig. 4(C) was slightly higher than previously reported experimental values (12.7; Shera et al., 2002). However, using the alternative method for evaluating cochlear tuning based on simulated BM impulse responses (see the black diamonds corresponding to BMIR-0 dB peSPL) yielded values that matched well the human SFOAE-derived -vs-frequency tuning values (SFOAE: SGO2010; Shera et al., 2010) and iso-response psychoacoustic forward masking measures (SGO2010-isoR; Oxenham and Shera, 2003).
BM-derived tuning at higher stimulus levels (white diamonds; BMIR-70 dB peSPL) reflects cochlear filter widening as a consequence of increasing values of the double pole of as the stimulus intensity surpasses the BM compression threshold. Tuning at these higher stimulus levels is hard to quantify experimentally using SFOAEs because the tuning ratio is not known at higher stimulus levels. Further, the high suppressor levels necessary to estimate the slopes of the tuning curves limit psychoacoustic approaches.
To compare the model's tuning to that resulting from other commonly adopted methods in physiological and psychoacoustic studies, was also computed from iso-response HiSR AN fiber tuning curves (AN-isoR). Iso-response tuning curves were determined by finding the stimulus level producing a 10% increment in the AN firing rate for 50-ms long pure-tones with frequencies near the CF of the fiber. s were estimated from the tips of the tuning-curves using the fiber's CF divided by the bandwidth of a rectangular filter that had the same power as the filter found by inverting the tuning curves. Tuning derived from the simulated iso-response AN tuning curves was markedly less sharp than that estimated from SFOAE metrics or BM impulse responses, and provided a close match to human iso-response values for frequencies below 4 kHz (Eustaquio-Martín and Lopez-Poveda, 2011). However, the simulated iso-response AN tuning did not match other iso-response psychoacoustic results (Oxenham and Shera, 2003), suggesting that iso-response AN tuning in the model matches temporal-masking curve estimates (Eustaquio-Martín and Lopez-Poveda, 2011) better than forward-masking estimates (Oxenham and Shera, 2003).
C. ABR wave-V latency
Figure 5 compares simulated ABR latencies, defined as the time difference between the wave-V peak and the onset of the stimulus, to data from the literature (panel A) as well as to other ABR model implementations (panel B). Note that when literature studies referenced their data to dB hearing level (HL) (i.e., hearing level) or dB SL (i.e., sensation level), the stimulus levels were compensated by 42 dB to translate dB HL/SL to dB peSPL. The value of 42 dB is based on the average detection threshold of an 80 μs-click for a small group of normal-hearing listeners using insert earphones (Etymotic Research ER-2, Elk Grove Village, IL).
FIG. 5.
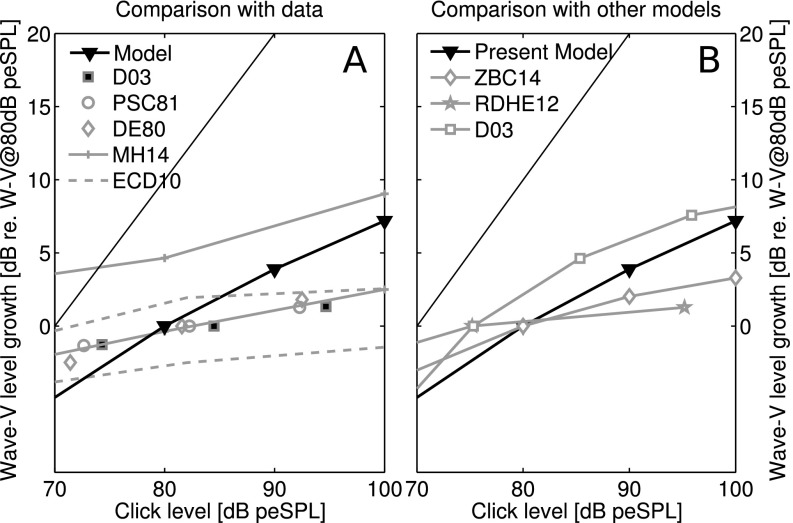
Simulated ABR wave-V latency for increasing intensity 80-μs clicks. (A) Comparison of the ABR wave-V latency a function of stimulus intensity. Simulations are plotted twice: once regularly, once with a constant offset of 3.5 ms to allow a comparison of the latency-intensity slope to the data reported in the literature for normal hearing listeners (Strelcyk et al., 2009, SCD09; Dau, 2003, D03; Prosser and Arslan, 1987, PA87; Jiang et al., 1991, JZSL91; Serpanos et al., 1997, SOG97). Note that literature data reported for stimulation at dB HL or dB SL was corrected for by 42 dB peSPL, corresponding to the detection threshold for the click. The SCD09 dataset was obtained by fitting a power-law function to the raw-data points pooled over all normal-hearing subjects. The PA87 dataset (dashed) shows three curves of the dataset, where the bottom and top curve correspond to the 5% and 95% confidence interval, respectively, and the middle to the mean latency over all listeners. (B) Comparison of the simulated wave-V latency to simulations performed with existing models: the AN model of Zilany et al. (2014) combined with the Nelson and Carney (2004) CN and IC model (ZBC14), and the ABR models of Rønne et al. (2012) (RDHE12), and Dau (2003) (D03).
Figure 5(A) shows that simulated ABR wave-V latencies were about 3.5 ms shorter than those reported from experimental results. This discrepancy may reflect that measured scalp-responses are generated by the superposition of fields produced by multiple neural elements (including the lateral lemnisci), rather than solely due to the ventral CN-IC pathway, which is the dominant source in our model (see Voordecker et al., 1988; Melcher and Kiang, 1996; Ponton et al., 1996). Additionally, the model did not impose any synaptic delays on the responses from intermediate nuclei, such as the superior olivary complex. Thus, our model assumptions likely both underestimate the delays of responses from different generators and ignore some generators that likely contribute to the wave-V peak response, which could account for some of the latency differences between the simulated and measured wave-V peak latencies. Thus, when using the model to evaluate level-dependent characteristics of peripheral auditory responses to broadband sounds, it is more appropriate to examine changes in latency rather than absolute values.
The simulated ABR wave-V latencies capture how ABR wave-V latency changes as a function of stimulus intensity for a number of human ABR studies in normal-hearing listeners (Strelcyk et al., 2009, SCD09; Dau, 2003, D03; Prosser and Arslan, 1987, PA87; Jiang et al., 1991, JZSL91; Serpanos et al., 1997, SOG97). When comparing our model simulations to other computational ABR and auditory-nerve models (e.g., the AN model of Zilany et al., 2014 combined with the Nelson and Carney, 2004 CN and IC model−ZBC14; ABR models of Rønne et al., 2012−RDHE12; Dau, 2003−D03), our model better accounts for decreases in ABR wave-V latency (1.3 ms per 40 dB, compared to 1.2–2 ms per 40 dB reported for normal-hearing listeners in Gorga et al., 1985; Dau, 2003; Elberling et al., 2010; Strelcyk et al., 2009). However, earlier ABR models capture absolute ABR latencies better than our model because the delays in the AN to ABR transfer function in those models was built into the unitary response to fit measured ABR responses, rather than the result of any explicit modeling of the timing of responses from intermediate brainstem processing centers (Dau, 2003; Rønne et al., 2012).
D. ABR wave-V growth
Figure 6 compares simulations of ABR wave-V level growth as a function of stimulus level to existing literature data (panel A) and to simulations from other ABR models (panel B). Examining ABR wave-V level growth functions rather than absolute level allowed for a fairer comparison across the varied studies. ABR wave-V growth functions were constructed by normalizing the simulated ABR wave-V levels by the ABR response to an 80-dB-peSPL click. Existing data reported in dB SL or HL were translated to dB peSPL using a 42 dB compensation, after which the reported levels were normalized to the reported stimulus level closest to that of 80 dB peSPL. Despite the simplification of the representation here, it is clear that all reported datasets show compressive growth at high-stimulus levels for normal-hearing listeners. Simulated ABR wave-V growth is less compressive than reported in experimental results, with an overall slope of 12 dB/30 dB (close to the implemented BM compression ratio of 0.4 dB/dB). Comparison with human experimental data suggests that more BM compression can be added in future model implementations to improve the correspondence between model and data. However, it is not clear whether the overall BM compression slope is the dominant predictor of ABR growth. For instance, it is possible that changes in the local excitation pattern with changes in level affect which tonotopic regions dominate responses, and thus affect the observed wave-V compression. If so, the overall BM compression slope may not be the primary factor determining the overall wave-V growth rate. ABR growth may also depend on the percentage of LoSR vs HiSR AN fibers in listeners with normal-hearing thresholds (Furman et al., 2013). In addition, because different stages of the pathway show different amounts of compression, the growth of potentials observed on the scalp likely depends on the relative strength of the contributions of different processing stages and how these responses sum as the neural population responding to sound grows (Okada et al., 1997).
FIG. 6.
Simulated ABR wave-V growth to increasing intensity 80-μs-clicks. (A) Comparison of simulated ABR wave-V growth to literature data that was normalized by the ABR level reported to the stimulus intensity closest to 80 dB peSPL to allow for comparison across studies. Literature data reported in dB HL or dB SL was corrected for by 42 dB peSPL. Experimental ABR wave-V levels collected in normal-hearing listeners are shown (Dau, 2003, D03; Picton et al., 1981, PSC81; Don and Eggermont, 1978, DE78; Maloff and Hood, 2014, MH14; Elberling et al., 2010; ECD10). The EDC10 and MH14 datasets show the boundaries of the mean results plus one standard deviation (top curve) and mean results minus 1 standard deviation (bottom curve) (B) Comparison of simulated ABR wave-V growth to simulations performed with existing ABR models: Zilany et al. (2014) combined with the Nelson and Carney (2004) CN and IC model (ZBC14), Rønne et al. (2012; RDHE12), and Dau (2003; D03).
E. Combined ABR and OAE latency measures
In the present study, the excitation pattern and time-dependent synchronous summation across different tonotopic sections at the level of the AN and IC depend on how the BM excitation, IHC, and middle-ear filtering shape the inputs to the AN/CN and IC stages of the model. Even though none of the frequency-dependent characteristics of those neural processing stages were calibrated to capture level-dependent properties of population responses, the simulations in Figs. 5 and 6 show that the present approach captures realistic level-dependent changes in ABRs. By using a cochlear model that simulates frequency-dependent changes of cochlear tuning in combination with a low-order IHC filter and relatively frequency-invariant AN thresholds, the current model depends on a minimal number of free parameters, but better accounts for ABR latency-intensity characteristics (1.3 dB/40 dB) than existing functional ABR model approaches (<0.5 dB/40 dB).
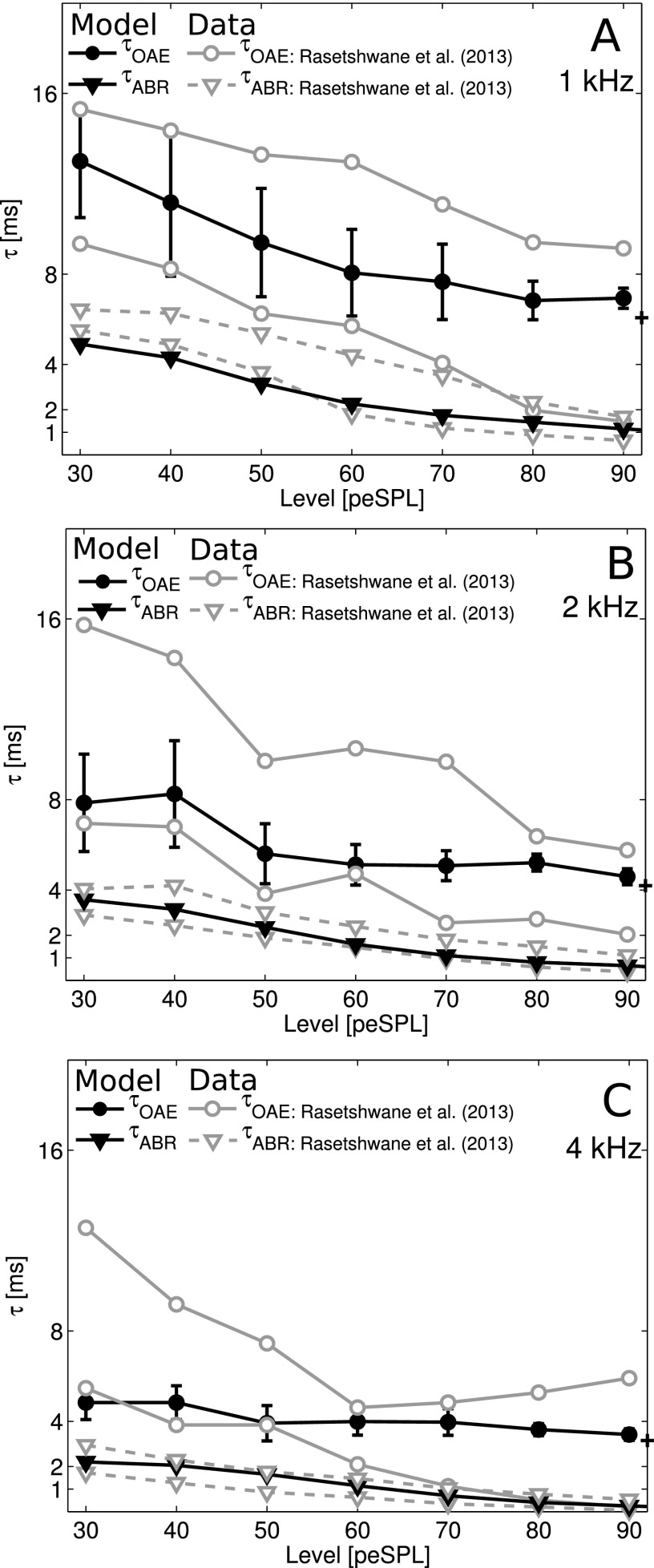
The transmission-line description of the cochlea adopted here is particularly practical because it allows BM processing to be isolated and evaluated independently of any later neural processing. In the future, the model can be refined to better fit both OAE and ABR measurements. Figure 7 evaluates how level affects peripheral processing in the model and compares it to both OAE and ABRs recorded in the same listeners (Rasetshwane et al., 2013). Each of the panels in Fig. 7 shows intensity functions of tone-burst OAE latency () simulated for windowed ms long tone-bursts (center frequencies reported in the corresponding panel: 1, 2, and 4 kHz). Simulations are plotted along with the across-subject mean responses, plus and minus the across-subject standard deviation (top and bottom dashed lines; Rasetshwane et al., 2013). The panels also depict simulated and recorded forward-latency, , a metric that allows for a direct comparison between the latency-intensity functions reported in the literature and the model simulations (see also Sec. V).
FIG. 7.
OAE and ABR latencies to -ms long tone-bursts with center frequencies of 1 (A), 2 (B), and 4 kHz (C). Simulations to Hanning windowed tone-bursts were compared to the data recorded in the study of Rasetshwane et al. (2013) that used a Blackmann-windowed toneburst of the same duration (14, 16, and 21 subjects for test frequencies of 1, 2, and 4 kHz, respectively). The Rasetshwane et al. (2013) data were shown using the boundaries of their observations: the top and bottom curve indicates the mean observations plus and minus one standard deviation across the subject mean, respectively. Simulated latency (circles) was calculated from the maximum of the zero-padded ear-canal recording (stimulus-duration +0.5 ms). The crosses on the right edge of the plot show the minimal possible latencies that could be obtained using this zero-padding method. Standard deviations were calculated over 25 frozen model subjects, each with a different placement of the random BM irregularities giving rise to different . Simulated (triangles) represent the forward ABR latency calculated as the wave-V latency from the start of the stimulus to the maximum of the ABR wave-V, subtracted with a constant delay representing a synaptic and neural delay (5 ms in humans, 3 ms in the model). Subject populations were the same as for the OAE simulations.
Overall, Fig. 7 shows that the model simulations fall within the range reported in Rasetshwane et al. (2013). It is worth noting that the measured estimates of have greater variability than the estimates of in the same group of listeners, and that this is captured in the model simulations. In the model, subject-dependent differences in BM irregularities can produce dramatic differences in reflection-source OAEs, which affect the measure (Verhulst and Shera, 2015). These results suggest that is more robust to subject-dependent differences in BM irregularities than is . Across stimulus levels, was fit best for the 1 kHz condition; the simulated latency-intensity slopes for the 2 and 4 kHz conditions were shallower than found experimentally, but still within range. Discrepancies between the experimental and simulated may be due in part to difficulty in determining the peak latency of tone-burst evoked OAEs, which sometimes exhibit multiple peaks in response to the stimulus (Verhulst and Shera, 2015). If the measured emissions had multiple peaks, the present definition of , which ensures we find the first of two such peaks, might tend toward shorter latencies than the energy-weighted group delay reported from the human data (Rasetshwane et al., 2013). Simulated latency-intensity functions better fit the data in the 2 and 4 kHz range than the 1 kHz range, where the model latency was shorter than the experimental latency for low stimulus levels.
Small adjustments in auditory filter tuning parameters and/or the CF-dependent shape of the BM nonlinearity function and IHC filter characteristics could yield more precise fits to the experimental data. Here, the model parameters were set to match human values across CF and the 0.4 dB/dB compressive nonlinearity. With this approach, the model fits the latencies of human tone-burst OAEs reasonably well, despite the fact that the small number of free parameters were determined solely on the basis of human estimates. This independent calibration and validation of the model's BM processing are encouraging, suggesting that the model's excitation patterns (the input to the ascending AN/CN/IC model stages) were realistic.
IV. DISCUSSION AND PERSPECTIVES
Because the present model accounts for level-dependent properties of human ABRs, it is worthwhile to ask which aspects of the model are responsible for capturing the level-dependence of ABRs. Given that only population responses can be obtained in humans and that in animals, it is difficult to obtain single-unit responses at multiple measurement sites, it is especially important to study the relationship between simulated excitation patterns generated from single-unit responses at many CFs and their relationship to the associated population responses. In addition, it is enlightening to explore why previous models do not account for ABR latency-vs-intensity characteristics. Examining how each stage of processing contributes to the modeled ABR response at different stimulus levels can elucidate which aspects of the neural excitation patterns (e.g., cochlear dispersion, or excitation strength at specific CFs) critically influence level-dependent changes in ABR responses.
A. From broadband excitation patterns to population responses
Figures 8 and 9 compare excitation patterns in different model stages for the present model and the AN model of Zilany et al. (2014), which is very similar to the AN models used as preprocessors for the ABR models of Dau (2003) and Rønne et al. (2012). To allow fair direct comparisons across the models, we fixed the instantaneous firing rate of Lo, Me, and HiSR fibers to 1, 5, and 60 spikes/s [see Eq. (6)] in all of the models considered here. This means that the refractoriness and long-range dependence of AN firing developed in Zilany et al. (2014) were excluded in our simulations of their model. Note that the same CN and IC model (Nelson and Carney, 2004) was connected to the different AN models when simulating ABR wave-III and wave-V responses [i.e., Eqs. (12) and (13)].
FIG. 8.
(Color online) BM Excitation patterns and AN firing thresholds across CF. (A) BM excitation patterns to 80-μs-clicks for intensities of 40, 60, 80, and 100 dB peSPL normalized to the 40–dB 1-kHz rms level of excitation. Simulations are shown for the present model (black) and that of Zilany et al. (2014; gray). (B). Single-unit AN firing thresholds to a 50-ms pure-tone at CF obtained using a 10% increment of SR criterion in the present and Zilany et al. (2014) model. Results are compared to the human threshold of hearing (ISO, 2003) and to the single-unit auditory-nerve recordings in cat for HiSR fibers (Liberman, 1978).
FIG. 9.

From broadband excitation to population responses. (A) and (D) Maximum instantaneous firing rate patterns across CF (irrespective of the latency at which the maximum occurred) within each CF for an 80-μs click at 40, 60, 80, and 100 dB peSPL. Maximum instantaneous rates are shown for the present model (black) and that of Zilany et al. (2014; gray dashed) at the level of the AN (panel A), and IC (panel D). At each CF, contributions from 19 AN fibers of three subtypes were included (see text). In panel D, the same CN and IC models were adopted for simulations with both the Zilany et al. (2014) model and the current model. (B) and (E). Latency at which maximum instantaneous firing rate in panels (A) and (D) occurred at each CF. (C) and (F). Temporal response profiles obtained by summing up all energy across CF, both at the level of the AN (wave-I, panel C) and IC (wave-V, panel F) at each time point. Whereas the wave-I amplitudes (C) were not normalized, the wave-V amplitudes (F) were scaled to their maximum to make it simpler to explore how peak latency changes.
Figure 8(A) shows BM excitation patterns to 80-μs click stimuli while Fig. 8(B) plots the frequency dependence of simulated AN thresholds, which are an important factor in determining how BM excitation is transmitted to ascending model stages in each frequency channel. While Zilany et al. modeled the characteristic 4 kHz ear-canal resonance, which enhances sensitivity to that frequency in free-field or headphone listening (ISO, 2003), the current model does not include any ear canal resonance; the excitation pattern depends only on the middle-ear transfer function. The present model thus simulates hearing using insert earphones (which is often the case when recording ABRs), and cannot account for the 4 kHz dip in human hearing thresholds [see also Fig. 8(B)].
The mismatch between the growth of the BM excitation patterns in Fig. 8(A) and that of the ABR wave-Vs in Fig. 6 demonstrates that ABR growth is not determined by BM compression alone. Although the BM excitation patterns in the Zilany et al. (2014) model grow more linearly than the 0.4 dB/dB compression ratio included in the current model, the ABR wave-V growth curves simulated using the Zilany et al. (2014) model are more compressive than those produced by our model. This suggests that the frequency dependence of AN thresholds may influence which cochlear regions dominate ABR responses, and thus the overall growth and latency of the ABR.
Even though the present model did not implement strong frequency dependence in the AN equations [Eqs. (6)–(11)], simulated AN thresholds in Fig. 8(B) (determined as the stimulus level required to increase firing rate by 10% over SR) vary with frequency. The shape of the simulated AN fiber thresholds across CF in the model arise due to how the middle-ear, BM and inner-hair-cell transduction shaped the inputs to the AN fibers at each CF. While both models yielded HiSR AN fiber thresholds that match the human hearing threshold with reasonable agreement (with the exception of failing to capture the 4 kHz ear-canal resonance dip in the present model), there is an important difference between the implementations that may impact how BM and IHC excitation drives the AN fibers. Whereas the AN thresholds in the Zilany et al. (2014) model family are parametrically fit to match cat data (Liberman, 1978), they are determined by how BM and IHC excitation drive AN fibers in the present model, without altering any free parameters. In addition, while the present model includes LoSR fibers with thresholds up to 40 dB higher than those of HiSR AN fibers (consistent with animal results; e.g., see Fig. 10 of Liberman, 1978), the AN thresholds in the Zilany et al. (2014) model do not span this range. Further, the simulations in the ABR models of Dau (2003) and Rønne et al. (2012) were based on HiSR fiber populations alone. Because the growth rates of ABR wave-I are more compressive in noise-exposed animals that have lost LoSR fibers (Furman et al., 2013), a faithful representation of different SR fiber types may be important for capturing supra-threshold ABR growth.
The level-dependence of latency and amplitude of population responses arises through a complex interaction between cochlear excitation, dispersion, the strength of the contributions from different AN fiber types, and differences in thresholds across the population of AN fibers. Therefore, analysis of how simulated excitation patterns vary with input level in the AN and IC can help elucidate why different classes of models differ in their ability to capture intensity-dependent changes in ABR wave-V latency. Figures 9(A)–9(C) show different aspect of the model AN responses computed for a population of 19 fibers (13 HiSR, 3 MeSR, and LoSR fibers). Figure 9(A) shows the maxima of the total firing rate at each CF, computed by summing the instantaneous AN firing rate across the population of all fibers for each CF. Figure 9(A) does not provide information about the time at which each CF channel reached its maximum; therefore Fig. 9(B) plots the latencies corresponding to the instantaneous firing rate maxima at each CF. Regions of large synchrony are characterized by shallower slopes across CF. Last, Fig. 9(C) shows the normalized wave-I waveform obtained by summing up instantaneous firing rates across the population of fibers at each characteristic frequency as a function of time. Here, the amplitude and corresponding latency of the wave-I is determined by those firing rate amplitudes in CF channels that showed large synchrony across multiple CF channels in Fig. 9(B).
Whereas the maximal AN firing patterns in Fig. 9(A) for the lowest stimulated level (40 dB peSPL) look similar in the two models, consistent with the fact that they have similar AN thresholds [compare lowest solid and dashed lines in Fig. 9(A)], the patterns differ greatly for the higher stimulus levels. In the current model, activity in the maximum instantaneous-rate pattern shifts basal-ward as stimulus level increases; however, in the Zilany et al. (2014) model the 4 to 8 kHz frequency region dominates the instantaneous-rate maxima across all stimulus levels. As a consequence of this relative intensity invariance of AN excitation, the simulated population wave-I response in the Zilany model decreases by only 0.8 ms as stimulus level increases [Fig. 9(C)]. In contrast, in the current model, the wave-I latency shifts by 1.25 ms for the same 40 dB stimulus level increase [Fig. 9(C)].
The same CN and IC model equations were used for both the Zilany and current AN model to simulate the wave-V waveform and associated patterns of single-unit IC response maxima and latencies [Figs. 9(D)–9(E)]. In the current model, the simulated wave-V latencies shift by 1.3 ms across the tested input levels; however, using the Zilany model as the input to the CN and IC model, the latency shifts by only 0.15 ms for a 40 dB stimulus level increase [Fig. 9(F)]. The Zilany AN model yields a smaller decrease in wave-V latency with changes in level because in that model, even though the responses in the 0.5–4 kHz range grow with level, responses in the 4–8 kHz region still dominate peak responses at all stimulus levels. In contrast, the current model shows excitation in the 4–8 kHz CF region that increases to the point that the short-latency, high-CF channels reduce the wave-V latency as stimulus level increases.
Analysis suggests that our model was better than previous models in capturing level-dependent properties of human ABRs by allowing BM excitation patterns to drive the AN fibers [see Fig. 9(A)], without introducing excessive low-pass filtering to model the IHCs (i.e., second order low-pass filter here vs seventh order filter in the Zilany model) or a strong frequency dependence in AN fiber thresholds (in contrast to the strong frequency dependence of the Vsat parameter used in the Zilany model family). Even though realistic cochlear filter-tuning parameters have been shown to improve the ABR latency-vs-intensity slope slightly (see Rønne et al., 2012 and Zilany et al., 2014 vs Dau, 2003), no previous models achieved shifts of the ABR wave-V latency larger than 0.5 ms/40 dB. The model analysis provided in Figs. 8 and 9 shows that a model capturing the spread of AN excitation as a function of stimulus level and including realistic AN thresholds mimics changes in ABR latencies with stimulus level like those observed experimentally.
B. Implications for ABR source generators
The instantaneous-rate maxima and onset synchrony patterns across CF and their relationship to the latency of population responses in Figs. 8 and 9 show that the interplay between which cochlear regions are firing synchronously and the relative strength of responses at different CFs affect the ABR response. Because ABR characteristics reflect how energy at each point in time sums across the cochlear partition, reduced cochlear dispersion at the highest simulated frequencies yields the most synchronous responses (e.g., Don and Eggermont, 1978; Dau et al., 2000). However, high frequency channels do not necessarily contribute a great deal of amplitude to the total response, as shown in Figs. 9(A) and 9(D). In the present model, responses of individual frequency channels were most synchronous above 6 kHz at the level of the AN, and above 4 kHz at the level of the IC. This difference in synchrony properties for the AN and IC stages is the result of CN/IC processing that would not be captured by a unitary-response kernel model, like some earlier functional ABR models (Dau, 2003; Rønne et al., 2012). Furthermore, in our model, the range of CFs contributing to synchronous firing increased to apical frequencies as stimulus level increased [see Figs. 9(B) and 9(E)].
The range of cochlear frequency regions dominating the population response has also been investigated experimentally. Using high-pass masking noises has a large effect on wave-I and wave-III, demonstrating the dominance of higher frequency portions of the cochlear partition in these responses. In contrast, the entire cochlear partition, including the apical regions, contributes to wave-V in human ABRs (Don and Eggermont, 1978). In the current model, IC response latencies vary less across CF than do AN response latencies, which helps explain these experimental observations [see Figs. 9(B) and 9(E)]. Further, several studies have shown that frequency regions below 2.5 kHz contribute to ABR generation in notched noise paradigms (e.g., Don and Eggermont, 1978; Abdala and Folsom, 1995). Those frequency regions also contribute large amplitudes to the total excitation pattern in the current model. However, the latencies of the simulated wave-V response in Fig. 9(F) are dominated by contributions of high frequency CFs, which exhibit good synchrony between neighboring channels [Fig. 9(E)]. This assertion is further supported by the neurograms in Fig. 10, which shows the relationship between dispersion and response amplitude for simulated wave-I and -V responses at 80 dB peSPL.
FIG. 10.
Neurograms of the AN and IC modeling stages. (A) Time-frequency representation of single-unit AN responses to a 80 dB-peSPL click indicating that the ABR wave-I peaks near 0.5–2 ms as a consequence of synchronous summation of energy across the 8–15 kHz CFs. The vertical inset shows the normalized weights of the peak amplitudes at each CF showing that the 1–2 kHz region contributed most strongly in amplitude to the wave-I response. (B) Time-frequency representation of the single-unit IC responses showing that the simulated ABR wave-V is arises through synchronous firing of onset IC responses across the 2–6 kHz CF regions.
Even though the current model qualitatively captures key characteristics of ABR wave-I and wave-V in response to click stimuli, additional model simulations to clicks, tone-bursts, or chirps (Dau et al., 2000; Elberling et al., 2010; Rasetshwane et al., 2013) presented in high-pass or band-pass masking noise (e.g., Don and Eggermont, 1978; Abdala and Folsom, 1995) should be used to further test and refine broadband response characteristics of the model. In such ABR masking paradigms, it is crucial to evaluate both response latency and amplitude. For example, even though masking studies show that the response latency of a click ABR in quiet is most similar to that of narrow-band responses from the 3–10 kHz region (Fig. 5 of Don and Eggermont, 1978), wave-V amplitudes of noise-masked responses can be equally high for narrow-band ABRs down to 0.5 kHz (Fig. 8 of Don and Eggermont, 1978). This implies that low-frequency regions can generate ABRs, but that in an unmasked condition, their relative contribution is much less than the contributions of higher-frequency channels, which fire with greater synchrony than lower-frequency channels, where cochlear dispersion is greater. The simulated IC neurograms in Fig. 10(B) support this view, showing that at 80 dB peSPL, the latency of the ABR wave-V (3.6 ms) matches that of the 2 to 6 kHz cochlear region, even though responses between 1 and 10 kHz have a great enough amplitude that they could contribute significantly to the total response (and thus could influence the wave-V latency) if they added in phase.
The model simulations show that the relative contributions of different CF channels to the population response differ across processing stages. In overall agreement with the experimental findings, the model did produce a more uniform excitation across CF for IC responses than for AN responses [compare results in Figs. 9(A) and 9(D)]. This is a consequence of the fact that the CN/IC model attenuates responses from low-frequency CFs relative to responses from high-frequency CFs, which could have implications for how wave-I and -V amplitude change as a consequence of stimulus alterations or frequency-specific hearing loss. For example, consider a hearing loss that elevates hearing thresholds above 2 kHz, reducing the relative contributions of those frequency regions. In such a case, wave-I responses are likely dominated by responses from the 1–2 kHz region (e.g., see Don and Eggermont, 1978), whereas wave-V responses would likely reflect contributions from CFs between 0.5 and 2 kHz. Depending on the exact timing of responses from those contributing CF regions, wave-V amplitude might be reduced less by the hearing loss than wave-I. How hearing loss affects the relative strength of different CF channels' contributions to wave-I and wave-V can be tested experimentally at sound levels for which both normal and hearing-impaired listeners have a measureable wave-I response. Exploring how wave-V and wave-I amplitudes are related individual audiogram shapes would help to determine whether the adopted CN/IC model adequately captures which CF channels dominate contributions to ABR wave-I and wave-V.
Additionally, when presenting clicks at an equally high SPL for hearing-impaired and normal-hearing listeners, the current model suggests that the shape of the audiogram will impact the slope of the latency-vs-intensity curve, because the audiogram shape will determine which frequency regions (and associated single-unit onset latencies) dominate the overall latency. Together with the observation that longer-latency LoSR fibers have little effect on the onset latency of population responses (Taberner and Liberman, 2005; Buran et al. 2010; Bourien et al., 2014), sloping hearing losses may yield longer-than-normal latencies because the low-frequency channels dominate the response at low SPLs, whereas high-level SPLs could yield normal latencies as high-frequency regions of the cochlea are recruited at higher stimulus levels. Increased slopes of latency-vs-intensity ABR curves have been observed for several sloping-audiogram listeners in the study of Strelcyk et al. (2009; i.e., 2-kHz derived-band ABR), and in an early study by Gorga et al. (1985) who reported ABR latency-vs-intensity curves for several audiometric hearing loss configurations. In context with the current model framework, these experimental findings suggest that spread of excitation across stimulus level, and to a lesser degree individual changes in filter width (and associated single-unit onset latency reductions), are dominant in determining ABR wave-V latency. Interactions between changes in single-unit properties and broadband excitation as a consequence of hearing loss can easily be studied using the current modeling framework, which offers a means to develop more sensitive diagnostic tests based on population responses such as the ABR and EFR.
C. Model strengths and limitations
1. Strengths
The model presented here has only a few free parameters, but accounts well for both single-unit responses and level-dependent characteristics of population responses (OAEs and ABR wave-V). Human OAE measurements were used to calibrate the broadband characteristics of BM processing. In the model, the input to the AN fibers is largely determined by how BM and IHC excitation changes with stimulus level. The resulting model predicts that wave-V latency decreases by 1.3 ms as level increases by 40 dB, in line with experimental observations. The model also predicts tone-burst OAEs and ABRs latency-vs-intensity curves that match experimental findings in the 1–4 kHz range (Rasetshwane et al., 2013; Strelcyk et al., 2009; Dau, 2003; Prosser and Arslan, 1987; Jiang et al., 1991; Serpanos et al., 1997).
The improvements in the broadband characteristics of the model over earlier functional ABR models were not achieved at the cost of poorer fits of single-unit AN/CN/IC fiber properties. While the stimulus-level-dependent permeability function in the AN equations [Eqs. (6)–(10)] were modified from earlier AN models (Zilany and Bruce, 2006; Zilany et al., 2009; Zilany et al., 2014), the amplitude-modulation and rate-level characteristics of single-unit AN fibers (Fig. 3) remain similar to existing implementations (Zilany and Bruce, 2006, Zilany et al., 2009). Even though instantaneous firing rates were not explicitly fit to physiological data, the model predicts key level-dependent properties (Fig. 3, and Fig. 3 of Sachs and Abbas, 1974). Because the proportion of LoSR AN fibers was set to be similar to that reported in animal models [Eq. (11); see Fig. 10 of Liberman, 1978), the present model captures response properties relevant for understanding how cochlear neuropathy affects responses to onset transients and amplitude-modulated signals.
Last, the present ABR model uses a cochlear model in which cochlear gain and BM filter bandwidth at each longitudinal position are controlled by a single parameter, the location in the complex frequency plane of the double pole of the BM admittance, (Zweig, 1991; Shera, 2001; Verhulst et al., 2012). By allowing to vary with position along the BM, the model is able to account for known variations in human cochlear filter tuning and OAE delays with CF (Fig. 4). Further, dynamic and stimulus-dependent variations in cochlear tuning that simulate the compressive nonlinearity of the cochlear amplifier were implemented by letting depend on the amplitude of the local BM velocity. Although this approach is functional and ignores the complicated details of cochlear micromechanics, it greatly facilitates the process of tailoring the model to approximate profiles of cochlear hearing loss in individual subjects, as determined using the audiogram or OAE measures. The model framework thus provides a means to study how outer-hair-cell related gain loss and cochlear neuropathy interact and affect OAEs and ABRs.
2. Limitations
The ABR model ignores several aspects of cochlear responses that may influence broadband and level-dependent characteristics of measured population responses.
-
(1)
For a model in which the BM velocity predominantly drives the AN fibers, the middle-ear and IHC filtering, which shape the input to the AN, largely determine cochlear responses. Even though the model simulated AN thresholds that qualitatively match how human hearing thresholds vary across frequency [Fig. 8(B)], it did not model the known frequency-dependence of the shear drive between BM vibration and IHC receptor potential (e.g., Guinan, 2012). This is in contrast to previous AN models, which implemented a low-order filter to account for the frequency dependence of the shear drive between the modalities (e.g., Shamma et al., 1986; Sumner et al., 2002; Sumner et al., 2003). Because the BM to IHC transduction depends on multiple mechanisms (e.g., shear and fluid drives; Guinan, 2012), a functional description of this process is complicated. However, a faithful representation should be included in future modeling efforts, as it can influence the phase and amplitudes of the CF channels that contribute to the population response.
-
(2)
This study focused on one family of previous AN models (Heinz et al., 2001; Zhang et al., 2001; Zilany and Bruce, 2006; Zilany et al., 2009; Zilany et al., 2014; Ibrahim and Bruce, 2010); and did not evaluate how the present model performs using other available AN models as preprocessors (e.g., Meddis, 1986; Sumner et al., 2002; Sumner et al., 2003). While these other models have similar AN fiber properties (Zhang et al., 2005), they model BM processing, IHC transduction, and CF-dependence of AN thresholds differently than in the AN model family considered here. Additional studies are needed to explore how using different AN models as inputs to our functional ABR model affects the simulated responses.
-
(3)
The model predicts that ABR latency decreases by 1.3 ms as input click level increases by 40 dB. This result falls within the range of experimental results from humans, although it is at the lower edge of the reported values (1.2–2 ms; Gorga et al., 1985; Dau, 2003; Elberling et al., 2010). Future work could explore whether higher slopes (ms/dB) could be achieved by changing the model parameters such that stimulus level increments cause larger relative changes in which CFs dominate the wave-V response. The level dependence of the ABR latency might also depend on retro-cochlear mechanisms. For instance, even for electrically evoked ABRs (which bypass BM processing and directly stimulate the AN), ABR latency is known to decrease over a large range with the magnitude of the stimulating current (Abbas and Brown, 1991).
-
(4)
The present model only quantifies changes in ABR wave-I, wave-III, and wave-V peaks as a function of stimulus level (or hearing impairment); it does not capture all aspects of scalp-recorded ABR waveforms. Although the model scales peak wave amplitudes to approximate average normal-hearing ABR amplitudes (via the scaling parameters), inter-wave delays were not set to match realistic values.
V. CONCLUSION
The current model modifies existing ABR models by (1) modeling cochlear processing as a nonlinear transmission-line, which captures across-frequency aspects of human cochlear filter tuning; (2) letting BM and IHC excitation drive AN fibers, without adding CF-dependent parameters that influence AN thresholds; (3) adopting SR-dependent AN fiber thresholds; and (4) adding a functional description of the CN and IC processing stages. With these modifications, the model accounts for level-dependent characteristics of human ABR wave-V and OAE responses while maintaining level-dependent characteristics of single-unit AN fibers. Because the model was designed to minimize the number of free parameters while allowing frequency-dependent aspects of cochlear gain loss and AN fiber populations to be controlled through simple parameters, it can be used as a research tool to predict how various hearing pathologies interact and affect human OAE and ABR responses.
ACKNOWLEDGMENTS
The authors thank Philip Joris, Mike Heinz, Laurel Carney, Ian Bruce, Muhammad Zilany, Filip Rønne, James Harte, Andrew Oxenham, Stephen Neely, Alessandro Altoè, Enrique Lopez-Poveda, and two anonymous reviewers for discussions related to the development and presentation of the model. This work was supported by R01 DC003687 (C.A.S.), a fellowship from the Office of Assistant Secretary of Defense for Research and Engineering (B.G.S.C.), DFG Cluster of Excellence EXC 1077/1 “Hearing4all” (S.V.), and Grant Number T32 DC00038 from the National Institute on Deafness and Other Communication Disorders (G.M.).
APPENDIX
The following section lists all the equations necessary to solve the three-store diffusion model by Westerman and Smith (1988) as implemented here. The model consists of three reservoirs: the global (G), local (L) and immediate store (I), each with their associated concentration (C) and volume (V). The global reservoir is that on the inside of the inner-hair-cell with infinite volume, and instantaneous firing rate is given at the output of the immediate store. Neurotransmitter material can move from the global to local and immediate store to the synaptic cleft depending on the permeability (P) between the stores. The following equations compliment Eqs. (6)–(10). The concentration of synaptic material in the immediate and local volumes is given by the following differential equations:
| (A1) |
| (A2) |
If , the following equations for the immediate and local concentrations are used instead
| (A3) |
| (A4) |
The concentrations at are given by
| (A5) |
The local and global permeability along with the local volume are given by
| (A6) |
| (A7) |
| (A8) |
The ratio between the rapid and short-time adaptation strength ( and ) is a free parameter in the model and was chosen here
| (A9) |
| (A10) |
Using
| (A11) |
The immediate volume of the three-store diffusion model is given by
| (A12) |
| (A13) |
| (A14) |
The following equations complete the model description:
| (A15) |
| (A16) |
Note that and in the current implementation correspond to and in the Zilany et al. (2009); Zilany et al. (2014) implementations.
Parts of the work by S.V. were conducted at the Center of Computational Neuroscience and Neural Technology, Boston University, 677 Beacon Street, Boston, MA 02215, USA and Department of Otology and Laryngology, Harvard Medical School, MEEI, 243 Charles Street, Boston, MA 02114, USA.
References
- 1. Abbas, P. J. , and Brown, C. J. (1991). “ Electrically evoked auditory brainstem response: Growth of response with current level,” Hear. Res. 51(1), 123–137. 10.1016/0378-5955(91)90011-W [DOI] [PubMed] [Google Scholar]
- 2. Abdala, C. , and Folsom, R. C. (1995). “ Frequency contribution to the click‐evoked auditory brain‐stem response in human adults and infants,” J. Acoust. Soc. Am. 97(4), 2394–2404. 10.1121/1.411961 [DOI] [PubMed] [Google Scholar]
- 3. Allen, J. B. (1980). “ Cochlear micromechanics—a physical model of transduction,” J. Acoust. Soc. Am. 68(6), 1660–1670. 10.1121/1.385198 [DOI] [PubMed] [Google Scholar]
- 4. Altoè, A. , Pulkki, V. , and Verhulst, S. (2014). “ Transmission line cochlear models: Improved accuracy and efficiency,” J. Acoust. Soc. Am. 136(4), EL302–EL308. 10.1121/1.4896416 [DOI] [PubMed] [Google Scholar]
- 5. Bharadwaj, H. , Masud, S. , Mehraei, G. , Verhulst, S. , and Shinn-Cunningham, B. (2015). “ Individual Differences Reveal correlates of hidden hearing deficits,” J. Neurosci. 35(5), 2161–2172. 10.1523/JNEUROSCI.3915-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Bharadwaj, H. , Verhulst, S. , Shaheen, L. , Liberman, M. C. , and Shinn-Cunningham, B. (2014). “ Cochlear Neuropathy and the coding of supra-threshold sound,” Front. Sys. Neurosci. 8, 26. 10.3389/fnsys.2014.00026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Bourien, J. , Tang, Y. , Batrel, C. , Huet, A. , Lenoir, M. , Ladrech, S. , Desmadryl, G. , Nouvian, R. , Puel, J. L. , and Wang, J. (2014). “ Contribution of auditory nerve fibres to compound action potential of the auditory nerve,” J. Neurophys. 112(5), 1025–1039. 10.1152/jn.00738.2013 [DOI] [PubMed] [Google Scholar]
- 88. Buran, B. N. , Strenzke, N. , Neef, A. , Gundelfinger, E. D. , Moser, T. , and Liberman, M. C. (2010). “ Onset coding is degraded in auditory nerve fibers from mutant mice lacking synaptic ribbons,” J. Neurosci. 30(22), 7587–7597. 10.1523/JNEUROSCI.0389-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Burkard, R. F. , Eggermont, J. J. , and Don, M. (2007). Auditory Evoked Potentials: Basic Principles and Clinical Application ( Lippincott Williams & Wilkins, Baltimore, MD: ), Chap. 11, pp. 229–253. [Google Scholar]
- 9. Dau, T. (2003). “ The importance of cochlear processing for the formation of auditory brainstem and frequency following responses,” J. Acoust. Soc. Am. 113, 936–950. 10.1121/1.1534833 [DOI] [PubMed] [Google Scholar]
- 99. Dau, T. , Wegner, O. , Mellert, V. , and Kollmeier, B. (2000). “ Auditory brainstem responses with optimized chirp signals compensating basilar-membrane dispersion,” J. Acoust. Soc. Am. 107(3), 1530–1540. 10.1121/1.428438 [DOI] [PubMed] [Google Scholar]
- 10. Delgutte, B. , Hammond, B. M. , and Cariani, P. A. (1998). “ Neural coding of the temporal envelope of speech: Relation to modulation transfer functions,” in Psychophysical and Physiological Advances in Hearing, edited by Palmer A. R., Rees A., Summerfield A. Q., and Meddis R. ( Whurr, London: ), pp. 595–603. [Google Scholar]
- 11. Don, M. , and Eggermont, J. J. (1978). “ Analysis of the click-evoked brainstem potentials in man using high-pass noise masking,” J. Acoust. Soc Am. 63(4), 1084–1092. 10.1121/1.381816 [DOI] [PubMed] [Google Scholar]
- 12. Elberling, C. , Callø, J. , and Don, M. (2010). “ Evaluating auditory brainstem responses to different chirp stimuli at three levels of stimulation,” J. Acoust. Soc. Am. 128, 215–223. 10.1121/1.3397640 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Eustaquio-Martín, A. , and Lopez-Poveda, E. A. (2011). “ Isoresponse versus isoinput estimates of cochlear filter tuning,” J. Assoc. Res. Otolaryngol. 12(3), 281–299. 10.1007/s10162-010-0252-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Freeman, D. M. , and Weiss, T. F. (1990a). “ Hydrodynamic forces on hair bundles at low frequencies,” Hear. Res. 48, 17–30. 10.1016/0378-5955(90)90196-V [DOI] [PubMed] [Google Scholar]
- 15. Freeman, D. M. , and Weiss, T. F. (1990b). “ Hydrodynamic forces on hair bundles at high frequencies,” Hear. Res. 48, 31–36. 10.1016/0378-5955(90)90197-W [DOI] [PubMed] [Google Scholar]
- 16. Frisina, R. D. , Smith, R. L. , and Chamberlain, S. C. (1990). “ Encoding of amplitude modulation in the gerbil cochlear nucleus: I. A hierarchy of enhancement,” Hear. Res. 44(2), 99–122. 10.1016/0378-5955(90)90074-Y [DOI] [PubMed] [Google Scholar]
- 17. Furman, A. C. , Kujawa, S. G. , and Liberman, M. C. (2013). “ Noise-induced cochlear neuropathy is selective for fibers with low spontaneous rates,” J. Neurophys. 110(3), 577–586. 10.1152/jn.00164.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Glasberg, B. R. , and Moore, B. C. (1990). “ Derivation of auditory filter shapes from notched-noise data,” Hear. Res. 47(1), 103–138. 10.1016/0378-5955(90)90170-T [DOI] [PubMed] [Google Scholar]
- 19. Goldstein, J. L. , Baer, T. , and Kiang, N. Y. S. (1971). “ A theoretical treatment of latency, group delay, and tuning characteristics for auditory-nerve responses to clicks and tones,” in Physiology of the Auditory System, edited by Sachs M. B. ( National Education Consultants, Baltimore, MD: ), pp. 133–141. [Google Scholar]
- 20. Gorga, M. P. , Neely, S. T. , Dierking, D. M. , Kopun, J. , Jolkowski, K. , Groenenboom, K. , Tan, H. , and Stiegemann, B. (2007). “ Low-frequency and high-frequency cochlear nonlinearity in humans,” J. Acoust. Soc. Am. 122, 1671–1680. 10.1121/1.2751265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Gorga, M. P. , Worthington, D. W. , Reiland, J. K. , Beauchaine, K. A. , and Goldar, D. E. (1985). “ Electrophysiological techniques in audiology and otology—some comparisons between auditory brain-stem response thresholds, latencies and the pure-tone audiogram,” Ear. Hear. 6(2), 105–112. 10.1097/00003446-198503000-00008 [DOI] [PubMed] [Google Scholar]
- 22. Greenwood, D. D. (1961). “ Critical bandwidth and the frequency coordinates of the basilar membrane,” J. Acoust. Soc. Am. 33(10), 1344–1356. 10.1121/1.1908437 [DOI] [Google Scholar]
- 23. Gu, J. W. , Herrmann, B. S. , Levine, R. A. , and Melcher, J. R. (2012). “ Brainstem auditory evoked potentials suggest a role for the ventral cochlear nucleus in tinnitus,” J. Assoc. Res. Otolaryngol. 13(6), 819–833. 10.1007/s10162-012-0344-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Guinan, J. J., Jr. (2012). “ How are inner hair cells stimulated? Evidence for multiple mechanical drives,” Hear. Res. 292(1–2), 35–50. 10.1016/j.heares.2012.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Hämäläinen, M. , Hari, R. , Ilmoniemi, R. J. , Knuutila, J. , and Lounasmaa, O. V. (1993). “ Magnetoencephalography—theory, instrumentation, and applications to noninvasive studies of the working human brain,” Rev. Mod. Phys. 65(2), 1–93. 10.1103/RevModPhys.65.413 [DOI] [Google Scholar]
- 26. Heinz, M. G. , Zhang, X. , Bruce, I. , and Carney, L. (2001). “ Auditory nerve model for predicting performance limits of normal and impaired listeners,” Acoust. Res. Lett. Online 2, 91–96. 10.1121/1.1387155 [DOI] [Google Scholar]
- 27. Hickox, A. E. , and Liberman, M. C. (2014). “ Is noise-induced cochlear neuropathy key to the generation of hyperacusis or tinnitus?,” J. Neurophys. 111(3), 552–564. 10.1152/jn.00184.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Ibrahim, R. A. , and Bruce, I. A. (2010). “ Effects of peripheral tuning on the auditory nerve's representation of speech envelope and temporal fine structure cues,” in The Neurophysiological Bases of Auditory Perception ( Springer, New York: ), pp. 429–438. [Google Scholar]
- 28.ISO (2003). ISO 226, “ Acoustics–Normal equal-loudness-level contours” (International Organization for Standardization, Geneva, Switzerland).
- 29. Jackson, B. S. , and Carney, L. H. (2005). “ The spontaneous-rate histogram of the auditory nerve can be explained by only two or three spontaneous rates and long-range dependence,” J. Assoc. Res. Otolaryngol. 6(2), 148–159. 10.1007/s10162-005-5045-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Jepsen, M. L. , Ewert, S. D. , and Dau, T. (2008). “ A computational model of human auditory signal processing and perception,” J. Acoust. Soc. Am. 124(1), 422–438. 10.1121/1.2924135 [DOI] [PubMed] [Google Scholar]
- 31. Jiang, Z. D. , Zheng, M. S. , Sun, D. K. , and Liu, X. Y. (1991). “ Brainstem auditory evoked responses from birth to adulthood: Normative data of latency and interval,” Hear. Res. 54(1), 67–74. 10.1016/0378-5955(91)90137-X [DOI] [PubMed] [Google Scholar]
- 32. Johannesen, P. T. , and Lopez-Poveda, E. A. (2008). “ Cochlear nonlinearity in normal-hearing subjects as inferred psychophysically and from distortion-product otoacoustic emissions,” J. Acoust. Soc. Am. 124(4), 2149–2163. 10.1121/1.2968692 [DOI] [PubMed] [Google Scholar]
- 105. Joris, P. X. , Schreiner, C. E. , and Rees, A. (2004). “ Neural processing of amplitude-modulated sounds,” Phys. Rev. 84(2), 541–577. 10.1152/physrev.00029.2003 [DOI] [PubMed] [Google Scholar]
- 33. Joris, P. X. , and Yin, T. C. (1992). “ Responses to amplitude-modulated tones in the auditory nerve of the cat,” J. Acoust. Soc. Am. 91(1), 215–232. 10.1121/1.402757 [DOI] [PubMed] [Google Scholar]
- 34. Krishna, B. S. , and Semple, M. N. (2000). “ Auditory temporal processing: Responses to sinusoidally amplitude-modulated tones in the inferior colliculus,” J. Neurophys. 84(1), 255–273. [DOI] [PubMed] [Google Scholar]
- 35. Kujawa, S. G. , and Liberman, M. C. (2009). “ Adding insult to injury: Cochlear nerve degeneration after “temporary” noise-induced hearing loss,” J. Neurosci. 29, 14077–14085. 10.1523/JNEUROSCI.2845-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Langner, G. , and Schreiner, C. E. (1988). “ Periodicity coding in the inferior colliculus of the cat. I. Neuronal mechanisms,” J. Neurophys. 60(6), 1799–1822. [DOI] [PubMed] [Google Scholar]
- 37. Liberman, M. C. (1978). “ Auditory-nerve response from cats raised in a low-noise chamber,” J. Acoust. Soc. Am. 63, 442–455. 10.1121/1.381736 [DOI] [PubMed] [Google Scholar]
- 38. Liberman, M. C. , Dodds, L. W. , and Pierce, S. (1990). “ Afferent and efferent innervation of the cat cochlea: Quantitative analysis using light and electron microscopy,” J. Comp. Neurol. 301, 443–460. 10.1002/cne.903010309 [DOI] [PubMed] [Google Scholar]
- 39. Lin, H. W. , Furman, A. C. , Kujawa, S. G. , and Liberman, M. C. (2011). “ Primary neural degeneration in the Guinea pig cochlea after reversible noise-induced threshold shift,” J. Assoc. Res. Otolaryngol. 12(5), 605–616. 10.1007/s10162-011-0277-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Lopez-Poveda, E. A. , and Eustaquio-Martín, A. (2006). “ A biophysical model of the inner hair cell: The contribution of potassium currents to peripheral auditory compression,” J. Assoc. Res. Otolaryngol. 7(3), 218–235. 10.1007/s10162-006-0037-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Maloff, E. S. , and Hood, L. J. (2014). “ A comparison of auditory brain stem responses elicited by click and chirp stimuli in adults with normal hearing and sensory hearing loss,” Ear. Hear. 35(2), 271–282. 10.1097/AUD.0b013e3182a99cf2 [DOI] [PubMed] [Google Scholar]
- 42. Meddis, R. (1986). “ Simulation of mechanical to neural transduction in the auditory receptor,” J. Acoust. Soc. Am. 79(3), 702–711. 10.1121/1.393460 [DOI] [PubMed] [Google Scholar]
- 43. Melcher, J. R. , and Kiang, N. (1996). “ Generators of the brainstem auditory evoked potential in cat III: Identified cell populations,” Hear. Res. 93(1), 52–71. 10.1016/0378-5955(95)00200-6 [DOI] [PubMed] [Google Scholar]
- 44. Neely, S. T. , Norton, S. J. , Gorga, M. P. , and Jesteadt, W. (1988). “ Latency of auditory brain-stem responses and otoacoustic emissions using tone-burst stimuli,” J. Acoust. Soc. Am. 83(2), 652–656. 10.1121/1.396542 [DOI] [PubMed] [Google Scholar]
- 45. Nelson, P. C. , and Carney, L. H. (2004). “ A phenomenological model of peripheral and central neural responses to amplitude-modulated tones,” J. Acoust. Soc. Am. 116, 2173–2186. 10.1121/1.1784442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Oertel, D. (1983). “ Use of brain slices in the study of the auditory system: Spatial and temporal summation of synaptic inputs in cells in the anteroventral cochlear nucleus of the mouse,” J. Acoust. Soc. Am. 78(1), 328–333. [DOI] [PubMed] [Google Scholar]
- 46. Okada, Y. C. , Wu, J. , and Kyuhou, S. (1997). “ Genesis of MEG signals in a mammalian CNS structure,” Electroencephalogr. Clin. Neurophysiol. 103, 474–485. 10.1016/S0013-4694(97)00043-6 [DOI] [PubMed] [Google Scholar]
- 90. Oxenham, A. J. , and Shera, C. A. (2003). “ Estimates of human cochlear tuning at low levels using forward and simultaneous masking,” J. Assoc. Res. Otolaryngol. 4(4), 541–554. 10.1007/s10162-002-3058-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Palmer, A. R. , and Russell, I. J. (1986). “ Phase-locking in the cochlear nerve of the guinea-pig and its relation to the receptor potential of the inner hair-cells,” Hear. Res. 24(1), 1–15. 10.1016/0378-5955(86)90002-X [DOI] [PubMed] [Google Scholar]
- 48. Picton, T. W. (2011). Human Auditory Evoked Potentials ( Plural Publishing Inc., Oxford, UK: ), Chap. 8, pp. 213–245. [Google Scholar]
- 49. Picton, T. W. , Stapells, D. R. , and Campbel, K. B. (1981). “ Auditory evoked potentials from the human cochlea and brainstem,” J. Otolaryngol. Suppl. 9, 1–41. [PubMed] [Google Scholar]
- 50. Ponton, C. W. , Moore, J. K. , and Eggermont, J. J. (1996). “ Auditory brain stem response generation by parallel pathways: Differential maturation of axonal conduction time and synaptic transmission,” Ear. Hear. 17(5), 402–410. 10.1097/00003446-199610000-00006 [DOI] [PubMed] [Google Scholar]
- 51. Prosser, S. , and Arslan, E. (1987). “ Prediction of auditory brainstem wave V latency as a diagnostic tool of sensorineural hearing loss,” Int. J. Audiol. 26(3), 179–187. 10.3109/00206098709078420 [DOI] [PubMed] [Google Scholar]
- 52. Purcell, D. W. , John, S. M. , Schneider, B. A. , and Picton, T. W. (2004). “ Human temporal auditory acuity as assessed by envelope following responses,” J. Acoust. Soc. Am. 116(6), 3581–3593. 10.1121/1.1798354 [DOI] [PubMed] [Google Scholar]
- 53. Puria, S. (2003). “ Measurements of human middle ear forward and reverse acoustics: Implications for otoacoustic emissions,” J. Acoust. Soc. Am. 113(5), 2773–2789. 10.1121/1.1564018 [DOI] [PubMed] [Google Scholar]
- 54. Rasetshwane, D. M. , Argenyi, M. , Neely, S. T. , Kopun, J. G. , and Gorga, M. P. (2013). “ Latency of tone-burst-evoked auditory brainstem responses and otoacoustic emissions: Level, frequency, and rise-time effects,” J. Acoust. Soc. Am. 133, 2803–2817. 10.1121/1.4798666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Recio, A. , and Rhode, W. S. (2000). “ Basilar membrane responses to broadband stimuli,” J. Acoust. Soc. Am. 108(5), 2281–2298. 10.1121/1.1318898 [DOI] [PubMed] [Google Scholar]
- 56. Recio, A. , Rich, N. C. , Narayan, S. S. , and Ruggero, M. A. (1998). “ Basilar-membrane responses to clicks at the base of the chinchilla cochlea,” J. Acoust. Soc. Am. 103(4), 1972–1989. 10.1121/1.421377 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Relkin, E. M. , and Doucet, J. R. (1991). “ Recovery from prior stimulation. I: Relationship to spontaneous firing rates of primary auditory neurons,” Hear. Res. 55(2), 215–222. 10.1016/0378-5955(91)90106-J [DOI] [PubMed] [Google Scholar]
- 58. Rhode, W. S. , and Greenberg, S. (1994). “ Encoding of amplitude-modulation in the cochlear nucleus of the cat,” J. Neurophys. 71(5), 1797–1825. [DOI] [PubMed] [Google Scholar]
- 59. Rhode, W. S. , and Smith, P. H. (1985). “ Characteristics of tone-pip response patterns in relationship to spontaneous rate in cat auditory nerve fibers,” Hear. Res. 18, 159–168. 10.1016/0378-5955(85)90008-5 [DOI] [PubMed] [Google Scholar]
- 92. Robles, L. , and Ruggero, M. A. (2001). “ Mechanics of the mammalian cochlea,” Phys. Rev. 81(3), 1305–1352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Rønne, F. M. , Dau, T. , Harte, J. M. , and Elberling, C. E. (2012). “ Modeling auditory evoked brainstem responses to transient stimuli,” J. Acoust. Soc. Am. 131, 3903–3913. 10.1121/1.3699171 [DOI] [PubMed] [Google Scholar]
- 60. Russell, I. J. , Cody, A. R. , and Richardson, G. P. (1986). “ The responses of inner and outer hair-cells in the basal turn of the guinea-pig cochlea and in the mouse cochlea grown in vitro,” Hear. Res. 22(1–3), 199–216. 10.1016/0378-5955(86)90096-1 [DOI] [PubMed] [Google Scholar]
- 61. Russell, I. J. , and Sellick, P. M. (1983). “ Low-frequency characteristics of intracellularly recorded receptor potentials in guinea-pig cochlear hair-cells,” J. Phys.-London 338, 179–206. 10.1113/jphysiol.1983.sp014668 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Sachs, M. B. , and Abbas, P. J. (1974). “ Rate versus level functions for auditory‐nerve fibers in cats: tone‐burst stimuli,” J. Acoust. Soc. Am. 56(6), 1835–1847. 10.1121/1.1903521 [DOI] [PubMed] [Google Scholar]
- 63. Schaette, R. , and McAlpine, D. (2011). “ Tinnitus with a normal audiogram: Physiological evidence for hidden hearing loss and computational model,” J. Neurosci. 31(38), 13452–13457. 10.1523/JNEUROSCI.2156-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Sellick, P. M. , and Russell, I. J. (1980). “ The response of inner hair-cells to basilar-membrane velocity during low-frequency auditory stimulation in the guinea-pig cochlea,” Hear. Res. 2(3–4), 439–445. 10.1016/0378-5955(80)90080-5 [DOI] [PubMed] [Google Scholar]
- 65. Sergeyenko, Y. , Lall, K. , Liberman, M. C. , and Kujawa, S. G. (2013). “ Age-related cochlear synaptopathy: An early-onset contributor to auditory functional decline,” J. Neurosci. 33(34), 13686–13694. 10.1523/JNEUROSCI.1783-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Serpanos, Y. C. , O'Malley, H. , and Gravel, J. S. (1997). “ The relationship between loudness intensity functions and the click-ABR wave V latency,” Ear. Hear. 101, 2151–2163. 10.1097/00003446-199710000-00006 [DOI] [PubMed] [Google Scholar]
- 67. Shamma, S. A. , Chadwick, R. S. , Wilbur, W. J. , Morrish, K. A. , and Rinzel, J. (1986). “ A biophysical model of cochlear processing—intensity dependence of pure-tone responses,” J. Acoust. Soc. Am. 80(1), 133–145. 10.1121/1.394173 [DOI] [PubMed] [Google Scholar]
- 68. Shera, C. A. (2001). “ Intensity-invariance of fine time structure in basilar-membrane click responses: Implications for cochlear mechanics,” J. Acoust. Soc. Am. 110(1), 332–348. 10.1121/1.1378349 [DOI] [PubMed] [Google Scholar]
- 95. Shera, C. A. , and Guinan, J. J., Jr. (1999). “ Evoked otoacoustic emissions arise by two fundamentally different mechanisms: A taxonomy for mammalian OAEs,” J. Acoust. Soc. Am. 105(2), 782–798. 10.1121/1.426948 [DOI] [PubMed] [Google Scholar]
- 97. Shera, C. A. , Guinan, J. J., Jr , and Oxenham, A. J. (2002). “ Revised estimates of human cochlear tuning from otoacoustic and behavioral measurements,” Proc. Nat. Acad. Sci. U.S.A. 99(5), 3318–3323. 10.1073/pnas.032675099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Shera, C. A. , Guinan, J. J., Jr , and Oxenham, A. J. (2010). “ Otoacoustic estimation of cochlear tuning: Validation in the chinchilla,” J. Assoc. Res. Otolaryngol. 11, 343–365. 10.1007/s10162-010-0217-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Shera, C. A. , and Zweig, G. (1991). “ A symmetry suppresses the cochlear catastrophe,” J. Acoust. Soc. Am. 89(3), 1276–1289. 10.1121/1.400650 [DOI] [PubMed] [Google Scholar]
- 71. Strelcyk, O. , Christoforidis, D. , and Dau, T. (2009). “ Relation between derived-band auditory brainstem response latencies and behavioral frequency selectivity,” J. Acoust. Soc. Am. 126(4), 1878–1888. 10.1121/1.3203310 [DOI] [PubMed] [Google Scholar]
- 72. Sumner, C. J. , Lopez-Poveda, E. A. , O'Mard, L. P. , and Meddis, R. (2002). “ A revised model of the inner-hair cell and auditory-nerve complex,” J. Acoust. Soc. Am. 111(5), 2178–2188. 10.1121/1.1453451 [DOI] [PubMed] [Google Scholar]
- 73. Sumner, C. J. , O'Mard, L. P. , Lopez-Poveda, E. A. , and Meddis, R. (2003). “ A nonlinear filter-bank model of the guinea-pig cochlear nerve: Rate responses,” J. Acoust. Soc. Am. 113(6), 3264–3274. 10.1121/1.1568946 [DOI] [PubMed] [Google Scholar]
- 87. Taberner, A. M. , and Liberman, M. C. (2005). “ Response properties of single auditory nerve fibers in the mouse,” J. Neurophysiol. 93(1), 557–569. [DOI] [PubMed] [Google Scholar]
- 74. Vannucci, G. , and Teich, M. C. (1978). “ Effects of rate variation on the counting statistics of dead-time-modified Poisson processes,” Opt. Commun. 25(2), 267–272. 10.1016/0030-4018(78)90322-X [DOI] [Google Scholar]
- 75. Verhulst, S. , Dau, T. , and Shera, C. A. (2012). “ Nonlinear time-domain cochlear model for transient stimulation and human otoacoustic emission,” J. Acoust. Soc. Am. 132, 3842–3848. 10.1121/1.4763989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Verhulst, S. , Harte, J. M. , and Dau, T. (2011). “ Temporal suppression of the click-evoked otoacoustic emission level-curve,” J. Acoust. Soc. Am. 129(3), 1452–1463. 10.1121/1.3531930 [DOI] [PubMed] [Google Scholar]
- 77. Verhulst, S. , and Shera, C. A. (2015). “ Relating the variability of toneburst otoacoustic emission and auditory brainstem response latency to the underlying cochlear mechanics,” in 12th Mechanics of Hearing Workshop, edited by Karavitaki D. and Corey D. ( AIP, Melville, NY: ), in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Voordecker, P. , Brunko, E. , and de Beyl, Z. (1988). “ Selective unilateral absence or attenuation of wave V of brain-stem auditory evoked potentials with intrinsic brain-stem lesions,” Arch. Neurol. 45(11), 1272–1276. 10.1001/archneur.1988.00520350110027 [DOI] [PubMed] [Google Scholar]
- 79. Weiss, T. F. , and Rose, C. (1988). “ A comparison of synchronization filters in different auditory receptor organs,” Hear. Res. 33(2) 175–179. 10.1016/0378-5955(88)90030-5 [DOI] [PubMed] [Google Scholar]
- 80. Westerman, L. A. , and Smith, R. L. (1988). “ A diffusion model of the transient response of the cochlear inner hair cell synapse,” J. Acoust. Soc. Am. 83, 2266–2276. 10.1121/1.396357 [DOI] [PubMed] [Google Scholar]
- 81. Zhang, X. D. , and Carney, L. H. (2005). “ Analysis of models for the synapse between the inner hair cell and the auditory nerve,” J. Acoust. Soc. Am. 118(3), 1540–1553. 10.1121/1.1993148 [DOI] [PubMed] [Google Scholar]
- 82. Zhang, X. D. , Heinz, M. G. , Bruce, I. C. , and Carney, L. H. (2001). “ A phenomenological model for the responses of auditory-nerve fibers: I. Nonlinear tuning with compression and suppression,” J. Acoust. Soc. Am. 109, 648–670. 10.1121/1.1336503 [DOI] [PubMed] [Google Scholar]
- 83. Zilany, M. S. A. , and Bruce, I. C. (2006). “ Modeling auditory-nerve responses for high sound pressure levels in the normal and impaired auditory periphery,” J. Acoust. Soc. Am. 120(3), 1446–1466. 10.1121/1.2225512 [DOI] [PubMed] [Google Scholar]
- 84. Zilany, M. S. A. , Bruce, I. C. , and Carney, L. H. (2014). “ Updated parameters and expanded simulation options for a model of the auditory periphery,” J. Acoust. Soc. Am. 135(1), 283–286. 10.1121/1.4837815 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Zilany, M. S. A. , Bruce, I. C. , Nelson, P. C. , and Carney, L. H. (2009). “ A phenomenological model of the synapse between the inner hair cell and auditory nerve: Long-term adaptation with power-law dynamics,” J. Acoust. Soc. Am. 126, 2390–2412. 10.1121/1.3238250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Zweig, G. (1991). “ Finding the impedance of the organ of corti,” J. Acoust. Soc. Am. 89(3), 1229–1254. 10.1121/1.400653 [DOI] [PubMed] [Google Scholar]