Abstract
Objectives
Studies of cancer recurrences and second primary tumors require information on outcome dates. Little is known about how well electronic health record-based algorithms can identify dates or how errors in dates can bias analyses.
Research Design
We assessed rule-based and model-fitting approaches to assign event dates using a previously published electronic health record-based algorithm for second breast cancer events (SBCE). We conducted a simulation study to assess bias due to date assignment errors in time-to-event analyses.
Subjects
From a cohort of 3152 early stage breast cancer patients, 358 women accurately identified as having had an SBCE served as the basis for this analysis.
Measures
Percent of predicted SBCE dates identified within +/−60 days of the true date was the primary measure of accuracy. In the simulation study, bias in hazard ratios (HRs) was estimated by averaging the difference between HRs based on algorithm-assigned dates and the true HR across 1000 simulations each with simulated N=4000.
Results
The most accurate date algorithm had a median difference between the true and predicted dates of 0 days with 82% of predicted dates falling within 60 days of the true date. Bias resulted when algorithm sensitivity and specificity varied by exposure status, but was minimal when date assignment errors were of the magnitude observed for our date assignment method.
Conclusions
SBCE date can be relatively accurately assigned based on a previous algorithm. While acceptable in many scenarios, algorithm-assigned dates are not appropriate to use when operating characteristics are likely to vary by the study exposure.
INTRODUCTION
Algorithms to identify cancer recurrence using claims data are increasingly common.1–6 Prior studies using algorithms have classified individuals with respect to whether or not an event has occurred. However, most studies have not assigned or validated an event date even though such dates are critical for most epidemiologic studies, especially time-to-event analyses. Our goals in the present analysis were to assess: 1) the accuracy in assigning second breast cancer event (SBCE) date based on a previously published algorithm;1 and 2) the implications of errors in date assignment when estimating exposure-outcome associations.
A prior manuscript presented a “menu” of algorithms to identify SBCE from which users can select algorithms based on the relative importance of sensitivity, specificity, and positive predictive value (PPV) for their study.1 Presumably, investigators who use a high sensitivity algorithm and verify results through chart abstraction can also abstract SBCE date. We therefore focused the present date assignment analysis on the high specificity algorithm (Figure 2 in Chubak et al.1), which is recommended when chart abstraction is not planned, date confirmation is not possible and tumor registry data are available.7 We conducted a secondary analysis focusing on the high specificity algorithm that did not rely on tumor registry data (Figure 5 in Chubak et al.1) to increase the applicability of our results to settings in which only claims data are available.
In addition to providing guidance for using the previously published algorithms in time-to-event analyses, this manuscript outlines an approach that other studies can use to develop date algorithms and assess impact of algorithm errors on study results.
METHODS
Development of date algorithm
We previously developed and validated SBCE classification algorithms in a population-based cohort of 3152 stage I and II breast cancer patients diagnosed with cancer while members of an integrated healthcare delivery system in western Washington state.1 The high specificity algorithm (Figure 2 in Chubak et al.1) used cancer-related procedure (ICD-9 and CPT) and diagnosis (ICD-9) codes capturing care received within the integrated delivery system as well as externally (via claims), along with Surveillance, Epidemiology and End Results (SEER) program cancer registry records to identify SBCE. In developing the algorithm, we also used pharmacy records as potential predictors; however, these did not improve the algorithm’s validity. With the exception of SEER tumor registry data, the algorithm used only data that would be available in claims databases.
Of 407 chart-reviewed SBCE in this population, the algorithm correctly identified 358 SBCE. Using the same dataset in which the SBCE classification algorithm was developed, we first tested rule-based approaches to assign SBCE date based on the variables in the classification algorithm that identified women as having an SBCE (i.e., two visits with a code for a secondary malignant neoplasm within 60 days and occurring >365 days after primary diagnosis; a second breast cancer record in the SEER program cancer registry; or mastectomy >180 days after primary breast cancer). Our first approach was to assign SBCE date by using the date of the variable that classified the woman as having an SBCE. We next tried assigning SBCE by using the earliest date of the three variables that could classify a woman as having had an SBCE (Appendix Figure 1). We also explored building prediction models for time to SBCE.
Figure 1.
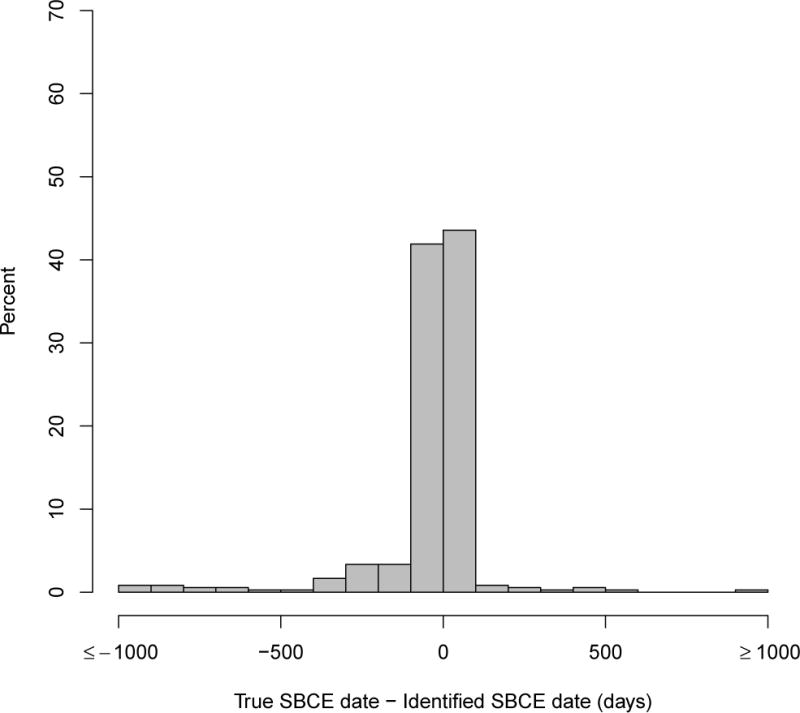
Distribution of days between estimated and true second breast cancer event (SBCE) date among persons with true SBCE
SBCE: second breast cancer event. The occurrence and dates of true SBCE were obtained from chart abstraction and the Surveillance, Epidemiology and End Results (SEER) cancer registry.
We also published a high specificity algorithm that did not rely on SEER cancer registry data (Figure 5 in Chubak et al.1). This algorithm can be implemented when only claims data (procedure and diagnosis codes) are available. We tested rule-based approaches to data classification using this algorithm as well.
Assessment of date algorithm accuracy
The true date of SBCE was abstracted from medical records. During chart review, pathological confirmation of a recurrence or second primary breast cancer was used as the SBCE date; when a pathological diagnosis date was unavailable, the date from imaging or other clinical diagnosis was abstracted. To assess the accuracy of different date assignment algorithms, we compared the difference in algorithm-assigned SBCE dates to the true date among true positives (N=358), as previously determined by chart abstraction. A priori, we defined our primary accuracy measure to be the percent of predicted SBCE dates identified within +/−60 days of the true date. We used histograms to examine the distribution of date error overall and by type of SBCE (i.e., local recurrence, regional recurrence, distant recurrence, and second primary breast cancer). For the eight most extreme outliers, we further investigated patient medical records to understand the source of the error.
Simulation study
Relying on imperfect algorithms to identify SBCEs and assign their dates could bias study results. We therefore conducted a simulation study to investigate whether the SBCE classification algorithm and the newly developed SBCE date assignment algorithm would be adequate for epidemiologic studies. We investigated bias from using the algorithm-assigned dates in a hypothetical study of the effect of a non-time-varying binary covariate on time to SBCE. Data were simulated as follows:
Exposure simulation. We first randomly assigned 50% of the population to the exposure group and 50% to no exposure.
True SBCE date simulation. We simulated a true SBCE date from an exponential distribution with rate 0.05 for unexposed individuals and 0.075 for exposed individuals, corresponding to a true hazard ratio of 1.5.
Censoring. We next simulated censoring times from a Weibull (shape =2.1, scale = 7). Parameters of the censoring distribution were chosen so that the distribution resembled that of censoring times observed in our sample. Individuals with true SBCE dates prior to censoring times were considered true events. Those with censoring times prior to true SBCE dates were considered censored.
Date misclassification simulation. We assumed several values for algorithm sensitivity (S) and specificity (P) (see Table 2) and used these to simulate algorithm-assigned event or censoring status. The sensitivity and specificity in the exposed and unexposed groups were chosen such that the weighted average gave the sensitivity and specificity observed in the total population. The overall sensitivity of the algorithm was 0.89.1 In the analyses where we varied sensitivity and specificity, we set the sensitivity in the exposed group to 0.86. That “forced” the sensitivity in the unexposed group to be 0.91 in order to preserve the overall sensitivity in the total population at 0.89. Given how high the overall sensitivity was, we were limited in how different the sensitivities could be between any two groups. Changes in sensitivity forced changes in specificity in order to keep the overall misclassification rate constant. For true events, we simulated algorithm-assigned event status from a Bernoulli(S). Thus (1-S)% of true events were misclassified by the algorithm as censored observations. Similarly, for individuals whose true status was censored, we simulated algorithm-assigned event status from a Bernoulli(1-P), resulting in (1-P)% of censored observations being misclassified by the algorithm as false-positive events.
Date accuracy simulation. Finally, for true-positive events we generated algorithm-assigned dates by adding normally distributed random error with mean and variance as given in Table 2 to the simulated true SBCE date. For false positive events, the algorithm-assigned date was simulated from a Weibull (shape = 1.1, scale = 3.1). This distribution was chosen to resemble that of the observed algorithm-assigned SBCE dates among false-positives in our data.
Table 2.
Bias in hypothetical study results due to errors in algorithms identifying and assigning dates to second breast cancer events
| Scenario | Description | Mean Estimated hazard ratio | Percent bias* |
|---|---|---|---|
| 1 | Exposure† is unrelated to errors in outcome classification and date assignment Date error in unexposed and exposed (years): mean=0, SD=1 Example: Exposure is a genetic factor, such as CYP2D6 genotype |
1.47 |
−2.2% |
| 2 | SBCE are detected later in exposed group Date error in unexposed (years): mean=−0.25, SD=1; exposed: mean=0.25, SD=1) Example: Exposure is annual vs. biennial follow-up visits, where all SBCEs are eventually detected, albeit at different times. |
1.51 |
0.4% |
| 3 | SBCE are detected earlier and with more precision in the exposed group Date error in unexposed (years): mean=0.25, SD=1.25; exposed: mean=−0.25, SD=0.75) Example: People who are exposed (e.g., medication users) visit their providers more frequently |
1.49 |
−0.9% |
| 4 | SBCE are detected later and with less precision in the exposed group Date error in unexposed (years): mean=−0.25, SD=0.75; exposed: mean=0.25, SD=1.25) Example: People who are exposed (e.g., high body mass index) visit their providers less frequently |
1.44 | −3.8% |
| 5 | SBCE sensitivity is higher and specificity is lower in the exposed group vs. unexposed, but no difference in date error Classification accuracy in unexposed: sensitivity = 0.86, specificity = 0.99; exposed: sensitivity = 0.91, specificity = 0.982 Date error in unexposed and exposed (years): mean=0, SD=1 Example: Exposure is provider type and certain providers tend to give more diagnosis codes than others |
1.60 | 6.5% |
| 6 | SBCE sensitivity is higher and specificity is lower in the exposed group vs. unexposed, and SBCE are detected earlier and with more precision in the exposed group Classification accuracy in unexposed: sensitivity = 0.86, specificity = 0.99; exposed: sensitivity = 0.91, specificity = 0.982 Date error in unexposed (years): mean=0.25, SD=1.25; exposed: mean=−0.25, SD=0.75 Example: People who are exposed (e.g., medication users) come in more frequently and get more procedure and diagnosis codes |
1.62 | 8.1% |
SCBE: second breast cancer events; SD: standard deviation
Relative to true hazard ratio of 1.5
In all scenarios, exposure was binary and non-time-varying
After simulating the data, we fit a Cox proportional hazards model using algorithm-assigned dates as event times. Percent bias in the hazard ratios was estimated by averaging the difference between hazard ratios based on algorithm-assigned dates and the true hazard ratio (1.5) across 1000 simulations and dividing by the true hazard ratio. Each simulated population consisted of 4000 individuals (2000 exposed and 2000 unexposed).
RESULTS
The most accurate date assignment approach, defined by percent of predicted SBCE dates identified within +/−60 days of the true date, was to use the earliest date among any of the variables that could classify a woman as having an SBCE (Appendix Figure 1). None of the prediction models performed as well; we therefore present only the results of the rule-based analysis. Figure 1 shows the distribution of error in date assignment for this approach. Overall, the median difference between the true and predicted dates was 0 (interquartile range: −13 to 5) days. Forty-six percent of SBCE dates were estimated within +/−7days of the truth, and 82% within +/−60 days). Dates were estimated more accurately for second primary breast cancers than recurrences (Table 1, Appendix Figure 2). Among women with an SBCE, those whose first breast cancer was local, small, node negative, estrogen-receptor positive, or diagnosed in later years (2004–2006) tended to have SBCE event dates identified more accurately by the algorithm than women with larger tumors, positive nodes, estrogen-receptor negative tumors, or who were diagnosed earlier in time.
Table 1.
Factors associated with the accuracy of an algorithm to identify date of second breast cancer events.
| Absolute difference in date of true and predicted second breast cancer event date (in days)
|
||||
|---|---|---|---|---|
| <30 days N = 272 (76.0%) |
31–60 days N = 23 (6.4%) |
61–90 days N = 8 (2.2%) |
>90 days N = 55 (15.4%) |
|
| Age, mean (SD), y | 60.3 (13.4) | 60.2 (15.5) | 54.6 (15.2) | 61.7 (15.5) |
| Study follow-up, mean (SD), y | 7.6 (3.9) | 7.7 (3.8) | 7.6 (3.8) | 5.8 (3.6) |
|
| ||||
| n (row %) | n (row %) | n (row %) | n (row %) | |
|
| ||||
| Characteristics of second breast cancer event
|
||||
| Type | ||||
| Recurrence | 185 (70.3) | 18 (6.8) | 8 (3.0) | 52 (19.8) |
| Second primary | 87 (91.6) | 5 (5.3) | 0 (0) | 3 (3.2) |
| Method of diagnosis | ||||
| Clinical | 60 (71.4) | 5 (6.0) | 2 (2.4) | 17 (20.2) |
| Pathological | 171 (74.7) | 15 (6.6) | 6 (2.6) | 37 (16.2) |
| Extent of second breast cancer event | ||||
| In situ | 23 (95.8) | 0 (0) | 0 (0) | 1 (4.2) |
| Local | 94 (85.5) | 11 (10.0) | 0 (0) | 5 (4.5) |
| Regional | 19 (48.7) | 2 (5.1) | 2 (5.1) | 16 (41.0) |
| Distant | 132 (72.9) | 10 (5.5) | 6 (3.3) | 33 (18.2) |
| Year of second breast cancer event | ||||
| 1993–1995 | 5 (55.6) | 0 (0) | 0 (0) | 4 (44.4) |
| 1996–1999 | 49 (64.5) | 5 (6.6) | 4 (5.3) | 18 (23.7) |
| 2000–2003 | 95 (79.8) | 10 (8.4) | 1 (0.8) | 13 (10.9) |
| 2004–2006 | 64 (73.6) | 7 (8.0) | 3 (3.4) | 13 (14.9) |
| 2007–2011 | 59 (88.1) | 1 (1.5) | 0 (0) | 7 (10.4) |
| Age at second breast cancer event, y | ||||
| 20–29 | 0 (0) | 0 (0) | 1 (100) | 0 (0) |
| 30–39 | 7 (63.6) | 1 (9.1) | 0 (0) | 3 (27.3) |
| 40–49 | 31 (73.8) | 3 (7.1) | 0 (0) | 8 (19.0) |
| 50–59 | 68 (77.3) | 5 (5.7) | 4 (4.5) | 11 (12.5) |
| 60–69 | 62 (78.5) | 6 (7.6) | 1 (1.3) | 10 (12.7) |
| 70–79 | 59 (77.6) | 3 (3.9) | 2 (2.6) | 12 (15.8) |
| ≥80 | 45 (73.8) | 5 (8.2) | 0 (0) | 11 (18.0) |
| Characteristics first primary cancer
|
||||
| Year of primary diagnosis, n (%) | ||||
| 1993–1995 | 68 (73.9) | 5 (5.4) | 2 (2.2) | 17 (18.5) |
| 1996–1999 | 105 (77.8) | 11 (8.1) | 4 (3.0) | 15 (11.1) |
| 2000–2003 | 72 (73.5) | 6 (6.1) | 1 (1.0) | 19 (19.4) |
| 2004–2006 | 27 (81.8) | 1 (3.0) | 1 (3.0) | 4 (12.1) |
| Age at first primary breast cancer diagnosis, y | ||||
| 20–29 | 0 (0) | 0 (0) | 1 (33.3) | 2 (66.7) |
| 30–39 | 13 (76.5) | 2 (11.8) | 0 (0) | 2 (11.8) |
| 40–49 | 51 (78.5) | 4 (6.2) | 2 (3.1) | 8 (12.3) |
| 50–59 | 68 (77.3) | 5 (5.7) | 2 (2.3) | 13 (14.8) |
| 60–69 | 64 (79.0) | 5 (6.2) | 1 (1.2) | 11 (13.6) |
| 70–79 | 52 (73.2) | 5 (7.0) | 2 (2.8) | 12 (16.9) |
| ≥80 | 24 (72.7) | 2 (6.1) | 0 (0) | 7 (21.2) |
| Stage† | ||||
| Local | 199 (80.6) | 19 (7.7) | 1 (0.4) | 28 (11.3) |
| Regional | 73 (65.8) | 4 (3.6) | 7 (6.3) | 27 (24.3) |
| Distant | ||||
| Tumor size† | ||||
| ≤20 mm | 178 (82.0) | 16 (7.4) | 3 (1.4) | 20 (9.2) |
| 21–49 mm | 88 (65.7) | 7 (5.2) | 5 (3.7) | 34 (25.4) |
| ≥50 mm | 6 (85.7) | 0 (0) | 0 (0) | 1 (14.3) |
| Positive node† | ||||
| No nodes examined | 28 (70.0) | 4 (10.0) | 0 (0) | 8 (20.0) |
| All negative | 175 (82.2) | 15 (7.0) | 1 (0.5) | 22 (10.3) |
| Positive | 69 (65.7) | 4 (3.8) | 7 (6.7) | 25 (23.8) |
| ER and PR status† | ||||
| ER positive | 200 (78.7) | 15 (5.9) | 6 (2.4) | 33 (13.0) |
| Both ER and PR negative | 55 (67.1) | 8 (9.8) | 2 (2.4) | 17 (20.7) |
| Other | 17 (77.3) | 0 (0) | 0 (0) | 5 (22.7) |
| Surgery, n (%)† | ||||
| No surgery | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| Lumpectomy | 170 (79.1) | 15 (7.0) | 3 (1.4) | 27 (12.6) |
| Mastectomy | 102 (71.3) | 8 (5.6) | 5 (3.5) | 28 (19.6) |
| Unknown surgery type | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
| Radiation therapy† | ||||
| No | 99 (70.7) | 8 (5.7) | 4 (2.9) | 29 (20.7) |
| Yes | 171 (79.2) | 15 (6.9) | 4 (1.9) | 26 (12.0) |
| Unknown | 2 (100) | 0 (0) | 0 (0) | 0 (0) |
| Chemotherapy† | ||||
| No | 158 (79.0) | 13 (6.5) | 3 (1.5) | 26 (13.0) |
| Yes | 113 (72.0) | 10 (6.4) | 5 (3.2) | 29 (18.5) |
| Unknown | 1 (100) | 0 (0) | 0 (0) | 0 (0) |
| Adjuvant Hormonal therapy† | ||||
| No | 144 (73.1) | 16 (8.1) | 4 (2.0) | 33 (16.8) |
| Yes | 125 (79.1) | 7 (4.4) | 4 (2.5) | 22 (13.9) |
| Unknown | 3 (100) | 0 (0) | 0 (0) | 0 (0) |
SD = standard deviation; ER = estrogen receptor; PR = progesterone receptor; SEER = Surveillance, Epidemiology and End Results program of the National Cancer Institute
Second breast cancer event status (second primary breast cancer or recurrent breast cancer) was determined by medical chart review.
Ascertained from SEER cancer registry data.
Our investigation of the most extreme cases suggested that the algorithm occasionally estimated the SBCE date to be several years later than the true date because it captured the date of the second SBCE and missed the date of the first SBCE. When the algorithm estimated the date to be much earlier than the true date, this was generally because we our date assignment rule based the SBCE date on the earliest of the nodes. The node that actually classified the patient would have provided the correct date. However, that approach did not, overall, perform as well.
For the classification algorithm designed for use without registry data (Figure 5 in Chubak et al.1), the best among tested approaches for determining SBCE data was to use the earliest of: first date of two visits with a secondary malignant neoplasm code within 60 days of each other and occurring >365 days after primary breast cancer; date of a visit with a code for breast carcinoma in situ occurring >120 days after the primary breast cancer; and second date of two consecutive radiation therapy visits ≥ 78 days apart. Estimated SBCE date was within +/− 7 days of the truth for 38.4% of cases; 70% were within +/−60 days.
Our simulation study showed that if date error is unrelated to exposure status, bias in the hazard ratio estimate is minimal (Table 2, scenario 1). If sensitivity and specificity of the SBCE classification algorithm are unrelated to exposure but date accuracy varies by exposure, bias will be small (scenarios 2, 3, and 4). However, if sensitivity and specificity of SBCE classification are related to exposure (scenarios 5 and 6), bias large enough to qualitatively affect data interpretation can result even if date error is unrelated to exposure. This may occur, for example, if exposed persons have more frequent healthcare contacts and receive more procedure and diagnosis codes. Results were generally similar when we changed exposure prevalence and the “true” hazard ratio in the simulated population (not shown).
DISCUSSION
Electronic health records-based algorithms are increasingly being used for epidemiologic and health services research, as they provide an efficient means of ascertaining health outcomes and health-care related exposures and covariates. Most published studies of algorithms do not assign or validate event dates, even though many epidemiologic and health services studies rely on event dates. A previously published SBCE classification algorithm1 is an example of one whose potential usefulness in future studies is not fully realized without assignment and validation of event date. We therefore conducted this study to make that algorithm more useful for research and to outline an approach that developers of other algorithms can use to improve the usability of their algorithms.
We conclude that using the previously published SBCE classification algorithm will not meaningfully bias results of time-to-event analyses if its sensitivity and specificity do not vary by exposure status, even if date ascertainment error varies by exposure group. Exposures for which we would expect the algorithm to have similar sensitivity and specificity in unexposed and exposed people include genotypes, certain patient characteristics, or even frequency of use of certain health services. The key requirement is that similar diagnosis and procedure codes would appear in unexposed and exposed persons who have SBCEs, even if the those codes appear later in one versus the other of the exposure groups. For example, people with higher body mass index (BMI) may visit their healthcare provider less frequently and thus may be diagnosed with an SBCE later than people with a lower BMI. If diagnosis and procedures codes are similar between exposure groups, we would not expect much bias in the results of a study on the association between BMI and SBCE risk, even if diagnosis and procedure codes occur later in the group that comes in less frequently (i.e., those with higher BMI). Another scenario where we might not expect much bias would be the study of an exposure that caused a shift in distribution of SBCE type (e.g., a higher percent of SBCEs are distant recurrences in exposed persons compared to unexposed persons). This situation could lead to differences in date precision between groups because, as Table 1 demonstrates, date precision varies by SBCE type. However, our simulations show bias is minimal when only the date precision varies across exposure groups.
We have demonstrated, however, that bias can result when sensitivity and specificity of the SBCE classification algorithm vary by exposure group. Variation in operating characteristics of SBCE classification algorithm by exposure status could arise in several scenarios, such as when either the exposed or unexposed group does not receive the same clinical examinations and therefore lack diagnosis or procedure codes. This could occur if, for example, medication users receive certain clinical exams when they come in frequently for refills or check-ups but healthy non-users do not receive as complete a clinical work-up. This underlying healthcare utilization pattern would also, most likely, lead to different precision in dates across groups. In such a scenario, the hazard ratio from a study examining the relationship between medication use and SBCE risk could be biased. It is therefore important for investigators to think carefully about whether SBCE classification algorithm’s operating characteristics are likely to vary according to the exposure under study. If so, the algorithm should not be used.
In situations where use of the SBCE classification algorithm is appropriate, our findings enhance its usability by providing users with a way to assign SBCE date in time-to-event analyses, one of the most important types of analyses for understanding the risk of SBCEs. The approach used in this manuscript can be applied to other algorithms to understand the potential impact for bias based on errors in event date ascertainment. Understanding the circumstances under which use of algorithms is, and is not, appropriate is critical for ensuring valid results from epidemiologic and health services research that relies on administrative data.
Acknowledgments
Funding This work was supported by the National Cancer Institute at the National Institutes of Health: (R21CA143242 to J.C., R01CA149365 to T.O., R01CA09377 to Rebecca Silliman, U01CA063731 to D.S.M.B, R01CA120562 to Denise Boudreau, and U19CA79689 to Ed Wagner); and the American Cancer Society (CRTG-03–024-01-CCE to D.S.M.B). The collection of cancer incidence data used in this study was supported, in part, by the Cancer Surveillance System of the Fred Hutchinson Cancer Research Center, which is funded the Surveillance, Epidemiology and End Results (SEER) Program of the National Cancer Institute (contract numbers N01-CN-67009 and N01-PC-35142) with additional support from the Fred Hutchinson Cancer Research Center and the State of Washington. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the American Cancer Society.
APPENDICES
Appendix Figure 1.
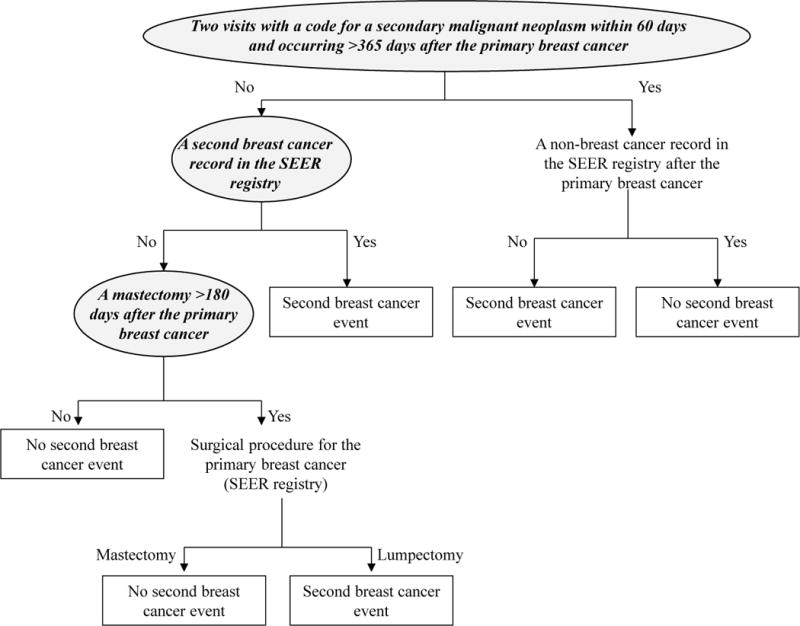
Algorithm to classify occurrence of second breast cancer event with high specificity and positive predictive value (adapted from Figure 2 in Chubak J, Yu O, Pocobelli G, et al. Administrative Data Algorithms to Identify Second Breast Cancer Events Following Early-Stage Invasive Breast Cancer. J Natl Cancer Inst. Apr 30 2012;104(12):931–940, by permission Oxford University Press). The most accurate date algorithm was to assign SBCE date as the earliest date among variables that could classify a woman as having an SBCE (indicated in shaded ovals with bold italics text).
Appendix Figure 2.
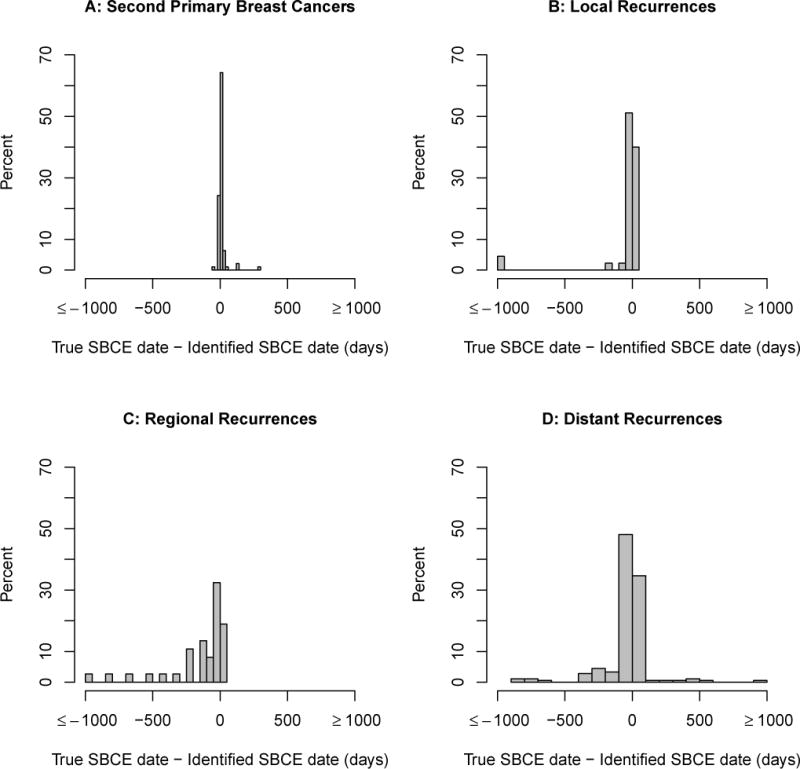
Distribution of days between estimated and true second breast cancer event (SBCE) date among persons with true SBCE, by SBCE type. (A) Second primary breast cancers; (B) Local recurrences; (C) Regional recurrences; (D) Distant recurrences.
References
- 1.Chubak J, Yu O, Pocobelli G, et al. Administrative Data Algorithms to Identify Second Breast Cancer Events Following Early-Stage Invasive Breast Cancer. J Natl Cancer Inst. 2012;104:931–940. doi: 10.1093/jnci/djs233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Earle CC, Nattinger AB, Potosky AL, et al. Identifying cancer relapse using SEER-Medicare data. Med Care. 2002;40:IV-75–81. doi: 10.1097/00005650-200208001-00011. [DOI] [PubMed] [Google Scholar]
- 3.McClish D, Penberthy L, Pugh A. Using Medicare claims to identify second primary cancers and recurrences in order to supplement a cancer registry. Journal of Clinical Epidemiology. 2003;56:760–767. doi: 10.1016/s0895-4356(03)00091-x. [DOI] [PubMed] [Google Scholar]
- 4.Lamont EB, Herndon JE, II, Weeks JC, et al. Measuring Disease-Free Survival and Cancer Relapse Using Medicare Claims From CALGB Breast Cancer Trial Participants (Companion to 9344) J Natl Cancer Inst. 2006;98:1335–1338. doi: 10.1093/jnci/djj363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hassett MJ, Ritzwoller DP, Taback N, et al. Validating Billing/Encounter Codes as Indicators of Lung, Colorectal, Breast, and Prostate Cancer Recurrence Using 2 Large Contemporary Cohorts. Med Care. 2012 doi: 10.1097/MLR.0b013e318277eb6f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Warren JL, Mariotto A, Melbert D, et al. Sensitivity of Medicare Claims to Identify Cancer Recurrence in Elderly Colorectal and Breast Cancer Patients. Med Care. 2013 doi: 10.1097/MLR.0000000000000058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chubak J, Pocobelli G, Weiss NS. Tradeoffs between accuracy measures for electronic health care data algorithms. Journal of Clinical Epidemiology. 2012;65:343–349. doi: 10.1016/j.jclinepi.2011.09.002. e342. [DOI] [PMC free article] [PubMed] [Google Scholar]


