Quantification of cell size using temporal diffusion spectroscopy

Abstract

Purpose

A new approach has been developed to quantify cell sizes and intracellular volume fractions using temporal diffusion spectroscopy with diffusion-weighted acquisitions.

Theory and Methods

Temporal diffusion spectra may be used to characterize tissue microstructure by measuring the effects of restrictions over a range of diffusion times. Oscillating gradients have been used previously to probe variations on cellular and subcellular scales, but their ability to accurately measure cell sizes larger than 10 μm is limited. By combining measurements made using oscillating gradient spin echo (OGSE) and a conventional pulsed gradient spin echo (PGSE) acquisition with a single, relatively long diffusion time, we can accurately quantify cell sizes and intracellular volume fractions.

Results

Based on a two compartment model (incorporating intra- and extracellular spaces), accurate estimates of cell sizes and intracellular volume fractions were obtained in vitro for (i) different cell types with sizes ranging from 10 to 20 μm, (ii) different cell densities, and (iii) before and after anti-cancer treatment.

Conclusion

Hybrid OGSE-PGSE acquisitions sample a larger region of temporal diffusion spectra and can accurately quantify cell sizes over a wide range. Moreover, the maximum gradient strength used was lower than 15 G/cm, suggesting that this approach is translatable to practical MR imaging.

Introduction

Cell size plays an important role in affecting the functional properties of cells from the molecular to the organismal level, such as cellular metabolism (1), proliferation (2) and tissue growth (3). For cancer diagnosis and prognosis, measurements of cell size have been widely used to differentiate cancer types (4) and monitor treatment-induced apoptosis (5). In addition to cell size, other microstructural information on a subcellular length scale, such as nuclear sizes, also provides insights into the functional properties of cancer cells. For example, nuclear size has been used to diagnose tumors (6) and distinguish low- from high-grade tumors (7). Conventionally, both cellular (e.g. cell size and cellularity) and subcellular (e.g. nuclear size and nuclear-to-cytoplasm ratio) information is obtained via invasive biopsy. However, biopsy is limited by various clinical complications, including pain, hemorrhage, infection, and even death (8). Therefore, a non-invasive technique with the capability of detecting tissue microstructural information on both cellular and subcellular length scales would be of great interest for clinical and research applications.

Diffusion-weighted MRI (DWI) provides a non-invasive way to map the diffusion properties of tissue water molecules that are affected by restrictions and hindrances to free movement, and is thereby able to provide information on tissue microstructure. Conventionally, an effective mean diffusion rate, the apparent diffusion coefficient (ADC), is obtained by using motion-sensitizing pulsed gradient spin echo (PGSE) pulse sequences to probe water displacements. ADC values are potentially affected by various tissue properties, including cellularity (9,10), cell size (11), nuclear size (12), and membrane permeability (13). ADC values therefore reflect overall diffusion effects and are not specific for any single parameter such as cell size. More elaborate methods have also been developed to map mean compartment size in porous media or tissues. Diffusion-diffraction effects (14) have been reported to successfully characterize the mono-dispersed cell sizes of erythrocytes (15), but fail in most real biological tissues due to the heterogeneous distribution of cell sizes. Q-space imaging generates a displacement probability distribution function that can provide apparent compartment sizes in biological tissues. Unfortunately, estimates of cell size are biased in practice because of methodological limitations (for example, the short-gradient pulse approximation (16) is usually not met, and only relatively low gradient strengths are available on regular MRI systems (17)) and the inherent complexity of real biological tissues (e.g. the existence of multiple compartments (17) and coexisting inflammation (18)). To overcome these problems, multi-compartment models that mimic real tissues have been developed to more accurately characterize cell size. For example, models that include more than one compartment and/or the effects of membrane permeability have been used to assess axon sizes in bovine optic nerve (19), to characterize axon size distributions in vitro (20) and in vivo (21), and to quantify mean axon size in the corpus callosum of human (22) and monkey brain (23). In addition, as an extension of the PGSE method, the double-PGSE sequence has been used to measure cell size and anisotropy in fixed yeast cells (24). However, despite these successes, subcellular microstructural information has not been obtainable by practical PGSE-based methods. One reason is that PGSE sequences typically employ a diffusion time of 20–80 ms in vivo due to hardware limitations. Thus, the characteristic diffusion length probed by water molecules is on the order of 5–20 μm, which is similar to the distance between hindering cell membranes of typical eukaryotic cells. As a result, PGSE measurements are sensitive to cellularity in biological tissues, but cannot isolate the effects of subcellular structures (< 5 μm). Consequently, conventional PGSE methods are suited to characterize cell sizes and cell densities in biological tissues non-invasively, but do not in practice provide information on subcellular microstructure.

Oscillating gradient spin echo (OGSE) sequences have emerged as a novel means to obtain much shorter effective diffusion times by replacing bipolar diffusion-sensitizing gradients in PGSE methods with oscillating gradients (25–27). Previous reports have shown that OGSE measurements, even at moderately low frequencies, are capable of detecting restrictions to water diffusion over a short spatial scale (< 5 μm) which is usually not accessible by conventional PGSE methods (25). Moreover, by varying the oscillation frequency (f), temporal diffusion spectra can be obtained to provide more comprehensive information about biological tissues at both cellular and subcellular length scales (28,29). OGSE sequences have been successfully implemented and used to measure abnormal brain metabolites (30) and treatment-induced variations in organelles (31), nuclear size changes after anti-cancer therapy (32) and hypoxia-ischemia (33,34). Recently, there has been increasing interest in using OGSE methods to measure axon sizes (35–37). However, despite these successes in probing microstructure, the ability of OGSE sequences that use harmonic waveforms to probe relatively large cell sizes is, ironically, limited by the maximum achievable diffusion time within the constraints of practical echo times. In typical cosine-modulated OGSE methods, the effective diffusion time Δ_diff = 1/(4f) = δ/(4N), where f is the frequency, δ is the duration of diffusion gradient, and N is the number of oscillations in each gradient (25). Hence, even for a very long gradient duration of 100 ms, the maximum achievable Δ_diff = 25 ms, corresponding to a diffusion distance ≈ 10 μm if the diffusion coefficient is 2 μm²/ms. Such a relatively short displacement significantly decreases the ability to quantify larger cell sizes (e.g. 10 – 20 μm), which is typical in tumors. Moreover, long gradient durations and lower frequencies in practice may not be used because of signal losses caused by T₂ relaxation. As an example, as shown in our recent histology-validated measurements using OGSE to measure mean axon diameters, dimensions in the range 1 to 5 μm were measured accurately, but the axon diameters larger than 6 μm were significantly underestimated (37).

For a general time-dependent gradient, the diffusion-weighted MR signal can be expressed as (25)

$$S=S_{0}exp\left[-\frac{1}{\pi }\underset{0}{\overset{\infty }{\int }}\mathbf{F}(\omega )\mathbf{D}(\omega )\mathbf{F}(-\omega )d\omega \right],$$ (1)

where F(ω) is the Fourier transform of the time integral of the diffusion gradient, and D(ω) is the frequency-dependent diffusion tensor that contains microstructural information. With appropriately designed gradient waveform (e.g. cosine-modulated), F(ω) can serve as a well-defined sampling function and hence D(ω), the temporal diffusion spectrum, can be obtained. However, due to hardware limitations, it is impossible to achieve all frequencies in practice, and hence only a segment of a diffusion spectrum can be acquired. For a conventional PGSE sequence, in which δ is the gradient pulse width and Δ is the diffusion time, $\mid F(\omega ,\mathrm{\Delta })\mid =\gamma \delta \mathrm{\Delta }G\frac{sin(\omega \delta /2)sin(\omega \mathrm{\Delta }/2)}{(\omega \delta /2)(\omega \mathrm{\Delta }/2)}$, which therefore samples low frequency regions of the spectrum that are difficult to sample with oscillating waveforms. In Figure 1, the spectrum is divided into two regions by the grey band, representing the readily accessible spectral ranges for PGSE (left) and OGSE (right) methods, separately. For the diffusion spectra of restricted water diffusion inside impermeable spheres (Figure 1), the rise in apparent diffusion coefficient in response to an increase in the frequency is the key to extract cell size (37). In order to measure the size of spheres smaller than 10 μm, an appropriate observation window can be chosen in the OGSE-accessible region to capture the rising portion of the curve. However, as the cell size becomes larger, the spectra in the right region are almost flat and the observation window needs to extend to the PGSE-accessible region. In the current study, 40 and 80 Hz OGSE measurements and PGSE with a diffusion time of 52 ms (labeled by vertical dash line in Figure 1) were combined, corresponding to an observation window with Δ_diff from 3.13 to 52 ms. We hypothesized that such a combination would cover a broader segment of the temporal diffusion spectrum and enable the quantification of larger cell sizes (up to 20 μm). In the rest of the paper, this hypothesis is elucidated and validated using both computer simulations and well-characterized cell culture experiments.

Figure 1.

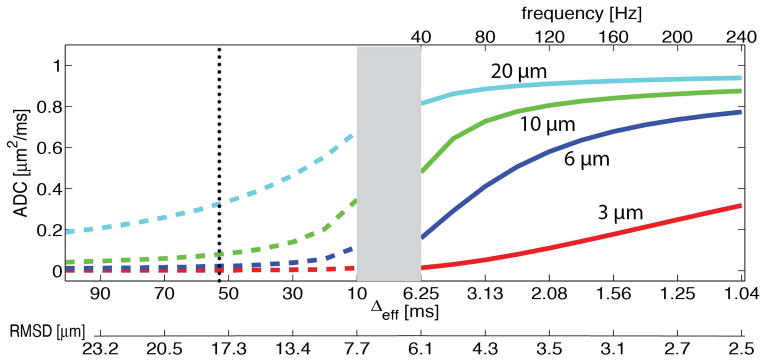
Diffusion spectra of restricted water diffusion inside impermeable spheres with diameters of 3, 6, 10, and 20 μm. The grey band divides the spectrum into two regions, representing the readily accessible spectral ranges for PGSE (left) and OGSE (right) methods, separately.

Methods

Diffusion signal modeling

We assume that the diffusion-weighted signals of cell samples can be expressed as the sum of signals arising from intra- and extracellular spaces, namely,

$$S=f_{in}·S_{in}+(1-f_{in})·S_{ex},$$ (2)

where f_in is the water volume fraction of intracellular space, and S_in and S_ex are the signal magnitudes per volume from the intra- and extracellular spaces, respectively. The water exchange between intra- and extracellular spaces is omitted, as suggested in the CHARMED model (38).

Cells are modeled as spheres despite the significant variations of cell shape in realistic tissues. The analytical expressions of OGSE signals in some typical geometrical structures, e.g. cylinders and spheres, have been derived previously (39). For OGSE measurements of diffusion within impermeable spheres using cosine-modulated gradient waveforms, the intracellular diffusion signal can be expressed as

$$\begin{array}{l}{S}_{in}(\mathit{OGSE})=exp(-2{(\gamma g)}^2{\mathrm{\sum }}_n\frac{B_n{\lambda }_n^2{D_{in}}^2}{{({\lambda }_n^2{D_{in}}^2+4{\pi }^2{f}^2)}^2}\{\frac{({\lambda }_n^2{D_{in}}^2+4{\pi }^2{f}^2)}{{\lambda }_n{D}_{in}}\left[\frac{\delta }{2}+\frac{\mathit{sin}(4\pi f\delta )}{8\pi f}\right]-1+\\ \mathit{exp}(-{\lambda }_n{D}_{in}\delta )+\mathit{exp}(-{\lambda }_n{D}_{in}\mathrm{\Delta })(1-\mathit{cosh}({\lambda }_n{D}_{in}\delta ))\left\}\right)\end{array}$$ (3)

where D_in is the intracellular diffusion coefficient, f is the oscillation frequency, δ is the gradient duration, Δ is the separation of two diffusion gradients, λ_n, B_n are structure dependent parameters containing sphere diameter. The accuracy of Eq.(3) has been validated by computer simulations (39) and phantom experiments (40). Note that, if f→0, a cosine-modulated OGSE pulse degenerates into a conventional PGSE pulse and hence Eq.(3) becomes

$$S_{in}(\mathit{PGSE})=exp(-2{\left(\frac{\gamma g}{D_{in}}\right)}^2{\mathrm{\sum }}_n\frac{B_n}{{\lambda }_n^2}\{{\lambda }_n{D}_{in}\delta -1+exp(-{\lambda }_n{D}_{in}\delta )+exp(-{\lambda }_n{D}_{in}\mathrm{\Delta })(1-cosh({\lambda }_n{D}_{in}\delta ))\}).$$ (4)

Therefore, Eqs.(3) and (4) describe intracellular diffusion signals obtained using OGSE and PGSE methods, respectively, and the microstructural parameters (i.e. λ_n and B_n, as well as sphere diameter) can be fit simultaneously using these equations.

Currently, only a narrow range of frequencies (less than 160 Hz) may be sampled with clinically achievable gradient strengths (< 15 G/cm). Under such circumstances, the ADC values for the extracellular space have been reported to show a linear dependence on the oscillating-gradient frequency (37). As a result, the extracellular diffusion signal can be modeled as a linear function of gradient frequency, namely,

$$S_{ex}(\mathit{OGSE})=exp[-b(D_{ex0}+{\beta }_{ex}·f)],$$ (5)

where D_ex0 is a constant and β_ex is the slope of extracellular diffusion coefficient with respect to frequency f, which contains information on structural dimensions but may not be simply assigned to any specific morphological feature in the tissue. If f→0, a cosine-modulated OGSE pulse degenerates into a conventional PGSE pulse and Eq.(5) becomes:

$$S_{ex}(\mathit{PGSE})=exp[-{bD}_{ex0}]$$ (6)

Simulation

Biological tissue was modeled as a two-compartment system, consisting of intracellular and extracellular spaces, without any water exchange between these two compartments. Cells were modeled as a collection of densely packed spheres on a face-centered cube (FCC) (12). The following diffusion and morphological parameters were used in the simulation: D_in= 1 μm²/ms, D_ex= 2 μm²/ms, cell diameter = 2.5, 5, 10, 15, 20, and 25 μm, intra-cellular volume fraction = 43%, 51%, and 62%. A finite difference method was employed, and further details of the computational aspects of the simulations have been reported elsewhere (41). Diffusion-weighted signals were simulated for both OGSE and PGSE sequences with the same parameters set in the cell culture experiments.

Cell Preparation

Two sets of cell experiments, designated as “A” and “B”, were performed. Experiment “A” was designed to measure cell sizes for different types of cells at different densities, while experiment “B” was designed to characterize the changes in the tumor cell size before and after anti-cancer treatment. In experiment “A”, murine erythroleukemia (MEL) and human promyelocytic leukemia K562 cells, purchased from American Type Culture Collection (ATCC, Manassas, VA), were cultured in DMEM medium supplemented with 10% FBS, 50 U/ml penicillin, and 50 μg/ml streptomycin (Invitrogen, CA) under standard culture conditions in a humidified incubator maintained at 5% CO₂ and 37 °C. Cells were spread every three days by 1:10 dilution and cell density was limited to be no more than 0.8 ×10⁶ cells/ml. All cell samples were collected, washed with PBS, and then fixed with 4% paraformaldehyde in PBS for over 2 hours. After fixation, cells were washed, and transferred to a 0.65ml Eppendorf tube. In order to obtain different cell densities, tubes were divided into three groups and centrifuged (Bio-rad microcentrifuge) at three different centrifugal forces (200, 1000, and 6000 g) for 2 minutes to result in three different cell densities. The liquid on the top was carefully removed, and the residual cell pellets, whose net weights were around 150 to 200 mg, were used for NMR measurements.

In experiment “B”, nab-paclitaxel (Abraxane) treated MDA-MBA-231 cells were used to mimic the effects of anti-cancer therapy on cell sizes. Abraxane is an FDA-approved mitotic inhibitor drug used in the treatment of breast, lung and pancreatic cancers (43, 44). It interrupts cell division during the mitotic (M) phase of the cell cycle when two sets of fully formed chromosomes are supposed to separate into daughter cells. Cells are thereby trapped in the M phase and then undergo apoptosis. Note that cells significantly increase their sizes during the M phase, and hence the cell size can be used a surrogate biomarker to monitor the efficacy of Abraxane treatment. Human breast cancer cells MDA-MBA-231 are highly metastatic and show a positive response to Abraxane treatment. MDA-MB-231 cells were cultured in the same way as MEL and K562 cells. After that, a half of the MDA-MB-231 cells were treated with 200nM of Abraxane for 24 hours. All cell samples were collected, washed with PBS, and then fixed with 4% paraformaldehyde in PBS for over 2 hours. After fixation, cells were washed, and transferred to a 0.65ml Eppendorf tube. Tubes were centrifuged (Bio-rad microcentrifuge) at 1000g for 2 minutes.

NMR measurements

All measurements were performed on a 7.0-T, 16-cm bore Varian DirectDrive^™ spectrometer (Varian Inc. Palo alto, CA). As described in ‘cell preparation’ section, MEL and K562 cells were prepared at three different cell densities (low, medium and high) with 4 samples at each density. Nine b-values evenly distributed between 0 and 2000 s/mm² were used in both PGSE and OGSE measurements. The OGSE pulse sequence substitutes the two bipolar diffusion-sensitizing gradients in PGSE with two apodized cosine-modulated gradients. Details of the OGSE pulse sequence can be found in (42). For PGSE experiments, diffusion gradient durations were δ=4 ms, and separation Δ=52 ms. The OGSE method measured frequencies at 40, 80, and 120 Hz with δ/Δ=25/30 ms. Note that the echo times (TE=60 ms) for both PGSE and OGSE measurements were the same to minimize relaxation effects.

Data analysis

The PGSE and OGSE diffusion signals were fit to Eq. (1)-(5) with five unknown variables: cell diameter d, intracellular diffusion coefficient D_in, intracellular volume fraction f_in, and extracellular parameters D_ex0 and β_ex (see Eq.(5)), using the lsqcurvefit function in Matlab (Mathworks, Natick, MA). The constraints for fitting parameters were: 0 ≤ d ≤ 40 μm, 0≤ f_in ≤ 1, 0 ≤ D_in ≤3.0 μm²/ms, 0 ≤ D_ex0 ≤ 3.0 μm²/ms, and 0 ≤ β_ex ≤ 2 μm². Randomly-generated initial parameters values were used. To ensure the global minimum was reached, the fitting was repeated 100 times for each sample, and the analyses corresponding to the smallest fitting residual were chosen as the final results.

Statistical Analysis

The correlations between fitted and preset intracellular volume fractions was assessed using Kendall’s tau correlation coefficient (43). The differences in MR-derived cell sizes and intracellular volume fractions among the cell samples having different densities (Figure 5) were summarized using means and standard deviations, and compared by one-way ANOVA. The differences in the other three fitted parameters (D_in, D_ex0, and β_ex) among the cell samples having different densities (Figure 6) were summarized using means and standard deviations, and compared by one-way ANOVA. All the tests were two-sided and a p-value of 0.05 or less was taken to indicate statistical significance. Statistical analyses were performed using OriginPro 9.0 (OriginLab. Northampton, MA).

Figure 5.

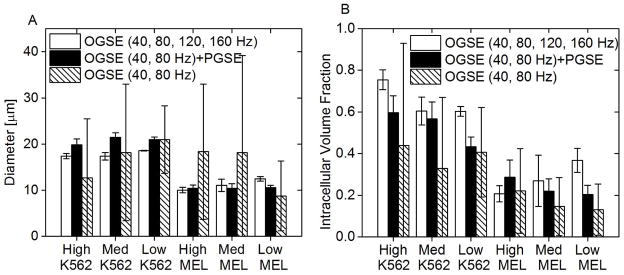
Diameter (left) and intracellular volume fractions (right) fitted from three combinations of OGSE and PGSE signals for K562 and MEL cells at three different densities: high, medium, and low. It is noted that varying cell density does not affect the fitted cell size for the same type of cells regardless of the data combination (p>0.05).

Figure 6.

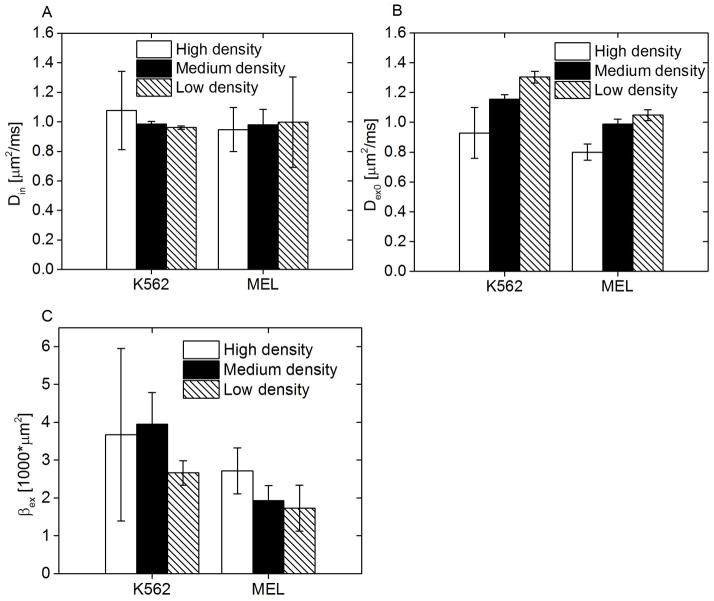
Fitted D_in, D_ex0, and β_ex for K562 and MEL cells at different cell densities: low, medium, and high.

Results

Simulation

For model systems mimicking tightly packed cells of diameter ranging from 2.5 to 25 μm and various intracellular volumes (43%, 51%, and 62%), both the OGSE signals with frequencies ranging from 40 to 160 Hz and the PGSE signals with a single long diffusion time of 48 ms were obtained from simulations. The size and intracellular volume fraction were fitted from three different combinations of the simulated data, including OGSE at 40 and 80 Hz, OGSE at 40 and 80 Hz + PGSE, and OGSE at 40, 80, 120, and 160 Hz. The cutoff frequencies, 80 and 160 Hz, are determined by two different maximum gradient strengths, 15 and 40 G/cm, corresponding to readily achievable gradient strengths on regular animal scanners and those with advanced human gradient coils (44), respectively. Figure 2A shows the fitted mean sizes of cells at three different densities. The OGSE method employing a maximum gradient strength of 15 G/cm is sufficient to extract the sizes of the cells smaller than 8 μm, while it underestimates the sizes of the cells larger than 8 μm. For cells larger than 8 μm, the accuracy of size measurement can be significantly improved by incorporating either PGSE or more OGSE data with more frequencies. Correlations between fitted and preset intracellular volume fractions are shown in Figure 2B and were measured via Kendall’s concordance coefficient. The calculated value of Kendall’s coefficient was 0.6 (p=0.0007), 0.75 (p<0.0001), and 0.72 (p<0.0001) for OGSE at 40 and 80 Hz, OGSE at 40 and 80 Hz + PGSE, and OGSE at 40, 80, 120, and 160 Hz, respectively. The fact that our proposed combination has a strong correlation demonstrates that this approach is a useful tool for the quantification of the intracellular volume fraction.

Figure 2.

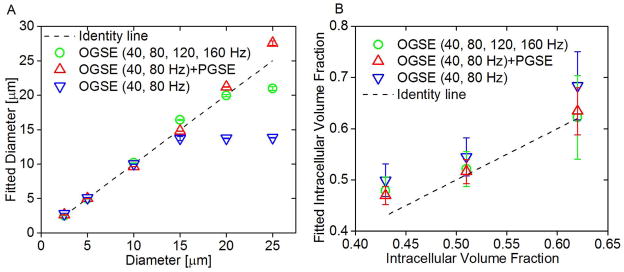
(A) Correlation between fitted diameters and preset diameters in simulations. Fitted diameters generated from three different combinations of OGSE and PGSE signals, mean ± std (n=3, with three different intracellular volume fractions: 43%, 51%, and 62%) vs. preset diameters. The dot line represents the identity line. (B) Fitted intracellular volume fraction generated from three different combinations of OGSE and PGSE signals, mean ± std (n=6, with cell size ranging from 2.5 to 25 μm) vs. preset intracellular volume fractions. The dot line represents the identity line.

Cell size measurements with different cell types and densities

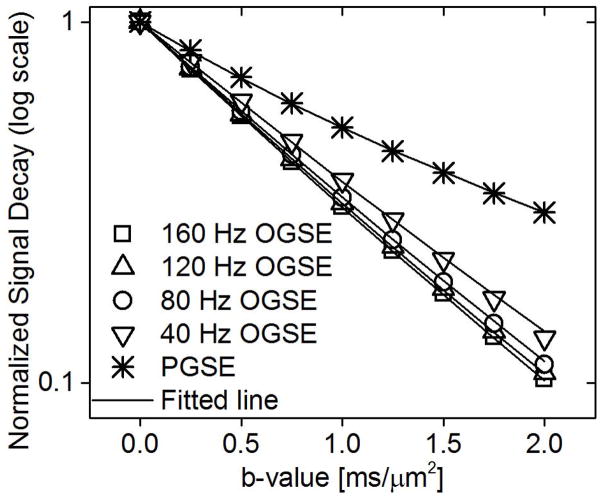
Representative OGSE and PGSE signals for a sample K562 cell pellet with medium density are shown in Figure 3. As expected, the diffusion-weighted signals decay faster as the effective diffusion time decreases. The PGSE signals were significantly higher than OGSE signals, indicating that lower effective diffusion rates were obtained at longer diffusion times. The solid lines represent the fits from Eq (1).

Figure 3.

Typical OGSE and PGSE signals for the K562 cell pellet which was centrifuged at a centrifugal force of 1000g. The solid line represents the fit using Eq(1)–(5).

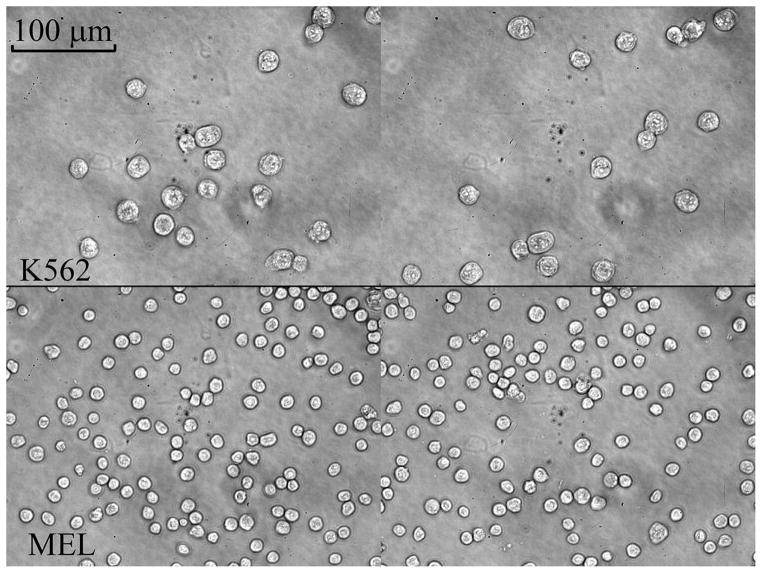
Figure 4 shows typical 40x microscope images for K562 (top) and MEL (bottom) cells. It is evident that K562 cells are much larger than MEL cells. The area of each cell was calculated from these light microscope images using an auto-segmentation program written in Matlab, and then converted to a diameter assuming each cell is a sphere. The area-weighted diameters (29) for K562 and MEL, which were determined from approximate 1000 cells, were 20.94±1.08 and 11.74±1.30 μm, respectively.

Figure 4.

Typical 40x light microscopy pictures for K562 (top) and MEL (bottom) cells.

Figure 5 compares the diameters (A) and intracellular volume fractions (B) fitted from three combinations of diffusion-weighted signals for K562 and MEL cells at three different densities. The two parameters extracted from 40 and 80 Hz OGSE signals have dramatic variations among the samples having the same cell types and the same densities, indicating that the combination of 40 and 80 Hz OGSE signals does not generate reliable results under these experimental conditions.

Using the high-frequency OGSE data, the mean diameters for K562 and MEL cells at three densities are close to the microscope-derived diameters. However, one-way ANOVA revealed that the diameters for the samples at low density are significantly larger than those from the high (p= 0.04 and 0.005 for K562 and MEL, respectively) and medium densities (p= 0.03 and 0.04 for K562 and MEL, respectively). Similarly, the mean intracellular volume fractions for MEL cells at high density are significantly lower than those for the low density (p=0.004), suggesting that this combination of OGSE signals does not estimate the intracellular volume fraction reliably.

By contrast, by combining the PGSE and low-frequency OGSE signals, the fitted cell sizes are not only consistent with microscope-derived sizes (Table 1) but also insensitive to the variations in cell density (p>0.05), indicating this approach is accurate for size quantification and robust to varying cell densities. Moreover, the intracellular volume fractions for cell samples of high density are significantly higher than that for low-density samples (p=0.02 and 0.03 for K562 and MEL, respectively). The medium-density samples were not differentiated from the other two densities (p>0.05).

Table 1.

Fitted and microscope-derived diameters for K562 and MEL cells at different cell densities: low, medium, and high.

	Density			Light microscope
	high	medium	low
K562	19.82±1.30	21.5±0.98	20.96±0.60	20.94±1.08
MEL	10.42±0.72	10.46±0.98	10.6±0.48	11.74±1.30

In Figure 6, the other three parameters (D_in, D_ex0, and β_ex) obtained from the combination of PGSE and low-frequency OGSE signals are displayed. D_in remains almost constant for different cell densities and cell types. D_ex0 increases with the decreasing cell density (p<0.05), possibly because of the increased extracellular tortuosity. β_ex does not show any apparent correlation with the cell density (p>0.05).

Cell size measurements with anti-cancer treatment

Abraxane is used to trap cells in the M phase and then undergo apoptosis. It is known that cells significantly increase their sizes during the M phase. Our microscope observations (Figure 7) confirm that Abraxane-treated cells are larger on average than the untreated MDA-MBA-231 cells. MRI-derived cell sizes are close to the area-weighted diameters calculated from light microscopy (table 2), indicating that the proposed approach is capable of quantifying increases in cell sizes in response to anti-cancer treatment. Table 3 shows the other four parameters (D_in, f_in, D_ex0, and β_ex) for Abraxane-treated and non-treated cells. The intracellular volume fraction became larger after treatment most likely due to the increase of individual cell size, although the packing density for large cells was lower than small cells. The extracellular diffusion coefficient (D_ex0) increased in the cell samples with larger cells, presumably due to the increased mean restricting distances in the extracellular spaces. Note that the changes of D_in may not reflect the true values because the applied gradient frequencies were not high enough to sensitize the intracellular free diffusion (40).

Figure 7.

Typical 40x light microscopy pictures for non-treated (top) and Abraxane-treated (bottom) MDA-MBA-231 cells. It is noted that most cells are not spherical.

Table 2.

Fitted and microscope-derived diameters for non-treated and Abraxane-treated MDA-MBA-231 cells.

	Fitted	Light microscope
Non-treated	14.9±1.58	15.72±1.84
Abraxane-treated	22.24±0.36	22.48±0.9

Table 3.

Fitted D_in, Intracellular volume fraction, D_ex0, and β_ex for non-treated and Abraxane-treated MDA-MBA-231 cells.

	Din (μm2/ms)	Intracellular volume fraction (%)	Dex0 (μm2/ms)	βex (1000*μm2)
Non-treated	0.62±0.018	42±6.8	0.84±0.047	4.2±0.39
Abraxane-treated	0.76±0.0012	59±2.3	1.00±0.029	4.17±0.87

Discussion

Various microstructural features of tumors, such as the cellularity, cell size, and nuclear size, play an important role in the diagnosis and prognosis of cancer. Conventionally, these parameters are obtainable only from invasive biopsy. Diffusion-weighted MRI provides a means to probe cellular characteristics of biological tissues non-invasively, and hence is potentially a viable approach for non-invasively obtaining critical information about cancer. Although PGSE and OGSE sequences are often conceived of as different, the theory of temporal diffusion spectroscopy shows how the information obtainable from different sequences is related. While OGSE implementation allow probing of the high frequency regions of a diffusion spectrum, PGSE has some advantages in practice for assessing low frequency values of the spectrum, a region that appears critical for accurately estimating the sizes of larger scale structures. PGSE methods are sensitive to cell size and cellularity, but relatively insensitive to subcellular microstructures. By contrast, OGSE methods are more sensitive to features that restrict diffusion at a subcellular scale, such as nuclear size, but in practice are not well suited to measuring larger structures. Our PGSE measurements with a single long diffusion time (52 ms) sample the diffusion spectra close to f → 0, extending the range of OGSE spectral data. By sampling a sufficient range of frequencies, a larger range of cell sizes (6 – 20 μm) can be accurately measured. This combination extends the ability of diffusion measurements to probe microstructural parameters over a broader range of length scales, from subcellular scales to large cell sizes. This more comprehensive information may have significant potential in cancer imaging.

Although it is possible to implement both conventional PGSE or OGSE methods to characterize cell dimensions and subcellular scales, respectively, this strategy is time-consuming and hence impractical in clinics. Previous studies have reported one hour scanning for PGSE-based methods to obtain mean axon diameter of human corpus callosum (22) and 2.5 hours to obtain the mean cell size of mouse tumors (45). Multi-frequency and multi-b-value OGSE measurements are also time-consuming especially with a limited signal-to-noise ratio (SNR) (37). In the current study, we report a novel approach to combine OGSE and PGSE measurements with a single, long diffusion time. Such an approach significantly improves the ability of OGSE methods to accurately measure large cell size (up to 20 μm) with slightly increased scanning time. Therefore, both cellular and subcellular information can be obtained by such an approach in limited scanning time, which may be of crucial interest in practice.

Both the simulations and cell culture experiments demonstrate that the temporal diffusion data obtained with combined PGSE and OGSE measurements enable an accurate in vitro estimation of cell size ranging from 10–20 μm using a maximum gradient strength of 15 G/cm. This gradient strength is available with the recently developed Connectome gradient coil, which provides a gradient strength up to 30 G/cm for human heads. Even for normal gradient coils with relatively low gradient strength, e.g. < 8 G/cm per channel, on regular MRI machines, it is still possible to employ our method. For example, a gradient duration δ = 25 ms was used in this work. Since the b value is proportional to δ³ and G², a gradient strength of 7.5 G/cm can result in the same b values used in the current study with δ = 40 ms, a typical gradient duration for human OGSE studies (46,47). This means that our proposed approach is directly translatable to current human imaging, although it will benefit significantly from more advanced gradient coils.

It is also shown that incorporating more high-frequency OGSE data improves the accuracy of cell size estimates for large cells. The high-frequency OGSE data are considered to have higher sensitivity to detect small dimensions, so it is interesting that they helped make the measurements of larger cell sizes more accurate. As discussed previously, the rise in apparent diffusion coefficient in response to an increase in the frequency is the key to extract cell size (37). As shown in the curves with 10 – 20 μm in Figure 1, ADCs kept increasing at 120 and 160 Hz, indicating that these OGSE frequencies are still sensitize to large cell size ranging from 10 20 μm. When more and more frequencies that sensitize the cell size were included in the cell size fitting, more accurate results were obtained even if those relatively higher frequencies had lower sensitivities to large cell size. However, this broader frequency range method shows larger errors compared with our approach in measuring large cell size. For example, as shown in figure 5A, our approach led to 5.34%, 2.67%, and 0.08% deviations from the microscopy-derived diameters for K562 cells at high, medium, and low densities, respectively, while the broader frequency method led to deviations of 16.97%, 17.16% and 11.36%. More importantly, the acquisitions of high-frequency OGSE data covering the same range of b-value need very high gradient strength (40 G/cm), which limits the clinical use of this approach.

The water exchange between intra and extracellular spaces was assumed negligible in the current study. This assumption has been used in previous OGSE studies (28,32,48), because the effective diffusion time of the OGSE measurement is usually much shorter (< 5 ms) compared with the intracellular lifetime of water molecules (49,50). However, the precise effect of water exchange on diffusion measurements in vivo remains unclear. The incorporation of PGSE measurements with a long diffusion time makes this method more likely to be affected by water exchange than typical OGSE methods. In addition, membranes of tumor cells may have altered permeability resulting from either treatment or tumor development (51). Therefore, the influence of water exchange effects on the proposed approach needs to be further investigated, especially for in vivo studies. A more complex model which can account for water exchange between intra and extracellular spaces, such as the Karger model (52), will be investigated in a future study.

The current study used a simplified model which describes cells as homogenous spheres without nuclei. Interestingly, cell sizes fitted by this sphere model are reasonably accurate for non-spherical MDA-MBA-231 cells (Figure 7), suggesting that this method may not be very sensitive to variations in cell shape. This is encouraging since cells in real biological tissues are usually not spherical. On the other hand, it has been found in computer simulations and in vivo studies that a change of nuclear size can affect high-frequency OGSE signals (12,28). A change of nuclear size is widely observed in many biological processes, such as necrosis and apoptosis induced by cancer treatment. Therefore, it will be valuable to develop a more comprehensive model and broader range of measurements to be able to quantitatively characterize cell size, cell density, and nuclear size. If successful, this could provide more quantitative tissue characterization of tumors.

Fitted intracellular volume fractions also show a good correlation with cell densities. However, it is technically demanding to perform the histology validation for in vitro cell pellets. As an alternative, it has been reported that the intracellular volume fraction can be extracted from changes of diffusion-weighted signal in the extracellular space, resulting from the administration of Gadolinium-based contrast agent which changes the T1 of the extracellular space only (51). Efforts to compare intracellular volume fractions generated from these two methods are in progress.

Conclusion

Temporal diffusion spectroscopy combining a single long diffusion time PGSE and low-frequency OGSE measurements, was developed for accurately measuring relatively large cell sizes (10–20 μm). Using this method, accurate cellular sizes were obtained with a weak gradient strength of 15 G/cm, in different cancer cells and at three different cell densities. Size changes in breast cancer cells MDA-MBA-231 in response to chemotherapy were also detected. These findings were confirmed by light microscopy and confirm the potential of this method for providing microstructural information non-invasively to assist better diagnosis and prognosis of cancer.