Correction and optimization of a T2-based approach to map blood oxygenation in small cerebral veins

Abstract

Purpose

Cerebral venous blood oxygenation (Y_v) is an important biomarker in brain physiology and function. The present study proposes a procedure to provide a quantitative map of the brain's intravascular Y_v.

Theory

The method is based on a pulse sequence, T₂-Relaxation-Under-Phase-Contrast (TRUPC) MRI, with post-processing approaches to correct eddy-current effects.

Methods

A complete scan protocol consists of four TRU-PC scans sensitized to large and small vessels with anterior-posterior and foot-head flow-encoding directions, and the data are analyzed conjunctively. Eddy-current correction was performed by fitting the tissue phase to a hyperplane, and then subtracting the eddy-current phase from the measured vessel phase. The reproducibility of the Y_v-maps was examined in five participants. Sensitivity of the Y_v map to a caffeine challenge was studied in another five participants.

Results

Removal of eddy-current induced artifact allowed for the correction of T₂ measurements, as demonstrated in vivo and with simulation. A Y_v-map depicting all vessels in the slice can be obtained with the proposed protocol. Test-retest variability of the Y_v-map was 3.7±1.2%. Y_v reduction can be reliably detected (P<0.001) following the caffeine ingestion.

Conclusion

With the proposed TRU-PC protocol and eddy-current correction procedure, an accurate, vessel-specific Y_v map of the human brain can be obtained.

Introduction

The brain is a highly energetic organ, utilizing significant fractions of oxygen under basal conditions (1). Alterations in oxygen utilization have been noted in healthy ageing (2-4), and in diseases such as Mild Cognitive Impairment (5), Multiple Sclerosis (6), and addiction (7). One important facet to quantifying brain oxygen metabolism is the reliable measurement of venous blood oxygen saturation (Y_v) (8). Several MRI approaches have been proposed to measure blood oxygen saturation non-invasively (9-26). One line of these methods is based on a calibratable relationship between blood T₂ and Y_v (9,10,14,27,28). That is, one can measure the blood T₂ in vivo, and then convert the blood T₂ to Y_v with a known calibration plot (29).

Most oximetry techniques measure the blood oxygenation on a whole brain level at the posterior portion of the superior sagittal sinus. The Y_v measurements in “only” large vessels lack a certain spatial specificity because of blood mixing as it travels down the vascular path. The Y_v measured in a particular vascular segment will represent the oxygen saturation from blood entering the vasculature at that point, along with contributions from previous vascular segments. This “washout” effect in large vessel scans averages aberrant Y_v values from affected regions with normal Y_v values from other regions, such that disease-related changes in physiology are difficult to detect, motivating us to image small veins.

Recently, a non-invasive method exploiting this principle to examine vessel-specific Y_v in the brain, named T₂-Relaxation-Under-Phase-Contrast (TRU-PC) MRI, was reported (13,30). TRU-PC uses Phase Contrast (PC) MRI to separate pure blood signal from the surrounding static tissue (31-33), and a CPMG T₂-preparation (34,35) to measure blood T₂, which is converted to Y_v. TRU-PC MRI has been shown to provide reliable assessment of oxygenation in major veins, including the superior sagittal sinus, straight sinus, great vein, and internal cerebral vein (13,30). In this way, TRU-PC of large vessels is able to look at regional variations of oxygen extraction fraction throughout the brain, but may still suffer from the “washout” effect in large vessel scans. Thus, the mapping of oxygenation in small cortical veins, though not yet well established, may provide region-specific metabolic information.

In the present report, we aim to optimize TRU-PC acquisition and analysis procedures to map the oxygenation of the entire mid-sagittal vasculature, including both the small draining veins (1-2mm in diameter) and the major veins. In order to effectively measure blood signal with a large range of flow velocities and directions, four TRU-PC scans with two cutoff velocities (V_enc) and two flow-encoding directions are performed and their data are conjunctively analyzed. We found that the strong flow-encoding gradients required to image the small veins resulted in spurious signals in static tissue. Therefore, we conducted optimization and correction of the TRU-PC technique for accurate Yv evaluation in small, slow-flowing veins. To mitigate eddy-current effects induced by the flow-encoding gradients (which are particularly pronounced in low V_enc scans) we implemented a correction algorithm and demonstrated that the correction improves the accuracy of blood T₂ estimation. Test-retest reproducibility of the maps is quantified. Finally, we show that the vessel-specific Y_v maps are sensitive to physiological changes with a caffeine challenge.

Theory

Detrimental effects of eddy-currents on PC MRI

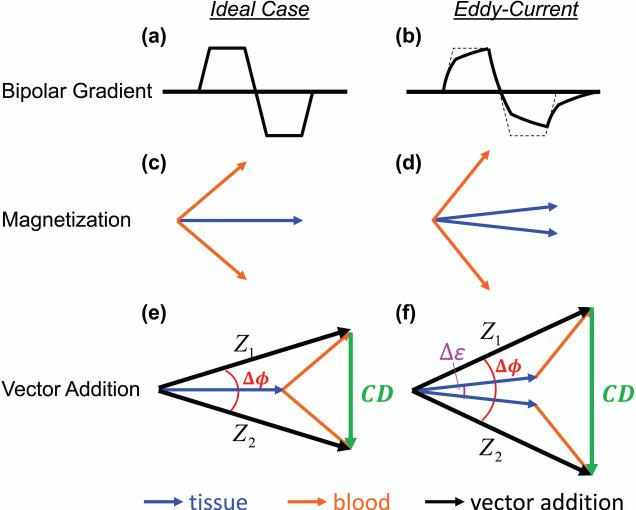
PC MRI requires two separate scans, in each of which a bipolar gradient is used to encode flow information. The polarity of the gradient is usually reversed between the two scans. PC MRI relies on the assumption that positive and negative lobes of the velocity encoding gradient have identical areas-under-curve (Figure 1a), so that no net phase will be obtained for a stationary spin (Figure 1c). However, in the presence of gradient-induced eddy-currents (Figure 1b), this is no longer the case. A net phase is added to both stationary and moving spins (Figure 1d) (36).

Figure 1.

The resulting magnetization vectors in response to Phase Contrast (PC) MRI for the ideal case, and the case of eddy-currents. The ideal bipolar gradient is shown in (a). In (b) the bipolar gradient has been distorted by the presence of eddy-currents. (c) The ideal tissue magnetization (blue vector, overlapping between two schemes) and blood magnetization (orange vector) resulting from the positive and negative bipolar gradient schemes. (d) Eddy-currents cause the tissue and blood magnetizations to accumulate additional phase. (e) The vector addition (black arrow) of tissue and blood magnetization for the ideal case, given by Z₁ and Z₂, and the Complex Difference (CD) vector (green arrow), which only contains information from blood. (f) In the presence of eddy-currents, incomplete subtraction of the tissue vectors causes the CD to contain information from both blood and tissue. The quantity δϕ is the measured phase difference between Z₁ and Z₂. The quantity δε is the phase error induced by eddy-currents.

Eddy-currents are generated during the “switching” of the bipolar gradients, and their magnitudes are determined by how fast and large the switching is (since eddy-currents are opposing the flux of the changing magnetic field). To image the low blood velocity flowing through a small vessel, large gradients must be employed, with a high slew rate to minimize echo times (TE). Thus, the eddy-currents in a low Venc scan will be larger in magnitude than the eddy-currents generated in a high Venc scan.

Figures 1e and f illustrate how eddy-currents affect the MR data measured in PC MRI. The total signal acquired from each scan (Z₁ and Z₂) is the vector addition from both blood (orange vector in Figure 1e) and tissue (blue), but the resulting (ideal) Complex-Difference (CD) only contains contribution from blood (Figure 1e). However, if eddy-currents are present (Figure 1f), the CD includes additional signal sources. In the example illustrated in Figure 1f, the amplitude of CD is increased, but it could also be decreased. The phase difference between Z₁ and Z₂, Δφ, is also effected because it contains an additional tern, Δε, associated with the eddy-currents. The magnitude of the vectors Z₁ and Z₂ are not affected by the eddy-currents.

In TRU-PC, the blood T2 is calculated from the CD images, which ideally only contain blood signal. However, in the presence of eddy-currents, spurious tissue signal can also contribute to the CD image, which will affect the quantified T2. Whether the T2 is under or overestimated depends on the sign of the eddy-current induced phase relative to the sign of the blood phase. When the eddy-current induced phase Δε is positive, the T₂ is overestimated, and when Δε is negative, the T₂ is underestimated. This is because, when Δε is positive, the eddycurrent induced tissue signal contribution is of the same sign as the blood signal. Since the tissue T₂ is longer than venous blood T₂ at 3T (28), the measured T₂ becomes greater. The opposite is true when Δε is negative.

Correction of eddy-current effects

Let us define the additional phase difference caused by eddy-currents as:

$$\Delta \epsilon =\Delta {\varphi }_{measured}-\Delta {\varphi }_{true}$$ [1]

where measured δϕ_measured is the measured phase difference between Z₁ and Z₂; true δϕ_true is the true phase difference. Therefore, once Δε can be estimated, we will be able to obtain true δϕ_true. It is important to note that, although Δε is defined upon the total signal vectors, Z₁ and Z₂, its amplitude is approximately the same as that of the tissue and blood components (Figure 1f). In other words, the eddy-current induced phase errors are the same in tissue and in blood such that,

$$\Delta \epsilon =\Delta {\epsilon }_{tissue}=\Delta {\epsilon }_{blood}$$ [2]

Fortunately, the effects of eddy-currents on tissue, δε_tissue, are relatively easy to estimate since Δϕ_true,tissue = 0 Thus, from Eq. [1], we have

$$\Delta {\epsilon }_{tissue}=\Delta {\varphi }_{measured,tissue}$$ [3]

Therefore, one can use δϕ_measured image and mask it to only preserve the tissue voxels. One can then fit δϕ_measured spatially to a hyperplane, similar to methods previously developed by Langham, et al. to remove field-inhomogeneities in gradient-echo images (37). Briefly, δϕ_measured in tissue is modeled to have contributions from six different field terms.

$$\Delta {\varphi }_{measured,tissue}=c_1+c_{2}X+c_{3}Y+c_{4}XY+c_5{X}^2+c_6{Y}^2$$ [4]

in which the coefficients c₁ to c₆ describe the amount of contribution from each of the 0^th order, 1^st order, and 2^nd order terms, (1, X, Y,...Y²), and are determined by least squares fitting. The data from all effective TE (eTE) values are fitted conjunctively as their eddy-currents effects are identical.

Then, for any vessel voxels, Δε can be estimated from the corresponding values on the hyperplane and can be used to compute Δϕ_true = δϕ_measured − δε. The corrected CD can be calculated using the law of cosines (38):

$$CD=\sqrt{{\mid Z_1\mid }^2+{\mid Z_2\mid }^2-2\mid Z_1\mid \mid Z_2\mid \cos \left(\Delta \varphi \right)}$$ [5]

which can be fitted as a function of eTE to obtain blood T₂. Note again, that the magnitude of the vectors Z₁ and Z₂ are not affected by the eddy-currents, thus they do not need to be corrected (only Δϕ needs to be corrected for eddy-current effects).

Numerical simulation of the effects of eddy-currents on T₂ estimation

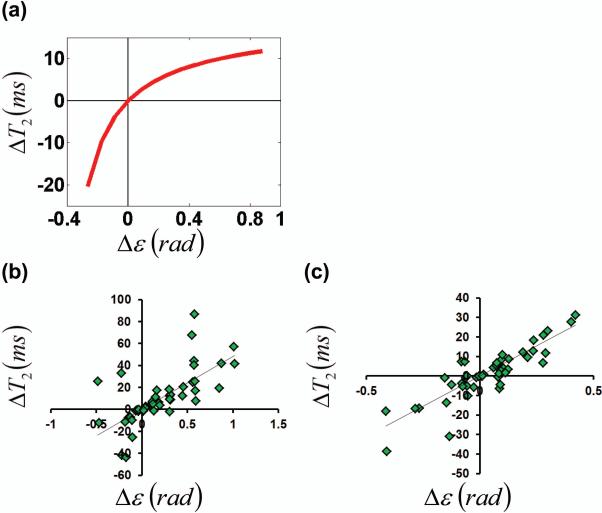
To assess the effects of eddy-currents on the measured T₂ from a theoretical perspective, numerical simulation was performed in which the bias in T₂,δT₂ = T_{2,measured blood} − T_{2,true blood}, was calculated as a function of Δε. The Z₁ and Z₂ vectors were simulated by assuming a blood volume fraction of 0.2 and a tissue fraction of 0.8, with the following parameters, T_2,tissue=95ms (39), T_1,tissue=1200ms (39), T_2,blood=75ms (29), T_1,blood=1600ms (40). The flow-encoding gradients were assumed to generate a true,blood Δϕ_true,blood of 180° in the blood compartment (using a Venc=5 cm/sec). The relationship between ΔT₂ and Δε is represented with a 2D plot and the simulation results were compared to experimental data.

Materials and Methods

General

Experiments were performed on a total of 10 healthy subjects (age 29±6 years, range 21-40, 6 Males) using a 3 Tesla MRI scanner (Philips Healthcare, Best, The Netherlands). The protocol was approved by the local Institutional Review Board. The body coil was used for RF transmission, and a 32-channel head coil was used for receiving.

MRI experiment

To capture the complete mid-sagittal cerebral vasculature, four separate TRU-PC scans were employed: two scans sensitized to the small vessels, and two scans sensitized to the large vessels. One small-vessel scan was acquired with flow-encoding in Anterior-Posterior (AP) direction, while the other small-vessel scan was acquired with flow encoding in Foot-Head (FH) direction. This covered all possible vessels with sagittal in-plane flow. The two large-vessel scans were also acquired in AP and FH. The MR protocols for the large-vessel and small-vessel scans were similar, but with differences in flow-encoding cut-off velocity (Venc) (Venc_large=15cm/s (30), Venc_small=3cm/s for Male, and 5cm/s for Female). The slight difference in Venc_small between male and female was due to gender differences in blood flow (2,3).

The general imaging parameters applicable to all TRU-PC scans were as follows: single 2D slice, FOV=200×200mm², Acquisition matrix=276×83, in-plane acquisition voxel size=0.72×2.41mm², Reconstruction matrix=400×400, slice thickness=5mm, single k-line acquisition per TR; T₂-preparation module used composite block pulses (90x-180y-90x) with τ_CPMG=10ms and MLEV-16 phase-cycling scheme (41); two effective TEs (eTE=0 and 40ms) were used. A shortest possible TE was used, which ranged from 5.0ms to 7.2ms depending on Venc and encoding direction. The total scan time for all four scans was 13min and 20sec (2min 50sec for each large vessel scan, and 3min 50sec for each small vessel scan). The TRU-PC data was exported from the scanner as complex images.

Prior to the TRU-PC scans, a Susceptibility Weighted Image (SWI) (42) was also acquired to guide the selection of veins. The SWI protocol was as follows: 3D gradient echo readout, sagittal orientation, AP phase encoding, read-out BW=80Hz, FOV=200×200mm², acquisition matrix = 400x333, reconstruction matrix=400×400, Sensitivity Encoding (SENSE) reduction factor = 2 (43) in Posterior direction, 13 slices, slice thickness=2mm, slice gap=0mm, TR=40ms, TE=25ms, FA=20°, scan duration=1:23min.

In five of the participants, the above-described protocol was performed twice to examine the test-retest reproducibility of the results. In the other five participants, the protocol was repeated following the ingestion of a 200mg caffeine tablet (NoDoz®, Novartis Consumer Health, Inc., New York, NY, USA) to test the sensitivity of the proposed protocol to known vascular challenges. The subjects were scanned before and after the ingestion of 200mg caffeine. Though caffeine is known to lower baseline Y_v by reducing the cerebral blood flow via vasoconstriction (44), the V_enc of the TRU-PC acquisition was not changed for the caffeine scanning session. Between sessions, the subjects were removed from the MRI scanner. Repositioning of the subject occurred exactly 60min after ingestion of caffeine.

Image processing

From the original complex images Z₁ and Z₂, three new images were computed: the magnitude of Z1 (|Z₁|) the magnitude of Z2 (|Z₂|), and the phase difference (Δϕ_measured). Then, for estimation of blood T₂ without eddy-current correction, one can simply calculate the pure blood signal using Eq. [5] for each eTE value and fit the blood signal as a function of eTE.

For estimation of blood T₂ with eddy-current correction, additional processing steps were used. We first estimated the eddy-current induced phase difference, Δε, as described in the Theory section. This was performed by fitting the measured tissue voxel phase, Δϕ_{measured,tissue}, to a hyperplane using Eq. [4]. Note that voxels containing vessels should be removed from the image before fitting. This was carried out using the SWI image. Specifically, the SWI data was first processed using the Signal Processing in NMR (SPIN) software (MRI Institute for Biomedical Research, Detroit, MI) and in-house Matlab scripts to generate a minimum intensity projection (mIP) SWI image. With SPIN, the SWI phase image was high-pass filtered (64×64 Hamming), and a “phase mask” was created as described in Reference (45). The phase mask was multiplied with the magnitude image five times to enhance the veins. A minimum intensity projection (mIP) across the four center SWI slices was used for the remaining processing in Matlab. To create the tissue mask, the voxels with signal intensity <25% of maximum intensity (presumably veins) as well as its immediately adjacent voxels (less than three voxels in distance) were excluded. Voxels with high signal intensity (>10% maximum signal) in large vessel PC MRI and the immediately adjacent voxels (less than three voxels in distance) were also excluded.

Once the eddy-current induced phase difference δε was obtained, Δϕ_measured could be corrected to yield Δϕ_true. Then, Eq. [5] could again be used to calculate the corrected pure blood signal, from which corrected blood T₂ could be estimated.

A blood T₂ map was generated in which only voxels that were identified as venous voxels in SWI had meaningful values. All other voxels in the map were set to be zero. For each venous voxel, the four data sets using large and small vessel Venc and AP and FH flow-encoding directions were averaged if they meet the signal inclusion thresholds. Specifically, if the SNR of the blood signal was greater than 4 and the phase difference Δϕ was greater than 0.05 radians, then the data from that scan was included in averaging. To improve signal stability in the voxel-wise map, the signal from neighboring non-zero voxels was averaged in an 8.5 mm radius (35 × 35 voxel kernel), and subsequently used in the T₂-fitting. The T₂ was then converted to Y_v using a known calibration plot (29), assuming a hematocrit of 41% (46).

Statistical and quantitative analysis

To quantitatively examine the effect of eddy-current correction on the T₂ estimation, region-of-interest (ROI) analysis was performed in the five subjects who underwent reproducibility study. This analysis focused on the small-vessel TRU-PC data as their eddy-currents are more prominent. Five ROIs were drawn in each data set, generating a total of 50 data points (5 subjects × 5 ROIs × 2 repetitions). The T₂ values before and after eddy-currents correction were compared with a paired t-test. Furthermore, we examined the relationship between ΔT₂(=T_{2,uncorrected} −T_2,corrected) and Δε in a 2D scatter plot, and compared this result to the simulation result. This analysis was carried out separately for AP and FH flow encoding directions.

To further demonstrate that eddy-current correction improves the accuracy of Y_v estimation in small veins, we used large vessel Y_v as a reference, with the assumption that small vessel Y_v should be similar to the large vessel that it joins. Specifically, a small vessel ROI was drawn on the small vessel scan, and an adjacent large vessel ROI was drawn on the large vessel scan. A total of 10 adjacent large-vessel-small-vessel ROIs were drawn (5 from Anterior-Posterior scans, 5 from Foot-Head scans). Scatter plot between small and large vessel Y_v was examined, separately for uncorrected and corrected data. We hypothesized that the two types of vessels should show a better correspondence of Y_v in the corrected data. To increase the dynamic range of data, this analysis was performed on the caffeine challenge images.

The reproducibility of the method was assessed by calculating a voxel-wise Coefficient of Variation (CoV) (47) for all voxels designated as veins. The effect of caffeine was assessed by comparing the difference between baseline and caffeine Y_v-maps on a voxel-by-voxel basis, and with t-statistic.

Results

Eddy-currents correction in TRU-PC MRI

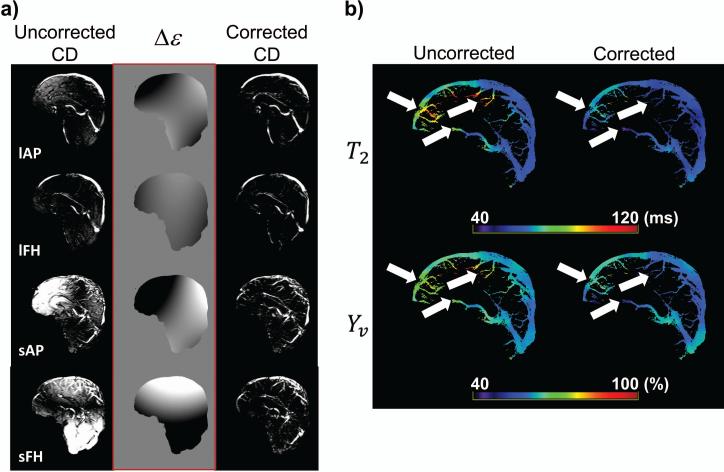
The effect of the eddy-current correction on the CD images can be seen by visually comparing uncorrected and corrected images of all four TRU-PC scans (Figure 2a). The artifactual tissue signal is minimal in the large vessel protocol (lAP, lFH), but becomes prominent in the small vessel protocols (sAP, sFH) due to increased gradient strength. It is also evident from the four hyperplanes (middle column, Figure 2a) that the eddy-current induced phase is dependent on the flow encoding direction.

Figure 2.

The effect of eddy-current correction. (a) A set of representative uncorrected and corrected CD images, as well as the Δε hyperplane calculated for the correction algorithm. Shown are the eTE=0ms images for all four TRU-PC scans (sensitized to different flow directions and blood velocities). lAP: large vessel in Anterior-Posterior, lFH: large vessel in Foot-Head, sAP: small vessel in Anterior-Posterior, sFH: small vessel in Foot-Head. (b) The uncorrected and corrected T₂ maps (in ms), and respective Y_v maps (in %). The eddy-current correction modifies the T₂ and Y_v (white arrows).

Shown in Figure 2b are representative uncorrected and corrected T₂ maps, and the corresponding Y_v maps. In regions of eddy-current induced phase error (white arrows in Figure 2b), the T₂ cannot be accurately estimated in the uncorrected image, but is modified upon removal of the artifact, which then falls into a more physiologically meaningful range. The T₂ differences directly translate to Y_v differences. Averaging across the entire brain, the T₂ before correction (80.2±7.7ms) is significantly higher than after correction (74.2±8.3%), (P=0.006). Similarly, the average Y_v before correction (69.0±3.3%) is significantly higher than the Y_v after correction (66.4±3.8%), (P=0.006). Each subject's average T2 and Yv values before and after correction are reported in Table 1. The significance between uncorrected and corrected T2 (or Yv) values was tested with a two-tailed paired Student's t-test.

Table 1.

The effect of eddy-current correction on average T2 and Yv values.

Subject	T2 (ms) (uncorrected)	T2 (ms) (corrected)	Yv (%) (uncorrected)	Yv (%) (corrected)
S01	81.8	73.8	69.7	66.3
S02	89.2	86.8	72.8	71.9
S03	83.9	75.3	70.6	66.9
S04	77.2	71.5	67.8	65.4
S05	68.8	63.7	63.9	61.4
Average ± Stdev	80.2 ± 7.7	74.2 ± 8.3	69.0 ± 3.3	66.4 ± 3.8
P-value (paired t-test)	P=0.006		P=0.006

Although the general trend is that the eddy-currents cause T₂ to become longer (i.e. ΔT₂ is positive), some voxels manifested the opposite effect. Numerical simulation was therefore performed to understand this observation. Figure 3a shows simulation results, which describe the effects of eddy-currents on blood T₂ estimation. When the eddy-current induced phase Δε is positive, the T₂ is overestimated, and when Δε is negative, the T₂ is underestimated.

Figure 3.

Effects of eddy-current correction on blood T₂ estimation. (a) Bloch simulation: the amount of blood T₂ correction is related to the amount of eddy-current induced phase error. (b) In vivo: the T₂-Δε relationship in AP. (c) In vivo: the T₂-Δε relationship in FH. Both flow-encoding directions mimic the relationship predicted in (a).

This simulation result is confirmed by the in vivo data. Figures 3b and c showed scatter plots between ΔT2 and Δε from various ROIs on the TRU-PC small vessel scans, for AP (Figure 3b, R=0.6842, P<0.0001) and FH (Figure 3c, R=0.8758, P<0.0001) flow-encoding direction, respectively.

Reproducibility and sensitivity to caffeine challenge

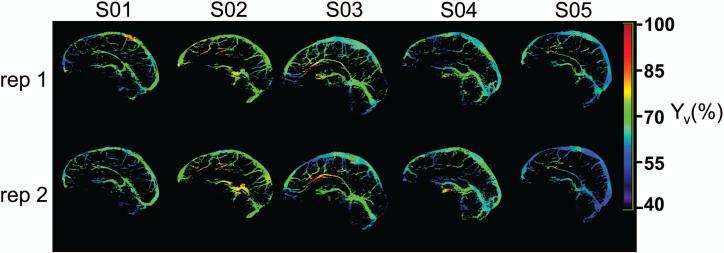
Test-retest reproducibility of (corrected) Y_v maps is shown in Figure 4 for all five subjects. The good visual agreement between repetition 1 and 2 is promising. Quantitatively, the proposed mapping method is relatively stable, with an average voxel-wise CoV of 3.7±1.2%. Linear regression of the voxel-wise R₂(=1/T₂) relationship between repetition 1 and 2 also shows good agreement (slope=1.03). Table 2 documents the average Yv values for repetition 1 and 2, before and after eddy-current correction.

Figure 4.

Test-retest reproducibility of corrected Y_v maps (in %) for five subjects.

Table 2.

The effect of eddy-current correction on average Yv values, for repetition 1 and 2.

Subject	Repetition 1		Repetition 2
	Yv (%) (uncorrected)	Yv (%) (corrected)	Yv (%) (uncorrected)	Yv (%) (corrected)
S01	70.0	67.3	69.3	65.2
S02	72.4	71.9	73.2	72.0
S03	70.8	67.3	70.4	66.6
S04	67.2	65.0	68.5	65.8
S05	65.8	63.4	62.0	59.4
Average ± Stdev	69.2 ± 2.7	67.0 ± 3.2	68.7 ± 4.1	65.8 ± 4.5

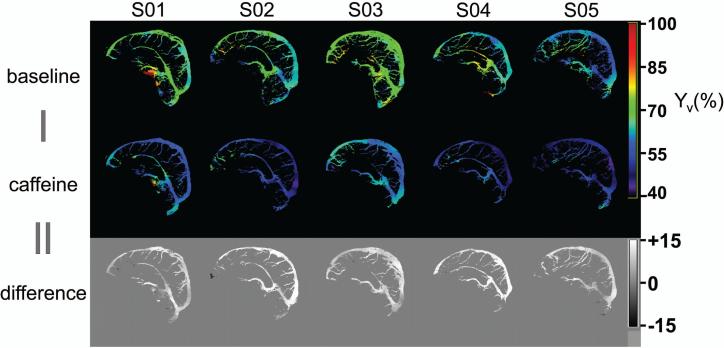
In an additional five subjects, the sensitivity to a caffeine challenge was tested. The (corrected) Y_v-maps at baseline and after caffeine ingestion are shown in Figure 5, along with the difference images. As expected, the Y_v after caffeine ingestion is reduced (including the pial vessels), suggesting excellent sensitivity to physiological changes. The average voxel-wise Y_v is significantly lower (P<0.001) after caffeine ingestion (54.7±4.6%) compared to baseline (66.4±3.7%), resulting in an average voxel-wise Y_v difference of 11.6±2.4%. Table 3 documents the average Yv values for baseline and caffeine conditions, before and after eddy-current correction.

Figure 5.

Corrected Y_v maps (in %) at baseline and after ingestion of caffeine for five subjects, along with voxel-wise difference maps (in %).

Table 3.

The effect of eddy-current correction on average Yv values, for baseline and caffeine conditions.

Subject	Baseline		Caffeine
	Yv (%) (uncorrected)	Yv (%) (corrected)	Yv (%) (uncorrected)	Yv (%) (corrected)
S01	70.4792	68.3725	64.1458	58.8990
S02	67.7939	65.7894	57.4593	52.0917
S03	72.8162	70.8012	63.6802	60.4533
S04	68.7396	66.1960	55.8583	51.4197
S05	65.2361	60.7926	57.4959	50.8798
Average ± Stdev	69.0 ± 2.8	66.4 ± 3.7	59.7 ± 3.9	54.7 ± 4.6

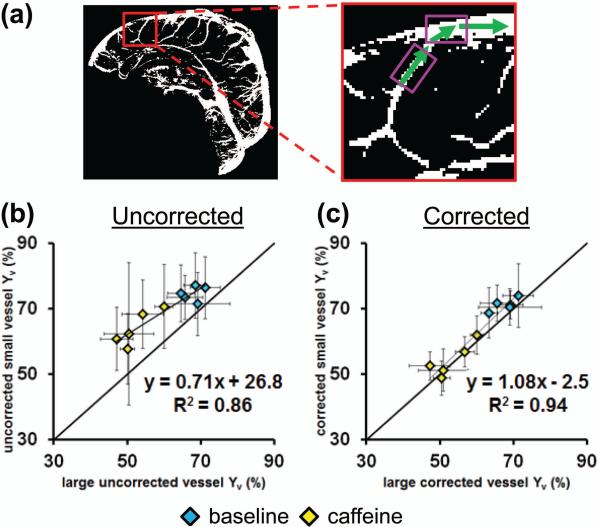
Finally, we examined whether Y_v measured in small vessels are consistent with that in large vessels. Before eddy-current correction, the small vessel Y_v was observed to be greater than the Y_v of the large vessels (Figure 6b). After correction, the small vessel Y_v matches the large vessel Y_v with a close to unity relationship (Figure 6c, slope=1.08, R=0.9671, P<0.001), again suggesting that the proposed eddy-current correction scheme promotes a more accurate Y_v measurement.

Figure 6.

The relationship between measured Y_v in adjacent small and large vessels. (a) A representative vessel mask with zoomed inset shows that the blood from small vessels will travel into the adjacent large vessel segment. The pink boxes show sample ROI selections to probe the relationship between small vessels and large vessels. The relationship (b) before, and (c) after eddy-current correction for baseline (blue diamonds) and after ingestion of caffeine (yellow diamonds) (N=5). The error bars represent standard deviation across 10 Y_v values (5 from Anterior-Posterior scans, 5 from Foot-Head scans).

Discussion

The present work is a follow-up study of a recently proposed technique, T2-Relaxation-Under-Phase-Contrast (TRU-PC). The proof-of-principle of this technique was shown independently by two groups, Krishnamurthy et al. (30) and Jain et al. (13), but primarily focused on large veins using a Venc of 15-20 cm/sec. The present study aims to push the envelope of this technique for the measurement of oxygenation in small veins (using a low Venc of 3 or 5 cm/sec). At this velocity range, we found that the strong flow-encoding gradients generated eddy-currents, resulting in an incomplete cancellation of static tissue. The presence of static tissue in the venogram can compromise the evaluation of blood oxygen saturation, resulting in either an under- or over-estimation of Yv. Therefore, we sought to optimize and correct the TRU-PC images during post-processing to recover an accurate Yv of small, slow-flowing veins. While the present study does not represent the contribution of an original, completely new technique, we believe that the optimization of a recently developed technique is also valuable to receive wide adaptation and to direct it towards clinical application.

This study proposed a practical protocol to provide a voxel-by-voxel map of cerebral venous oxygenation in the human brain, with considerations of sensitivity to both major veins and small veins. Sequences tailored toward small veins tend to generate considerable eddy-currents effects. Thus, a correction method was proposed and its efficacy was demonstrated with simulations and in vivo experiments. The optimized protocol was tested in terms of its reproducibility and ability to detect known oxygenation-altering challenges.

Motivation for vessel-specific Y_v measurements

Several studies have shown that whole-brain oximetry techniques (12,17,47,48) provide a robust estimation of cerebral oxygenation and metabolic rate, but inherently lack spatial specificity. A “vessel-specific” imaging technique will instead promote a more regional measurement of Y_v and CMRO₂.

Anticipating such a need, we previously showed the feasibility of the TRU-PC technique to small draining vessels (30). However, based on our imaging technique at that time, we were only able to provide ROI Y_v values, and only vessels with a predefined flow direction were detectable. With the new mapping technique presented in this paper, we are now able to produce a map of the entire mid-sagittal vasculature with arbitrary flow direction, including small draining veins.

Comparison with other vessel-specific Y_v techniques

Recently, another group has also proposed vessel-specific Y_v measures with Quantitative Susceptibility Mapping (QSM) (25). QSM directly quantifies the susceptibility of a voxel by finding the source of the measured fields (49). By relating the susceptibility with the amount of deoxyhemoglobin, the Y_v of a venous segment can be estimated with QSM.

The QSM-Y_v technique produces realistic 3D representations of the brain's volumetric venous vasculature, but we believe that TRU-PC MRI might offer several advantages compared to the QSM technique. For one, unlike QSM, TRU-PC does not require the empirical choice of a reference tissue, which could unintentionally bias the QSM-Y_v measurement. It has also been shown that the presence of flow could impact the reconstruction of the field map used in the QSM-Y_v quantification (50). Since blood is intrinsically flowing, an immediate bias will be observed in the QSM technique, and must be recovered with mathematical modeling. The T₂ measurements in TRU-PC are not influenced by flow because the non-slice-selective CPMG T₂-preparation is stable in the presence of flow (51).

On the other hand, TRU-PC requires the blood to be flowing, and may not be able to register vessels that have little or no flow. Conditions of low flow could arise in disease states, such as infarction or venous thrombosis (52). In this case, QSM-Y_v would be superior to TRUPC, in that it could register the presence of low-velocity blood. Thus, the choice of Y_v measurement technique depends on specific clinical population of interest.

Eddy-current induced phase errors

The presence of eddy-currents in small vessel scans is a nuisance that could lead to gross Y_v quantification errors (range of −22.6% to 37.5%, average of 2.6%). The phenomenon is diminished in large vessel scans, simply because the flow-encoding gradients are smaller. The use of a second order polynomial to estimate eddy-currents was predicted by Bernstein, et al (36), and has been successfully used to correct PC MRI data (53). With the simple formulation proposed by Langham, et al (37), we showed that the correction effectively removes the phase error due to eddy-currents, and improves the Y_v quantification accuracy.

Langham, et al. applied their technique to gradient echo images, and phase-based oximetry measurements. In this study, we have expanded upon Langham, et al.'s work, and applied their technique to Phase Contrast MRI to correct a T2-based oximetry technique. Thus, we have appropriately tailored our study towards the effects of eddy-currents on T2 measurements using TRU-PC. Most methods remove eddy-current induced phase in vessels based on ROIs of adjacent static tissue (54). However, this is susceptible to biases induced by subjective ROI selections and is not practical for voxel-by-voxel mapping studies. The method of fitting a hyperplane takes into account the eddy-current pattern over the entire image, and is less labor-intensive.

Practical considerations in the proposed TRU-PC protocol

One challenge of mapping the entire vasculature is maintaining reasonable scan durations. The proposed TRU-PC protocol includes four separate scans (large and small vessels with AP and FH flow-encoding directions), thus the total scan duration could be greater than 30 minutes if no other adjustments are made. We therefore made several changes to reduce the scan duration. One is that we reduced the number of eTEs acquired, from the original 3 to 2. The longest TE value in the previous protocol was removed. In principle, the lower number of data points (eTEs) could reduce the fitting reliability. In practice, we found that the CoV of 3.7±1.2% is similar to the previously reported CoV of 3.5±1.0% (30). This may be because 1) the longer eTE data are noisy to start with; 2) the average of four difference scans could recover some of the data stability. We also slightly reduced the image resolution in the phase-encoding direction, thereby further shortening the scan duration. The lower resolution means that more static tissue spins would contribute to the voxel signal measured. But the use of the flowing-encoding gradients should be able to preserve only the blood signal in the final Complex-Difference image. With these improvements, the total duration of the proposed TRU-PC protocol is 13min and 20sec.

Limitations of the study

We note that additional measurement bias could stem from a sub-optimal T₂-prep, especially in the presence of B₁ inhomogeneity. Simulations show that a 10% error in B₁, could bias the T₂ values as much as 2.5ms, which translates to a Y_v bias of 1.1% (assuming T₂=75ms, Hct=41%). Thus, it is important for T₂-based oximetry to have a robust preparation of the magnetization. This can be controlled experimentally through adiabatic refocusing (51) or B₁ shimming (55).

The phase errors removed with the hyperplane have been attributed to eddy-currents, but may also contain some contribution from concomitant fields. In our image reconstruction, we did not calculate the concomitant fields, which could be considered a limitation. Methods have been described that calculate the precise amount of concomitant fields based on the pulse sequence, the gradient geometry, and the position of each voxel from the isocenter (36). It would be ideal to disentangle the contribution from eddy-currents and concomitant fields, though the computations are resource intensive, and calculations are specific to each scanner. Thus, to maintain a generic algorithm, we chose to remove all phase errors with the hyperplane, and generalize them to eddy-current induced phase errors.

Another limitation of this study is that hematocrit was not measured, but rather assumed to be a uniform 41% across the entire vascular path. The T₂-Y_v conversion depends on Hct (29), and the Hct should ideally be measured. It is known that the hematocrit in the capillary bed is lower than the hematocrit in the large draining veins (46), but it is unknown in which vascular segment the Hct returns to the hematocrit measurable with a blood-draw. Since the diameter of the vessels in question (>1mm) are much larger than the diameter of a red blood cell (8μm) (56), we assume that the hematocrit does not change across the vessels that are visible with TRU-PC. Ideally, the Hct-T₁ relationship (40) could be exploited in a similar manner to measure the vessel-specific hematocrit for use in the T₂-Y_v conversion.

A major limitation of this study is that only a single mid-sagittal slice of the brain was acquired. Ideally, a whole-brain 3D coverage should be used to capture all veins of the brain. This was not feasible in this study due to scan duration limitations. The brain's anatomy has a highly symmetric organization, where most of the major draining vessels are positioned in the mid-sagittal, and the small vessels joining these veins are mostly visible in this plane as well. However, there are numerous other major draining veins (transverse sinus, sigmoid sinus, jugular vein, cavernous sinus, petrosal sinus, basal vein, superficial sylvian vein, trolard vein, etc.) that this study could not image, simply because we used a 2D single-slice acquisition scheme. Future studies should focus on expanding the coverage of TRU-PC acquisition, to include more vessels of the brain.

Conclusion

We have demonstrated that the mid-sagittal vessel-specific Y_v can be mapped on a voxelby-voxel basis with T₂-based oximetry. A procedure to remove eddy-currents induced artifact was used to correct the Y_v measurement. We demonstrated that the Y_v maps are reproducible and sensitive to physiological changes.