Sensitivity of Chemical Shift-Encoded Fat Quantification to Calibration of Fat MR Spectrum

Abstract

Purpose

To evaluate the impact of different fat spectral models on proton density fat-fraction (PDFF) quantification using chemical shift-encoded (CSE) MRI.

Material and Methods

Simulations and in vivo imaging were performed. In a simulation study, spectral models of fat were compared pairwise. Comparison of magnitude fitting and mixed fitting was performed over a range of echo times and fat fractions. In vivo acquisitions from 41 patients were reconstructed using 7 published spectral models of fat. T2-corrected STEAM-MRS was used as reference.

Results

Simulations demonstrate that imperfectly calibrated spectral models of fat result in biases that depend on echo times and fat fraction. Mixed fitting is more robust against this bias than magnitude fitting. Multi-peak spectral models showed much smaller differences among themselves than when compared to the single-peak spectral model. In vivo studies show all multi-peak models agree better (for mixed fitting, slope ranged from 0.967–1.045 using linear regression) with reference standard than the single-peak model (for mixed fitting, slope=0.76).

Conclusion

It is essential to use a multi-peak fat model for accurate quantification of fat with CSE-MRI. Further, fat quantification techniques using multi-peak fat models are comparable and no specific choice of spectral model is shown to be superior to the rest.

Introduction

Nonalcoholic fatty liver disease (NAFLD) is the most common chronic liver disease, affecting up to 30% of the adult U.S population (1). NAFLD is a risk factor for diabetes and cardiovascular disease, and can progress into cryptogenic cirrhosis and hepatocellular carcinoma (2,3). The diagnosis of NAFLD requires assessment of intracellular triglycerides in hepatocytes. Chemical shift-encoded (CSE) water fat imaging enables accurate quantification of proton density fat fraction (PDFF) over the entire liver. Compared with liver biopsy and single voxel MR spectroscopy (MRS) (4), CSE-MRI provides non-invasive spatially resolved quantification of liver fat. 3D coverage of the entire liver can be acquired within a single breath-hold (5–8). Extensive validation of confounder-corrected quantitative CSE-MRI have demonstrated equivalence of these methods to MRS (5–7,9–11)

In CSE-MRI, multiple images are acquired with increasing echo time (TE). A water image (W) and a fat image (F) are calculated by fitting the acquired data at each voxel to a signal model based on the chemical shift between fat and water (6,7). Fat fraction is then calculated as F/(W+F). To ensure that the calculation yields proton density fat-fraction (PDFF), a fundamental property of tissue that reflects the concentration of triglycerides (12), several confounding factors must be addressed. Such confounders include B₀ inhomogeneity (13), T1 bias (14,15), T2* signal decay (15–18), eddy currents (19,20), noise bias (14), and the spectral complexity of fat (18,21).

Compared with water, which has a single spectral peak, the complex structure of triglyceride molecules leads to complex and heterogeneous proton chemical shifts within the molecule. The different chemical shifts observed in a number of functional groups in fat molecules give rise to multiple peaks of fat signal in proton-based MRI. In early CSE-MRI techniques, a single-peak fat model (methylene peak) was generally assumed. However, this single-peak model accounts for only 70% of the total fat protons (22). A recent study showed that the single-peak model results in a biased estimate of PDFF that can be corrected by using a multi-peak spectral model of fat (21). In principle, the use of such a model requires independent estimation of the amplitude (and potentially other spectral parameters) of every fat peak. However, due to limited number of echo times typically acquired in CSE-MRI, it is not possible to individually resolve each fat peak. Consequently, CSE-MRI using a pre-calibrated multi-peak fat spectral model have been proposed (15,17,21), where the relative amplitudes and chemical shift of fat peaks are assumed to be known parameters. Therefore, compared with the single-peak model, no additional variables (degrees of freedom) are introduced into the estimation problem.

Pre-calibrated multi-peak models have been derived by MR spectroscopy or using dedicated CSE-MRI experiments with a large number of echo times (17,22,23). However, different models have been derived and applied in different studies. The various models differ in the number of peaks, chemical shift between peaks and relative amplitudes of the peaks. Although techniques using different spectral models have been validated for accurate fat quantification or water fat separation, there is no consensus as to which spectral model should be used.

The impact on PDFF estimation from the choice of spectral model of fat is unknown, and this lack of standardization has potential impact on the reproducibility of CSE-MRI for quantifying fat. The purpose of this study is to evaluate the sensitivity of PDFF mapping to the choice of multi-peak fat model by simulation and in vivo liver fat quantification.

Theory

In chemical shift-encoded (CSE) MRI, the acquired signal in a voxel in the presence of water and fat can be generally described as:

$$s_n=e^{i(\mathrm{\Delta }{\omega }_0·T{E}_n)}·(W{e}^{i{\varphi }_{0,w}}{e}^{-R2}{w}^{\ast }·T{E}_n+F{E}^{i{\varphi }_{0,f}}·{\sum }_{p=1}^P{\alpha }_p{e}^{i2\pi ·f_p·T{E}_n}{e}^{-R{2_p}^{\ast }·T{E}_n})$$ (1)

where s_n is the signal acquired at the n^th echo time TE_n, Δω₀, is the frequency offset due to local B₀ off-resonance ϕ_0,w, ϕ_0,f are the initial phase of water and fat signal. The signal consists of one water peak and P fat peaks. W and F are the sum of all water signal and fat signal, respectively. The R2* decay rate of water is R2_W*. The relative amplitude, relative frequency shift, and R2* decay rate of the p^th fat peak are denoted as α_p, f_p and R2*_p, respectively. In general, ϕ_0,w, ϕ_0,f, Δω₀, R2_W*, α₁… α_P, f₁… f_P, R2*₁… R2*_p are the unknown parameters to be estimated.

In CSE-MRI, due to imaging time constraints, 6 echoes with maximum echo time of approximately 10–20ms (at 1.5T) are typically acquired, providing limited spectral resolution. To achieve robust water fat separation, the number of unknowns can be reduced by introducing assumptions to the general signal model in Eq (1). Two major and well-validated assumptions are commonly used 1) R2* of water and all fat peaks are all assumed to be equal (7,24), 2) the relative amplitude and chemical shift of all fat peaks are assumed to be known a priori based on other experimental data (17,21) (i.e. pre-calibrated fat spectrum). These assumptions lead to the following simplified signal model (18):

$$s_n=e^{i(\mathrm{\Delta }{\omega }_0·T{E}_n)}·(W{e}^{i{\varphi }_{0,w}}+F{e}^{i{\varphi }_{0,f}}·{\sum }_{p=1}^P{\alpha }_p{e}^{i2\pi ·f_p·T{E}_n})e^{-R{2}^{\ast }·T{E}_n}$$ (2)

where α_p, f_p are the known (ie: pre-calibrated) relative amplitude and frequency shift of the p^th fat peak. In a typical CSE-MRI acquisition, signals from multiple echoes acquired are fit, on a voxel-by-voxel basis, using the signal model in Eq (2) to estimate the six unknown parameters W, F, ϕ_0,w and ϕ_0,f, Δω₀, and R2*. A PDFF map then can be calculated using separated water and fat images, including correction for noise bias effects (14). This signal model has been successfully applied for PDFF quantification, and validated using MR spectroscopy-based fat quantification as a reference (6,7).

Further, eddy current effects can lead to undesired phase shifts between different echoes, introducing errors in CSE fat quantification. To address this challenge, fitting is often performed after taking magnitude of both sides of Eq (2), ie: “magnitude” fitting. When the phase in equation 2 is preserved, this is referred to as “complex” fitting. Magnitude fitting is relatively immune to eddy current related phase errors but suffers from reduced noise performance compared with complex fitting (25). Alternatively, a mixed fitting technique has been proposed where only the phase of the first echo is discarded in “single echo train” acquisitions. Mixed fitting results in good robustness to phase errors relative to complex fitting, and improved noise performance relative to magnitude fitting (20).

The specific choice of pre-calibrated multi-peak fat model differs considerably between studies and there is no consensus as to which is the best and most appropriate spectrum to use. In recent works, Hamilton et al., measured the human liver fat spectrum as a 6-peak and a 9-peak model using spectroscopy on a 3T GE system (22). Ren et al., characterized the human subcutaneous and bone marrow fat spectrum using a 7-peak model, measured at 7T, using single-voxel stimulated echo acquisition mode STEAM spectroscopy (23). Wokke et al., derived 4- and 5-peak fat models by merging peaks that are close together in the 6-peak model(26). Yu et al., applied a self-calibrated fat quantification method which calibrated human liver fat spectrum on a 1.5T system as a 3 peak model (17).

The differences in number of peaks, frequency shifts relative to water, and relative amplitudes are summarized in Table 1. Among these fat models, 6,7 and 9-peak models are most commonly used in CSE fat quantification. The 9-peak model has been adopted by Berglund et al. (27), 6-peak model has been adopted by Hernando et al. (18), Hines et al. (7), Meisamy et al. (6). The 7-peak model has been used by Jonker et al. (28). An additional 3-peak model and 5-peak model have also been reported by Yokoo et al. (5,9).

Table 1.

List of different multi-peak spectral models of fat used in this work.

Peaks	Frequency relative to water (ppm)	Relative amplitude (%)	Reference
1	−3.4	100	n/a
3	0.73, −2.49, −3.29	8, 17, 75	Yu (17)
4	0.73, −2.49, −3.27, −3.68	8, 15, 72, 4	Wokke (26)
5	0.73, −2.35, −2.54, −3.27, −3.68	8, 5, 10, 72, 4	Wokke (26)
6	0.6, −0.5, −1.95, −2.6, −3.4, −3.8	4.7, 3.9, 0.6, 12, 70, 8.8	Hamilton (22) Hernando (18) Meisamy (6) Hines (7)
7	0.61, −1.93, −2.45, −2.67, −3.11, −3.4, −3.8	4.2, 1.5, 6.6, 9.6, 7.1, 62.7, 8.3	Ren (23), Jonker (28), Zhong (10)
9	0.59, 0.49, −0.5, −1.95, −2.46, −2.68, −3.1, −3.4, −3.8	3.7, 1, 3.9, 0.6, 5.8, 6.2, 5.8, 64.2, 8.8	Hamilton (22), Berglund (27)

Materials and Methods

Simulations

As part of a computer simulation, each spectral model of fat was compared with all other models in a pairwise manner. Specifically one model was used to generate a test signal (as the “true” fat model) at each TE, and the other spectral model (as the estimator fat model) was used to fit the test signals to estimate PDFF. All frequencies are based on 1.5T imaging. For each pair of spectral models of fat test signals were generated using the signal model in Eq (2) for simulated voxels with fat fractions ranging from 1% to 40%, and a fixed R2* of 40s⁻¹ (typical for 1.5T liver imaging (29)). No noise were added. A combination of 6 echoes starting at 1.2ms, and spaced by 2.0ms were adopted. The initial phase of water and fat was assumed 0, and the initial field inhomogeneity was 2ppm. No eddy current induced phase was added to the first echo. Nevertheless, the phase of the first echo was discarded for both the magnitude and mixed fitting algorithms to better approximate the in vivo situation (20,25).

The PDFF was estimated by fitting the test signals to equation 2 using both magnitude and mixed fitting algorithms, using a different signal model as the estimator fat model. The estimated PDFF was then compared to the true PDFF using linear regression to determine the bias. This simulation was performed for all possible pairs of the fat models listed in Table 1.

Next, the effect of the choice of echo times on the PDFF bias caused by multi-peak model mismatch was also evaluated using simulations. Each combination contains 6 echoes with initial echo time (TE_min) and echo spacing (ΔTE) both ranging from 0ms to 3ms. For this simulation, the fat fraction was 30%, R2* = 40s⁻¹, field strength 1.5T. Signal was generated using the 6-peak model reported by Hamilton et al. as the “true” fat model and PDFF was estimated with 1, 3, 5, 7, 9-peak models. No noise was added to the test signals since we were evaluating the effects of bias in these simulations. Bias was calculated for each echo combination studied.

In vivo liver fat quantification

In vivo liver datasets from 41 patients were also analyzed. Data acquisition was performed on GE Signa HDxt 1.5T scanners, with either an 8-channel cardiac coil or an 8-channel torso coil. This dataset has been analyzed by previous studies (6,7) for different purposes, but reprocessed specifically and uniquely for this study.

CSE data were obtained using an investigational version of a multi-echo spoiled gradient echo (SGRE) sequence. All images were acquired in axial plane and obtained during a single 21s breath-hold, with the following imaging parameters: readout direction R/L, matrix size 256×128, 2D autocalibrated parallel imaging (30) with a nominal acceleration factor of 2 in both phase encoding directions, for an effective acceleration factor of 2.2 (due to central autocalibration lines), slice thickness 10mm, 24 slices, flip angle 5°, TR=13.7–14.9ms, BW=±125kHz, mono-polar readout (flyback gradients), 6 echoes, TE_min=1.2ms,ΔTE=2.0ms. PDFF maps using the multi-echo SGRE data were reconstructed twice using each fat model listed in Table 1, once using magnitude fitting and once using mixed fitting algorithms, respectively for a total of 14 reconstructions for each dataset. Due to eddy current induced phase, pure complex fitting was not performed since phase shifts on the first echo caused by eddy currents were known to create bias. T1 bias was minimized by using a low flip angle and by performing a retrospective T1 correction for any residual T1 related bias (7) assuming a T1 of 568ms for water and 343ms for fat (31). Initial field maps were stabilized with a 3D graph cut algorithm (not publicly available through water-fat toolbox) (32). Mixed fitting and magnitude fitting were performed using Levenberg-Marquardt least-square fitting algorithm.

A single voxel STEAM-MRS spectrum was also acquired in a single breath-hold in every subject to provide a reference standard for fat fraction (33). MRS data were acquired in the right lobe of liver during a 21s breath-hold at 5 echo times (10, 20, 30, 40, 50 ms) enabling T2 correction. Typical voxel size was 20 × 20 × 25 mm³, TR=3500ms, 2048 readout points, 1 average, and spectral width = ±2.5 kHz. MRS-PDFF was estimated from STEAM-MRS data. MRS data of individual coils were first combined using a singular-value decomposition (SVD) based method (34) implemented in Matlab (Mathworks, Natick, MA). In jMRUI (35), individual signal peak areas were estimated using the coil-combined data at each echo time with the AMARES (36) algorithm and prior knowledge as described by Hamilton et al. (22). Peak area estimates over all echo times were then fit into a mono-exponential curve for the estimation of peak-specific T2 and T2-corrected peak areas. Subsequently, total water and fat signals were calculated as the summation of their individual peak areas. MRS-PDFF was calculated as the ratio of T2 corrected total fat signal and the sum of T2-corrected water and fat signals (35,37).

For each patient, a region-of-interest (ROI) was co-localized with the STEAM voxel in the slice closest to the center of STEAM voxel. The PDFF was measured in a 20 × 20 mm² voxel and the two adjacent slices to match the STEAM voxel closely. MRI-based PDFF was then calculated by averaging the PDFF values within the three ROI’s. This procedure was repeated for reconstructions using each spectral model of fat and fitting algorithms. The same ROI’s were used for all reconstructions of the same patient to achieve perfectly co-registered MRI-PDFF values.

For each patient, STEAM PDFF were linearly regressed against 14 MRI-based PDFF values. 95% confidence intervals and p values were generated from applying a t-test to the estimate of slopes and intercepts to determine whether slopes are significantly different from 1 and intercepts are significantly different from 0 (ie: p_slope<0.05 or p_intercept<0.05).

Results

Simulations

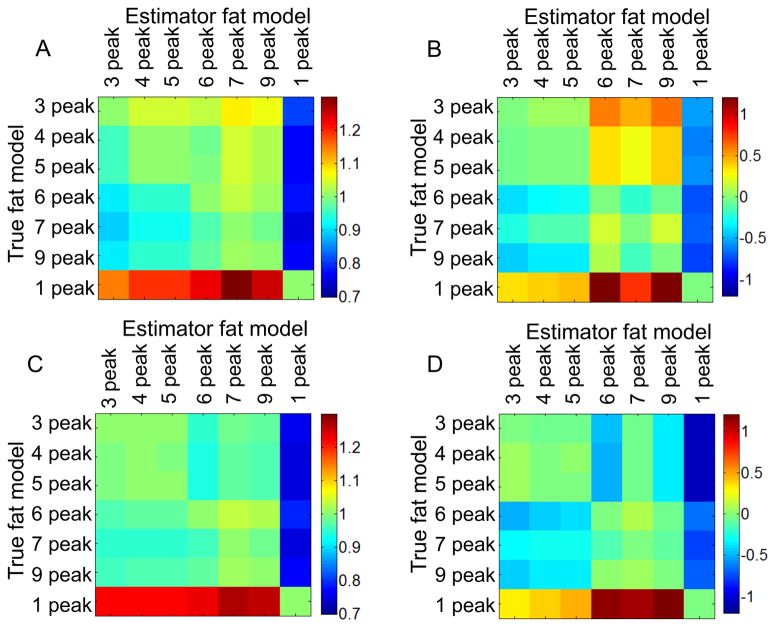
In pairwise comparisons, for each pair of spectral models of fat, estimated PDFF was linearly regressed against true PDFF with excellent correlation (r² > 0.998) as expected. Thus, slopes close to 1 and intercepts close to 0 reflect equivalence between compared models. In Figure 1, A) C) show slopes, B) D) show intercepts in comparison of each pair of spectral models when magnitude fitting (A,B) and mixed fitting (C,D) were used as fitting algorithms. Each row shows the slope between a particular spectral model (“true” fat model) and every other model (estimator fat model) in each column. Between a single-peak model and any multi-peak model, greater errors were observed between estimated fat fraction and true fat fraction (slope< 0.79 or slope>1.22, |intercept| up to 1.20% for mixed fitting, slope<0.82 or slope>1.15, |intercept| up to 1.56% for magnitude fitting). Between any two multi-peak models, improved agreement was demonstrated: 0.94<slope<1.03, −0.51%<intercept<0.10% for mixed fitting, 0.89< slope<1.08, −0.39%<intercept<0.60% for magnitude fitting.

Figure 1.

Multi-peak models demonstrate better agreement with each other than with the single peak spectral model of fat. Results are from simulations comparing, in a pairwise manner, different spectral models of fat. The color coding plots the slope (A, C) and intercept (B, D) from linear regression of estimated PDFF with true fat fraction, for magnitude fitting (A,B) and mixed fitting (C, D).

Figure 2 presents simulation results for the absolute bias in estimated PDFF over a range of initial echo times and echo spacings. Horizontal and vertical axes show echo spacing and initial echo times, respectively. The top row was reconstructed using mixed fitting and the bottom row was reconstructed using magnitude fitting. A clear dependence of bias on echo combination is seen for both fitting algorithms. For magnitude fitting, there is a range of echo combinations (near TE_min=1.25ms, ΔTE=2.3ms) that result in over 10% absolute bias regardless of the fat model used in estimation. For mixed fitting, the bias changes more gradually with echo times, and remains relatively low for lower initial echo times and echo spacings.

Figure 2.

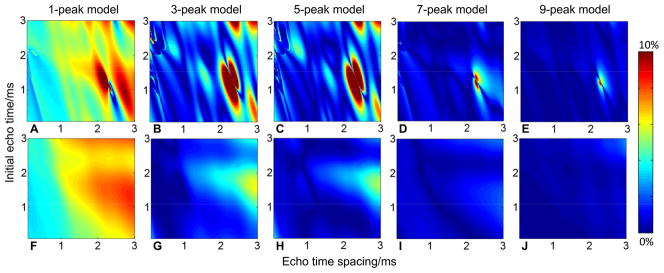
In general, mixed fitting has lower bias than magnitude fitting and is less sensitive to the choice of spectral model of fat. Absolute biases from simulated PDFF estimate resulting from difference between “true” fat model (6-peak model) and estimator fat model (1-, 3-, 5-, 7-, 9-peak models) are presented for mixed fitting (A, B, C, D, E) and for magnitude fitting (F, G, H, I, J). The bias is shown to be a function of echo times. For certain echo time combinations, magnitude fitting can lead to large bias (>10%) even from small model differences, while mixed fitting had lower bias. particularly for 7-peak and 9-peak models

In vivo liver fat quantification

Figure 3 shows representative PDFF maps of a patient calculated using several spectral models of fat, for both mixed fitting and magnitude fitting algorithms. A clear PDFF offset can be observed between reconstructions using single-peak model and multi-peak models. Over all patients, linear regression showed strong correlation between STEAM PDFF and all MRI-based PDFF values (r²>0.962). Further, slopes and intercepts of these regressions were calculated and are shown in Table 2, including the 95% confidence intervals and p values generated from t-tests. Multi-peak models with both fitting algorithms exhibit better agreement with the MRS as reflected by the values of slopes and intercepts. Only 1-peak (p_slope=3.76·10⁻¹³ in magnitude fitting p_slope=5.00·10⁻¹⁶ in mixed fitting) model and 7-peak (p_slope =4.42·10⁻² ) in magnitude fitting and mixed fitting) models were significantly different from the reference. Despite being significantly different from the reference, 7-peak model has much closer agreement with the reference than single–peak model (slope=1.05 compared with 0.76 for single-peak model).

Figure 3.

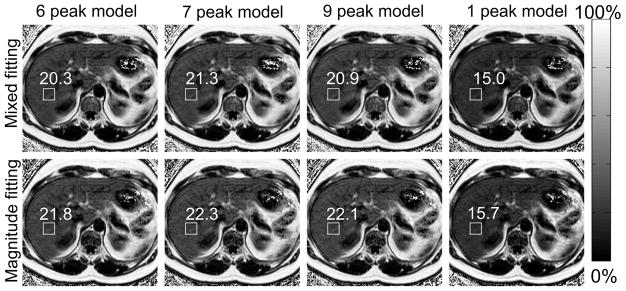
Single-peak model produced substantially different liver fat fraction using 6-, 7-, and 9-peak spectral models of fat. PDFF maps from one patient reconstructed using mixed fitting (top row) and magnitude fitting (bottom row) for 4 different spectral models of fat. T2-corrected STEAM MRS-PDFF was 20.9% in this patient. The location of the steam voxel and Co-localized MRI-PDFF measurements are shown in the figure.

Table 2.

All multi-peak fat models agree closely with the reference standard (MRS-PDFF), as evidenced by regression results. Results of the linear correlation of MRI-PDFF and MRS-PDFF are tabulated for the 7 spectral models and the two fitting methods. Coefficient of determination, slope and intercept of the linear regression are all listed, including 95^th percentile confidence intervals. Overall, multi-peak models including 7-peak model demonstrate better correlation and agreement with MRS than single-peak model as reflected by the values of slope and intercept estimate. No significant difference (p=0.05) was observed for multi-peak models expect 7-peak model using both fitting methods. Further, mixed fitting demonstrates slightly stronger correlation and agreement than does magnitude fitting, although the differences are small.

ββ	R2	Slope [95th CI]	p-value (slope)	Intercept (%)[95th CI]	p-value (intercept)
Magnitude Fitting
1-peak	0.974	0.770 [0.726, 0.814]	3.755·10−13	−0.406 [−0.891, 0.078]	0.098
3-peak	0.962	0.952 [0.900,1.004]	0.068	−0.284 [−0.852, 0.284]	0.318
4-peak	0.974	0.967 [0.916,1.019]	0.210	−0.295 [−0.868, 0.278]	0.304
5-peak	0.974	0.967 [0.916, 1.019]	0.214	−0.293 [−0.866, 0.279]	0.307
6-peak	0.978	1.035 [0.979, 1.091]	0.219	−0.282 [−0.907, 0.334]	0.357
7-peak	0.977	1.060 [0.988, 1.109]	0.041	−0.287 [−0.912, 0.349]	0.372
9-peak	0.970	1.050 [0.993, 1.107]	0.083	−0.287 [−0.914, 0.339]	0.360
Mixed Fitting
1-peak	0.978	0.760 [0.723, 0.797]	4.996·10−15	−0.421 [−0.830,−0.012]	0.044
3-peak	0.979	0.967 [0.920,1.013]	0.151	−0.317 [−0.829, 0.194]	0.217
4-peak	0.979	0.975 [0.929,1.021]	0.281	−0.326 [−0.838, 0.185]	0.205
5-peak	0.979	0.975 [0.929,1.022]	0.292	−0.324 [−0.835, 0.188]	0.209
6-peak	0.982	1.008 [0.964, 1.053]	0.703	−0.373 [−0.864, 0.118]	0.133
7-peak	0.983	1.047 [1.001, 1.092]	0.044	−0.313 [−0.813 0.188]	0.214
9-peak	0.981	1.045 [0.997, 1.092]	0.063	−0.358 [−0.880 0.164]	0.174

Discussion

In this study we have analyzed the sensitivity of MRI-based CSE fat quantification to the choice of spectral model of fat, using both computer simulations and in vivo data acquired in patients. Spectral models of fat from previously published studies were used in this analysis and it was demonstrated that all multi-peak models showed greater accuracy for quantifying fat than the single-peak model. In addition, mixed fitting showed better agreement between the spectral models than magnitude fitting. Overall, these data demonstrate that multi-peak spectral modeling of fat is essential for accurate estimation of PDFF. However, no compelling evidence has been found to support any specific multi-peak spectral model of fat over the rest.

Among the discussed multi-peak spectral models of fat, the 7-peak model by Ren et al. was calibrated in subcutaneous fat while the others were all measured in liver. The results shown in this study indicate the 2 fat depots have similar fat spectral peaks. 3-peak (1.5T) and 7-peak (7T) models are also calibrated at different field strengths compared with other models (3T). The fact that these models are relatively interchangeable, suggests that MR spectroscopy is a reproducible tool for the measurement of fat spectrum in scanners at different field strength (1.5T – 7T).

In all signal estimation problems, bias will be introduced when there is discrepancy between the underlying physics (eg. true spectral model) and the signal model used in the estimation of the parameters of interest. In the case of PDFF estimation, the resulting bias will depend on factors such as the true PDFF and the choice of echo times and fitting method (eg: magnitude vs mixed fitting).

The choice of echo times is an important component of CSE-MRI based fat quantification. It has been shown that the choice of echo times has a large impact on the noise performance of the technique (13,38). Further, previous studies have shown that bias due to temperature-related effects (ie: model mismatch) is heavily influenced by the choice of echo times, and also the fitting method (39). In this study, we have shown that bias created by discrepancies in the true spectral model and the estimator model will depend on the choice of echo times. Interestingly, the bias increased markedly with longer echo spacing. Bias can be limited by shortening initial echo time and echo time spacing. It was also important to note that mixed fitting was more robust to changes in echo time (ie: had less bias) than magnitude based fitting, which is consistent with the study by Hernando et al. (39). This may explain the observation by Heba (40) that using a shorter echo train length may improve the accuracy of PDFF quantification using magnitude based fitting. A discrepancy between the underlying physics and the spectral model used in CSE-MRI may explain why using fewer echoes appears to lead to less bias, as shown in that study.

This study has several limitations. Small differences between a spectral model of fat used for PDFF estimation and the actual spectra will reduce accuracy. However, we have demonstrated that the accuracy of PDFF quantification is relatively insensitive to different spectral models. Therefore, it is likely that errors introduced by small discrepancies in the spectral model relative to the true spectra are much smaller than the variability due to noise and other unrelated confounders. Large patient populations may be necessary to detect errors introduced by errors in the spectral model. Although, published data suggest relative uniformity in the triglyceride spectra across patients (22), variability in the spectra between patients could also introduce additional variability in the estimated PDFF. A second limitation is that all in vivo data and simulations were acquired at 1.5T. However, quantitative CSE-MRI is increasingly frequently performed on 3T scanners. The difference between these two platforms may result in different optimal echo times, which impacts the relative importance of the spectral models. In addition, this study did not consider the presence of liver iron overload. The high R2* introduced by the presence of iron may affect the relative impact of different fat models. Furthermore, all in vivo data were acquired at the same echo time not allowing further in vivo validation of the echo time dependence of fat signal model related bias. Overall, however, we believe that the conclusions drawn by this study will, in all likelihood, extend to 3T and when R2* is higher, although further work would be needed to confirm this speculation. Finally, this study is limited to “single R2*” signal models, where the R2* decay is assumed common for water and fat signals. Although dual R2* signal models have been proposed and studied in CSE-MRI, single R2* models have superior noise performance (18,24), have been shown to be accurate and robust (6,7), and the assumption that the R2* of water and fat peaks are very similar has been experimentally validated (24).

In conclusion, multi-peak spectral modeling of fat is essential for accurate estimation of tissue fat concentration, as measured by the proton density fat-fraction. Although spectral modeling is necessary, no specific choice of spectral model was shown to be superior, so long as one of the multi-peak models discussed in this work is used. Echo time combinations, such as shorter echo times, and the use of mixed fitting may be useful to minimize the impact of any model imperfections.