Abstract
Vascular smooth muscle cells’ primary function is to maintain vascular homeostasis through active contraction and relaxation. In diseases such as hypertension and atherosclerosis, this function is inhibited concurrent to changes in the mechanical environment surrounding vascular smooth muscle cells. It is well established that cell function and extracellular mechanics are interconnected; variations in substrate modulus affect cell migration, proliferation, and differentiation. To date, it is unknown how the evolving extracellular mechanical environment of vascular smooth muscle cells affects their contractile function. Here, we have built upon previous vascular muscular thin film technology to develop a variable-modulus vascular muscular thin film that measures vascular tissue functional contractility on substrates with a range of pathological and physiological moduli. Using this modified vascular muscular thin film, we found that vascular smooth muscle cells generated greater stress on substrates with higher moduli compared to substrates with lower moduli. We then measured protein markers typically thought to indicate a contractile phenotype in vascular smooth muscle cells and found that phenotype is unaffected by substrate modulus. These data suggest that mechanical properties of vascular smooth muscle cells’ extracellular environment directly influence their functional behavior and do so without inducing phenotype switching.
Keywords: arterial mechanics, extracellular matrix, atherosclerosis, hypertension, vascular muscular thin film
1 INTRODUCTION
Vascular smooth muscle cells (VSMCs), the most numerous cell type in arteries, are responsible for maintaining vascular homeostasis through active contraction and relaxation. However, in vascular pathologies, contractile function can be inhibited. This loss of function often corresponds with changes in the mechanical environment to which the cells are exposed. For example, while healthy vessels have a small-strain Young’s modulus of 30kPa (Fung, 2004), atherosclerotic plaques are composed of soft lipid pools, with Young’s moduli of ~50Pa (Loree et al., 1994), surrounded by stiff, fibrous caps, with moduli of 0.5–2.0MPa (Lee et al., 1991). In hypertension, increased collagen content leads to increased vessel stiffness (Ooshima et al., 1974). The mechanical properties of the extracellular environment, such as the substrate modulus in vitro, can directly impact cell behavior (Discher et al., 2005) including cell motility (Isenberg et al., 2009; Peyton and Putnam, 2005; Wong et al., 2003; Zaari et al., 2004), differentiation (Engler et al., 2006), focal adhesion formation (Peyton and Putnam, 2005), proliferation (Brown et al., 2005; Klein et al., 2009; McDaniel et al., 2007), and cytoskeletal organization (Engler et al., 2006; Griffin et al., 2004). In VSMCs, substrate mechanics affect migration (Isenberg et al., 2009; Peyton and Putnam, 2005; Wong et al., 2003), proliferation (McDaniel et al., 2007), and sensitivity to growth factors (Brown et al., 2010). However, it is unknown how substrate mechanical properties affect the key function of VSMCs: contractile force generation. We hypothesize that VSMC contractility is altered by perturbations of extracellular mechanics associated with vascular pathologies.
VSMC contractility is controlled chronically through switching between two distinct phenotypes (Chamley-Campbell et al., 1979; Owens, 1995). The differentiated, mature contractile phenotype has a spindle-shaped morphology, expresses higher levels of proteins associated with the contractile apparatus, and exhibits limited migration and proliferation (Owens, 1995; Rensen et al., 2007). VSMCs with a synthetic phenotype are rhomboid in shape, are highly migratory and proliferative, and synthesize extracellular matrix proteins, such as collagen and elastin (Owens et al., 2004; Rensen et al., 2007). In atherosclerosis, VSMCs switch from a contractile to synthetic phenotype and migrate from the media to the intima of the artery (Hao et al., 2003; Owens, 1995). In vitro, non-confluent VSMCs cultured on stiff substrates express contractile phenotype markers at higher levels than on soft substrates, though this difference declines in confluent VSMCs (Sazonova et al., 2011). Currently, it is unclear whether substrate mechanics-related phenotype expression affects VSMC functional contractility.
In vitro methods, traction force microscopy (TFM) (Munevar et al., 2001) and microfabricated Post-Array-Detectors (mPADs) (Tan et al., 2003), have previously been used to study the effects of substrate mechanics on cell force generation (Califano and Reinhart-King, 2010; Fu et al., 2010). However, these systems evaluate force generation of a single cell or a small group of cells (Ting et al., 2012), and do not capture tissue-scale functional contractility. This distinction is important because in vivo VSMCs exist within cell-dense medial lamellae wrapped concentrically around the vessel (Humphrey, 2002). Additionally, in vitro VSMCs with increased cell-cell contacts exhibit a more contractile in vivo-like behavior than sparsely seeded VSMCs (Cao et al., 2010), and VSMCs with in vivo-like alignment express a more contractile phenotype than disorganized, but confluent, cells (Williams et al., 2011). Thus, it is important to recapitulate in vivo structure to study VSMC function in vitro. We have previously developed vascular muscular thin film (vMTF) (Alford et al., 2010) technology to evaluate VSMC stress generation in aligned, confluent vascular lamellae mimics, but to date all vMTF studies have been performed with a single substrate modulus (Alford et al., 2011a; Alford et al., 2011b; Hald et al., 2014; Win et al., 2014). Thus, it is unclear how extracellular mechanical properties affect contractile function in confluent VSMCs with in vivo-like structure.
Here, we describe a modified vMTF method for determining the effect of substrate modulus on functional contractility of a confluent layer of VSMCs. We find increasing substrate modulus corresponds with increasing VSMC contractility. However, this increase in cell stress generation occurs without changes to VSMC tissue architecture or phenotype.
2 METHODS
2.1 Polydimethysiloxane Mechanical Characterization
Polydimethylsiloxane (PDMS) 184 (Dow Corning, Midland, MI) was mixed and degassed in an AR-100 mixer (Thinky, Tokyo, Japan) at base to cross linker ratios of 50, 40, 30, 20, 15, and 10. PDMS 527 (Dow Corning) was similarly mixed and degassed at component A to component B ratios of 0.5, 0.6, 0.7, 0.8, 0.9, and 1. Each formulation was cured at 90°C in a dog-bone shaped mold and uniaxial tensile tests were conducted in triplicate. The Young’s modulus was determined from the stress-strain curve. PDMS 184 and PDMS 527 Young’s moduli (E) varied by E = 3448e−0.1172x and E = 306.67e−3.829x, respectively, where x is the formula’s ratio. These functions were used to calculate the recipes for each substrate modulus: 10kPa – 0.9 (A:B; PDMS 527), 50kPa – 0.47 (A:B; PDMS 527), 100kPa – 0.29 (A:B; PDMS 527), 1MPa – 10.6 (base:cross linker; PDMS 184).
2.2 Variable-Modulus vMTF Fabrication
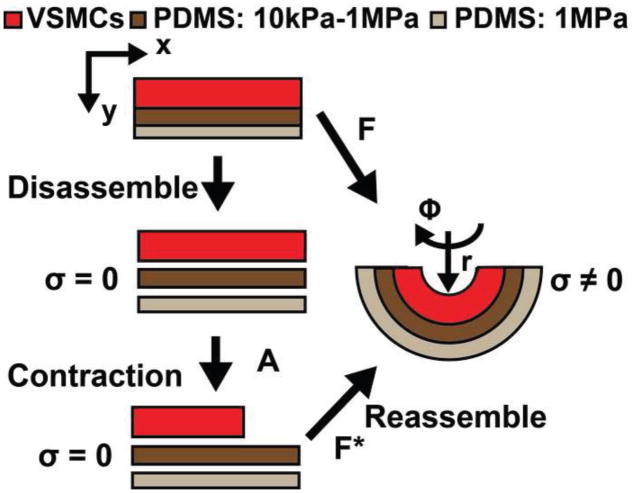
Clean, 22mm coverslips were spin coated with poly(N-isopropylacrylamide) (PIPAAm) (Polysciences, Warrington, PA) (Fig. 1, steps 1, 2). Then a 10–12μm thick layer of variable modulus (10kPa, 50kPa, 100kPa, 1MPa) PDMS doped with green fluorescent microspheres (Polysciences) was spin coated and cured at 90°C (Fig. 1, step 3). Next, a 5–10μm thick layer of PDMS at 1MPa was spin coated and cured at 90°C (Fig. 1, step 4). A ~5mm strip of tape was placed across the diameter of a clean, 25mm coverslip and a ~5μm layer of 1MPa PDMS 184 was spin coated (Fig. 1, steps 5–7). Prior to curing, the tape was removed and the 22mm coverslip was inverted and placed on the 25mm coverslip. The two coverslips were then cured at 90°C bonding the PDMS surfaces (Fig. 1, step 8). The constructs were submerged in ddH2O overnight, dissolving the PIPAAm layer, releasing the 22mm coverslip, and revealing the variable modulus substrate (Fig. 1 steps 9, 10). The final construct was composed of three layers: 1) supportive base layer 2) variable modulus layer 3) arterial lamella tissue layer (Fig. 2A). This inverse layer construction method was developed to prevent the development of residual stress in the released films (see Supplemental Materials). PDMS thicknesses were acquired with a P10 Tencor profilometer (KLA-Tencor, Milpitas, CA).
Figure 1.
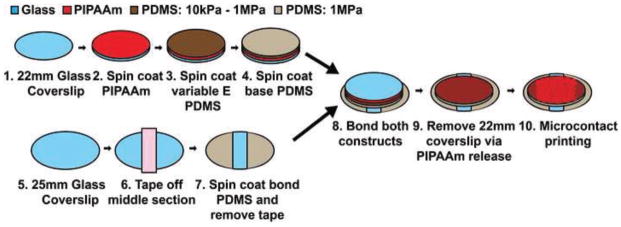
Variable Modulus vMTF Fabrication.
Figure 2.
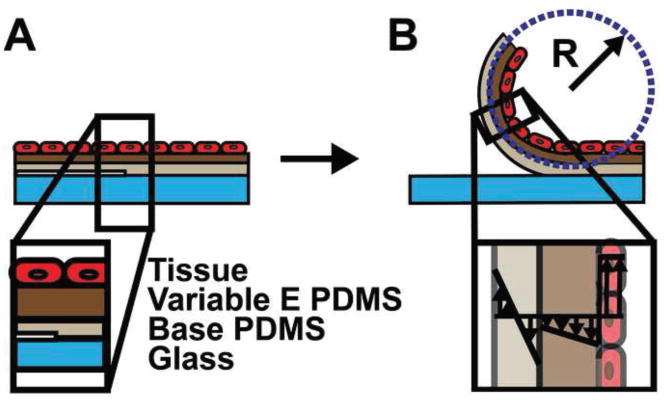
Variable modulus vascular muscular thin film structure. A. Side view of each layer in the three layer MTF. B. Film release yields a curved beam. The radius of curvature (R) is used to calculate the stress in the tissue layer. Inset: Transmural stress distribution.
2.3 Cell Culture
Human umbilical artery VSMCs were purchased from Lonza (Walkersville, MD) and cultured in M199 culture medium (Mediatech, Manassas, VA), 10% fetal bovine serum (GIBCO, Grand Island, NY), 50U/ml penicillin (GIBCO), 50U/ml streptomycin (GIBCO), 10mM HEPES (GIBCO), 1X MEM non-essential amino acids (GIBCO), 2mM L-glutamine (Sigma Aldrich, St. Louis, MO), 3.5g/L glucose (Sigma Aldrich), and 2mg/L vitamin B-12 (Sigma Aldrich). VSMCs were kept in 5% CO2 at 37°C and all experiments were conducted using passages 5–7. Prior to all experiments the tissues were serum starved for 24h to induce an in vivo-like phenotype (Han et al., 2006).
2.4 Tissue Construction
Microcontact printing was used to construct arterial lamella tissue mimics as in our previous publications (Alford et al., 2011a; Alford et al., 2011b; Win et al., 2014). Briefly, extracellular matrix protein, fibronectin (BD Biosciences, Radnor, PA), was stamped onto the PDMS substrate surface in 10μm parallel lines with 10μm pitch and VSMCs were seeded at 57,000 cells/cm2.
2.5 Immunofluorescent Imaging and Quantification
Tissues were fixed with 4% paraformaldehyde (Electron Microscopy Sciences, Hatfield, PA), permeabilized with 0.05% Triton (Sigma Aldrich), and blocked in 10% bovine serum albumin (Thermo Fisher Scientific, Waltham, MA) for 1h. F-actin, nuclei, smooth muscle alpha-actin, and N-cadherin were stained with fluorophore-conjugated phalloidin (Life Technologies, Carlsbad, CA), DAPI (Life Technologies, Grand Island, NY), fluorophore-conjugated anti-α smooth muscle actin antibody (1A4; Sigma Aldrich), and anti-N-cadherin antibody (GC-4; Sigma Aldrich) with secondary Alexa Fluor 546 goat anti-mouse IgG (Life Technologies), respectively. Tissues were imaged using an Olympus IX81ZDC confocal microscope (Olympus, Shinjuku, Tokyo). Actin and nuclear alignment were determined as in Alford et al. (2011b) using immunofluorescent staining and custom MATLAB software to determine the orientation order parameter (OOP). Anti-paxillin antibody (Abcam, Cambridge, MA) was used to stain for focal adhesions and imaged at 60x with an Olympus IX81ZDC confocal microscope (Olympus). Image processing with ImageJ was completed using rolling ball threshold and a single application of dilation and erosion. Particle analysis was conducted for particles between 0.11μm (Coyer et al., 2012) and 23μm (Kim and Wirtz, 2013). Tissue thickness was measured using confocal stacks of phalloidin labelled f-actin (Alford et al., 2010).
2.6 Variable-Modulus vMTF Experimental Protocol
The construct was placed in 37°C, 1X, pH 7.4 Tyrode’s buffer and cut eight times parallel to tissue alignment and two orthogonal to the initial eight (Hald et al., 2015), leaving two rows of four, semi-detached, curved variable-modulus vMTFs with the VSMCs on the concave surface (Fig. 2B). After 15min of equilibration, the variable-modulus vMTF VSMCs were serially stimulated with increasing concentrations of endothelin-1 (Sigma Aldrich) every 10min; 500pM, 5nM, 50nM, and 500nM. Finally, 100μM rho-kinase inhibitor HA-1077 (Sigma Aldrich) was added for 30min. Fluorescent and bright field images were acquired every 30s using a Lumar V12 stereomicroscope (Zeiss, Oberkochen, Germany). These images were used to determine the 2D projection length of the film, which was used to evaluate its radius of curvature (Win et al., 2014). Data was analyzed using ANOVA and pairwise comparisons were made using the Tukey test in MATLAB.
2.7 Stress Analysis
The stress in the tissue layer was determined by utilizing finite volumetric growth theory (Rodriguez et al., 1994) modified for pseudo-contraction (Ramasubramanian and Taber, 2008), as in our previous work (Fig. 3) (Alford et al., 2010). The variable-modulus vMTF is treated as an incompressible three-layer beam in both moment and radial force equilibrium. The PDMS layers undergo shear-free bending, while the tissue layer contracts. Each layer is modeled as a Neo-Hookian material, and the thickness of each layer is experimentally determined (See Methods 2.2 and 2.5).
Figure 3.
Schematic representation of volumetric pseudo-contraction applied to variable modulus vMTF to calculate cell stress. F is the deformation gradient tensor. F* is the elastic deformation tensor. A is the active deformation tensor.
The deformed geometry is mapped to the undeformed by
| (1) |
where k and λ are constants (Fig. 3). The experimentally-determined radius of curvature is assumed to be the vMTF midline (rm) so that
| (2) |
where h is the deformed film thickness, and ri and ro are the inner and outer radii of the film in the deformed configuration. The observed deformation of the beam is represented by the deformation gradient tensor, F, given by
| (3) |
where λi is the stretch ratio in i the principal direction (Fig. 3). We assume plane strain deformation (λZ = 1). Incompressibility then gives
| (4) |
The VSMCs are assumed to only contract in the direction of alignment, along the length of the variable-modulus vMTF. The cellular active stretch ratio (λa) represents the stress-free shortening the cells would undergo if not constrained by the PDMS layers. Thus, the total active deformation tensor (Fig. 3) is given by
| (5) |
The PDMS is passive, so APDMS = I. The elastic deformation tensor defines the deformation from the contracted zero-stress configuration to the current observed configuration and is given by
| (6) |
where is the elastic stretch ratio in the i principal direction (Fig. 3). The observed deformation is the product of the active and elastic deformations;
| (7) |
Therefore,
| (8) |
All layers are represented by Neo-Hookean strain energy density functions, given by
| (9) |
where μ is the shear modulus and is the first elastic strain invariant, defined as
| (10) |
The Cauchy stress of the cell layer is a function of elastic deformation, and defined as,
| (11) |
where p is a Lagrange multiplier. The radial and moment equilibrium equations and boundary conditions are given by:
| (12) |
| (13) |
| (14) |
Given rm, the undeformed thickness, and μ for each layer, the active stretch ratio (λa) and the deformed thickness (h) of the variable-modulus vMTF in the radial direction was solved with Nelder-Mead minimization and used to calculate the Cauchy stress in the cell layer. The cell strain was determined by ε = λθcell − 1.
2.8 Western Blotting
Tissues were lysed with RIPA buffer (100mM Tris (pH 7.4) (Sigma Aldrich), 4M Urea (Sigma Aldrich), 5mM EDTA (Sigma Aldrich), 0.5% SDS (Sigma Aldrich), 0.5% Nonidet P-40 (Sigma Aldrich), and protease inhibitor cocktail (Complete mini, Roche)) 36h after seeding. 15μg of total protein for each sample was run through a 4–15% Tris-HCL gel (Bio-Rad, Hercules, CA) at 120V for 2h. Then the samples were transferred to 0.2μm PVDF membrane (Bio-Rad). The following primary antibodies were incubated overnight at 4°C: smoothelin (Abcam), Calponin (Santa Cruz Biotechnology, Dallas, TX), Caldesmon (Santa Cruz Biotechnology), and β-actin (Santa Cruz Biotechnology). Protein bands were visualized after 1h incubation in LICOR secondary antibodies on the LICOR Odyssey (LICOR, Lincoln, NE). Image Studio Lite Version 3.1 was used to quantify protein amounts via densitometry. Each protein band value was normalized to its respective β-actin loading control and then normalized to the 10kPa substrate construct.
2.9 Inhibition of N-cadherin
Tissues were seeded in cell media supplemented with either 10μg/ml neutralizing anti-N-cadherin antibody or 10μg/ml nonimmune mouse immunoglobulin G (Sigma Aldrich) (Lyon et al., 2010). After 12h, tissues were serum starved for 24h in serum free cell media supplemented with 10μg/ml of the respective antibody with which they were initially seeded. VSMC functional contractility for each condition was assessed as described in Methods 2.6 and 2.7. Data was analyzed using two-way ANOVA and Holm-Sidak test.
3 RESULTS
3.1 Tissue Structure
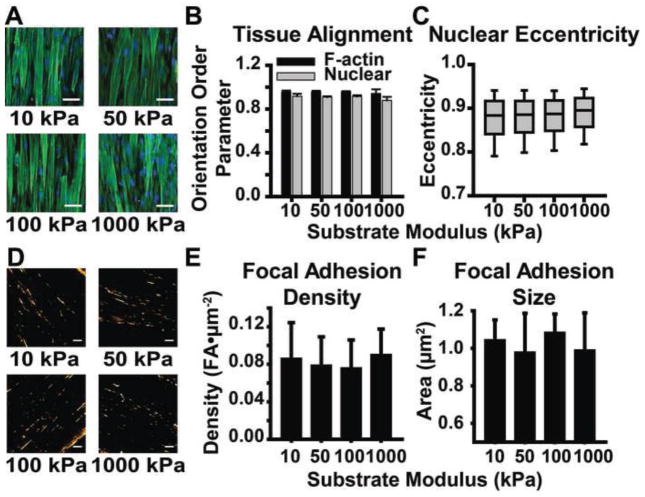
Organization of the actin cytoskeleton (Peyton and Putnam, 2005), focal adhesions (Peyton and Putnam, 2005), and nuclei (Lovett et al., 2013), can be influenced by substrate mechanics. We first asked whether tissue architecture and cellular structure in VSMC-dense lamellar mimics are affected by substrate modulus. Actin and nuclear structure were quantified from immunofluorescent staining (Fig. 4A) to obtain tissue thickness and actin and nuclear orientation order parameter (OOP), as previously described (Alford et al., 2011b). Tissue thickness was unchanged by substrate modulus (4.6±0.06μm, 4.7±0.2μm, 4.8±0.3μm, and 4.7±0.2μm for 10kPa, 50kPa, 100kPa, and 1000kPa modulus substrates, respectively). F-actin and nuclear alignment were independent of substrate modulus, with both showing high alignment for all substrate moduli (Fig. 4B). Nuclear eccentricity, which has previously been shown to correlate with cell contractility (Alford et al., 2011b), was also independent of substrate modulus (Fig. 4C). Focal adhesion plaque density and size were found to be consistent across all substrates (Fig. 4D–F). Taken holistically, tissue architecture was not affected by substrate mechanics.
Figure 4.
Engineered arterial lamella tissue mimic structural characterization. A. Representative images of engineered arterial lamella tissue mimics on each substrate modulus. Scale bar: 50μm. Green: F-actin Blue: Nuclei B. F-actin and nuclear alignment for each substrate modulus. Mean±SD (n = 3) C. Nuclear eccentricity on each substrate modulus. (n = 3) D. Representative images of focal adhesions on each substrate modulus. Scale bar: 10μm. Orange: Paxillin E. Focal adhesion density on each substrate modulus. Mean±SD (n = 3). F. Focal adhesion size on each substrate modulus. Mean±SD (n = 3).
3.2 VSMC Functional Contractility
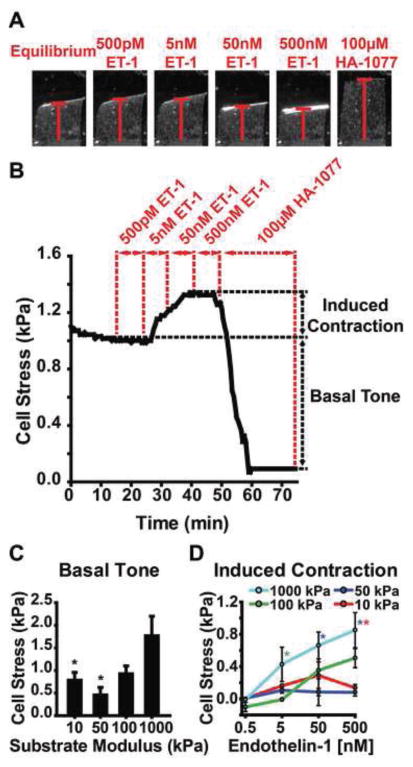
To test the effect of substrate modulus on the functional contractility of VSMCs, we used a variable-modulus vMTF (see Methods for details). Contraction stress generated by the VSMCs bends the PDMS beam (Fig. 5A), and the curvature, obtained from the projection length (Fig. 5A), is used to calculate the stress in the cell layer. In vivo, arteries maintain a homeostatic basal tone allowing them to contract or relax, quickly altering vessel resistance to sustain blood flow and endothelial shear stress (Humphrey, 2002). Changes in both the passive and active pressure-diameter curves have been observed in hypertensive vessels (Cox, 1979; Fridez et al., 2002; Matsumoto and Hayashi, 1994), suggesting functional changes in contractility are indicative of disease initiation and progression. To capture both the basal tone and induced contraction, we serially stimulated the variable-modulus vMTFs with increasing doses of endothelin-1 (ET-1) followed by rho-kinase inhibitor HA-1077 (Fig. 5A). Basal tone was determined from the change in stress between the equilibrated and post-HA-1077-treated VSMCs (Fig. 5B). Induced contraction was determined from the change between the equilibrated VSMCs and the stress at the end of each ET-1 treatment (Fig. 5B).
Figure 5.
VSMC functional contractility increases with increasing substrate modulus. A. Bright field images show corresponding time points of variable modulus vMTF film. Red bar indicates film projection length. B. Representative temporal stress curve for 50kPa film. C. Basal tone for varying substrate moduli. Mean±SEM (n = 18, 12, 21, 20, respectively) p<0.05 compared to 1000kPa. D. Induced contractility for varying substrate moduli. Mean±SEM (n = 18, 13, 17, 14 [n = 20, 13, 21, 20], respectively [n for 50nM]). Significant with respect to substrate modulus with matching asterix color (p<0.05).
Using the variable-modulus vMTFs, we found that basal tone generally increases with increasing substrate modulus. Contraction by VSMCs on 1000kPa modulus substrates was significantly greater than for those on 10kPa and 50kPa substrates (Fig. 5C). ET-1 induced contraction displayed an expected dose-response behavior and, as with basal tone, increased with increasing substrate modulus (Fig. 5D). Tissues constructed on substrates with 1000kPa moduli generated significantly greater stress in response to 500nM ET-1 than those on 10kPa and 50kPa substrates (Fig. 5D). We also measured the maximum cell strain and observed no trend (−0.76±0.08%, −0.52±0.09%, −0.98±0.09%, and −0.76±0.13%, for 10kPa, 50kPa, 100kPa, and 1000kPa, respectively). Overall, we found a distinct relationship between substrate modulus and functional VSMC contractility, such that VSMC tissues cultured on substrates with a higher modulus exhibit increased contractility.
3.3 VSMC Phenotype
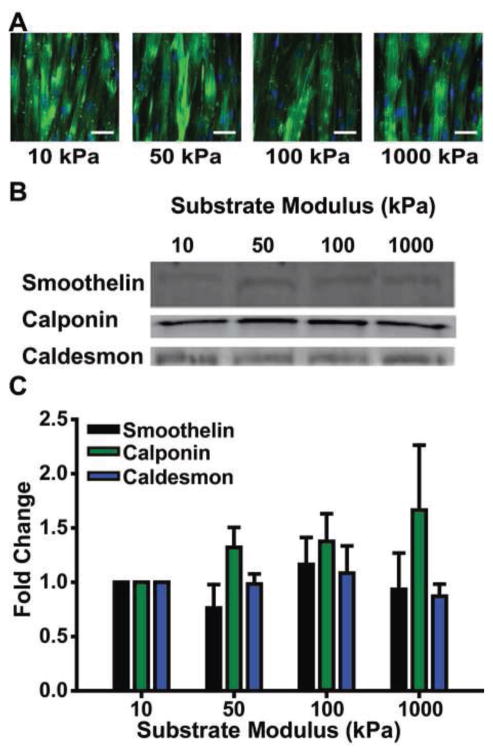
VSMC phenotype modulation can be indicative of vascular dysfunction; for example, VSMCs switch from a contractile to synthetic phenotype in atherosclerosis (Hao et al., 2003; Owens, 1995) and hypertension (Olivetti et al., 1980). VSMC phenotype modulation also occurs in response to mechanical perturbations (Alford et al., 2011a), suggesting that changes in mechanics in these diseases may play a role in the observed phenotype switch. We hypothesized that changes in phenotype expression were responsible for the altered contractility measured using variable-modulus vMTFs. VSMC phenotype is typically assessed by measuring the relative expression of several contractile phenotype protein markers (Rensen et al., 2007). We performed immunofluorescent staining of smooth muscle alpha-actin (Fig. 6A) and Western blots of smoothelin, caldesmon, and calponin (Rensen et al., 2007) in arterial lamella tissue mimics (Fig. 6B). No statistically significant substrate-dependent phenotype expression was observed (Fig. 6C).
Figure 6.
VSMC phenotype is not dependent on substrate modulus. A. Representative images of smooth muscle alpha-actin in engineered arterial lamella tissue mimics on each substrate. Scale bar: 50μm Green: Smooth muscle alpha-actin Blue: Nuclei B. Representative Western blots of contractile phenotype markers; smoothelin, calponin, and caldesmon for VSMC tissues exposed to either a substrate modulus of 10kPa, 50kPa, 100kPa, or 1000kPa. C. Protein expression quantification of contractile phenotype markers for VSMC tissues exposed to either a substrate modulus of 10kPa, 50kPa, 100kPa, 1000kPa. Fold change is with respect to VSMC tissues exposed to a substrate modulus of 10kPa (n = 5, 10, and 3, respectively). Mean±SEM.
3.4 Effect of N-cadherin on Contractility
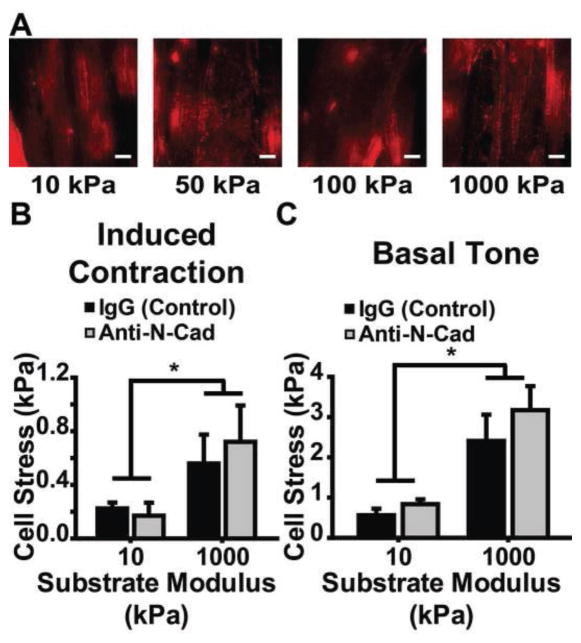
To elucidate the role of cell-cell binding in substrate-dependent VSMC stress-generation, we studied the effect of N-cadherin inhibition on contractility. First, we stained tissues built on each substrate for N-cadherin (Fig. 7A). Next, we used a neutralizing antibody to inhibit N-cadherin binding during tissue formation on 10kPa and 1000kPa substrate vMTFs and tested the VSMC contractility. We found no difference in either the induced contraction or basal tone between the IgG control and the anti-N-cadherin construct for either substrate (Fig. 7B, C) and N-cadherin inhibition did not affect the previously observed increase in contractility for tissues on 1000kPa compared to tissues on 10kPa (Fig. 7B, C). This suggests that N-cadherin-mediated cell-cell binding interactions are not responsible for substrate modulus dependent VSMC contractility.
Figure 7.
Substrate modulus sensitivity of VSMC contractility is not affected by N-cadherin. A. Representative images of N-cadherin for engineered arterial lamella tissue mimics on each substrate. Scale bar: 10μm. Red: N-cadherin B. 50nM ET-1 induced contraction for engineered arterial lamella tissue mimics with either neutralizing anti-N-cadherin or IgG on 10kPa and 1000kPa modulus constructs (n = 11, 12, 13, and 10 for 10kPa IgG, 10kPa anti-N-cadherin, 1000kPa IgG, and 1000kPa anti-N-cadherin, respectively). Mean±SEM. C. Basal tone for engineered arterial lamella tissue mimics with either neutralizing anti-N-cadherin or IgG on 10kPa and 1000kPa modulus constructs (n = 11, 12, 13, and 10 for 10kPa IgG, 10kPa anti-N-cadherin, 1000kPa IgG, and 1000kPa anti-N-cadherin, respectively). Mean±SEM. * = p<0.05.
4 DISCUSSION
Healthy arterial function requires acute dynamic control of the vessel lumen through active contraction and dilation to maintain blood pressure and flow. However, vascular pathologies can perturb vessel mechanics and function. Hypertension leads to arterial wall thickening (Humphrey, 2002), increased stiffness (Matsumoto and Hayashi, 1994; Sharma and Hollis, 1976), and decreased compliance (Armentano et al., 1991). Hypertension rat models exhibit drastic shifts in vessel pressure-diameter curves, indicating a direct connection between mechanical perturbation of the vessel and its functional behavior (Matsumoto and Hayashi, 1994). Notably, when the active and passive vessel behaviors are examined separately, the active stresses rapidly adapt within the first four days, while the passive behavior remains consistent, suggesting that modulation of functional contractility is a key player in vascular mechano-adaptation (Fridez et al., 2002). Macroscopically, atherosclerosis is the stiffening of the arteries (Cecelja and Chowienczyk, 2012; Nabel et al., 1988). However, microscopically, atherosclerotic plaques are heterogeneous and include lipid-dense regions that are much softer than healthy vascular tissue (Loree et al., 1994). A common treatment for atherosclerosis is stenting with metal meshes, which are much stiffer than native tissue, to provide structural support along the vessel wall (Bedoya et al., 2006). One common link between these diseases is a change in the mechanical environment to which VSMCs in the vessel are exposed. Here, we find that in the absence of any other extrinsic factors, the mechanical properties of VSMCs’ extracellular environment directly affect their primary function – contraction.
Substrate modulus affects cell migration (Chan and Odde, 2008; Peyton and Putnam, 2005; Zaari et al., 2004), differentiation (Engler et al., 2006), cytoskeleton organization (Engler et al., 2006; Griffin et al., 2004), and focal adhesion organization (Peyton and Putnam, 2005). In VSMCs, migration (Isenberg et al., 2009; Peyton and Putnam, 2005; Wong et al., 2003), proliferation (McDaniel et al., 2007), and platelet-derived growth factor sensitivity (Brown et al., 2010) are affected by substrate modulus. However, Sazonova et al. (2011) found that substrate stiffness modulates expression of focal adhesion proteins talin, vinculin, and β1-integrin in low density VSMC cultures, but not at high density (Sazonova et al., 2011), demonstrating that there is a fundamental difference between sub-confluent and confluent cultures of VSMCs. Additionally, cell and tissue architecture within dense cultures can also affect VSMC behavior. VSMCs that are patterned into aligned tissues with elongated cell architecture exhibit a more contractile phenotype compared to non-patterned VSMCs (Williams et al., 2011), and cell architecture within a confluent tissue layer affects phenotype expression (Win et al., 2014). Here, we find that VSMC phenotype in an organized confluent layer does not depend on substrate modulus.
The variable-modulus vMTF system shown here provides a novel platform to examine how substrate modulus affects functional contractility in confluent, aligned, in vivo-like VSMCs. And our finding of increased contraction with increasing substrate modulus at the tissue scale reinforces substrate-dependent single cell traction previously reported (Califano and Reinhart-King, 2010; Lo et al., 2000; Oakes et al., 2014). Our technique is versatile, as the variable substrate modulus can be tuned to mimic both pathological and physiological mechanical environments present in vascular disease and could be expanded to other polymers as well (McCain et al., 2014). Notably, we found increased contraction in tissues constructed on stiffer substrates in the absence of phenotype switching or structural reorganization. This result is consistent with a number of whole artery findings. Cox found that in the normal physiological range, muscular arteries (renal, internal thoracic, iliac, and mesenteric artery) have higher incremental moduli than does the elastic carotid artery (Cox, 1978a). He further showed that the muscular arteries generate a maximum contractile stress twice that of the carotid artery (Cox, 1978b). Fridez et al. (2002) found that in the first four days following induced hypertension, VSMC contractility significantly increases. This is notable because, due to the exponential-like stress-strain behavior of the passive vessel, hypertension increases the incremental modulus of the VSMCs’ surroundings in the early state of remodeling. Our results suggest that these phenomena are linked to VSMC functional adaptation in response to extracellular mechanical properties.
Tissue growth and remodeling play important roles in maintenance of vascular integrity. A finer understanding of how vascular tissues adapt in response to stimuli could facilitate patient-specific models of vascular disease (Ionasec et al., 2010; Kuhl et al., 2007; Taylor and Figueroa, 2009; Werner et al., 2009). Current models consider how extracellular matrix remodeling affects global vessel properties, but not how it affects VSMC function (Alford et al., 2008; Alford and Taber, 2008; Gleason et al., 2004; Schmid et al., 2010). Our results suggest that VSMC function is dynamic and may change both temporally and spatially in response to changes in extracellular matrix mechanics, suggesting that artery growth and remodeling models need to account for extracellular mechanics-induced VSMC functional changes to accurately model diseased tissue. Finally, a goal of tissue engineering is development of small artery vascular replacements (Conte, 1998). Mechanical environment, as influenced by scaffold material selection, is an important factor to produce functional engineered blood vessels (Grassl et al., 2002; Huang and Niklason, 2014; Syedain et al., 2014). Our results suggest that scaffold properties are important not only for vessel integrity, but for healthy VSMC functional behavior.
Supplementary Material
Residual stress in the variable modulus vMTF due to different fabrication methods. A. Film curvature that develops due to thermal mismatch between the two layers. B. Film curvature that develops due to chemical interactions between the two different Sylgard polymer recipes (184 and 527) that interface between the two layers. C. Film curvature the develops when the construct is fabricated inverted, such that the layer two is cured first and then layer one.
Acknowledgments
We gratefully acknowledge our funding sources (NIH 1R03EB016969-01 (PWA) and AHA 15PRE21790000 (KES)), the fabrication resources at the Minnesota Nano Center (MNC), and image processing resources at the University of Minnesota University Imaging Centers (UIC). Parts of this work were carried out in the Characterization Facility, University of Minnesota, a member of the NSF-funded Materials Research Facilities Network via the MRSEC program.
Footnotes
CONFLICT OF INTEREST STATEMENT
We certify that there is no conflict of interest with any financial organization regarding the material discussed in the manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alford P, Humphrey J, Taber L. Growth and remodeling in a thick-walled artery model: effects of spatial variations in wall constituents. Biomechanics and Modeling in Mechanobiology. 2008;7:245–262. doi: 10.1007/s10237-007-0101-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alford PW, Dabiri BE, Goss JA, Hemphill MA, Brigham MD, Parker KK. Blast-induced phenotypic switching in cerebral vasospasm. Proceedings of the National Academy of Sciences. 2011a;108:12705–12710. doi: 10.1073/pnas.1105860108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alford PW, Feinberg AW, Sheehy SP, Parker KK. Biohybrid thin films for measuring contractility in engineered cardiovascular muscle. Biomaterials. 2010;31:3613–3621. doi: 10.1016/j.biomaterials.2010.01.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alford PW, Nesmith AP, Seywerd JN, Grosberg A, Parker KK. Vascular smooth muscle contractility depends on cell shape. Integr Biol (Camb) 2011b;3:1063–1070. doi: 10.1039/c1ib00061f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alford PW, Taber LA. Computational study of growth and remodelling in the aortic arch. Computer Methods in Biomechanics and Biomedical Engineering. 2008;11:525–538. doi: 10.1080/10255840801930710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armentano R, Simon A, Levenson J, Chau NP, Megnien JL, Pichel R. Mechanical pressure versus intrinsic effects of hypertension on large arteries in humans. Hypertension. 1991;18:657–664. doi: 10.1161/01.hyp.18.5.657. [DOI] [PubMed] [Google Scholar]
- Bedoya J, Meyer CA, Timmins LH, Moreno MR, Moore JJE. Effects of Stent Design Parameters on Normal Artery Wall Mechanics. Journal of Biomechanical Engineering. 2006;128:757–765. doi: 10.1115/1.2246236. [DOI] [PubMed] [Google Scholar]
- Brown XQ, Bartolak-Suki E, Williams C, Walker ML, Weaver VM, Wong JY. Effect of substrate stiffness and PDGF on the behavior of vascular smooth muscle cells: implications for atherosclerosis. Journal of cellular physiology. 2010;225:115–122. doi: 10.1002/jcp.22202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown XQ, Ookawa K, Wong JY. Evaluation of polydimethylsiloxane scaffolds with physiologically-relevant elastic moduli: interplay of substrate mechanics and surface chemistry effects on vascular smooth muscle cell response. Biomaterials. 2005;26:3123–3129. doi: 10.1016/j.biomaterials.2004.08.009. [DOI] [PubMed] [Google Scholar]
- Califano JP, Reinhart-King CA. Substrate Stiffness and Cell Area Predict Cellular Traction Stresses in Single Cells and Cells in Contact. Cell Mol Bioeng. 2010;3:68–75. doi: 10.1007/s12195-010-0102-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao Y, Poon YF, Feng J, Rayatpisheh S, Chan V, Chan-Park MB. Regulating orientation and phenotype of primary vascular smooth muscle cells by biodegradable films patterned with arrays of microchannels and discontinuous microwalls. Biomaterials. 2010;31:6228–6238. doi: 10.1016/j.biomaterials.2010.04.059. [DOI] [PubMed] [Google Scholar]
- Cecelja M, Chowienczyk P. Role of arterial stiffness in cardiovascular disease. JRSM Cardiovascular Disease. 2012;1 doi: 10.1258/cvd.2012.012016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chamley-Campbell J, Campbell GR, Ross R. The smooth muscle cell in culture. Physiol Rev. 1979;59:1–61. doi: 10.1152/physrev.1979.59.1.1. [DOI] [PubMed] [Google Scholar]
- Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- Conte MS. The ideal small arterial substitute: a search for the Holy Grail? FASEB J. 1998;12:43–45. doi: 10.1096/fasebj.12.1.43. [DOI] [PubMed] [Google Scholar]
- Cox RH. Passive mechanics and connective tissue composition of canine arteries. Am J Physiol. 1978a;234:H533–541. doi: 10.1152/ajpheart.1978.234.5.H533. [DOI] [PubMed] [Google Scholar]
- Cox RH. Regional variation of series elasticity in canine arterial smooth muscles. Am J Physiol. 1978b;234:H542–551. doi: 10.1152/ajpheart.1978.234.5.H542. [DOI] [PubMed] [Google Scholar]
- Cox RH. Comparison of arterial wall mechanics in normotensive and spontaneously hypertensive rats. American Journal of Physiology - Heart and Circulatory Physiology. 1979;237:H159–H167. doi: 10.1152/ajpheart.1979.237.2.H159. [DOI] [PubMed] [Google Scholar]
- Coyer SR, Singh A, Dumbauld DW, Calderwood DA, Craig SW, Delamarche E, Garcia AJ. Nanopatterning reveals an ECM area threshold for focal adhesion assembly and force transmission that is regulated by integrin activation and cytoskeleton tension. J Cell Sci. 2012;125:5110–5123. doi: 10.1242/jcs.108035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Discher DE, Janmey P, Wang Y-l. Tissue Cells Feel and Respond to the Stiffness of Their Substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix Elasticity Directs Stem Cell Lineage Specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- Fridez P, Makino A, Kakoi D, Miyazaki H, Meister JJ, Hayashi K, Stergiopulos N. Adaptation of conduit artery vascular smooth muscle tone to induced hypertension. Ann Biomed Eng. 2002;30:905–916. doi: 10.1114/1.1507326. [DOI] [PubMed] [Google Scholar]
- Fu J, Wang YK, Yang MT, Desai RA, Yu X, Liu Z, Chen CS. Mechanical regulation of cell function with geometrically modulated elastomeric substrates. Nat Methods. 2010;7:733–736. doi: 10.1038/nmeth.1487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung YC. Biomechanics: Mechanical Properties of Living Tissues. 2. Springer Science and Business Media; New York, NY: 2004. [Google Scholar]
- Gleason RL, Taber LA, Humphrey JD. A 2-D model of flow-induced alterations in the geometry, structure, and properties of carotid arteries. J Biomech Eng. 2004;126:371–381. doi: 10.1115/1.1762899. [DOI] [PubMed] [Google Scholar]
- Grassl ED, Oegema TR, Tranquillo RT. J Biomed Mater Res. Vol. 60. Wiley Periodicals, Inc; United States: 2002. Fibrin as an alternative biopolymer to type-I collagen for the fabrication of a media equivalent; pp. 607–612. [DOI] [PubMed] [Google Scholar]
- Griffin MA, Sen S, Sweeney HL, Discher DE. Adhesion-contractile balance in myocyte differentiation. Journal of Cell Science. 2004;117:5855–5863. doi: 10.1242/jcs.01496. [DOI] [PubMed] [Google Scholar]
- Hald ES, Steucke KE, Reeves JA, Win Z, Alford PW. Long-term vascular contractility assay using genipin-modified muscular thin films. Biofabrication. 2014;6:045005. doi: 10.1088/1758-5082/6/4/045005. [DOI] [PubMed] [Google Scholar]
- Hald ES, Steucke KE, Reeves JA, Win Z, Alford PW. Microfluidic Genipin Deposition Technique for Extended Culture of Micropatterned Vascular Muscular Thin Films. 2015:e52971. doi: 10.3791/52971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han M, Wen JK, Zheng B, Cheng Y, Zhang C. Serum deprivation results in redifferentiation of human umbilical vascular smooth muscle cells. Am J Physiol Cell Physiol. 2006;291:C50–58. doi: 10.1152/ajpcell.00524.2005. [DOI] [PubMed] [Google Scholar]
- Hao H, Gabbiani G, Bochaton-Piallat ML. Arterial Smooth Muscle Cell Heterogeneity: Implications for Atherosclerosis and Restenosis Development. Arteriosclerosis, Thrombosis, and Vascular Biology. 2003;23:1510–1520. doi: 10.1161/01.ATV.0000090130.85752.ED. [DOI] [PubMed] [Google Scholar]
- Huang A, Niklason L. Engineering of arteries in vitro. Cellular and Molecular Life Sciences. 2014;71:2103–2118. doi: 10.1007/s00018-013-1546-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer-Verlag; New York: 2002. [Google Scholar]
- Ionasec RI, Voigt I, Georgescu B, Wang Y, Houle H, Vega-Higuera F, Navab N, Comaniciu D. Patient-specific modeling and quantification of the aortic and mitral valves from 4-D cardiac CT and TEE. Medical Imaging, IEEE Transactions on. 2010;29:1636–1651. doi: 10.1109/TMI.2010.2048756. [DOI] [PubMed] [Google Scholar]
- Isenberg BC, DiMilla PA, Walker M, Kim S, Wong JY. Vascular Smooth Muscle Cell Durotaxis Depends on Substrate Stiffness Gradient Strength. Biophysical Journal. 2009;97:1313–1322. doi: 10.1016/j.bpj.2009.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim DH, Wirtz D. Focal adhesion size uniquely predicts cell migration. Faseb j. 2013;27:1351–1361. doi: 10.1096/fj.12-220160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein EA, Yin L, Kothapalli D, Castagnino P, Byfield FJ, Xu T, Levental I, Hawthorne E, Janmey PA, Assoian RK. Cell-cycle control by physiological matrix elasticity and in vivo tissue stiffening. Curr Biol. 2009;19:1511–1518. doi: 10.1016/j.cub.2009.07.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhl E, Maas R, Himpel G, Menzel A. Computational modeling of arterial wall growth. Attempts towards patient-specific simulations based on computer tomography. Biomech Model Mechanobiol. 2007;6:321–331. doi: 10.1007/s10237-006-0062-x. [DOI] [PubMed] [Google Scholar]
- Lee RT, Grodzinsky AJ, Frank EH, Kamm RD, Schoen FJ. Structure-dependent dynamic mechanical behavior of fibrous caps from human atherosclerotic plaques. Circulation. 1991;83:1764–1770. doi: 10.1161/01.cir.83.5.1764. [DOI] [PubMed] [Google Scholar]
- Lo CM, Wang HB, Dembo M, Wang Y-l. Cell Movement Is Guided by the Rigidity of the Substrate. Biophysical Journal. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loree HM, Tobias BJ, Gibson LJ, Kamm RD, Small DM, Lee RT. Mechanical properties of model atherosclerotic lesion lipid pools. Arterioscler Thromb. 1994;14:230–234. doi: 10.1161/01.atv.14.2.230. [DOI] [PubMed] [Google Scholar]
- Lovett DB, Shekhar N, Nickerson JA, Roux KJ, Lele TP. Modulation of nuclear shape by substrate rigidity. Cellular and molecular bioengineering. 2013;6:230–238. doi: 10.1007/s12195-013-0270-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyon CA, Koutsouki E, Aguilera CM, Blaschuk OW, George SJ. Inhibition of N-cadherin retards smooth muscle cell migration and intimal thickening via induction of apoptosis. J Vasc Surg. 2010;52:1301–1309. doi: 10.1016/j.jvs.2010.05.096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto T, Hayashi K. Mechanical and dimensional adaptation of rat aorta to hypertension. Journal of biomechanical engineering. 1994;116:278–283. doi: 10.1115/1.2895731. [DOI] [PubMed] [Google Scholar]
- McCain ML, Agarwal A, Nesmith HW, Nesmith AP, Parker KK. Micromolded gelatin hydrogels for extended culture of engineered cardiac tissues. Biomaterials. 2014;35:5462–5471. doi: 10.1016/j.biomaterials.2014.03.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDaniel DP, Shaw GA, Elliott JT, Bhadriraju K, Meuse C, Chung KH, Plant AL. The stiffness of collagen fibrils influences vascular smooth muscle cell phenotype. Biophys J. 2007;92:1759–1769. doi: 10.1529/biophysj.106.089003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munevar S, Wang Y-l, Dembo M. Traction Force Microscopy of Migrating Normal and H-ras Transformed 3T3 Fibroblasts. Biophysical Journal. 2001;80:1744–1757. doi: 10.1016/s0006-3495(01)76145-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nabel EG, Ganz P, Gordon JB, Alexander RW, Selwyn AP. Dilation of normal and constriction of atherosclerotic coronary arteries caused by the cold pressor test. Circulation. 1988;77:43–52. doi: 10.1161/01.cir.77.1.43. [DOI] [PubMed] [Google Scholar]
- Oakes PW, Banerjee S, Marchetti MC, Gardel ML. Geometry regulates traction stresses in adherent cells. Biophys J. 2014;107:825–833. doi: 10.1016/j.bpj.2014.06.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olivetti G, Anversa P, Melissari M, Loud AV. Morphometry of medial hypertrophy in the rat thoracic aorta. Lab Invest. 1980;42:559–565. [PubMed] [Google Scholar]
- Ooshima A, Fuller GC, Cardinale GJ, Spector S, Udenfriend S. Increased collagen synthesis in blood vessels of hypertensive rats and its reversal by antihypertensive agents. Proc Natl Acad Sci U S A. 1974;71:3019–3023. doi: 10.1073/pnas.71.8.3019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Owens GK. Regulation of differentiation of vascular smooth muscle cells. Physiological Reviews. 1995;75:487–517. doi: 10.1152/physrev.1995.75.3.487. [DOI] [PubMed] [Google Scholar]
- Owens GK, Kumar MS, Wamhoff BR. Molecular regulation of vascular smooth muscle cell differentiation in development and disease. Physiol Rev. 2004;84:767–801. doi: 10.1152/physrev.00041.2003. [DOI] [PubMed] [Google Scholar]
- Peyton SR, Putnam AJ. Extracellular matrix rigidity governs smooth muscle cell motility in a biphasic fashion. J Cell Physiol. 2005;204:198–209. doi: 10.1002/jcp.20274. [DOI] [PubMed] [Google Scholar]
- Ramasubramanian A, Taber LA. Computational modeling of morphogenesis regulated by mechanical feedback. Biomech Model Mechanobiol. 2008;7:77–91. doi: 10.1007/s10237-007-0077-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rensen SS, Doevendans PA, van Eys GJ. Regulation and characteristics of vascular smooth muscle cell phenotypic diversity. Neth Heart J. 2007;15:100–108. doi: 10.1007/BF03085963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodriguez EK, Hoger A, McCulloch AD. Stress-dependent finite growth in soft elastic tissues. Journal of Biomechanics. 1994;27:455–467. doi: 10.1016/0021-9290(94)90021-3. [DOI] [PubMed] [Google Scholar]
- Sazonova Olga V, Lee Kristen L, Isenberg Brett C, Rich Celeste B, Nugent Matthew A, Wong Joyce Y. Cell-Cell Interactions Mediate the Response of Vascular Smooth Muscle Cells to Substrate Stiffness. Biophysical Journal. 2011;101:622–630. doi: 10.1016/j.bpj.2011.06.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmid H, Watton PN, Maurer MM, Wimmer J, Winkler P, Wang YK, Rohrle O, Itskov M. Impact of transmural heterogeneities on arterial adaptation: application to aneurysm formation. Biomech Model Mechanobiol. 2010;9:295–315. doi: 10.1007/s10237-009-0177-y. [DOI] [PubMed] [Google Scholar]
- Sharma MG, Hollis TM. Rheological properties of arteries under normal and experimental hypertension conditions. Journal of Biomechanics. 1976;9:293–300. doi: 10.1016/0021-9290(76)90051-8. [DOI] [PubMed] [Google Scholar]
- Syedain ZH, Meier LA, Lahti MT, Johnson SL, Tranquillo RT. Implantation of completely biological engineered grafts following decellularization into the sheep femoral artery. Tissue Eng Part A. 2014;20:1726–1734. doi: 10.1089/ten.tea.2013.0550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan JL, Tien J, Pirone DM, Gray DS, Bhadriraju K, Chen CS. Cells lying on a bed of microneedles: An approach to isolate mechanical force. Proceedings of the National Academy of Sciences. 2003;100:1484–1489. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor CA, Figueroa CA. Patient-specific modeling of cardiovascular mechanics. Annu Rev Biomed Eng. 2009;11:109–134. doi: 10.1146/annurev.bioeng.10.061807.160521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ting LH, Jahn JR, Jung JI, Shuman BR, Feghhi S, Han SJ, Rodriguez ML, Sniadecki NJ. Flow mechanotransduction regulates traction forces, intercellular forces, and adherens junctions. Am J Physiol Heart Circ Physiol. 2012;302:H2220–2229. doi: 10.1152/ajpheart.00975.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werner R, Ehrhardt J, Schmidt R, Handels H. Patient-specific finite element modeling of respiratory lung motion using 4D CT image data. Med Phys. 2009;36:1500–1511. doi: 10.1118/1.3101820. [DOI] [PubMed] [Google Scholar]
- Williams C, Brown XQ, Bartolak-Suki E, Ma H, Chilkoti A, Wong JY. The use of micropatterning to control smooth muscle myosin heavy chain expression and limit the response to transforming growth factor β1 in vascular smooth muscle cells. Biomaterials. 2011;32:410–418. doi: 10.1016/j.biomaterials.2010.08.105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Win Z, Vrla GD, Steucke KE, Sevcik EN, Hald ES, Alford PW. Smooth muscle architecture within cell-dense vascular tissues influences functional contractility. Integr Biol (Camb) 2014;6:1201–1210. doi: 10.1039/c4ib00193a. [DOI] [PubMed] [Google Scholar]
- Wong JY, Velasco A, Rajagopalan P, Pham Q. Directed Movement of Vascular Smooth Muscle Cells on Gradient-Compliant Hydrogels†. Langmuir. 2003;19:1908–1913. [Google Scholar]
- Zaari N, Rajagopalan P, Kim SK, Engler AJ. Photopolymerization in Microfluidic Gradient Generators: Microscale Control of Substrate Compliance to Maniupulate Cell Response. Advanced Materials. 2004;16:2133–2137. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Residual stress in the variable modulus vMTF due to different fabrication methods. A. Film curvature that develops due to thermal mismatch between the two layers. B. Film curvature that develops due to chemical interactions between the two different Sylgard polymer recipes (184 and 527) that interface between the two layers. C. Film curvature the develops when the construct is fabricated inverted, such that the layer two is cured first and then layer one.