Abstract
This work describes methodology for evaluating laboratory models of head impact biomechanics. Using this methodology, we investigated: how closely does twin-wire drop testing model head rotation in American football impacts? Head rotation is believed to cause mild traumatic brain injury (mTBI) but helmet safety standards only model head translations believed to cause severe TBI. It is unknown whether laboratory head impact models in safety standards, like twin-wire drop testing, reproduce six degree-of-freedom (6DOF) head impact biomechanics that may cause mTBI. We compared 6DOF measurements of 421 American football head impacts to twin-wire drop tests at impact sites and velocities weighted to represent typical field exposure. The highest rotational velocities produced by drop testing were the 74th percentile of non-injury field impacts. For a given translational acceleration level, drop testing underestimated field rotational acceleration by 46% and rotational velocity by 72%. Primary rotational acceleration frequencies were much larger in drop tests (~100Hz) than field impacts (~10Hz). Drop testing was physically unable to produce acceleration directions common in field impacts. Initial conditions of a single field impact were highly resolved in stereo high-speed video and reconstructed in a drop test. Reconstruction results reflected aggregate trends of lower amplitude rotational velocity and higher frequency rotational acceleration in drop testing, apparently due to twin-wire constraints and the absence of a neck. These results suggest twin-wire drop testing is limited in modeling head rotation during impact, and motivate continued evaluation of head impact models to ensure helmets are tested under conditions that may cause mTBI.
Key terms: Mild traumatic brain injury (mTBI), six degree of freedom kinematics, twin-wire drop testing, head impact model, rotational acceleration and velocity
INTRODUCTION
Of the 2–4 million sports-related mild traumatic brain injuries (mTBI) in the U.S. each year, over half occur in football (Gessel et al., 2007; Langlois et al., 2006; Lincoln et al., 2011). Football helmets are worn to mitigate the risk of injury, but their purpose, function, and efficacy are the source of much debate. Some studies suggest modern helmets may not protect against mTBI better than helmets developed 20–80 years prior (Bartsch et al., 2012; Cantu et al., 2012; Rowson et al., 2013; Viano et al., 2012). This controversy has motivated the question: are helmets effective in conditions that cause mTBI?
Rapid head rotation is thought to cause mTBI by shearing brain tissue and straining axons in tension (Gennarelli et al., 1998; Giordano and Kleiven, 2014; Holbourn, 1943). In primates, translational acceleration induced traumatic coma only when combined with rotational acceleration (Ommaya and Gennarelli, 1974). Animal, physical, analytic, and finite element models found that the severity and direction of head rotation was commensurate with traumatic coma, neurological impairment, tissue strain, and diffuse axonal pathology (Gennarelli et al., 1982; Kleiven, 2006; Margulies et al., 1990; Margulies and Thubault, 1992; Smith et al., 2000). These findings have motivated direct measurement of human head rotation during head impact (Bartsch and Samorezov, 2013; Camarillo et al., 2013; Rowson et al., 2011) and the development of criteria to predict mTBI using rotation measurements (Newman, 1986; Newman et al., 2000b; Ommaya and Hirsch, 1971). In a field study of football mTBI (Hernandez et al., 2014), criteria that used rotation measurements predicted injury better than the translation-only criteria used in safety standards (Gadd, 1966; Versace, 1971).
Despite studies implicating rotation in mTBI, helmet safety testing may not model head rotation in football head impacts. For 40 years, helmet safety standards defined by the National Operating Committee on Standards for Athletic Equipment (NOCSAE) (NOCSAE, 2012a,b) have used a drop test that was developed to reproduce severe TBI conditions commensurate with head translational acceleration (Gurdjian et al., 1953, 1966). However, laboratory drop testing has been used to model mTBI risk, as in the STAR rating system (King, 2012; Rowson and Duma, 2011, 2012) and other recent helmet efficacy studies (Forbes et al., 2013; Johnston et al., 2014; Rowson et al., 2013). Although drop testing suitably models the frequency characteristics of translational acceleration in football head impacts (Gwin et al., 2010), drop testing and other laboratory models such as horizontal linear impacting (Camarillo et al., 2013; NOCSAE, 2006; Rowson et al., 2011; Viano et al., 201) and pendulum testing (Bartsch et al., 2012; Pellman et al., 2003), have not been demonstrated to reproduce human head rotation in football head impacts because no such methodology exists.
Our objective was two-fold: (a) describe methodology for evaluating laboratory head impact models using field measurements, and (b) use this methodology to investigate the degree to which laboratory twin-wire drop tests model human head rotation in American football head impacts. To that end, we compared six degree of freedom (6DOF) measurements of football head impacts to drop tests performed at typical impact sites and velocities. Using stereo high speed video, we compared 6DOF measurements of a single football head impact to a drop test reconstruction.
MATERIALS AND METHODS
Field measurements
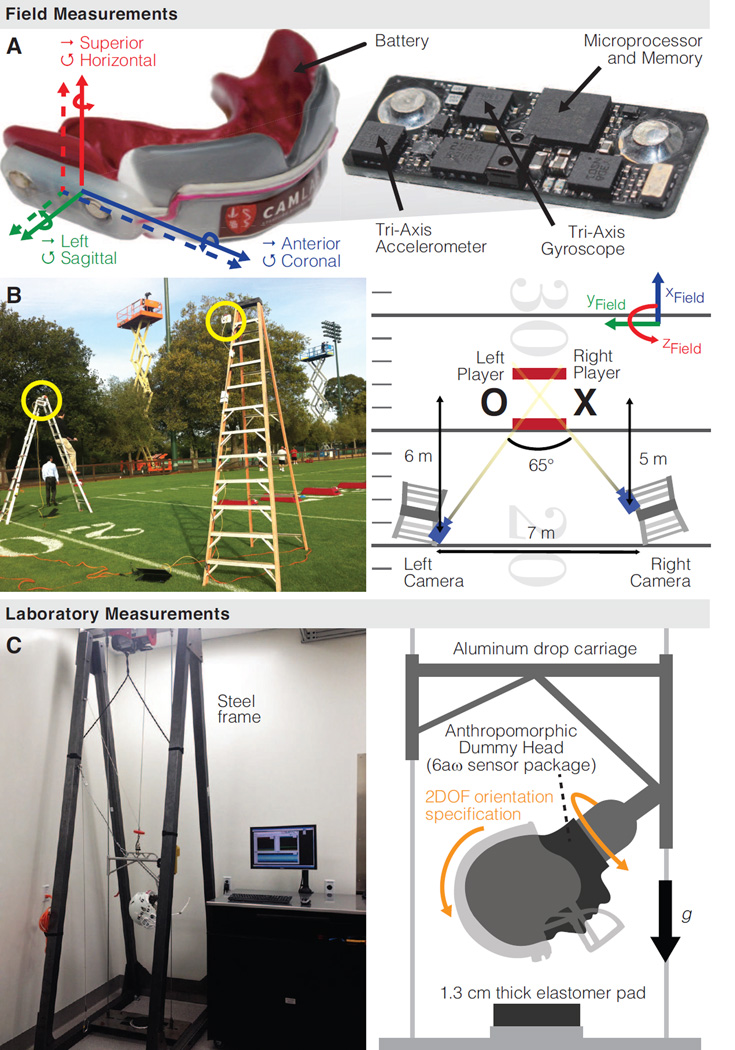
We measured 421 American football (video-confirmed) head impacts in 6DOF using instrumented mouthguards (Fig. 1A) (Hernandez et al., 2014). These head impacts were collected from 30 collegiate football players over 15 games and practices of varying intensity (66 total athlete-events). Of these head impacts, two resulted in the diagnosis of mTBI by a sideline clinician: one loss of consciousness (LOC) injury, and one self-reported injury. Human subjects protocols were approved by the Stanford Institutional Review Board (IRB No. 21304). All head impacts were confirmed in video as player head contact with another head, body, or ground. The kinematic accuracy of the instrumented mouthguards was previously characterized in laboratory testing (Camarillo et al., 2013; Hernandez et al., 2014).
Figure 1. Field and laboratory data collection.
(A) Custom-fit mouthguards measured head impacts in full six degree of freedom (6DOF) using a tri-axis accelerometer and tri-axis gyroscope. (B) stereo high speed video cameras were 7 m apart, 3.5 m elevated above the field, at a 5–6 m down-field distance from the impact, and formed a 65° triangulation angle. (C) Twin-wire drop test and anthropomorphic dummy head
To understand aggregate field trends, we reconstructed a single head impact that was measured in high resolution on the drop test. Stereo high speed video of a single in vivo head impact was collected to estimate initial impact conditions (impact location on helmet and relative impact speed) that were used to set up a laboratory reconstruction of the impact. As part of a routine football practice drill, two players lined up approximately 3 m apart and engaged in head-to-head contact following an auditory cue. The drill was filmed with two high definition, high speed cameras (Phantom Miro LC-320S, Vision Research, Wayne, NJ) in 1920 × 1080 resolution at 2500 frames s−1. The cameras were configured in a stereo setup on two ladders (Fig. 1B).
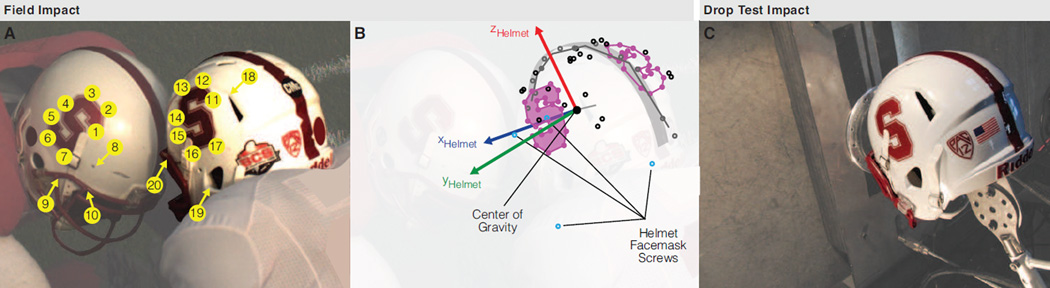
To estimate the orientation and velocity of the players’ helmets at impact, we tracked fiducial markers in stereo video and resolved helmet motion in three-dimensional (3D) space (Fig. 2A). We used the Camera Calibration Toolbox for MATLAB (California Institute of Technology, CA)(Heikkila and Silven, 1997; Zhang and Way, 1999) to triangulate the 3D position of each fiducial marker in a field-fixed reference frame using a 23×17 calibration grid of 50.8 mm squares (Fig. 2B). We also digitized the 3D position of the fiducial markers in a helmetfixed reference frame (FaroArm, FARO Technologies, Coventry, United Kingdom) (Fig. 2B). Assuming the video-tracked points are related by this helmet-fixed (rigid body) frame, we determined the rotation of each helmet in the field-fixed frame using a least-squares optimization (Horn et al., 1988). In the helmet and field frames, we computed the mean velocity of all 10 points on the helmet in the 10 frames (4 ms) before helmet contact. The difference between the helmet velocity vectors was used to determine the relative impact speed and orientation.
Figure 2. Head impact reconstruction setup.
(A) 2D pixel location of 20 fiducial markers (10 on each helmet) were tracked in stereo high speed video to resolve (B) the position, orientation, and velocity of a helmet-fixed reference frame for each player. In the camera reference frame, video tracking and stereo triangulation produced average x-y-z errors of [1, 1.5, 1] mm in tracking fiducial marker locations, over the 10 frames/4 ms before helmet contact, with respect to their (true) digitized locations. (C) Drop test reconstruction was set to match initial conditions for the player in the right. From the available discrete head orientations in twin-wire drop testing (Fig. 1C), the closest helmet impact location was within 5 cm of the impact location in the field. In the field frame, the x-y-z translational velocity of the player’s helmet was [0.3, 0.8, −1.3] m/s while the velocity of the opposing player’s helmet was [−0.3, −1.4, −0.3] m/s. The magnitude of the vector difference between these values (2.4 m/s) corresponded to the relative impact speed of the players and was reconstructed by a 0.3 m drop. Due to physical limitations of twin-wire drop testing, reconstructing the helmet contact location produced a velocity orientation error of 28°
Laboratory measurements
Laboratory testing was performed on a twin-wire drop test (Fig. 1C) similar to that used by NOCSAE (NOCSAE, 2012b). The drop test is a 3DOF system consisting of an aluminum drop carriage that slides along taut twin wires: 2 discrete DOF for orientation (sagittal and horizontal) of a dummy head attached to the drop carriage and 1 continuous DOF for the height from which the dummy head is dropped onto a 1.3 cm thick elastomer pad. The anthropomorphic dummy head was instrumented with a 6aω sensor package (six accelerometers and three gyroscopes)(Kang et al., 2011) recording at 10 kHz, and has been used in previous laboratory studies (Camarillo et al., 2013; Hernandez et al., 2014).
To compare with aggregate field data, drop tests were weighted to represent typical field exposure according to impact location and drop heights defined by the STAR helmet rating protocol (Rowson and Duma, 2011) (Table 1). STAR exposure was grouped into four impact locations that match site definitions described in the NOCSAE helmet standard (NOCSAE, 2012a) and those used here. Five drop heights were selected to approximate the heights specified in the STAR protocol; 0.61 and 1.52 m are also equivalent to the minimum and maximum drop heights specified by the NOCSAE helmet standard. Five tests were performed at each combination of impact location and drop height (100 tests total) (Table 1). Exposure frequency was calculated for individual impact locations and drop heights using distribution functions defined by the STAR study. These represent the frequency of a given impact location and severity (correlated with drop height) per 1000 impacts (Rowson and Duma, 2011).
Table 1. Drop testing and field exposure weighting.
Five tests were performed at each drop height/impact location. Each impact was weighted (duplicated) n times, where n equals typical field exposure per 1000 head impacts (Rowson and Duma, 2011)
| Drop Height (m) |
Field exposure per 1000 impacts by drop location and height (# tests) | ||||
|---|---|---|---|---|---|
| Front | Rear | Side | Top | Total | |
| 0.20 | 268 (5) | 281 (5) | 150 (5) | 132 (5) | 831 (20) |
| 0.41 | 42 (5) | 27 (5) | 8 (5) | 20 (5) | 97 (20) |
| 0.61 | 23 (5) | 8 (5) | 3 (5) | 10 (5) | 44 (20) |
| 0.91 | 9 (5) | 2 (5) | 1 (5) | 4 (5) | 16 (20) |
| 1.52 | 5 (5) | 1 (5) | 1 (5) | 5 (5) | 12 (20) |
| Total | 347 (25) | 319 (25) | 163 (25) | 171 (25) | 1000 (100) |
An additional drop test was performed to reconstruct the single in vivo head impact measured in stereo high speed video during a football drill. The dummy head was attached to the drop carriage so that the impact location approximated the impact location on the helmet of the player in the right in the field video (Fig. 2A,C). The drop height was selected to match the magnitude of the relative impact velocity of the helmets in the field. High speed video of the laboratory reconstruction was collected for comparison with high speed video of the field impact.
Data analysis
We compared head biomechanics in field and laboratory impacts using kinematic mTBI criteria as defined by Hernandez et al. (2014). The mouthguards measured 6DOF kinematics 10 ms before the acceleration trigger and 90 ms after; over this period, we computed two 3DOF translation-only criteria (peak translational acceleration, and Severity Index (SI) (Gadd, 1966)), two 3DOF rotation-only criteria (peak rotational acceleration and peak rotational velocity), and two 6DOF translation and rotation criteria (Head Impact Power (HIP) (Newman et al., 2000b), and Generalized Acceleration Model of Brain Injury (GAMBIT)(Newman, 1986)). Peak acceleration and velocity were given by the largest observed value in each vector magnitude (L2-norm). SI is the criteria used by NOCSAE to certify helmets (NOCSAE, 2012b). HIP and GAMBIT were two of the strongest predictors of human mTBI among 18 mTBI criteria (Hernandez et al., 2014).
Since acceleration duration has been implicated in mTBI, we compared the frequency content of field and laboratory impacts. For each impact, we computed the power spectral density (PSD) using a Fast Fourier Transform (FFT) normalized to span [0,1], of each component of translational acceleration, rotational acceleration, and rotational velocity to identify the primary frequency content. For performing FFT, field data was zero-padded to match the 1 Hz resolution of laboratory data, which had 10× higher sampling rate. To compare aggregate distributions of frequency content independent of signal amplitude (e.g. initial velocity, drop height, etc.), we computed the mean of the normalized PSDs across all field impacts and weighted drop tests.
Statistical analyses were performed to compare the likeness of field and laboratory impacts. A 1D two-sample Kolmogorov-Smirnov (KS) test was performed to compare histogram shape and location of field and laboratory kinematic criteria data, with a low p-value indicating field and laboratory samples significantly differ and are likely to originate from different 1D distributions. For pairs of peak kinematic measurements, we compared the overlap of field and laboratory distributions using a 2D two-sample KS test.
RESULTS
Aggregate distributions
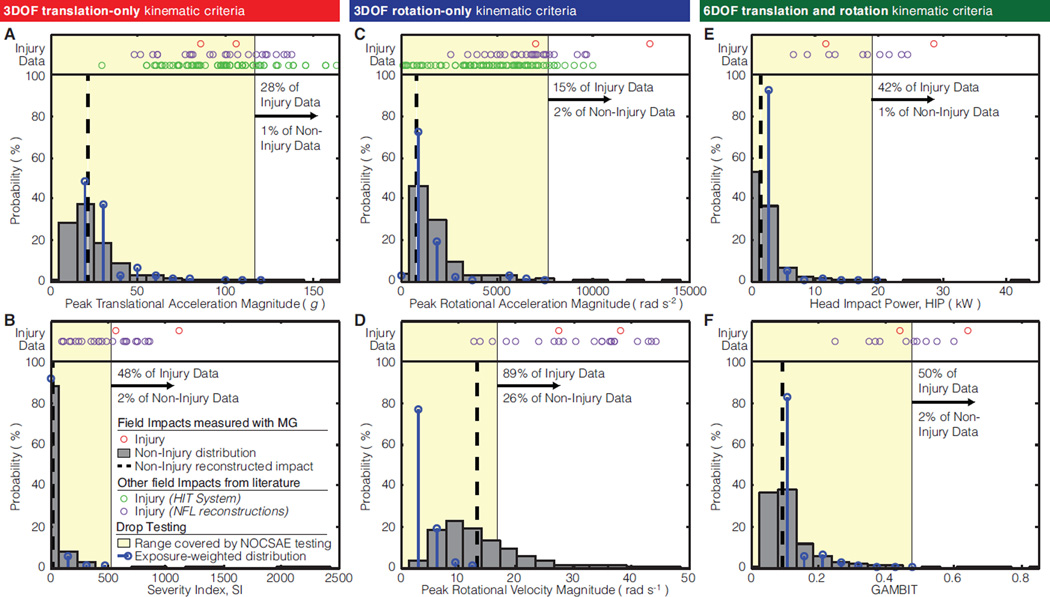
The highest severity NOCSAE standard drop tests (drop height of 1.52 m) produced peak translational accelerations (117 g) that covered all but 28% if the injury impacts (72nd percentile) and 1% of the non-injury field impacts (99th percentile) (Fig. 3A). For Severity Index (SI), NOCSAE’s standard criteria for helmet certification, drop testing (534) covered all but 2% of the field data, but only half of the injuries (Fig. 3B). Peak rotational acceleration covered the greatest portion of injury impacts, all but 16% (Fig. 3C). The 6DOF criteria, HIP and GAMBIT, also covered the vast majority of non-injury impacts (all but 1% and 2%, respectively), but were among the criteria that covered the least injury impacts (all but 42% and 60%, respectively) (Fig. 3E,F). Among all criteria, the peak rotational velocities generated by the highest NOCSAE drop tests (17 rad s−1) covered the fewest injury (all but 89%) and non-injury (all but 26%) impacts (Fig. 3D).
Figure 3. Aggregate distributions of kinematic criteria.
Field data for six kinematic criteria is plotted against the range of values produced by the highest drop heights in the NOCSAE standard protocol on the twin-wire drop test (yellow region) and exposure-weighted distribution of drop test data (black bars). We also compared the range covered by NOCSAE to 116 mTBI impacts recorded in previous studies: n = 2 using our instrumented mouthguards (red circles) (Hernandez et al., 2014), n = 89 using the Head Impact Telemetry System (HITS) (green circles) (Broglio et al., 2011; Duma and Rowson, 2009; Guskiewicz et al., 2007; Rowson et al., 2012), and n = 25 using NFL reconstructions (purple circles) (Newman et al., 2000a,b; Pellman et al., 2003).
With the exception of rotational velocity, drop testing produced kinematic criteria distributions that were not different than field impacts (p > 0.1) (Fig. 3). Drop testing and field distributions were more similar for the two translation-only criteria: SI (Fig. 3B), followed by translational acceleration which was slightly overestimated by drop testing (Fig. 3A). The drop test distribution of peak rotational velocity was skewed left and different than the field distribution (p < 0.01) (Fig. 3D).
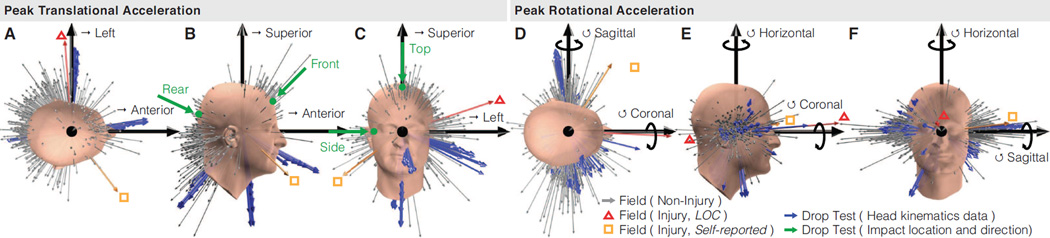
Although drop testing and field impacts yielded similar distributions of peak translational and rotational acceleration, the directions of peak acceleration were dissimilar (Fig. 4). Drop testing produced translational acceleration clusters corresponding to replicate impacts at specific impact locations, with less variety than what subjects experienced in the field. Over 44% of our field impacts, but no drop tests, had a translational acceleration direction with a positive superior component (Fig. 4B–C). Rear drop tests, weighed heaviest by the STAR helmet rating protocol, produced anterior accelerations that were relatively uncommon in our field impact dataset (Fig. 4B). In the laboratory impacts, impact direction did not align exactly with the resulting direction of peak translational acceleration, with Side impacts having the largest average difference in angle (19°), followed by Rear (10°), Top (8°), and Front (6°) impacts. Drop testing and our field impacts produced peak rotational accelerations with more comparable variety (Fig. 4D–F). Sagittal plane rotations were the most common rotations in our field and laboratory data, but were of lower magnitude in drop testing.
Figure 4. Aggregate distributions of peak acceleration directions.
Direction and relative amplitude of (A–C) peak translational acceleration and (D–F) peak rotational acceleration was described by component values at the time when magnitude was peak and is given for field impacts (gray arrows) and laboratory drop tests (blue arrows). Impact directions and locations are labeled in green
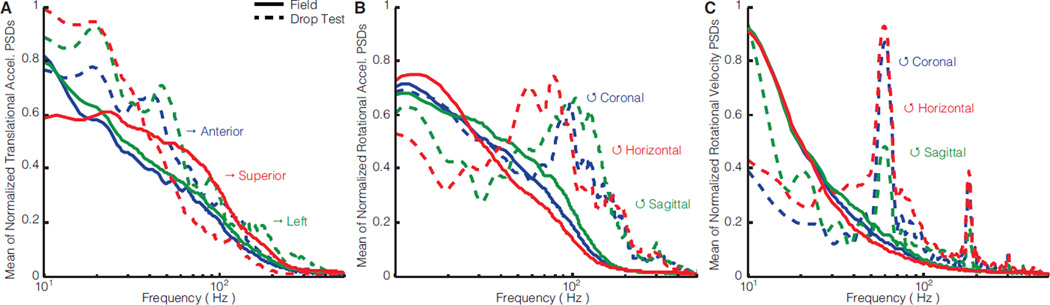
Acceleration amplitude/direction differences between field impacts and drop tests were consistent with frequency content differences (Fig. 5). On average across all directions, field impacts produced primary frequencies of translational acceleration, rotational acceleration, and rotational velocity that were similarly low (10–30 Hz). Drop testing also produced translational accelerations with low primary frequencies (10–20 Hz) (Fig. 5A). However, drop testing produced noticeably more high frequency content (60–120 Hz) than field impacts in rotational acceleration and velocity (Fig. 5B,C). In all rotational components except coronal for acceleration and sagittal for velocity, the high frequency content (60–120 Hz) exceeded the peaks on the low end (10–20 Hz).
Figure 5. Aggregate distributions of frequency content.
Mean of normalized power spectral density (PSD) is compared between field (solid lines) and laboratory (dotted lines) for all 3 directions of (A) translational acceleration, (B) rotational acceleration, and (C) rotational velocity. Peaks correspond to common primary frequencies independent of signal amplitude and impact severity (e.g. initial velocity, drop height, etc.).
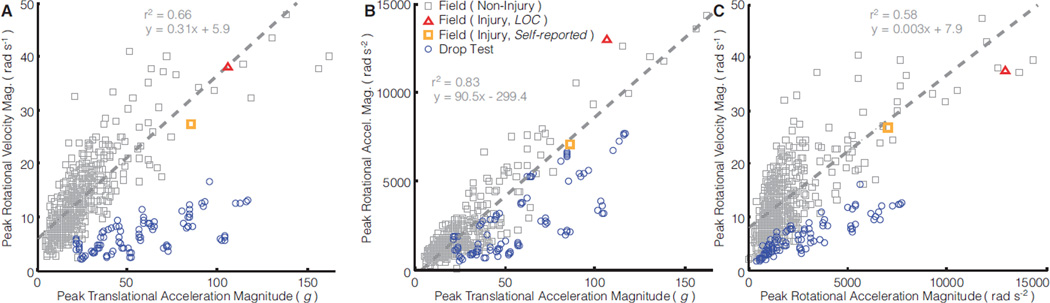
While field impacts and drop tests produced similar distributions of translational and rotational accelerations, the relationship between these measures differed (Fig. 6). Drop testing differed from field impacts for three pairs of kinematic measurements (p < 0.01) (Fig. 6). For a given translational acceleration, drop testing underestimated a linear fit of field rotational velocities by an average of 72% (Fig. 6A), and rotational accelerations by an average of 46% (Fig. 6B). For a given rotational acceleration, drop testing underestimated a linear fit of field rotational velocities by an average of 59% (Fig. 6C).
Figure 6. Aggregate distributions of kinematic measurement combinations.
Field and laboratory data are plotted for combinations of peak kinematic measurements. For the field data, we performed linear regression of one peak kinematic measurement (independent variable) on another (dependent variable); drop test under-/over-estimation of the dependent variable for a given independent variable value was compared with this linear model
Single impact reconstruction
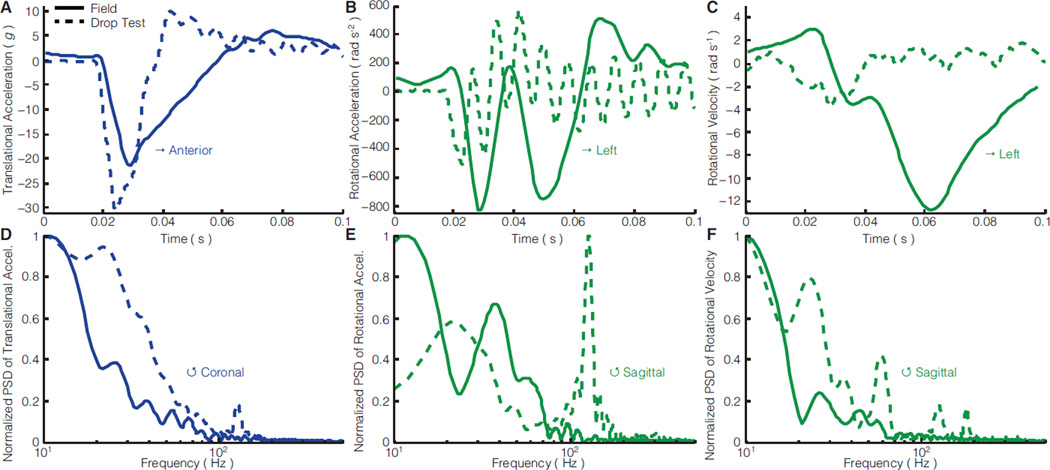
The reconstructed field impact was typical and representative of the aggregate distributions (Fig. 3). Before impact, the field (player on right) and drop test helmets approached similar impact locations at similar speeds (Fig. 7A–B,D–E). The player’s helmet rotated down approaching the impact (positive sagittal rotational velocity up to t = 0.03 s), and after impact, rotated back slightly (negative sagittal rotational velocity from t = 0.03 – 0.04 s) as his neck appeared to compress and couple with his torso (rotational velocity inflection at t = 0.04 s). His body and head then continued to rotate together backward at a faster velocity (Fig. 7C, Fig. 8C, Movie S1). In contrast, the drop test helmet did not rotate appreciably (Fig. 7D).
Figure 7. Single impact reconstruction response.
Comparison of head motion 25 ms before, at, and 150 ms after impact for a field impact and drop test reconstruction
Figure 8. Single impact reconstruction kinematics.
Kinematics and power spectral density (PSD) in primary motion directions of a mostly sagittal plane field impact and a drop test reconstruction with similar initial conditions. In all three kinematic measurements, the drop test and field impact produced multiple direction changes (zero-crossings), however, these were generally faster in drop testing
Kinematic measurements were consistent with video. A mostly sagittal plane impact, translational acceleration was primarily anterior-posterior where drop testing overestimated the field peak by 40% (Fig. 8A). Sagittal rotational acceleration and velocity in drop testing underestimated the field peaks by 40% and 70%, respectively (Fig. 8B,C). The field impact and drop test produced similar low primary frequencies (10–20 Hz) in anterior-posterior translational acceleration (Fig. 8D). However, drop testing produced more high frequency content in sagittal rotational acceleration (120 Hz) and velocity (60 Hz) compared to the field impact (Fig. 8E).
DISCUSSION
The study objective was two-fold: (a) describe methodology for evaluating laboratory models of head impact biomechanics using field measurements, and (b) use this methodology to investigate how closely twin-wire drop tests model human head rotation in football head impacts. We compared field head impact measurements with drop tests at heights and impact locations representative of typical field exposure. To understand aggregate trends, we also reconstructed a typical in vivo head impact on the drop test. The results suggest twin-wire drop testing does not model human head rotation in football head impacts.
Compared to field head impacts, drop testing generally under-rotated the head. The rotational velocity distribution produced by drop testing significantly differed (under-estimated) from field data, and did not cover the vast majority of mTBI impacts and the upper quartile of non-injury impacts. Field impacts and drop tests produced similar peak rotational accelerations amplitudes. Yet independent of signal amplitude (e.g. initial velocity, drop height, etc.), drop testing typically produced more high frequency content than field impacts and thereby produced lower amplitude rotational velocities (high acceleration sustained for shorter intervals), a trend consistent among aggregate distributions and the single reconstructed impact. High frequency rotation dynamics may be less relevant to mTBI – for the same rotational acceleration amplitude, a lower frequency (longer impulse duration) impact produces more brain strain (Ji and Zhao, 2014; Kleiven, 2006; Yoganandan et al., 2008) and significant changes in activity and emotional-type behaviors following mTBI in rodents (Stemper et al., 2014). High rotational velocity, which we observed in field impacts and not in drop tests, has been thought to induce brain strain and has been predictive of mTBI (Margulies and Thubault, 1992; Newman et al., 2000b; Ommaya and Hirsch, 1971; Rowson et al., 2012; Takhounts et al., 2013; Weaver et al., 2012). Ommaya and Hirsch (1971) proposed a human mTBI tolerance of 30 rad s−1, well above the range covered by our NOCSAE drop tests.
Twin-wire drop testing generally reproduced field translational accelerations with drop heights of 1.52 m or less. But for a given translational acceleration, drop testing substantially underestimated rotational acceleration and rotational velocity. Drop testing did not produce translational and rotational criteria levels experienced in many mTBI impacts measured using our instrumented mouthguards (Hernandez et al., 2014), the Head Impact Telemetry System (HITS) (Broglio et al., 2011; Duma and Rowson, 2009; Guskiewicz et al., 2007; Rowson et al., 2012), and NFL video reconstructions (Newman et al., 2000a,b; Pellman et al., 2003), most surprising in the case of Severity Index (SI), the NOCSAE standard criteria, which missed half. Drop tests at higher-than-standard heights may cover mTBI-level kinematics and other peak rotational kinematics below injury, but translational accelerations would far exceed what is typical in the field. Modeling a biofidelic relationship between translation and rotation may be key for helmet testing, as several studies have predicted mTBI with a combination of translation and rotation acceleration measurements (Greenwald et al., 2008; Newman, 1986; Newman et al., 2000b; Rowson and Duma, 2013). Improper modeling of this relationship may encourage helmet design optimization for a combination of translation and rotation that is not likely to be experienced in the field by human users.
Physically, head under-rotation in twin-wire drop testing was likely due to rigid neck and twin-wire constraints. Higher frequency dynamics imply a stiffer system. Dummy head attachment to a rigid neck, and constraint of the drop carriage to motion along stiff twin wires, are specified in the NOCSAE standard. In our drop testing, horizontal and sagittal head rotational acceleration had similar frequency content but least approximated field impacts. In the most common impact locations (Front and Rear), head rotation in the horizontal and sagittal planes cause the drop carriage to torque the twin wires about a stiff transverse axis perpendicular to the length of the wire and may explain why these rotations contain higher frequency content. Drop testing likely models coronal rotations better in Front and Rear drops because these rotations cause a torque on the twin wires about a softer, axial axis. If so, drop test wire tension may affect head rotation frequency, and could perhaps be tuned to improve the fidelity of this or alternative laboratory models. Others have suspected the rigid neck under-rotates in drop testing, and have adopted a non-rigid neck in horizontal linear impact testing (Camarillo et al., 2013; NOCSAE, 2006; Rowson et al., 2011; Viano et al., 2012) and pendulum testing (Bartsch et al., 2012; Pellman et al., 2003). A recent revision to the STAR rating system applied to hockey helmets has also made use of a non-rigid neck (Rowson et al., 2015). These studies use the Hybrid III anthropomorphic neck, which was developed for vehicle crash testing and not tuned for modeling sport-related head impacts. Gwin et al. (2010) found that laboratory testing with the Hybrid III neck produced impact dynamics with a damping factor and period of natural oscillation that far exceeded in vivo football impacts. Higher damping and lower natural frequency may not affect head translational and rotational acceleration as these typically peak before substantial head displacement. However, the system characteristics identified by Gwin et al. 2010 imply that the Hybrid III neck may be less stiff than a braced football player, which could affect head translational and rotational acceleration by slowing the dynamics (Gwin et al. 2010). Ultimately, these models have not been evaluated against field measurements of head impact translation and rotation.
Differences in acceleration directions between field and laboratory impacts suggest more physical limitations of drop testing. Almost half of our field head impacts had a positive superior component of translational acceleration direction. However, drop testing is physically limited by the carriage, neck, and twin wires for producing the impact directions necessary to induce this kind of acceleration. Instead, the present study weighted rear head impacts most according to the STAR protocol field exposure estimates (Rowson and Duma, 2011). However, anterior accelerations were relatively uncommon in our field data, suggesting a potential need to re-assess typical field exposure. Impact direction is defined in 6DOF: 3DOF for the head location that was impacted (which is typically all that is estimated and reported) and 3DOF for the closing velocity direction at impact (which is typically excluded). For example, head acceleration measurements are not sufficient to fully define 6DOF impact direction without additional measurements of impact or neck reaction forces (Allison et al., 2014; Crisco et al., 2004). Exposure may be better expressed as a function of acceleration direction output. Yet even then, twin-wire drop testing only allows 2DOF orientation of the head (sagittal and horizontal plane rotation), and would be limited in reproducing arbitrary 6DOF impact directions that may occur in the field as with our single impact reconstruction.
The present study presents methodology for evaluating laboratory models of field head impact biomechanics. These analyses may help assess the fidelity of existing and future laboratory head impact models for producing acceleration amplitudes, directions, and frequencies experienced in the field. A similar evaluation study by Gwin et al. (2010) found that frequency characteristics of translational acceleration were similar between drop testing and field head impacts (as we did here), but did not evaluate drop testing for rotation. Here we considered numerous criteria that were most predictive of injury (Hernandez et al., 2014) and compared a single head impact reconstruction to visualize aggregate trends. We used high definition, high speed stereo video to expand on previous reconstructions of NFL impacts that used standard broadcast video (Pellman et al., 2003). This novel dataset is the first to precisely measure initial conditions (i.e. relative velocity, impact location, and impact direction) prospectively using high speed video and directly measure head acceleration for a full speed head-to-head football impact.
This study has several limitations to mention. One limitation is uncertainty in the field measurements, which came from instrumented mouthguards that were validated for kinematic accuracy in a laboratory testing that may not capture field conditions specific to a human user (Camarillo et al., 2013; Hernandez et al., 2014). Despite potential sources of error, the methodology proposed in this study could be performed with other field sensor data. Two NOCSAE standard impact locations (Front Boss and Rear Boss) (NOCSAE, 2012a) were not included here as there is no exposure weighting information provided for these impact locations in the STAR rating system study. However, head impacts in these locations typically produce lower accelerations than the head impacts studied here (Forbes et al., 2013; Gwin et al., 2010). The theoretical capability of drop testing is limited here by the size of the device and spatial constraints in a laboratory environment; here we report ranges for the highest specified drop height in the NOCSAE standard and STAR helmet rating protocol. A non-standard headform was used in the present study, however, it has been used in previous laboratory studies and has similar mass and inertia properties as the 50th percentile male human head (Camarillo et al., 2013). Findings from a single reconstruction of a typical impact are preliminary, and additional reconstructions would provide a more complete evaluation of drop testing.
Despite these limitations, our evaluation of a laboratory head impact model indicates limitations of twin-wire drop testing for modeling head rotation in football head impacts. If rotation is indeed clinically significant, drop testing may not be sufficient to test and certify helmets under conditions that cause mTBI. Given the current helmet controversy, and the need to evaluate helmets under conditions that may cause mTBI, twin-wire drop testing may need to be replaced or modified to include a flexible neck. Some groups have already been working to incorporate rotation into helmet testing (Rowson et al., 2015). NOCSAE has announced they will be amending their standard in the next year or two to include a flexible neck model (NOCSAE, 2014). Methodology similar to that used in the present study may help lend credence to a head impact model and its future use for helmet certification.
Supplementary Material
Acknowledgements
We thank the Stanford Department of Athletics (Palo Alto, CA) for enabling this research, notably Scott Anderson, Director of Athletic Training, and Mike Gleeson, Video Director. We thank Rebecca Shultz and James Mattson for collecting high speed video data. We thank X2 Biosystems (Seattle, WA) for sharing mouthguard architecture and the twin-wire system. The study was supported by the National Institutes of Health (NIH) National Institute of Biomedical Imaging and Bioengineering (NIBIB) 3R21EB01761101S1, David and Lucile Packard Foundation 38454, and by the NIH Clinical and Translational Science Award 1UL1 RR025744 for the Stanford Center for Clinical and Translational Education and Research (Spectrum).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement: The authors have no personal financial conflict of interests related to this study.
REFERENCES
- Allison MA, Kang YS, Bolte JH, Maltese MR, Arbogast KB. Validation of a helmet-based system to measure head impact biomechanics in ice hockey. Medicine & Science in Sports & Exercise. 2014;46(1):115–123. doi: 10.1249/MSS.0b013e3182a32d0d. [DOI] [PubMed] [Google Scholar]
- Bartsch A, Benzel E, Miele V, Prakash V. Impact test comparisons of 20th and 21st century American football helmets. Journal of Neurosurgery. 2012;116(1):222–233. doi: 10.3171/2011.9.JNS111059. [DOI] [PubMed] [Google Scholar]
- Bartsch A, Samorezov S. Cleveland Clinic intelligent mouthguard: a new technology to accurately measure head impact in athletes and soldiers. Proceedings of SPIE 8723, Sensing Technologies for Global Health, Military Medicine, and Environmental Monitoring III. 2013;8723:1–8. [Google Scholar]
- Broglio SP, Schnebel B, Sosnoff JJ, Shin S, Feng X, He X, Zimmerman J. The biomechanical properties of concussions in high school football. Medicine & Science in Sports & Exercise. 2011;42(11):2064–2071. doi: 10.1249/MSS.0b013e3181dd9156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camarillo DB, Shull PB, Mattson J, Shultz R, Garza D. An instrumented mouthguard for measuring linear and angular head impact kinematics in American football. Annals of Biomedical Engineering. 2013;41(9):1939–1949. doi: 10.1007/s10439-013-0801-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantu RC, Bishop P, Duma SM, Gennarelli TA, Greenwald RM, Guskiewicz K, Mueller F, Halstead PD, Hoshizaki TB, King A, Putukian M. Letter to the editor: helmets. Journal of Neurosurgery. 2012;117(1):187–189. doi: 10.3171/2011.12.JNS112108. [DOI] [PubMed] [Google Scholar]
- Crisco JJ, Chu JJ, Greenwald RM. An algorithm for estimating acceleration magnitude and impact location using multiple nonorthogonal single-axis accelerometers. Journal of Biomechanical Engineering. 2004;126(6):849–854. doi: 10.1115/1.1824135. [DOI] [PubMed] [Google Scholar]
- Duma SM, Rowson S. Every newton hertz: A macro to micro approach to investigating brain injury; Proceedings of the 31st International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC); 2009. pp. 1123–1126. [DOI] [PubMed] [Google Scholar]
- Forbes JA, Zuckerman SL, He L, McCalley E, Lee YM, Solomon GS, Halstead PD, Sills AK. Subdural hemorrhage in two high-school football players: post-injury helmet testing. Pediatric Neurosurgery. 2013;49:43–49. doi: 10.1159/000355121. [DOI] [PubMed] [Google Scholar]
- Gadd CW. Use of a weighted impulse criterion for estimating injury hazard; Proceedings of the 10th Stapp Car Crash Conferfence, SAE Paper No. 660793, SAE Paper; 1966. pp. 164–174. [Google Scholar]
- Gennarelli TA, Thibault LE, Adams JH, Graham DI, Thompson CJ, Marcincin RP. Diffuse axonal injury and traumatic coma in the primate. Annals of Neurology. 1982;12(6):564–574. doi: 10.1002/ana.410120611. [DOI] [PubMed] [Google Scholar]
- Gennarelli TA, Thibault LE, Graham DI. Diffuse axonal injury: an important form of traumatic brain damage. Neuroscientist. 1998;4(3):202–215. [Google Scholar]
- Gessel LM, Fields SK, Collins CL, Dick RW, Comstock RD. Concussions among United States high school and collegiate athletes. Journal of Athletic Training. 2007;42(4):495–503. [PMC free article] [PubMed] [Google Scholar]
- Giordano C, Kleiven S. Evaluation of axonal strain as a predictor for mild traumatic brain injuries using finite element modeling. Stapp Car Crash Journal. 2014;58:29–61. doi: 10.4271/2014-22-0002. [DOI] [PubMed] [Google Scholar]
- Greenwald RM, Gwin JT, Chu JJ, Crisco JJ. Head impact severity measures for evaluating mild traumatic brain injury risk exposure. Neurosurgery. 2008;62(4):789–798. doi: 10.1227/01.neu.0000318162.67472.ad. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurdjian ES, Lissner HR, Latimer FR, Haddad BF, Webster JE. Quantitative determination of acceleration and intracranial pressure in experimental head injury; preliminary report. Neurology. 1953;3(6):417–423. doi: 10.1212/wnl.3.6.417. [DOI] [PubMed] [Google Scholar]
- Gurdjian ES, Roberts VL, Thomas LM. Tolerance curves of acceleration and intracranial pressure and protective index in experimental head injury. Journal of Trauma. 1966;6(5):600–604. doi: 10.1097/00005373-196609000-00005. [DOI] [PubMed] [Google Scholar]
- Guskiewicz KM, Mihalik JP, Shankar V, Marshall SW, Crowell DH, Oliaro SM, Ciocca MF, Hooker DN. Measurement of head impacts in collegiate football players: impact biomechanics and acute clinical outcome after concussion. Neurosurgery. 2007;61(6):1244–1253. doi: 10.1227/01.neu.0000306103.68635.1a. [DOI] [PubMed] [Google Scholar]
- Gwin JT, Chu JJ, Diamond SG, Halstead PD, Crisco JJ, Greenwald RM. An investigation of the NOCSAE linear impactor test method based on in vivo measures of head impact acceleration in American football. Journal of Biomechanical Engineering. 2010;132(1):011006. doi: 10.1115/1.4000249. [DOI] [PubMed] [Google Scholar]
- Heikkila J, Silven O. A four-step camera calibration procedure with implicit image correction. Proceedings of the 1997 IEEE Conference on Computer Vision and Pattern Recognition. 1997:1106–1112. [Google Scholar]
- Hernandez F, Wu LC, Yip MC, Laksari K, Hoffman AR, Lopez J, Grant GA, Kleiven S, Camarillo DB. Six degree of freedom measurements of human mild traumatic brain injury. Annals of Biomedical Engineering. 2014:1–16. doi: 10.1007/s10439-014-1212-4. (In press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holbourn AHS. Mechanics of head injuries. Lancet. 1943;242(6267):438–441. [Google Scholar]
- Horn BKP, Hilden HM, Negahdaripour S. Closed-form solution of absolute orientation using orthonormal matrices. Journal of the Optical Society of America. 1988;5(7):1127–1135. [Google Scholar]
- Ji S, Zhao W. A pre-computed brain response atlas for instantaneous strain estimation in contact sports. Annals of Biomedical Engineering. 2014:1–19. doi: 10.1007/s10439-014-1193-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston JM, Ning H, Kim J-E, Kim Y-H, Soni B, Reynolds R, Cooper L, Andrews JB, Vaidya U. Simulation, fabrication and impact testing of a novel football helmet padding system that decreases rotational acceleration. Sports Engineering. 2014:1–10. [Google Scholar]
- Kang Y-S, Moorhouse K, Bolte JH. Measurement of six degrees of freedom head kinematics in impact conditions employing six accelerometers and three angular rate sensors (6aω configuration) Journal of Biomechanical Engineering. 2011;133(11):111007. doi: 10.1115/1.4005427. [DOI] [PubMed] [Google Scholar]
- King AI. Comments on Rowson and Duma (2011) Annals of Biomedical Engineering. 2012;40(12):2510–2511. doi: 10.1007/s10439-012-0659-4. [DOI] [PubMed] [Google Scholar]
- Kleiven S. Evaluation of head injury criteria using a finite element model validated against experiments on localized brain motion, intracerebral acceleration, and intracranial pressure. International Journal of Crashworthiness. 2006;11(1):65–79. [Google Scholar]
- Kleiven S. Predictors for traumatic brain injuries evaluated through accident reconstructions. Stapp Car Crash Journal. 2007;51:81–114. doi: 10.4271/2007-22-0003. [DOI] [PubMed] [Google Scholar]
- Langlois JA, Rutland-Brown W, Wald MM. The epidemiology and impact of traumatic brain injury: a brief overview. Journal of Head Trauma Rehabilitation. 2006;21(5):375–378. doi: 10.1097/00001199-200609000-00001. [DOI] [PubMed] [Google Scholar]
- Lincoln AE, Caswell SV, Almquist JL, Dunn RE, Norris JB, Hinton RY. Trends in concussion incidence in high school sports: a prospective 11-year study. American Journal of Sports Medicine. 2011;39(5):958–963. doi: 10.1177/0363546510392326. [DOI] [PubMed] [Google Scholar]
- Margulies SS, Thibault LE, Gennarelli TA. Physical model simulations of brain injury in the primate. Journal of Biomechanics. 1990;23(8):823–836. doi: 10.1016/0021-9290(90)90029-3. [DOI] [PubMed] [Google Scholar]
- Margulies SS, Thibault LE. A proposed tolerance criterion for diffuse axonal injury in man. Journal of Biomechanics. 1992;25(8):917–923. doi: 10.1016/0021-9290(92)90231-o. [DOI] [PubMed] [Google Scholar]
- Newman JA. A generalized acceleration model for brain injury threshold (GAMBIT); Proceedings of the 1986 International Conference on the Biomechanics of Impact (IRCOBI); 1986. pp. 121–131. [Google Scholar]
- Newman JA, Barr C, Beusenberg M, Fournier E, Shewchenko N, Welbourne E, Withnall C. A new biomechanical assessment of mild traumatic brain injury, part 2: results and conclusions. Proceedings of the 2000 International Conference on the Biomechanics of Impact (IRCOBI) 2000a:223–233. [Google Scholar]
- Newman JA, Shewchenko N, Welbourne E. A proposed new biomechanical head injury assessment function - the maximum power index. Stapp Car Crash Journal. 2000b;44:215–247. doi: 10.4271/2000-01-SC16. [DOI] [PubMed] [Google Scholar]
- NOCSAE. Standard linear impactor test method and equipment used in evaluating the performance characteristics of protective headgear and faceguards. National Operating Committee on Standards for Athletic Equipment (NOCSAE) 2006:1–6. (Paper No. ND081-04m04) [Google Scholar]
- NOCSAE. Standard performance specification for newly manufactured football helmets. National Operating Committee on Standards for Athletic Equipment (NOCSAE) 2012a:1–6. (Paper No. ND001- 11m12) [Google Scholar]
- NOCSAE. Standard test method and equipment used in evaluating the performance characteristics of protective headgear/equipment. National Operating Committee on Standards for Athletic Equipment (NOCSAE) 2012b:1–30. (Paper No. ND001-11m12) [Google Scholar]
- NOCSAE. NOCSAE board approves first helmet standard to address concussion forces [Press release] National Operating Committee on Standards for Athletic Equipment (NOCSAE) 2014 (Retrieved from http://nocsae.org/wp-content/uploads/2011/10/NOCSAE-June-Board-Meeting-release-FINAL-6-20-14.pdf). [Google Scholar]
- Ommaya A, Hirsch A. Tolerances for cerebral concussion from head impact and whiplash in primates. Journal of Biomechanics. 1971;4(1):13–21. doi: 10.1016/0021-9290(71)90011-x. [DOI] [PubMed] [Google Scholar]
- Ommaya AK, Gennarelli TA. Cerebral concussion and traumatic unconsciousness. Correlation of experimental and clinical observations of blunt head injuries. Brain. 1974;97(4):633–654. doi: 10.1093/brain/97.1.633. [DOI] [PubMed] [Google Scholar]
- Pellman EJ, Viano DC, Tucker AM, Casson IR. Concussion in professional football: reconstruction of game impacts and injuries. Neurosurgery. 2003;53(4):799–812. doi: 10.1093/neurosurgery/53.3.799. [DOI] [PubMed] [Google Scholar]
- Rowson B, Rowson S, Duma SM. Hockey STAR: A methodology for assessing the biomechanical performance of hockey helmets. Annals of Biomedical Engineering. 2015:1–15. doi: 10.1007/s10439-015-1278-7. (In press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowson S, Beckwith JG, Chu JJ, Leonard DS, Greenwald RM, Duma SM. A six degree of freedom head acceleration measurement device for use in football. Journal of Applied Biomechanics. 2011;27(1):8–14. doi: 10.1123/jab.27.1.8. [DOI] [PubMed] [Google Scholar]
- Rowson S, Daniel RW, Duma SM. Biomechanical performance of leather and modern football helmets. Journal of Neurosurgery. 2013;119:805–809. doi: 10.3171/2013.3.JNS121735. [DOI] [PubMed] [Google Scholar]
- Rowson S, Duma SM. Development of the STAR evaluation system for football helmets: integrating player head impact exposure and risk of concussion. Annals of Biomedical Engineering. 2011;39(8):2130–2140. doi: 10.1007/s10439-011-0322-5. [DOI] [PubMed] [Google Scholar]
- Rowson S, Duma SM. The Virginia Tech Response. Annals of Biomedical Engineering. 2012;40(12):2512–2518. [Google Scholar]
- Rowson S, Duma SM. Brain injury prediction: assessing the combined probability of concussion using linear and rotational head acceleration. Annals of Biomedical Engineering. 2013;41(5):873–882. doi: 10.1007/s10439-012-0731-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowson S, Duma SM, Beckwith JG, Chu JJ, Greenwald RM, Crisco JJ, Brolinson PG, Duhaime A-C, McAllister TW, Maerlender AC. Rotational head kinematics in football impacts: an injury risk function for concussion. Annals of Biomedical Engineering. 2012;40(1):1–13. doi: 10.1007/s10439-011-0392-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith DH, Nonaka M, Miller R, Leoni M, Chen XH, Alsop D, Meaney DF. Immediate coma following inertial brain injury dependent on axonal damage in the brainstem. Journal of Neurosurgery. 2000;93(2):315–322. doi: 10.3171/jns.2000.93.2.0315. [DOI] [PubMed] [Google Scholar]
- Stemper BD, Shah AS, Pintar FA, McCrea M, Kurpad SN, Glavaski-Joksimovic A, Olsen C, Budde MD. Head rotational acceleration characteristics influence behavioral and diffusion tensor imaging outcomes following concussion. Annals of Biomedical Engineering. 2014;43(5):1071–1088. doi: 10.1007/s10439-014-1171-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takhounts EG, Craig MJ, Moorhouse K, McFadden J, Hasija V. Development of brain injury criteria (BrIC) Stapp Car Crash Journal. 2013;57:243–266. doi: 10.4271/2013-22-0010. [DOI] [PubMed] [Google Scholar]
- Versace J. A review of the Severity Index; Proceedings of the 15th Stapp Car Crash Conference, SAE Paper No. 710881; 1971. pp. 771–796. [Google Scholar]
- Viano DC, Withnall C, Halstead D. Impact performance of modern football helmets. Annals of Biomedical Engineering. 2012;40(1):160–174. doi: 10.1007/s10439-011-0384-4. [DOI] [PubMed] [Google Scholar]
- Weaver AA, Danelson KA, Stitzel JD. Modeling brain injury response for rotational velocities of varying directions and magnitudes. Annals of Biomedical Engineering. 2012;40(9):2005–2018. doi: 10.1007/s10439-012-0553-0. [DOI] [PubMed] [Google Scholar]
- Yoganandan N, Li J, Zhang J, Pintar FA, Gennarelli TA. Influence of angular acceleration-deceleration pulse shapes on regional brain strains. Journal of Biomechanics. 2008;41(10):2253–2262. doi: 10.1016/j.jbiomech.2008.04.019. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Way OM. Flexible camera calibration by viewing a plane from unknown orientations. Proceedings of the 7th IEEE Conference on Computer Vision. 1999;1:666–673. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.