A Model of Extracellular Enzymes in Free-Living Microbes: Which Strategy Pays Off?

Abstract

An initial modeling approach was applied to analyze how a single, nonmotile, free-living, heterotrophic bacterial cell may optimize the deployment of its extracellular enzymes. Free-living cells live in a dilute and complex substrate field, and to gain enough substrate, their extracellular enzymes must be utilized efficiently. The model revealed that surface-attached and free enzymes generate unique enzyme and substrate fields, and each deployment strategy has distinctive advantages. For a solitary cell, surface-attached enzymes are suggested to be the most cost-efficient strategy. This strategy entails potential substrates being reduced to very low concentrations. Free enzymes, on the other hand, generate a radically different substrate field, which suggests significant benefits for the strategy if free cells engage in social foraging or experience high substrate concentrations. Swimming has a slight positive effect for the attached-enzyme strategy, while the effect is negative for the free-enzyme strategy. The results of this study suggest that specific dissolved organic compounds in the ocean likely persist below a threshold concentration impervious to biological utilization. This could help explain the persistence and apparent refractory state of oceanic dissolved organic matter (DOM). Microbial extracellular enzyme strategies, therefore, have important implications for larger-scale processes, such as shaping the role of DOM in ocean carbon sequestration.

INTRODUCTION

Dissolved organic matter (DOM) in the oceans is one of the largest active reservoirs of organic carbon in the biosphere (1). An intricate web of biotic (e.g., photosynthesis, viral lysis, and grazing) and abiotic (e.g., photodegradation and aggregation) processes contribute to the physical and chemical complexity of DOM (2–4). However, DOM is almost exclusively exploited by the bacterioplankton (5, 6). Microbes face several challenges when consuming DOM. While small molecules approximately 600 to 800 Da in size can be taken up directly (7, 8), larger compounds need to be enzymatically hydrolyzed outside the cell before uptake. This two-phase system of hydrolysis and subsequent uptake is a rate-limiting step of microbial enzymatic degradation (9–11), and a mechanistic understanding of these processes, therefore, is of global biogeochemical relevance. Furthermore, the bacterioplankton are faced with the challenges of spatial heterogeneity (12, 13) and individual compounds at extremely dilute concentrations (14–16). For a microbe, there is presumably a delicate balance between the substrate encounter rate and the energy cost associated with carrying and maintaining an enzymatic apparatus for substrate uptake.

It has been proposed that bacteria have adapted to the “landscape” of marine DOM by two very different trophic strategies. Copiotrophs use a “feast and famine” strategy where they proliferate from low abundances upon exposure to high substrate levels (17), such as in association with detrital aggregates or phytoplankton blooms. Copiotrophs are distinguished by traits indicating specialization, such as rapid uptake and high growth rates, chemotaxis, and motility (18, 19). In contrast, oligotrophs are generally smaller and are suggested to have streamlined genomes, to lack motility, and to possess broad uptake systems (18). The oligotrophs are numerically the most abundant fraction among the free-living bacteria, as exemplified by the ubiquitous SAR11 clade (20, 21), while the abundance of the copiotrophs reflects the environment's resource concentration (13).

Extracellular enzymes are an important bacterial trait, regardless of the trophic strategy. Extracellular hydrolytic enzymes are located outside the cell membrane and differentiate into two groups: (i) attached enzymes, which are kept associated with the surface of the cell, either tethered to or integrated into the membrane, and (ii) free enzymes, which are released into solution by the cell (22). Both groups of extracellular enzymes are observed in natural seawater (23–29), but it is difficult to assess the relative ecological significance of the two enzyme strategies. It is assumed that the enzyme deployment strategy is associated with the lifestyle of the microbe. For particle-associated microbes, the free-enzyme strategy is profitable due to high nutrient concentrations on particles (30), and significant enzyme activities have been measured on particles (31, 32). For free-living microbes utilizing DOM, the ambient substrate field is radically different. Here, it has been hypothesized that surface-attached enzymes represent the most cost-efficient strategy, as free enzymes should not be profitable due to the dilute nature of DOM (22, 33). To our knowledge, existing methodologies employed for assessing natural microbial communities in seawater are not able to determine the location of extracellular enzymes relative to the cell or to quantify the fraction of enzymes associated with the surface of the cell. Consequently, only the contribution of dissolved enzymatic activity to total enzyme activity, in size-fractionated water, is commonly reported (24–26, 34). The contributions of free enzymes have been observed to be highly variable, which is not in line with the hypothesis that surface-attached enzymes are the most cost-efficient strategy. However, many processes may mask a potential signal of actively released extracellular enzymes from microbes, e.g., zoo- and phytoplankton activities (35–37), escaped enzymes from particles (30, 32, 38), active enzymes on cell fragments (28), or release of enzymes due to cell lysis during sample filtration.

In this study, we developed a mathematical model that provides a theoretical framework to examine the enzyme strategies of free-living, heterotrophic bacteria. The model is applied to identify the optimal enzyme deployment strategy for a single nonmotile cell and whether there is an ambient substrate concentration below which enzymatic production ceases to be profitable to the cell. Finally, we speculate on the enzyme strategy implications for the DOM landscape in the oceans.

MATERIALS AND METHODS

Physical scenario.

In order to assess the substrate-foraging strategies of marine bacteria, a mathematical description of substrate uptake is made. For this, we assume a stationary bacterium, spherical with radius a (Table 1), releasing a hydrolytic extracellular enzyme (E) at a rate Q. The enzyme spreads in all directions, transported by molecular diffusion with diffusivity D_E, while degrading exponentially in time with decay rate α. For the enzymatic reaction, we assume conditions with concentrations below the K_m (the substrate concentration at which the reaction rate is half of the saturation concentration), i.e., first-order kinetics. The efficiency of the catalytic reaction rate, β, is the ratio between the K_m and k_cat (a direct measure of catalytic reaction under saturation), also referred to as the specificity constant. As the model operates at concentrations far below saturation, the enzyme reaction time is secondary. The enzymes hydrolyze a high-molecular-weight (HMW) substrate, referred to here as polymers (P), to produce a low-molecular-weight (LMW) substrate, referred to as monomers (M). The monomers are small enough to be transported across a bacterial cell membrane and subsequently utilized by the cell. Upon collision between the cell and a polymer, the polymer is reflected off the cell surface, while a collision between a monomer and the cell surface results in uptake. Upon collision between an enzyme and a polymer, we assume a catalytic reaction. The outcomes of the above-mentioned collision types are based on the theory of collisional limit (39), which predicts that the close proximity of many different receptors and enzymes on a cell surface makes the cell surface uniformly reactive, resulting in a binding or catalytic event with every encounter. However, in the case of enzymes not present on the cell surface (i.e., a free-enzyme strategy), the polymer is ultimately reflected. In this simplified description, we consider only those polymers that are suitable substrates for the specific enzyme, and we assume that the reaction between an enzyme and a polymer always yields as a product one monomer, which is a suitable substrate for the cell. The model is parameterized in carbon units.

TABLE 1.

Parameters central to the enzyme model

Symbol	Description	Unit	Value
α	Enzyme (E) decay rate	1/s	1/(7 × 24 × 3,600)a
β	Reaction constant	m3/(s mol)	4.1 × 103b
DE	Diffusivity of enzymes	m2/s	5 × 10−11
DM	Diffusivity of monomer	m2/s
DP	Diffusivity of polymer	m2/s	5 × 10−11
a	Radius of spherical cell	m	0.3 × 10−6c
Q	Production rate of enzyme	mol/s	1.8 × 10−24
P∞	Background polymer concn	mol/m3	P∞d

^aBased on measurements of extracellular enzymes in seawater (34, 41).

^bAlso called the specificity constant and defined as k_cat/K_m for the specific enzyme-substrate complex. The value is based on an average of bacterial psychrophilic and mesophilic α-amylases (40).

^cTypical cell size of planktonic marine bacteria (64).

^dThe oceans typically contain 30 to 80 μmol C kg⁻¹ in the dissolved organic carbon fraction (65), and from the perspective of a single planktonic cell, the potential substrate field would indeed appear infinite.

Partial differential equations.

We assume a steady state and rotational invariance, so the concentrations of enzymes and substrates P and M are functions of the distance to the center of the bacterium (r). The three concentrations are therefore governed by the following partial differential equations (PDE):

$$\dot{E}=D_E\Delta E-\alpha E=0$$ (1)

$$\dot{P}=D_P\Delta P-\beta EP=0$$ (2)

$$\dot{M}=D_M\Delta M-\beta EP=0$$ (3)

Here, Δ is the Laplacian, which with rotational invariance and in spherical coordinates is equivalent to the following equation for the enzyme concentration and similarly for P and M: ΔE = r⁻²(r²E′), where E = E(r) and E′ = dE/dr. The PDE for the enzyme (equation 1) describes a balance between diffusive transport and exponential decay, while the equations for P (equation 2) and M (equation 3) describe similar balances between diffusive transport and reaction terms from the enzymatic reaction; the enzyme kinetics are approximated with first-order mass action, assuming that substrate concentrations are low. These equations were solved by both analytical and numerical methods (see the supplemental material).

Boundary conditions.

The far-field concentration of P is fixed at P_∞, while the boundary condition at the surface of the bacterium is a P′(a) of 0, corresponding to reflection. In contrast, M vanishes at the surface, due to absorption, and in the far field. We consider only monomers produced by enzymes and enzymes produced by the cell, as any background concentration of M and E simply would give rise to an extra monomer uptake, independent of enzyme strategies, making it unnecessarily complex to assess the impact of each enzyme strategy. The enzyme concentration vanishes in the far field, while the boundary condition at the surface of the bacterium is given by the production rate Q of enzymes.

Diffusion of solutes.

The diffusion coefficient of a solute in seawater is dependent on the water temperature and salinity altering the viscosity of the water and on the solute characteristics. However, as there is a relatively small range of temperatures and salinities for the majority of the ocean volume (meso- and bathypelagic zones), their influence is disregarded in this work. The size, hydrophobicity, and charge of dissolved solutes generally control their diffusivities in seawater. In the model, however, the diffusivity of DOM (i.e., polymer) is regulated by molecular weight (MW) only, for simplicity (see the supplemental material, section 5). The diffusivity of the DOM polymer and enzyme will be on the same order of magnitude as long as the MW ratio is no larger than 1,000. Hence, we have set both to have a size of 100 kDa, which results in a diffusivity of 5 × 10⁻¹¹ m²/s. Diffusion, in turn, determines how fast the microbe encounters substrate and how a single free-living cell perceives its ambient DOM field.

Model: fluxes and efficiency.

From solving the PDEs, we calculate the flux of M (J_M) to the cell. In order to simplify further analysis, we examine J_M, measured relative to a maximum potential flux of P (J_P) (i.e., a hypothetical cell that is capable of assimilating P directly), which here represents the diffusive flux to a sphere. This provides an estimate of the efficiency (ε) of the extracellular enzyme strategy, which is nondimensional.

$$\epsilon =\frac{J_M\left(a\right)}{J_P}=\frac{4\pi a^2{D}_M{M}^{\prime }\left(a\right)}{4\pi a{D}_P{P}_{\infty }}$$ (4)

The efficiency will always be less than 1 but asymptotes to 1 as the decay rate of the enzyme decreases or enzyme production increases.

To apply this model, we take the perspective of the cell and aim at optimizing the efficiency (ε) with respect to enzyme diffusivity (D_E).

Cost of enzyme.

The cost of enzyme production relative to utilized substrate (M) also has to be considered. The net carbon gain (J_C) is as follows:

$$J_C=m_M{J}_M\left(a\right)-m_{E}Q$$ (5)

i.e., the harvest of carbon from monomer assimilation minus the expenses involved in producing enzymes. Here, m_M and m_E are the carbon contents of the monomer and enzyme, respectively, and we assume m_E is equal to 1,000 m_M. The net gain increases with the ambient concentration of P and becomes positive at a threshold concentration which we denote$P_{\infty }^{*}$. Thus, at concentrations below$P_{\infty }^{*}$, the enzyme will not return enough carbon to the cell to cover the expenses of producing the enzyme. For free enzymes, the threshold concentration is as follows:

$$P_{\infty }^{*}=\frac{m_E}{m_M}\frac{\alpha }{\beta }\left(1+\sqrt{\frac{D_E}{\alpha a^2}}\right)$$ (6)

With enzyme diffusion at zero (i.e., cell-attached enzymes), the equation simplifies, so that$P_{\infty }^{*}$ depends only on the cost (m_E/m_M), the decay rate (α), and the enzymatic reaction rate (β).

$$P_{\infty }^{*}=\frac{m_E}{m_M}\hspace{0.17em}\frac{\alpha }{\beta }$$ (7)

The enzyme cost, decay rate, and reaction rate inputs are kept constant when comparing the free- and attached-enzyme strategies. The enzyme kinetics are based on the average of kinetic measurements of bacterial psychrophilic and mesophilic α-amylases (40), and the decay rate of the enzyme is set to 7 days, based on in situ measurements (34, 41).

Reference data.

Reference data, based on published measurements from a range of prokaryotic extracellular enzymes (Table 2), are used to assess the importance of enzyme size in relation to diffusivity (see Fig. 2A, range of shaded area) and parameterize the importance of the enzymatic reaction rate (β) for the efficiency of the enzyme strategy (see Fig. 4). The data pertain to prokaryotic extracellular enzymes operating at natural temperature and pH values. We acknowledge that the data are not an exhaustive collection. Neither measurements nor estimates of the lifetime are available for the specific enzyme data, and it is therefore set to 7 days unless otherwise specified, based on in situ measurements (41).

TABLE 2.

Enzyme reference data collected for prokaryotic extracellular enzymes^a

Enzyme	Size (kDa)	Reaction rate (β) (μmol/liter s−1)b	Source
α-Amylase	50	8.1	40
α-Amylase	55	0.1	40
α-Glucosidase	65	0.02–2.15	66
β-Glucosidase	50	0.00006–2.17	67
Alkaline phosphatase	94	1.8–2.5	68
Alkaline protease	26.55	107–1,480	69
Alkaline (H)protease	28	0.0045–0.13	70
Alkaline (N)protease	27	0.0081–0.174	70

^aThe data are not exhaustive; however, to our knowledge, the maximum and minimum size values are close to the boundaries of known prokaryotic extracellular enzymes. The data illustrate the relatively large biological variability in extracellular enzymes.

^bEnzymes with reaction rates in ranges were measured on more than one substrate, and only maximum and minimum values are shown.

FIG 2.

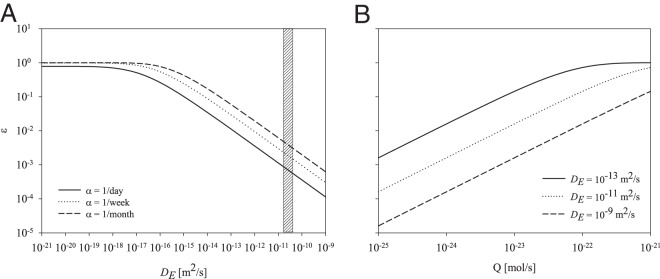
(A) Effects of enzyme decay rate (α) and enzyme diffusivity (D_E) on the efficiency (ε) of the enzyme. The plotted decay rates (1/1, 1/7, and 1/30 days) are based on in situ measurements (34, 41). The gain in efficiency by decreasing the enzyme decay rate is relatively small compared to what can be gained by an attached enzyme (diffusivity approaching zero). The range of the shaded area symbolizes the effect enzyme size/mass has on enzyme diffusivity based on molecular mass data collected from the literature (Table 2). The size variation (27 to 94 kDa) of the measured enzymes causes a relatively small variation in diffusivity. (B) Impacts of enzyme production (Q) and enzyme diffusivity (D_E) on the efficiency of the enzyme.

FIG 4.

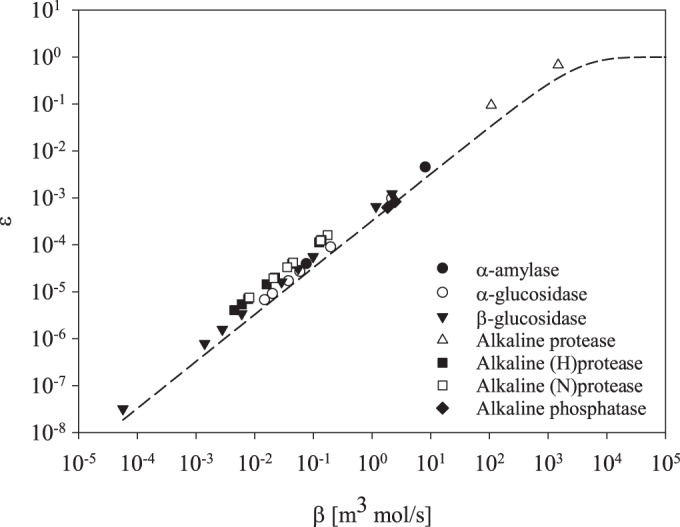
The model predicts a linear relationship between the reaction rate (β) and the efficiency (ε) of an enzyme as long as conditions are under saturation. The faster an enzyme carries out the catalytic reaction, the more efficiently it produces monomers. Each point is based on published data on prokaryotic enzyme kinetics (see the references in Table 2). This illustrates the impact of the enzyme reaction rate and how difficult it is to parameterize.

Concentration fields of enzymes, polymers, and monomers.

The model does not require the computation of monomer concentration fields, but they are useful for illustrative purposes. The monomer concentrations depend on monomer diffusivity. Simple results are obtained if the monomer diffusivity equals the polymer diffusivity. In that case, the monomer concentration can be computed as follows (see the supplemental material):

$$M\left(r\right)=P_{\infty }-\frac{a}{r}\left(P_{\infty }-P\left(a\right)\right)-P\left(r\right)$$ (8)

We should point out that our model is idealized, and among the ignored effects are advective loss and changes in metabolic demands. Transports at these small scales are generally diffusion dominated, as the Péclet numbers are below 1. The Péclet number in our model and the effect of advection are examined in the supplemental material, section 6. A cell may undergo changes in metabolic demands during its lifetime, which will presumably affect the threshold concentration at which it will be energetically beneficial to produce an enzyme. This is highly difficult to parameterize and is secondary to the aim of our model and, therefore, is kept static.

RESULTS

Predicted concentration fields of enzymes, polymers, and monomers.

Dimensionless concentration fields of enzymes, polymers, and monomers are computed with the model using default values for all parameters except enzyme diffusivity (Fig. 1). With a D_E value of 10⁻²¹ m²/s, the enzymes are effectively surface attached and reside in a very thin layer around the cell. Polymers diffuse to the cell, where they almost all react with enzymes; hence, the polymer field resembles that of a cell that absorbs polymers directly. However, not all monomers are absorbed by the cell, so at greater distances from the cell, the monomer concentration resembles that resulting from a point source. For enzymes with a very low diffusivity (D_E = 10⁻¹⁵ m²/s), the enzyme cloud around the cell already has a noticeable extent and the maximum monomer concentration is found at significant distance from the cell (Fig. 1C). For enzyme diffusivities faster than 10⁻¹² m²/s, enzyme decay has no noticeable effect on the enzyme concentration field, which is indistinguishable from the 1/r scaling. In terms of dimensional quantities, the enzyme concentration at the cell surfaces decreases with the diffusivity as follows:

$$E\left(a\right)=\frac{Q}{4\pi a}\frac{1}{D_E+a\sqrt{D_E\alpha }}$$ (9)

(see the supplemental material). As a result, when the enzyme diffusivity is high, the polymer concentration is not 0 at the cell surface and, indeed, increases with enzyme diffusivity. When D_E is >10⁻¹² m²/s, i.e., at realistic values for free enzymes, the enzyme cloud is dilute, and the polymer concentration slightly decreases near the cell, while the monomer concentration is consistently low.

FIG 1.

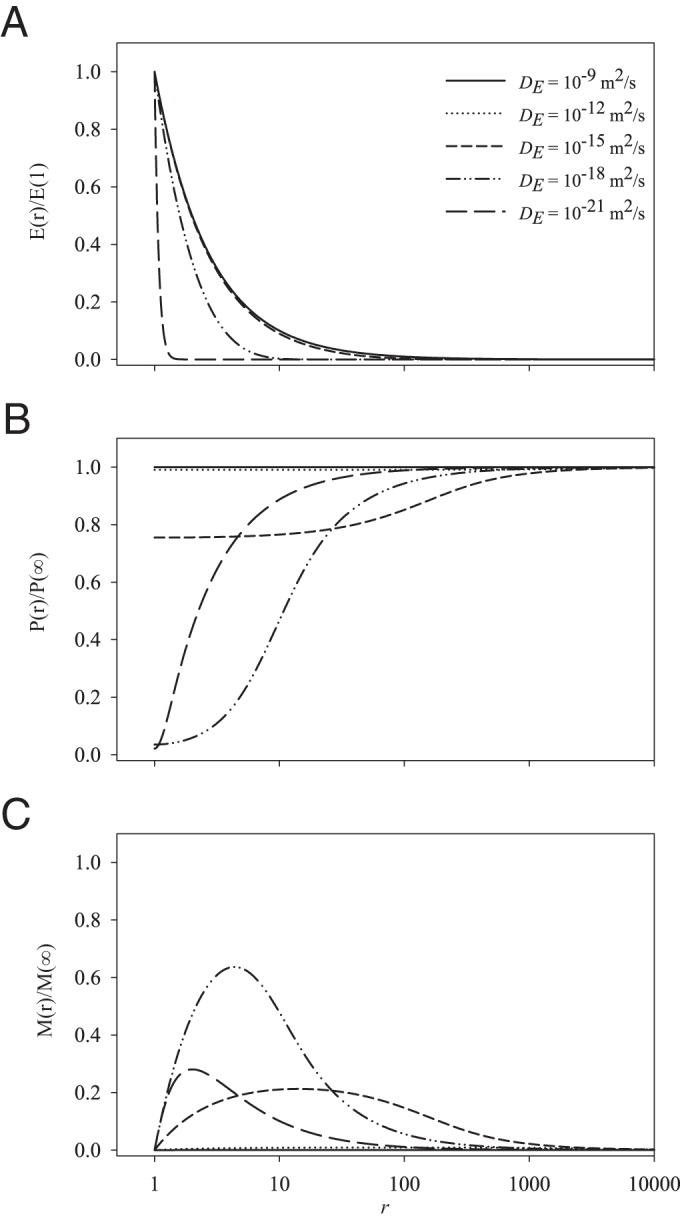
Dimensionless concentration fields of enzymes (E) (A), polymers (P) (B), and monomers (M) (C) as computed from the model for different values of enzyme diffusivity, with the remaining model parameters fixed at default values. Although the dimensionless enzyme concentration fields are similar, there are great differences between the dimensional fields of P and M.

Enzyme efficiency in regard to diffusivity, decay, and production rate.

The cell can optimize uptake efficiency (ε), defined by equation 4, through decreasing the enzyme decay rate (α), increasing enzyme production (Q), or decreasing the enzyme diffusivity (D_E) (Fig. 2). Efficiency is the ratio of monomer uptake compared to direct uptake of polymers. The uptake efficiency decreases with an increase in enzyme diffusivity (Fig. 2A). As the diffusivity approaches zero, the enzymes distribute themselves close to the cell and effectively become surface attached. For default parameter values, surface-attached enzymes (D_E = 0 m²/s) have approximately 100-times-higher yield in efficiency than free enzymes with realistic diffusivities (D_E, ∼5 × 10⁻¹¹ m²/s). In comparison, increasing the enzyme lifetime from 1 to 30 days results in less than 10-times-higher yield in efficiency (Fig. 2A). Furthermore, the enzyme decay rate has less impact on the efficiency as enzyme diffusivity approaches zero (Fig. 2A). For the producing cell, having attached enzymes appears to be the most efficient, resulting in a monomer yield significantly greater than what can be achieved by free enzymes.

Increase in enzyme production is another parameter that also allows the cell to increase enzyme efficiency and is calculated at three different diffusivity values (Fig. 2B). Efficiency increases with enzyme production, Q, initially linearly (note that the slope in log-log is 1, indicating a linear relationship) but eventually saturating at 1, qualitatively similar to a Holling type II functional response (Fig. 2B). A given efficiency may be obtained with high production of high-diffusivity enzymes or with low production of low-diffusivity enzymes. Below saturation, a factor 10 increase in production and a factor 100 increase in diffusivity will, together, result in an unchanged efficiency.

The results show that when enzyme diffusivity approaches zero, the efficiency of the enzyme approaches its optimum use. An enzyme with diffusivity close to zero corresponds to having the enzyme attached to the cell surface.

Total production versus harvest of monomers.

Whether a strategy is profitable for a single cell depends on the amount of monomers that reaches that cell. In order to compare attached and free enzymes, we plot, as a function of enzyme diffusivity, both monomer production and total absorption of monomers (Fig. 3). Low-range diffusivity values represent attached enzymes, and high diffusivity values (10⁻¹² to 10⁻¹¹ m²/s) represent the free-enzyme strategy. The amount of monomers an enzyme produces increases with increasing diffusivity and reaches maximum values when entering the diffusivity range of free enzymes. However, in contrast, the fraction of monomers being absorbed by the cell declines when approaching the diffusivity range of free enzymes. Attached enzymes produce fewer monomers than free enzymes but result in a monomer cloud around the cell (Fig. 1), which effectively leads to almost all of the monomers being harvested by that cell. Free enzymes produce a distinctively different monomer field (Fig. 1), with the majority of monomers being lost from the parent cell through diffusion.

FIG 3.

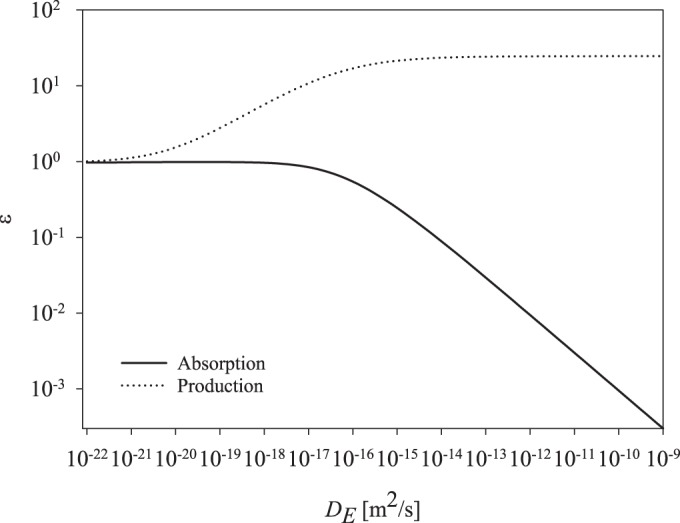
Model predictions of monomer uptake and production by the parent cell as a function of the enzyme diffusivity. As the diffusivity approaches values (10⁻¹¹ to 10⁻¹⁰ m²/s) expected for free enzymes, the enzyme achieves the highest monomer production. However, the amount of monomers harvested by the cell in that diffusivity range is very small. In contrast, the attached enzyme (diffusivity approaching zero) is less efficient in producing monomers, but effectively all the monomers produced are taken up by the cell, yielding a high efficiency for attached enzymes.

When it pays to produce.

Another way to compare the two enzyme strategies is to calculate the substrate concentration each strategy requires in order to return enough monomers to cover enzyme production. The free-enzyme strategy comes with a diffusional loss of both enzymes and monomers. Therefore, the threshold concentration of substrate required for an enzyme strategy to be profitable is defined by a combination of the respective enzyme cost, enzyme reaction rate, decay rate, and diffusivity (equation 6). For a cell to invest in the free-enzyme strategy requires a substrate concentration of 3.3 μmol/liter in order to produce and return enough monomers to compensate for the enzyme cost. For the attached-enzyme strategy, the diffusional loss can be disregarded, simplifying the equation for the threshold concentration (equation 7). This results in attached enzymes being a profitable strategy down to a concentration of 0.4 nmol/liter.

DISCUSSION

Model assumptions.

The model assumes that both enzyme concentrations and substrate concentrations are much smaller than the Michaelis constant (typically denoted K_M). This implies that simple linear enzyme kinetics apply and that the enzyme kinetics are in quasi-steady state (42). While substrate concentrations are very low in the environments we are concerned with, low enzyme diffusivity implies high enzyme concentrations near the cell. In this case, the simplification of the enzyme kinetics will imply slightly exaggerated estimates for the uptake, since enzyme-substrate complexes can diffuse away. The steady-state assumption also applies to the diffusive transport, as is standard in this type of study (e.g., Vetter et al. 30), even if the time required to achieve diffusive steady state may well exceed the lifetime of the cell.

The assumption that cells are nonmotile is based on the fact that nonmotile bacteria dominate oligotrophic waters, as exemplified by the ubiquitous SAR11 clade (20, 21). However, if swimming is to be considered, at realistic cell swimming speeds, the effect is predominantly insignificant, which in part is due to the small cell size, which results in small Péclet numbers. The effect of swimming on monomer uptake is slightly positive for attached enzymes and negative for free enzymes (see the supplemental material, section 6) (43). Specifically, for free enzymes (as plotted in the supplemental material) (Fig. 2), swimming speeds of ≤30 μm/s have little to no effect while swimming speeds of 100 μm/s and greater will cause an increasingly negative effect on uptake as the cell moves away from the enzyme activity. With an enzyme diffusivity of 10⁻¹⁰ m²/s, a 10-fold reduction in uptake is reached at swimming speeds of 340 μm/s. For attached enzymes, swimming will increase uptake, and this becomes noticeable at swimming speeds above 30 μm/s.

For simplicity, we chose to model a single type of enzyme and substrate where each enzyme-polymer encounter results in a single monomer, while the remaining polymer is considered waste. A single cell applying multiple, functionally different extracellular enzymes simultaneously should have little impact on our model, which investigates the deployment strategy. We acknowledge that in nature the hydrolysis process may be considerably more complex. For instance, enzyme reactions may not produce directly usable biomolecules, or some enzyme-polymer systems may produce several biomolecules from a single substrate molecule. The existence of endo- and exoacting enzymes leads to an even more complicated web of possible interactions between enzymes and substrates. Moreover, an extracellular enzyme in nature is most likely not restricted to a single compound but can hydrolyze a specific bond in a range of similar compounds. However, the substrate in the model can alternatively be perceived as different compounds that all contain the same chemical bond and that yield the same product upon hydrolysis. To our knowledge, information about the variation within naturally occurring extracellular enzymes is at present limited. Resolving the specificity and mode of action of predominant extracellular enzymes in seawater would be an important future advancement, which could refine the predictions in the model.

Enzyme efficiency in regard to diffusivity, decay, and production rate.

Decreasing the decay rate of the enzyme allows the enzyme to encounter and hydrolyze more substrate in its lifetime and results in more monomers being harvested by the parent cell, thus increasing the efficiency. However, the gain is modest, since longer-lived free enzymes will hydrolyze substrate at greater distances from the parent cell, resulting in greater diffusional loss of monomers. This is indicated by the relatively small difference in efficiency between the three decay rates. The decay rates are based on recent studies suggesting lifetimes of days to weeks for extracellular enzymes in seawater (34, 41). From the perspective of the producing cell, enzyme lifetimes grossly exceeding this would diminish in importance due to diffusional loss of the hydrolysis products and eventually the enzyme. This becomes clear from Fig. 2A, as the cell harvests more monomers through attached enzymes as opposed to free enzymes with a lifetime of 30 days. However, attached enzymes will also benefit from longer lifetimes, allowing the cell to decrease the production of enzymes and still maintain the same harvest of monomers. Several studies have observed major contributions of dissolved enzymes to total enzyme activity in seawater (25, 26, 34). In this context enzyme lifetimes of weeks can potentially affect microbial growth and consequently carbon turnover rates in the oceans.

The next parameter to consider is the enzyme production rate, which greatly affects the efficiency. Upregulated enzyme production can compensate for diffusive loss of enzymes, thereby increasing enzyme substrate encounter rates closer to the cell and resulting in more monomers being harvested by the cell. Producing more enzymes, however, is an expensive way to optimize the yield of an enzyme strategy, since it will increase the cell's demand for nutrients and energy (43–45). Substrate (energy) availability for microbes decreases with depth in the ocean (1), so particularly for deep-sea bacteria, increased production rates will not be beneficial, especially when considering the yield of monomers obtained through attached enzymes (i.e., decrease of enzyme diffusivity).

The reaction rate is another parameter that is critical for enzymatic hydrolysis of substrates. Published reaction rates are highly variable (Fig. 4) and reflect differences in substrate specificity, temperature, and pH optima for individual enzymes and substrates. The reaction rate is a key parameter because the faster the catalytic reaction, the more monomers will be produced by the enzyme. However, as this applies to both free and attached enzymes, the reaction rate becomes irrelevant for comparison of the two enzyme strategies.

The results indicate that the best approach to optimize the efficiency of an extracellular enzyme is to lower enzyme diffusivity. This can be achieved via two mechanisms. The first is to produce larger enzymes, which increases the molecular size and thereby lowers the diffusivity. We investigate this by taking published data on extracellular enzymes (Table 2) and estimating their diffusivity based on molecular mass. The effect of enzyme size on diffusivity is small (Fig. 2A, span of shaded area), despite relatively large size variation (27 to 94 kDa). The small effect of the molecular mass of the enzyme indicates that enzyme size alone cannot compensate for the difference in efficiency between free and attached enzymes. The second mechanism to decrease enzyme diffusivity is by anchoring the enzyme to the surface of the cell, making it stationary in relation to the cell and theoretically equating to a diffusivity of zero. By having the enzyme attached, the hydrolytic reaction occurs in the vicinity of the cell, which results in a substantial share of the monomer production being harvested by the parent cell. This indicates that attached enzymes are the most cost-efficient strategy when considering solitary cells.

Total production versus harvest of monomers.

To further compare the strategies, monomer production and absorption of those monomers by the parent cell are plotted as a function of enzyme diffusivity. Free enzymes yield a greater production of monomers than attached enzymes, but only a small fraction of those monomers are harvested by the cell. This supports the previous results from the model showing free enzymes to be a less rewarding strategy from the perspective of the parent cell (Fig. 2) and indicates a trade-off where attached enzymes produce fewer monomers than free enzymes but effectively all of the monomers produced by attached enzymes are harvested by the parent cell (Fig. 3). The additional production of monomers by free enzymes does not profit the parent cell; however, it would benefit other cells in the community, which, together with the significant increase in the monomer yield, illustrates the power of the free-enzyme strategy. This has been demonstrated for particulate substrates, where the high substrate densities lead free enzymes to be profitable (30, 46). Although the strategy of free enzymes presumably is costly, producing them may also be favorable for free-living cells through cooperative efforts (47, 48). Indeed, several studies have shown extracellular enzyme regulation by quorum-sensing mechanisms as a means of enhancing the fitness gain offered by such cooperative traits (49–51). For cells to engage in cooperation, several variables must align: close proximity to neighbors, relatedness, and resource density are key (52–54). Particles and phytoplankton blooms present ideal conditions for promoting cooperation between cells. Thus, free enzymes may be a relevant strategy for the free-living fraction of microbes when considered in the context of cooperation or under favorable resource concentrations.

When it pays to produce.

Another interesting comparison between the two enzyme strategies is to consider at which substrate concentration enough monomers will return to the cell to cover the cost of producing the enzyme. This would also further explore the idea of free enzymes as a viable strategy for free-living cells. We have already established that free enzymes come with a diffusional loss of both enzyme and monomers compared to attached enzymes. The remaining parameters (i.e., enzyme cost, decay rate, and reaction rate) were kept constant to compare the free- and attached-enzyme strategies.

The total cost of producing an enzyme is a poorly understood parameter. It depends on several metabolic factors, such as the growth efficiency of the cell and how much of the carbon allocated to biomass is channeled into extracellular enzymes. Bacterial growth efficiency alone can vary between 1 and 80% (55), depending on environmental parameters, which illustrates the difficulty in constraining the cost of an enzyme. Therefore, we disregard metabolic variability between microbes and across environments in the model, which in any case supposedly influence the threshold concentrations of both strategies equally. We seek to compare the two enzyme strategies; therefore, less importance can be placed on the specific input values of enzyme cost, decay rate, and reaction rate, as they are kept constant. One could imagine that the biological variability of extracellular enzymes and substrates elicits an equivalent variability in the threshold concentration. The results provide an indication of the order of magnitude of substrate concentrations required to support either strategy. To compensate for the diffusional loss of both enzyme and monomers, a free-enzyme strategy requires substrate concentrations in the micromolar range in order to produce and return enough monomers to pay for its own carbon cost. For the attached enzyme, the diffusional loss could be disregarded, which results in the attached enzyme being profitable below nanomolar concentrations. Interestingly, the deployment strategy itself has a significant impact on the threshold concentration, thus suggesting that how an enzyme is deployed can optimize the performance of extracellular enzymes and how much substrate needs to be present in order for an enzyme to be viable to produce. We emphasize that specific threshold concentrations will vary with the kinetics of each unique extracellular enzyme and as such may differ from the above-mentioned concentration thresholds.

In the oceans, specific compounds of the major biochemical classes, carbohydrates and amino acids, fluctuate between concentrations on the nanomolar scale to below the detection limit, depending on season and depth (14, 15, 56). This corresponds well to the low threshold concentrations we find for attached enzymes in the model. Presumably, attached enzymes are cost-effective enough to drive concentrations of specific compounds down and maintain them at nanomolar levels. This implies that extracellular enzymes (both free and attached) play an active role in shaping the DOM pool in the oceans. In addition, most specific DOM compounds likely exist at very low concentrations, which would strongly select against the use of free enzymes. However, we interpret the higher threshold concentration (micromolar) for the free enzymes in our model to indicate significantly different conditions under which this strategy is advantageous. Phytoplankton blooms could create optimal conditions for releasing free enzymes, as senescent stages of blooms are known to produce and temporarily accumulate certain classes of compounds (e.g., carbohydrates and amino acids) at high concentrations in the water column (57, 58). Another environment is within and around organic particulates, which can be considered nutrient hot spots in the water column. They provide substrate concentrations high enough for free enzymes to be profitable. This is consistent with the conclusions drawn for enzyme strategies of particle-associated bacteria (30).

It is important to keep in mind that although a single compound may be extremely dilute in the oceans (14), extracellular enzymes may exhibit relatively relaxed substrate specificity within their class of substrates (59). It is possible that such enzymatic flexibility allows an enzyme to target enough suitable compounds to reach substrate concentrations in the nano- to micromolar range. However, a “broad” substrate range is relative, as enzymes have both structural and chemical challenges when hydrolyzing a compound. The varying reaction rates of similar enzymes on different compounds (Fig. 4) indicate high biochemical variation in how an enzyme interacts with its substrates.

The initial modeling effort reported here is not intended to replace empirical data but to uncover relationships that are not identified with current methods. The model suggests that deployment of attached enzymes is the most efficient foraging strategy for a free-living cell under oligotrophic conditions, such as those found at depth in most of the global ocean. However, our model does not suggest that the two strategies are mutually exclusive. For the solitary cell, deployment of free enzymes still provides an advantage over no enzymes under high substrate concentrations. Furthermore, the free enzymes result in substantial hydrolytic reactions, forming large and dilute clouds of monomers that never reach the parent cell but may benefit bacteria at the community level. This suggests that free enzymes may be a viable strategy, even for free-living cells, if substrate utilization is viewed as a cooperative effort. Combined with a long enzyme lifetime, even small amounts of free or escaped enzymes from the free-living fraction of microbes could contribute significantly to the dissolved-enzyme activity. Interestingly, this may present an alternate explanation for high enzyme activities, which recent studies have attributed primarily to dissolved enzymes (26, 34, 60) and which are currently believed to originate from particles (26, 32).

Extracellular enzymes are the first step in microbial DOM processing, and our results indicate that a threshold concentration for viable enzyme-based degradation exists. Individual substrates below such a threshold concentration would be less attractive for biological utilization, thus making the compound persist at low concentrations. The combination of an enzyme threshold concentration and the dilute nature of individual compounds could explain the persistence and apparent refractory state of some compounds in oceanic DOM. This aligns with the hypothesis that a large fraction of DOM in the oceans persists primarily due to dilute concentrations (61–63) and calls for further experiments and methodological developments to further investigate this. Extracellular enzymes and how microbes utilize them in response to ambient DOM carry important implications for microbial ecology and the microbial impact on carbon sequestration in the ocean as DOM.