Melting of iron determined by X-ray absorption spectroscopy to 100 GPa

Significance

There is a long-standing controversy over the melting curve of Fe at high pressure as determined from static laser heated diamond anvil cell and dynamic compression studies. X-ray absorption spectroscopy measurements are used here as a criterion to detect melting under pressure. Confronted with a diversity of obtained melting curves, this technique, used at such pressure and temperature conditions, is eligible to be at the forefront to probe Earth's deep interior. Furthermore, the experiment reported here holds promise for addressing important issues related to the structure and phase diagram of compressed melts, such as the existence of structural complexity (polyamorphism) in the liquid phase or the extent of icosahedral ordering whose investigation has been limited until now to ambient conditions.

Abstract

Temperature, thermal history, and dynamics of Earth rely critically on the knowledge of the melting temperature of iron at the pressure conditions of the inner core boundary (ICB) where the geotherm crosses the melting curve. The literature on this subject is overwhelming, and no consensus has been reached, with a very large disagreement of the order of 2,000 K for the ICB temperature. Here we report new data on the melting temperature of iron in a laser-heated diamond anvil cell to 103 GPa obtained by X-ray absorption spectroscopy, a technique rarely used at such conditions. The modifications of the onset of the absorption spectra are used as a reliable melting criterion regardless of the solid phase from which the solid to liquid transition takes place. Our results show a melting temperature of iron in agreement with most previous studies up to 100 GPa, namely of 3,090 K at 103 GPa.

Iron is the principal constituent of the Earth’s core (1), and knowledge of its melting curve at inner core boundary (ICB) conditions is one of the major concerns in geophysics. At the ICB, corresponding to a depth of 5,150 km and to a pressure of 330 GPa, the solid inner core melts and the outer core is liquid. Even though the temperature at which the solid core becomes liquid should be adjusted to take into account the effects of light elements in the solid and liquid cores, the knowledge of the melting temperature of iron is an important fixed point in the thermal profile of Earth’s interior. Earth’s magnetic field is generated by a dynamo in the liquid iron core that has a convection motion as a result of cooling of the overlying mantle. Because the melting temperature of iron puts a constraint on the thermal gradient across the core–mantle boundary and the heat flow from the core, it represents the key to understand Earth’s dynamo and therefore the implications to the terrestrial magnetic field.

A considerable effort has been expended to study the melting of iron at high pressure both theoretically (2–5) and experimentally, but this has led to considerable discrepancies in the estimates of the temperature in the center of Earth. This discrepancy, as large as 2,000 K at ICB conditions (330 GPa), has a significant impact on dynamic and thermal evolution models. The numerous studies have been summarized in several recent papers (6, 7).

Besides shock compression, laser heating in diamond anvil cells (LHDAC) allows one to generate the very high pressure and temperature conditions of Earth’s core. In LHDAC studies, the maximum pressure for which iron melting temperatures have been reported is 200 GPa (8, 9), but the difference in the melting temperature in these measurements exceeds 1,000 K. Even the two most recent studies using synchrotron X-ray diffraction (XRD) and X-ray Mössbauer techniques (8, 10) show melting temperatures differing by 800 K at 100 GPa. The difficulty in measuring the melting temperature is particularly concerning, given that two X-ray diffraction measurements, carried out at the same beamline at the European Synchrotron Radiation Facility (ESRF) (8, 11), led to a difference in the melting temperature of 980 K at 130 GPa.

Here we report a determination of the solid–liquid phase boundary of iron compressed to over 100 GPa in an LHDAC by means of energy-dispersive X-ray absorption spectroscopy (EDXAS) using a well calibrated optical system and a novel sample encapsulating technique, which avoids chemical reactions and deterioration of the sample geometry.

X-ray absorption spectroscopy (XAS) provides structural information within a few angstroms around the photoabsorbing atom, and therefore maintains the same sensitivity and accuracy regardless of the physical state of the investigated sample (crystalline, amorphous, or liquid). This is a considerable asset with respect to diffraction techniques in which the onset of melting appears as a weak diffuse halo superimposed onto strong Bragg reflections from partially molten sample and sample environment. Similarly to diffraction techniques, X-ray absorption near edge structure (XANES) spectra may distinguish different crystallographic phases, but, in addition, it may shed some light on the electronic structure. A further advantage with respect to other methods is that, given its chemical selectivity, the XANES spectra contain solely the signal relative to the absorbing element, without any interference of the container or experimental environment. This is particularly convenient when the sample environment is particularly bulky, such as at high-pressure conditions. From the XANES part of the spectrum, it is possible to retrieve the coordination geometry of the atom of interest and its speciation, giving information about possible chemical reactions that may occur at specific conditions of the sample. EDXAS allows fast (from nanoseconds to a few seconds per spectrum depending on the experimental conditions) acquisition of the whole spectrum with a small (<5 μm) X-ray focal spot. These are significant advantages for studies of molten systems at high pressure with in situ LHDAC, in which samples are small and unstable under laser heating. In a previous exploratory study (12), EDXAS was coupled to an in situ LHDAC to follow the structural evolution of Fe up to 3,000 K and 80 GPa, assessing the capability of the method for melting diagnostics. A major issue in EDXAS studies is that the sample is required to maintain uniform thickness during heating and melting over an area larger than the synchrotron X-ray beam diameter. For this reason, particular care has been taken in the sample preparation (see Materials and Methods and Supporting Information).

Results

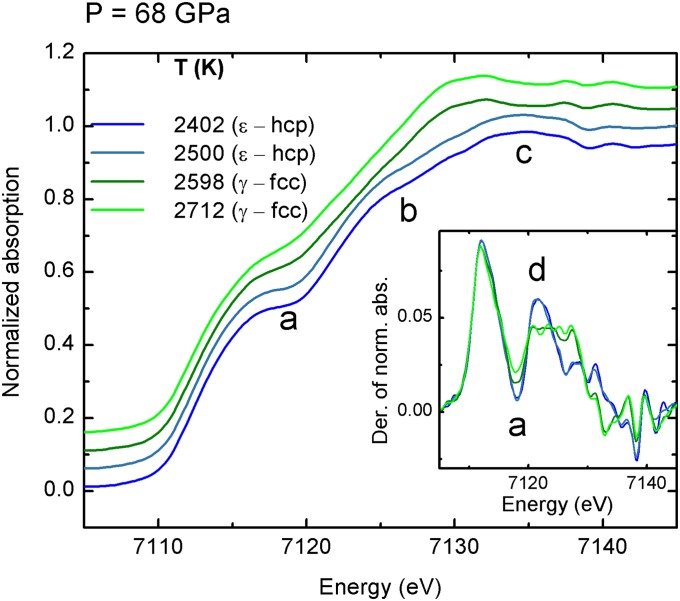
Fig. 1 shows some illustrative XANES spectra of iron between 2,400 K and 2,710 K along the 68-GPa heating series. The XANES spectra were normalized to one absorption event and are shown together with their derivatives (Fig. 1, Inset). They show evidence of a structural phase transition that, according to the well-established iron phase diagram in this P–T range, can be attributed to ε-Fe (hcp) to γ-Fe (fcc) transition. The spectra collected at lower temperature (blue curves) depict features typical of the ε-hcp phase (13), characterized by a pronounced shoulder in the onset of the absorption, that gives rise to a plateau (feature “a”), followed by a bump (feature “b”) and by a maximum (feature “c”). Upon heating (green curves), some changes occur: plateau “a” is smoothed out, bump “b” disappears, and maximum “c” shifts to lower energy (14, 15). These modifications are even more evident in the derivatives of the spectra (Fig. 1, Inset). At the transition, the deep minimum in the derivative corresponding to the plateau in the normalized spectra, both indicated as “a,” becomes more shallow, and peak “d” (originating from bump “b”) flattens out to a constant value between ∼7,120 eV and ∼7,128 eV. These changes are observed for all heating series (see Supporting Information) in agreement with the known ε-hcp to γ-fcc phase boundary.

Fig. 1.

XANES spectra of iron recorded at 68 GPa with increasing temperature through the ε-hcp to γ-fcc phase transition. The blue curves correspond to the ε-hcp structure, and the green curves correspond to the γ-fcc phase. (Inset) The derivatives of the XANES spectra are reported.

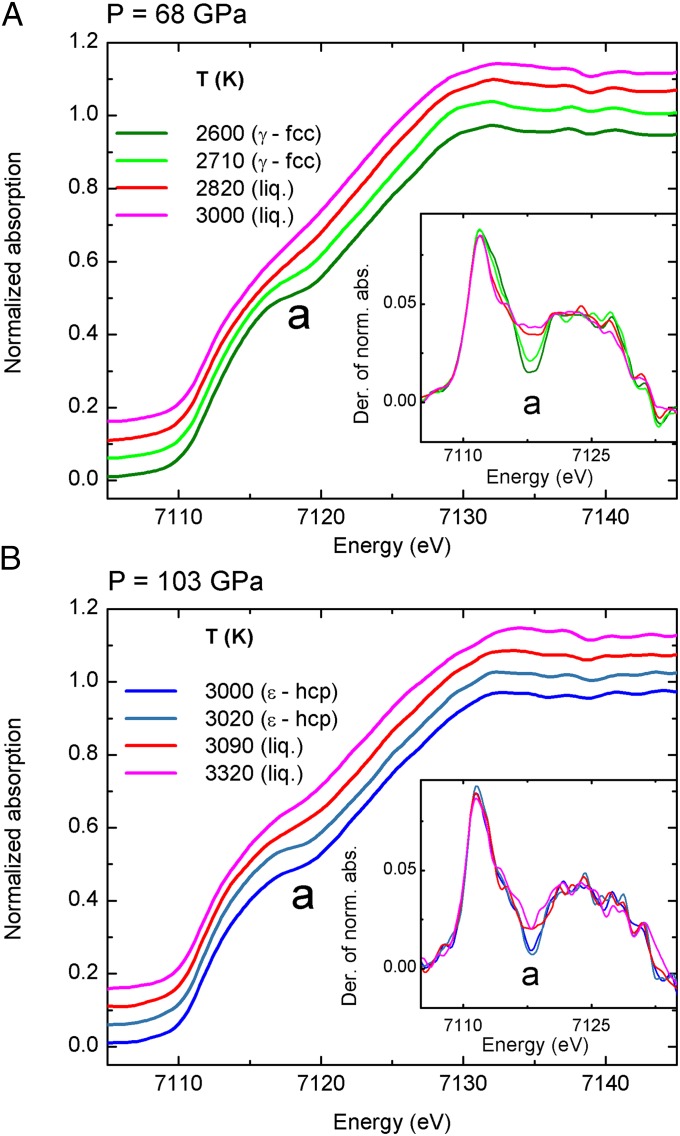
Fig. 2 shows XANES spectra through the solid to liquid phase transitions at 68 GPa from 2,600 K to 3,000 K (Fig. 2A) and at 103 GPa from 3,000 K to 3,320 K (Fig. 2B). The modifications of the onset of the absorption can be used as a signature for the solid to liquid phase transition. At the solid (either γ-fcc or ε-hcp) to liquid phase transition, the data show a discontinuous behavior. The derivatives of the XANES highlight this change, with minimum “a” flattening abruptly.

Fig. 2.

XANES spectra of iron recorded at 68 GPa (A) and 103 GPa (B) with increasing temperature through the γ-fcc to liquid (A) and the ε-hcp to liquid (B) phase transition. (Insets) The derivatives of the XANES spectra are reported.

The energy region around plateau “a” between 7,115 eV and 7,120 eV is the most sensitive to disruptions in crystalline order. This part of the spectrum is affected by broadening with increasing temperature, ascribed by recent density functional theory (DFT) based theoretical calculations (16) to the thermal motion of the atoms. However, at melting, either from ε-hcp or γ-fcc, the broadening increases discontinuously following the breakdown of crystalline order characteristic of the liquid phase. A similar effect has been observed at all of the recorded pressures (see Supporting Information). The K edge XANES of iron involves, in the dipole approximation, the electronic transition from the 1s to the empty 4p states (17). The observed smoother absorption onset in the liquid phase can therefore be attributed to a broader distribution of empty 4p states as a consequence of the lack of crystalline order. The same effect of discontinuous broadening in the XANES spectra has not only been theoretically predicted by DFT calculations on iron at high temperature and pressure conditions (16) but has also been observed experimentally at the solid to liquid transition in other transition metals such as Cu (18) and Ni (19) at ambient pressure. In these studies, the solid to liquid phase transition was additionally confirmed by combined X-ray diffraction measurements.

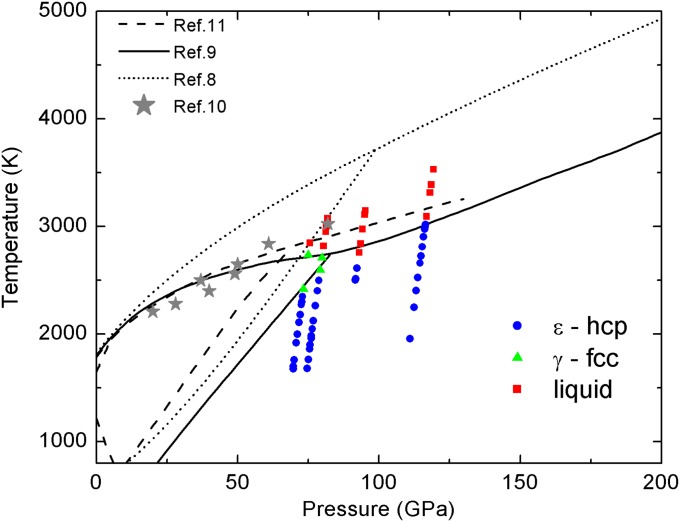
Fig. 3 shows the P–T conditions at which all of the XANES measurements have been collected. Different symbols and colors correspond to ε-Fe (blue dots), γ-Fe (green triangles) and liquid Fe (red squares) phases as determined from the XANES spectra. Phase boundaries reported in refs. 8–11 are also shown for comparison. The phase diagram is reported with thermal pressure corrections (10).

Fig. 3.

P–T conditions at which XANES spectra were collected. Blue dots correspond to ε-hcp Fe. Green triangles correspond to γ-fcc Fe. Red squares correspond to liquid Fe. Half thermal pressure has been considered. This has been determined from Fe phonon density of states to 151 GPa (10). Phase boundaries for iron from other experimental studies are also shown (solid black line, ref. 9; dashed black line, ref. 11; dotted line, ref. 8; stars, ref. 10).

Discussion

In the context of continuous efforts to provide additional experimental data toward resolving the discrepancy in the measured melting curve of Fe at high pressure, the results here reported are an independent measurement of the melting curve obtained by an experimental technique different from those used in previous experimental studies. The XAS experiment provides continuous monitoring of the changes of both the atomic and electronic structure as a function of temperature, and it is optimally suited to detect the onset of order–disorder or solid–liquid transitions. The melting criterion here adopted is based on changes occurring in the near-edge region of the absorption spectrum (XANES) that is known to be less affected by thermal damping and by the noise associated with extreme experimental conditions. We show here that the detection of the new phase does not appear gradually as a weak background superimposed to a much larger signal as in XRD methods but as a discontinuous change in the XANES signal that has similar amplitude with respect to that in the solid phase. This is an advantage of XANES over XRD because, in a partially molten sample caused by temperature instabilities (11), the signature of the melting has the same intensity as that of the solid sample whereas, in XRD, the diffused halo characteristic of the liquid sample is weak with respect to the signal coming from the solid part of the sample. This is especially true when phenomena defined as “recrystallization” (11) or “fast crystallization” (8) occur, giving rise to intense Bragg peaks.

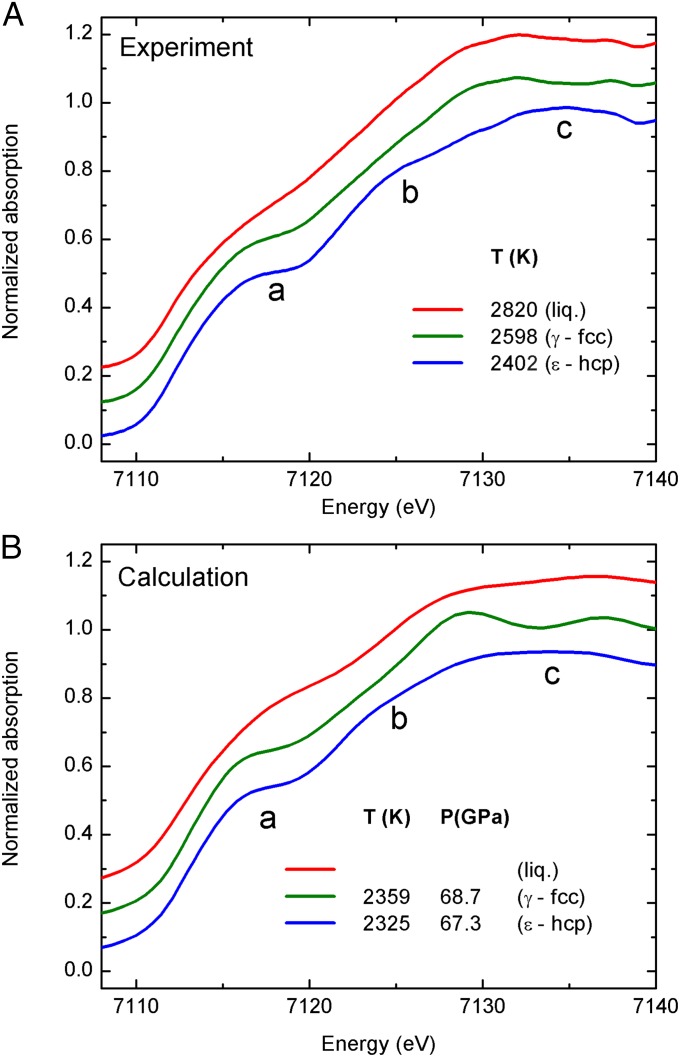
Fig. 4 reports a comparison between the experimental XANES recorded at 68 GPa at different temperatures (blue line, ε-Fe (hcp); green line, γ-Fe (fcc); red line, liquid iron) compared with full multiple-scattering calculations to simulate the XANES region of the spectra at thermodynamic conditions comparable to the experimental ones (the details of the calculations are reported in Supporting Information). Concerning the hcp to fcc transition, the calculations confirm the flattening of the bump “b” and the shifts of the maximum “c” to lower energy. On the other side, the XANES calculation of iron in the fcc phase shows a second maximum just above 7,135 eV which is less evident in the experimental data presented in this work. As well, the smoothing of the plateau “a” discussed before on Fig. 1 is less pronounced in the calculated XANES. Approximations used for the theoretical XANES calculations could be invoked to explain these discrepancies. More interesting, instead, is the behavior of the onset of the absorption that has been used in discussing Fig. 2 as a signature for the solid to liquid phase transition. In fact, consistent with the experimental data, the XANES calculation shows the same modifications of plateau “a” between 7,115 eV and 7,120 eV in the liquid phase with respect to the solid phases characteristic of the disruption of the crystalline order.

Fig. 4.

Experimental XANES spectra of iron recorded at 68 GPa (A). Calculated XANES spectra of iron in the ε-hcp phase (blue line), γ-fcc phase (green line), and liquid phase (red line) (B).

The present results show excellent agreement for the ε-Fe (hcp) to γ-Fe (fcc) transition reported earlier (6, 7), and the present melting data are in agreement with most previous studies up to 100 GPa resulting in a flat melting curve near 3,000 K at that pressure range. This is in stark disagreement with the recent XRD study by Anzellini et al. (8). The latter reports a much steeper melting curve at that pressure range and a melting temperature that is 700 K higher than the majority of all previous studies (6). This difference has significant implications for estimating the temperature in Earth’s interior, which determines the value of the temperature jump at the core–mantle boundary, which is key for calculating the core–mantle heat flow, inner core age, dynamo models, and cooling history of Earth. Although an accurate extrapolation of the present data to Earth’s core conditions is difficult given the limited number of experimental data above the triple point, our results are in agreement with the majority of diamond anvil cells (DACs) measurements in the 100-GPa pressure range (7) and with previous data to 200 GPa (9). The latter suggests a melting temperature of iron below 5,000 K when extrapolated to ICB conditions.

The experimental method here reported paves the way for extensive studies of molten metals at extreme pressures. For liquids, it is known that frustration, defined as the presence of locally preferred structures incompatible with the crystal periodicity, may have important consequences in the melting. For molten iron, together with other metals with partially filled d bands, liquid frustration was proposed as an explanation for the low slope of the melting curve (20). In the present work, the analysis is focused on the features of the near-edge region of the XAS spectrum because they are clear fingerprints for the occurrence of melting. However, previous studies have demonstrated that XAS is capable to evidence the existence and extent of preferred local geometries in molten metals at ambient conditions (18, 19). Therefore, beyond geophysical implications, the present results may be used to investigate the structure of compressed liquid Fe and possibly validate the hypothesis on the presence of frustration.

Materials and Methods

The pressure is generated using a Boehler–Almax plate DAC equipped with monocrystalline conical diamond anvils (21) of 250–300 μm of diameter. A rhenium gasket is preindented to a thickness 40 μm. A hole of 100 μm diameter is then drilled on the culet imprint.

The sample container consists of two discs of sapphire manufactured using a combination of micropolishing and focused ion beam milling (FIBM). The cavity dimension of 18 μm diameter and 6 μm depth is chosen to optimize the synchrotron beam condition at the beamline ID24 (22) at ESRF. The single-crystal capsule and its lid are embedded in very fine-grained (3–5 μm grain size) dried Al₂O₃ powder, which molds around the capsule to prevent fracture during loading and after laser heating. One ruby grain of 2–3 μm size was also mixed with the Al₂O₃ powder (see Supporting Information).

The principal optical layout of the laser heating and temperature measurement system is very similar to the one described in ref. 23. The major difference is that the optical components do not interfere with the direct X-ray beam, allowing true simultaneous measurements of temperature from both sides of the sample as well as the X-ray absorption spectra. Further details are given in Supporting Information.

The XAS measurements in transmission geometry are carried out at the dispersive extended X-ray absorption fine structure (EXAFS) beamline ID24 at ESRF (22). The size of the beam at the sample is of 5 × 5 μm² FWHM. Spectra are recorded using a CCD-based position sensitive detector. Pixel energy calibration is obtained by measuring spectra on a metallic Fe foil at ambient conditions. XAS spectra are collected every few seconds before, during, and after heating in four different runs in the pressure range 63–103 GPa and temperatures up to 3,530 K. For each heating cycle, the laser power is ramped up incrementally and kept constant for several seconds to record the XAS spectrum and light emission to measure the temperature. Pressures are determined before and after heating cycles using both ruby and the Raman spectra of the diamond anvil tips (24), with the accuracy within 2 GPa at the highest pressure achieved. After several heating cycles, these pressures are within 5 GPa. XANES spectra of the same sample are recorded at the beginning of each heating cycle and show that chemical reactions of the sample with the environment, if any, occur for a fraction of the sample that is below the XANES detection limit. Moreover, in each cycle we find the same transition temperatures within the experimental error. See Supporting Information for additional experimental details.

Extended Data

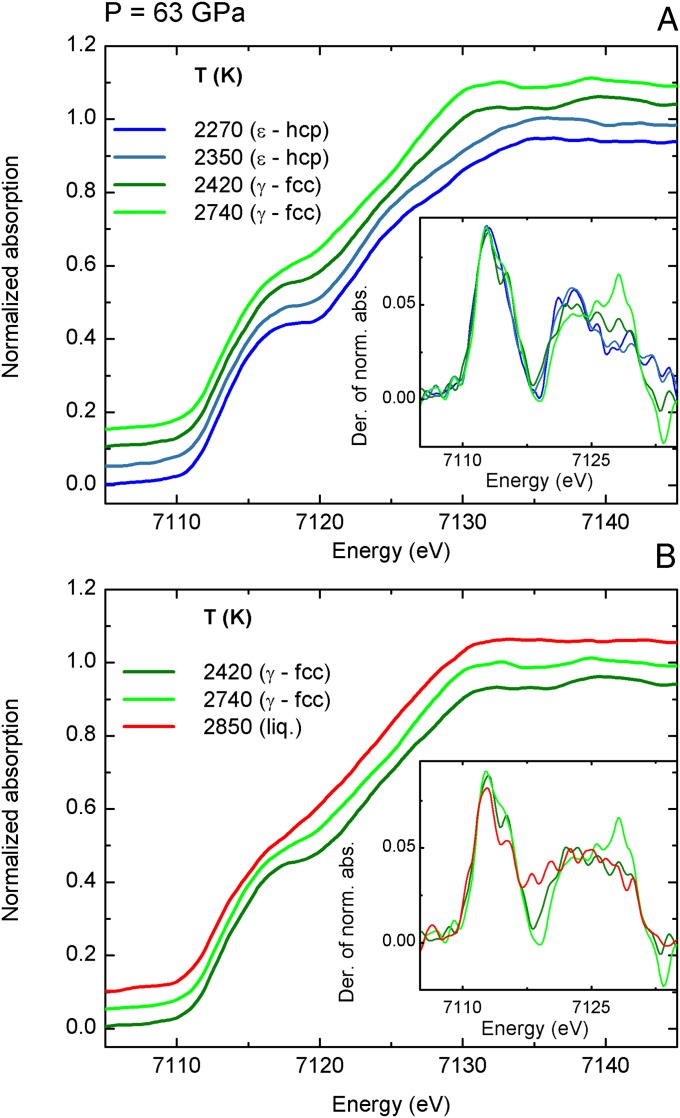
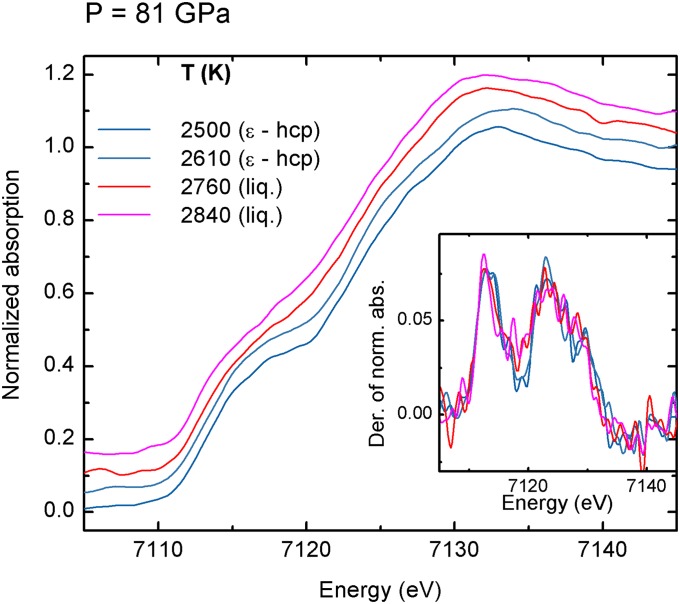
XANES spectra of iron recorded at 63 GPa and at 81 GPa are shown in Figs. S1 and S2.

Fig. S1.

XANES spectra of iron recorded at 63 GPa with increasing temperature through the ε-hcp to γ-fcc (A) and from the γ-fcc to liquid (B) phase transition. (Insets) The derivatives of the XANES spectra are reported.

Fig. S2.

XANES spectra of iron recorded at 81 GPa with increasing temperature through the ε-hcp to liquid phase transition. (Inset) The derivatives of the XANES spectra are reported.

Sample Preparation

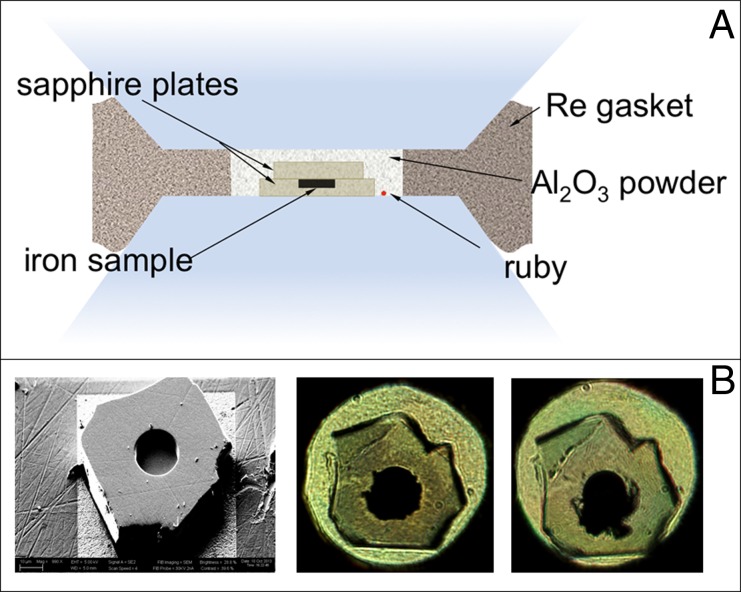
The sample loading is sketched in Fig. S3A. The sample container consists of two discs of sapphire manufactured using a combination of micropolishing and FIBM (Fig. S3B, Left). The cavity dimension of 18 μm diameter and 6 μm depth is chosen to optimize the synchrotron beam condition at the beamline ID24 (22) at ESRF. The single-crystal capsule and its lid are embedded in very fine-grained Al₂O₃ powder, which molds around the capsule to prevent fracture during loading and after laser heating (Fig. S3B, Center and Right).

Fig. S3.

(A) Schematics of the sample loading. (B) Sample containment using single-crystal sapphire. (Left) Disk before loading. The disk is 10 μm thick, with a cavity 18 μm in diameter and 6 μm deep machined with FIBM. The iron sample with the same dimensions is laser-cut from a foil. (Center) Picture in transmitted light taken at 24 GPa before heating. The capsule shows no sign of cracks. (Right) Picture taken at 100 GPa after three heating/melting events.

X-Ray Absorption Spectroscopy Experiment

The XAS measurements in transmission geometry are carried out at the dispersive EXAFS beamline ID24 at ESRF (22). The electron energy and the maximum current are 6 GeV and 200 mA, respectively. The gap of the undulator is optimized to have the maximum of the first harmonic in the energy range 6,900–7,300 eV. The optics includes a pair of silicon mirrors in a Kirkpatrick–Baez geometry at grazing angle of 3 mrad followed by a Si (111) polychromator crystal in the Bragg geometry and an additional vertical focusing Si mirror at grazing angle of 3.5 mrad. The size of the beam at the sample is 5 × 5 μm² FWHM. Spectra are recorded using a CCD-based position sensitive detector. Pixel energy calibration is obtained by measuring spectra on a metallic Fe foil at ambient conditions.

XAS spectra are collected every few seconds before, during, and after heating in four different runs in the pressure range 63–103 GPa and temperatures up to 3,530 K. For each heating cycle, the laser power is ramped up incrementally and kept constant for several seconds to record the XAS spectrum and light emission to measure the temperature.

Pressure Measurements

Pressures were determined before and after heating cycles using both ruby and the Raman spectra of the diamond anvil tips (24) with the accuracy within 2 GPa at the highest pressure achieved. After several heating cycles, these pressures were within 5 GPa. In the cell configuration used in this study, with an Al₂O₃ pressure medium, the thermal pressure contribution could be as much as 30% as reported elsewhere (10). The phase diagram with the thermal pressure corrections reported by Jackson et al. (10) determined from Fe phonon density of states to 151 GPa (25) is reported in Fig. 3.

Laser Heating Setup and Temperature Measurements

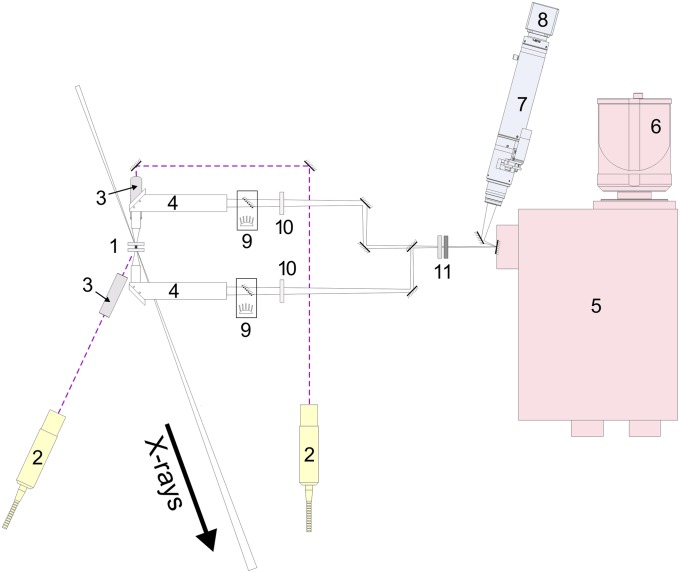
Fig. S4 shows a schematic of the optical layout of the laser heating and temperature measurement system. A DAC (site 1) is mounted in a water-cooled copper holder. Two 1,070-nm IR fiber lasers (site 2) are focused on both sides of the sample with lenses with 50-mm focal length (site 3). Each laser has a maximum power of 120 W. The sample image is collected by custom objectives (site 4) with 16.7× magnification, and then projected on the entrance of the spectrometer (site 5). We use a standard Czerny–Turner-type spectrometer (Acton SP2300; Princeton Instruments) with focal length of 300 mm, equipped with a planar holographic grating having a density of 150 grooves per millimeter. Optical spectra in a wide visible to near-IR range (420–950 nm) are recorded with a 2D back-illuminated CCD from Princeton Instruments (model PIXIS-400) (site 6) with a 1,340 × 400 pixel matrix cooled down to −75 °C, which provides high sensitivity and quantum efficiency combined with low dark current for exposure times varying from 10 ms to several seconds. The entrance slit of the spectrometer is replaced with a front-surface mirror featuring two holes of ∼35 μm diameter each, vertically separated for collecting the upstream and downstream spectral stripes on the same CCD frame. The temperature probe size therefore is nominally 2 μm. The motorized zoom microscope produced by the Navitar company (site 7) is focused on the spectrometer entrance mirror, providing a sharp and clean image with the help of a digital CCD video camera (KP-FD32F model; Hitachi Kokusai) (site 8), needed for precise sample and lasers alignment. The integrated coaxial illumination modules (site 9) allow sample visualization in transmitted and/or reflected light. We use two notch filters (site 10) to remove the laser radiation, and two neutral density absorbing filters (site 11) to prevent saturation at high temperatures.

Fig. S4.

ID24 laser heating setup layout: 1, DAC; 2, IR fiber lasers; 3, laser focusing lenses (F = 50 mm); 4, imaging objectives; 5, optical spectrometer for analyzing thermal emission from the sample; 6, CCD detector; 7, a motorized zoom microscope with the color CCD video camera (site 8) for sample imaging and alignment; 9, coaxial LED illumination modules; 10, notch (laser line removal) filters; 11, neutral density (gray) absorbing filters. X-ray direction is shown with a thick arrow.

A critical part of the microscopic optical pyrometry measurements is the choice of imaging optics. The system uses a right angle objective holding both a front optical achromatic lens (0.5” diameter, F = 30 mm) and a back achromatic lens (1” diameter, F = 500 mm) (Fig. S5). Both lenses were purchased from Thorlabs.

Fig. S5.

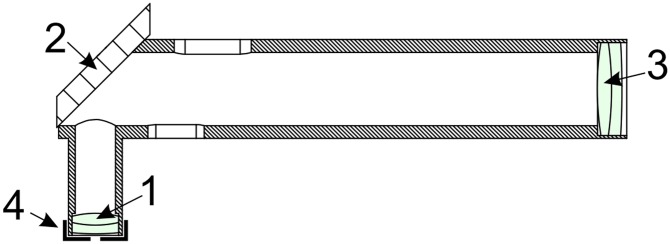
Imaging objective design: 1, front achromatic lens (F = 30 mm); 2, a front-surface mirror mounted at 45°; 3, back achromatic lens (F = 500 mm); 4, removable front iris aperture used to eliminate chromatic aberrations during temperature measurements.

During temperature measurement, a concentric iris with 3 mm diameter is inserted in front of the first lens to minimize chromatic aberrations (see ref. 23). With the iris removed, the optical resolution and throughput is maximized, making relative alignment of the X-ray beam, lasers, and spectrometer entrance straightforward (the X-ray spot becomes visible due to the X-ray excited luminescence in the diamond and sapphire capsule). With the iris in place, chromatic aberrations in the range 450–950 nm are reduced to a negligible level at the cost of a slight loss of spatial resolution. As a result, the temperature is analyzed from a ∼5-μm spot, which matches perfectly the X-ray spot size and therefore the sample area probed by XAS measurements. Here we report the details of the alignment: (i) A flat and uniform part of the sample is centered on the X-ray spot. The quality of the XAS spectrum confirms that X-rays illuminate a homogeneous portion of the sample. (ii) With increasing the CCD camera exposure time, the X-ray spot is visualized using the fluorescence excited in diamond anvil and pressure medium. (iii) The position of the objectives is adjusted so that the sample is in focus and the X-ray spot position perfectly matches the spectrometer entrance hole from both sides of the sample. (iv) With all of the filters removed, the position of the IR heating laser spot is adjusted along with the focusing lens position to produce a large (typically 40–50 μm) laser spot at the desired position. This alignment is performed at a minimal laser power (∼150 mW), so no heating occurs. This alignment procedure guarantees a relative position of X-ray beam and temperature probed area to match within ∼1 μm precision.

The relative alignment between the X-ray and optical probe is an essential part of the experiment. Modern synchrotron X-ray beams are as small as a few microns, whereas radial thermal gradients in a laser-heated DAC can reach several hundred degrees per micrometer. A quite small (∼5 μm) mismatch between temperature probe and X-ray beam can easily produce temperature measurement error on the order of 500 K or more. During laser heating, an experimentalist can only observe the hot spot from the sample, not the X-ray beam position. Therefore, if a misalignment of the hot spot position relative to the spectrometer entrance occurs, this would be immediately noticed and corrected. At the same time, if some X-ray spot misalignment occurs, it cannot be seen immediately, nor can it be found postfactum from data reduction. Thus, small misalignments would more likely result in temperature overestimations (in other words, X-rays probe a colder part of the sample). We believe that this can explain some of the discrepancies between different experiments on iron melting curves using a laser-heated DAC.

The high resolution and the numerical aperture of the optical system in combination with the discrete heating strategy (i.e., the laser is on for 2–3 s only) allowed us to verify X-ray alignment continuously, and to minimize the risk of misalignments of any kind. The discrete heating also dramatically decreases total heat dissipation in a DAC, which is the main reason for sample and optics drifting in space.

The IR heating lasers are focused to a point to produce the flattest possible temperature profile across the sample, and the powers of the lasers are adjusted to produce identical temperatures on both sides of the sample. The absence of chromatic aberrations is verified by measuring the image sharpness at different wavelengths and also by moving/displacing the objective by 0.1 mm toward and away from the sample while having a stable hot spot at moderate temperatures (∼2,200 K); temperature readings were identical within ±100 K.

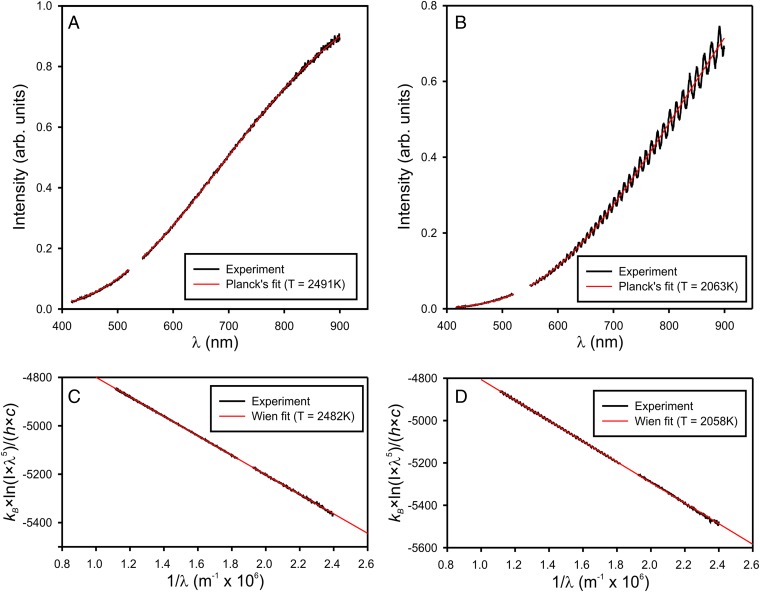
The emitted spectra from the sample are fitted within a gray-body approximation (constant emissivity) to the Planck’s function in the 500- to 950-nm range, after applying an instrumental response correction. Two examples of corrected experimental spectra and the corresponding Planck’s fits are shown in Fig. S6 A and B. A small spectral region around 532 nm cut off by the notch filters is omitted.

Fig. S6.

Two examples of Planck’s temperature fits with and without etaloning in the pressure medium at 2,491 K (A) and 2,063 K (B), and their respective representations in a linear form within Wien’s approximation (C and D).

The spectral correction coefficients are calculated from a reference spectrum (i.e., the thermal emission signal collected from a calibrated tungsten filament lamp of known temperature). Perfectly parallel thin platelets of sapphire, such as those used for sample confinement, are known to produce significant interference (etaloning) of visible light, which is recorded as intensity oscillations (Fig. S6B). These oscillations, however, do not affect temperature fits, because their period is much shorter than the fitting range.

According to Planck’s law, a black body at temperature T emits electromagnetic radiation of intensity at a given wavelength λ given as

$$I=\frac{2h{c}^2}{{\lambda }^5\left(exp\left(\raisebox{1ex}{$hc$}\!\left/ \!\raisebox{-1ex}{$\lambda k_{B}T$}\right.\right)-1\right)}$$ [S1]

where h and k_B are the Planck’s and Boltzmann’s constants and c is the speed of light. Within the gray-body approximation used in this study, a constant emissivity parameter ε is applied (0 < ε ≤ 1) and

$$I=\epsilon \frac{2h{c}^2}{{\lambda }^5\left(exp\left(\raisebox{1ex}{$hc$}\!\left/ \!\raisebox{-1ex}{$\lambda k_{B}T$}\right.\right)-1\right)}.$$ [S2]

There is a commonly used Wien’s approximation to the Planck’s law, which is valid if

$$\raisebox{1ex}{$hc$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.\gg k_{B}T.$$

In this approximation, Eq. S2 turns into

$$I=\epsilon \frac{2h{c}^2}{{\lambda }^{5}exp\left(\raisebox{1ex}{$hc$}\!\left/ \!\raisebox{-1ex}{$\lambda k_{B}T$}\right.\right)}.$$ [S3]

The major advantage of the Wien’s approximation is that it implies a linear relation between 1/λ and $\left[k_{B}ln\left(I{\lambda }^5\right)\right]/hc$, and the slope is given by the inverse temperature. Temperature fitting in this case is reduced to a simple linear regression. Fig. S6 C and D show these linear representations of the spectra in Fig. S6 A and B. Wien’s fits differ from Planck’s fits by less than 10 K.

Data Analysis

The spectra are normalized to one absorption event by using the ATHENA program (26). In the normalization procedure, a line is regressed to the data in the preedge region from −40 eV to −10 eV before E₀ (E₀ is assigned as the maximum of the first derivative), and a quadratic polynomial is regressed in the normalization range between 30 eV and 230 eV after E₀. The normalization constant J (absorption jump) is evaluated by extrapolating the preedge and postedge lines to E₀ and subtracting the E₀ crossing of the preedge line from the E₀ crossing of the postedge line. Then, the preedge line is extrapolated to all energies in the measurement range of the data and subtracted from the raw data. The preedge subtracted data are then divided by J. Then, the difference in slope and quadrature between the preedge and postedge lines is subtracted from the data after E₀. After this procedure, the preedge portion of the data are on the y = 0 axis, and the oscillatory part of the data are up to the y = 1 line. The normalized and flattened data are smoothed by using the default algorithm implemented in the ATHENA program, and, finally, the first derivative is calculated on the normalized, flattened, and smoothed data.

XANES Calculations

The ab initio XANES simulations reported in Fig. 4 are obtained by full multiple-scattering calculations using the FEFF9.6.4 package (27). We use a self-consistent energy-dependent exchange correlation Hedin–Lundqvist potential. Self-consistency is obtained by successively calculating the electron density of states, electron density, and Fermi level at each stage of the calculation within a cluster of 4.3 Å radius (corresponding to ∼40 atoms) centered on the atom for which the density of states is calculated, and then iterated. Full multiple-scattering XANES calculations are carried out for a larger cluster (∼130 atoms) centered on the photoabsorber. All multiple-scattering paths within this atomic cluster are summed to infinite order. For the crystalline phases ε-Fe (hcp) and γ-Fe (fcc), calculations are based on a single atomic cluster built using the structural parameters reported in refs. 6, 11, and 28. Debye–Waller factors for each path calculated using the correlated Debye Model are included in the simulations of the solid phases to take into account the thermal disorder.

For the calculation of the XANES spectrum of the liquid phase, a single atomic cluster is not representative of the structural disorder of the system. Therefore, we use the Empirical Potential Structure Refinement (EPSR) method (29) to generate atomic clusters consistent with the structure factor S(Q) measured experimentally by XRD at ambient pressure and 1,833 K (30). EPSR simulations are performed in a 1,000-atom cubic simulation box with a constant Lennard–Jones potential and an empirical term iteratively refined to reproduce the experimental structure factor. XANES calculations are performed for several equilibrium configurations on clusters of radius 6.5 Å around a photoabsorber selected at random within the simulation box. To take into account the effect of pressure on the liquid structure, the interatomic distances are contracted by 10%. The final spectrum is then obtained by averaging spectra obtained over 15 different XANES spectra calculations. The XANES spectrum calculated by using this approach shows the same modifications of plateau “a” between 7,115 eV and 7,120 eV in the liquid phase with respect to the solid phases observed experimentally and is consistent with spectral calculations based on atomic clusters generated by ab initio methods (15, 16).