Hybridization in Three Dimensions: A Novel Route toward Plasmonic Metamolecules

Abstract

Plasmonic metamolecules have received much interest in the last years because they can produce a wide spectrum of different hybrid optical resonances. Most of the configurations presented so far, however, considered planar resonators lying on a dielectric substrate. This typically yields high damping and radiative losses, which severely limit the performance of the system. Here we show that these limits can be overcome by considering a 3D arrangement made from slanted nanorod dimers extruding from a silver baseplate. This configuration mimics an out-of-plane split ring resonator capable of a strong near-field interaction at the terminations and a strong diffractive coupling with nearby nanostructures. Compared to the corresponding planar counterparts, higher values of electric and magnetic fields are found (about a factor 10 and a factor 3, respectively). High-quality-factor resonances (Q ≈ 390) are produced in the mid-IR as a result of the efficient excitation of collective modes in dimer arrays.

The past decade has seen an ever growing interest in plasmonic resonators as building blocks of numerous and variegated nanophotonics components,¹⁻³ ranging from optical biosensors⁴ to metasurfaces,⁵ from optical tweezers⁶ to nanolasers.⁷ The first pioneering studies on isolated nanoparticles and nanorods highlighted the enhancements of scattering and electric field produced by these structures, thanks to localized surface plasmon resonances.⁸ Later on it has been realized that by combining two or more resonators into near-field-interacting multiplets, usually referred to as metamolecules,⁹ a wide range of hybrid plasmonic resonances can be obtained,¹⁰⁻¹⁵ often classified as bright or dark modes,¹⁵⁻¹⁷ depending on their excitability by far-field illumination. Broadly speaking, the excitation of bright hybrid modes may lead to huge electric¹⁸⁻²⁰ and magnetic²¹ field enhancements, taking advantage of nanometric gaps between the coupled resonators. On the other hand, the indirect excitation of dark modes can give rise to higher quality-factor resonances.^19,22−25 In addition, the coherent diffractive coupling between isolated metamolecules can produce collective phenomena, which may dramatically amplify or inhibit the overall optical features.^{22,23,26−29}

Currently, most of the contributions on the subject focused on planar nanoresonators, namely with small aspect ratios, because these configurations are compatible with standard fabrication techniques.³⁰ However, a number of severe limitations have been pointed out for planar structures.³¹⁻³⁵ Dipole resonators oscillating parallel to the substrate interface scatter most of the power in out-of-plane directions.³¹ This determines a poor and anisotropic diffractive coupling between antennas with consequently relatively low collective resonance quality factors. Another well-known issue is the strong influence exerted by the presence of a high refractive index substrate on the optical properties of planar nanoantenna arrays.^27,32−35 It has been shown that a progressive increase of the dielectric asymmetry of the system affects both the isolated resonator properties, red-shifting and broadening the resonances,^34,35 and the collective modes of the systems, which can be dramatically reduced or even completely suppressed.^27,32−35 Although index matching techniques can be adopted,²⁷ these may create nontrivial problems in practical applications of the resonant arrays, such as sensing.

The additional degree of freedom provided by the third spatial dimension may help to overcome these limitations. Going in this direction, first achievements were obtained by considering arrays of single vertical nanorods protruding normally to the substrate plane.^31,36−40 However, analogously to the case of horizontal resonators, the most interesting phenomena are found when two or more 3D nanostructures are coupled together by near-field interaction, combining the advantages offered by tridimensionality with the variegate hybrid resonance scenarios produced by near-field coupling. For example, the simplest near field coupling can be achieved by pairing two vertical and parallel nanorods (dimer). Upon pairing, the plasmonic resonance characterizing the isolated vertical antenna splits up into two hybrid modes, respectively symmetric and antisymmetric in charge distribution, often referred to as antibonding and bonding, respectively.¹⁰ However, as we shall show, in this side-by-side vertical configuration, only the antibonding mode turns out to be accessible by far-field illumination, whereas the bonding one remains dark, similar to the case of side-by-side planar nanorod dimers.¹⁰ In order to make the bonding mode accessible to far-field illumination more complex spatial arrangements have to be considered.

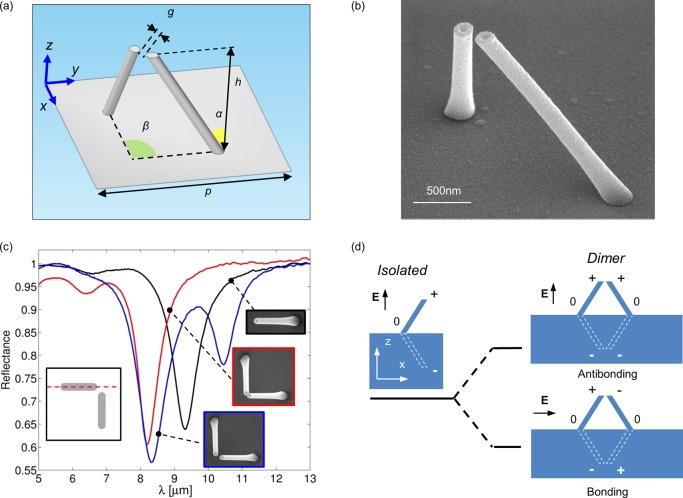
Here we propose the plasmonic dimer layout depicted in Figure 1a. It consists of a pair of high-aspect-ratio slanted silver nanorods supported by a silver baseplate and separated by a nanometric gap (details on the geometrical parameters are reported in the figure caption). The advantage of considering such an exotic configuration is manifold. The rods are efficiently near-field coupled by means of the nanometric gap separation between their terminations. We will show that both bonding and antibonding modes become bright and then excitable by far-field illumination. The excitation of both modes is proved to be independent of each other and tunable as a function of different geometrical parameters, thus enabling interesting spectral engineering opportunities. In addition, thanks to the quadrupolar nature of the bonding resonance, a high magnetic field enhancement can be produced in the area subtended by the metamolecule, which actually can be viewed as a slanted 3D split-ring resonator.⁴¹ Finally, dimers are arranged in regular arrays in order to promote diffracting far-field couplings that are intrinsically much more efficient than those achievable in 2D planar configuration. In fact vertical resonators, unlike planar ones, mainly scatter light in directions parallel to the substrate surface thus redirecting light toward the neighbor dimers and increasing the fraction of coupled light.³⁶

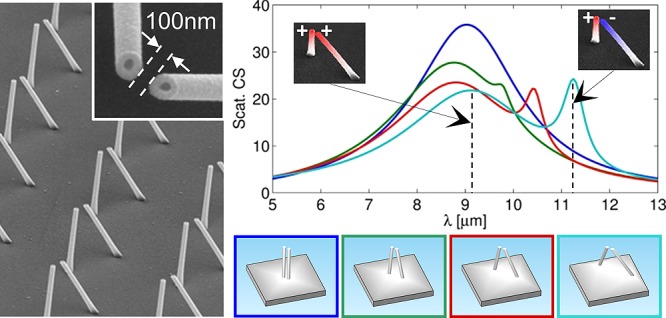
Figure 1.

(a) Scheme of slanted silver nanorod dimer on silver substrate. In the most general case, these nanorods are characterized by a nonzero tilt angle, α, and by a nonzero angle β between the rods planes. (b) Scanning electron microscope images of the fabricated structures. (c) Experimental reflectances of arrays of single tilted rods (black), pairs of touching tilted rods (namely gap g = 0, red line) and rod dimers with gap g = 100 nm (blue). Right insets report SEM images of the three cases. Geometrical parameters are α = 30°, β = 90°, h = 1.8 μm, and p = 4.5 μm. Nonpolarized light impinges at 25° along the scattering plane depicted in the left inset. The impinging angle is kept fixed for all of the experimental and simulative results presented in the paper. (d) Energy splitting of the isolated tilted rod resonance upon dimerization, and schematic representation of real and image charge distribution at resonances with corresponding exciting electric field orientations.

Periodic arrays of slanted nanorod dimers were fabricated by means of a recently presented technique relying on low energy secondary electrons emitted during the process of focused ion beam milling.^42,43 A SEM picture showing an example of fabricated nanorod dimer is reported in Figure 1b. Fabrication details are already described elsewhere^42,43 and here reported in the Supporting Information 1. The final structures consist of hollow metal nanotubes with a diameter of 160 nm and silver wall thickness of 30 nm while their length can range from hundreds of nanometers to several microns.

In Figure 1c, we compare the experimental reflectance of a slanted dimer array (blue line) with that one of an array of single tilted rods (black line). In the same plot, we report also the reflectance of a slanted dimer with rods connected at the extremity, namely gap g = 0 nm (red line). The presented measurements were performed by Fourier transform infrared spectroscopy, carried out with a commercial micro-FTIR (ThermoFisher iS50) in the spectral range of 5–15 μm. Nonpolarized illumination impinges at fixed impinging angle of 25° and scattering plane parallel to one of the rods (red dashed line in left inset of Figure 1c). As is seen, the single reflectance dip observed in the case of single rod array splits up into two in the case of dimer array with nonzero gap. The lower energy dip, in particular, is closely related to the presence of the gap. In fact, when the gap is reduced to zero (connected rods) we observed just a single resonance (red curve), which spectrally matches the higher energy dip observed for the separated dimer arrays, while the lower energy dip disappears.

The metallic baseplate plays a crucial role in determining the observed optical properties of these structures, which can be interpreted by means of the method of images,⁴⁴ considering the baseplate to be a perfectly conducting surface. Charges and currents located in the substrate rearrange themselves in a mirror-like way, that is, the metallic baseplate can be replaced with a mirror image of the resonator, endowed with opposite surface charge distribution. The dip found in the case of the single rod arrays can thus be viewed as the fundamental dipolar resonance of an equivalent free-standing rod with double length,⁴⁴ as schematically depicted in Figure 1d. Similarly, it can be easily realized that two resonances are expected for the rod dimers, corresponding to the two possible oscillation modes of real and image charges (Figure 1d). This closely resembles the case of side-by-side planar nanorod dimers, widely discussed in literature,¹⁰ with the difference that here the dipole moments are aligned vertically. The two observed experimental dips correspond to the excitation of the bonding and antibonding modes,¹⁰ the former being at lower energy with antisymmetric charge distribution (antiparallel electric dipole moments), and the latter being at higher energy with symmetric charge distribution (parallel electric dipole moments).

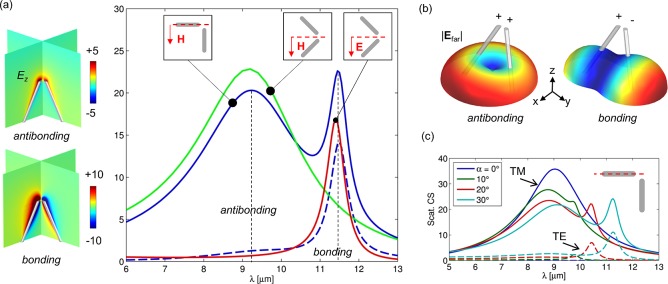
To verify this interpretation, we performed electromagnetic finite elements simulations (COMSOL Multiphysics software⁴⁵) of an isolated slanted rod dimer in order to separate the near-field intradimer coupling effects from the interdimer coupling ones. The rods were modeled as slanted silver cylinders with sharp edge terminations. We verified that the effect of nonzero edge curvature radii on the optical behavior is negligible (see Supporting Information 2). Results in case of a dimer with the same geometrical parameters of the fabricated sample (see Figure 1 caption) are reported in Figure 2. The blue solid curve in Figure 2a represents the calculated scattering cross section in case of a transverse magnetic (TM)-polarized plane wave impinging at 25° with scattering plane parallel to one of the two rodss (as schematized in the inset). We clearly observe two peaks, which correspond to the excitation of the two resonances, antibonding (shorter wavelength) and bonding (larger wavelength). This can be readily verified by inspecting the z-component of the electric field at resonances (Figure 2a, insets).

Figure 2.

Scattering simulations of an isolated slanted nanorods dimer with same geometrical parameters as in Figure 1. (a) Solid lines are the scattering cross sections (CS) in the three illumination conditions sketched in the insets, while the blue dashed line is the absorption CS corresponding to the blue solid scattering CS. Values are normalized to the geometrical CS. Insets on the left show the E_z fields at peak wavelengths in two cross sections of the structures. Field values are normalized to the impinging light amplitude and saturated to arbitrary values to better evidence their distribution. (b) Scattering far-field patterns at resonant wavelengths. (c) Scattering cross-section spectra for different tilting angles α of the dimers and illumination condition as sketched in the inset (for TM and TE polarized light as indicated by the arrows).

A further check of the resonances interpretation is provided by looking at the scattering far-field patterns at resonances, reported in Figure 2b. For the antibonding resonance, we find a doughnut-shaped emission pattern with maximum isotropic emission in all directions parallel to the metal baseplate. This is compatible with a dipolar-like emission with dipole moment oriented in the z-direction.^44,46 As anticipated, this effect strongly improves the far-field diffractive coupling because light impinging on a dimer is redirected toward its neighbors. In fact, it can be noticed that the antibonding peak in the scattering cross section of isolated dimer (Figure 2a) is much broader than the corresponding reflectance dip in Figure 1c (blue line). This is due to array effects that substantially modify the antibonding-resonance properties. Conversely, at bonding resonance (Figure 2c) the emission pattern has two maxima in the direction connecting the two rods, which is very similar to the far-field produced by a pair of closely spaced vertical dipole emitters with π-phase shift between each other.^44,46 In such a case, as we shall see, array effects only weakly affect the position and the width of the resonance.

It is worth to underline that in the proposed nanorods arrangement both the bonding and antibonding modes are bright for suitable far-field excitation. As a matter of fact, the antibonding mode is excited in the presence of an impinging electric field having a nonzero z-component. On the other hand, the bonding mode is excited by a nonzero electric field component in the direction parallel to the dimer interaxis. To evidence this aspect, we report the simulations in the case of impinging light wave vector parallel to the symmetry plane of the dimer and consider TM and transverse electric (TE) polarized light impinging (see corresponding insets in Figure 2a). The scattering cross sections for these two illumination conditions are reported in Figure 2a (green and red lines). Clearly, it is possible to selectively excite either the antibonding resonance with TM polarization or the bonding resonance with TE polarization.

Beside the illumination conditions, it is also important to notice that the access to the bonding resonance is made possible thanks to the particular slanted geometry. The tilt angle α of the rods introduces a horizontal component in the electronic oscillation, which enables coupling with the corresponding exciting electric field projection. This is demonstrated in Figure 2c, where the scattering cross sections for different tilting angles α are reported for TM and TE polarized illumination. As presented in these plots, the bonding resonance is absent in the case of α = 0 and gradually appears with increasing α. Interestingly, the spectral location of the antibonding resonance remains almost unaltered, and this is the first evidence of how this resonance is only slightly dependent on geometrical details of the dimer. A similar behavior is found when varying the angle of aperture β between the two rods (see Supporting Information 3 for more details).

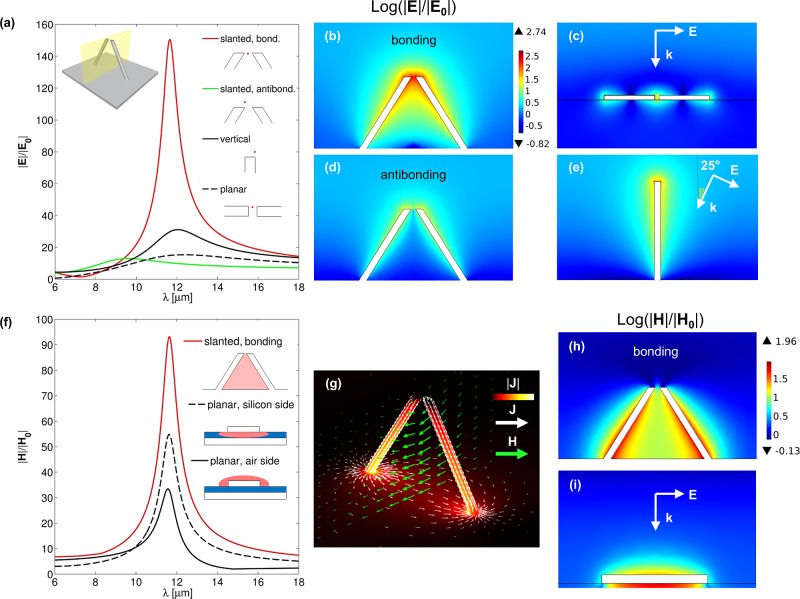
While the scattering cross section presents two peaks of comparable intensity, by looking at the absorption cross section in Figure 2a (blue dashed line) a much more pronounced peak is observed in correspondence of the bonding resonance. This is correlated to a strong field enhancement (FE) at the rods terminations and within the gap. We address in detail this feature of the bonding resonance by considering the case of coplanar slanted nanorods, namely α = 30°, β = 180°, and TE polarized light impinging with scattering plane parallel to the dimer symmetry plane (Figure 3a, inset). This is the optimal condition for bonding mode excitation, because the projection of the geometry along the impinging field is maximized (see Supporting Information 3). All other geometrical parameters are as in Figure 1 and in particular we consider a 100 nm wide gap. In Figure 3a, the red line reports the electric FE spectrum at the center of the gap in the case of TE polarized impinging light, exciting thus the bonding mode. A maximum enhancement of 150 is predicted for the electric field amplitude. To better evidence the extent of the FE in this configuration, we consider as references a planar nanorod dimer on silicon substrate with same gap width and metal cross sectional area (Figure 3c), and a single vertical nanorod on silver substrate (Figure 3e). The illumination of the two structures is schematized in the figures. In both cases, the nanorod lengths have been tuned in order to produce the fundamental resonance at the same wavelength as the slanted dimer antibonding oscillation. The black dashed and solid lines in Figure 3a report respectively the FE at the gap center of the planar dimer, and the FE calculated 50 nm above the vertical rod termination (see Figure 3a, inset). As can be seen, the FE predicted for the tilted dimer largely exceeds those calculated in the two reference structures. In particular, it is 1 order of magnitude higher than in case of planar dimer. The electric FE maps at resonant wavelengths in vertical cross sections, Figure 3b,c,e, further highlight the very different performances of the three architectures. A maximum electric FE of 310 is calculated at a distance of 10 nm from the rod edge. It is interesting to further compare the FEs of the bonding resonance of the slanted dimer with that one at antibonding resonance. The green solid line in Figure 3a represents the FE in case of antibonding resonance, calculated 50 nm above one of the antenna edges, while Figure 3e reports the corresponding FE map at the resonant wavelength. As can be expected, the FE in this case is comparable to the one obtained for the single straight rod and thus much lower than for the bonding resonance.

Figure 3.

Comparison of electric (a–e) and magnetic (f–i) properties of the slanted nanorod dimer with reference structures. The slanted dimer geometry and illumination considered are depicted in (a), left inset. It has the same geometrical parameters as in Figure 1 except for β = 180°. (a) Comparison of electric FEs spectra for the structures (b–e). Fields are taken in representative positions, as schematized in the legend. The red curve denotes the field at the gap center of the slanted dimer for TE-polarized illumination and scattering plane as depicted in the inset. The green curve is the FE for the same structure with TM-polarized illumination and calculated 50 nm above the antenna terminations. The solid black line is the FE in case of vertical antenna on silver substrate, calculated 50 nm above the antenna edge; the black dashed line is the FE at the center of a planar dimer antenna on silicon substrate with gap size of 100 nm. (f) Comparison of the maximum magnetic FE for the slanted dimer bonding resonance (red line) with the maximum FEs in case of a planar silver antenna on 70 nm thick silicon layer on a silver substrate. Field maxima are calculated over the respective spatial regions shaded with red in the schematics. (g) Surface current distributions (white arrows and color map) and magnetic field in the middle plane (green arrows) for the slanted dimer at bonding resonance. (h,i) Magnetic FE maps at resonant wavelengths. The lengths of the reference structures considered (c,e,i) have been tuned in order to resonate at the same wavelength of the slanted antenna bonding resonance. They are 1800 nm for (c), 2450 nm for (e), and 1700 nm for (i).

Beside the strong electric field localization in the gap region, we notice that our structure is expected to create also a high magnetic field in the area subtended by the nanorods. In fact, owing to the conductive substrate connecting the two rods, at bonding resonance an oscillating loop current is produced, analogous to those observed in split-ring resonators.⁴¹ This is shown in Figure 3g, where the local surface current density (white arrows and colormap) and the resulting magnetic field in the midplane (green arrows) are visualized (see also the Supporting Information Movie). As can be seen, the resonant dimer can then be viewed as a magnetic dipole with magnetic dipole moment parallel to the baseplate surface. In Figure 3f, the red solid line reports the maximum magnetic FE calculated in the dimer cross section as a function of wavelength, while the magnetic FE map at resonance is reported in Figure 3h. As it can be expected, the strongest H field is found close to the antenna regions presenting the highest surface charge currents, namely at the antenna basements (compare with Figure 3g). Magnetic FE values as high as 90 are obtained. To assess the magnetic performance of the structure, we consider one of the most studied magnetic nanoantenna configurations, namely a planar nanorod on a dielectric-coated metallic substrate (Figure 3i).⁴⁷ We assume here the dielectric to be silicon. Geometrical details of the simulated structure are reported in Figure 3 caption. By illuminating this antenna with normally impinging light polarized along the antenna axis it is possible to excite a magnetic resonance, thanks to the mirror symmetry provided by the metal substrate.⁴⁷ At resonance, a high magnetic field is obtained in the silicon region between antenna and substrate. In Figure 3f, the black dashed and solid black lines report respectively the maximum magnetic field in the silicon layer and in the air superstrate as a function of wavelength, while the field distribution at resonance is reported in Figure 3i. As shown in Figure 3f, the slanted nanorod dimer provides a higher magnetic FE, which reaches a factor of 3 when the maximum magnetic field in air is considered for the planar dimer.

While the most interesting properties of the bonding resonance concern field enhancements, the antibonding is interesting from the scattering efficiency point of view, which translates into strong diffractive coupling between nearby nanorod dimers. As introduced above, it is important to observe that, because the nanorods scatter as vertically oriented electric dipoles for both resonances the electric field scattered in directions parallel to the xy plane is necessarily polarized along z. The scattered field is thus optimally oriented for the excitation of the antibonding resonance in nearby dimers. By contrast, the bonding resonance cannot be diffractively excited, because it requires an exciting field with a nonzero horizontal component. Consequently, we expect the antibonding resonance to give rise to much more pronounced interdimer coupling effects than the bonding resonance.

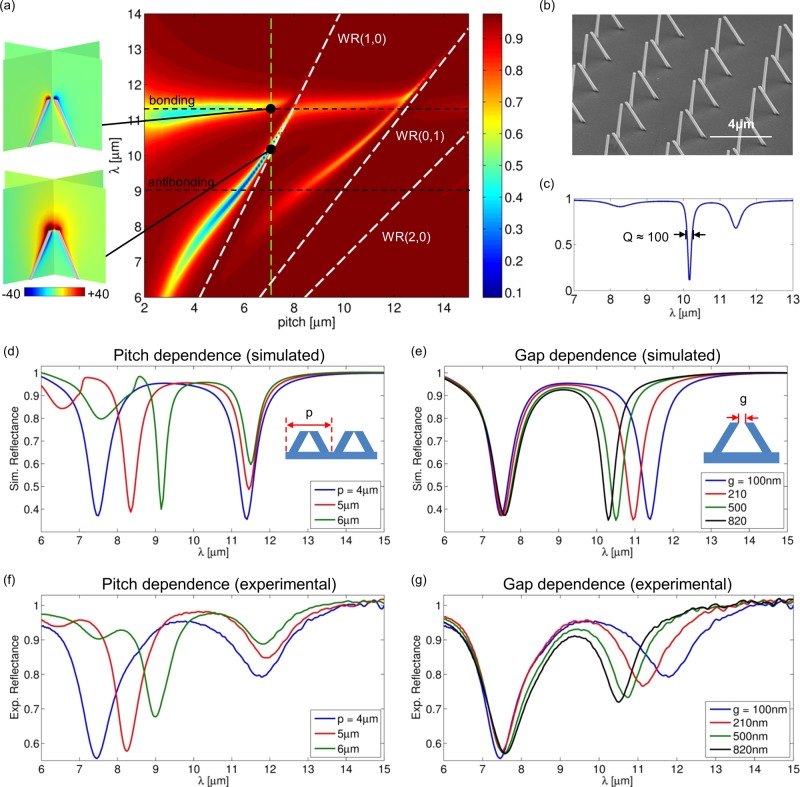
We study in detail this aspect by scattering simulations of squared dimer arrays considering the same dimer geometrical parameters as in the Figure 1 caption with TM polarized illumination and scattering plane as in Figure 1c. The calculated total reflectance as a function of impinging wavelength and array pitch is reported in Figure 4a.

Figure 4.

(a) Simulated total reflectance of a slanted nanorod dimer array with illumination condition as in the inset of Figure 1c, as a function of pitch and wavelength. Geometrical parameters are the same reported in Figure 1. The bonding and antibonding resonant wavelengths of the isolated structures are marked with horizontal black dashed lines, while Wood–Rayleigh anomalies are marked with white dashed lines. The insets report the E_z field maps in two sample configurations. (b) SEM micrograph of a fabricated sample. (c) Cross section of the map in (a) corresponding to the green dashed line. (d,e) Simulated 0th order reflectance (averaged between TE and TM polarizations) of an array with gap g = 100 nm for three sample pitches, (d), and of an array with p = 4 μm for some values of gap g, (e). (f), (g) Corresponding experimental reflectances.

For reference, the spectral locations of the single-dimer resonances are marked in the map with black dashed lines. A horizontal resonant region, almost independent of the pitch, is evident in the map, which is crossed by a number of narrow strongly pitch-dependent resonances. The E_z field maps in two sample configurations (insets of Figure 4a) reveal that the horizontal resonant region corresponds to the bonding while the sharp dips are the antibonding resonance. As expected, owing to the efficient scattering along the baseplate surface, the antibonding resonance shows a strong pitch dependence. For a given grating pitch and light impinging angle, the in-phase superposition of the field scattered by each dimer along the baseplate surface takes place at specific wavelengths, usually denoted as Wood–Rayleigh (WR) anomalies.⁴⁸ They are marked with white dashed lines in Figure 4a and are found when the following equation is satisfied

with m, n being integers, k_x = ê_xk₀ sin(θ) is the in-plane component of the impinging light momentum, k₀ is the vacuum light wave vector, G_x,y = ê_x,y(2π/p) are the reciprocal lattice basis vectors, and p is the pitch of the array both in x- and y- directions. The spectral overlap of the (n,m) = (1,0) and (0,1) WR anomalies with the broad single-dimer antibonding resonance produces the sharp Fano-like dips observed in Figure 4a (sometimes called surface lattice resonances).^{23,26−29,49} Analogous mechanisms of collective resonance generation have been widely described for horizontal nanorod arrays.⁴⁹ This phenomenon arises because at WR anomalies one of the diffracted waves travels at a grazing angle along the surface of the substrate and hence interacts with the nearby array elements. From the plot reported in Figure 4c, corresponding to the vertical green dashed line in Figure 4a, we observe that the Fano resonance quality factor can be as large as 100. By optimizing the grating pitch and illumination conditions, this value can be further raised up to 390 (see Supporting Information 4), which is almost an order of magnitude higher than the typical Q-factors reported in case of horizontal plasmonic nanorod arrays at mid-infrared wavelengths (of the order of tens).⁴⁹⁻⁵¹ Indeed, as already mentioned, when light impinges on planar nanorods it is mainly back scattered or transmitted into the substrate, as expected from a classical dipole that oscillates in the substrate plane and therefore emits out of the plane (normally to the direction the oscillation). This results in a relatively poor diffractive coupling efficiency, taking place only along the direction normal to the planar nanorod axis. By contrast, the depth of the spectral dips found in 3D resonators evidences the efficient coupling in this configuration, while the presence of features along both (0,1) and (1,0) anomalies demonstrates that this coupling takes place isotropically along the substrate surface.

For what concerns the bonding resonance, we notice in Figure 4a that the only nontrivial reflectance variations as a function of the grating pitch correspond to the crossing points with the antibonding resonances. In these configurations the scattered field produced by the bonding resonance can excite the antibonding one, opening a channel of diffractive coupling between the dimers. Far from the crossing points, as expected, the bonding reflectance dip does not depend on the grating pitch, and its spectral location is almost identical to that one of the insulated dimer. This reveals the inherent intradimer character of this resonance.

The different intercoupling behaviors of the two resonances have been experimentally verified. Figure 4d,f reports respectively the simulated and measured reflectance spectra of nanorod arrays with g = 100 nm and different pitches. As can be seen, an excellent agreement between simulated and measured spectral dip locations is found. It can be noticed, however, that the experimental bonding resonance dips result broader and less pronounced than the simulated ones. This effect can be ascribed to the different sensitivity of the two resonances to the geometrical details of the unitary cell. At the bonding resonance in particular, the opposite sign of the charges on the two nanorod terminations yields a strong capacitive coupling, resulting in a marked dependence on the gap size. This is shown in Figure 4e,g, in which we report respectively the simulated and experimental reflectance for arrays with fixed pitch of 4 μm and different gaps. As can be expected, the gap dependence of the resonant wavelength becomes stronger with decreasing of the gap size due to an increased near field coupling. For larger gap sizes (>500 nm) the dip stabilizes at a fixed wavelength. The reason why the bonding dips appear generally broader and shallower than the simulated ones is explained by considering the experimental fabrication error in realizing a monodispersed gap size within a nanorod array, which has, in our case, a variability of ±10 nm. The resulting reflectance dip is thus an average and is consequently smeared out.

By contrast, the antibonding resonance appears almost totally insensitive to the gap size. Moreover, the grating pitch is experimentally controlled with a higher precision. This explains the good agreement between experiment and simulations for the corresponding reflectance dip.

Figure 4, panels d,f and e,g, shows that we can almost independently tune the spectral location of the two resonances by tuning different geometrical parameters: gap size for the bonding resonance and grating pitch for the antibonding resonance. This can be useful in practical applications of the presented structure, allowing an easy engineering of the resonant spectrum according to the particular needs. Furthermore, by properly tuning the parameters one can spectrally overlap bonding and antibonding resonances, and the spectral location of the crossing point can itself be tuned.

In conclusion, we numerically and experimentally investigated the optical properties of high-aspect-ratio out-of-plane metallic slanted nanorod dimers standing on a metallic substrate. The proposed architecture mimics a 3D split-ring resonator with nanometric gap. We showed that the tiny gap between the nanorods enables a strong near-field coupling between the rods, resulting in the splitting of the single rod resonance into two hybrid dimer modes, bonding and antibonding. The tilt of the structure on the other hand is shown to be the key feature enabling the excitation of the bonding resonance of the structure by far-field illumination. This resonance yields both remarkable electric field enhancements at the nanorods terminations (a factor 310 calculated at 10 nm from the nanorods edge) and magnetic-field enhancements at the nanorod basement (a factor 90). The antibonding resonance, instead, is characterized by an efficient lateral scattering of light, yielding a strong interdimer interaction, which is shown to produce high-quality-factor collective resonances (up to Q = 390). A final valuable feature of the proposed structure is the possibility to freely tune the resonance wavelengths as a function of different geometrical parameters (gap size for the bonding, array pitch for the antibonding resonance). This property can be particularly important for sensing applications in which the resonance of the structure has to be tuned to those ones of the target molecule. In Supporting Information 5, we report experimental evidence that molecules of interest can be deposited onto the slanted nanorods terminations without damaging the architecture itself, provided a proper deposition process and/or a suitable nanorods geometry are chosen.

Several interesting applications can be envisaged for the presented structure. In fact, the electric and magnetic hot spots as well as the efficient diffractive interdimer coupling can be smartly associated with other interesting morphological properties of this full-3D architecture, such as the hollow cores of the nanorods, which may be exploited as nanochannels for molecule injection in microfluidic chips, or the presence of a suspended nanogap, which may enable to study the optical properties of target molecules placed on its boundary surfaces without any kind of influence from the substrate This may pave the way to the development of extremely compact multifunctional biosensing platforms, combining optical-based functionalities with micro- and nanoparticle trapping, microfluidics, and electrical probing.^43,52

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.5b01437.

• Supporting Information 1: Fabrication of slanted nanorod dimers arrays; Supporting Information 2: effect of rounded edges on the simulation results; Supporting Information 3: role of the β angle in the optical properties of the slanted rods dimers; Supporting Information 4: high-quality-factor lattice resonances optimization; Supporting Information 5: proof-of-concept molecule deposition on top of slanted nanorod dimers. (PDF)

• Supporting Information Movie: magnetic field and surface current distributions for two optical cycles in case of a slanted dimer at bonding resonance. (AVI)

The authors declare no competing financial interest.