Habit learning by naïve macaques is marked by response sharpening of striatal neurons representing the cost and outcome of acquired action sequences

SUMMARY

Over a century of scientific work has focused on defining the factors motivating behavioral learning. Observations in animals and humans trained on a wide range of tasks support reinforcement learning (RL) algorithms as accounting for the learning. Still unknown, however, are the signals that drive learning in naïve, untrained subjects. Here, we capitalized on a sequential saccade task in which macaque monkeys acquired repetitive scanning sequences without instruction. We found that spike activity in the caudate nucleus after each trial corresponded to an integrated cost-benefit signal that was highly correlated with the degree of naturalistic untutored learning by the monkeys. Across learning, neurons encoding both cost and outcome gradually acquired increasingly sharp phasic trial-end responses that paralleled the development of the habit-like, repetitive saccade sequences. Our findings demonstrate a novel integrated cost-benefit signal by which RL and its neural correlates could drive naturalistic behaviors in freely behaving primates.

INTRODUCTION

Habits, in the form of sequential actions that are performed repeatedly, seemingly without thought, are a ubiquitous part of our lives. Despite their importance in the structure of daily life, little is known about how habits and stereotyped action sequences are formed and about the neural systems supporting their formation, particularly in naturalistic situations in primates. In rodents, chronic, long-term recordings have been made in the striatum during the acquisition of instructed habitual tasks (Barnes et al., 2005; Costa et al., 2004; Jin et al., 2014; Jog et al., 1999; Kimchi and Laubach, 2009; Smith and Graybiel, 2013). An observation from this prior work was that neural activity in the striatum at the end of the task, when the animal has completed its decision and before it reaches reward, evolves through the course of learning. It has further been shown that these end signals become impervious to reward devaluation, indicating that they likely are part of the neural signature of acquired habits (Smith and Graybiel, 2013). The precise function of these acquired neural task-end signals is an open question. Because this activity occurs at the completion of the task, i.e., when the decisions and actions necessary to obtain reward are complete, it is likely that they could mark such completion by setting or resetting neural circuits mediating the behavior, thereby facilitating the learning of habitual, repetitive action sequences. Similar task-end signals have been observed in well-trained primates performing sequences of saccades; brief peaks of activity occur just after completion of the last saccade of an instructed saccade sequence and before reward delivery (Fujii and Graybiel, 2003, 2005). The course of development of such end-related activity in the primate is still unknown. Nor is it known whether such signals would develop in primates never instructed to learn specific action-sequences. We addressed these issues in the experiments reported here.

Many mechanisms have been proposed to drive the formation of such sequential actions and habits (Dezfouli and Balleine, 2012; Graybiel, 2008; Smith and Graybiel, 2014), one of which is reinforcement learning (RL). RL algorithms gradually converge on which actions to take in different situations (states) so as to minimize the difference between predicted outcomes and obtained outcomes (Sutton and Barto, 1998). RL models have been extensively applied to model the acquisition of both simple and complex behaviors (Barraclough et al., 2004; Chukoskie et al., 2013; Daw et al., 2005, 2006), including movement sequences (Amemori et al., 2011; Desrochers et al., 2010; Dezfouli and Balleine, 2012), but the nature of the feedback error signal used in the uninstructed development of sequential, habit-like behaviors remains unclear.

With RL theory as a foundation, there are at least three candidate driving forces that could compose the neural task-end signal and drive subsequent learning behavior: reward, cost, and combinations of reward and cost. First, conventional RL algorithms use a learning rule to maximize the total amount of expected reward, and RL agents (animals, people, or machines) use information about the value of each state. Neurons in the striatum represent both values and rewards (Cai et al., 2011; Histed et al., 2009; Lau and Glimcher, 2007; Yamada et al., 2011, 2013; Yanike and Ferrera, 2014). Additionally, the specific coding of the difference between the actual and expected reward, reward prediction error (RPE), has been found in the striatum of humans (Daw et al., 2006; O'Doherty et al., 2004; Tanaka et al., 2004), monkeys (Asaad and Eskandar, 2011), and rodents (Stalnaker et al., 2012).

A second RL strategy is to minimize the total amount of effort to perform the behavior by locally adjusting the behavior according to the difference between the actual and expected effort to complete movements in each trial. Such performance prediction errors (PPEs) could be quantified as the effortful cost of the movements. The field of machine learning has often used such values to drive control systems (Harris et al., 1999; Zhao et al., 2010), but little is known about cost signals in the brain. Studies in humans and rats have suggested that cost variables may be represented in the striatum, as they relate to the effort of responding quickly (Mazzoni et al., 2007; Niv, 2007), the costs of the movements themselves (Gepshtein et al., 2014), and cognitive effort (Schouppe et al., 2014). Yet to be studied is the potential role of cost signals in acquisition of naturalistic sequential behaviors. Only recently has a third strategy using RL been emphasized, in which elements involving both reward and cost are explicitly considered as driving forces (Collins and Frank, 2014). Whether variables related to reward or cost, or to both, are employed as the feedback error signals in spontaneous, untutored formation of action sequences in naïve primates has been unclear. Previous studies have examined the short-term acquisition of new stimulus-response associations (Asaad and Eskandar, 2011; Histed et al., 2009; Kawagoe et al., 1998; Pasupathy and Miller, 2005; Samejima et al., 2005; Watanabe and Hikosaka, 2005; Williams and Eskandar, 2006), but none have examined the composition of neural learning signals starting from the naïve state and extending for months of behavioral experience.

Taking as a clue the appearance of end signals in the striatum following learning, we tracked neural activity in the caudate nucleus (CN) to determine how such signals develop during naturalistic learning as naïve monkeys developed stereotyped scanning sequences without instruction. We then tested how these signals related to the potential RL drivers of reward, cost, and combined reward and cost. We capitalized on the use of an uninstructed free scan task in which naïve monkeys naturally form habitual eye movement patterns without explicit supervision (Desrochers et al., 2010). In this scan task, monkeys, without instruction, generated eye movements to scan a grid of dots presented to them, eventually found a pseudorandomly placed baited target and received reward. We found that in an RL model, the cost, defined as the difference between the actual and expected distance that the eyes traveled in a trial (PPE), could both generate and account for the evolution of the monkeys’ eye movement patterns. Here, we used this same cost variable along with the outcome of each trial (reward/no reward) to probe the activity of striatal neurons during the task-end period (scan-end in this paradigm). We asked whether such signals would emerge in striatal neurons during the spontaneous acquisition of stereotyped action sequences; how, if so, such signals might relate to the progression of natural sequence learning; and on finding them, how they were related to the candidate RL model driving forces. We demonstrate that phasic scan-end activity of striatal neurons representing both cost and outcome parallels the gradual changes in the saccade patterns performed as they became more refined and habitual. We propose that these scan-end signals could provide a mechanism by which the natural formation of habit-like stereotyped action sequences can occur in naïve primates.

RESULTS

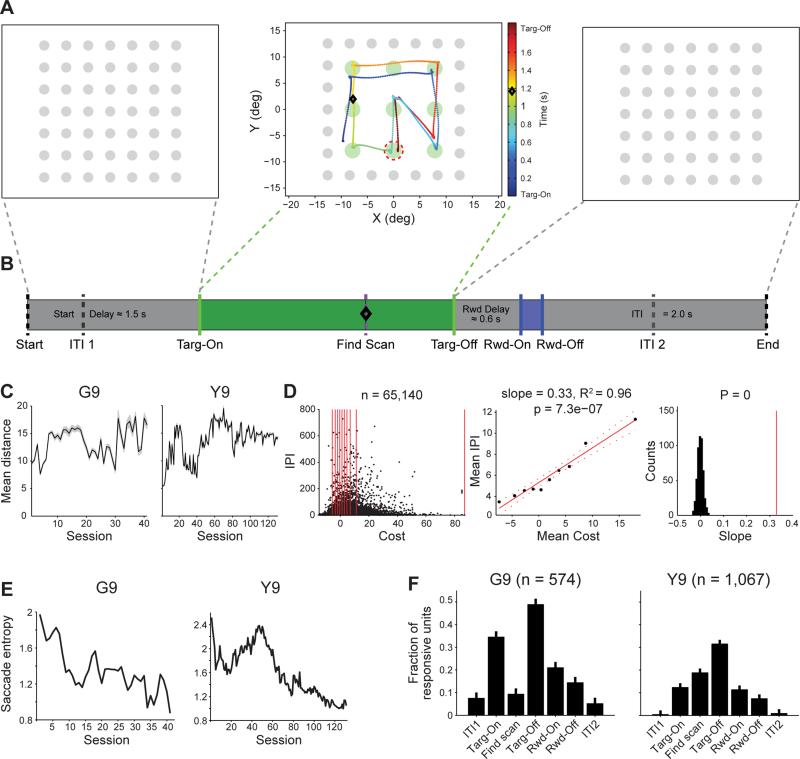
We recorded from arrays of approximately 100 chronically implanted, independently moveable electrodes (Feingold et al., 2012) in the CN of two monkeys, G and Y, throughout up to 202 days of acquisition and performance of the free-viewing scan task (Figures 1A, 1B and S1A). Each monkey freely scanned a presented grid of four or nine green target dots (Targ-On). After a variable delay to prevent the monkey from immediately completing the trial (Delay Scan, mean 1.5 s), one of the target dots was baited according to a pseudorandom schedule (Find Scan). When the monkey's gaze entered the baited target, the green target grid was immediately extinguished (Targ-Off), and the gray target grid reappeared. After a variable delay (Reward Delay, 0.4-0.8 s), a reward was delivered, the inter-trial interval (ITI) began, and a trial considered as “correct” was completed. While the green targets were on, the only requirement was that the monkey's gaze remained in the area defined by the green target grid; trials in which the monkey looked away from the green target grid before finding the baited target were considered as error trials. As soon as the monkey committed an error, the green target grid was extinguished (Targ-Off), and the trial proceeded directly to the ITI. Therefore, error trials contained the same events as correct trials, with the exception of the onset (Rwd-On) and offset (Rwd-Off) of reward delivery, and Find Scan if the monkey made an error before the Delay Scan time had elapsed.

Figure 1. Behavior and Neural Responses during Task Periods.

(A) Sample sequence of viewing screens in single trial. Gray targets appear on black background (left). The monkey scans green targets until a randomly chosen target is captured (middle). Then, the green targets grid turns off (right). Black diamond indicates time (on color bar) and position (on grid) of monkey's gaze when the target (red dashed circle) became bated with reward (not signaled to the monkey).

(B) Sequence of task events, with mean of variable duration (Start Delay, Delay Scan, Reward Scan, and Reward Delay) or fixed duration. Dashed lines indicate events not observable by the monkey. ITI1 (0.5 s after trial start) and ITI2 (1 s before trial end) were used to examine neural responses immediately prior to and after each trial, respectively.

(C) Mean (± SEM) saccade distance (from Targ-On to Targ-Off) for each session in G9 (left) and Y9 (right).

(D) Correlation between trial-by-trial cost and inter-pattern interval (IPI, number of intervening trials between two trials with the same stereotyped scan pattern; see Supplemental Information). All trials containing any of the most frequent sequences in G9 and Y9 are shown as dots in the left panel. Note that the distribution appears skewed because the density of values less than zero cannot be accurately represented; the distribution is centered around zero with a median cost value of 1.2. Middle panel shows means for 10 bins containing the same number of trials (bin edges indicated by red lines in left) and line fit. Right panel shows results of shuffling the IPI and cost 500 times and computing the slope for each. Actual slope (middle) indicated by red line. No shuffled slope was greater than actual.

(E) Entropy of target-to-target transition probabilities across training sessions.

(F) The mean fraction (± SEM) of units with significant responses to task events across sessions (see Supplemental Information).

See also Figure S1.

We previously reported the behavioral results from this task (Desrochers et al., 2010). In brief, both monkeys performed the task well, at ~70% correct across sessions. Despite the complete lack of instruction, both monkeys spontaneously formed their own repetitive, stereotyped eye-movement patterns as they scanned the target grid for the baited target. We found potential driving forces of these saccade patterns on two time scales. First, we defined the cost, or PPE, as the difference between the total distance that the monkeys’ eyes traveled while scanning the target grid in each trial (actual distance) and the mean distance across trials (expected distance). The mean total distance that the monkeys’ eyes traveled either did not significantly change or reached asymptote very rapidly across sessions (first non-significant line slope G9: session 1, Y9: session 34; Figures 1C and S1B). By definition, the mean cost values also did not change across sessions; they always varied around zero. When we minimized this cost-related variable in an RL algorithm, it captured gradual transitions in the saccade patterns towards those that were more efficient, i.e., the specific pattern that was repeated within the trial traversed shorter distances to cover all the targets. Thus the algorithm mimicked the behavior of the monkeys, wherein the mean total distance did not change, but the monkeys more efficiently visited the targets within each trial. Here, we updated previous results relating the trial-by-trial change in the total distance to how frequently individual patterns were selected for performance, and found that this same cost variable could drive the selection of stereotyped saccade sequences in the following trials (Desrochers et al., 2010). If the monkeys performed a short (or low-cost) trial, then they tended to perform that same sequence again with few or no intervening trials. Conversely, if they performed a long (or high-cost) trial, then they waited a greater number of trials before performing that sequence again (Supplemental Information, Figures 1D and S1C). Thus, the cost variable was capable of driving both the trial-by-trial selection of stereotyped action sequences and the overall progression towards efficiency in how the sequences covered the targets.

Second, we found across-session increases in the repetitiveness of the saccade patterns, regardless of which pattern was being performed. We measured the repetitiveness of the saccade patterns by converting the eye movements for each session to transition probabilities between each pair of targets and then by calculating the entropy of this transition matrix. This increase in repetitiveness was reflected in both correct and error trials by the steady decline in the entropy across sessions (see Supplemental Information; Figures 1E and S1D). Here we show the results of recordings made during learning, focusing on the 9-target task during which the behavior was more consistent across the two monkeys (see Supplemental Information for all 4-target analyses in monkeys G and Y).

Across all sessions, we isolated 1,641 striatal units for study, 574 units from the CN of monkey G in the 9-target task (G9) and 1,067 units from the CN of monkey Y in the 9-target task (Y9). To determine the most relevant task period for units in the striatum of this free scan task, we generated histograms (20 ms bins) for all of the 400 ms windows before or after each event for each unit in each session. If the firing rate of a unit in a 400 ms event window was greater than two standard deviations above the mean firing rate (calculated across all trial time, not just in 400 ms windows) for four or more consecutive bins, then that unit was defined as significantly responsive in that event window.

We found that different proportions of units in the CN exhibited significant responses to the seven examined event windows (G9: F_6,280 = 62, Y9: F_6,910 = 66; p's < 0.0001; Figures 1F and S1E). Those units with significant responses specifically in one or more of the Targ-On, Targ-Off, Rwd-On, and Rwd-Off event windows we defined as task responsive (TR); this group comprised ~50% of all recorded CN units. Across all event windows and sessions, the greatest proportion of units (G9: 49%, Y9: 32%) responded significantly in the 400 ms after Targ-Off event window (p < 0.05, post hoc Tukey test).

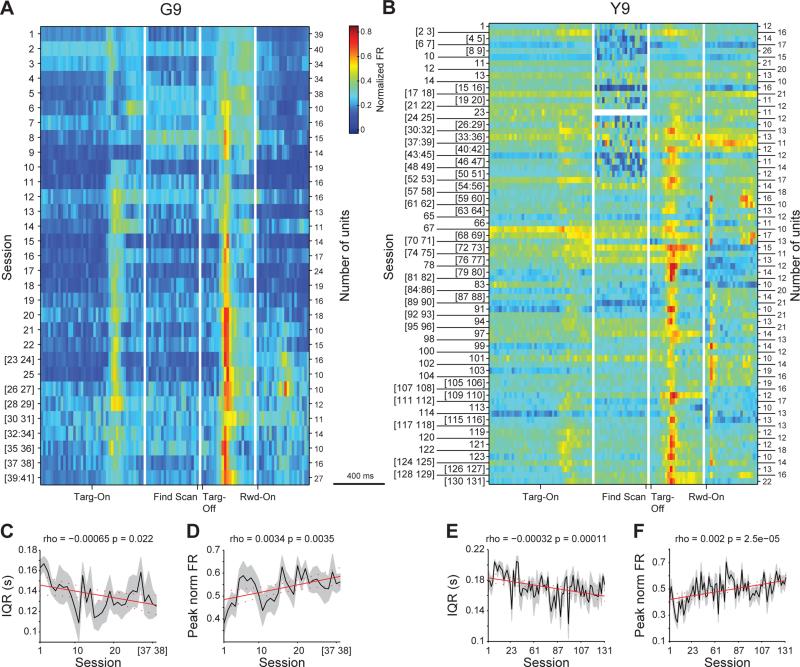
To examine the activity of the CN units across behavioral learning, we normalized each unit's firing in peri-event windows so that zero was the minimum and one was the maximum firing rate of that unit. Because later sessions often had fewer well isolated units than earlier sessions, and because we did not want to bias the analysis toward sessions with fewer cells, we then binned sessions together until there were at least 10 units in each bin, and we calculated the mean firing rate for each group of binned sessions (Figures 2A, 2B, S2A and S2B; binned by single sessions: Figures S2C and S2F). In addition to confirming the predominance of Targ-Off responses, we observed the gradual development of Targ-On (Supplemental Information; Figures S2K-S2P) and Targ-Off (Figures 2C-2F, S2D, S2E, S2G and S2H) activity through learning. Such task-bracketing activity has been previously observed in the striatum of rodents and monkeys performing instructed tasks (e.g., Fujii and Graybiel, 2005; Jog et al., 1999, see Discussion). Our observation of this task-bracketing pattern provides the first demonstration of the development of this activity pattern in naïve non-human primates freely acquiring their own idiosyncratic stereotyped action sequences. Strikingly, there was a commonality to this patterning across the different scan patterns that the monkeys performed as they continued over months of training. We focused on the Targ-Off window for the subsequent analyses because units with Targ-Off responses, the most abundant subtype, fired at the time that crucial RL variables, namely trial outcome and cost, could first be evaluated.

Figure 2. Changes in Activity Patterns of Striatal Neurons across Learning.

(A and B) All units recorded in monkey G (A) and monkey Y (B). Activity of each unit was normalized to minimum-to-maximum (0-1) scale. Units were binned across sessions, if necessary, so that there were at least 10 units in each bin. Each row shows the average activity of all units (20 ms bins, color indicates normalized firing rate) in that session bin across the following peri-event windows (divided by vertical white lines): Targ-On (−0.4 to 0.4 s), Find Scan (−0.4 to 0 s), Targ-Off (0 to 0.4 s), and Rwd-On (0 to 0.4 s; only for correct trials). (C and E) Response sharpness (mean ± SEM) in the Targ-Off window, as measured by IQR, increases across sessions (binned as in A) in monkeys G (C) and Y (E). Regression lines (red) shown with confidence intervals (red dashed).

(D and F) Average peak firing (± SEM) of all units across sessions in the Targ-Off window for monkeys G (D) and Y (F), calculated as the mean normalized firing rate in the center two quartiles around the median firing time.

See also Figure S2.

CN Units Represent Trial-by-Trial Outcome and Cost

To determine whether the scan-end signal could be composed of neuronal activity representing the RL variables of trial outcome and/or cost, we examined the trial-by-trial neuronal activity in the Targ-Off window. Importantly, although the outcome of the trial (correct/error) was simply associated with receipt of reward (reward/no-reward), the Targ-Off window occurred before the earliest possible time that the animal could receive reward and was temporally dissociated from the randomized timing of reward delivery. Thus, the spike activity at Targ-Off could not be attributed to reward delivery itself. We estimated the cost (PPE) as the difference between the actual and expected eye movement distance, the measure that we previously found to be a driving force in an RL model of the monkeys’ scanning behavior (Desrochers et al., 2010) and that we found to be superior as a driving force to other potential driving forces including distance, reward rate, the number of fixation/saccades, and saccade entropy. The RL models using these alternate factors took longer to reach steady-state and did not converge on the optimal path as did the RL model using cost. Distance was simplified to be the geometric distance: one unit was the horizontal or vertical distance between adjacent targets.

With outcome and cost as potential driving forces of behavioral acquisition, we adopted a multivariate regression approach to find the best variable to account for the activity of each neuron. We found that the regressors were correlated with one another, but we found that there was no multicollinearity problem as determined by Belsley collinearity diagnostics (all condition indices < 18, see Supplemental Information). We performed a stepwise linear regression to predict the trial-by-trial firing rate in the 400 ms after Targ-Off using terms for outcome, cost, and the interaction of the two variables (see Experimental Procedures).

Because the monkeys were free to move their eyes, we wanted to eliminate the possibility that changes in firing could be related to changes in the timing of the monkeys’ saccades. Thus, for this and subsequent analyses, we excluded the approximately 15% of units in the Targ-Off window (Eye category; Figures 3A, 3B, S3A and S3B) for which we found a significant correlation (Pearson's, p < 0.05) between saccade and spike onset times (Supplemental Information, Figures S2I-S2P). As a further control, we tested for and verified the fact that the distribution and variability of the final eye position at Targ-Off did not change across sessions (t₃₉'s < 2, p's > 0.05, Supplemental Information).

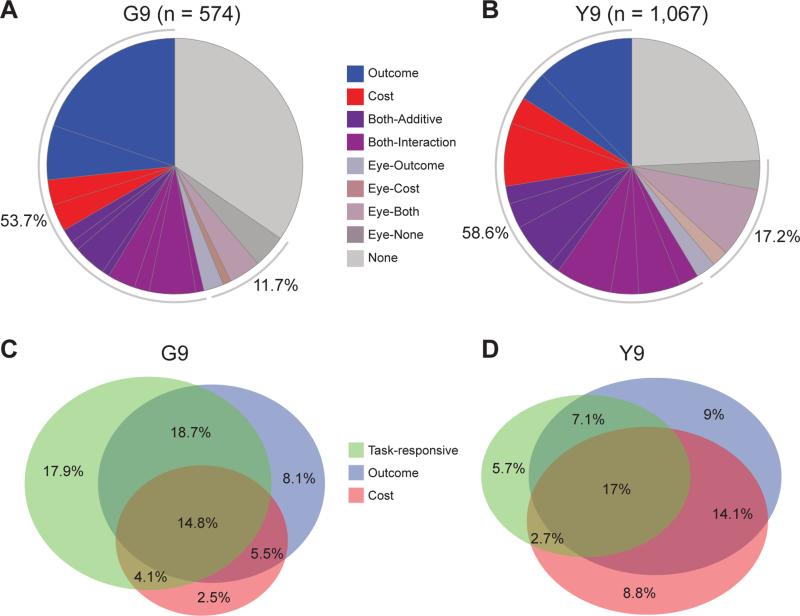
Figure 3. Response Categories of CN Units.

(A and B) Percentage of units categorized as Outcome, Cost, and Both (Additive and Interaction types) units recorded in monkeys G (A) and Y (B) across sessions. Signs (“+”, “−”, or combination) indicate the sign of the coefficient in the regression (for Both units, signs for Outcome and Cost shown, respectively, toward perimeter and towards center). Units correlated with eye movement times (Eye) are not further broken down into subtypes based on the sign of the coefficient.

(C and D) Venn diagrams showing percentage of each unit type. Eye units were excluded. Overlap of Outcome and Cost units represents Both units.

See also Figure S3.

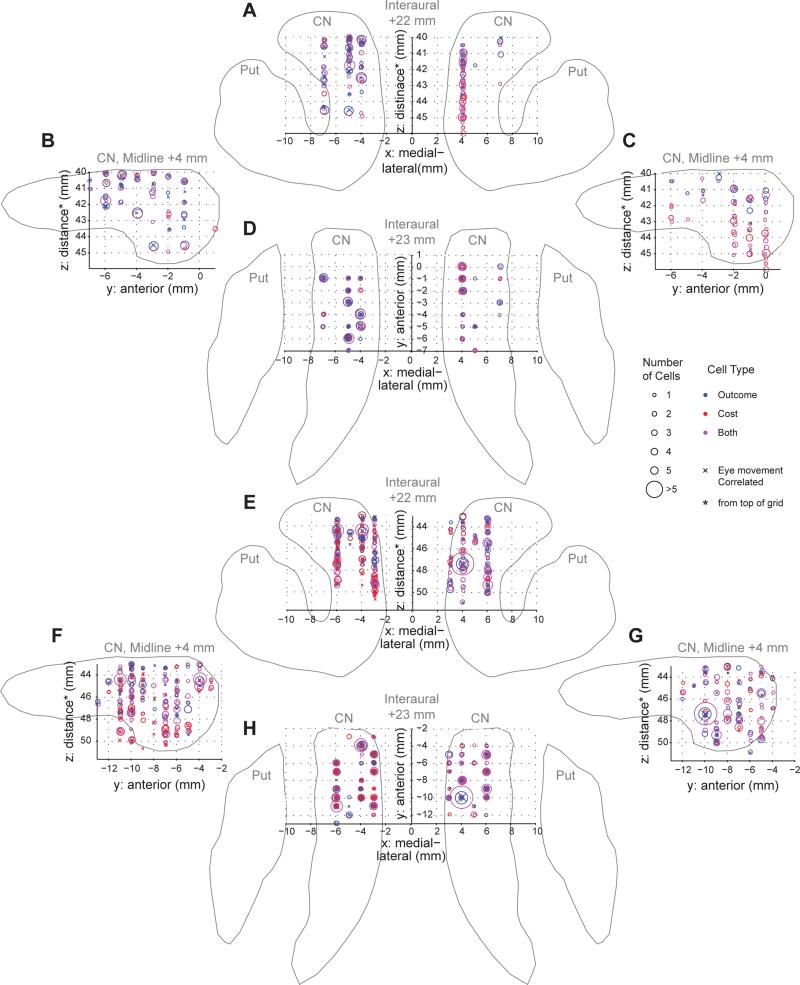
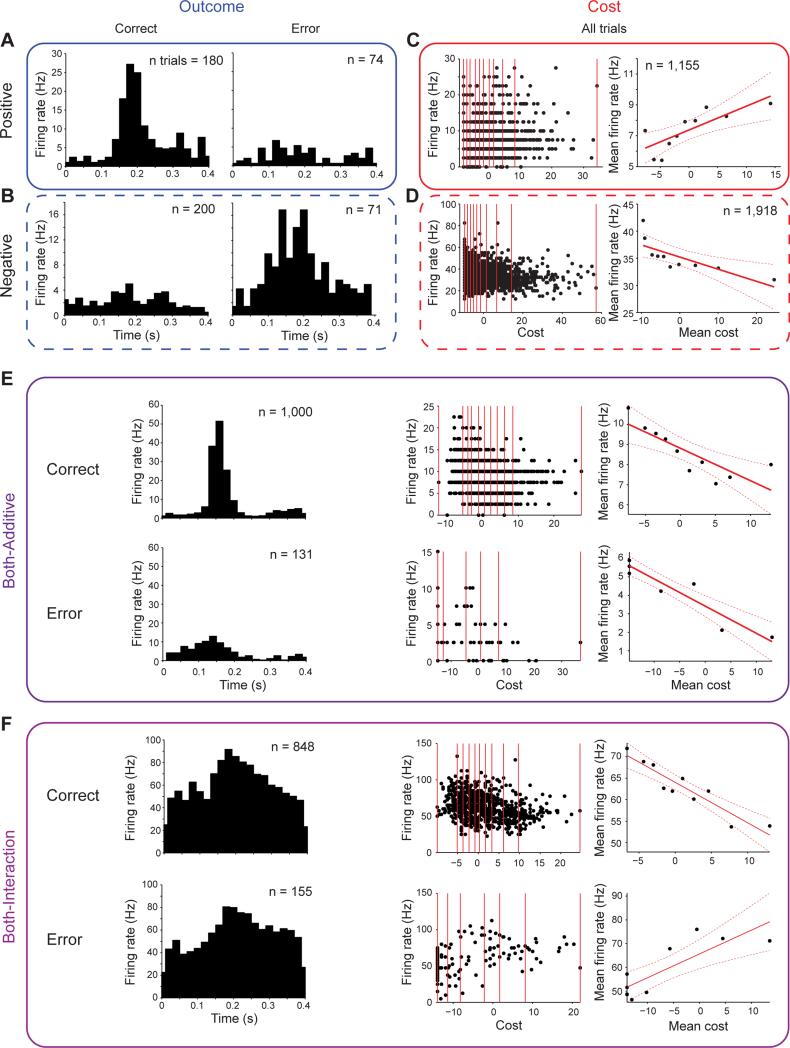
We found units with significant coefficients (p < 0.05), both positive and negative, in the linear regression for different combinations of the outcome, cost, and interaction terms. These units were physically distributed throughout the head and body of the CN (Figure 4). We defined as Outcome units those units for which the regression contained only a significant term for outcome (i.e., not for cost or the interaction of outcome and cost). Outcome units with positive coefficients responded with higher firing rates for correct trials (Outcome-positive units; Figure 5A); negative coefficients indicated greater firing for error trials (Outcome-negative units; Figure 5B). Cost units were defined as those for which only the cost term was significant. Cost-positive units fired more when the actual trial distance was greater than the expected mean distance (Figure 5C); conversely, Cost-negative units fired more when the trial distance was less than the expected distance (Figure 5D).

Figure 4. Recording Locations of Outcome, Cost and Both Units.

(A-D) Coronal view (A), sagittal view of left (B) and right (C) hemisphere, and axial view (D) of bilateral recording locations in G9. Outline of the striatum showing the CN and putamen (Put) is drawn for reference and does not represent exact border. The location of individual electrode tracks was verified in histological sections of each monkey's brain. Zero in the anterior/posterior (y) direction is the center of the grid used for implanting electrodes.

(E-H) The same as A-D but for recording locations in Y9.

Figure 5. Response Patterns of Single CN Units in Relation to Outcome and Cost.

(A and B) Units with a greater response in correct (left) trials (Outcome-positive unit, A) and with a greater response in error (right) trials (Outcome-negative unit, B). Plots show activity during 0.4 s period after Targ-Off (time 0).

(C and D) Trial-by-trial firing rate relative to cost (left) and mean firing rate with regression line (red line) and 95% confidence bounds (red dashed lines, right) for Cost-positive (C) and Cost-negative (D) units, plotted as in Figure 1D.

(E and F) Both-Additive (E) and Both-Interaction (F) units. Histograms as in A and B and correlations with change in cost as in C and D are shown for correct (top) and error (bottom) trials. All units recorded in monkey G.

There were two different ways that a unit's regression could simultaneously contain significant terms for both outcome and cost variables. Units with significant terms for outcome and cost without a significant interaction term were defined as Both-Additive units (Figure 5E). Those units with a significant interaction term were defined as Both-Interaction units (Figure 5F). Both-Additive and Both-Interaction unit types could be divided into four subtypes according to the sign of the coefficient for the Outcome and Cost terms: Outcome and Cost positive, Outcome and Cost negative, Outcome positive and Cost negative (Both-Additive example: Figure 5E), and Outcome negative and Cost positive (negative Both-Interaction example: Figure 5F). For subsequent analyses, we collected all units that simultaneously represented outcome and cost into a single category (Both), which contained the Both-Additive and Both-Interaction subtypes.

We found that each of these unit categories consisted of ~15% of recorded units across sessions, with ~60% of units representing some combination of the outcome or cost variables (Figures 3A, 3B, S3A and S3B). The fraction found for each unit type did not change significantly across sessions: no unit-type fractions exhibited significant correlations with session number across either animal (Pearson's p's > 0.05). This stability supports the general finding that cost (and outcome) are constant driving forces towards optimality throughout training (Figure 1C, see also Desrochers et al., 2010). Outcome, Cost, and other TR units formed separate but overlapping distributions; more than 60% of the TR units were also categorized as being either Outcome or Cost types (Figures 3C, 3D, S3C and S3D).

We validated the distinctions among Outcome, Cost and Both units by examining the mean peri-event time histogram in the Targ-Off window of each category separately during correct (rewarded) and error (no reward) trials. Outcome units exhibited a clear separation of responses in correct and error trials, confirming their classification as such (Figures S3E and S3F). Conversely, Cost units showed little or no separation between responses in correct and error trials, consistent with their coding a performance variable and not the outcome (Figure S3G). Units classified as Both did show a difference in mean response to correct and error trials (Figure S3H). Further, as shown by the pseudocolor plots illustrating the mean firing across trial events across sessions (Figures S3I and S3J), activity at Targ-Off sharpens in both correct and error trials. In the period during and after reward delivery, there is very little, if any, response of the Both units to reward itself, as was similarly observed across all units (Figures 2A and 2B). These findings demonstrate that these unit classes exhibit separable physiological responses.

To verify the robustness of the unit classifications, we performed additional, separate regressions employing variations in the calculation of the cost variable as well as alternative regression methods. Variations in the calculation of the cost variable were created by sampling different trials to estimate the mean distance (Supplemental Information). With these alternative cost variables, separate regressions were found to have distributions of unit types nearly identical to the distribution of unit types found with the original definition of cost presented above (two-sample Kolmogorov-Smirnov test, p's > 0.9, Figures S4A and S5A). To test the validity of the stepwise regression approach, we further performed four additional linear regressions using All Possible Subset and Ridge regression with Akaike and Bayesian information criteria for model selection (Supplemental Experimental Procedures, Amemori et al., 2015). The resulting distributions of unit types again did not differ from the distributions obtained with stepwise regression as presented above (Kolmogorov-Smirnov test p's > 0.3, Figures S4B and S5B). The finding that the classification of units used here was not changed with alternative calculations of the cost variable or regression methods provided further evidence for the distinctions among units with these response types in the CN.

It is not surprising that units in the CN responded to the outcome of the trial (Cai et al., 2011; Histed et al., 2009; Lau and Glimcher, 2007; Yamada et al., 2011, 2013; Yanike and Ferrera, 2014), but our findings additionally demonstrate a novel striatal representation of cost. Approximately half of the CN units represented behavioral cost in some manner, and this cost variable was the same variable that we previously found to drive the uninstructed formation of habitual eye movement patterns in these naïve monkeys (Figure 1D; Desrochers et al., 2010). Taken together, these results suggested that the CN units representing one or both of the outcome and cost variables could contribute to driving the acquisition of repetitive behavioral sequences resembling habitual behaviors.

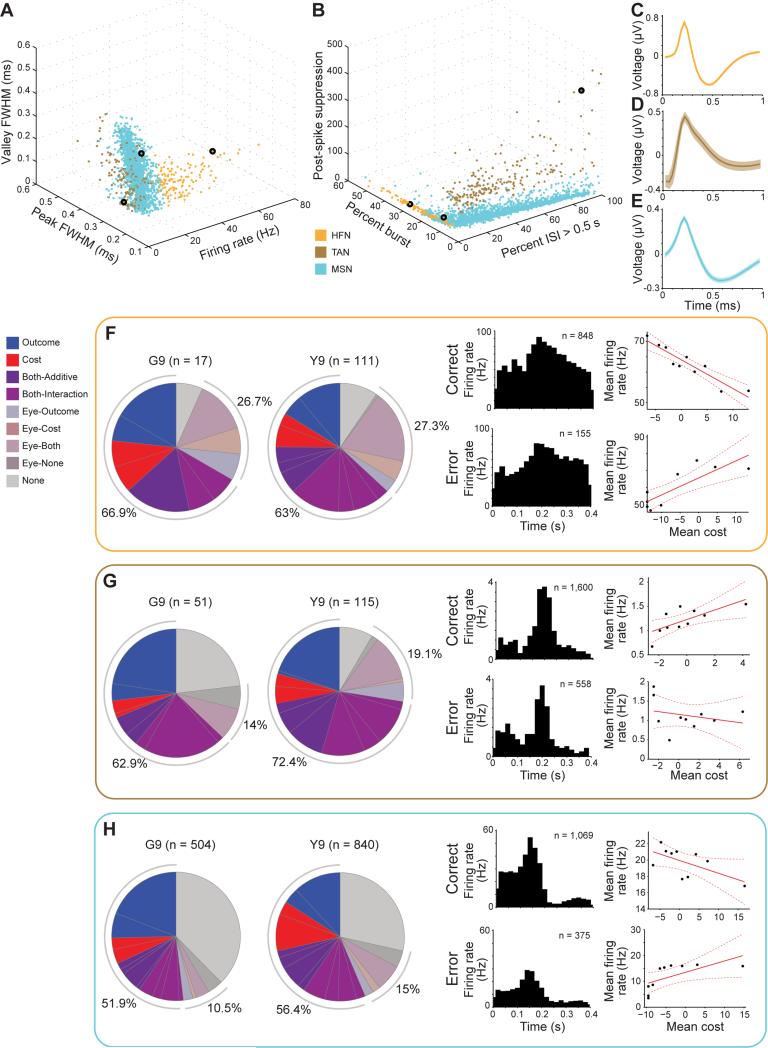
We classified each unit as belonging to one of three putative neuronal types in the striatum (see Supplemental Experimental Procedures; Figures 6A, 6B and S3K): high-firing neurons (HFNs; Figure 6C), tonically active neurons (TANs; Figure 6D), and medium spiny neurons (MSNs; Figure 6E). Outcome, Cost, Eye and combinations of these categories were all included within each of these putative neuronal types (Figures 6F-6H). The distribution of units in each category for each putative neuronal type was not significantly different from the overall distribution (Figures 5A and 5B; two-sample Kolmogorov-Smirnov test, p's > 0.05). Because there were similar distributions of Outcome and Cost units for each putative neuronal type, to analyze the maximum number of units possible in each session across learning, we grouped together all three neuronal types (putative HFN, TAN, and MSN) in subsequent analyses. We note that we do not assume that the identification of the putative neuronal types is fully accurate, or that the activity patterns and computations of these putative neuronal types are the same under all conditions. Rather, we report that in the context of activity in the Targ-Off window, the putative striatal neuronal types represented the relevant variables in concert and so could be grouped by response type.

Figure 6. HFN, TAN, and MSN Classification.

(A) All HFNs (orange), TANs (brown) and MSNs (blue) recorded in monkeys G and Y, plotted in 3-D by spike parameters used to classify HFNs: firing rate, peak full width at half maximum (FWHM) and valley FWHM.

(B) All units recorded in both monkeys, plotted in 3-D by firing pattern parameters use to classify TANs: percent of spikes with long (> 0.5 s) interspike intervals (ISIs), percent of spikes in a burst (two or more spikes within 10 ms) and post-spike suppression (see Methods).

(C-E) Mean wave forms of an HFN (C), TAN (D) and MSN (E) indicated by black circles in A and B.

(F-H) Response categories for HFNs (F), TANs (G) and MSNs (H) as in Figures 3A and 3B, and single units from the Both category of each unit type as in Figure 5.

See also Figure S3K.

CN Units Exhibit Changes across Learning

Because the predominant Targ-Off activity (Figure 2) was not constant across sessions, but rather, appeared to evolve across learning, we next asked how the neural cost and outcome feedback representations that we found in the Targ-Off period developed across task performance sessions. We found that trial-by-trial cost not only could contribute to an adaptive behavioral shift and selection of sub-optimal action sequences (Figures 1D and S1C), but also could be correlated with behavioral changes across sessions as measured by the entropy and efficiency of the saccade patterns (Figures 1C, 1E, S1B and S1D) (Desrochers et al., 2010). We therefore asked whether there were neural changes that were correlated with these behavioral changes across sessions. Unit responses, normalized for the population analyses shown in Figures 2, 7A and 7B, were not normalized in the analyses that follow.

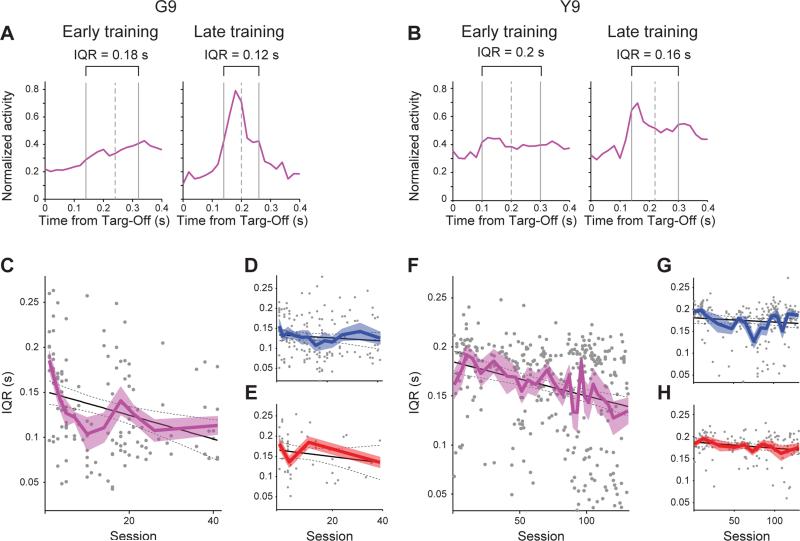
Figure 7. Inter-Quartile Range (IQR) Through Learning.

(A and B) IQR illustrated on the mean normalized firing rate histograms from Both units recorded early (left, mean of first five session bins) and late (right, mean of last five session bins) in training for monkeys G (A) and Y (B). Dashed line indicates median spike time.

(C) IQR of individual Both units (dots) across sessions in monkey G with correlation line (solid) and confidence intervals (dashed) in black. Mean IQRs (± SEM) in consecutive session bins (as in Figure 2) are shown in color.

(D-H) Same as in C but for Outcome (D) and Cost (E) units in monkey G, and Both (F), Outcome (G) and Cost (H) units in monkey Y.

See also Figures S4, S5 and S6.

To quantify a property of the neural activity that might reflect neural efficiency in encoding learning-related variables, we measured the sharpness of the activity in the Targ-Off window (Barnes et al., 2005; Jog et al., 1999). We used the inter-quartile range (IQR) of the spiking activity for the estimate of sharpness. For each unit in each session, we determined the IQR first by creating a histogram across all trials of the spike activity in the 400 ms Targ-Off window, and then by dividing the total number of spikes into four time bins (quartiles) so that each quartile contained the same number of spikes (but could have a varying width in time). Examples of time-bin boundaries that resulted from this procedure are shown as gray vertical lines on the sample histograms in Figures 7A and 7B. Then, by definition, the time boundary between the second and third quartiles (dashed gray line) is the median spike time, and the time between the first and fourth quartiles is the IQR. If the spike rate were greater in the middle of the 400-ms Targ-Off window, then the IQR would be shorter, as less time would be needed to bin a greater number of spikes. Thus IQR provided a measure of the sharpness of dispersion of the spike activity in the scan-end time window (Figures 7A and 7B).

To measure how the Targ-Off IQR of spike activity changed across sessions, we correlated for each unit the IQR and the session number in which the unit was recorded. Correlations were calculated for all units within each category over all sessions without any binning (gray points and black line fits in Figures 7C-7H), but for display purposes, we binned sessions together until there were at least 10 units of that category in each bin and plotted the mean IQR across those units in each bin (colored lines; Figures 7C-7H). We found that only the IQR of those units in the Both category showed significant correlations with steady decreases in IQR across sessions in G9 (Pearson's rho = −0.29, p < 0.001; Figure 7C) and Y9 (rho = −0.26, p < 0.0001; Figure 7F) and a significant interaction between session and category for both animals (ANCOVA, F_{2,321; 615}'s > 3, p's < 0.05). Further, these changes in IQR, the measure of dispersion of the Targ-Off window spiking, were not due to overall changes in firing time or rate as there were no consistent changes across sessions and across unit categories in either the median spike times or non-normalized firing rates of units (Figure S6). The IQR of Outcome and Cost units did not exhibit correlations across sessions for either monkey (rho's > −0.18, p's > 0.05; Figures 7E-7H).

Because the chronic electrodes were gradually lowered across training sessions, it was essential to dissociate the effects of training and electrode depth on IQR. We compared units in the Both category recorded earlier in training to those recorded at the same relative depth later in training, and found a significant decrease in the IQR of those units, even though they were recorded at the same depth (t₁₇ = 2.3, p < 0.05). Further, there were no differences across sessions among the recorded depths in the different unit categories (Outcome, Cost, and Both; F's < 1.4, p's > 0.5). Therefore, differences in IQR could not be due to differences in depth (see Supplemental Information for further details). In addition, these across-session dynamics were not solely a feature of categories derived from stepwise regression; nearly all of the results obtained with the stepwise regression model were replicated with the four alternative regression models (Figures S4C and S5C).

At the single-trial level, the decrease in the IQR of the Both units could have been due to more precisely aligned responses or narrowing of these responses, or to a combination of these variables. To test these potential underlying activity patterns, we employed two measures for each unit in each trial: the median spike time and the IQR of the spike times in the Targ-Off window. Then, as a measure of variability of those measures, we calculated the IQR of the trial-by-trial IQRs and the IQR of the trial-by-trial median spike times. We performed this analysis on each unit on each session. Changes in the variability of these measures tell us whether, in each trial, the units exhibited narrower responses (decrease in IQR of IQR) or more precisely aligned responses (decrease in IQR of median). We found, that the sharpening effect in Both units was associated with more tightly aligned responses, as there was a significant decrease in the IQR of the median spike times across sessions (G9: rho = −0.36, p < 0.001; Y9: rho = −0.19, p < 0.001), but no decrease in the IQR of the IQRs across sessions (G9: rho = 0.03, p > 0.7; Y9: rho = 0.14, p < 0.01). The difference in the slopes of these two measures was significant across sessions, with a significant measure × session interaction (G9: F_1,266 = 10.8, p < 0.01; Y9: F_1,630 = 18.4, p < 0.001).

In sum, we found a gradual sharpening of the neural responses in the Targ-Off window across training only in the CN units that were the most highly dimensional, i.e., the Both units that concurrently represented the outcome and cost variables. The finding that it is the alignment of responses across trials that produces the decrease in IQR of the Both units across sessions suggests that the firing of the population of units would also be more precisely aligned within a single trial. This alignment could serve as a predictor of efficacy and as a factor favoring spike-timing-dependent plasticity.

We next searched for a link between this neural activity and the behavioral acquisition observed across sessions. A candidate correlate for the changes in the efficiency of the saccade patterns across sessions was the distance measure (total distance the monkey's eyes traveled while scanning) from which the cost variable was calculated. However, the fluctuations in scan distance due to the efficiency of the saccade patterns executed were relatively small in comparison to the fluctuations due to the random trial to trial placement of the baited target, and therefore the mean distance did not change across sessions (Figure 1C). Moreover, because the cost variable was defined as a fluctuation around this mean distance, cost itself always had a mean around zero across sessions. The behavioral measure that we did previously find to reflect the shift towards optimality across sessions was the repetitiveness of the saccade patterns (Desrochers et al., 2010). Repetitiveness was measured by saccade pattern entropy (see Supplemental Experimental Procedures, Figure 1E). Increases in repetitiveness indicated decreases in entropy, as there was less variability in the probability of moving (making saccades) from one target to any other target. We therefore calculated the correlation of each unit's Targ-Off IQR with the saccade pattern entropy in the session during which it was recorded (Figures S7 and S8). For display purposes, units were binned across sessions so that there were at least 10 units per bin, and the mean entropy was calculated for each bin across the sessions included in that bin (Figure 8).

Figure 8. Correlation between Saccade Entropy and IQR.

(A) Saccade entropy versus IQR in the Targ-Off window plotted for Both units in monkey G using the same bins as in Figure 2. Each point represents the mean across all the sessions contained in that session bin. For illustrative purposes only, regression lines (solid) and 95% confidence intervals (dashed) are shown.

(B-F) Same as in A but for Outcome (B) and Cost (C) units in monkey G, and Both (D), Outcome (E), and Cost (F) units in monkey Y.

See also Figures S7 and S8.

The responses of the Both units (Figures 8A and 8D) exhibited highly significant correlations between the neural scan-end activity sharpness (IQR) and the entropy of the behavioral saccade behavior (G9: Spearman's rho = 0.35, p < 0.0001; Y9: rho = 0.16, p < 0.01). By contrast, neither Outcome unit responses alone nor Cost unit responses alone were significantly correlated with entropy in either monkey (Spearman's rho's < 0.1, p's > 0.1), and there was a significant interaction between unit category and saccade pattern entropy for both animals (ANCOVA, F_{2,321; 615}'s > 3, p's < 0.05).

These results were reinforced by analyses with the alternative regression methods employed using All Possible Subset and Ridge regression with Akaike and Bayesian information criteria for model selection (Figures S4D and S5D). Further, we attempted to determine whether the effects of the number of sessions could be separated from the effects of entropy on these correlations. Although there was some evidence for an independent correlation between entropy and IQR with the effects of session number removed, the results indicated that session number, reflecting length of exposure to the task, and entropy are both important learning-related variables not clearly separable in this context (Supplemental Information). Finally, these changes were not driven by overall changes in firing peak or rate, as there was no consistent relationship between median firing time or firing rate and entropy across the unit types (Figures S7 and S8), further emphasizing the sharpening of the Targ-Off responses as a critical parameter related to the gradual refinement of the saccade patterns as naïve monkeys perform a free-viewing scan task, without explicit instruction.

DISCUSSION

Here we have shown that as naïve monkeys learn without explicit training to scan target arrays effectively to receive rewards, subsets of neurons in the striatum acquire representations of key learning variables: trial outcome and behavioral cost. Over the many sessions of this untutored behavioral learning, populations of striatal neurons developed accentuated firing at the beginning and end of the stereotyped scans, and their end-responses became progressively sharpened in close relation to the increases in the habitual repetitiveness of the scanning behaviors. Notably, only those neurons with both outcome and cost representations exhibited such across-session sharpening of the scan-end responses. The conjunction of these learning variables in the same neurons in the striatum could provide precisely the update signal necessary for the monkeys to improve in the efficacy of their saccade patterns, narrowing the scan-end signaling temporally to provide signals compatible with spike-timing dependent plasticity. These findings suggest a novel mechanism by which the striatum could participate in the formation of natural, untutored habitual behaviors.

Pronounced Scan-End Activity Develops in the Primate Striatum during Natural, Untutored Learning

In each monkey, without explicit behavioral training and across the performance of different scan patterns during behavioral learning, the activity of many neurons in the striatum developed phasic responses at the beginning and end of the saccade sequences. This ‘beginning-and-end’ pattern resembles the task-bracketing patterns found in rodents given explicit training on cued and goal-directed sequential tasks (Barnes et al., 2005; Jog et al., 1999) and the enhanced phasic responses of units in the prefrontal cortex and striatum neurons at the beginning and end of instructed sequences of saccades (Fujii and Graybiel, 2003, 2005). These parallel findings suggest that self-initiated, untutored learning can be accompanied by re-patterning of striatal firing resembling that found in instructed learning. By focusing on striatal activity at the end of each scanning period, when feedback error signals could be used in the uninstructed development of habitual behaviors, we found that this scan-end activity could represent key RL variables including PPE (cost), RPE (outcome), or both. The activity of striatal neurons that encoded both outcome and cost was highly correlated with the degree to which the scan patterns performed were repetitive, raising the possibility that the end signals could be a biomarker of the degree of learning or habit formation.

Dynamic Cost and Outcome Representation in the Striatum

We have shown that the activity of populations of striatal neurons dynamically correlates with measures of learning on two time scales: behavioral adaptation on a trial-by-trial basis and an across-session acquisition of optimal behavioral sequence production. We found that the PPE derived for each trial affects the subsequent selection of the most frequent patterns performed. This finding was not specific to particular most-frequent saccade patterns, suggesting that this influence represents an overall mechanism by which sub-optimal pattern selection could be signaled in the striatum. Further, even though the patterns’ changes can appear rather abrupt on a macro scale (across sessions) (Desrochers et al., 2010), we have shown that they can be driven by relatively small trial-by-trial changes that nudge the behavior in the direction of optimality, thus producing a gradual shift with less efficient patterns being performed less frequently and more efficient patterns being performed more frequently. The activity of many striatal neurons exhibited correlations with this same cost variable, and thus these activities were correlated with trial-by-trial changes in behavioral learning.

The sharpening of the end signals, as evidenced by decreases in IQR of the Both units, was produced by a more precise alignment of responses trial-by-trial. This finding suggests that the population firing of the striatal neurons recorded could become more aligned within a single trial, potentially enabling Hebbian mechanisms to link these neurons together in networks. These mechanisms potentially could produce greater efficacy, on a trial-by-trial basis, of communicating signals to downstream targets of the striatal neurons. Given that we have shown that the cost variable is a driving force in both optimal habit-like formation across sessions and trial-by-trial basis adaptation, and that the outcome of trials (presence or absence of reward) is generally accepted as a driving force in trial-by-trial basis adaptation, we hypothesize that the dynamics of the response of these neurons across sessions could also be an important part of the learning process and the neural activity that underlies it. Alternatively, a greater alignment of the Targ-Off signal could indicate that the signal has become more predictive of subsequent behavior as training progressed. Further investigation will be necessary to explore these and other potential mechanisms.

Critically, the subpopulation of striatal end-responsive neurons that represented both cost and outcome, but not the subsets of cost-responsive neurons or outcome-responsive neurons alone, exhibited long-term, cross-session changes in firing pattern: their spike activity underwent a gradual sharpening that was highly correlated with the increases in repetitiveness of the scanning movements that the monkeys exhibited across training sessions. In work in rodents, the degree of sharpening of striatal responses was found to correlate with the degree of habit formation (e.g., Barnes et al., 2005; Smith and Graybiel, 2013). Our findings suggest that an aspect of local striatal spike density at scan-end, combining information about cost and outcome, is available in the striatum as a putative teaching signal for natural, uninstructed learning in non-human primates.

Extensive work has shown that outcomes, in the form of rewards or values, are represented during learning in the CN in addition to the error associated with reward prediction (Asaad and Eskandar, 2011; Daw et al., 2006; Histed et al., 2009; Lau and Glimcher, 2007; O'Doherty et al., 2004; Stalnaker et al., 2012; Tanaka et al., 2004; Yamada et al., 2011, 2013; Yanike and Ferrera, 2014). There is a much smaller body of work specifically pertaining to the representation of cost in the dorsal striatum. Of note is the fact that, according to our findings, changes in firing rate due to differences in cost are relatively small in comparison to changes related to reward outcome (e.g., see Fig. 5E Outcome versus Fig. 5E Cost). This difference could account for the relative paucity of reports of cost signals in the striatum: the changes in activity due to these factors are relatively small, and a large parametric range of values is required to detect them.

The cost variable that we found to be related to the Targ-Off spike responses of CN neurons was the same cost variable that we earlier found to be a better driver than reward of the RL algorithm that modeled the monkeys’ free scanning patterns (Desrochers et al., 2010). A prediction error in cost is not commonly used in modeling an adaptive change in behavior, but it bears resemblance to variables in traditional models of sequential (Squire, 2004) and non-sequential (Gomi and Kawato, 1993; Ito, 2008; Kawato and Gomi, 1992; Marr, 1969; Wolpert and Ghahramani, 2000) motor skill learning thought to be represented in the cerebellum (Kitazawa et al., 1998; Medina and Lisberger, 2008). Most computational models of sequential movements, however, have emphasized the use of reward prediction error as the feedback signal (Berns and Sejnowski, 1998; Dolan and Dayan, 2013; Doya, 2000; Gläscher et al., 2010; Hikosaka et al., 1999). Here we suggest, as predicted by our cost-based RL model (Desrochers et al., 2010), that subsets of neurons in the striatum of macaque monkeys represent at trial end the same cost variable identified behaviorally.

Many studies have investigated the representation of effort in the neocortex (see Rushworth et al., 2011 for review), and both theoretical and experimental work specifically relating the effort of actions to the striatum has focused on cost/benefit trade-offs in motor tasks, positing a role of dopamine in their representation (Niv, 2007), or in decision-making tasks in which cost and benefit are combined variables to be judged in guiding actions (Amemori and Graybiel, 2012; Friedman et al., 2015). In human patients with Parkinson's disease, depleted levels of striatal dopamine are accompanied by decreases in efficient planning and execution of tasks (Gepshtein et al., 2014; Mazzoni et al., 2007), compatible with a function for the striatum in representing cost itself in such motor targeting tasks. Downstream targets of the striatum, components of the direct and indirect pathways, also have been implicated in performance prediction error monitoring (Tan et al., 2014). Moreover, the notion of cost has been extended from the motor domain by showing that mental effort can be represented by activations in the CN in humans (Schouppe et al., 2014). The findings presented here help to fill a gap in this domain by showing that the specific neural encoding of conjunctions of outcome and cost can parallel not only single movements or decisions, but also the acquisition and execution of complex, naturalistic self-taught behaviors in the primate.

Questions for Further Study

Our findings are, per force, limited to the neuronal population that we sampled with the ~100 electrodes chronically implanted across the striatum of each monkey. We have not obtained proof that the scan-end activity that we report is causally responsible for the naturalistic learning that we observed. Furthermore, we focused on activity occurring in the Targ-Off window, after the movements have been completed for the trial, in order to examine potential feedback signals, but we recognize that other changes occurred during the months of the recording periods. When examining the entire trial-time series as a whole, it was evident that the beginning of the movement sequence was also highly represented, as part of a beginning and end pattern.

The specific content of the scan-start (Targ-On) signal is an intriguing avenue for future research. A subset of the task-start signals recorded in the prefrontal cortex of monkeys performing instructed sequences of saccades were found to be directly linked to increases or decreases in task-end activity (Fujii and Graybiel, 2003). Also, in the scan task that we used here, CN activity at Targ-On appeared to be independent of the execution of individual eye movements. These observations suggest that CN activity at Targ-On may represent the same kind of activity previously observed in the prefrontal cortex to mark the initiation of stereotyped action sequences, but in an uninstructed context. It is possible that these signals at the beginning and end of sequences of uninstructed movements are intimately tied to predictions about performance and outcome. If so, it is reasonable to suggest that their dysfunction could contribute to deficits in initiating and terminating commonplace movement sequences, such as those observed in patients with Parkinson's disease.

Other task periods also hold promise for future investigation. Howe et al. (2013) found, with fast-scan cyclic voltammetry, that dopamine release in the striatum of rats ramps up with the progress towards a distant goal in a maze. This observation suggests that there could be a gradual dopamine signal that ramped up through the progress of scanning; it will be important to determine whether this dopamine signal is related to the end signal that we describe here. Further, although we have shown that cost drives the acquisition of repetitive action sequences in general, an important open question is how neural activity in this scanning period relates to the previously described individual habit-like sequences themselves (Desrochers et al., 2010).

End-Boundary Activity as a Higher Order Form of Neural Representation Related to Learning

The fact that action boundary activity of this kind has been reported in both rodents (Barnes et al., 2005; Jin and Costa, 2010; Jin et al., 2014; Jog et al., 1999; Smith and Graybiel, 2013) and in over-trained primates (Fujii and Graybiel, 2003, 2005), and now our evidence that this boundary activity exists in monkeys performing uninstructed sequences of movements of their own, suggests that signals marking the end of successful performance are a fundamental feature of behavioral learning of repetitive behaviors and habits. Moreover, the end-boundary activity sharpening of a subpopulation integrating cost and outcome signals that evolves over time is remarkably similar to the reduction in the variability of neural responses previously reported in rodents learning a T-maze task (Barnes et al., 2005). These converging lines of evidence across different species and tasks suggest that the eye-movement sequences that the individual monkeys performed were represented by the action boundaries developed during months of exposure to the scan task. This commonality suggests that the beginning-and-end patterning, including the prominent end-related activity analyzed here, represents a higher order representation not only of scan-end signaling itself, but also of task structure, coordinately built up through the learning process.

EXPERIMENTAL PROCEDURES

Two adult female monkeys (Macaca mulatta, ~5.9 kg each, monkeys G and Y) were studied in the experiments. All procedures were performed as approved by Massachusetts Institute of Technology's Committee on Animal Care. The details of the surgical procedures and chronic recording method was previously published (Feingold et al., 2012), and a summary is provided in Supplemental Experimental Procedures.

The two monkeys were experimentally naïve prior to the first day of exposure to the free-viewing scan task, as they were not exposed to any explicit task training (on any task) prior to the first day of recording. They were only trained to be transferred from their home cage to the primate chair in the laboratory and to sit quietly in the chair with their head stabilized prior to the first day of neural recording. The free-viewing scan task and the related analyses of behavioral data have been previously described in detail (Desrochers et al., 2010); therefore, a summary is provided in Supplemental Experimental Procedures.

One Y4 session and one Y9 session were excluded due to data loss. Session blocks with fewer than 55% rewarded trials were included only if performance in other blocks indicated the monkey was sufficiently motivated to perform the task, and session blocks with fewer than 40 rewarded trials were not included in analyses (~4% excluded overall). All analyses were done in Matlab.

For each session, the probability of the monkey fixating each target in the green target grid following a fixation of each of the targets in the target grid was calculated to allow formation of the transition probabilities for that session. The entropy of the transition probabilities for each session (q) was defined as:

$$E=-\sum _i{q}_i\sum _j{q}_{ij}{\log }_2{q}_{ij}$$

where q_i is the probability of observing target i, and q_ij is the probability of observing target j followed by target i.

The trial-by-trial cost was calculated in the following manner. First, the distance measured from Targ-On to Targ-Off in each trial was simplified to be the geometric distance, so that the horizontal or vertical distance between two adjacent targets was equal to one. The mean distance was calculated over all trials in a single session and then was subtracted from the distance traveled in each trial to yield an estimate of the trial-by-trial cost (Δ distance). A positive cost would mean that the distance in the current trial was greater than the mean distance; a negative cost would mean the distance in the current trial was shorter than the mean distance.

Units were separated from noise manually and with templates using Offline Sorter (Plexon, Inc.). We used established methods (Thorn and Graybiel, 2014) to classify units as HFNs, TANs, or MSNs (see Supplemental Experimental Procedures).

The stepwise regression with the firing rate (number of spikes) in the Targ-Off window (400 ms) as the response variable was initialized with an intercept, outcome (as a categorical variable for correct and error trials), cost, and an interaction term.

$$\text{Firing rate}\sim 1+\text{Outcome}+\text{Cost}+\text{Outcome:Cost}$$

The criterion to add or remove terms was the p-value for an F-test of the change in the sum of squared error. Terms were added if p < 0.05 and removed if p > 0.10.

Highlights.

• During sequence learning, macaque striatal neurons encode integrated cost-benefit

• These signals mark ends of saccade sequences acquired without explicit training

• With learning, the cost-benefit end signals sharpen via population spike alignment

• This sharpening is tightly coupled to decreasing entropy of the sequences acquired