Abstract
Key points
The brain makes decisions by means of races between neural units representing alternative choices.
In the present study, we record the eyemovements made in the Wheeless task, when a visual stimulus is followed after a short delay by another stimulus demanding a different response.
The behaviour can be very precisely described as a race between three independent decision processes: one Go process for each of the responses, and a Stop process that tries to cancel the first, now erroneous, response.
To explain the high success rate for cancellation that we observe, the onset time for the Stop process must be some 10–20 ms shorter than for Go.
As well as extending our understanding of the dynamics of complex decision‐making, this task provides a rapid, non‐invasive method for quantifying disorders of higher neural function.
Abstract
The brain makes decisions by means of races between neural units representing alternative choices, and such models can predict behaviour in decision tasks in a precisely quantitative way. But what is less clear is how soon after the stimulus the race actually starts. In the present study, we re‐visit a complex decision experiment: the Wheeless task, in which a saccadic stimulus is followed after a short delay by a second stimulus, with the subject sometimes making a saccade to the first, now inappropriate, stimulus, and sometimes going straight to the correct one. We demonstrate that a simple model with three accumulator units, two ‘Go’ and one ‘Stop’, can then account in detail for the individual responses made, as well as their timing. This complex decision‐making behaviour is predicted directly for each individual subject by their performance in a simple step saccadic task, which identifies the two free parameters that are specific for each subject. By contrast to previous assumptions, we find that it is necessary for the onset time of the Stop unit to be shorter than for Go by 10–20 ms. This suggests a specifically fast mechanism for altering responses in situations where urgent action is needed to prevent an impending error.
Abbreviation
- K–S
Kolmogorov–Smirnov
Introduction
It is generally assumed that the brain makes decisions as a result of accumulating relevant information by a quasi‐Bayesian process until the resultant probability reaches a threshold that justifies action. How long this takes will depend on the dynamics of the rise‐to‐threshold, and quantitative analysis of reaction times has provided a great deal of information about the underlying decision mechanisms. But what about when things go wrong?
An example is when a second stimulus appears very soon after the first, which makes the first response inappropriate: when driving, for example, and the crossing lights turn green but a pedestrian steps in front and you stop yourself from hitting the accelerator. In the laboratory, a popular example is the countermanding task: subjects are told to cancel their response to a stimulus if a second one appears (Logan & Cowan, 1984; Logan et al. 1984; Carpenter, 1988; Hanes & Schall, 1995; Hanes & Carpenter, 1999; Boucher et al. 2007; Camalier et al. 2007; Emeric et al. 2007). Because the accumulation process is noisy, countermanding is probabilistic; sometimes it succeeds, sometimes it does not. If the delay D before the second stimulus is long, the probability of successful countermanding is low because the decision process has almost reached completionbut rises steadily as D is reduced.
It is not difficult to model all of the above with two accumulating decision units: one (Go) leading to the response and a second (Stop) causing immediate cancellation of the impending movement (Fig. 1) (Logan & Cowan, 1984; Logan et al. 1984; Hanes & Schall, 1995; Hanes & Carpenter, 1999). Specifically, one can instantiate the two units using LATER (Carpenter & Williams, 1995; Carpenter, 2012), a Bayesian model that can provide quantitatively accurate predictions of the stochastic behaviour of individual subjects in this and other more complex tasks (Hanes & Carpenter, 1999; Noorani & Carpenter, 2011; Noorani et al. 2011; Noorani & Carpenter, 2013; Noorani, 2014; Noorani & Carpenter, 2014). Such a race between Go and Stop processes has recently been demonstrated for neurons in the basal ganglia during countermanding (Schmidt et al. 2013), and similar activity is probably found whenever impending actions must be cancelled (Noorani & Carpenter, 2014).
Figure 1. A model for countermanding .
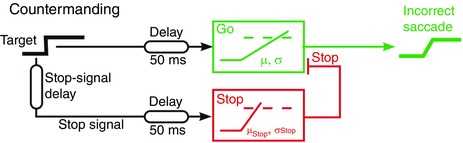
When the target appears, it triggers a rise of activity in a Go decision unit that would normally initiate a response on reaching threshold. However, if a stop signal is presented (after the stop‐signal delay), it triggers a Stop decision unit that cancels the Go unit if it reaches its threshold first. Because of variability in the rates of rise of the decision signals in different trials, sometimes cancellation may be successful and sometimes not.
A related but less artificial task can provide even more information about how neural decisions alter when circumstances suddenly change: the Wheeless task, which was introduced almost 50 years ago but subsequently investigated only sporadically (Wheeless et al. 1966; Komoda et al. 1973; Carlow et al. 1975; Becker & Jürgens, 1979; Camalier et al. 2007). It can be regarded as a special case of the more general double‐step task (Westheimer, 1954), in which a saccadic target is presented in two successive positions with a short intervening delay; the relationships between different versions of the basic task have been usefully discussed by Ramakrishnan and Murthy (2013). In the Wheeless task, a target steps to one side at the start of the trial; in control trials, it remains there but, on other trials, randomly interleaved, after a delay D, it jumps to the corresponding location on the opposite side (Fig. 2). No specific countermanding instructions are needed: subjects are told simply to follow the target with their eyes. As with countermanding, behaviour is probabilistic: on some trials, they make a saccade to the first target (a type A response), which is followed by a saccade to the second (a type C response), whereas sometimes they go straight to the final position (a type B response). In general, the proportion of type A responses, p(A), is an increasing function of D (Fig. 4).
Figure 2. The Wheeless task .
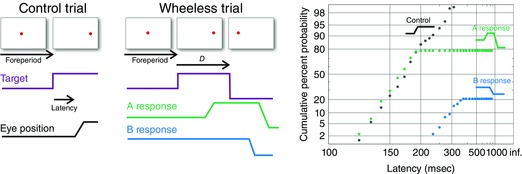
Left: in a control trial, after a random foreperiod, the target steps to one side and the subject makes a saccade to follow it after a delay: the latency or reaction time.In the Wheeless task, such trials are randomly interleaved with trials (middle) in which, after a delay D, the target steps to the opposite side. The subject may then respond by making two saccades: one to the first position (an A response, grey) followed by one to the second (a C response), or may jump straight to the second (a B response, black). Right, reciprobit plots of reaction times from one subject in this experiment, showing cumulative frequency as a function of reciprocal latency. The distribution for A responses (grey) is initially similar to that for controls (open circles) but then stops at a level dependingupon D (whose value here was 100 ms). The B responses (black) are greatly delayed but rise in a similar manner to a steady level.
Figure 4. Dependence of p(A) and μstop on D .
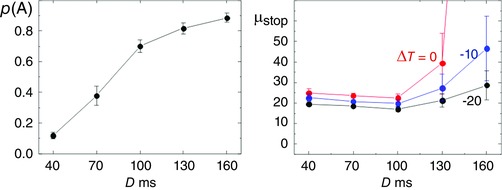
Left: average values of p(A), rising monotonically as D increases. Right: average best‐fit values of μstop for three different values of ΔT, of the Stop signal afferent delay relative to that for Go; with no reduction (ΔT = 0) the value rises catastrophically beyond D = 130 ms; for ΔT = −10 ms, μstop still rises but less dramatically; for ΔT = −20 ms, μstop does not alter significantly with D. Averages are across all subjects; error bars indicate 1 SE; μstop is shown in Hz.
Although this relationship between p(A) and D can provide some information about the underlying mechanisms, very much more can be learnt (as with countermanding) by examining the distributions of reaction times of latencies of the different types of response in the task. A helpful way to represent the outcome of such experiments is to plot these distributions cumulatively. Using a probit scale for the cumulative frequency, and a reciprocal scale for latency (a reciprobit plot), in control trials, we should then obtain a straight line. This is because, in LATER, the rate of rise varies from trial to trial with a Gaussian distribution, such that the reciprocal of latency is also Gaussian (Carpenter & Williams, 1995; Carpenter, 2012). An example is shown in Figure 2 for D = 100 ms. The cumulative probabilities are plotted as a fraction of the total number of trials for that category, leading to distributions that level off at p(A) (for A), or 1‐p(A) for B. It can be seen that the earlier responses to A follow the same distribution as the controls, and that the effect of the second stimulus effectively cuts the cumulation short, initiating a corresponding cumulation of the B response
A great advantage of the Wheeless task is that there is at least one response in every trial, whereas, in countermanding, a large number of trials generate no response at all, such that there is nothing to measure; from an experimenter's point of view, it is therefore a great deal more efficient, with three different classes of response (A, B and C) for which attemptscan be made to predict the distributions. It is also more natural than countermanding in that no explicit instructions to cancel are required: cancellation simply follows implicitly if subjects are just told to follow the target.
In the present study, we examine latency distributions for the three different kinds of responses (A, B and C) made in the Wheeless task and, from these, we deduce a simple model that, despite having very few parameters, predicts the quantitative details of the responses by individual subjects, providing much more information about the Stop process, as well as how it is triggered. In particular, the time needed to detect a situation where the Stop unit needs to abort the original response is shown to be significantly shorter than that needed to detect the existence and location of primary targets to initiate Go units. We suggest that there are two functionally distinct routes by which incoming stimuli influence a decision: one that triggers directed actions, and one that recognizes and aborts unwanted impending actions, with the increased speed of the latter reflecting the simpler nature of the associated detection process.
Methods
Participants
After having provided their informed consent, eight subjects (six males, two females, age mean ± SD 27.9 ± 6.8 years) participated in the experiments, which were performed in accordance with the Declaration of Helsinki and had received Local Ethical Committee approval. None of the subjects had visual defects other than deuteranopia for participant F, and refractive errors, which were corrected as necessary: the authors comprised two of the subjects; the other subjects were not informed about the purpose of the experiments. Data from one participant had to be discarded because of over‐noisy raw records.
Stimuli
We created the stimuli on a calibrated and linear CRT display (GDM‐F520 monitor, resolution 800 × 600; Sony, Tokyo, Japan), with a refresh rate of 100 Hz synchronized to the timing of data collection, viewed at a distance of 1 m to provide a visual subtense of 22 × 17 deg. The target elements consisted of black dots of diameter 0.3 deg, with the peripheral targets centred horizontally at 4 deg to left or right of the centre, on a uniform white background (CIE x = 0.283, y = 0.299, Lum = 107.8 cd m−2). The visual surrounds were arranged to have a similar luminance, aiming to minimize the effect of after‐images or field adaptation.
Recording
Eye movements were measured using a dual differential infrared reflection binocular oculometer (Ober et al. 2003) (Ober Consulting, Poznan, Poland) with a 250 Hz bandwidth, and linear to 7% within a range of ±30 deg. The oculometer was positioned on the bridge of the nose, with the subject's head resting comfortably on a chin‐rest. Its output was sent to a ViSaGe system (Cambridge Research Systems Ltd, Rochester, UK) sampling at 100 Hz in exact synchrony with the screen frame rate to prevent uncertainties arising from interrupts and other interference from Windows processes; the ViSaGe in turn interfaced with the recording and stimulation application SPIC (Carpenter, 1994) running on a PC, which also generated the stimuli.SPIC detects saccades in real time using a criterion based on velocity and acceleration (normally 50 deg s−1 and 2500 deg s−2); however, after each run, we checked the individual saccadic traces manually and excluded from further consideration any containing obvious artefacts (as a result of blinks, headmovements or lapses of attention) or occurring with a latency of less than 80 ms.
Protocols
Each trial began with presentation of the central target during a foreperiod whose duration varied randomly between 0.5 s and 3 s in a non‐ageing manner (Oswal et al. 2007), followed by presentation of one of the peripheral targets, randomly on the right or left. On experimental trials, which formed half of the total and occurred at random, this was followed after an interval D by the target moving to the mirror‐image target position on the opposite side of the screen: experimental trials were randomly interleaved with possible values of D: 40, 70, 100, 130 and 160 ms. Each trial ended 600 ms after presentation of the first stimulus, with an inter‐trial period of 100 ms before the start of the next. One hundred such trials constituted a block, and each participant undertook a run of six blocks, with rest and refreshment in between as required. The subjects were told to look at the targets presented on the screen and to follow them with their eyes when they moved; we deliberately did not draw attention to the fact that that there were interleaved control and experimental trials or that, in the latter, the target would jump to a new position. Before a session, they were allowed to practise, usually for 20–30 trials, to ensure that they understood the task.
Analysis
SPIC recorded distributions of latencies of A responses (i.e. to the location of the first stimulus), of B responses (i.e. that go direct to the location of the second stimulus) and of the correction saccades to the second stimulus that normally follow the first response (C responses), as well as of the saccades generated in the control trials. The individual distributions of control latencies were fitted in SPIC to determine the best‐fit values for each subject of the corresponding LATER parameters (μ and σ, mean ± SD of the underlying Gaussian distribution of the rate of rise of the cumulation) by minimization of the one‐sample Kolmogorov–Smirnov statistic (Kolmogorov, 1941; Smirnov, 1948) (K–S 1); this is a conventional optimization that can be performed analytically and does not demand iterative simulation. In doing this, we assumed an overall invariant delay T go, as a result of synaptic and conduction delay and activation of photoreceptors and muscle cells and detection, which was held constant at 50 ms: the critical question of how much of that delay is afferent rather than efferent is discussed below. These values are shown in Table 1.
Table 1.
Individual parameter values
| Participant | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | A | B | C | D | E | F | G |
| μ | 8.34 | 6.26 | 8.42 | 6.94 | 8.83 | 8.75 | 7.56 |
| σ | 2.05 | 0.67 | 2.34 | 2.13 | 2.79 | 2.28 | 1.87 |
Values are the mean ± SD(μ, σ) of the rate of rise of the Go units as estimated from the control trials, for each participant (expressed in Hz).
Simulations
We used SPIC to run MonteCarlo simulations of the behaviour in the experimental trials, using a model described in detail below, finding values of the parameter μStop (the mean rate of rise of the cumulation unit of the stop process) for each subject and condition by reiterative minimization of the two‐sample Kolmogorov–Smirnov test (K–S 2) in simulated runs of 300 trials each (Table 2). The general procedures have been described previously (Noorani et al. 2011; Noorani & Carpenter, 2013). Because of the greater stochastical complexity of the model, compared to fitting the controls, this fitting cannot be performed analytically, and must necessarily introduce slightly more uncertainty concerning the optimality of the values that are obtained. This is of course true of any ‘best fit’ procedure, whether analytical or iteratively stochastic: unless infinite time is available in which to scan the n‐dimensional space of possible parameter values, there must always be a degree of uncertainty, and this is particularly true of non‐parametric tests such as the Kolmogorov–Smirnov test. The simulation fitting performs an adaptive exploration of the region around the previous best estimate, reducing the size of the corresponding simplex (the Amoeba procedure; Press et al. 2007) each time, until no further significant improvement occurs. In this case, some 10–20 iterations are typically required; the robustness of the procedure can be judged from Table 2, which shows the results from a sequence of such iterations to estimate μStop on an identical set of observations, with over 95,000 individual trials. The values of μ and σ for the Go units for each subject were simply those previously obtained analytically from the control trials, and thus comprise fixed parameters for each subject. Other parameters (σstop, and two parameters, τ and L, which describe lateral inhibition) that appeared to be less critical were estimated globally (over all conditions) for the group of subjects as a whole and no attempt was made to find optimum values for individuals, aiming to reduce the number of unnecessary free parameters. Therefore, the only free parameter for each subject in each condition was μStop.
Table 2.
Iterative simulation fitting
| Sequence | Iterations | Trials | p(K–S)A | p(K–S)B | μstop |
|---|---|---|---|---|---|
| 1 | 16 | 4800 | 0.71 | 0.96 | 15.88 |
| 2 | 17 | 5100 | 0.51 | 0.97 | 16.25 |
| 3 | 23 | 6900 | 0.71 | 0.92 | 15.83 |
| 4 | 20 | 6000 | 0.64 | 0.91 | 15.89 |
| 5 | 17 | 5100 | 0.73 | 0.94 | 15.88 |
| 6 | 16 | 4800 | 0.81 | 0.87 | 15.80 |
| 7 | 8 | 2400 | 0.67 | 0.93 | 16.50 |
| 8 | 22 | 6600 | 0.58 | 0.97 | 15.48 |
| 9 | 13 | 3900 | 0.38 | 0.94 | 15.80 |
| 10 | 19 | 5700 | 0.64 | 0.97 | 15.99 |
| 11 | 9 | 2700 | 0.44 | 0.97 | 15.91 |
| 12 | 22 | 6600 | 0.73 | 0.95 | 15.80 |
| 13 | 12 | 3600 | 0.38 | 0.94 | 15.78 |
| 14 | 13 | 3900 | 0.44 | 0.97 | 15.65 |
| 15 | 15 | 4500 | 0.81 | 0.86 | 15.82 |
| 16 | 14 | 4200 | 0.58 | 0.91 | 16.29 |
| 17 | 13 | 3900 | 0.71 | 0.84 | 16.26 |
| 18 | 19 | 5700 | 0.61 | 0.89 | 16.49 |
| 19 | 14 | 4200 | 0.51 | 0.86 | 16.31 |
| 20 | 16 | 4800 | 0.58 | 0.92 | 15.90 |
The results of a sequence of 20 independent iterative simulation fits for μstop in a representative single subject (B) with D = 100 ms, showing the degree of robustness of the final estimated value. Each fit reiterates until no further significant improvement occurs, with the number of iterations and therefore trials (300 trials per iteration) varying stochastically in each case (the Iterations and Trials columns); the data derive from a total of 95,400 trials; the mean estimate of μstop is 15.98 Hz (SEM= 0.06). p(K–S)A and p(K–S)B are the significance values for the resultant K–S tests in each case for the A and B response distributions, respectively.
Results
Controls
The distributions of latencies in the control trials (50% of all trials: grey points) (Fig. 3) had the linear form predicted by LATER, providing the data for estimating the LATER parameters μ and σ of the Go units, for each subject, by minimization of the K–S 1 (P values: 0.50, 0.89, 0.26, 0.85, 0.34, 0.46, 0.89). These parameters vary quite widely from one subject to another, reflecting intersubject variations that are nevertheless extremely stable over time, as is characteristic of reaction times in general (Carpenter, 2012; Antoniades et al. 2013b) (Table 1).
Figure 3. Observed and simulated A responses .
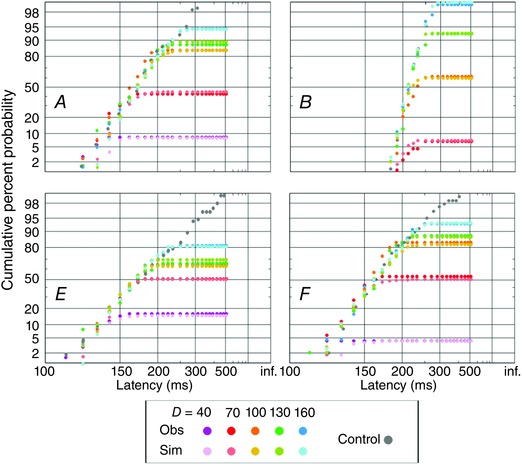
Reciprobit plots of distributions of latencies for A responses are shown (as in Fig. 2) for four subjects (participants A, B, E and F): actual observations (more saturated colours) are shown, as well as simulated data (less saturated) from the model.
The A responses
As noted in the Introduction, behaviour in the experimental trials was stochastic. For a given value of the interval D, in a proportion p(A) of the trials, the subject made two successive saccades to the first and second target locations (a type A response) and, in the remainder, the subject would make a single saccade straight to the final target location (a type B response). As previously reported (Wheeless et al. 1966; Komoda et al. 1973; Carlow et al. 1975; Becker & Jürgens, 1979; Camalier et al. 2007), p(A) increased monotonically with D (Fig. 4, left).
Figure 3 shows reciprobit plots of the distributions of latencies of the A responses for each value of D. In these ‘incomplete’ plots, the cumulative percentages are of the number of responses as a fraction of the total number of trials, rather than simply of A‐trials alone, such that they asymptote finally to a level representing p(A). The distributions initially rise along the same cumulant as the controls, corresponding to the period before the appearance of the second target, during which the behaviour must inescapably be identical in the two cases, before levelling off.
In this respect, the A responses are very similar to the uncancelled responses in a countermanding task, and a similar model should predict both. However, we found that applying a model such as in Fig. 1 to our Wheeless data failed in one crucial respect. The problem is illustrated schematically in Fig. 5. In a countermanding trial, the stop stimulus, after the inevitable ‘physiological’ afferent delay, starts the Stop unit, which eventually reaches threshold and, in effect, slices into the distribution for control trials, cancelling all of the responses that would otherwise have occurred. If we take the afferent delay to be identical for the target and for the stop stimulus, then there is an absolute minimum value for p(A) that cannot be reduced, however rapidly the Stop unit rises to threshold. Were we to observe a smaller value of p(A), we would be forced to conclude either that the system is capable of precognition or that the assumption of equal afferent delays for the Go and Stop pathways is incorrect, and that the latter is faster and able to overtake the former.
Figure 5. Timing relationships in countermanding and Wheeless trials .
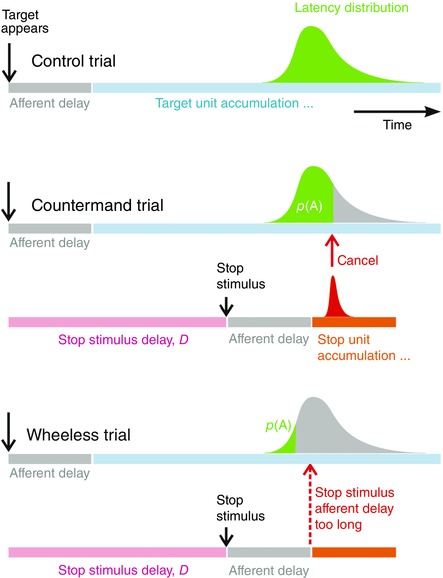
Top: countermanding. After an afferent delay, assumed the same as for the original stimulus, a stop stimulus initiates a stop process that cancels the responses that would otherwise have occurred (grey area), leaving behind a proportion p(A) of trials that remain uncancelled (black). Bottom: wheeless. Even if the stop process is taken to be infinitely fast (dotted arrow), if the two afferent delays are assumed identical, it is impossible to explain the small proportion p(A) of A responses actually observed (black). It must be concluded that the afferent delay for the stop process is shorter than that for Go.
For two of our subjects, with the largest values of D, this is exactly what we found: the control distributions were being ‘sliced’ earlier than would be physically possible even if the rate of rise of the Stop unit, μStop, were to be infinite. By modelling with different afferent delays for the Stop unit, we estimated that, for both of these subjects, it would have to be some 5 ms shorter than the afferent delay for the Go unit to make the observations possible, albeit with an implausibly infinite value for μS. If this difference, ΔT (= T stop – T go) is −10 ms, the values of μstop needed to fit the observations are still anomalously large (Fig. 4, right; Table 2) but, with ΔT = −20 ms, the necessary values for μstop, averaged across all subjects, are not significantly different for D = 160 ms compared to the other values of D (two‐tailed t test, P = 0.194). Because it is always possible to trade off different values of ΔT against variations in μstop, there is no absolute conclusion, except that our data show that ΔT must be at least −5 ms and probably lies in the range −10 to −20 ms (as shown in Fig. 6; which also adds, to Fig. 1, an explicit distinction between afferent delays and the corresponding efferent delays that must include such factors as muscle activation, nerve conduction and neuromuscular synaptic delay). It is important to note that this argument makes no assumptions about any aspect of the model except the values of the delays in each case; for the two instances mentioned, the Stop signal must be initiated earlier if causality is not to be violated. Nor is it simply the result of some individual statistical anomaly. From Fig. 4, it clear that is an increased ΔT regularizes the data across all subjects.
Figure 6. Model for the Wheeless A responses .
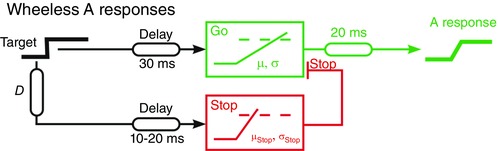
This is closely similar to that for countermanding (Fig. 1) but with the overall fixed delay divided between afferent and efferent components, and the former shorter for the Stop signal than for Go.
Table 3 shows best‐fit values for μStop, assuming ΔT = −10 ms, and Fig. 3 shows the corresponding simulated distributions, all of which fit the observations for all subjects and values of D, with Pnever less than 0.1. As noted above, at this value of ΔT, discrepantly large values of μstop are still needed to fit the observations for some subjects, suggesting that ΔT should be larger still.
Table 3.
μStop
| Participant | |||||||
|---|---|---|---|---|---|---|---|
| D (ms) | A | B | C | D | E | F | G |
| 40 | 22 | 20 | 19 | 19 | 22 | 31 | 25 |
| 70 | 22 | 19 | 19 | 19 | 22 | 23 | 22 |
| 100 | 18 | 16 | 19 | 19 | 29 | 18 | 20 |
| 130 | 21 | 15 | 24 | 21 | 63 | 26 | 22 |
| 160 | 22 | 15 | 45 | 18 | 90 | 26 | 110 |
The best‐fit values for μStop are shown (Hz) for all participants and each value of D, using a model in which ΔT, the difference between the afferent delays for Go and Stop, is taken to be −10 ms. Other parameters (τ and L, time‐constant and degree of lateral inhibition, and σstop) were invariant across subjects (τ = 67 ms, L = 2%, σstop = 5.0 Hz).
The B responses
Having obtained best‐fit values for μStop by analysis of the A responses, it should in principle be possible to predict latency distributions for the B responses as well. A simple independent race model, with a second Go unit having exactly the same parameters μ and σ as the original A unit, and with the same afferent delay, does indeed generate simulated distributions very similar to what is observed, although with some systematic discrepancies. In particular, for small D, they predict slightly shorter latencies for B responses than are actually observed, as if the original A stimulus was exerting some kind of transient inhibitory effect, of a kind that has been noted before between interacting saccadic targets (Hanes & Carpenter, 1999; Noorani et al. 2011). We found that these discrepancies could almost be eliminated by adding a simple mechanism of lateral inhibition, of a kind frequently introduced in such models (Hanes & Carpenter, 1999; Leach & Carpenter, 2001; Findlay & Gilchrist, 2003) between the units (Fig. 7), having an exponential decline with a time constant τ of 67 ms and a relatively small (L = 2%) maximum effect (in other words, the rate of rise of one unit is reduced by 2% compared to that of the other); these values did not need to be varied between subjects, and we made no attempt to determine their optimum values. The observed and simulated latency distributions for B responses, using this model, are shown in Fig. 8, left. In general, the correspondence is very good, despite the obvious idiosyncratic differences between subjects, and in no case (across all subjects and D‐values) was P less than 0.1 (K–S 2).
Figure 7. A model for the entire system .
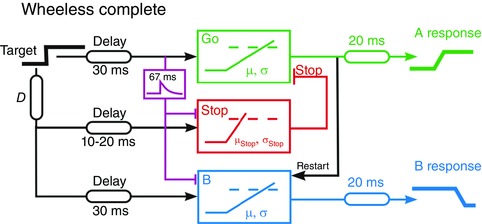
A third decision unit for the B responses (blue) is added to the model shown in Fig. 6, and transient inhibition with a time‐constant of 67 ms acts on both the Stop and B units. When an A response occurs, the B unit is retriggered to generate the second saccade (C) that lands on the final position of the target. The values of μ and σ for each subject are taken directly from their performance in the control task.
Figure 8. Observed and simulated B responses and C responses .
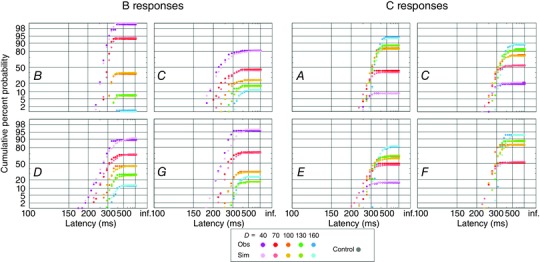
Reciprobit plots of latencies of B (left) and C (right) responses for all subjects and all values of D, with saturated colours representing observed data, and unsaturated colours representing simulated data (as in Fig. 3).
The C responses
A complete model should also be able to predict the timing of the final corrective saccades (C responses). In a previous study (Noorani & Carpenter, 2014), we showed that, in the anti‐saccade task, the final corrective saccades made after an initial incorrect response could be accurately modelled very simply, if the LATER unit corresponding to these saccades is triggered when the unit for the original response reached its threshold. We incorporated the same mechanism in our Wheeless model, with the additional and inescapable proviso that the unit could not be triggered until the second target had actually appeared (and allowing for the afferent delay). Observed and predicted distributions of latencies of C responses, according to this model (which requires no extra parameters) are shown in Fig. 8 (right); the fits are all satisfactory (K–S 2: P > 0.05 for all conditions and subjects).
Figure 9 compares observed and predicted proportions of type A responses and median latencies of B and C responses.
Figure 9. Performance of the model .
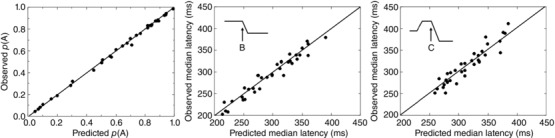
Comparison of observed and predicted values of p(A) (left), of median latencies for B responses (middle) and C responses (right), across all subjects and D values. The R 2 values are 0.998, 0.948 and 0.828, respectively.
Discussion
Although race models have been used to describe simple or choice reaction times for several decades, only relatively recently has it been realized that they can also model more complex decisions. In the present study, we have revisited a classic example of such a task, showing that a simple model with three decision units can explain the reaction time behaviour in considerable quantitative detail. Moreover, it needs only one free parameter for each subject, with the others being invariant between subjects or derived from control data; indeed, if the larger value of ΔT is accepted, no individual free parameter is required at all: the entire behaviour for any particular subject can be predicted from the reaction times in their control trials.
The precision of the model provides further information about quantitative aspects of cancellation and error correction, implying in particular that the mechanism for stopping an impending disaster appears to be specialized for unusually fast initiation. Specifically, if the Go and Stop afferent delays are equal, and even allowing μstop to be infinite, such that the stop unit acts instantaneously, for larger values of D, the model generates more type A responses than are actually observed. The inescapable conclusion is that the afferent delay of the Stop unit is shorter than the Go unit by some 10–20 ms; this then predicts the correct proportions of responses in the task with values for μStop for each subject that no longer have to alter with D. This is in contrast to what has previously been reported for the countermanding task, or other tasks such as anti‐saccades that require a Stop unit (Logan et al. 1984; Hanes & Schall, 1995; Hanes & Carpenter, 1999).
Fast neural onset time
The time lapse between a stimulus and the onset of the decision rise‐to‐threshold, an aspect of decision modelling that has tended to be glossed over, comprises two logically distinct components. First, there is an irreducible afferent delay T in including photoreceptor activation, synaptic delays and conduction; second, especially where stimuli are complex, noisy or distributed in space, there is the time T det taken for stimulus detection (Reddi, 2001; Reddi et al. 2003; Carpenter et al. 2009; Smith & Ratcliff, 2009). In addition, there is an irreducible efferent delay T out, comprising motor neuron conduction, efferent synaptic delay and muscle activation time. The sum of these three components constitutes the overall fixed delay, designated T go or T stop depending upon which of the decision units is being considered.
It is surprisingly difficult to make robust estimates of these delays (Luce, 1986). For quantitative modelling of reaction times to simple stimuli, it is generally adequate to use a ballpark value combining the afferent and efferent components, T often being taken to be some 50 – 60 ms (Thompson et al. 1997; Hanes & Carpenter, 1999; Noorani & Carpenter, 2013). One might hope to estimate an upper bound for this value by examining the very shortest visual saccadic latencies, in early or express saccades; however, it is very difficult to make the necessary allowance for any background, spontaneous, rate of saccadic initiation. A recent study examining monkey colour‐discrimination times in a saccadic task (Stanford et al. 2010) generated a rather long estimate (∼100 ms) for T, although much of this is probably a result of the time needed to discriminate colour. In Fischer's classic work on human express saccades (Fischer & Ramsperger, 1984; Fischer et al. 1993), for gap tasks, the peak of the express distributions is ∼100 ms, with a skirt that extends perhaps down as far as 70–80 ms; however, although the gap task is excellent at encouraging a larger number of express responses, one cannot be sure whether the earliest responses are in effect to the gap rather than the target itself. Similarly, the fastest responses to step or overlap targets have such dramatically short latencies (<20 ms) that they cannot possibly represent visually‐driven responses.
For more complex modelling, we need to separate the efferent and afferent components. Estimates of T out suggest some 4–10 ms from firing in the abducens nucleus, and perhaps 20 ms from the colliculus (Robinson, 1972; Sparks, 1986; Sylvestre & Cullen, 1999); the latter is the value that we use in our modelling. For T in, we have the additional complication that the time to activate photoreceptors increases at low light levels, and that different populations of optic nerve fibres conduct at different velocities, and respond to different aspects of the stimulus. With high‐contrast targets under light‐adapted conditions, and where colour discrimination is not an issue, one is justified in ignoring the spread of latencies characteristic of central regions, and considering only the shortest that are consistently observed. Two classic studies provide such data, relating to the primate lateral geniculate nucleus and visual cortex (V1), reporting minimum latencies of 16 ms and 18 ms, respectively (Maunsell & Gibson, 1992; Maunsell et al. 1999); although otherstudies have reported rather larger values (Nowak et al. 1995), perhaps as a result of using different stimuli, it is the minimum that is relevant here. Collicular latencies are longer (Goldberg et al. 1972; Sparks, 1986; Dorris et al. 1997; Bell et al. 2006) but less relevant: if the primary function of the colliculus is localization rather than decision, there is no particular hurry for the relevant information. Overall, one must conclude that the irreducible minimum time for information to reach V1 is ∼15–20 ms. Taken together, all of these values represent tight constraints, although they are compatible with the 20 ms of delay that we assume for the model's output, as well as our input delays of 30 ms for Go units and 10–20 ms for Stop.
As noted above, a process of detection may have to be accomplished before the decision unit itself is activated. Although the changes in this detection time resulting from manipulation of stimuli can be measured (Carpenter et al. 2009; Smith & Ratcliff, 2009), it is almost impossible to estimate an absolute minimum value for it. It probably depends on what it is that has to be detected: longer for colour discrimination, for example, or when contrasts are low (Thompson et al. 1996; Carpenter, 2004; Carpenter et al. 2009; Noorani et al. 2011). Similarly, manipulations of the countermanding task can alter the time of decision activity onset rather than its rate of rise (Salinas & Stanford, 2013). Pouget et al. (2011) correspondingly argue that systematically increased latencies after unsuccessful countermanding trials are the result of a delay in onset time of accumulation by the neurons responsible for movement initiation in the frontal eye fields and superior colliculus, rather than a change in other race model parameters. It is not unreasonable to suggest that onset time could be longer when, for a Go unit, a target must both be identified and localized compared to what is needed for a Stop unit; simply to register that something has changed probably making the forthcoming movement redundant. In the anti‐saccade task, to model the distribution of latencies an additional delay is needed, in advance of the Go unit, to calculate the required location of the saccadic destination, different from where the actual visual target is (Zhang & Barash, 2000; Noorani & Carpenter, 2013).
One may well wonder why shortening of the Stop onset time relative to Go was not previously observed in models of the countermanding task. One reason could be that, in countermanding, the stop signal is typically a central visual stimulus no different from the initial target at the start of a trial, and subjects have to be told beforehand that it represents a cancellation command. In other words, it is an arbitrary signal that requires prior instruction and learning. By contrast, in the Wheeless task this signal is implicit, requiring no prior instruction. It is therefore a simpler and more natural stop signal. However, it is also true that, with the exception of the work by Pouget et al. (2011), models of the implied race process in countermanding have tended to assume, in the absence of specific evidence, that the two fixed delays, T go and T stop, were identical. As noted by by Hanes & Carpenter (1999), in such models, the parameters for the Stop process are not almost as tightly constrained by the data as for the Go process, and an increase in μstop can be traded off against an increase in T stop (Fig. 10, left) without introducing unacceptable discrepancies with observed distributions. For example, although Hanes and Carpenter (1999), assuming T stop to be identical to T go with a value of 60 ms, found best‐fit values for μstop of 13–14 Hz, it is easy to show by simulation that the data can be equally well fitted by taking μstop to be the same as in the present study (∼24 Hz), and increasing ΔT to +26 ms. Figure 10 (plot B) compares the simulated distributions (100 trials each) of the uncancelled responses in each of these two cases: the distributions are statistically indistinguishable (Fig. 10, plot B). In other words, although, in the Wheeless task, the simplicity of the stop signal results in a shortening of T, which considerably constrains the timing parameters, the arbitrary and learnt nature of countermanding means that different combinations of afferent delay and assumed μstop may not be experimentally discriminable, such that no firm conclusions can be reached about the underlying values either of μstop or of the afferent delay.
Figure 10. Modifying the countermanding model .
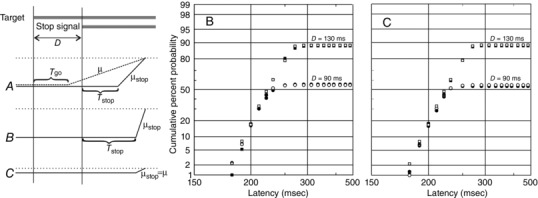
In the original model, there is a race between a Go unit and a Stop unit, which starts after a delay D; both have the same fixed delay T go = T stop, although μstop is greater than μgo, such that the Stop process frequently overtakes the Go (A, left), with the decision signal reaching the threshold level (dotted line) sooner. Estimates of μstop in countermanding are smaller than we have observed for the Wheeless task, although the original countermanding behaviour can be accurately simulated with the increased value for μstop if T stop is increased as well, relative to T go. The results of such a simulation are presented in reciprobit plot B, which shows uncancelled responses in countermanding trials, with ΔT = 0 (filled symbols: μstop = 13.8 Hz, σstop = 3.0 Hz) and ΔT = +26 ms (open symbols: μstop = 24.0 Hz, σstop = 5.0 Hz). Simulations are shown for D = 90 ms and D = 130 ms; for all cases, μ = 6.11 Hz, σ = 1.05 Hz and T go = 60 ms. Each simulation is of 1,000 trials, and the distributions for each value of D are not significantly different (P > 0.5, K–S 2). Furthermore, by assuming a reduced threshold level for the stop process (C, left), the values of μ and σ for the Stop unit can be the same as for the Go unit. Reciprobit plot C compares simulated reaction times, as in B, for the original model and for one in which μstop = μgo and σstop = σgo: the distributions are again statistically indistinguishable (P > 0.5, K–S 2).
Finally, it is worth also emphasizing that, in LATER, there is another fundamental parameter that determines the shape of the distribution, namely the threshold level, S T. Indeed, there is a redundancy necessarily built into the model, in that changes in S T are indistinguishable in their effects from proportional changes in μ and σ because, essentially, it is simply a scaling factor. Nevertheless, there are circumstances such as changes in urgency, when the behaviour of the system is more simply described as a change in S T, and also, from a functional point of view, more naturally because S T in Bayesian terms is an embodiment of the balance between speed and risk (Reddi & Carpenter, 2000). This could certainly be expected to apply to the stop process, and it is arguably more natural to attribute the rapidity of the corresponding LATER process to increased urgency rather than to increased μ (Fig. 10), although, in previous accounts, the difference between the Stop and Go processes has generally been expressed in terms of alterations in μ. Figure 10(plot C) demonstrates that the same countermanding simulation discussed previously can be performed just as satisfactorily by assuming not that S T is the same for Stop and Go but that μstop and μgo are identical (and also σstop and σgo), with a corresponding lowering of S T for the Stop process to ∼25% of its previously assumed value. This approach has something to recommend it with respect to future modelling studies not just because it offers a more functionally plausible explanation for the speed of the Stop decision process, but also because it eliminates one more free parameter from what is already a very economically sparse model.
One can of course speculate on why the Stop unit appears to have a privileged access to a faster activation pathway compared to a Go unit. Two possible reasons come to mind, concerning the underlying mechanism and the possible functional consequences. To simply detect something unexpected has occurred requires less in the way of signal‐processing than recognizing a specific and localized stimulus that demands a correspondingly specific response, and, in many situations, almost any unexpected behaviour (e.g. a change in the size of the stimulus, or of the colour of the background) can inhibit the ongoing accumulation (Singh & Carpenter, 2010). In addition, one can argue that an inappropriate uncancelled response delays the final correct response, as is apparent in the B and C responses shown in Fig. 8, and of course it also implies a needless expenditure of energy.
Relationshipwith previous models
A model with a similar architecture to ours has previously been proposed for the Wheeless task and other more general two‐step paradigms by Camalier et al. (2007). This model has also been used for an identical task in clinical studies to identify deficits in stop reaction times in Parkinson's disease and schizophrenia patients (Joti et al. 2007; Thakkar et al. 2015), although the focus was on mean reaction times rather than detailed individual distributions. Although the basic arrangement of the Stop unit and two separate Go units is the same, it did not incorporate specific afferent delays, and the decision units were not explicitly identified; rather, a generic Weibull function with three free parameters was used to provide empirical fits to latency distributions, with the two Go units being allowed to have different parameters. Moreover, we show the stop unit has a shorter intrinsic delay by 10–20 ms or so, which they did not find: indeed, their model assumes that the units start immediately on presentation of a stimulus, rather than after an onset delay. We now know from neural recordings that onset time is an important feature of neural decision activity influencing reaction time (Stanford et al. 2010; Pouget et al. 2011) and must be recognized as an important parameter in neural race models.
We implemented several different models, comparing how well they succeeded in explaining latency distributions. As previously emphasized by Camalier et al. (2007), and as already been noted by Carpenter (1988), without a Stop unit, one cannot explain the delayed distribution of B responses. Similarly, Ramakrishnan et al. (2012) demonstrated that a model with a stop unit provided the best description of data from macaques under conditions of frontal eye field manipulation in the same task. We have seen that it is necessary for the onset time of Stop to be shorter than for the Go unit because, otherwise, the values of μStop are unacceptably high, or the observed p(A) cannot be simulated at all. Lateral inhibition is also required because, without it, the model predicts systematically faster distributions of B and C responses than actually occur.
For correction responses, an alternative model is to let the second Go unit continue after the first one wins, rather than have it restart: in other words, after the A response is initiated, the B unit continues accumulating, triggering the correction response when it reaches threshold. Although Camalier et al. (2007) used this alternative version to model the overall proportions of corrections, it could not entirely predict the variation in their incidence across subjects. In the present study, by plotting the correction latency distributions in full as reciprobit plots, we find that their alternative architecture only predicts very fast corrections and does not satisfactorily account for the entire distribution. With the race re‐starting, our model predicts the entire correction distribution satisfactorily, including variation between subjects.
Future
One conclusion is that detecting a target for use in the decision process is faster when the stimulus means that an impending action needs to be cancelled compared to when its existence and location must be determined for the purpose of initiating a new directed action. The former is certainly the simpler task and, on those grounds alone, one might well expect the corresponding detection process to be faster: furthermore, it is less risky, in the sense that stopping an action reduces rather than increases energy expenditure. Such a view is supported by recent neural recordings in the basal ganglia of rats during the countermanding task: the subthalamic nucleus, representing the stop process, was activated very quickly, within 15 ms of the stop signal onset, much as in the model of Wheeless presented here (Schmidt et al. 2013). Such a fast time would leave no allowance for prefrontal cortical input to the basal ganglia, which is probably important in humans. However, the rats in this task were probably very well trained, implying alternative mechanisms for the stop process such as thalamic–subthalamic nucleus plasticity. Of course, it is not entirely impossible that the difference in speed reflects the existence of two distinct pathways, rather than a simplified process of detection.
Simple‐minded interpretations need to be avoided. For example, although the superior colliculus is a shorter physical pathway from the retina compared to the frontal eye fields, recordings suggest that collicular activation latencies are longer (Maunsell & Gibson, 1992; Nowak et al. 1995; Maunsell et al. 1999) and, in general, it is important to avoid the category mistake of claiming to make deductions about neural locations from purely behavioural data. The aimof neuroscience is not neophrenology (or not entirely neophrenology; Carpenter, 2012) but, instead, the provision of detailed functional explanations of behaviour; if nothing else, the present study demonstrates that this is not a wholly unrealistic goal. The specific model presentedhere advances our understanding of the task, as well as our ability to use it in such studies, by enabling a detailed prediction of all reaction time distributions at the level of the individual subject.
Finally, this approach also has clinical implications: measurements of saccadic latency distributions in simple tasks are increasingly used as measures of high‐level neural performance, particularly in neurodegenerative disorders (Temel et al. 2009; Ghosh et al. 2010; Krismer et al. 2010; Perneczky et al. 2011; Burrell et al. 2012). The Wheeless task is easy to implement in a clinical setting (Joti et al. 2007; Thakkar et al. 2015). Similar to the currently popular anti‐saccade task (Antoniades et al. 2013a), it can provide additional information about more complex decision processes but more rapidly. Being a more natural task than the anti‐saccade, it is simpler for subjects to understand, and an important consideration in testing patients with cognitive disorders. Making neurology both data‐rich and determinedly quantitative is key to better understanding subtypes of impairment, as well as evaluating the consequences of different forms of therapy.
Additional information
Competing interests
The authors declare that they have no competing interests.
Author contributions
The authors contributed equally to conceiving and designing the experiments; collecting, analysing and interpreting data; and writing the paper. The experiments were carried out in Gonville and Caius College, Cambridge.
Funding
This work was funded by a grant to RHSC from Gonville and Caius College, Cambridge.
References
- Antoniades C, Ettinger U, Gaymard B, Gilchrist I, Kristjánsson A, Kennard C, Leigh RJ, Noorani I, Pouget P, Smyrnis N, Tarnowski A, Zee DS & Carpenter RHS (2013a). An internationally standardized antisaccade protocol for clinical use. Vision Res 84, 1–5. [DOI] [PubMed] [Google Scholar]
- Antoniades CA, Xu Z, Carpenter RH & Barker RA (2013b). The relationship between abnormalities of saccadic and manual response times in Parkinson's disease. J Parkinson's Dis 3, 557–563. [DOI] [PubMed] [Google Scholar]
- Becker W & Jürgens R (1979). An analysis of the saccadic system by means of double‐step stimuli. Vision Res 19, 967–983. [DOI] [PubMed] [Google Scholar]
- Bell AH, Meredith MA, Opstal AJV & Munoz DP (2006). Stimulus intensity modifies saccadic reaction time and visual response latency in the superior colliculus. Exp Brain Res 174, 53–59. [DOI] [PubMed] [Google Scholar]
- Boucher L, Palmieri TJ, Logan GD & Schall JD (2007). Inhibitory control in mind and brain: an interactive race model of countermanding saccades. Psychol Rev 114, 376–397. [DOI] [PubMed] [Google Scholar]
- Burrell JR, Hornberger M, Carpenter RHS, Kiernan MC & Hodges JR (2012). Saccadic abnormalities in frontotemporal dementia. Neurology 78, 1816–1823. [DOI] [PubMed] [Google Scholar]
- Camalier CR, Gotier A, Murthy A, Thompson KG, Logan GD, Palmieri TJ & Schall JD (2007). Dynamics of saccade target selection: race model analysis of double step and search step saccade production in human and macaque. Vision Res 47, 2187–2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlow T, Dell'Osso LF, Troost BT, Daroff RB & Birkett JE (1975). Saccadic eye movement latencies to multimodal stimuli. Vision Res 15, 1257–1262. [DOI] [PubMed] [Google Scholar]
- Carpenter RHS (1988). Movements of the Eyes. Pion, London. [Google Scholar]
- Carpenter RHS (1994). SPIC: a PC‐based system for rapid measurement of saccadic responses. J Physiol(Proc) 480, 4P. [Google Scholar]
- Carpenter RHS (2004). Contrast, probability and saccadic latency: evidence for independence of detection and decision. Curr Biol 14, 1576–1580. [DOI] [PubMed] [Google Scholar]
- Carpenter RHS (2012). Analysing the detail of saccadic reaction time distributions. Biocyb Biol Eng 32, 49–63. [Google Scholar]
- Carpenter RHS, Reddi BAJ & Anderson AJ (2009). A simple two‐stage model predicts response time distributions. J Physiol 587, 4051–4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter RHS & Williams MLL (1995). Neural computation of log likelihood in the control of saccadic eye movements. Nature 377, 59–62. [DOI] [PubMed] [Google Scholar]
- Dorris MC, Paré M & MUnoz DP (1997). Neuronal activity in monkey superior colliculus related to the initiation of saccadic eye movements. J Neurosci 17, 8566–8579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emeric EE, Brown JW, Boucher L, Carpenter RHS, Hanes DP, Harris R, Logan G, Mashru RN, Paré M, Pouget P, Stuphorn V, Taylor TT & Schall JD (2007). Influence of history on saccade countermanding performance by humans and macaque monkeys. Vision Res 47, 35–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Findlay JM & Gilchrist ID (2003). Active Vision: The Psychology of Looking and Seeing. Oxford University Press, Oxford. [Google Scholar]
- Fischer B & Ramsperger E (1984). Human express saccades: extremely short reaction times of goal directed eye movements. Exp Brain Res 57, 191–195. [DOI] [PubMed] [Google Scholar]
- Fischer B, Weber H, Biscaldi M, Aiple F, Otto P & Stuhr V (1993). Separate populations of visually guided saccades in humans: reaction times and amplitudes. Exp Brain Res 92, 528–541. [DOI] [PubMed] [Google Scholar]
- Ghosh B, Rowe J, Carpenter R, Calder A, Peers P, Lawrence A & Hodges J (2010). Saccadic correlates of cognition in progressive supranuclear palsy. J Neurol Neurosurg Psychiatry 81, E29. [Google Scholar]
- Goldberg SJ, Hull CD & Buchwald NA (1972). Intracellular responses of two populations of neurons in the cat abducens nucleus. Anat Rec 172, 316–317. [Google Scholar]
- Hanes DP & Carpenter RHS (1999). Countermanding saccades in humans. Vision Res 39, 2777–2791. [DOI] [PubMed] [Google Scholar]
- Hanes DP & Schall JD (1995). Countermanding saccades in macaque. Vis Neurosci 12, 929–937. [DOI] [PubMed] [Google Scholar]
- Joti P, Kulashekhar S, Behari M & Murthy A (2007). Impaired inhibitory oculomotor control in patients with Parkinson's disease. Exp Brain Res 177, 447–457. [DOI] [PubMed] [Google Scholar]
- Kolmogorov A (1941). Confidence limits for an unknown distribution function. Ann Math Statist 23, 525–540. [Google Scholar]
- Komoda MK, Festinger L, Phillips LJ, Duckman HR & Young RA (1973). Some observations concerning saccadic eye movements. Vision Res 13, 1009–1020. [DOI] [PubMed] [Google Scholar]
- Krismer F, Roos JCP, Schranz M, Graziadei IW, Mechtcheriakov S, Vogel W, Carpenter RHS & Zoller H (2010). Saccadic latency in hepatic encephalopathy: a pilot study. Metab Brain Dis 25, 285–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leach JCD & Carpenter RHS (2001). Saccadic choice with asynchronous targets: evidence for independent randomisation. Vision Res 41, 3437–3445. [DOI] [PubMed] [Google Scholar]
- Logan GD & Cowan WB (1984). On the ability to inhibit thoughts and action: a theory of an act of control. Psychol Rev 91, 295–327. [Google Scholar]
- Logan GD, Cowan WB & Davis KA (1984). On the ability to inhibit responses in simple and choice reaction time tasks: a model and a method. J Exp Psychol Hum Percept Perform 10, 276–291. [DOI] [PubMed] [Google Scholar]
- Luce RD (1986). Response Times: Their Role in Inferring Elementary Mental Organization. Oxford University Press, London. [Google Scholar]
- Maunsell JHR, Ghose GM, Assad JA, McAdams CJ, Boudreau CE & Noerager BD (1999). Visual response latencies of magnocellular and parvocellular LGN neurons in macaque monkeys. Vis Neurosci 16, 1–14. [DOI] [PubMed] [Google Scholar]
- Maunsell JHR & Gibson JR (1992). Visual response latencies in striate cortex of the macaque monkey. J Neurophysiol 68, 1334–1344. [DOI] [PubMed] [Google Scholar]
- Noorani I (2014). LATER models of neural decision behavior in choice tasks. Front Integr Neurosci 8, 67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noorani I & Carpenter RHS (2011). Full reaction time distributions reveal the complexity of neural decision‐making. Eur J Neurosci 33, 1948–1951. [DOI] [PubMed] [Google Scholar]
- Noorani I & Carpenter RHS (2013). Antisaccades as decisions: LATER model predicts latency distributions and error responses. Eur J Neurosci 37, 330–338. [DOI] [PubMed] [Google Scholar]
- Noorani I & Carpenter RHS (2014). Restarting a neural race: anti‐saccade correction. Eur J Neurosci 39, 159–164. [DOI] [PubMed] [Google Scholar]
- Noorani I, Gao MJ, Pearson BC & Carpenter RHS (2011). Predicting the timing of wrong decisions. Exp Brain Res 209, 587–598. [DOI] [PubMed] [Google Scholar]
- Nowak LG, Munk MHJ, Girard P & Bullier J (1995). Visual latencies in areas V1 and V2 of the macaque monkey. Vis Neurosci 12, 371–384. [DOI] [PubMed] [Google Scholar]
- Ober JK, Przedpelska‐Ober E, Gryncewicz W, Dylak J, Carpenter RHS & Ober JJ (2003). Hand‐held system for ambulatory measurement of saccadic durations of neurological patients. In Modelling and Measurement in Medicine, ed. Gajda J, pp.187–198. Komitet Biocybernityki i Inzyneierii Biomedycznej PAN, Warsaw. [Google Scholar]
- Oswal A, Ogden M & Carpenter RHS (2007). The time‐course of stimulus expectation in a saccadic decision task. J Neurophysiol 97, 2722–2730. [DOI] [PubMed] [Google Scholar]
- Perneczky R, Ghosh BC, Hughes L, Carpenter RH, Baker RA & Rowe JB (2011). Saccadic latency in Parkinson's disease correlates with executive function and brain atrophy, but not motor severity. Neurobiol Dis 43, 79–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouget P, Logan GD, Palmieri TJ, Boucher L, Paré M & Schall JD (2011). Neural basis of adaptive response time adjustment during saccade countermanding. J Neurosci 31, 12604–12612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT & Flannery BP (2007). Numerical Recipes: The Art of Scientific Computing. Cambridge University Press, Cambridge. [Google Scholar]
- Ramakrishnan A & Murthy A (2013). Brain mechanisms controlling decision making and motor planning. Prog Brain Res 202, 321–345. [DOI] [PubMed] [Google Scholar]
- Ramakrishnan A, Sureshbabu R & Murthy A (2012). Understanding how the brain changes its mind: microstimulation in the macaque frontal eye field reveals how saccade plans are changed. J Neurosci 32, 4457–4472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddi B & Carpenter RHS (2000). The influence of urgency on decision time. Nat Neurosci 3, 827–831. [DOI] [PubMed] [Google Scholar]
- Reddi BAJ (2001). Decision making: the two stages of neuronal judgement. Curr Biol 11, 603–606. [DOI] [PubMed] [Google Scholar]
- Reddi BAJ, Asrress KN & Carpenter RHS (2003). Accuracy, information and response time in a saccadic decision task. J Neurophysiol 90, 3538–3546. [DOI] [PubMed] [Google Scholar]
- Robinson DA (1972). Eye movements evoked by collicular stimulation in the alert monkey. Vision Res 12, 1795–1808. [DOI] [PubMed] [Google Scholar]
- Salinas E & Stanford TR (2013). The countermanding task revisited: fast stimulus detection is a key determinant of psychophysical performance. J Neurosci 33, 5668–5685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt R, Leventhal DK, Mallet N, Chen F & Berke JD (2013). Canceling actions involves a race between basal ganglia pathways. Nat Neurosci 16, 1118–1124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh M & Carpenter RHS (2010). Saccadic latency with unexpected distraction. Proc Physiol Soc 19, PC229. [Google Scholar]
- Smirnov NV (1948). Table for estimating the goodness of fit of empirical distributions. Ann Math Statist 19, 279–281. [Google Scholar]
- Smith PL & Ratcliff R (2009). An integrated theory of attention and decision making in visual signal detection. Psychol Rev 116, 288–317. [DOI] [PubMed] [Google Scholar]
- Sparks DL (1986). Translation of sensory signals into commands for control of saccadic eye movements: role of the primate superior colliculus. Physiol Rev 66, 118–171. [DOI] [PubMed] [Google Scholar]
- Stanford TR, Shankar S, Massoglia DP, Costello MG & Salinas E (2010). Perceptual decision‐making in less than 30 milliseconds. Nat Neurosci 13, 379–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sylvestre PA & Cullen KE (1999). Quantitative analysis of abducens neuron discharge dynamics during saccadic and slow eye movements. J Neurophysiol 82, 2612–2632. [DOI] [PubMed] [Google Scholar]
- Temel Y, Visser‐Vandewalle V & Carpenter RHS (2009). Saccadometry: a novel clinical tool for quantification of the motor effects of subthalamic nucleus stimulation in Parkinson's disease. Exp Neurol 216, 481–489. [DOI] [PubMed] [Google Scholar]
- Thakkar K, Schall JD, Logan GD & Park S (2015). Response inhibition and response monitoring in a saccadic double‐step task in schizophrenia. Brain Cogn 95, 90–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson KG, Bichot NP & Schall JD (1997). Dissociation of visual discrimination from saccade programming in macaque frontal eye field. J Neurophysiol 77, 1046–1959. [DOI] [PubMed] [Google Scholar]
- Thompson KG, Hanes DP, Bichot NP & Schall JD (1996). Perceptual and motor processing stages identified in the activity of macaque frontal eye field neurons during visual search. J Neurophysiol 76, 4040–4055. [DOI] [PubMed] [Google Scholar]
- Westheimer G (1954). Eye movement responses to a horizontally moving visual stimulus. Arch Ophthalmol 52, 932–941. [DOI] [PubMed] [Google Scholar]
- Wheeless LL, Boynton RM & Cohen GH (1966). Eye‐movement responses to step and pulse‐step stimuli. J Opt Soc Am 56, 956–960. [DOI] [PubMed] [Google Scholar]
- Zhang M & Barash S (2000). Neuronal switching of sensorimotor transformations for antisaccades. Nature 408, 971–975. [DOI] [PubMed] [Google Scholar]


