PDMS Elastic Micropost Arrays for Studying Vascular Smooth Muscle Cells

Abstract

This paper describes the design, modeling, fabrication and characterization of a micromachined array of high-density 3-dimensional microposts (100×100) made of flexible material (silicone elastomers) for use to measure quantitatively the cellular traction force and contractile events in isolated vascular smooth muscle cells (VSMCs). The micropost array was fabricated with diameters ranged from 3 to 10 μm, with edge to edge spacing of 5, 7 and 10 μm, and with a height to diameter aspect ratio up to 10. VSMCs exerted larger basal traction forces when they were grown on stiffer micropost arrays. These basal traction forces were 80% larger in control VSMCs than in VSMCs in which integrin linked kinase (ILK) was knocked down using shRNA. The addition of Angiotensin II (ANGII) led to VSMC contraction as evidenced by an increased traction force exerted on the microposts under the cell. This ANGII induced contractile response and change in traction force on the microposts was not observed in VSMCs lacking ILK. Following treatment of VSMCs with Cytochalasin D to depolymerize the actin cytoskeleton, the VSMCs exhibited relaxation that was apparent as a significant reduction in the measured traction force exerted on microposts under the cell. Overall, this study demonstrates the usefulness of micropost arrays for study of the contractile responsiveness of VSMC and the results indicate that ILK plays a critical role in the signaling pathways leading to the generation of substrate traction force in VSMC.

1. Introduction

Vascular smooth muscle cells (VSMCs) comprise the mechanically active component of the blood vessel wall endowing it with the ability to constrict and dilate. This vasoregulation occurs through the transmission of mechanical force from the cells to the external environment. Thus the processes of force generation and transmission play an important function role in defining the mechanical efficiency of VSMCs in the vascular wall [1,2]. Techniques for quantitative assessment and measurement of force generation at the level of single cells and at focal adhesion sites where cells interact with their substrate have been limited by technical difficulties. However, recent technical advances in micropost fabrication have permitted development of nanostructured devices that allow questions concerning cell force generation and transmission to its environment to be quantitatively investigated.

Many techniques have been developed to detect the traction forces generated by cells on a flexible continuum substrate. One example is the use of a thin silicone substrate such as polydimethylsiloxane (PDMS) where cells cultured on the substrate cause it to deform by applying force to the substrate and thereby produce wrinkled pattern on it [3]. Another approach employs the use of fluorescent beads-embedded polyacrylamide gels where the cultured cells generate traction forces that deform the gel structure. The deformation is then be detected by observing and tracking the movement of the embedded beads. These techniques have led to significant improvements in our understanding of spatial and temporal aspects of force generation in cells. However, a limitation of these approaches is that they cannot determine precisely the location, magnitude and directional vector of point forces [3–8]. To overcome this limitation, other techniques have been developed to quantitatively measure cell traction forces including cantilever beams which measure the cell traction forces, micro-fabricated microgrippers, atomic force microscope (AFM) tips or micro-needles in conjunction with photodiode, carbon fiber beams or carbon nanotubes, magnetic beads and optical tweezers [9–16]. These approaches, although highly quantitative are limited to measuring force at a single site on a cell. These limitations were overcome by the development of high-density elastomeric micropost arrays [17–24]. Using the micropost array approach, cells attach and spread across the top of regularly ordered microposts. Since each post is discrete, it can act as an independent cantilever and detect the cell traction force independently at the site where it contacts the cell. Analysis requires only a spring constant and a measurement of the micropost deflection from acquired images of the micropost array. Currently, this technique appears to be among the most effective for quantitative measurement of force at multiple sites between a cell and its substrate. Micropost array technologies have been used to analyze cells such as cardiac fibroblasts, cardiac myocytes, smooth muscle cells, and cell monolayers and detect significantly large contractile forces at the edge of the cell and cells such as tendon fibroblast with weaker contractile force [7,14,20,17,12].

The objective of our work is to improve the micropost array fabrication process in order to produce high aspect ratio microposts that could be used to measure small changes of traction force when exposed to AngII- a factor in human body that has a vessel constriction effect, and is commonly known to induce VSMC contraction, and compared it with that of the VSMC relaxation effect by Cytochalasin D, and cells with ILK expression reduced. In present work, we successfully fabricated high aspect ratio (up to 10) PDMS micropost arrays. Using these micropost arrays we have shown that VSMCs that grown on a stiffer micropost array substrates generate larger traction forces than those grown on a softer micropost array. In addition, the highly sensitive high-aspect ratio micropost arrays were able to pick-up the change of VSMC contraction forces that occur in an in vivo situation. We have demonstrated that ANGII caused a significant increase in VSMC cell traction force that was not observed in cells with ILK expression reduced. Depolymerization of the actin cytoskeleton with Cytochalasin D reduced traction force exerted by the VSMC on the micropost array and confirmed the involvement of the cytoskeleton in our system.

2. Micropost design and modeling

The device was designed with array of high-density 3-D microposts (100×100) made of flexible material (silicone elastomers) with known physical and chemical properties. The 3-D flexible environment allowed the study of the cell-substrate distribution of traction forces exerted by VSM cells on the micropost array. This device was used to measure the traction forces generated by VSM cells attached to them. It is important to note that the stiffness of the micropost depends on the geometry and material used. Therefore PDMS was used to create the micropost with appropriate mechanical properties and biocompatibility for cells to favorably grow on them. Initially, the micropost’s top surfaces were treated and coated with extracellular matrix proteins (collagen or fibronectin) in order to enhance the surface properties and enable the cells to attach to them. Once the cells start moving (expand or contract), the posts will bend. This post-deflection was measured using phase contrast microscopy and was translated into traction force using beam-bending theory. In the linear regime, the post behaves similar to a spring such that the deflection is directly proportional to the force applied by the attached cells. Hence the traction forces can be quantified by determining the deflection of each post.

The micropost was treated as a cylindrical cantilever beam, one end was fixed to the substrate and the other end was free. The relationship between force, F, and free end displacement, x, for a cylindrical beam can be determined using the theory of cantilever beam bending (Euler-Bernoulli Beam Theory) [6,10,12,25].

$$F=Kx=(K_{\mathrm{t}}+K)x_{\mathrm{d}}$$ (1)

$$\mathrm{K}=[x_{\mathrm{d}}/(x-x_{\mathrm{d}})]K_{\mathrm{t}}=(3\mathrm{\pi }{ED}^4/64L^3)$$ (2)

where E, D, L, K, K_t, and x are the Young’s modulus, the diameter, the height, the spring constant and the displacement of the micropost, respectively. K_t and x_d are the spring constant and displacement of the AFM cantilever beam. Therefore, the Young’s modulus of PDMS can be calculated after measuring the spring constant of the micropost and it can then be used as a calibrated value for determining the force.

Finite element analysis (FEA) using Coventorware simulation package were employed to determine the micropost geometry, the deflection as a function of force applied on the top surface of the micropost, and hence provided an accurate prediction of their performance. Three models were studied in this paper. In these models, the micropost’s base was assumed to have a rectangular shape with thickness and area of 500 μm and 250×250 μm², respectively. The experimentally measured Young Modulus was used in all models (1.38 MPa), and the simulation was performed at the same temperature as the cell environment (23°C) [26]. In addition, the mesh size in the simulation ranged from 10×50 to 70×360 that was sufficient to obtain accurate results. The convergence was accomplished when mesh density increased and a mesh size of 45×230 was chosen to model the behavior of the PDMS micropost. In the first model, the force-deflection relationship was investigated. The micropost diameters and heights were fixed at 5 μm and 25 μm, respectively. The bottom of the micropost’s base was fixed and a shear force was applied to the center of its top surface and ranged between 0 to 60 nN. The deflections corresponding to different levels of shear forces were computed as shown in figure 1a. For example, a 15 nN force was able to cause a noticeable deflection to the post by 2.55 μm. It should be noted that the post was deflected linearly when the traction force was between 0 – 40 nN. In second model, the height-deflection relationship was determined. The height of the micropost was varied between 0–25 μm, and the diameter and applied force were fixed to 5 μm, and 15 nN, respectively as shown in figure 1b. A deflection of 2.52 μm was achieved for a post with a height of 25 μm (figure 1c). In the third model, diameter-deflection relationship was determined by varying post diameter from 3 to15 μm and fixing post height and applied force to 25 μm and 15 nN, respectively. The simulation result is shown in figure 1d. The micropost was also simulated with a rigid anchor (without base) and compared with the one with a base. The results showed a slight difference of 2.5%. For example, the deflection of a micropost with diameter and height of 5 μm, and 25 μm, respectively and under a constant force of 15 nN with and without base were 2.55 μm and 2.60 μm, respectively. A mask was designed and fabricated based on the modeling results, the following dimensions were included in the mask: the post diameters were 3, 5, 7, and 10 μm, the spacing were 5, 7, and 10 μm.

Fig. 1.

The relationship between a) the micropost deflection and the lateral force (diameters and heights were fixed at 5 μm and 25 μm, respectively), b) the micropost deflection and the micropost height (the diameter and applied force were fixed to 5 μm, and 15 nN, respectively), c) the micropost deflection and the micropost diameter (post height and applied force were fixed to 25 μm and 15 nN, respectively), d) schematic of FEA model for a micropost with a lateral force exerted on its top. The post’s diameter, height, and force are 5 μm, 25 μm, 15 nN, respectively. The simulations were performed using Coventorware finite element tool.

3. Device fabrication

The micropost arrays were fabricated using standard microlithography and replica-molding techniques in the following sequence: 1) a photoresist layer (Shipley 1813 and 1827) was first patterned on a 3″ silicon wafer (figure 2a), which was initially cleaned with piranha solution for 15 minutes, to form openings at locations corresponding to the microposts; 2) silicon micromold was formed by etching micro-holes with high aspect ratio using a Deep Reactive Ion Etching System (Alcatel DRIE AMS-100) (See figure 2b); 3) the wafer was cleaned again with Pirhana solution and the natural oxide layer was removed using Hydrofluoric acid (HF); 4) the wafer was treated with a vapor of hexamethyldisilazane reagent in vacuum desiccators for 15 minutes.

Fig. 2.

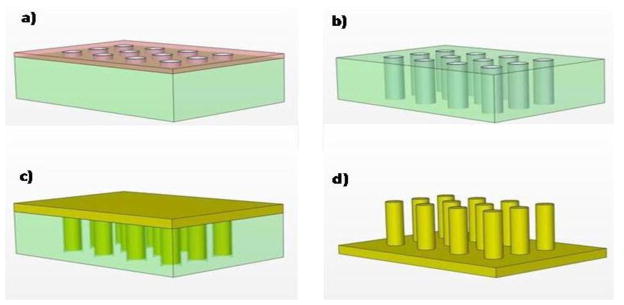
Micropost array fabrication process, a) after photolithography and patterning circles which corresponds to post diameter, b) after deep Si etching to create Si mold with high aspect ratio, c) after pouring and curing PDMS, d) after peeling off cured PDMS from the mold.

This step proved to be crucial for preventing the PDMS from sticking to the substrate due to reduction of PDMS’s surface tension to the silicon mold and hence facilitated peeling off the posts from the mold after being cured; 4) the wafer was diced into 2×2 cm², each containing 4 arrays and was placed in a Petri dish and a PDMS, prepared by mixing the resin (Sylgard 184 Silicon Elastomer Kit, Dow Corning) with curing agent (10:1), was poured over them. The PDMS - wafer mold were placed inside a vacuum at 65°C for 24 hours (figure 2c). The long baking time was needed to completely cure the PDMS in the high aspect ratio mold. This step was necessary for successfully removing the micropost from the mold. 5) After the PDMS was cured, it was peeled off manually creating the micropost arrays (figure 2d). Each of the removed samples was cut into 4 arrays and they were ready for cell culturing experiment. The microposts were fabricated with diameter ranged between 3–10 μm, height between 5–40 μm and spacing of 5–10 μm. The best aspect ratio achieved was 10. In this case the post diameter and height were 3 μm and 30 μm, respectively. Scanning electron micrographs of the fabricated arrays are shown in figure 3.

Fig. 3.

Scanning Electron Micrographs (SEMs) of microposts with diameter, height, and spacing of a) 10 μm, 30 μm, 7 μm, b) 3 μm, 20 μm, 7 μm; c) 3 μm, 25 μm, 7 μm c), 3 μm, 30 μm, 5 μm; respectively.

4. Vascular smooth muscle cell studies using micropost array

4.1 Measurements of Young’s Moduli and Spring Constants

We have measured the Young’s Modulus and stiffness of PDMS and used them as a calibrated value for determining the traction forces of VSMCs. The measurements were performed on over 50 microposts divided between four set with small and large dimensions that were cured at room temperature or 65 °C for the same duration (24 hours). The small dimension and large dimension microposts are referred to microposts with diameter (D) and height (H) of 3.3–9.2 μm, 10–27 μm, 16.1–26.7 μm and 30–42.9 μm, respectively. A range of forces was applied on the surface of the micropost using an AFM cantilever beam with a spring constant of 0.06 N/m (Veeco Company). The applied forces and the corresponding micropost displacements were recorded in real time by computer and their relation was obtained by using Matlab program. This step was repeated several times to remove the system noise and measurement error. The calibration of the microposts starts by measuring the sensitivity of AFM against a glass substrate, and measuring the indentation of PDMS substrate by applying force between 0–60 nN. In the former case, there was no indentation during the measurement. The deflection of the micropost was determined by applying force using AFM on its free end and by subtracting the PDMS indentation (σ) and the deflection of AFM cantilever beam (d) from Z-travel of the cantilever beam’s base (z). The deflection is given by x=z−d−σ. For this analysis, we assumed the microposts have uniform material properties such that the deflection is equivalent to the corresponding traction force divided by the spring constant. The calibrated results show that a low value Young’s Modulus of PDMS was found in small-scale and large-scale microposts that were cured at room temperature (0.936±0.037 MPa and 0.543±0.032 MPa, respectively), while microposts that were cured at 65 °C had higher Young’s Modulus values of 1.378±0.162 MPa and 1.090±0.090 MPa, respectively. The p-values of all data sets were much less than 0.001 which verifies that there is significant variation between compared data sets. The results indicate that the posts cured at higher temperature were stiffer than posts cured at room temperature. The comparison between small and large microposts that were cured at the same temperature indicates that the speed of curing of the micropost was influenced by the dimensions of micropost. The large size of a given micropost will slow the curing process in the silicon mold compared to those of smaller size. The exact diameter and height of the micropost was measured using scanning electron microscopy (SEM), and the same size and fabrication regime for micropost, used in the cell experiments, was used to determine the Young’s Modulus. For example, the spring constants of the microposts with diameter, height and spacing of 5 μm, 25 μm, and 7 μm; and 3 μm, 25 μm 5 μm, respectively are 8.12 nN/μm and 1.05 nN/μm, respectively. The Young’s Modulus in both cases was 1.378±0.162 MPa.

4.2 Preparation for Cell Study

We have successfully cultured VSMCs on the fabricated high aspect ratio microposts with two different micropost geometries of diameter, height and spacing of 5 μm, 25 μm, and 7 μm, and 3 μm, 25 μm, 5 μm, respectively. Figure 4 shows an SEM micrograph of VSMC grown on two dimensional micropost array. This micropost array was first treated with oxygen plasma for 45 seconds and then exposed with UV light for 30 minutes to sterilize them before using the arrays for cell culturing. VSMCs enzymatically isolated from skeletal muscle arterioles from male Sprague-Dawley rats (250–350 g) were cultured on top of the micropost arrays and incubated for 2 days before image acquisition experiment. The cells on arrays were imaged using an Olympus Fluoview 1000 confocal microscope with 60X water objective. A series of wide field optical images were captured by scanning the micropost array from the micropost bottom to the micropost top. A single pixel in the wide field optical image represents a square area of 400×400 nm² which corresponds to minimum measured traction force for the two types of microposts of 1.62 nN and 0.21 nN, respectively, which represents the resolution of our force measurement system using these microposts. The largest measurable traction force was limited by the spacing between adjacent posts. It was 97.08 nN, and 8.73 nN for the two micropost geometries, respectively. The microposts with no cells attached maintained their erect position and were unchanged when emerging in the media solution through the cell experiment (See Figure 5). In order to verify that the micropost without cells maintained a stable position during the experiment, the top and bottom positions of the same post were compared initially. It was found that there was no position change of the micropost without cell contact in these images that proved that the microposts with such geometry were able to stand stably and vertically in the solution. For example, Figure 5 shows the micropost array (with diameter, height and spacing of 5 μm in 25 μm, and 7 μm, respectively) used in cell study experiment. By calculating the center position of each micropost in both bottom and top images, the average deflection of posts with no cell is 0.348 pixel which is less than the minimum detectable displacement. Therefore, motion noise contributions from deflections of microposts with no cells on top were negligible. The microposts at the cell’s edge had an average deflection of 16.26 pixels (with standard error of 2.17) while the ones at the center of the cell have the average deflection of 2.34 pixels (with standard error of 2.17). This experiment demonstrated that the cells were exerting higher traction forces at the cell margin the in the cell center region and shown that the micropost array was able to measure the traction force of VSMCs effectively and accurately.

Fig. 4.

Single VSMCs grown on two micropost arrays with diameter, height, and spacing of a) 7 μm, 25 μm, and 7 μm. The dehydration (freezing) process of the VSMC on the microposts causes them to squeeze together due to shrinkage of the cell. We were not able to capture good images of cells on high aspect microposts.

Fig. 5.

Wide field optical images of single VSMC grown on micropost array with 5μm in diameter, 25μm in height and 7μm in spacing, (a) recorded at the top of micropost array (b) recorded at bottom of the micropost array, respectively.

4.3 Description of Cell Study

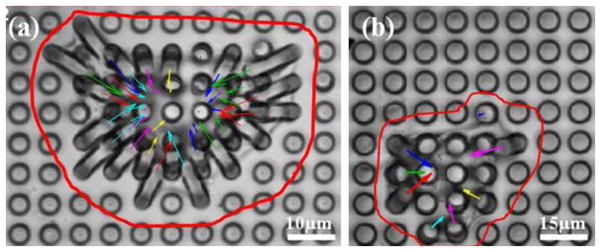
The effects of Integrin-linked kinase (ILK), a serine/threonine protein kinase implicated in signaling pathways involved in VSMCs adhesion, proliferation and migration were analyzed by measuring the traction forces exerted by VSMCs on the microposts [27]. Two groups of VSMCs were studied, the first was a control group, while the second group consisted of the VSMC cells in which ILK expression was reduced using a shRNA approach and designated as VSMC-ILK cells. The control and ILK cells were grown on top of PDMS micropost arrays. The cells were grown on separate micropost arrays with the same geometry in a 35 mm culture dish for 2 days. The optical images of the cells were recorded using Olympus Fluoview1000 confocal microscope. These images were used to determine the magnitude of the micropost deflection and map the distribution traction forces. Figure 6 shows the wide field optical images of a single control VSMC and a VSMC-ILK grown on separate micropost arrays with same geometry, and the corresponding force distributions maps. The arrows (force vectors) in both figure panels (a and b) point towards the direction of deflection to display the force vector and the arrow lengths are proportional to the magnitude of the traction force applied to the corresponding micropost. The results demonstrate that the traction forces of VSMCs cell point toward the cell’s physical center. The analysis of traction forces also shows that the forces are small around the center region of the cell compared to higher forces near the cell edge. It was also found that there was no notable difference in general morphology between control VSMC and VSMC-ILK.

Fig. 6.

Wide field optical images of single a) control VSMC and b) VSMC-ILK grown on micropost array with diameter, height and spacing of 5 μm, 25 μm and 7 μm, respectively.

In the second part of the experiment, Angiotensin II (ANG II), a potent vasoconstrictor hormone, was diluted to 10⁻⁵ M/ml by Dulbecco’s Phosphate-Buffered Saline buffer (DPBS) and then added to both groups of cells. The effect of ANGII on the cells was analyzed by measuring the subsequent change in micropost deflections. This process was recorded by camera at 10 frames/min scanning rate for 30 minutes beginning immediately after addition of ANGII. After 30 minutes, Cytochalasin D (CYTO), an agent that depolymerizes the f-actin cytoskeleton, was diluted to 10⁻⁷ M/ml by DPBS and added to the cells. Images were continuously recorded for 40 minutes after application of Cytochalasin D. The responses of two groups of VSMCs with respect to ANG II and CYTO were obtained and compared by recording and analyzing the images to quantify the deflection of the microposts.

5. Results and Discussion

Control VSMCs and VSMCs-ILK have been grown on micropost arrays with different geometries. Two examples are shown in figure 7 and figure 8 respectively. It should be noticed that the arrows’ length in figure 7a and 8a has been magnified 8 times to make those arrows long enough to been seen. The same experiment was repeated 5 times to verify the repeatability. Table I shows the experimental results of average deflection of the microposts and the corresponding traction force generated by control VSMCs and VSMCs-ILK. The results demonstrate that control VSMCs and VSMCs-ILK tend to exert larger traction force when they grow on stiffer micropost array. However, the traction forces generated by control VSMCs are more than 80% larger than that generated by VSMCs-ILK when the same size of micropost array was used. The P-values of controlled VSMCs and ILK cells grown on 3 μm and 5 μm micropost arrays are 9.75×10⁻⁰⁶ and 6.24×10⁻⁰⁶ which shows the extinguished traction force from these two types of cells.

Fig. 7.

Wide field optical images of single control VSMC grown on micropost array with a) 3 μm in diameter, 25 μm in height and b) 5μm in diameter, 25 μm in height, respectively. The arrow’s length in figure 7a is magnified 8 times to make it long enough to be seen.

Fig. 8.

Wide field optical images of single control VSMC-ILK grown on micropost array with a) 3 μm in diameter, 25 μm in height and b) 5 μm in diameter, 25 μm in height, respectively. The arrow’s length in figure 8a is magnified 8 times to make it long enough to be seen.

TABLE I.

Average deflection of the micropost and corresponding traction force generated by cells on micropost array. D is the deflection of the micropost, F is the traction force applied on micropost. C and I represent the control VSMCs and VSMC-ILK, respectively.

VSMCs	Post diameter and height 3 μm, 25 μm				Post diameter and height 5 μm, 25 μm
	D (μm)		F (nN)		D (μm)		F (nN)
	C	I	C	I	C	I	C	I
1	7.00	3.18	7.35	3.34	4.31	3.38	34.95	27.48
2	7.03	4.27	7.38	4.48	4.72	3.71	38.28	30.09
3	7.56	4.45	7.94	4.67	6.12	3.76	49.64	30.49
4	7.61	4.86	7.99	5.10	6.70	3.83	54.34	31.06
5	7.62	5.03	8.00	5.28	7.94	4.24	64.4	34.39
6	8.87	5.24	9.31	5.50	8.04	4.58	65.2	37.14

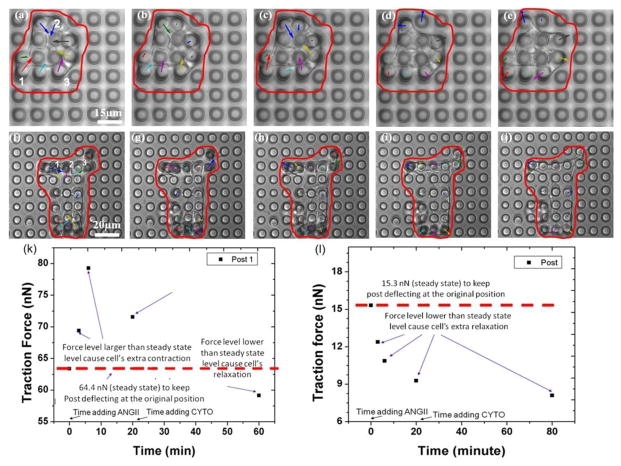
The dynamic change and traction force distribution map of a single control VSMC after adding ANG II followed by CYTO, are shown in Figure 9a–9e. The optical image recorded before adding ANGII to the control VSMCs (figure 9a) shows that control VSMCs generates a basal level traction force on the micropost array. The images recorded 3 minutes, 6 minutes and 20 minutes after adding ANGII are shown in Figure 9b to 9d, and in Figure 9e, 40 minutes after adding CYTO. Micropost labeled as 1 (in figure 9a) shows the deflection equivalent to the traction force of 63.4 nN (before adding ANGII). This force has increased to 69.4 nN (3 minutes after adding ANGII) and to 79.3 nN (6 min after adding ANGII). The traction force has decrease to 71.6 nN (20 minutes after adding ANGII). The results show that ANGII leads to significant contraction in the control VSMC. The cell contraction continued for 6 minutes. Then, the contraction subsided slightly. A pronounced relaxation (expansion) occurred 15 minutes after adding the CYTO to control VSMC and it persisted for 30 minutes. Figure 9k shows the traction force of control VSMC applied on post 1 as a function of observation time. The force applied to the post before adding ANGII (63.4 nN) reflects the steady state level. The contraction was noted as when the traction force applied at that time is larger than the steady state level and relaxation occurred when the force level is lower than the steady state level. The exact experiment has been repeated by 5 VSMCs.

Fig. 9.

Wide field optical images of single control VSMC (a–e) and VSMC-ILK (f–j) cell recorded in real time: (a) and (f) right before adding ANGII, (b)–(d) and (g)–(i) 3 minutes, 6 minutes and 20 minutes after adding ANG II, (e) and (j) 40 minutes after adding CYTO. The arrows’ length in b, c, g and h has been magnified 6 time times; the arrows’ length in d, e, i and j has been magnified 2 times to make arrows observable. (k) The traction force of control VSMC applied on post 1 (figure 9a) as a function of observation time. (l) The traction force of ILK cell applied on post 1 (Fig. 9f) as a function of observation time.

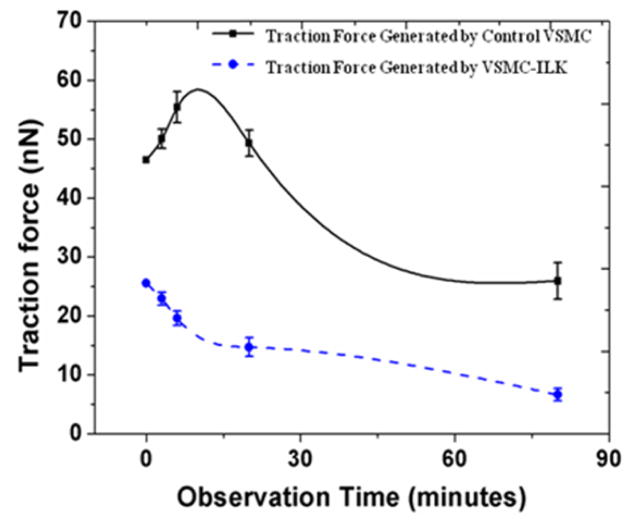
The dynamic changes and traction force distribution map of a single VSMC-ILK growing on a PDMS micropost array after adding ANG II and CYTO are shown in Figure 9f–9j. Similarly, the optical image recorded right before adding ANGII to the ILK cell (Figure 9f) show that VSMC-ILK also generates a basal traction force on the micropost array. The image recorded 3 minutes, 6 minutes and 20 minutes after adding ANGII to VSMC-ILK are shown in Figure 9g to 9i, and 40 minutes after adding CYTO to VSMC-ILK is shown in Figure 9j. Micropost labeled by 1 shows traction force of 15.32 nN (before adding ANGII). This force has been reduced to 12.39 nN (3 minutes after adding ANGII) and to 10.86 (6 min after adding ANGII). The traction force has been decrease to 9.28 nN by 20 minutes after adding ANGII). The results show that the reaction from VSMC-ILK is opposite to that of CK₄ cell during this period. The VSMC-ILK continues relaxing during the remainder of the observing process. The relaxation (expansion) occurs 15 minutes after adding the CYTO to VSMC-ILK and persisted approximately 30 minutes. Figure 9i shows the traction force of VSMC-ILK applied on post 1 as a function of observation time. The force applied to the post before adding ANGII (12.39 nN) is the basal level. Relaxation occurred at all time points since the force levels are lower than the steady state level. The experiments described in figure 9 were repeated on 6 VSMCs-ILK. Figure 10 shows the average forces in those 6 experiments applied by control VSMCs and VSMC-ILK on microposts, respectively, as a function of observation time. The error bar in the curve represents the standard error of the data set. Table II shows the average traction forces of the 6 repeated experiments and the corresponding standard errors. The solid and dot curve in figure 10 represents the dynamic change of average traction force applied on micropost by control VSMC and VSMC-ILK, respectively. The traction force applied by control VSMC continued to increase after adding ANGII to the cell bath and reached maximum at 6 minutes after ANGII. While there was no contraction found all through the dynamic study of VSMCs-ILK, suggesting that ILK plays an important role in mediating force generation in VSMC and in mediating the ANGII induced VSMC contraction.

Fig. 10.

The average traction force of control VSMC and VSMC-ILK applied on posts as a function of observation time. (The error bar represents the standard error of the measured traction forces)

TABLE II.

Traction force applied on post 1, 2, 3 in Figure 9f

Cells	Before experiment (nN)	ANGII 3min (nN)	ANGII 6min (nN)	ANGII 20min (nN)	CYTO 40min (nN)
Control-Avg.	45.50	51.51	59.22	48.95	29.06
Control-Std-Error	0.36	1.86	1.544	1.93	1.22
ILK-Avg.	27.44	22.52	20.64	15.13	8.98
ILK-Std-Error	0.19	0.30	0.47	0.45	0.22

ILK has been shown to directly interact with the cytoplasmic domain of integrins β1 and β3 [28], and has been implicated to play an important role as both a kinase and as a scaffolding protein in the focal adhesion (FA) structure [29,30]. Previous studies from our laboratory [31] have shown that knock-down of ILK expression level using an shRNA approach, enhanced integrin-mediated adhesions and FA formation but also resulted in a significantly lowered cortical stiffness of VSMC. This suggests that there may be lower mechanical force transmitted from the cell across the FA by way of the VSMC stress fibers. This observation is consistent with the current findings that ILK-knock-down in VSMC displayed a reduced traction force on the micro-posts. These findings raised the possibility that ILK silencing could weaken the VSMC contraction and their ability to apply stress to the external mechanical environment. Earlier studies in search of a target of the ILK’s kinase activity have suggested a role in calcium-independent myosin dephosporylation in WSMC [32,33], and in phosphorylation of the myosin phosphatase target subunit, thereby inhibiting the activity of myosin phosphatase [34]. These mechanisms provide possible explanation for the low traction forces observed in these studies and the reduced contractile response to AngII stimulation in the ILK-knock-down VSMCs. Together, these data provide further evidence to support a functional role of ILK in promoting transmission of force through Fas during contraction in VSMC.

6. Conclusion

The high aspect ratio PDMS micropost array was utilized for a traction force study of VSMCs. The smallest spring constant of the micropost is 1.05 nN/μm and the corresponding minimum detectable traction force is 0.21 nN. The control VSMCs cells and VSMCs-ILK were successfully grown on microposts array with two different geometries. It was found that both cell groups exert larger traction force when growing on stiffer micropost arrays. By comparing these two groups of VSMCs using the micropost arrays with the same size, it was observed that control VSMCs generate larger traction forces than VSMCs-ILK. It has also been found that VSMCs-ILK loses the ability to increase traction force following stimulation with ANGII when compared to control VSMCs. This demonstrates that ILK is important for the VSMC to develop and maintain substrate traction force and to alter traction force in response to agonists that activate the contractile apparatus.

Biographies

Qi Cheng (S’09) received the B.Sc. and M.Sc. degrees from Nanjing University of Science and Technology, Nanjing, China, in 2000 and 2003, respectively, and the M.Sc. degree from the Royal Institute of Technology (KTH), Sweden in 2006, all in electrical engineering. He completed his Ph.D in 2011 in electrical engineering at the University of Missouri, Columbia. His research interests include optimization of Si-Ge-O sensing material for uncooled infrared detection; optical, thermal, and mechanical design and modeling of uncooled tunable microbolometers; and micropost array biosensor for cardiovascular cell traction force studies. He is currently working at Intel Corporation, Hillsboro, Oregon.

Zhe Sun received Ph.D. degree in Engineering from Department of BioEngineering, The University of Toledo, U.S.A., in 2000. He now serves as Assistant Research Professor in the Dalton Cardiovascular Research Center, University of Missouri-Columbia, U.S.A. His current research interests include N-cadherin function as a mechano-sensor in Vascular Smooth Muscle Cells and the regulation of cerebral artery myogenic tone.

Gerald A. Meininger serves as Director of the Dalton Cardiovascular Research Center at the University of Missouri. He is a Margaret Mulligan Professor in Medical Research and appointed in the Department of Medical Pharmacology with adjunct appointments in the Departments of Biomedical Sciences and Biological Engineering. Prior to MU, Dr. Meininger was at Texas A&M University, for 25 years and was a Regents Professor, Director of the Division of Vascular Biology at the Cardiovascular Research Institute and Associate Department Head of the Medical Physiology. His research interests are in mechanobiology of the vascular wall and cell interactions with extracellular matrix.

Mahmoud Almasri received PhD in Electrical Engineering from Southern Methodist University in 2001. He is currently an associate professor with the Department of Electrical and Computer Engineering, University of Missouri, Columbia. From 2001 to 2002 he was a research scientist with General Monitors, Lake Forest CA. From 2002 to 2003 he was with Albanynanotech of Albany, NY as a post doctoral research associate, and from 2004 to 2005 he was with Georgia Institute of Technology as a post doctoral fellow. His research includes biosensors, capacitors for power harvesting, infrared detectors, MEMS Coulter counter, and uncooled infrared material and detectors.