Abstract
Major facilitator superfamily (MFS) is a large class of secondary active transporters widely expressed across all life kingdoms. Although a common 12-transmembrane helix-bundle architecture is found in most MFS crystal structures available, a common mechanism of energy coupling remains to be elucidated. Here, we discuss several models for energy-coupling in the transport process of the transporters, largely based on currently available structures and the results of their biochemical analyses. Special attention is paid to the interaction between protonation and the negative-inside membrane potential. Also, functional roles of the conserved sequence motifs are discussed in the context of the 3D structures. We anticipate that in the near future, a unified picture of the functions of MFS transporters will emerge from the insights gained from studies of the common architectures and conserved motifs.
Keywords: MFS transporters, energy coupling mechanisms, membrane potential, motif A
MFS Transporters
Major facilitator superfamily (MFS) is the largest class of secondary active transporters and is present in cells across all life kingdoms.1 So far, over 15,000 genes have been identified as encoding MFS transporters.2 For example, 25% of prokaryotic transporters belong to the MFS family,3 whereas in the human genome, genes coding for at least 110 MFS proteins have been identified.4 One of the defining features of transporters is that they commonly use the electrochemical potential of one substance, for example, from ATP hydrolysis (for primary active transport) or an ion gradient (for secondary active transport), to drive the transport of another substance (i.e., the substrate). Many MFS transporters utilize proton-motive force (PMF) to drive the transport process.5,6 In such cases, an MFS transporter often consumes one proton to transport one molecule of an electroneutral substrate. Thus, MFS transporters appear to be more energy-efficient in terms of the stoichiometric ratio of substrate to protons, compared to the other major class of active transporters, the ATP-Binding Cassette (ABC) transporters. The ABC transporters consume two ATP molecules (equivalent to about 6 protons) per transport cycle. On the basis of transport direction of the substrate relative to that of the driving substance, MFS transporters can be classified into symporters, antiporters, and, in case of a driving substance being absent, uniporters. Considering the countless types of molecules that a cell encounters during its lifespan, the number of transporter genes is quite small. Therefore, many transporters have to accommodate numerous types of ligands, and such poly-specificity is likely to be a common property of MFS transporters.7,8
This review discusses common energy-coupling mechanisms in MFS transporters, and uses PMF-driven electrogenic transporters as an example. Many parts of the discussion are, however, applicable to other types of secondary active transporters.
Two Major Conformations of the MFS Transporter
An alternating access mechanism for substrate transport was proposed by Jardetzky in 1966 for transporters.9 According to this mechanism, a transporter differs from a channel molecule in that a transporter does not open simultaneously to both sides of the membrane, whereas a channel molecule may. Thus, a transporter often has two major conformations, namely the inward-facing conformation (CIn) and the outward-facing conformation (COut), in which the substrate is accessible to the cytosol/cytoplasmic and periplasmic/extracellular space, respectively. Such a large conformational change not only drives the substrate transport, but may also permit the transporter to transduce signals.10 The key question that is associated with the alternating access model and remains unanswered to this day is as to how external driving-energy is coupled mechanistically to the physical conformational change of the transporter.
Analysis of crystal structures of MFS transporters, for example, LacY (PDB ID: 1PV7),11 GlpT/1PW4,12 FucP/3O7Q,13 and YajR/3WDO,14 revealed that these proteins possess a 12-transmembrane (TM) helix core consisting of two pseudo symmetrical domains, namely the N-domain (TMs 1−6) and the C-domain (TMs 7–12), and indeed have two major conformations, that is, the CIn and COut states (Fig. 1). Between the two domains there is a central cavity serving as both the binding site and transport path for the substrate. An MFS transporter usually consists of four, pseudo-symmetrical, three-helix repeats.15 The first helix in each repeat (i.e., TMs 1, 4, 7, and 10) contributes to the formation of the cavity, and is thus referred to as the cavity-helix. The second helix in each repeat (i.e., TMs 2, 5, 8, and 11) is usually long and curved, possessing a banana-like shape. Together, these four helices form the side walls of the central cavity, and are referred to as rocker-helices, to indicate the fact that they are directly involved in inter-domain conformational changes. The third group of helices (i.e., TMs 3, 6, 9, and 12) are located at both ends of the longest dimension of the TM core. They usually do not directly contribute to the formation of the cavity. However, they do contact the lipid bilayer, thus being involved in hydrophobic mismatch interactions with the surrounding membrane,16 and are referred to here as support-helices. On average, the TM region of support-helices are usually about one-turn shorter than that of the other two groups.17 Thus, during the major conformational change, support-helices are likely to move less than the other two groups of helices do, relative to the membrane. In order to specify the membrane-related position of a given residue, the membrane-embedded part (about 20 residues or five helix turns) of each TM helix are divided into five regions, and are numbered as 1−5 starting from the periplasmic side (not from the N- to C- termini of the TM helix) (Supporting Information Fig. S2 in Ref.17). For example, TM7.3 depicts the central region of TM7. The pseudo symmetrical architecture is a major structural feature of MFS transporters and forms the bases of our understanding of energy-coupling mechanisms.
Figure 1.
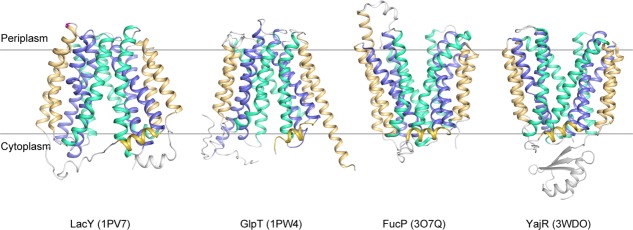
Representative crystal structures of MFS transporters. LacY/1PV7, GlpT/1PW4, FucP/3O7Q, and YajR/3WDO are shown in ribbon diagrams. Cavity helices are colored in blue, rocker helices in cyan, and support helices as well as the amphipathic helices α6–7 in golden.
On the bases of available crystal structures of MFS transporters, a rocker-switch hypothesis of the conformational change between the two major states, COut and CIn, was proposed, representing the mechanism behind the alternating access model suggested earlier.12 According to this mechanism, each the N- and C-domains maintain their structures as approximate rigid bodies and change their relative positions,18 allowing the central cavity to access the cytosol side of the membrane in the CIn state, and to the periplasmic side in the COut state. Nevertheless, rigid-body rotation based conformational change is not the only probable mechanism. Other types of non-MFS transporters may have different ways of using the alternating access mechanism.19 The rocker-switch mechanism has been investigated for MFS transporters that were solubilized in detergent. For example, double electron-electron resonance (DEER) has been used to monitor changes of inter-domain distances on both the periplasmic and cytosol side of the TM core, for example, in the sugar-H+ symporter LacY from Gram-negative Escherichia coli20 and in the drug-H+ antiporter LmrP from Gram-positive Lactococcus lactis.21 In these experiments, changes occurring at the inter-domain distance on the two sides of the membrane are often correlated reciprocally. Further, results from studies on chemical modifications, such as Cys-scanning (e.g., in LacY22,23), dicyclohexyl-carbodiimide (DCCD) reaction, and PEGylation (e.g., in MdfA24), also support the notion of a rocker-switch mechanism. Therefore, the “rocker switch”-like conformational alternation is a well-established mechanism that links the pseudo symmetry of the MFS structure to the alternating access mechanism of general transporters.
Energy Sources Driving Conformational Changes of MFS Transporters
Applying the rocker-switch model dictates that an MFS transporter functions by cycling its conformation between the two major states. From an enzymological point of view, the COut conformation can be considered as the ground state of a PMF-driven, electrogenic, MFS transporter; and the CIn conformation can be considered as the excited state (Fig. 2). Transition from the ground state to the excited state is energized by protonation inside the central cavity, whereas the transition from the excited state back to the ground state is more or less automatic, being driven by conformational energy stored in the excited state. A key question associated with the rocker-switch mechanism is how the two common functions of an MFS transporter are coupled, namely the protonation (or binding of other ions) and conformational alternation between the COut and CIn states.
Figure 2.
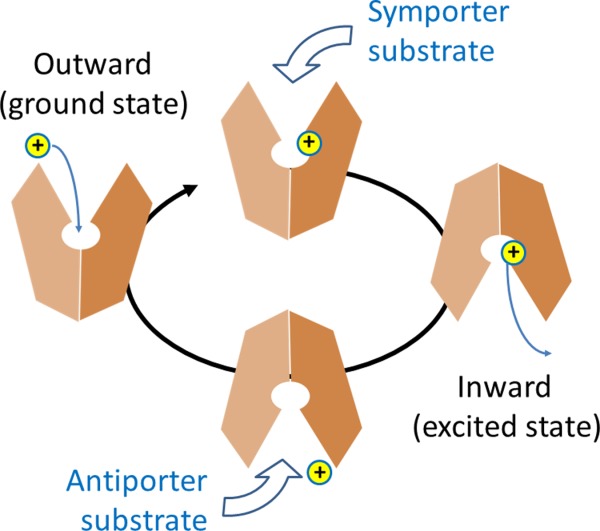
Schematic diagram of the transport cycle of MFS protein.
It is commonly accepted that in order for the MFS transporter to transport a substrate sustainably against its own concentration gradient (i.e., Δμ[S] ≝ RTln([S]R/[S]L)>0, where subscripts “L” and “R” stand for the loading and releasing states), external driving energy is essential. In addition, in the case of a charge-carrying substrate moving against the membrane potential, the electrochemical potential of the substrate (including an extra electrostatic energy term) must be compensated by an opposing term from the external driving energy. The total external energy of a PMF-driven transporter is ΔμΨ+Δμ[H+]+Δμ[S],5 and should be equal to the change of Gibbs free energy (ΔG, i.e. the negative value of the heat released to the environment) of the transport cycle. This free-energy change is necessarily to have a negative value according to the Second Law of thermodynamics. Within the total energy, the part of |ΔμΨ+Δμ[H+]| is considered to be the driving-energy, and Δμ[S] is the result of the transport cycle. In other words, part of the external driving-energy is used to move the substrate against its own electrochemical potential, and the rest is converted to heat. Thus, energy efficiency of the transport cycle may be defined as Δμ[S]/|ΔμΨ +Δμ[H+]| (< 1). At the micro-scale, an MFS transporter functions similarly to Maxwell’s Demon (in Theory of Heat, 1871), who senses a specific type of molecules (substrates) and opens a gate for them allowing a movement of the substrate against its concentration gradient. The entropy of the substrate decreases during the transport process, at an expense of part of the driving energy being converted to heat. The total entropy increases to satisfy the Second Law of thermodynamics.
Despite of this simple thermodynamic notion, the nature of the mechanism behind this energy-coupling process has to this day remained a mystery. Specifically, how does the binding of a 1-Da proton drive the large conformational change of a 50-kDa transporter such as MFS. Figure 3 shows energy diagrams for both a symporter and an antiporter (also see Appendices A and B for detailed discussion on energy terms). For any step of an isothermal-isobaric transport cycle, a positive term of ΔG must be coupled to a negative term(s), to keep the sum of ΔG negative.
Figure 3.
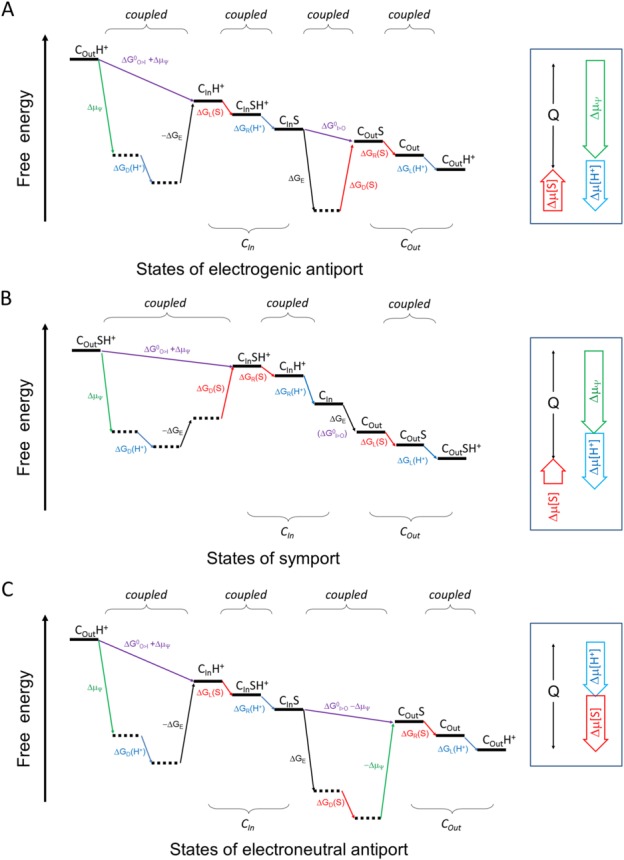
Schematic diagram of the energy landscape of MFS transporters. A: Electrogenic antiporter. B: Symporter. C: Electroneutral antiporter. The free-energy landscape plot describes the thermodynamic relationship between different states, without attention to kinetic issues. The plot must satisfy the First and Second Laws of thermodynamics. Horizontal lines represent states. Tilted lines represent transitions between states. Transitions associated with the proton are indicated in blue, those with the substrate in red, and those with ΔΨ in green. Subscripts L, R, D, and E stand for energy terms associated with loading, releasing, differential binding, and elastic, respectively. “I>O” and “O>I” stand for the CIn-to-COut and COut-to-CIn conformational changes, respectively. In principle, since the transport process cycles, choice of the starting point is arbitrary. In this sense the starting and ending states are identical, only being differed by the release of heat (Q) during one transport cycle. Thus, the end state must be below the starting state. Neighboring states may be coupled tightly. In such a case, their sequential order may be arbitrary. Locally, any transition of positive ΔG must be driven by a neighboring transition of a negative ΔG. (Also see Appendices).
The ΔG terms associated with chemical concentrations deserve some explanatory notes. The free energy change of a substrate, Δμ[S], can be divided into three terms: ΔGL(S), associated with substrate loading; ΔGD(S), what we call differential-binding energy between the loading and releasing states; and ΔGR(S), associated with substrate releasing. ΔGL(S) determines how easily the substrate may bind to the transporter (e.g., from the periplasm for a PMF-driven symporter); and ΔGR(S) determines how easily the substrate may be released from the transporter (e.g., into the cytosol for a PMF-driven symporter). Both ΔGL(S) and ΔGR(S) vary with the concentrations of the substrate on the two sides of the membrane, and may be coupled with energy terms of protonation/deprotonation. In contrast, ΔGD(S) does not change with the substrate concentrations on either side of the membrane, and thus is an intrinsic property of the transporter. In principle, ΔGD(S) is experimentally measurable (see Appendix C). A negative ΔGD(S) would indicate that the substrate-carrying conformational change from the loading state to the releasing state is thermodynamically favored, and thus it contributes in part to the driving force of the transport. The complex of the drug-H+ antiporter MdfA with its substrate TPP+ seems to fit this scenario24 [see Fig. 3(C)]. There, substrate binding stabilized the substrate-releasing state more than the substrate-loading state. In contrast, if ΔGD(S) is positive, the binding affinity is higher in the loading state than in the releasing state. It may favor substrate loading and/or releasing. Yet, in this case, external energy inputs are required to drive the conformational change, to overcome the positive ΔGD(S). The results of studies of the complex of the sugar-H+ symporter LacY with its substrates seem to fit this scenario20 [see Fig. 3(B)]. There, substrate binding stabilized the substrate-loading state. Similar discussions can also be made for the proton associated free energy terms (i.e., Δμ[H+] etc.).
As a corollary of the above discussion, formation of an intra-molecular hydrogen-bond (H-bond) (or a salt-bridge bond) within the transporter may stabilize a particular state of the transport cycle, but cannot be a driving force for thermodynamic cycle of the transport. In fact, the same H-bond must break later in the process, and the energy released from the H-bond formation has to be paid back from other sources. Nevertheless, such short-term energy gains may influence the kinetics, for example the rates, of individual step(s).
Protonation and Membrane Potential
Membrane potential-driving hypothesis
The plasma membranes of all living cells usually carry an electrostatic membrane potential (ΔΨ) of typically ∼100-mV magnitude. If effective monovalent ions that generate this membrane potential were uniformly distributed in a region of δth fraction of the membrane thickness on each side of the membrane, the required ion concentration would be estimated to be δ−1 millimolar. For example, if the membrane thickness were 30 Å and the ionic region were 3-Å thick (i.e., δ=0.1), the effective ion concentration would be 10 mM, a value that is biologically relevant. Such an ionic distribution is equivalent to 0.02 standard charges (i.e., the charge of an electron or a proton) per 1000 Å2 (an area value of the cross section of a typical membrane protein). Therefore, the membrane potential is a macroscopic physical property of the membrane. It is produced by fast Brownian motions of charge-carrying particles. Such clouds of charges on both sides of the membrane can be described best using an average-field hypothesis, which treats fast moving charges as a continuous distribution, especially when considering the slow motions of the major conformational changes of a typical transporter.
Why is membrane potential important for PMF-driven transporters? From an energetic point of view, for a 100-mV membrane potential, the free energy of transferring a proton across the membrane (ΔμΨ= FΔΨ, where F is the Faraday constant) is about −4 RT. In comparison, for a ΔpH of 0.6, corresponding free energy of transferring one proton (Δμ[Η+]= −2.3 RTΔpH) is about −1.4 RT. Some MFS transporters that function under alkaline pH conditions may even perform transport under a negative (i.e., acidic-inside) ΔpH.25 In addition, pH 7.6 (the typical pH inside a bacterial cell) is equivalent to ∼15 effective free protons per 1-μm3 volume, suggesting that a cell is necessarily subjected to fluctuation in pH. Since electrostatic membrane potential is universal to all living cells, it would have been biochemically and evolutionarily advantageous to select in favor of utilizing the membrane potential as part of the driving force for MFS transporters. In fact, the presence of a membrane potential increases the transport rate of LacY by a factor of over 20 (see Fig. 2 in Ref.26). Because the relative dielectric constant (εr) of an aqueous solvent (∼80) is much higher than that of a protein (∼1), the electrostatic field (E=ΔΨ/(εrd)) of a membrane potential is focused on the protein part of the MFS transporter (with an effective thickness of d<30 Å). In other words, in both COut and CIn states, the solvent-filled cavity of an MFS transporter does not bear a significant part of the electrostatic field. Because of this non-uniform distribution of the dielectric constants, an electrostatic field jumps between the cytoplasmic half (in the COut state) and the extracellular half (in the CIn state) of the transporter during the major conformational changes. Relative to the membrane, the positional shift of the field may be even larger than the movement of charged particle(s) within the transporter. It is the movement of the charged particle(s) relative to the electrostatic field that determines the energy levels of a transporter. It is noteworthy, however, that several reported crystal structures of MFS transporters have been presented in the so-called occluded conformation.18,27,28 Although such a conformation may represent a transient intermediate state of the conformational change, it is unlikely to be a stable state in the presence of membrane potential, and therefore should be treated as in vitro artifacts. If it were a stable state, the transport process would not be able to proceed. Taken together, ΔμΨ is a major part of the free energy input for a PMF-driven MFS transporter, especially for electrogenic transport.
For PMF-driven transport, both a symporter and an antiporter get protonated in the COut state and deprotonated in the CIn state. In the presence of a negative-inside membrane potential, a protonated site is necessarily subjected to an inward electrostatic force.14 This force is ∼5 pN in strength (i.e., ∼FΔΨ/(εrd)), which is comparable with forces of typical biological events at the molecular level.29–31 Here, we propose a simple, yet elegant hypothesis on how the major conformational changes in MFS are coupled to the free energy ΔμΨ (Fig. 4): Protonation provides a structural point for the electrostatic membrane potential to apply an inward force. Together with the force of a hydrophobic mismatch from the surrounding lipid bilayer, the electrostatic force generates a mechanic torque that promotes a relative rotation between the N- and C-domains, thus shifting the COut–CIn equilibrium toward the CIn state.14 The hydrophobic mismatch force that balances the electrostatic force is necessarily associated with many small deformations on the protein–lipid interface (either membrane bending or inward shift of the transporter). On the one hand, the electrostatic force and the sum of hydrophobic mismatch forces are of equal size but opposite in their directions, thus keeping the mass center of the TM core within the membrane (see Appendix D). On the other hand, the elongated shape of the MFS transporter (with the longest dimension defined by the distance between the two pairs of support-helices, that is, TMs 3, 6 and TMs 11, 12) ensures that, for each of the N- and C-domain, the two forces generate a mechanical torque. Interestingly, the same architecture of a central cavity containing titratable residues inside, together with an elongated overall shape is also observed in some non-MFS transporters, e.g., the MATE family of transporters.32,33 In addition, some other non-MFS transporters form elongated dimers, as exemplified in the LeuT family member, Arg+/Agm antiporter AdiC,34 and the NhaA family member, Na+/H+ antiporter NapA.35 One explanation for such widely used 3D architectures is that the hydrophobic mismatch effect is essential for the conformational changes involved in transport function. Importantly, the membrane potential-driving hypothesis provides a unified foundation to explain common mechanisms of energy coupling with conformational changes of electrogenic MFS transporters, regardless of types of substrates.
Figure 4.
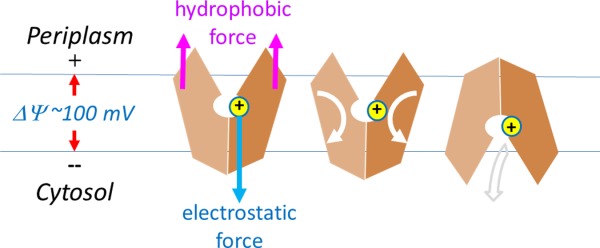
Membrane potential-driving hypothesis. Conformational changes driven by protonation are depicted. Directions of physical movements are shown in arrows.
In a more general sense, the combination of electrostatic and hydrophobic-mismatch forces determines the equilibrium position of a transporter (or any charge-carrying integral membrane protein) within the membrane.36 Changing either the membrane potential or the charge distribution of the transporter results in positional changes of the transporter relative the membrane, which in turn may affect chemical properties of the membrane protein and the kinetic equilibrium rates between its sub-states. For instance, in the MFS antiporter MdfA, a change in the electrochemical potential of H+ shifts the equilibrium between the CIn and COut states in the presence chloramphenicol (an electroneutral substrate).37 In fact, the interaction of a charge distribution with the membrane potential determines the orientation of an integral membrane protein in the membrane, and this is reflected in the widely accepted positive-inside rule (of charge distribution).38 ATP synthases and voltage-gated channels have been shown to utilize the membrane potential, either as a driving force or a means to regulate their gate functions.39,40 Recently, membrane potential-dependent conformational change was proposed to be responsible for the sealing of the peptide-conducting channel in the SecYEG translocon, thus preventing ion leakage during translocation of substrate peptides across the membrane.41 Such a membrane potential-dependent, positional equilibrium of membrane proteins also implicates that, an in vitro study, be it functional or structural, would deviate from the in vivo situation to some extent, because of both the absence of a membrane potential and altered hydrophobic mismatch.
Moreover, in an MFS transporter, not all ΔμΨ related energy is converted to heat in the COut-to-CIn step. Part of it may be stored in a form of elastic conformational energy (ΔGE) in the transporter-membrane system, and is released during the CIn-to-COut conformational change. The stored elastic conformational energy is the result of a balance between an external force (e.g., electrostatic force) and internal forces (e.g., those associated with a hydrophobic mismatch and other structural adjustments). In agreement with this elastic nature, the stored energy is roughly proportional (albeit not necessarily linearly) to the external force. Withdrawing the external force (e.g., by deprotonation) would result in the release of the elastic conformational energy. Taken together, membrane potential-dependent positional and conformational changes of a PMF-driven transporter during the COut-to-CIn conformational change are associated with elastic conformational energy stored in the CIn state, which may serve as a driving force for the CIn-to-COut conformational change.
Protonation sites
Proton-titratable residues are common features of PMF-driven MFS transporters, although their locations may vary from one transporter to another. All reported crystal structures of PMF-driven MFS transporters contain such titratable residues inside their central cavities (Supporting Information Table S2 in Ref.42), either acidic or histidine residues. For examples, E. coli LacY, the most extensively studied prokaryotic MFS transporter, contains a H322TM10.2–E325TM10.3 pair inside the central cavity, which is conserved in many sugar porters and essential for the PMF-driven transport.43 In E. coli YajR (a putative antiporter), H225TM7.3 and E320TM10.3 reside close to each other in the 3D structure and are the only two titratable residues inside the cavity.14 E. coli YbgH (a dipeptide-H+ antiporter) contains a conserved E21TM1.3 inside the central cavity, essential for protonation.42 While it is widely accepted that protonation is important for the transport process, the concept of interaction between protonation and membrane potential remains to be established.
According to our membrane potential-driving hypothesis, it is not necessary for protonation to be fixed at one position during the COut-to-CIn conformational change, provided that there exists one of the titratable residues inside the central cavity assuming the protonation status at any given time. A proton may potentially be transferred between two (or more) binding sites during the conformational change, depending on difference of the pKa values of the titratable sites. For example, the multidrug-resistance antiporter E. coli MdfA contains conserved E26TM1.4 and D34TM1.2 inside the central cavity, and both of them were shown to be required for transport activity.24 On the one hand, in the COut state, E26 is located at the apex of the cavity and buried more deeply than D34, suggesting a higher pKa for E26. Thus, E26 is likely to be the one that gets protonated in the COut state. In the CIn state, on the other hand, D34 is located at the new apex of the central cavity and becomes buried more deeply than E26. Thus, D34 becomes protonated in the CIn state in the absence of a substrate, while E26 becomes deprotonated. Therefore, during the COut-to-CIn transition, there appears to be a proton transfer occurring from E26 to D34, either directly (via a proton-relay path) or indirectly (e.g., by a dropping-and-picking mechanism).17 Similarly, in the fucose-H+ symporter FucP, a pair of acidic residues, D46TM1.2 and E135TM4.4, are located at the apex of the central cavity in the CIn and COut states, respectively, and flank the substrate from two sides.13 Mutations of either D46 or E135 results in activity loss of fucose uptake. In addition, of the two acidic residues, E135 is directly involved in substrate binding. Mutation of E135 abrogates the counter-flow activity (i.e., the ability of binding substrate), while that of D46 does not. These observations can be interpreted as following: in the COut state, substrate binding from the periplasmic side induces the protonation of E135 by expelling solvent from the vicinity of E135. This proton is transferred to D46 during the COut-to-CIn transition. After releasing the substrate into the cytosol, D46 becomes solvent-exposed and thus deprotonated. Therefore, proton transfer inside the central cavity during the COut-to-CIn transition may not be an isolated phenomenon.
For many non-MFS secondary active transporters, there exist two structural parts (or domains) that undergo conformational changes relative to each other during substrate transport.19 According to the membrane potential-driving hypothesis, the part that changes its electrostatic status in response to substrate binding is likely to be the one that moves more significantly, relative to the membrane. In agreement with such a prediction, the part that avoids charge-change is often involved in formation of an oligomer, which is likely to serve as the scaffold for the moving parts.34,35,44
Symporters, Antiporters, and Uniporters
Given their common energy-coupling mechanism, how can PMF-driven symporters, antiporters, and uniporters be distinguished from each other? A major functional difference between a symporter and an antiporter is whether the COut-to-CIn conformational change carries a substrate: Symporters do, but antiporters do not. Then, an interesting question arises as to whether it is possible for a given MFS transporter to function as a symporter for some substrates yet as an antiporter for others. If one proton was consumed for both uptake of one substrate and expelling of another per transport cycle, the process would be a PMF-driven exchanger, which is hypothetically possible but has so far rarely been reported. Moreover, if the influx and efflux were operating independently from each other, the transporter would allow a PMF-driven conformational change to occur in the absence of a substrate. Such a scenario would be equivalent to proton leakage and is likely to be detrimental for the cell. Thus, such a dual-functional MFS transporter is unlikely to exist. (Note, however, that E. coli KgtP transporter was reported to carry out both α-ketoglutarate uptake45 and arabinose efflux,46 albeit a detailed mechanistic analysis is still missing.) Logically, a symporter must couple substrate binding with protonation, and an antiporter requires competition of substrate binding with protonation (i.e., coupling of substrate binding with deprotonation). These notions are supported by early experimental data for several MFS transporters24,47 and are likely to be generally true for most cation (H+/Na+)-driven transporters of different types.48 In short, symporters and antiporters are fundamentally different from each other in terms of substrate-induced energy coupling. Therefore, it is important to understand the structural differences between symporters and antiporters.
Symporters
Since in symporters, protonation drives the COut-to-CIn conformational change, it is necessary that, for a symporter, protonation only occurs after substrate loading; otherwise, proton leakage might ensue. Under the condition that its substrate is present in limited amounts, a PMF-driven MFS symporter is likely to spend more time in its de-protonated COut state, waiting for the binding of a substrate that moves from the extracellular/periplasmic side to the central cavity (unless an allosteric mechanism exists for other regulatory factors to trigger the CIn-to-COut conformational change). To couple substrate binding with protonation, an ideal symporter should have the following properties: The pKa values of the proton-titratable sites in COut (i.e., pKa,out) in the absence of substrate binding is lower than pHOut, preventing premature protonation. Substrate binding from the outside increases pKa,out to above pHOut thus promoting protonation. In such a scenario, the free energy of substrate binding, ΔGL(S)= −RTln([S]Out/Kd,out), may be partially used to raise the pKa,out of the protonation site. In the CIn state, the pKa,in value before substrate release is higher than pHIn, preventing premature deprotonation. Substrate release decreases pKa,in to below pHIn thus promoting deprotonation. This paradigm implies that substrate loading in COut is not later than protonation, and substrate release in CIn is not later than deprotonation. In LacY, it is found that decreased affinity for sugar in the COut state at alkaline pH is due specifically to an increased reverse rate,49 suggesting that, under normal pH, sugar loading promotes protonation which in turn stabilizes sugar binding. In short, for a symporter, substrate binding is a prerequisite for proton binding.
How is such a mechanism applied in a symporter structure? At least two types of implementations have been observed in available structures of MFS symporters. One simple way is to change the micro-environment of the titratable residue by substrate binding, as exemplified in the above discussion on fucose binding to E135 of FucP.13 Furthermore, proton-titratable residues of symporters are often involved in a cluster of polar residues. Substrate binding may turn the cluster more electronegative, either by attracting positive charges away from the cluster, and/or by pushing negative charges toward the cluster and thus, the cluster becoming more electronegative and easier to become protonated. For example, in the crystal structure of E. coli LacY/1PV7, residues Y236TM7.2, D240TM7.1, R302TM9.1, K319TM10.1, H322TM10.2, and E325TM10.3 form a cluster of polar residues and are conserved in a number of sugar porters.11 This cluster may function as a proton-relay network, in which the H322–E325 pair is the titratable site. In E325 mutant variants, both uphill (PMF-driven) transport and substrate-induced proton uptake are abolished, while substrate affinities may even be increased relative to the wild-type form,50,51 suggesting that E325 is directly involved in protonation. In E. coli YbgH, a peptide-H+ symporter, the titratable residue E21TM1.3 is involved in a cluster of polar residues, some of which directly interact with the negatively charged carboxy group of the substrate dipeptide.42,52,53 Thus, substrate binding increases pKa of E21 (Fig. 5). Mutations at E21 as well as other residues in the polar cluster of YbgH result in loss of the transport activity.42 A very similar cluster of polar residues (including the so-called “ExxER” motif in TM1) is also observed in the crystal structure of the nitrate-H+ symporter, NTR1.1, from Arabidopsis (PDB ID: 4OH3).54 Taken together, substrate loading-induced increase of pKa,out may be a common event during symporter protonation.
Figure 5.
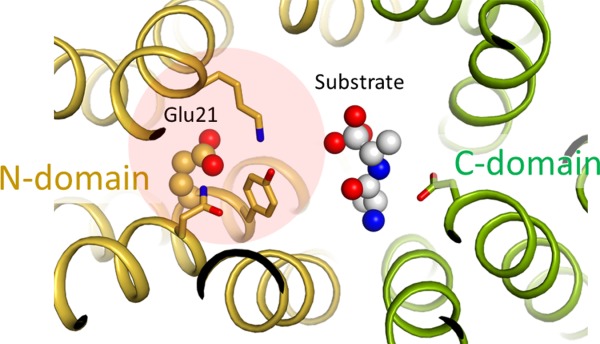
Coupling of substrate binding with protonation in symporters. Putative substrate binding site of E. coli YbgH (PDB ID: 4Q65). A model substrate (alafosfalin) is included based on superposition of a homologous complex crystal structure (4IKZ). Selected residues that are potentially important for substrate binding are shown in stick models. A cluster of polar residues (Q18, E21, Y22, and K118) potentially plays a role of coupling substrate binding with protonation at E21.
Antiporters
In contrast to symporters, under condition of limited substrate availability, a PMF-driven MFS antiporter would stay in the protonated CIn conformation, waiting for the binding of a substrate from the cytosol side (unless additional regulatory mechanisms exist). In an ideal case of the competition between substrate binding and protonation in an antiporter, the pKa,in values of the proton-titratable sites in the CIn state would be higher than pHIn in the absence of a substrate, preventing premature deprotonation; and substrate loading would decrease pKa,in to below pHIn thus promoting deprotonation. In the COut state, the pKa,out values of the titratable sites would be lower than pHOut in the presence of the substrate, preventing premature protonation. Substrate releasing would increase pKa,out to above pHOut thus promoting protonation. In short, in the case of an antiporter, substrate binding destabilizes the proton binding.
How, then, is such a mechanistic scheme implemented in an antiporter structure? In the CIn state, the titratable residues may be buried in a hydrophobic or electronegative environment to maintain a protonation state in the absence of a substrate. Substrate loading may make them either more accessible to hydrophilic groups or more electropositive; either way it would promote deprotonation. For example, in the multidrug-resistance antiporter, E. coli MdfA, D34TM1.2 is a potential titration site in the central cavity.55 In the CIn crystal structure of the MdfA-chloramphenicol complex, D34 is directly involved in substrate binding via H-bonds.17 In addition, it has been suggested that loading of a substrate may decrease pKa,in of this titratable site through interactions with the positively charged motif-B (see below). In another multidrug-resistance antiporter LmrP, the membrane-embedded acidic residue E327TM10.4 was found to be essential for high-affinity binding with the cationic substrate Hoechst-33342 and for proton transport.56 Upon interaction with substrates, this residue is believed to become more accessible to solvent, thus easier to get deprotonated.57 In E. coli YajR, the H225TM7.3–E320TM10.3 pair in the C-domain is the only titratable site inside the central cavity. In the COut state, this pair is away from the basic residue R108TM4.2 (i.e., the motif-B in the N-domain).14 In the putative CIn state, the H225–E320 pair is likely to approach closer to R108, presumably allowing substrate to trigger deprotonation. In general, because of different pKa,in values of the titratable sites inside the central cavity, substrates carrying different charges may induce differential deprotonation at distinct titratable sites. This might explain the observation that the efflux of different substrates is coupled to an influx of different stoichiometry of protons, with a net inward movement of +1 electric charge in each electrogenic transport cycle.56,58 The membrane potential ΔΨ can only be a driving force for substrate efflux if each excreted cationic substrate has a lower charge than the number of protons translocated.5 Such antiporters require multiple protonation sites that have pKa,in higher than pHIn in the absence of substrates, but can lower the pKa,in values in response to substrate binding. Taken together, a substrate loading-induced decrease of pKa,in may be a common event in the transport cycle of PMF-driven antiporters.
Uniporters and electroneutral transport
Uniporters mediate facilitated diffusion and, by definition, do not require proton translocation across the membrane as their driving force. Nevertheless, they may also utilize the negative-inside membrane potential if either the substrate influx carries positive charges or the substrate efflux carries negative charges. Although some MFS transporters are reported to carry out only uniport processes (e.g., GLUT1-4), both PMF-driven symporters and antiporters may behave like uniporters if under a strong concentration gradient of the substrate. For example, LacY was shown to carry out both symport and facilitated diffusion.26 Furthermore, many cationic compounds can be either exported or imported through the same MFS “antiporter,” depending on the direction and strength of the concentration gradient of the substrate between the two sides of the membrane.5 For example, LmrP may carry out both antiport and facilitated diffusion of cationic substrates.59 Also, Candida albicans Mdr1p usually expels a broad spectrum of electroneutral or cationic drugs in a PMF-driven manner; however, it has recently been shown that Mdr1p also uptakes a class of positively charged isoquinoline derivatives.60 Such uptake may be driven by ΔΨ via facilitated diffusion. Therefore, there appears to be no unique structural features that distinguish uniporters from either symporters or antiporters, except that in uniporters, substrate binding or release is not coupled in an obligatory manner to a particular protonation status.
Not all MFS transporters are driven by membrane potential-mediated electrostatic interaction. If the net charge change in the transport cycle is zero, the transport is called electroneutral [Fig. 3(C)]. An electroneutral transport is often defined by the fact as to whether the given transport process is independent of ΔΨ. In such cases, another favorable chemical potential has to serve as the thermodynamic driving force. However, since the presence of a membrane potential is a universal feature of all living cells, electrostatic interactions may play certain roles in affecting the kinetics of the transport process, even for electroneutral transport. For example, it would require at least a 55-fold concentration gradient (RTln55= 4 RT) for a monovalent charged substrate to move against a 100-mV membrane potential, and such a gradient would be unusual under physiological conditions. Therefore, the free-energy required for moving a charged substrate against the membrane potential is most likely compensated by an accompanied favorable charge movement along the membrane potential of either protons or ions. Electroneutral symport (i.e., H+/A− co-transport, where A− stands for a monovalent anionic substrate) has been briefly discussed before,5 for example, for uptake of some acidic substrates. The fungal H+-phosphate (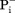 ) symporter PiPT is one such example (PDB ID: 4J05).61 Furthermore, electroneutral antiport (i.e., H+/B+ antiport, where B+ stands for a monovalent cationic substrate) is more commonly observed in multidrug exporters (e.g., MdfA58). In such cases, the energy barrier from the CIn state back to the COut state may be low, such that in the absence of net charge change, a negative ΔGD(s) is sufficient to stabilize the COut state, thus thermodynamically favoring the CIn-to-COut conformational change [see Fig. 3(C)].
) symporter PiPT is one such example (PDB ID: 4J05).61 Furthermore, electroneutral antiport (i.e., H+/B+ antiport, where B+ stands for a monovalent cationic substrate) is more commonly observed in multidrug exporters (e.g., MdfA58). In such cases, the energy barrier from the CIn state back to the COut state may be low, such that in the absence of net charge change, a negative ΔGD(s) is sufficient to stabilize the COut state, thus thermodynamically favoring the CIn-to-COut conformational change [see Fig. 3(C)].
As discussed in the Appendix A [Eq. 14 ], in the absence of an effect of a membrane potential (e.g., in electroneutral antiport), conformational changes between CIn and COut states would be driven by the sum of differential-binding energies of the transported substances (i.e., ΔGD(H+) +ΔGD(S)). These energy terms of differential binding are intrinsic properties of the transporter, but are not a function of substance concentrations. Their sum predicts whether influx or efflux of the substrate is thermodynamically favored at the steps of conformational changes, in the absence of effects of membrane potential. Nevertheless, since a membrane potential determines the equilibrium positions of both CIn and COut states, ΔGD(H+) and ΔGD(S) per se may be affected by ΔΨ, even in electroneutral transport. In addition, since different substrates may differ in their differential-binding energies between the CIn and COut states, their transport mechanisms in a given transporter are not necessarily the same. This is particularly true in the absence of a membrane potential, whereupon differential-binding energy becomes a major energy source.
Conserved Motifs
Despite the drastically different sizes, shapes, and chemical properties of their substrates as well as different protonation mechanisms, MFS transporters often contain several conserved motifs in addition to the 12-TM helix overall structure.62 Among them, motifs-A and -B are the most common. Such conserved motifs are likely to provide the structural basis of common functions of MFS transporters, for example, stabilizing one of the two major conformations and regulating or responding to either protonation or deprotonation.
Motif-A
3D motif-A
Motif-A (“GxxxD(+5)RxGRR”) is located in the intracellular loop L2–3 where it connects TMs 2 and 3, and is the most conserved motif in MFS transporters.6 For example, of 77 MFS proteins identified from the E. coli genome, 62 contain a putative motif-A (Supporting Information Table S4 in Ref.14). Although most available crystal structures of MFS transporters are determined in the CIn state, which is a non-functional state for motif-A, mutagenesis analyses have repeatedly shown that motif-A is essential for the transport activity in many MFS transporters.17,21,42,63–71 More importantly, in the COut crystal structure of YajR/3WDO,14 the motif-A is captured in its functional state [Fig. 6(A)]. This structure shows that the acidic residue D(+5) of the motif-A participates in an inter-domain charge-helix dipole interaction with the N-terminal end of TM11 from the C-domain. Other physical components of the motif-A and associated structural features include the following: (i) G(+1) interacts with conserved Gly residues from the N-terminal end of TM11 to ensure a tight packing between TMs 2 and 11 in the COut state [Fig. 6(A)]. (ii) D(+5), R(+9), and a conserved acidic residue from the C-terminal end of TM4 (i.e., TM4.5 region)66 form a charge-relay triad. (iii) G(+8) is required for an S-shaped turn of the L2–3 loop. (iv) R(+10) serves as the C-cap for TM6. (v) A conserved “PET(S)” motif at the loop C-terminal to TM6 stabilizes both R(+10) (using the mainchain carbonyl oxygen of the Pro residue) and the TM4.5 acidic residue of the charge-relay triad (using the sidechain hydroxyl group of Thr/Ser), and serves as an N-cap for TM3 (using the sidechain carboxylate group of the Glu residue) (see the crystal structures of MdfA/4ZOW, YajR/3WDO, and XylE/4GC0). (vi) A positively charged residue (prior to the TM11 N-terminal Gly) forms a salt-bridge with the TM4.5 acidic residue of the charge-relay triad in the COut state. Most of these residues have been shown in mutagenesis analyses to play important roles in substrate transport. For example, a mutation at Asp128TM4.5 significantly reduces the transport activity of LmrP.68 Mutations in the E. coli antiporter MdfA (e.g., S133F and A191T/V) that potentially disrupt the PET(S) motif affect the transport activity.37 Thus, the motif-A and its surrounding residues form a conserved “3D motif-A.” One important role played by this 3D motif-A is to regulate stability of the COut state.
Figure 6.
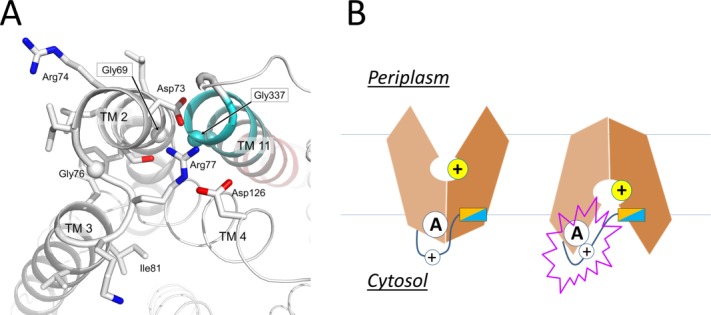
Active conformation of motif A of E. coli YajR. A: Side chains in motif A and Asp126 from the charge-relay triad are shown as stick models. Cα atoms of conserved Gly residues are shown as spheres. TM11 is colored from cyan at the N-terminal end to pink at the C-terminal end. B: Putative role of the inter-domain linker in regulating motif-A.
Amphipathic helix
Motif-A stabilizes the COut state. To initiate the COut-to-CIn conformational change, the COut state must be destabilized, which occurs in response to protonation inside the central cavity. How then does this 3D motif-A on the cytosolic side of the transporter sense and respond to protonation inside the central cavity? In nearly all known crystal structures of motif-A containing, PMF-driven, MFS transporters, the charge-relay triad is always accompanied by an inter-domain peptide (i.e., L6–7). These linker peptides contain a number of polar residues (often positively charged) as well as an amphipathic α-helix (α6–7) (Supporting Information Fig. S2 in Ref.14), the latter of which is likely to bind to the inner leaflet of the membrane. If this amphipathic α-helix maintains membrane association during an inward shift of the TM core, the inter-domain peptide will be stretched, resulting in a linker movement that likely interrupts the charge-relay triad of the motif-A [Fig. 6(B)]. For example, in the CIn crystal structure of NRT1.1/4OH3, a lysine residue from the linker peptide is found to insert into the charge-relay triad.54 In the CIn crystal structure of MdfA/4ZOW, D(+5) of motif-A is surrounded by positive residues from the motif-A as well as L6–7 loop. Moreover, in the crystal structures of several bacterial peptide transporters (POTs), an inter-domain, TM-helix pair is inserted between the two domains of the TM core, replacing α6–7, and is likely to move independently from the rest of the TM core.27,42,72 Thus, this helix-pair insert may function in a way similar to the amphipathic helix α6–7 in other 12-TM MFS structures. In support of such possibilities, mutations in the L6–7 that change the charge distribution or disrupt the amphipathic property of the α6–7 result in loss of transport activity.17,42,73 Interestingly, in the multidrug-resistance antiporter MdfA, mutation of S204 at the N-cap of α6–7 to a Pro residue enhanced the transport activity.37 Therefore, the L6–7 and associated amphipathic α6–7 are likely to play the roles of sensing protonation and regulating the stability of the 3D motif-A.
Motif-A hypothesis
Together, the above data support the “motif-A hypothesis”14: Protonation-induced, inward movement of the TM core relatively to the membrane is sensed by the amphipathic helix, α6–7. This helix further induces a conformational change in the L6–7 loop. Through the charge-relay triad, the positive charges of the loop weakens the inter-domain, charge-dipole interaction between D(+5) of the motif-A and TM11, thus destabilizing the COut state of the MFS transporter.
A-like motifs
Because of the internal symmetry of MFS transporters, motif-A could exist at four locations, namely L2–3, L5–6, L8–9, and L11–12. They are referred to as A-like motifs (or motifs-AL2–3, -AL5–6, -AL8–9, and -AL11–12). Among the four potential A-like motifs, AL2–3 and AL8–9 are located on the cytosol side, and AL5–6 and AL11–12 are located on the periplasmic side. Sequence analysis of E. coli MFS transporters has confirmed the existence of A-like motifs in all four locations.14 In some cases, more than one such motif exists in a given MFS transporter. For examples, E. coli YbgH contains the motifs-AL2–3 and -AL5–6.42 Mammalian multidrug-resistance antiporter Oct1 contains two complete sets of motif-A at both L2–3 and L8–9 on the cytoplasm side,6 and so does the fungal H+-phosphate symporter, PiPT (PDB ID: 4J05).61 Signature motifs of sugar porters [Supporting Information Figs. S1(B) and S2 in Ref.74] are in fact components of the 3D motif-AL2–3 and -AL8–9. These two motifs are found even in a non-PMF driven nitrate/nitrite exchanger, NarK75 (note that its homolog NarU is proposed to be a (Na+/K+)-(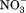 /
/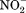 ) symporter76), indicating that the motif-A is not directly involved in proton translocation. Mutations in these A-like motifs were shown to reduce transport activities.42,71,77 Their main functions are likely to include stabilizing of the COut or CIn states. The precise mechanisms that regulate these A-like motifs in L5–6, L8–9, and L11–12 remain to be elucidated.
) symporter76), indicating that the motif-A is not directly involved in proton translocation. Mutations in these A-like motifs were shown to reduce transport activities.42,71,77 Their main functions are likely to include stabilizing of the COut or CIn states. The precise mechanisms that regulate these A-like motifs in L5–6, L8–9, and L11–12 remain to be elucidated.
Motif-B
Motif-B, “RxxqG” in TM4, is present in many MFS transporters,6 including a number of multidrug-resistance antiporters.7 According to the PFAM database,78 motif-B is the only high frequency site that contains a basic residue embedded in the TM region among MFS transporters (Supporting Information Fig. S2 in Ref.17). Of the 77 MFS proteins from E. coli, 13 transporters possessing the “RxxQG” motif are identified. Nine of them, namely EmrB, EmrY, HsrA, MdfA, MdtD, MdtL, MdtM, YajR, and YebQ, are annotated to be PMF-driven antiporters, and the remaining four (KgtP, ShiA, YdfJ, and YhjE) are symporters. This classification indicates that the simple presence of a motif-B is neither a necessary nor a sufficient condition for an MFS transporter to be an antiporter. In addition, in E. coli there are six “RTM4.2xx[S/T/C/H]G”-containing transporters, namely AraJ, Brc, DgoT, EntS, Fsr, and MhpT; and there are 14 other “RTM4.2xxxG”-containing transporters, including ExuT, GalP, MdtG, NanT, NepL, UhpC, XylE, YaaU, YcaD, YhhS, YjhB, YjiJ, YjjL, and YnfM. Hypothetically, a motif-B might appear in the four cavity-helices (i.e., TMs 1, 4, 7, and 10), which are related by the internal pseudo-symmetry of the MFS transporter. However, sequence analysis showed that the “RxxQG” sequence motif occurs only in the TM4.2 region. Further, two of the nine “RxxQG”-containing E. coli MFS antiporters (EmrB and EmrY) do not contain a motif-A. Thus, potential functions of the motif-B appear to be independent of the motif-A. More importantly, mutations in the motif-B in several MFS transporters have been shown to abolish all transport activity.17,65,71,79–81 Together, these data suggest that motif-B plays a common functional role in motif-B containing MFS transporters.
MdfA and YajR crystal structures
Among currently available crystal structures of MFS transporters, the canonical motif-B is only observed in E. coli YajR and MdfA.17 Similar to motif-A, motif-B is also accompanied by a number of residues that are conserved in the 3D structure but not contiguous in the primary sequence [Fig. 7(A)]. Together, they form a “3D motif-B” that contains an extended H-bond network.
Figure 7.
Structure and mechanism of the motif-B. A: Motif-B in the crystal structure of MdfA/4ZOW. Residues of the motif-B and surrounding conserved residues are shown in stick models. Backbone of the N- and C-domain is shown in tubes indicated in wheat and red, respectively. B: Schematic diagram of motif-B in regulating deprotonation.
Motif-B is unlikely to be directly involved in the inter-domain conformational change, because the 3D motif-B is embedded entirely in the N-domain. G(+5)TM4.3 residue of motif-B is more conserved than R(+1)TM4.2, even in MFS transporters carrying no motif-B, and allows a tight packing of TM4 with TM2. Thus, R(+1) appears to be the signature residue of motif-B. It carries a buried positive charge and breaks the H-bonding pattern of the neighboring TM1 helix.17 Both features are energetically costly, implicating important functions of the “3D motif-B.” Mutagenic analysis on MdfA shows that, among point mutations at R(+1), only the R(+1)H variant confers resistance to most antibiotics tested, the R(+1)K variant maintains partial drug-resistance activities, whereas R(+1)M/Q/E variants lose all activities.80 Results of drug-resistance assays on more extensive mutations in the 3D motif-B are in agreement with its importance in the transport activity.17
In the COut state, levels 1 and 2 of the cavity- and rocker-helices are accessible to solvents from the periplasmic side, thus the electrostatic field radiating from the motif-B is attenuated by the solvent, which is of a high dielectric constant [Fig. 7(B)]. In the CIn state, in contrast, levels 1 and 2 of the TM helices become buried inside the inter-domain interface, thus the positive electrostatic field of the motif-B is strengthened relatively to the COut state. In particular, the level 2 region would become more electropositive, thus potentially being able to promote deprotonation in the central cavity. For example, in the CIn crystal structure of MdfA/4ZOW [Fig. 7(A)], R112(+1) of the motif-B is 8 Å away from the protonation site D34TM1.2 in the N-domain. In comparison, in the putative CIn state of YajR, the titratable H225TM7.3–E320TM10.3 pair in the C-domain becomes closer to the motif-B than in the COut state of YajR/3WDO, thus favoring deprotonation in the CIn state. Therefore, effects of motif-B do not depend strictly on the location of the proton-titratable sites inside the central cavity.69 Furthermore, in multidrug-resistance antiporters, many of which contain motif-B, loading of substrates (which are often small hydrophobic molecules) from the cytosolic side may further strengthen the electrostatic field, namely by reducing the dielectric constant inside the cavity and/or by bringing in a positive charge into the cavity, thus promoting deprotonation.17 Taken together, in the CIn state the positive electrostatic field radiating from motif-B seems to be essential for regulating the protonation status of motif-B containing transporters.
B-like motifs
In members of the sugar porter (SP) subfamily of MFS, motif-B changes to “RxxxG” (where x stands for a hydrophobic residue).74 Some of SP transporters (e.g., GLUT1-4) are known as uniporters, while others (e.g., XylE) are PMF-driven symporters. In the crystal structure of XylE/4GC0, the side chain of Gln residue of the canonical motif-B is replaced by two ordered water molecules. The XylE structure also shows a pair of acidic residues, D27TM1.3–E206TM6.3 in the vicinity of R133TM4.2 of motif-B (“R133IIGG”), whereas those uniporters, instead, have electroneutral polar residues replacing the acidic pair. Therefore, the acidic pair in XylE is likely to be the potential protonation site, and its protonation status is probably influenced by R133. These acidic residues have recently been shown to be essential for the transport activity of XylE.82 In addition, this acidic-residue pair is located closely to the central cavity. By expelling solvent, substrate binding in the COut state increases the electronegativity of the acidic-residue pair, promoting protonation of the latter. Such a mechanism is another example of coupling protonation with substrate binding in symporters. Once in the CIn state, R133 decreases the electronegativity of the micro-environment of the acidic residue pair, promoting its deprotonation.
In the fungal H+-phosphate (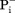 ) symporter PiPT, motif-B assumes a form of “R139VFLG”. In its CIn crystal structure (PDB ID: 4J05),61 the basic residue R139TM4.2 is stabilized by Q119TM3.2. Two acidic residues, D45TM1.3 and D48TM1.3, are located close to motif-B, and this pair is likely to be the protonation site. In the COut state, loading of the negative charged substrate into the cavity increases the electronegativity of the acidic-residue pair, promoting protonation. In the CIn state, the combination of enhanced positive electrostatic field of the motif-B and release of the negatively charged substrate promotes deprotonation.
) symporter PiPT, motif-B assumes a form of “R139VFLG”. In its CIn crystal structure (PDB ID: 4J05),61 the basic residue R139TM4.2 is stabilized by Q119TM3.2. Two acidic residues, D45TM1.3 and D48TM1.3, are located close to motif-B, and this pair is likely to be the protonation site. In the COut state, loading of the negative charged substrate into the cavity increases the electronegativity of the acidic-residue pair, promoting protonation. In the CIn state, the combination of enhanced positive electrostatic field of the motif-B and release of the negatively charged substrate promotes deprotonation.
Although the sugar-H+ symporter, E. coli LacY (PDB ID: 1PV7) does not possess a motif-B, a basic residue, R302TM9.2, is buried in the C-domain and located at the membrane-level similar to R(+1) of motif-B in the N-domain (e.g., R112TM4.2 of MdfA). This R302 is located near the potential protonation site, H322TM10.2–E325TM10.3 in LacY. Mutations at R302 abolish the proton translocation in LacY,43 and this observation may be explained using the mechanistic insights gained from studies of motif-B.
In all cases discussed above, the protonation site inside the central cavity is located on the cytosolic side of motif-B. Increasing the strength of a positive electrostatic field inside the central cavity in the CIn state relatively to the COut state seems to be a common mechanism of promoting deprotonation in MFS transporters.
Stability Balance Between the Two Conformations
The rocker-switch mechanism of MFS transporters suggests that a balance between the COut and CIn states is essential for the proper function of the transporters (see Appendix B). This notion has been supported by a number of studies. For example, point mutations in E. coli LacY that rescue a defective mutation at the D(+5) position of motif-AL2–3 on the cytosol side are found to be clustered around the motif-AL11–12 on the periplasmic side,77 implicating that balanced stabilities of the COut and CIn states are important for the transport function. Moreover, the C154TM5.2G point mutation is an extensively studied variant of LacY.83 This mutation is transport-inactive, while maintaining substrate binding (with affinity even higher than the WT).20 The crystal structure of detergent-solubilized C154G-LacY (PDB ID: 1PV7) was among the first reported MFS crystal structures11 and was found to assume the CIn conformation. It was speculated that the C154G mutation stabilized the CIn state; nevertheless, the WT-LacY crystal structure (PDB ID: 2V8N) was later reported to be also in the CIn-state.84 In fact, a crystallized conformation only suggests that it is a dominant population under the crystallization condition (including crystal packing). Moreover, a DEER study showed that in solution, C154G was predominantly in the COut state (Figs. 2.3 and 2.5 in Ref.20), while the WT assumed more equal distribution between the CIn and COut states (Figs. 2.2 and 2.4 in the same Reference). Since substrate binding per se is shown to stabilize the COut state,20 the tighter substrate binding in C154G seems to correlate with a more predominant COut conformation in solution than WT. Therefore, the lost transport activity of C154G is likely to be caused by the reduced stability in the CIn state. This corollary is in agreement with the close location of the mutation site to the inter-domain interface in the CIn crystal structure (1PV7). Intriguingly, the loss of transport activity of periplasmic-side mutation C154G can be rescued by secondary mutations on the cytosol side of the transporter.85 In particular, rescuing mutations include E130TM4.5C, K131TM4.5C, R134C, and G141TM5.5C. These mutations are potentially involved in the inter-domain interface in the COut state, presumably destabilizing the latter. Again, balanced stabilities of the two states appear to be important for transport activity. A similar balance was also shown to be important for E. coli POT transporter YbgH.42 Mutation D70A at the critical acidic residue of motif-AL2–3 on the cytosol side results in loss of transport activity, presumably by reducing the stability of the COut state. Such an activity loss can be reversed by another loss-of-function mutation on the periplasmic side, E163A/R297A, which reduces the CIn state stability by disrupting the motif-AL5–6 and a salt-bridge bond observed in the CIn crystal structure of YbgH/4Q65. In all three of the above studies, loss-of-function mutations on the cytosol side and on the periplasmic side can rescue each other. These results strongly suggest that the balance in stability between the COut and CIn states plays a key role in the transport activity of MFS transporters.
It is most likely that adjusting stabilities of the two major conformations is a common mechanism to regulate the activity of most alternating-access transporters, including MFS and non-MFS transporters. For example, transporters of the anti-acid system, for example, Arg+/Agm antiporter of E. coli AdiC (a member of the LeuT transporter family), preferentially perform the transport at low pH rather than neutral pH. According to its crystal structure (PDB ID: 3NCY34), a sensor for acidic condition is likely to be a cytosolic, inter-domain, salt-bridge bond, R78-D307, which is accompanied by Y74.86 This salt-bridge bond likely stabilizes the COut state, even in the presence of a bound substrate Arg+ ready to be transported. The interaction of Arg+ with membrane potential likely provides the driving force to the COut-to-CIn conformational change. In contrast, Y74 uses its positively charged edge of the sidechain aromatic ring as well as its hydroxyl group to decrease the pKa of D307, so that the strength of the salt-bridge bond is enhanced at neutral pH. However, at low pH D307 becomes protonated, and the salt-bridge bond dissolves more easily, thus shifting the COut-CIn equilibrium toward the CIn state. In addition, many MFS transporters contain rather large exo-membrane domains (e.g., E. coli XylE74 and YajR87), and such regulatory domains likely exert their functions through manipulating stability of certain states.
Concluding Remarks
In the past decade, structural studies on transporters have provided significant insights into the structural basis of the alternating access mechanism. In PMF-driven electrogenic MFS transporters, interaction of protonation and the negative-inside membrane potential provides a significant part of the driving energy for the COut-to-CIn conformational change. For symporters, substrate loading triggers the protonation in the COut state; while for antiporters, substrate loading triggers the deprotonation in the CIn state. Conserved motifs A and B of MFS transporters play important roles in common functions of MFS. Balanced stabilities between the COut and CIn states are essential for the transport function. Future work will be required to define and verify details of related mechanisms.
Acknowledgments
Authors thank Drs. Hong Qian and Taotao Wei for in depth discussion on the thermodynamics principles of the transport cycle. They also thank Dr. Torsten Juelich for linguistic assistance during the preparation of this manuscript.
A APPENDIX THERMODYNAMIC DESCRIPTION OF MFS TRANSPORTERS
In a transport process, the “external” Gibbs free energy includes terms of ΔμΨ, Δμ[H+], and Δμ[S].5 The following is true for a cycle of PMF-driven transport of (electrogenic) substrates:
| A1 |
(< 0. Q is the heat released in one transport cycle); where
| A1.1 |
| A1.2 |
| A1.3 |
(> 0, if the transport is against the substrate gradient. L and R stand for loading and releasing states, respectively).
Each term of external energy can be further divided into sub-terms (see Fig. 3).
| A2 |
| A2.1 |
(free energy of substrate loading);
| A2.2 |
(substrate-associated intrinsic differential free energy of the conformational change from the L to R state);
| A2.3 |
(free energy of substrate releasing).
Similarly, the following equations for proton-related free energies apply:
| (A3) |
| A3.1 |
(free energy of protonation in COut);
| A3.2 |
(protonation-associated intrinsic differential free energy of the COut-to-CIn step);
| A3.3 |
(free energy of deprotonation in CIn).
Further,
| A4 |
(where and
and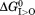 are free energy changes associated with conformational changes in the absence of membrane potential).
are free energy changes associated with conformational changes in the absence of membrane potential).
B APPENDIX KINETIC DESCRIPTION
A kinetic discussion can be made based on the “tightly coupled chemical model.”88 Based on the assumption that, in a symporter, substrate binding is coupled with protonation, the following equations apply:
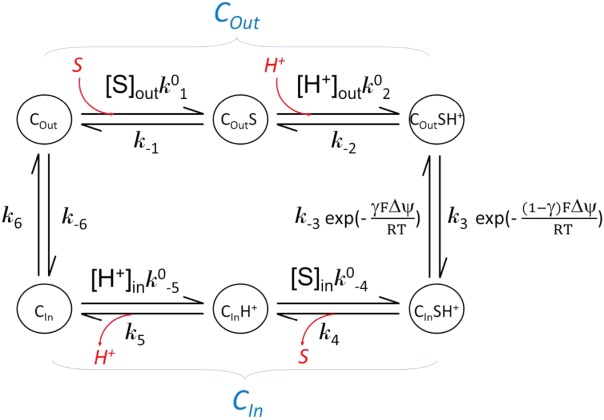
| B1 |
(where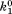 and
and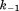 are forward and reversal kinetic coefficients for substrate loading);
are forward and reversal kinetic coefficients for substrate loading);
| B2 |
(where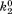 and
and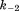 are forward and reversal kinetic coefficients for proton loading);
are forward and reversal kinetic coefficients for proton loading);
| B3 |
(where k3 and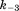 are forward and reversal kinetic coefficients for the COut-to-CIn conformational change in the absence of ΔμΨ);
are forward and reversal kinetic coefficients for the COut-to-CIn conformational change in the absence of ΔμΨ);
| B4 |
(where k4 and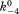 are forward and reversal kinetic coefficients for substrate releasing.);
are forward and reversal kinetic coefficients for substrate releasing.);
| B5 |
(where k5 and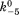 are forward and reversal kinetic coefficients for proton releasing.);
are forward and reversal kinetic coefficients for proton releasing.);
| B6 |
(where k6 and k−6 are forward and reversal kinetic coefficients for the CIn-to-COut conformational change).
In addition,
| B7 |
| B8 |
and
| B9 |
(i.e., the tightly coupled chemical model; equivalent to Eqs. 14).
Similarly, based on the assumption that in an antiporter substrate binding is coupled with deprotonation, one has the following diagram as well as equations similar to the above discussion for the symporter.
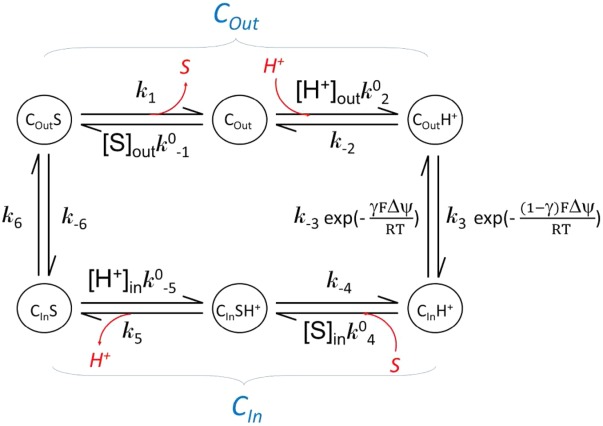
C APPENDIX KINETIC OF IN VITRO SUBSTRATE BINDING ASSAYS
Substrate binding is often studied in a solubilized form of a transporter. The results from such a binding assay usually represent transporters at different states with or without substrate bound. Major differences in kinetics of a membrane embedded transporter compared to the solubilized form are the lack of external driving force and identical substrate concentration for both substrate loading and releasing in the solubilized form. In the following, we assume that the transporter maintains the two major conformations in the soluble form as it does in the membrane. In addition, the affinity of substrate binding in each conformation is assumed to be the same in both the membrane embedded and the solubilized form. (This assumption may need to be verified in each case.) Each conformation is of distinct properties, in particular binding affinity (Kd) of the substrate. Note that Kd is related to binding enthalpy, ΔH, by the van’t Hoff equation. The kinetic relationship between these states is shown in the following scheme.
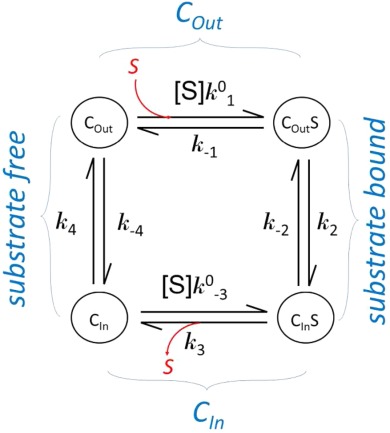
Equilibration Conditions
| C1.1 |
| C1.2 |
| C1.3 |
| C1.4 |
| C1.5 |
Although there are seven independent kinetic variables in Eq. 29, there are only three independent thermodynamic variables (e.g., equilibrium constants).
Dissociation Constants
| C2.1 |
| C2.2 |
| C2.3 |
| C2.4 |
| C2.5 |
| C2.6 |
Whilst dissociation constants Kd,1 and Kd,3 in the COut and CIn states, respectively, and their related free energy terms (ΔGL(S) and ΔGR(S)) are of interests, what is directly measurable in in vitro binding assays such as SPR, ITC, and SPA is usually the apparent dissociation constant of the mixture system, Kd,app.
Partition Between the COut and CIn Conformations
Here, we define the ratio of the concentration of transporters in both substrate-free and substrate-bound COut states to that of CIn states as conformational ratio f, which is a function of [S].
| C3.1 |
| C3.2 |
| C3.3 |
| C3.4 |
| C3.5 |
| C3.6 |
| C3.7 |
The coefficients f(0) and f(∞) are the COut–CIn conformational ratios in the absence of substrate and in super-high concentration of substrate, respectively. They are important properties of the transporter for a given substrate, and can be chosen as independent thermodynamic variables. Experimentally, the curve of f([S]), including f(0) and f(∞), can be measured with assays such as smFRET or DEER. The third independent variable, for example, Kd,3 can be determined by fitting the observed f([S]) curve with the calculated one using Kd,3 as a variable [in Eq. 42)].
In general, the Gibbs free-energy of conformational change from the COut to CIn state at the substrate concentration [S] is given by:
| C3.8 |
where the enthalpy ΔH and entropy ΔS terms are commonly considered to be independent of temperature. Further, let’s assume, for a given [S], f([S]) is measured at two temperatures, T1 and T2, with that ΔT≝ T2−T1 (> 0), T≝ (T1+T2)/2, and ΔT ≪ T. According to the van’t Hoff equation, the following is applied:
| C3.9 |
where f1 and f2 are the conformation ratios measured at T1 and T2, respectively. Therefore, by measuring f([S]) at two temperatures, one may determine ΔG, ΔH, and ΔS at any specified substrate concentration [S].
Distribution of the Transporters in the Four States
| C4.1 |
| C4.2 |
| C4.3 |
| C4.4 |
| C4.5 |
Of R1(0), R2(∞), R3(∞), and R4(0), three of them can be chosen as independent variables. The fourth one can be determined by the equation R1+R2+R3+R4=1 [i.e., Eq. 45].
Relationship Between Dissociation Constants and f([S])
| C5.1 |
| C5.2 |
| C5.3 |
| C5.4 |
| C5.5 |
It can be proved that Kd,1 is the substrate concentration at which 1/f([S]) equals (1/f(0) +1/f(∞))/2, that is, the mean of 1/f([S]). Kd,3 is the substrate concentration at which f([S]) equals (f(0) +f(∞))/2, that is, the mean of f([S]). Similarly, Kd,app. is the substrate concentration at which f([S]) equals (R1(0) +R2(∞))/(R3(∞) +R4(0)), that is, the ratio of the mean fraction of COut to that of CIn.
Further,
| C5.6 |
| C5.7 |
| C5.8 |
Differential Free Energy of Substrate Binding
| C6.1 |
| C6.2 |
ΔGD(S), which is determined solely by the ratio of f(∞) to f(0), is an important property of the transporter (a symporter in this case) for a given substrate. It indicates the thermodynamic preference of the substrate movement in the absence of external driving forces (e.g., membrane potential). When ΔGD(S)<0, the movement is inward; and when ΔGD(S)>0, the movement is outward.
D APPENDIX HOW TO ESTIMATE HYDROPHOBIC MISMATCH FORCES
The atomic solvation parameter (σ) of a membrane protein (MP) is estimated to be
| D1 |
(see Ref.89). In the absence of a charge–potential interaction, the MP is at an equilibrium position (i.e., Δx=0). Thus the hydrophobic mismatch force is
| D2.1 |
At a large displacement,
| D2.2 |
where c is the circumference of the MP (typically ∼100 Å). So, the larger the size of the MP is, the stronger the hydrophobic mismatch force may become. For a small rigid-body displacement, the hydrophobic mismatch force can be written as
| D2.3 |
where λ indicates the rigidity of the membrane. The larger λ is, the more sticky (dissipative) of the membrane–MP interface would be. Typically, λ is in the order of 10 Å.
In the presence of the membrane potential ΔΨ (or more precisely of a charge–potential interaction), the electrostatic force is
| D3 |
where F is the Faraday constant (typically FΔΨ ≈ 10 kJ/mol) and d is the membrane thickness (∼30 Å). Assuming a rigid-body displacement, at the equilibrium position the two forces balance each other:
| D4.1 |
Thus,
| D4.2 |
Note that (FΔΨ/d)Δx would be the electrostatic energy of the displacement, and (σc)Δx would be the hydrophobic mismatch energy assuming a constant maximum force during the displacement. Equation 46) suggests that even for a soft membrane (e.g., λ ≈ 10 Å), the displacement Δx caused by electrostatic interaction is likely to be small (unless the MP is not a rigid body, e.g. when there is a large conformational change).
Supporting Information
Additional Supporting Information may be found in the online version of this article.
Supporting Information Appendix
References
- Marger MD, Saier MH., Jr. ( A major superfamily of transmembrane facilitators that catalyse uniport, symport and antiport. Trends Biochem Sci. 1993;18:13–20. doi: 10.1016/0968-0004(93)90081-w. [DOI] [PubMed] [Google Scholar]
- Law CJ, Maloney PC, Wang DN( Ins and outs of major facilitator superfamily antiporters. Ann Rev Microbiol. 2008;62:289–305. doi: 10.1146/annurev.micro.61.080706.093329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saier MH, Jr, Beatty JT, Goffeau A, Harley KT, Heijne WH, Huang SC, Jack DL, Jahn PS, Lew K, Liu J, Pao SS, Paulsen IT, Tseng TT, Virk PS( The major facilitator superfamily. J Mol Microbiol Biotechnol. 1999;1:257–279. [PubMed] [Google Scholar]
- Brown S, Chang JL, Sadee W, Babbitt PC( A semiautomated approach to gene discovery through expressed sequence tag data mining: discovery of new human transporter genes. AAPS PharmSci. 2003;5:E1. doi: 10.1208/ps050101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poolman B, Konings WN( Secondary solute transport in bacteria. Biochim Biophys Acta. 1993;1183:5–39. doi: 10.1016/0005-2728(93)90003-x. [DOI] [PubMed] [Google Scholar]
- Paulsen IT, Brown MH, Skurray RA( Proton-dependent multidrug efflux systems. Microbiol Rev. 1996;60:575–608. doi: 10.1128/mr.60.4.575-608.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fluman N, Bibi E( Bacterial multidrug transport through the lens of the major facilitator superfamily. Biochim Biophys Acta. 2009;1794:738–747. doi: 10.1016/j.bbapap.2008.11.020. [DOI] [PubMed] [Google Scholar]
- Lyons JA, Parker JL, Solcan N, Brinth A, Li D, Shah ST, Caffrey M, Newstead S. Structural basis for polyspecificity in the POT family of proton-coupled oligopeptide transporters. EMBO Rep. 15:886–893. doi: 10.15252/embr.201338403. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jardetzky O( Simple allosteric model for membrane pumps. Nature. 1966;211:969–970. doi: 10.1038/211969a0. [DOI] [PubMed] [Google Scholar]
- Tetsch L, Jung K( How are signals transduced across the cytoplasmic membrane? Transport proteins as transmitter of information. Amino Acids. 2009;37:467–477. doi: 10.1007/s00726-009-0235-x. [DOI] [PubMed] [Google Scholar]
- Abramson J, Smirnova I, Kasho V, Verner G, Kaback HR, Iwata S( Structure and mechanism of the lactose permease of Escherichia coli. Science. 2003;301:610–615. doi: 10.1126/science.1088196. [DOI] [PubMed] [Google Scholar]
- Huang Y, Lemieux MJ, Song J, Auer M, Wang DN( Structure and mechanism of the glycerol-3-phosphate transporter from Escherichia coli. Science. 2003;301:616–620. doi: 10.1126/science.1087619. [DOI] [PubMed] [Google Scholar]
- Dang S, Sun L, Huang Y, Lu F, Liu Y, Gong H, Wang J, Yan N( Structure of a fucose transporter in an outward-open conformation. Nature. 2010;467:734–738. doi: 10.1038/nature09406. [DOI] [PubMed] [Google Scholar]
- Jiang D, Zhao Y, Wang X, Fan J, Heng J, Liu X, Feng W, Kang X, Huang B, Liu J, Zhang XC( Structure of the YajR transporter suggests a transport mechanism based on the conserved motif A. Proc Natl Acad Sci USA. 2013;110:14664–14669. doi: 10.1073/pnas.1308127110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madej MG, Dang S, Yan N, Kaback HR( Evolutionary mix-and-match with MFS transporters. Proc Natl Acad Sci USA. 2013;110:5870–5874. doi: 10.1073/pnas.1303538110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips R, Ursell T, Wiggins P, Sens P( Emerging roles for lipids in shaping membrane-protein function. Nature. 2009;459:379–385. doi: 10.1038/nature08147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heng J, Zhao Y, Liu M, Liu Y, Fan J, Wang X, Zhao Y, Zhang X. Substrate-bound structure of the E. coli multidrug resistance transporter MdfA. Cell Res. 2015 doi: 10.1038/cr.2015.94. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar H, Kasho V, Smirnova I, Finer-Moore JS, Kaback HR, Stroud RM( Structure of sugar-bound LacY. Proc Natl Acad Sci USA. 2014;111:1784–1788. doi: 10.1073/pnas.1324141111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi Y. Common folds and transport mechanisms of secondary active transporters. Ann Rev Biophys. 2013;42:51–72. doi: 10.1146/annurev-biophys-083012-130429. [DOI] [PubMed] [Google Scholar]
- Smirnova I, Kasho V, Choe JY, Altenbach C, Hubbell WL, Kaback HR( Sugar binding induces an outward facing conformation of LacY. Proc Natl Acad Sci USA. 2007;104:16504–16509. doi: 10.1073/pnas.0708258104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masureel M, Martens C, Stein RA, Mishra S, Ruysschaert JM, McHaourab HS, Govaerts C. Protonation drives the conformational switch in the multidrug transporter LmrP. Nat Chem Biol. 10:149–155. doi: 10.1038/nchembio.1408. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frillingos S, Kaback HR( Cysteine-scanning mutagenesis of helix VI and the flanking hydrophilic domains on the lactose permease of Escherichia coli. Biochemistry. 1996;35:5333–5338. doi: 10.1021/bi953068d. [DOI] [PubMed] [Google Scholar]
- Frillingos S, Sun J, Gonzalez A, Kaback HR( Cysteine-scanning mutagenesis of helix II and flanking hydrophilic domains in the lactose permease of Escherichia coli. Biochemistry. 1997;36:269–273. doi: 10.1021/bi9618629. [DOI] [PubMed] [Google Scholar]
- Fluman N, Ryan CM, Whitelegge JP, Bibi E. Dissection of mechanistic principles of a secondary multidrug efflux protein. Mol Cell. 47:777–787. doi: 10.1016/j.molcel.2012.06.018. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holdsworth SR, Law CJ( Multidrug resistance protein MdtM adds to the repertoire of antiporters involved in alkaline pH homeostasis in Escherichia coli. BMC Microbiol. 2013;13:113. doi: 10.1186/1471-2180-13-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viitanen P, Garcia ML, Kaback HR( Purified reconstituted lac carrier protein from Escherichia coli is fully functional. Proc Natl Acad Sci USA. 1984;81:1629–1633. doi: 10.1073/pnas.81.6.1629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newstead S, Drew D, Cameron AD, Postis VL, Xia X, Fowler PW, Ingram JC, Carpenter EP, Sansom MS, McPherson MJ, Baldwin SA, Iwata S( Crystal structure of a prokaryotic homologue of the mammalian oligopeptide-proton symporters, PepT1 and PepT2. EMBO J. 2011;30:417–426. doi: 10.1038/emboj.2010.309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quistgaard EM, Low C, Moberg P, Nordlund P( Metal-mediated crystallization of the xylose transporter XylE from Escherichia coli in three different crystal forms. J Struct Biol. 2013;184:375–378. doi: 10.1016/j.jsb.2013.09.009. [DOI] [PubMed] [Google Scholar]
- Schnitzer MJ, Visscher K, Block SM( Force production by single kinesin motors. Nat Cell Biol. 2000;2:718–723. doi: 10.1038/35036345. [DOI] [PubMed] [Google Scholar]
- Cocco S, Monasson R, Marko JF( Force and kinetic barriers to unzipping of the DNA double helix. Proc Natl Acad Sci USA. 2001;98:8608–8613. doi: 10.1073/pnas.151257598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S, Chistol G, Hetherington CL, Tafoya S, Aathavan K, Schnitzbauer J, Grimes S, Jardine PJ, Bustamante C( A viral packaging motor varies its DNA rotation and step size to preserve subunit coordination as the capsid fills. Cell. 2014;157:702–713. doi: 10.1016/j.cell.2014.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu M, Radchenko M, Symersky J, Nie R, Guo Y( Structural insights into H+-coupled multidrug extrusion by a MATE transporter. Nat Struct Mol Biol. 2013;20:1310–1317. doi: 10.1038/nsmb.2687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka Y, Hipolito CJ, Maturana AD, Ito K, Kuroda T, Higuchi T, Katoh T, Kato HE, Hattori M, Kumazaki K, Tsukazaki T, Ishitani R, Suga H, Nureki O( Structural basis for the drug extrusion mechanism by a MATE multidrug transporter. Nature. 2013;496:247–251. doi: 10.1038/nature12014. [DOI] [PubMed] [Google Scholar]
- Fang Y, Jayaram H, Shane T, Kolmakova-Partensky L, Wu F, Williams C, Xiong Y, Miller C( Structure of a prokaryotic virtual proton pump at 3.2 A resolution. Nature. 2009;460:1040–1043. doi: 10.1038/nature08201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C, Kang HJ, von Ballmoos C, Newstead S, Uzdavinys P, Dotson DL, Iwata S, Beckstein O, Cameron AD, Drew D( A two-domain elevator mechanism for sodium/proton antiport. Nature. 2013;501:573–577. doi: 10.1038/nature12484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang XC, Sun K, Zhang L, Li X, Cao C( GPCR activation: protonation and membrane potential. Protein Cell. 2013;4:747–760. doi: 10.1007/s13238-013-3073-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adler J, Bibi E( Determinants of substrate recognition by the Escherichia coli multidrug transporter MdfA identified on both sides of the membrane. J Biol Chem. 2004;279:8957–8965. doi: 10.1074/jbc.M313422200. [DOI] [PubMed] [Google Scholar]
- von Heijne G( Membrane protein structure prediction. Hydrophobicity analysis and the positive-inside rule. J Mol Biol. 1992;225:487–494. doi: 10.1016/0022-2836(92)90934-c. [DOI] [PubMed] [Google Scholar]
- Rastogi VK, Girvin ME( Structural changes linked to proton translocation by subunit c of the ATP synthase. Nature. 1999;402:263–268. doi: 10.1038/46224. [DOI] [PubMed] [Google Scholar]
- Tombola F, Pathak MM, Isacoff EY( How far will you go to sense voltage? Neuron. 2005;48:719–725. doi: 10.1016/j.neuron.2005.11.024. [DOI] [PubMed] [Google Scholar]
- Knyazev DG, Winter L, Bauer BW, Siligan C, Pohl P( Ion conductivity of the bacterial translocation channel SecYEG engaged in translocation. J Biol Chem. 2014;289:24611–24616. doi: 10.1074/jbc.M114.588491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y, Mao G, Liu M, Zhang L, Wang X, Zhang XC( Crystal structure of the E. coli peptide transporter YbgH. Structure. 2014;22:9–1. doi: 10.1016/j.str.2014.06.008. [DOI] [PubMed] [Google Scholar]
- Zhou Y, Jiang X, Kaback HR( Role of the irreplaceable residues in the LacY alternating access mechanism. Proc Natl Acad Sci USA. 2012;109:12438–12442. doi: 10.1073/pnas.1210684109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verdon G, Boudker O( Crystal structure of an asymmetric trimer of a bacterial glutamate transporter homolog. Nat Struct Mol Biol. 2012;19:355–357. doi: 10.1038/nsmb.2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seol W, Shatkin AJ( Escherichia coli kgtP encodes an alpha-ketoglutarate transporter. Proc Natl Acad Sci USA. 1991;88:3802–3806. doi: 10.1073/pnas.88.9.3802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koita K, Rao CV( Identification and analysis of the putative pentose sugar efflux transporters in Escherichia coli. PloS One. 2012;7:e43700. doi: 10.1371/journal.pone.0043700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smirnova I, Kasho V, Sugihara J, Vazquez-Ibar JL, Kaback HR( Role of protons in sugar binding to LacY. Proc Natl Acad Sci USA. 2012;109:16835–16840. doi: 10.1073/pnas.1214890109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu M, Symersky J, Radchenko M, Koide A, Guo Y, Nie R, Koide S( Structures of a Na+-coupled, substrate-bound MATE multidrug transporter. Proc Natl Acad Sci USA. 2013;110:2099–2104. doi: 10.1073/pnas.1219901110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smirnova IN, Kasho V, Kaback HR( Protonation and sugar binding to LacY. Proc Natl Acad Sci USA. 2008;105:8896–8901. doi: 10.1073/pnas.0803577105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franco PJ, Brooker RJ( Functional roles of Glu-269 and Glu-325 within the lactose permease of Escherichia coli. J Biol Chem. 1994;269:7379–7386. [PubMed] [Google Scholar]
- Smirnova I, Kasho V, Sugihara J, Choe JY, Kaback HR( Residues in the H+ translocation site define the pKa for sugar binding to LacY. Biochemistry. 2009;48:8852–8860. doi: 10.1021/bi9011918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steiner HY, Naider F, Becker JM( The PTR family: a new group of peptide transporters. Mol Microbiol. 1995;16:825–834. doi: 10.1111/j.1365-2958.1995.tb02310.x. [DOI] [PubMed] [Google Scholar]
- Daniel H, Spanier B, Kottra G, Weitz D( From bacteria to man: archaic proton-dependent peptide transporters at work. Physiology. 2006;21:93–102. doi: 10.1152/physiol.00054.2005. [DOI] [PubMed] [Google Scholar]
- Sun J, Bankston JR, Payandeh J, Hinds TR, Zagotta WN, Zheng N( Crystal structure of the plant dual-affinity nitrate transporter NRT1.1. Nature. 2014;507:73–77. doi: 10.1038/nature13074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal N, Fluman N, Siemion S, Bibi E( The secondary multidrug/proton antiporter MdfA tolerates displacements of an essential negatively charged side chain. J Biol Chem. 2009;284:6966–6971. doi: 10.1074/jbc.M808877200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazurkiewicz P, Driessen AJ, Konings WN( Energetics of wild-type and mutant multidrug resistance secondary transporter LmrP of Lactococcus lactis. Biochim Biophys Acta. 2004;1658:252–261. doi: 10.1016/j.bbabio.2004.06.004. [DOI] [PubMed] [Google Scholar]
- Mazurkiewicz P, Konings WN, Poelarends GJ( Acidic residues in the lactococcal multidrug efflux pump LmrP play critical roles in transport of lipophilic cationic compounds. J Biol Chem. 2002;277:26081–26088. doi: 10.1074/jbc.M203141200. [DOI] [PubMed] [Google Scholar]
- Lewinson O, Adler J, Poelarends GJ, Mazurkiewicz P, Driessen AJ, Bibi E( The Escherichia coli multidrug transporter MdfA catalyzes both electrogenic and electroneutral transport reactions. Proc Natl Acad Sci USA. 2003;100:1667–1672. doi: 10.1073/pnas.0435544100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolhuis H, Poelarends G, van Veen HW, Poolman B, Driessen AJ, Konings WN( The lactococcal lmrP gene encodes a proton motive force-dependent drug transporter. J Biol Chem. 1995;270:26092–26098. doi: 10.1074/jbc.270.44.26092. [DOI] [PubMed] [Google Scholar]
- Sun N, Li D, Fonzi W, Li X, Zhang L, Calderone R( Multidrug-resistant transporter mdr1p-mediated uptake of a novel antifungal compound. Antimicrob Agents Chemother. 2013;57:5931–5939. doi: 10.1128/AAC.01504-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen BP, Kumar H, Waight AB, Risenmay AJ, Roe-Zurz Z, Chau BH, Schlessinger A, Bonomi M, Harries W, Sali A, Johri AK, Stroud RM. Crystal structure of a eukaryotic phosphate transporter. Nature. 496:533–536. doi: 10.1038/nature12042. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulsen IT, Skurray RA( Topology, structure and evolution of two families of proteins involved in antibiotic and antiseptic resistance in eukaryotes and prokaryotes—an analysis. Gene. 1993;124:1–11. doi: 10.1016/0378-1119(93)90755-r. [DOI] [PubMed] [Google Scholar]
- Yamaguchi A, Someya Y, Sawai T( Metal-tetracycline/H+ antiporter of Escherichia coli encoded by transposon Tn10. The role of a conserved sequence motif, GXXXXRXGRR, in a putative cytoplasmic loop between helices 2 and 3. J Biol Chem. 1992;267:19155–19162. [PubMed] [Google Scholar]
- Jessen-Marshall AE, Paul NJ, Brooker RJ( The conserved motif, GXXX(D/E)(R/K)XG[X](R/K)(R/K), in hydrophilic loop 2/3 of the lactose permease. J Biol Chem. 1995;270:16251–16257. doi: 10.1074/jbc.270.27.16251. [DOI] [PubMed] [Google Scholar]
- Kimura T, Nakatani M, Kawabe T, Yamaguchi A( Roles of conserved arginine residues in the metal-tetracycline/H+ antiporter of Escherichia coli. Biochemistry. 1998;37:5475–5480. doi: 10.1021/bi973188g. [DOI] [PubMed] [Google Scholar]
- Someya Y, Kimura-Someya T, Yamaguchi A( Role of the charge interaction between Arg(70) and Asp(120) in the Tn10-encoded metal-tetracycline/H(+) antiporter of Escherichia coli. J Biol Chem. 2000;275:210–214. doi: 10.1074/jbc.275.1.210. [DOI] [PubMed] [Google Scholar]
- Bannam TL, Johanesen PA, Salvado CL, Pidot SJ, Farrow KA, Rood JI( The Clostridium perfringens TetA(P) efflux protein contains a functional variant of the Motif A region found in major facilitator superfamily transport proteins. Microbiology. 2004;150:127–134. doi: 10.1099/mic.0.26614-0. [DOI] [PubMed] [Google Scholar]
- Gbaguidi B, Mazurkiewicz P, Konings WN, Driessen AJ, Ruysschaert JM, Vigano C( Proton motive force mediates a reorientation of the cytosolic domains of the multidrug transporter LmrP. Cell Mol Life Sci. 2004;61:2646–2657. doi: 10.1007/s00018-004-4298-2. [DOI] [PubMed] [Google Scholar]
- Sigal N, Molshanski-Mor S, Bibi E( No single irreplaceable acidic residues in the Escherichia coli secondary multidrug transporter MdfA. J Bacteriol. 2006;188:5635–5639. doi: 10.1128/JB.00422-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hakizimana P, Masureel M, Gbaguidi B, Ruysschaert JM, Govaerts C( Interactions between phosphatidylethanolamine headgroup and LmrP, a multidrug transporter: a conserved mechanism for proton gradient sensing? J Biol Chem. 2008;283:9369–9376. doi: 10.1074/jbc.M708427200. [DOI] [PubMed] [Google Scholar]
- Pascual JM, Wang D, Yang R, Shi L, Yang H, De Vivo DC( Structural signatures and membrane helix 4 in GLUT1: inferences from human blood-brain glucose transport mutants. J Biol Chem. 2008;283:16732–16742. doi: 10.1074/jbc.M801403200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solcan N, Kwok J, Fowler PW, Cameron AD, Drew D, Iwata S, Newstead S( Alternating access mechanism in the POT family of oligopeptide transporters. EMBO J. 2012;31:3411–3421. doi: 10.1038/emboj.2012.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandal A, Kumar A, Singh A, Lynn AM, Kapoor K, Prasad R( A key structural domain of the Candida albicans Mdr1 protein. Biochem J. 2012;445:313–322. doi: 10.1042/BJ20120190. [DOI] [PubMed] [Google Scholar]
- Sun L, Zeng X, Yan C, Sun X, Gong X, Rao Y, Yan N( Crystal structure of a bacterial homologue of glucose transporters GLUT1-4. Nature. 2012;490:361–366. doi: 10.1038/nature11524. [DOI] [PubMed] [Google Scholar]
- Zheng H, Wisedchaisri G, Gonen T( Crystal structure of a nitrate/nitrite exchanger. Nature. 2013;497:647–651. doi: 10.1038/nature12139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan H, Huang W, Yan C, Gong X, Jiang S, Zhao Y, Wang J, Shi Y( Structure and mechanism of a nitrate transporter. Cell Rep. 2013;3:716–723. doi: 10.1016/j.celrep.2013.03.007. [DOI] [PubMed] [Google Scholar]
- Cain SM, Matzke EA, Brooker RJ( The conserved motif in hydrophilic loop 2/3 and loop 8/9 of the lactose permease of Escherichia coli. Analysis of suppressor mutations. J Membr Biol. 2000;176:159–168. doi: 10.1007/s00232001085. [DOI] [PubMed] [Google Scholar]
- Finn RD, Bateman A, Clements J, Coggill P, Eberhardt RY, Eddy SR, Heger A, Hetherington K, Holm L, Mistry J, Sonnhammer EL, Tate J, Punta M( Pfam: the protein families database. Nucleic Acids Res. 2014;42:D222–D230. doi: 10.1093/nar/gkt1223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewinson O, Padan E, Bibi E( Alkalitolerance: a biological function for a multidrug transporter in pH homeostasis. Proc Natl Acad Sci USA. 2004;101:14073–14078. doi: 10.1073/pnas.0405375101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigal N, Vardy E, Molshanski-Mor S, Eitan A, Pilpel Y, Schuldiner S, Bibi E( 3D model of the Escherichia coli multidrug transporter MdfA reveals an essential membrane-embedded positive charge. Biochemistry. 2005;44:14870–14880. doi: 10.1021/bi051574p. [DOI] [PubMed] [Google Scholar]
- Kapoor K, Rehan M, Kaushiki A, Pasrija R, Lynn AM, Prasad R( Rational mutational analysis of a multidrug MFS transporter CaMdr1p of Candida albicans by employing a membrane environment based computational approach. PLoS Comput Biol. 2009;5:e1000624. doi: 10.1371/journal.pcbi.1000624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wisedchaisri G, Park MS, Iadanza MG, Zheng H, Gonen T( Proton-coupled sugar transport in the prototypical major facilitator superfamily protein XylE. Nat Commun. 2014;5:4521. doi: 10.1038/ncomms5521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menick DR, Sarkar HK, Poonian MS, Kaback HR( cys154 is important for lac permease activity in Escherichia coli. Biochem Biophys Res Commun. 1985;132:162–170. doi: 10.1016/0006-291x(85)91002-2. [DOI] [PubMed] [Google Scholar]
- Guan L, Mirza O, Verner G, Iwata S, Kaback HR( Structural determination of wild-type lactose permease. Proc Natl Acad Sci USA. 2007;104:15294–15298. doi: 10.1073/pnas.0707688104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermolova NV, Smirnova IN, Kasho VN, Kaback HR( Interhelical packing modulates conformational flexibility in the lactose permease of Escherichia coli. Biochemistry. 2005;44:7669–7677. doi: 10.1021/bi0502801. [DOI] [PubMed] [Google Scholar]
- Wang S, Yan R, Zhang X, Chu Q, Shi Y( Molecular mechanism of pH-dependent substrate transport by an arginine-agmatine antiporter. Proc Natl Acad Sci USA. 2014;111:12734–12739. doi: 10.1073/pnas.1414093111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang D, Zhao Y, Fan J, Liu X, Wu Y, Feng W, Zhang XC( Atomic resolution structure of the E. coli YajR transporter YAM domain. Biochem Biophys Res Commun. 2014;450:929–935. doi: 10.1016/j.bbrc.2014.06.053. [DOI] [PubMed] [Google Scholar]
- Qian H. Cycle kinetics, steady state thermodynamics and motors—a paradigm for living matter physics. J Phys Condens Matter. 2005;17:S3783–S3794. doi: 10.1088/0953-8984/17/47/010. [DOI] [PubMed] [Google Scholar]
- Cymer F, von Heijne G, White SH(inpress. Mechanisms of integral membrane protein insertion and folding. J Mol Biol. 427:999–1022. doi: 10.1016/j.jmb.2014.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Appendix


