Abstract
The purpose of this article is to introduce and describe a statistical model that researchers can use to evaluate underlying mechanisms of behavioral onset and other event occurrence outcomes. Specifically, the article develops a framework for estimating mediation effects with outcomes measured in discrete-time epochs by integrating the statistical mediation model with discrete-time survival analysis. The methodology has the potential to help strengthen health research by targeting prevention and intervention work more effectively as well as by improving our understanding of discretized periods of risk. The model is applied to an existing longitudinal data set to demonstrate its use, and programming code is provided to facilitate its implementation.
Keywords: discrete time, survival analysis, mediation, onset, substance use
The purpose of this article is to introduce a statistical model that researchers can use to evaluate underlying mechanisms of behavioral onset and other time-to-event outcomes. Combining advantages from mediation analysis and discrete-time survival analysis, discrete-time survival mediation (henceforth referred to as DTSMed) supports investigations that seek to study pathways of event occurrence measured in discrete-time epochs such as months, school semesters, or years. Some examples of research where DTSMed would be applicable are examining underlying mechanisms of youth drug involvement onset, first relapse following treatment, early initiation of sexual activity, school expulsion, or criminal recidivism.
The DTSMed model has the potential to help strengthen health research in several ways. Namely, the model facilitates effective evaluation of prevention and intervention programs with time-to-event outcomes as well as informs the etiology of different public health concerns in a variety of domains. Previous research has demonstrated how studying mechanisms of change via mediation analysis can direct and refine evidence-based programming and prevention research, both by enhancing program evaluation and by helping to explain observed relations among variables (e.g., Chen, 2005; MacKinnon, 2008; Fairchild & McQuillin, 2010; Fairchild & Mackinnon, in press). Other research has argued how operationalizing the timing of event occurrence as a discrete-time survival outcome presents critical advantages over other methodologies including the (a) logistical and financial feasibility of periodic rather than continuous data collection, (b) ability to evaluate both time-varying and time-invariant predictors, (c) capacity to provide a pattern of risk probabilities for event occurrence over time, and (d) capability to effectively deal with censored observations (Singer & Willet, 1993; Willett & Singer, 1993; 2004). Censored observations are a hallmark of survival and event history data. Given that data collection lasts for a finite period of time, events of interest (e.g., death) will generally not be observed for everyone in a given sample. Censored data can be viewed as a type of missing data where one has partial information on missing observations rather than no information at all. For example, if death is not observed for a subject under observation, though the exact event time for that individual will remain unknown, there is certainty in the fact that the event will occur sometime after the end of the study (if it does at all). Note this scenario is referred to as right censoring in the survival literature.
Although DTSMed has the potential to inform research in a broad variety of areas, we demonstrate the need for the model in the context of early-onset substance involvement. Our reason for this choice is two-fold. Not only is substance abuse a critical public health problem that affects a variety of outcomes in numerous domains, but hypotheses about the timing of substance involvement onset lend themselves well to discrete-time survival methods in particular. We develop an argument for the relevance of DTSMed in this area in the following section, then formally present the statistical DTSMed model before applying it to an empirical example.
Substance Abuse: A Motivating Context
The Importance of Studying Substance Abuse
Substance abuse remains a major public health problem in the United States, with the excessive use and misuse of substances such as alcohol, tobacco, and illicit drugs relating to adverse health outcomes, increased risk of fatal and nonfatal injuries, violence, crime, and delinquency. The Centers for Disease Control and Prevention has identified tobacco and excessive alcohol use as the two leading behaviors responsible for a prevalence of chronic diseases, with tobacco and excessive alcohol ranking as the primary and third leading causes of preventable deaths in the United States each year, respectively (Centers for Disease Control and Prevention, 2011; Centers for Disease Control and Prevention, 2008; Mokdad, Marks, Stroup, & Gerberding, 2004; McGinnis & Foege, 1993). The economic costs that arise from substance abuse are also dire, with the burden of these costs extending beyond the individual user to include family members, employers, crime victims, health insurers, and the government (e.g., costs associated with health care, work productivity losses, property damage, and criminal justice system resources).
Why is Studying the Timing of Substance Involvement Onset so Crucial?
Beyond the broad scope risk and adverse societal consequences that substance abuse poses, there is specific concern about substance involvement by youth. Despite the decline of substance involvement among young people over the past decade, the prevalence and consequences of youth substance involvement nevertheless remain pronounced (Bouchery, Harwood, Sacks, Simon, & Brewer, 2011; Eaton et al., 2010; Johnston, O’Malley, Bachman, & Schulenburg, 2012). A growing number of studies suggest that early-onset substance involvement is associated with heightened risk for myriad adverse social, psychological, and behavioral outcomes including later accelerated substance abuse (e.g., Chambers, Taylor, & Potenza, 2003; Gil, Wagner, & Tubman, 2004; Griffin, Bang, & Botvin, 2010; Hingson, Heeren, Winter, & Wechsler, 2003; Peleg-Oren, Saint-Jean, Cardenas, Tammara, & Pierre, 2009; Robins & Przybeck, 1985; Slade et al., 2008). Overall findings support a key relationship between age of substance involvement initiation and the development of adverse outcomes, such that earlier substance involvement is detrimental. Unquestionably, early-onset substance involvement is a critical public health problem that calls for concerted efforts in prevention.
How Can We Ameliorate the Problem?
Given the heightened risk of problems associated with early substance involvement, understanding the motivating mechanisms associated with the timing of its onset and targeting the timing of onset in prevention can act as a crucial element in confronting substance abuse problems. By addressing malleable determinants of early substance involvement, prevention efforts can potentially delay substance involvement initiation and reduce risk of later adverse outcomes. Further, by exploring the underlying processes that drive observed relations between different risk and protective factors and substance involvement, prevention researchers can improve our scientific understanding of the behavior. Having appropriate analytic tools to design and evaluate programs, as well as methods to effectively explore underlying processes that can account for relations among variables, will help make these efforts maximally effective. One such method, the DTSMed model, can direct the empirical exploration of underlying processes driving the timing of substance involvement as well as guide formal evaluations of prevention programs in the area.
The DTSMed Model
The DTSMed model can be used to explain the relations between predictors and event occurrence or to design and evaluate programs intended to impact time-to-event outcomes. Employing the DTSMed model as an explanatory tool provides a vehicle to explore theoretically guided pathways of behavior and can lend insight into the etiological roots of health and behavioral problems that unfold over time. Alternatively, using the DTSMed model to design a program incites the researcher to identify behavioral determinants a priori to create interventions that influence those variables with the intention of preventing or delaying an event.
Coupling mediation analysis with discrete-time survival analysis, the DTSMed model conceptually explores how or why a predictor impacts the timing of experiencing an event. DTSMed parses the effect of a predictor on the timing of event occurrence into direct effect and indirect effects. The direct effect conveys the influence of a predictor on the timing of event occurrence, controlling for a mediator variable, and the indirect effect conveys the influence of a predictor on the timing of event occurrence through the mediator. The DTSMed model empirically estimates the impact of predictors on the timing of event occurrence via a logit link function, such that the outcome in analysis is a conditional log odds of the hazard probability of event occurrence. In the subsequent sections, we explicate both a regression approach to estimating DTSMed and a structural equation modeling (SEM)-based approach. The utility of considering an SEM variant of DTSMed involves the ability to incorporate measurement error as well as the capacity to estimate model frailties in complex models. The benefits of modeling frailties have been studied in continuous time survival models (Henderson & Oman, 1999; Hougaard, Myglegaard, & Borch-Johnsen, 1994). Note that in its simplest form, the SEM-based model provides maximum likelihood estimates of binary event indicator parameters equivalent to the hazard probability estimates from a logistic regression-based model. Before detailing model estimation, we first briefly review the methodological foundations of DTSMed for the reader.
Methodological Foundations
Mediation Analysis
Statistical mediation models permit the investigation of mechanisms underlying the relation of two or more other variables by explaining how or why the variables relate. Specifically, a mediator variable (M) transmits the influence of a predictor (X) onto an outcome (Y; Baron & Kenny, 1986; Judd & Kenny, 1981; MacKinnon, 2008; MacKinnon & Fairchild, 2009; MacKinnon, Fairchild, & Fritz, 2007). Given a relation between the mediator and an outcome, any influence of the predictor on the mediator should lead to change in the outcome as the mediator intercedes the relation between X and Y.
Given continuous M and Y variables, the single mediator model is defined as follows:
| (1) |
| (2) |
where b0 is the intercept in each equation, a is the regression coefficient relating X to M, c′ is the partial regression coefficient relating X to Y controlling for M, b is the partial regression coefficient relating M to Y controlling for X, and e1 and e2 are the corresponding residual terms for each equation (see Figure 1). The c′ coefficient defines the direct effect of X on Y. The product of the a and b coefficients, ab, conveys the indirect effect of X on Y through M and thus portrays the mediation process. The logic of this product of coefficients estimator derives from tracing rules for recursive models in path analysis (Wright, 1934).
Figure 1.
The single mediator model, where X = the independent variable, Y = the dependent variable, M = the mediator variable, a = the effect of the independent variable onthe mediator, b = the effect of the mediator on the outcome controlling for X, and c’ = the effect of X on Y controlling for M. Residual variances are denoted by e1 and e2.
Discrete-Time Survival Analysis
One uses discrete-time survival analysis to estimate effects when an outcome of interest involves event history or time-to-event data collected in discrete intervals of time. The methods support research questions that relate to the questions of “if” and “when” an outcome occurs by modeling subjects over time and estimating at which interval they first experience an event (e.g., Allison, 1982; Singer & Willet, 1991; Singer & Willet, 1993). Note that this article discusses univariate discrete-time survival analysis that considers the onset of a single, nonrepeatable target event. Discrete-time survival analysis lends insight into temporal windows of risk by providing information on the probability of event occurrence across time intervals. The focus of analysis is the hazard probability of an event or the conditional probability that a single nonrepeatable target event will occur in a particular time period, given that it has not occurred before that time (e.g., Allison, 1982; Singer & Willet, 1993; Willett & Singer, 1993):
| (3) |
where hij is the hazard probability for individual i at time period j and Ti is a discrete random variable representing the time period at which the event occurs for each individual. Hazard probabilities are conditional because an individual can only be at risk to experience the event in a given time period j if they have not already experienced the event beforehand. Like-wise, once an individual experiences the nonrepeatable event, they cannot be at risk to experience it again at a later time. The cumulative set of the conditional probabilities is called the hazard function and enumerates a distribution of hazard probabilities over time. When independent of predictors other than time itself, the hazard function is called a baseline hazard.
Although Cox (1972) originally proposed a nonparametric partial likelihood approach to estimating survival models with continuous time, the strategy is neither necessary nor ideal to implement with discrete-time data. Rather, one can use logistic regression and estimate parameters using maximum likelihood to demonstrate the hazard function’s dependence on time and predictors of interest (Allison, 1982; Singer & Willet, 1993). More recently, researchers have demonstrated an SEM-based approach to estimating discrete-time survival effects that also estimates parameters via maximum likelihood and offers capabilities beyond the logistic regression-based approach (Masyn, 2009; Muthén & Masyn, 2005).
Estimating the DTSMed Model
A Logistic Regression-Based Approach
With a single predictor, mediator, and outcome variable, two equations define the DTSMed model in the logistic regression-based approach:
| (4) |
| (5) |
where previously introduced terms retain their meaning from earlier equations, loge is the logit link function, denotes the marginal hazard probability of event occurrence given X and M, αj is a vector of time-specific intercept parameters (α1, … , αJ that relates each time interval to the conditional log odds of the baseline hazard probability of event occurrence, and Dij is a vector of J dummy codes (D1, … , DJ representing discrete-time intervals defined identically for all individuals through the last observation period, J. The c’ parameter demonstrates how X impacts the conditional log odds (i.e., the logit) of the baseline hazard probability of event occurrence controlling for the mediator, and the b coefficient illustrates how M impacts the conditional log odds of the baseline hazard probability controlling for the independent variable. All slope coefficients in the model are linear in the logit metric. Exponentiating a given slope coefficient gives a hazard odds ratio (hOR) for the predictor, illustrating the multiplicative increase (or decrease) in the hazard odds of risk of event occurrence associated with a one-unit change in the predictor.
As in the model outlined in Equations 1 and 2, the DTSMed model defines the mediated effect as ab and the direct effect as c’. Previous methodological work has advocated using ab to define mediation in logistic regression frameworks (MacKinnon & Dwyer, 1993; MacKinnon, Lockwood, Brown, Wang, & Hoffman, 2007). Null hypothesis significance testing of mediated effects in the DTSMed model can be conducted by estimating asymmetric bootstrapped confidence intervals (CIs) based on the empirical sampling distribution of ab or by estimating asymmetric confidence limits based on the distribution of the product of two random variables. Both approaches have been shown to have greater power and more accurate Type 1 error rates than normal theory standard error estimators, given the nonnormality of the ab distribution (e.g., MacKinnon et al., 2002). Once difficult to implement, these methods are now widely available and user friendly, given the integration of bootstrapping options in several statistical software packages as well as the creation of a program called “PROD-CLIN” which computes the distribution of the product test using user entered values of model parameter estimates (MacKinnon, Fritz, Williams, & Lockwood, 2007; Tofighi & MacKinnon, 2011). As with any interval estimate, if zero is included in a given CI, the mediated effect is not significant.
An SEM-Based Approach
With a single predictor, mediator, and outcome variable, two equations define the DTSMed model in the SEM-based approach:
| (6) |
| (7) |
where all terms retain their meaning from previous equations, η is a continuous latent variable representing underlying propensity for event occurrence, ej is a time-specific binary event indicator coding whether or not the event occurred in a given time interval, and τj is a vector of time-specific threshold parameters (τ1, … , τJ). The negative value of these threshold parameters will equal the value of the time-specific intercept parameters in the logistic regression specification:
| (8) |
A researcher can take the negative value of each time-specific threshold in the SEM-based approach to get the conditional log odds of the baseline hazard probability of event occurrence in a given time period. A path diagram of the SEM-based DTSMed model is shown in Figure 2.
Figure 2.
The structural equation modeling (SEM)-based DTSMed model, where X = the independent variable, M = the mediator, variable, η = the latent propensity for event occurrence, and ui − uj = binary indicators of event occurrence at each time period. The a, b, and c’ path coefficients retain their meaning from Figure 1.
As in the logistic regression-based specification of DTSMed, the mediated effect is defined by ab in the SEM-based approach and can be tested for statistical significance with either bootstrapped CIs or asymmetric CIs based on the sampling distribution of the product. Note that the log odds of the marginal hazard probabilities in the logistic regression-based approach are equivalent to the log odds of the event indicator probabilities in the SEM-based approach, such that maximum likelihood estimates of the event indicator probabilities in Equation 7 will equal maximum likelihood estimates of the marginal hazard probabilities in Equation 5. Note also that because the event indicators are driven by an underlying factor, η, the probabilities of the estimates are interpreted as latent response propensities for event occurrence rather than the hazard probability of event occurrence itself.
Assumptions of the DTSMED Model
Assumptions of the DTSMed model draw naturally from its component parts. Given that the DTSMed model analyzes mediation effects, it is assumed that (a) there is correct chronological ordering of the variables such that temporal precedence is preserved, (b) there are no reverse causality effects, and (c) there is no interaction between X and M. Given that discrete-time survival effects are evaluated, it is further assumed that (d) there is noninformative censoring, such that the censoring mechanism is independent of event occurrence, (e) there is a linear relation between the logit hazard and the predictors (i.e., X and M) such that differences in the logit hazard are linear for each unit change in a predictor, (f) values of X and M remain constant within a given time interval, (g) there is no unobserved heterogeneity in the hazard, such that fixed model coefficients sufficiently represent relations between predictors and the hazard function, and (h) the ratio of hazard functions with different values of X and M does not depend on time (i.e., proportionality). Note that the noninformative censoring assumption is crucial for local independence of the event outcomes. Although univariate discrete-time survival outcomes are conditionally independent by definition (i.e., an individual can only be at risk in a given time period if they have experienced the event beforehand and can no longer be at risk once they have experienced the event), if the censoring mechanism is not random then statistical inferences may be compromised.
Although it would not be viable to explore survival outcomes in purely cross-sectional data, it is worthwhile to caution against measuring X and M contemporaneously with each other and/or with the first measurement of Y. Measurements of X and M in the DTSMed model should precede the first measurement wave of the event outcome. The DTSMed model is causal in theory, but cross-sectional data and nonrandomized studies preclude inferring causal relations from the model unless statistical corrections are applied (e.g., Coffman, 2011; Jo, Stuart, MacKinnon, & Vinokur, 2011). The issue of causality in mediation analysis is an important area of research that we further consider in the discussion, but the importance of temporal precedence in the model is worthwhile expanding here. Although not a sufficient assumption for causality, lack of temporal precedence of variables in the DTSMed model undermines basic premises of analysis. Cross-sectional data only provide a snapshot of concurrent relations and estimating mediation in this context implicitly assumes stationarity and equilibrium, limiting the ability to compute accurate parameter estimates (Cole & Maxwell, 2003; Maxwell & Cole, 2007). Since mediation analysis seeks to explain the mechanisms by which an effect occurs and causes must precede effects in time, it is only sensible that mediation should be examined with longitudinal data. Moreover, variables take time to achieve their effects. Maxwell and Cole (2007) show several compelling examples where cross-sectional mediation models break down, arguing against their estimation generally and reflecting that such models are not able to provide reasonable conclusions about mediating processes. Although survival data are different from other longitudinal data in that there is only one outcome of interest (i.e., event time) rather than a series of repeated outcome measures, temporal precedence of the variables in the DTSMed model is still paramount. The researcher should also be mindful of both the timing and the duration of data collection, given that DTSMed considers how a mediated relation impacts the probability of event occurrence over a span of time (i.e., the hazard probability). Attention to the choice of measurement interval is also important to maximize the likelihood that an event will be captured, given that it occurs during the study period.
An Applied DTSMed Example
The Data and Hypothesis
To illustrate estimation and interpretation of parameters in the DTSMed model, we applied the methods to an available longitudinal data set where we could explore the etiology of early-onset smoking behavior. The data had annual assessments of children/youth, families, and teachers from age 5 to 14. Using the Mplus Version 7 software package (Muthén & Muthén, 1998–2012), we demonstrate the DTSMed analysis for both the logistic regression-based and the SEM-based approaches. A simplified example has been chosen not for its comprehensive or sophisticated conceptualization but rather for its utility in demonstrating application of the DTSMed model. The example reflects a single mediator model scenario with one continuous X variable, one continuous M variable, and a single discrete-time survival outcome, Y. Specifically, we examined whether parental depressive symptoms in kindergarten (X; drawn from the Parenting Stress Index; Abidin, 1990) impacted child externalizing behavior problems in fourth grade (M; as assessed by a teacher report of externalizing behavior problems on the Child Behavior Checklist; Achenbach, 1991), which was posited to subsequently impact the timing of smoking onset between Grades 5 and 9 (Y).
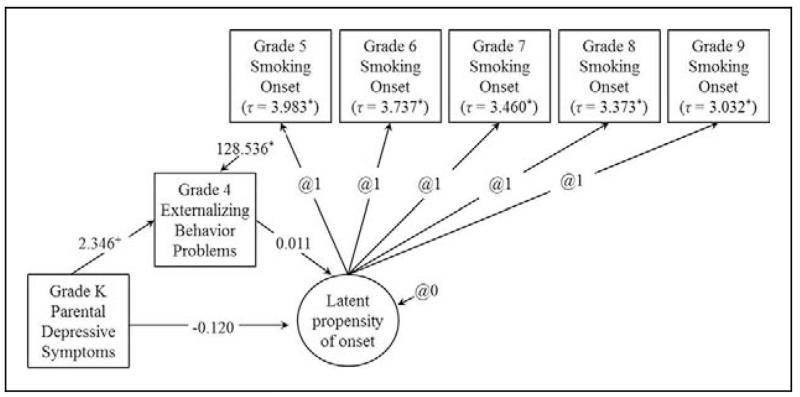
A path diagram of the applied example (in the SEM-based approach) is shown in Figure 3. Note that the assessment periods for each variable in the example were nonoverlapping to preserve temporal sequencing of the mediation model. The smoking onset outcome involved asking youth annually about their smoking involvement out of earshot of the caregiver to preserve confidentiality and potential validity of responses. A 6-month window of behavior (rather than a 30-day window) was considered at each assessment so as to minimize missing first smoking involvement no matter how infrequent. The sample consisted of 508 children, none of whom reported having puffed a cigarette prior to fifth grade.
Figure 3.
The structural equation modeling (SEM)-based DTSMed model for the applied example. The example explores the relation between parental depressive symptoms on smoking onset via child externalizing behavior problems. +indicates p < .05 and *indicates p < .001.
Conceivably, parental depressive symptoms when a child is young could disrupt parenting and child development, which in turn could affect adjustment trajectories of children including early substance involvement (e.g., Brook, Brook, Richter, & Whiteman, 2003; Dishion, Capaldi, & Yoerger, 1999). As well, a link between early conduct problems (i.e., externalizing behavior problems) and subsequent substance abuse has also been well documented, mostly in the general population and to some extent in specific populations (e.g., King, Iacono, & McGue, 2004). Relations between child externalizing behaviors (EBPs) and smoking behavior in particular have also been supported (Helstrom, Bryan, Hutchison, Riggs, & Blechman, 2004). With this in mind, we hypothesize that parental depressive symptoms in kindergarten will lead to an increase in fourth-grade EBPs, which will lead to an increased risk of early onset of smoking involvement. Testing the proposition explored here does not preclude several other influences from impacting smoking onset or from being included in comprehensive models.
Checking Assumptions
We examined several testable assumptions of the DTSMed model prior to running analysis models. First, we evaluated whether there was a violation of linearity in the predictors by performing the Box-Tidwell (1962) transformation test. Neither the interaction between X and its natural log (i.e., X × ln(X)) nor between M and its natural log (i.e., M × ln(M)) were significant, indicating that there was no nonlinearity in the relation between the logit of the predictors and the discrete-time survival outcome: bX × ln(X) = −1.235(1.057), p = .243 and bM × ln(M) = −.088(.073), p = .227. Second, we examined whether there was an XM interaction in the data; this coefficient was also nonsignificant, indicating that the data satisfied the assumption of no XM interaction: b = .010(.012), p = .419. Finally, we examined the tenability of the proportional hazard odds assumption by comparing the model fit of an SEM-based DTSMed model with the proportionality constraints intact (i.e., a model in which the factor loadings from the latent variable to each time point of the outcome were constrained to be equal) to a model where we relaxed the assumption. Results of a chi-square difference test between the models indicated no significant improvement in model fit, indicating that retaining the proportional hazard odds assumption was reasonable: Δχ2(Δdf) = 0.011(4), p > .999.
Conducting the Logistic Regression-Based DTSMed Analysis
Data Structure
When estimating a DTSMed model with the logistic regression-based approach, the data must conform to a person-period format (this step is not necessary if estimating DTSMed in the SEM-based approach). Unlike conventional data structures where each subject typically fills one line in the data set and their values on different measured variables appear in separate columns, a person-period data set contains multiple data records per subject, with each line corresponding to a different observation period for the outcome. Using observations from the applied example, Table 1 illustrates the comparison of a conventional data format to a person-period format for the reader.
Table 1.
Comparing Conventional Versus Person-Period Data Formats.
| Conventional data format | ||||||||
|---|---|---|---|---|---|---|---|---|
| ID | Censored | X | M | Y 1 | Y 2 | Y 3 | Y 4 | Y 5 |
| 001 | 1 | 0.104 | 78 | 0 | 0 | 0 | 0 | 0 |
| 002 | 1 | −0.007 | 46 | 0 | 0 | 0 | 0 | 0 |
| 003 | 0 | 0.215 | 61 | 0 | 0 | 0 | 1 | 0 |
| Person-period data format | ||||||||
| ID | D 1 | D 2 | D 3 | D 4 | D 5 | X | M | Y |
| 001 | 1 | 0 | 0 | 0 | 0 | 0.104 | 78 | 0 |
| 001 | 0 | 1 | 0 | 0 | 0 | 0.104 | 78 | 0 |
| 001 | 0 | 0 | 1 | 0 | 0 | 0.104 | 78 | 0 |
| 001 | 0 | 0 | 0 | 1 | 0 | 0.104 | 78 | 0 |
| 001 | 0 | 0 | 0 | 0 | 1 | 0.104 | 78 | 0 |
| 002 | 1 | 0 | 0 | 0 | 0 | −0.007 | 46 | 0 |
| 002 | 0 | 1 | 0 | 0 | 0 | −0.007 | 46 | 0 |
| 002 | 0 | 0 | 1 | 0 | 0 | −0.007 | 46 | 0 |
| 002 | 0 | 0 | 0 | 1 | 0 | −0.007 | 46 | 0 |
| 002 | 0 | 0 | 0 | 0 | 1 | −0.007 | 46 | 0 |
| 003 | 1 | 0 | 0 | 0 | 0 | 0.215 | 61 | 0 |
| 003 | 0 | 1 | 0 | 0 | 0 | 0.215 | 61 | 0 |
| 003 | 0 | 0 | 1 | 0 | 0 | 0.215 | 61 | 0 |
| 003 | 0 | 0 | 0 | 1 | 0 | 0.215 | 61 | 1 |
Note. X = the independent variable; Y = the dependent variable; M = the mediator variable.
Estimating the Model
The Mplus program code for the logistic regression-based DTSMed model appears in the appendix of this article, where uppercase characters indicate Mplus commands. Parameter estimates for the model are shown in Table 2. The intercept in the table gives the log odds of initiating smoking in ninth grade, since we modeled Grade 9 as the reference year in the dummy codes representing time. The αgrade5 to αgrade8 coefficients in the table compare the log odds of initiating smoking in year j back to the reference year. Adding the value of any given αj coefficient to the intercept in the table yields the log odds of initiating substance involvement in year j.
Table 2.
Logistic Regression-based Model Parameter Estimates for the Applied Example.
| Outcome Variable | Parameter | Estimate | Standard Error | Wald Test | p Value |
|---|---|---|---|---|---|
| M | Intercept | 58.484 | 0.355 | 164.547 | <.001 |
| a | 2.227 | 0.427 | 5.211 | <.001 | |
| Y | Intercept | −3.028 | 0.484 | −6.258 | <.001 |
| c ’ | −0.121 | 0.153 | 0.791 | .429 | |
| b | 0.011 | 0.007 | 1.518 | .129 | |
| α grade5 | −0.951 | 0.296 | −3.218 | .001 | |
| α grade6 | −0.705 | 0.280 | −2.521 | .012 | |
| α grade7 | −0.430 | 0.265 | −1.623 | .105 | |
| α grade8 | −0.340 | 0.266 | −1.282 | .200 | |
| α grade9 | na | na | na | na |
Note. Y = the dependent variable; M = the mediator variable. Parameter estimates associated with αgrade9 are all “na” as they are captured in the “intercept” coefficient, since Grade 9 is the reference group for time. Related, αj coefficients in the table refer to the difference between the α value for the reference group and the α value for a given time period j.
Regressing fourth-grade EBPs onto parental depressive symptoms in kindergarten using Equation 4 yielded an a path of 2.227(.427), p < .001 (see Table 2). This parameter estimate indicated that there was a significant effect of parental depressive symptoms on EBPs, such that a one-unit increase in parental depressive symptoms in kindergarten was associated with a 2.227 unit increase in subsequent child EBPs in the fourth grade. Regressing the event history outcome onto parental depressive symptoms and EBPs using Equation 5 yielded parameters estimates of c’ = −.121(.153), ns, and b = .011(.007), ns, respectively (see Table 2). The c’ path revealed that there was no significant effect of parental depressive symptoms on the log odds of initiating smoking in any given year, controlling for EBPs; the b parameter revealed that EBPs did not significantly impact the log odds of smoking onset, controlling for parental depressive symptoms. Although neither coefficient was significant, we explain the b coefficient further to demonstrate how readers can interpret model coefficients. The b parameter estimate signified that for every one-unit increase in EBPs, there was a corresponding .011-unit increase in the log odds of initiating smoking, controlling for parental depressive symptoms. Taking the inverse log of the coefficient by exponentiating base e to the power of the b coefficient gave a conditional hOR for EBPs of e(.011) = 1.011. Thus, for every one-unit increase in fourth-grade EBPs, the odds of initiating smoking in Grades 5–9 increased 1.1% when controlling for parental depressive symptoms in kindergarten. Multiplying the a and b parameters gave an estimate of the indirect effect of parental depressive symptoms on smoking onset via EBPs, ab = (2.227)(.011) = .024. Inputting these estimates and their standard errors into the PRODCLIN program indicated that the effect was not significant at α = .05: 95% CI [−.006, .059]. Interpreting this parameter estimate for demonstration purposes, ab showed that the mediated effect of parental depressive symptoms on smoking onset via EBPs yielded a .025-unit increase in the log odds of initiating smoking in Grades 5–9.
Conducting the SEM-Based DTSMed Analysis
Data Structure
Although the data need not conform to a person-period format when estimating the DTSMed as an SEM model, there are data structure requirements of which the reader should be aware. Specifically, the outcome variable, Y, must be coded in a specific manner to conduct the DTSMed analysis in an SEM framework (see Table 3). Like a conventional longitudinal data collection format, there must be different variables for each time point of Y, so that a unique binary event indicator can be created for each interval. If an individual does not experience the target event during the observation period, the binary event indicators are coded 0 across intervals. If an individual experiences the target event in a given interval, the binary event indicator associated with that interval is coded 1. Most importantly, once an individual experiences the target event, all subsequent binary event indicators are coded missing for the subject. Coding the outcome variable in this way not only defines the risk set and characterizes event timing for each individual but also hardwires information about censoring into the data such that there is no need for a separate censoring variable.
Table 3.
Illustrating How to Code Data for the SEM-Based DTSMed Analysis.
| Subject | X | M | Y 1 | Y 2 | Y 3 | Y 4 | Y 5 |
|---|---|---|---|---|---|---|---|
| 001 | 0.104 | 78 | 0 | 0 | 0 | 0 | 0 |
| 002 | −0.007 | 46 | 0 | 0 | 0 | 0 | 0 |
| 003 | 0.215 | 61 | 0 | 0 | 0 | 1 |
Note. X = the independent variable; Y = the dependent variable; M = the mediator variable; SEM = structural equation modeling.
Estimating the Model
The Mplus program code for the SEM-based DTSMed model appears in the appendix of this article, where uppercase characters indicate Mplus commands. Parameter estimates for the model are shown in Figure 3. Note that these estimates are comparable to those from the logistic regression-based approach and converge on the same conclusion of significance or nonsignificance, respectively. Recall that the negative value of a given time-specific threshold parameter, τ;j, in the SEM-based model will be equivalent to the time-specific intercept parameter in the logistic regression-based approach for a corresponding time interval. Recall also that to obtain time-specific intercepts in the logistic regression-based model, one needs to add the value of αj for the reference group to a given αj coefficient of interest.
As with the logistic regression-based approach, an estimate of the mediated effect can be obtained by multiplying the a and b paths from the program output: ab = (2.346)(0.011) = .026. Although bootstrapping is typically an option to obtain asymmetric confidence limits in Mplus, the program invokes a numerical integration estimator that is incompatible with bootstrapping when handling missing data on independent variables. One can easily obtain asymmetric CIs for the mediated effect via the PROD-CLIN program in these instances. Alternatively, one could manually create bootstrapped samples in another statistical software package such as SAS or R to be used as input for model estimation in Mplus. This approach is more computationally intensive, however, and necessarily has multiple stages that require advanced programming. Asymmetric CIs for the mediated effect from the Prodclin program were 95% CI [−0.011, 0.077]. Note that these estimates are comparable to those using results from the logistic regression-based model output.
Although we have shown that it is possible to estimate a simple mediation model with the SEM-based DTSMed approach, part of the utility of the SEM-based model is the ability to incorporate extensions beyond the capabilities of the logistic regression-based model. We consider one such extension for the reader here, incorporating measurement models into one or more predictor variables. To demonstrate estimation of an SEM-based DTSMed model that incorporates a measurement model into estimation, we reran the empirical example and modeled parental depressive symptoms at kindergarten as a latent variable. In this permutation, we considered parental depressive symptoms as an underlying construct that drove responses to the 9 items on the scale, rather than modeling a total summed scored for the scale as done in the original example (see Figure 4 for model diagram and parameter estimates).
Figure 4.
The structural equation modeling (SEM)-based DTSMed model for the applied example with a measurement model for the independent variable. +indicates p < .05 and *indicates p < .001.
How Did DTSMed Inform Our Understanding of Smoking Etiology in the Applied Example?
By analyzing our data with a DTSMed model, we were able to ascertain several pieces of information to enhance our understanding of smoking etiology in the sample under study. The a path of the DTSMed model indicated that parental depressive symptoms in kindergarten significantly impacted EBPs in fourth grade. Thus, we surmise that the failure to find mediation effects was likely not driven by a lack of relation between our predictor and mediator variables. On the other hand, the b path of the DTSMed model illustrated that the fourth-grade EBPs did not significantly impact the hazard odds of smoking onset in Grades 5–9, controlling for parental depressive symptoms. Therefore, the failure to find mediation effects was likely driven by the lack of relationship between the mediator and the outcome variables in this example. Given this information, we could choose to (a) try to improve measurement of the EBPs variable if we feel strongly that the purported relation should be supported or (b) revisit the conceptual theory underlying our research question (defined by the b path in the mediation model) to identify other plausible mechanisms of smoking onset (Chen, 2005; Fairchild & MacKinnon, in press).
Other aspects of the analysis are also informative. Plotting the observed hazard probabilities for each time period illustrates a chronology of risk across intervals in the observation period. Plotting these estimates in the sample shows us that the risk of experiencing smoking onset increases over time during fifth to ninth grades (see Figure 5). This is not unexpected given the age range of the sample under study. Interpreting these parameters identifies the hazard odds of initiating smoking in each time period given the fitted model. For example, taking the negative of the intercept estimate in Table 2, we see that the hazard odds of initiating smoking in ninth grade (i.e., the reference year for time) is e(−3.028) = .0484. Thus, the model predicts that approximately 1 in 20 children will experience smoking onset in ninth grade. We can also evaluate whether there are significant differences between the log odds of smoking onset in the reference year versus other years by inspecting the significance of the αj parameters in Table 2. These estimates show that the hazard odds of initiating smoking in Grade 5 or 6 are significantly less than the hazard odds of initiating smoking in Grade 9. Given that youth were at a higher risk of smoking onset during the middle school years, interventionists could use this information to consider targeting prevention in that period.
Figure 5.
The hazard function for the applied example.
Discussion
This article integrated the statistical mediation and discrete-time survival models to present a framework for evaluating mediators of event timing. The methodology shared here has the potential to inform a variety of research efforts across disciplines, improving our understanding of developmental periods of risk as well as enhancing our evaluation of prevention and intervention programs with time-to-event outcomes. In this examination, we considered the simplest case of DTSMed by demonstrating a single mediator and a single discrete-time outcome satisfying the proportional hazard odds assumption. Although the simplest case offers an appropriate starting point to describe basic model applications and parameter interpretation, there are valuable extensions of DTSMed that can be considered.
By modeling a statistical interaction between time and predictors of interest in the model, researchers can evaluate nonproportional hazard odds models that allow for the possibility that the effects of a predictor are not constant over time. Although there was no evidence to reject the proportional hazard odds assumption in our applied example, such models may be relevant when specific research hypotheses support the proposition that a given risk or protective factor has differential influence across developmental stages. Future research could also extend application of the DTSMed model to multivariate survival models to explore developmental sequences that consider repeated events over time. Such an extension would allow for studying mechanisms of change underlying recurring behaviors or behavioral cycling, lending insight into the etiology of detrimental outcomes like substance abuse relapse, school truancy, criminal recidivism, and work absenteeism or unemployment. In this context, it may also be useful to integrate latent classes into the SEM-based DTSMed model to evaluate how frailties impact the hazard function (Masyn, 2009; Muthén & Masyn, 2005).
Finally, we would be remiss not to address issues of causality in mediation analysis. Causal inference is a critical area of research that has been, and continues to be, studied within the context of mediation. Given random assignment of the independent variable, the a path in the mediation model can be interpreted as a causal estimate, but the b and c’ paths are not causal effects unless the sample is also randomly assigned to the levels of the mediator. Given the infrequency of such double randomization in research, model-implied causal relations are often tentative in mediation. Basic design and statistical strategies may help lend credibility to results in the absence of objective randomization. Some examples include using within subject designs, matching subjects, modeling covariates, or using propensity scores. Recent methodological advances have also made progress in developing alternative estimation methods for mediation that improve causal interpretation of model parameters (Imai, Keele, & Tingley, 2010; Lange & Hansen, 2011; Vanderweele, 2011). To this point, however, these potential outcome approaches have focused on binary predictor and mediator variable. Extending the models to accommodate continuous predictors and mediator variables will be an important new direction for the field (e.g., Schwartz, Li, & Mealli, 2011).
Although there is plenty of future research needed in the development of discrete-time survival mediation models, the DTSMed model presented here is an important first step in helping to understand underlying mechanisms of event occurrence. Such models facilitate evaluating programs that target time-to-event outcomes and may be particularly useful with regard to promoting effective prevention and intervention efforts in this context. Ultimately, advancing our understanding of what factors help determine the onset of different behaviors can improve our ability to affect those behaviors. Further, continuing to develop and refine models to examine mediation relations with a variety of different data types will continue to strengthen research in the health sciences more broadly.
Acknowledgments
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research was supported by the National Institute on Drug Abuse (R01DA030349).
Appendix
Mplus Program Code for Applied Example
| Code for the Logistic Regression-Based DTSM |
| TITLE: (a) |
| Logistic regression-based DTSM Example; |
| DATA: (b) |
| FILE IS example1.txt; |
| VARIABLE: (c) |
| NAMES ARE x m y5 y6 y7 y8 y9 event; |
| USEVARIABLES ARE x m y5 y6 y7 y8 y9 event; |
| CATEGORICAL = event; |
| MISSING ARE ALL (−999); |
| ANALYSIS: (d) |
| TYPE = GENERAL; |
| ESTIMATOR = MLR; |
| LINK = LOGIT; |
| ALGORITHM = INTEGRATION EM; |
| INTEGRATION = MONTECARLO (500); |
| MODEL: (e) |
| [x]; |
| x; |
| m ON x (p1); |
| [m]; |
| m; |
| event ON x (p2) m (p3) y5 y6 y7 y8 y9@0; |
| MODEL CONSTRAINT: (f) |
| NEW (ab); |
| ab = p1 * p3; |
| OUTPUT: (g) |
| SAMPSTAT; |
| CINTERVAL; |
| Programming Notes: |
In the TITLE command make a title for the analysis.
In the DATA command specify the data file. If the file is in the same location as the Mplus input file there is no need to specify a file path.
In the VARIABLE command name the variables as they appear in the dataset, specify the binary indicator indicating whether the event occurred in the observation period of Y as categorical, and identify the missing value code. If there are variables in the dataset that will not be estimated in the model, specify a subset of variables to use for analysis with the usevariables command.
In the ANALYSIS command specify a general model with ML estimation and robust standard errors; use a logit link function and the integration expectation maximization algorithm. Note that integration is necessary to deal with missing data on X. Specify the number of integration points to estimate in parentheses; we chose 500.
In the MODEL command estimate the mean and variance of X so that the program will treat it as endogenous and handle missing data on the variable. Estimate the a path of the mediation model by regressing M on X. Name the parameter in parentheses; we chose“p1.” Estimate the mean and variance of M. Regress the event outcome on X, M and the five time points of Y. Name the b and c’ parameters; we chose “p2” and “p3” respectively, and fix the loading associated with y9 to identify the reference group for time.
In the MODEL CONSTRAINT command define the indirect effect by creating a new variable and naming it in parentheses; we chose “ab.” Calculate the variable by computing the product of the p1 and p3 parameter estimates.
In the OUTPUT command specify sample statistics, confidence limits and any other information you deem useful.
| Code for the SEM-Based DTSM |
| TITLE: (a) |
| SEM-based DTSM Example; |
| DATA: (b) |
| FILE IS example2.txt; |
| VARIABLE: (c) |
| NAMES ARE x m y5 y6 y7 y8 y9; |
| USEVARIABLES ARE x m y5 y6 y7 y8 y9; |
| CATEGORICAL = y5 y6 y7 y8 y9; |
| MISSING ARE ALL (−999); |
| ANALYSIS: (d) |
| TYPE = GENERAL; |
| ESTIMATOR = MLR; |
| LINK = LOGIT; |
| ALGORITHM = INTEGRATION EM; |
| INTEGRATION = MONTECARLO (500); |
| MODEL: (e) |
| [x]; |
| x; |
| m ON x (p1); |
| [m]; |
| m; |
| factor BY y5@1 y6@1 y7@1 y8@1 y9@1; |
| [y5$1 y6$1 y7$1 y8$1 y9$1]; |
| factor@0; |
| factor ON x m (p2-p3); |
| MODEL CONSTRAINT: (f) |
| NEW (ab); |
| ab = p1 * p3; |
| OUTPUT: (g) |
| SAMPSTAT; |
| CINTERVAL; |
Programming Notes:
In the TITLE command make a title for the analysis.
In the DATA command specify the data file.
In the VARIABLE command name the variables as they appear in the dataset, specify the categorical outcomes to create binary event indicators for each time period, and identify the missing value code. Specify a subset of variables to use for analysis if applicable.
In the ANALYSIS command specify a general model with MLR estimation; use a logit link function and the EM integration algorithm. Specify the number of integration points to estimate in parentheses.
In the MODEL command estimate the mean and variance of X so that the program can handle any missing data. Estimate the a path of the mediation model by regressing M on X. Name the parameter. Estimate the mean and variance of M. Specify a proportional odds model for Y by creating a latent factor defined by the binary event indicators and constraining all the factor loadings to be equal. Freely estimate the thresholds for each time point. Fix the variance of the latent factor to zero. Estimate the b and c’ paths of the mediation model by regressing the latent factor on X and M. Name the parameters.
In the MODEL CONSTRAINT command define the indirect effect by naming the variable and calculating it using previously estimated parameters.
In the OUTPUT command request information you deem useful.
Footnotes
Declaration of Conflicting Interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- Abidin RR. Parenting stress index-manual. Rev. ed. Pediatric Psychology Press; Charlottesville, VA: 1990. [Google Scholar]
- Achenbach TM. Integrative Guide to the 1991 CBCL/4-18, YSR, and TRF Profiles. Department of Psychology, University of Vermont; Burlington, VT: 1991. [Google Scholar]
- Allison PD. Discrete-time methods for the analysis of event histories. In: Leinhardt S, editor. Sociological methodology. Jossey-Bass; San Francisco, CA: 1982. pp. 61–98. doi:10.2307/270718. [Google Scholar]
- Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. doi:10.1037/0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Bouchery EE, Harwood HJ, Sacks JJ, Simon CJ, Brewer RD. Economic costs of excessive alcohol consumption in the U.S., 2006. African Journal of Pathology and Microbiology. 2011;41:516–524. doi: 10.1016/j.amepre.2011.06.045. doi:10.1016/j.amepre.2011.06.045. [DOI] [PubMed] [Google Scholar]
- Box GEP, Tidwell PW. Transformation of the independent variables. Technometrics. 1962;4:531–550. [Google Scholar]
- Brook JS, Brook DW, Richter L, Whiteman M. Risk and protective factors of adolescent drug use: Implications for prevention programs. In: Sloboda Z, Bukoski WJ, editors. Handbook of drug abuse prevention: Theory, science, and practice. Kluwer Academic/Plenum; New York, NY: 2003. pp. 265–287. [Google Scholar]
- Centers for Disease Control and Prevention Smoking-attributable mortality, years of potential life lost, and productivity losses—United States, 2000–2004. The Morbidity and Mortality Weekly Report. 2008;57:1226–1228. [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention Health disparities and inequalities report—United States, 2011. The Morbidity and Mortality Weekly Report. 2011;60:101–109. [Google Scholar]
- Chen H. Practical program evaluation: Assessing and improving planning, implementation, and effectiveness. Sage; Thousand Oaks, CA: 2005. [Google Scholar]
- Coffman DL. Estimating causal effects in mediation analysis using propensity scores. Structural Equation Modeling. 2011;18:357–369. doi: 10.1080/10705511.2011.582001. doi:10.1080/10705511.2011.582001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole DA, Maxwell SE. Testing mediational models with longitudinal data: Questions and tips in the use of structural equation modeling. Journal of Abnormal Psychology. 2003;112:558–577. doi: 10.1037/0021-843X.112.4.558. doi:10.1037/0021-843X.112.4.558. [DOI] [PubMed] [Google Scholar]
- Chambers RA, Taylor JR, Potenza MN. Developmental neurocircuitry of motivation in adolescence: A critical period of addiction vulnerability. The American Journal of Psychiatry. 2003;160:1041–1052. doi: 10.1176/appi.ajp.160.6.1041. doi:10.1176/appi.ajp.160.6.1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DR. Regression models and life-tables (with discussion) Journal of the Royal Statistical Society, Series B. 1972;34:187–220. [Google Scholar]
- Dishion TJ, Capaldi DM, Yoerger K. Middle childhood antecedents to progression in male adolescent substance use: An ecological analysis of risk and protection. Journal of Adolescent Research. 1999;14:175–205. doi:10.1177/0743558499142003. [Google Scholar]
- Eaton DK, Kann L, Kinchen SA, Shanklin S, Ross J, Hawkins J, Wechsler H. Youth risk behavior surveillance—United States, 2009. The Morbidity and Mortality Weekly Report. 2010;59:1–148. [PubMed] [Google Scholar]
- Fairchild AJ, MacKinnon DP. Using mediation and moderation analyses to enhance prevention research. In: Sloboda Z, Petras H, editors. Advances in prevention science, Vol 1. Defining prevention science. in press. [Google Scholar]
- Fairchild AJ, McQuillin S. Evaluating mediation and moderation effects in school psychology: A presentation of methods and review of current practice. Journal of School Psychology. 2010;48:53–84. doi: 10.1016/j.jsp.2009.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gil AG, Wagner EF, Tubman JG. Associations between early-adolescent substance use and subsequent young-adult substance use disorders and psychiatric disorders among a multiethnic male sample in south Florida. American Journal of Public Health. 2004;94:1603–1609. doi: 10.2105/ajph.94.9.1603. doi:10.2105/AJPH.94.9.1603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffin KW, Bang H, Botvin GJ. Age of alcohol and marijuana use onset and weekly substance use and related psychosocial problems during young adulthood. Journal of Substance Use. 2010;15:174–183. doi:10.3109/14659890903013109. [Google Scholar]
- Helstrom AW, Bryan AD, Hutchison KE, Riggs PD, Blechman EA. Tobacco and alcohol use as an explanation for the association between externalizing behavior and illicit drug use among delinquent adolescents. Prevention Science. 2004;5:267–277. doi: 10.1023/b:prev.0000045360.23290.8f. doi:10.1023/B:PREV.0000045360.23290.8f. [DOI] [PubMed] [Google Scholar]
- Henderson R, Oman P. Effect of frailty on marginal regression estimates in survival analysis. Journal of the Royal Statistical, Society B. 1999;61:367–379. doi:10.1111/1467-9868.00182. [Google Scholar]
- Hingson R, Heeren T, Winter MR, Wechsler H. Early age of first drunkenness as a factor in college students’ unplanned and unprotected sex attributable to drinking. Pediatrics. 2003;111:34–41. doi: 10.1542/peds.111.1.34. doi:10.1542/peds.111.1.34. [DOI] [PubMed] [Google Scholar]
- Hougaard P, Myglegaard P, Borch-Johnsen K. Heterogeneity models of disease susceptibility, with application to diabetic nephropathy. Biometrics. 1994;50:1178–1188. doi:10.2307/2533456. [PubMed] [Google Scholar]
- Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychological Methods. 2010;15:309–334. doi: 10.1037/a0020761. doi:10.1037/a0020761. [DOI] [PubMed] [Google Scholar]
- Jo B, Stuart EA, MacKinnon D, Vinokur AD. The use of propensity scores in mediation analysis. Multivariate Behavioral Research. 2011 doi: 10.1080/00273171.2011.576624. doi:10.1080/00273171.2011.576624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston LD, O’Malley PM, Bachman JG, Schulenberg JE. Monitoring the Future national results on adolescent drug use: Overview of key findings, 2011. 2012 Retrieved from http://monitoringthefuture.org/pubs/monographs/mtf-overview2011.pdf.
- Judd CM, Kenny DA. Process analysis: Estimating mediation in treatment evaluations. Evaluation Review. 1981;5:602–619. doi:10.1177/0193841X8100500502. [Google Scholar]
- King SM, Iacono WG, McGue M. Childhood externalizing and internalizing psychopathology in the prediction of early substance use. Addiction. 2004;99:1548–1559. doi: 10.1111/j.1360-0443.2004.00893.x. doi:10.1111/j.1360-0443.2004.00893.x. [DOI] [PubMed] [Google Scholar]
- Lange T, Hansen JV. Direct and indirect effects in a survival context. Epidemiology. 2011;22:575–581. doi: 10.1097/EDE.0b013e31821c680c. doi:10.1097/EDE.0b013e31821c680c. [DOI] [PubMed] [Google Scholar]
- MacKinnon DP. Introduction to statistical mediation analysis. Erlbaum; Mahwah, NJ: 2008. [Google Scholar]
- MacKinnon DP, Dwyer JH. Estimating mediated effects in prevention studies. Evaluation Review. 1993;17:144–158. doi:10.1177/0193841X9301700202. [Google Scholar]
- MacKinnon DP, Fairchild AJ. Current directions in mediation analysis. Current Directions in Psychology. 2009;18:16–20. doi: 10.1111/j.1467-8721.2009.01598.x. doi:10.1111/j.1467-8721.2009.01598.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Fairchild AJ, Fritz MS. Mediation analysis. Annual Review of Psychology. 2007;58:593–614. doi: 10.1146/annurev.psych.58.110405.085542. doi:10.1146/annurev.psych.58.110405.085542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Fritz MS, Williams J, Lockwood CM. Distribution of the product confidence limits for the indirect effect: Program PROD-CLIN. Behavior Research Methods. 2007;39:384–389. doi: 10.3758/bf03193007. doi:10.3758/BF03193007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Brown CH, Wang W, Hoffman JM. The intermediate endpoint effect in logistic and probit regression. Clinical Trials. 2007;4:499–513. doi: 10.1177/1740774507083434. doi:10.1177/1740774507083434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychological Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. doi: 10.1037/1082-989X.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masyn K. Discrete-time survival factor mixture analysis for low-frequency recurrent event histories. Research in Human Development. 2009;6:165–194. doi: 10.1080/15427600902911270. doi:10.1080/15427600902911270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxwell SE, Cole DA. Bias in cross-sectional analyses of longitudinal mediation. Psychological Methods. 2007;12:23–44. doi: 10.1037/1082-989X.12.1.23. doi:10.1037/1082-989X.12.1.23. [DOI] [PubMed] [Google Scholar]
- McGinnis JM, Foege WH. Actual causes of death in the United States. Journal of the American Medical Association. 1993;270:2207–2212. doi:10.1001/jama.270.18.2207. [PubMed] [Google Scholar]
- Mokdad AH, Marks JS, Stroup DF, Gerberding JL. Actual causes of death in the United States, 2000. Journal of the American Medical Association. 2004;291:1238–1245. doi: 10.1001/jama.291.10.1238. doi:10.1001/jama.291.10.1238. [DOI] [PubMed] [Google Scholar]
- Muthén B, Masyn K. Discrete-time survival mixture analysis. Journal of Educational and Behavioral Statistics. 2005;30:27–58. doi:10.3102/10769986030001027. [Google Scholar]
- Muthén LK, Muthén BO. Mplus user’s guide. 7th ed. Muthén & Muthén; Los Angeles, CA: 1998-2012. [Google Scholar]
- Peleg-Oren N, Saint-Jean G, Cardenas GA, Tammara H, Pierre C. Drinking alcohol before age 13 and negative outcomes in late adolescence. Alcoholism: Clinical and Experimental Research. 2009;33:1966–1972. doi: 10.1111/j.1530-0277.2009.01035.x. doi:10.1111/j.1530-0277.2009.01035.x. [DOI] [PubMed] [Google Scholar]
- Robins LN, Przybeck TR. Age of onset of drug use as a factor in drug and other disorders. In: Jones CL, Battjes RJ, editors. Etiology of drug abuse: Implications for prevention. U.S. Government Printing Office; Washington, DC: 1985. pp. 178–193. [Google Scholar]
- Schwartz SL, Li F, Mealli F. A Bayesian semiparametric approach to intermediate variables in causal inference. Journal of the American Statistical Association. 2011;106:1131–1344. doi:10.1198/jasa.2011.ap10425. [Google Scholar]
- Singer JD, Willett JB. Modeling the days of our lives: Using survival analysis when designing and analyzing longitudinal studies of duration and timing of events. Psychological Bulletin. 1991;110:268–290. doi:10.1037/0033-2909.110.2.268. [Google Scholar]
- Singer JD, Willett JB. It’s about time: Using discrete-time survival analysis to study duration and the timing of events. Journal of Educational Statistics. 1993;18:155–195. doi:10.2307/1165085. [Google Scholar]
- Slade EP, Stuart EA, Salkever DS, Karakus M, Green KM, Ialongo N. Impacts of age of onset of substance use disorders on risk of adult incarceration among disadvantaged urban youth: A propensity score matching approach. Drug and Alcohol Dependence. 2008;95:1–13. doi: 10.1016/j.drugalcdep.2007.11.019. doi:10.1016/j.drugalcdep.2007.11.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tofighi D, MacKinnon DP. RMediation: An R package for mediation analysis confidence intervals. Behavior Research Methods. 2011;43:692–700. doi: 10.3758/s13428-011-0076-x. doi:10.3758/s13428-011-0076-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanderweele TJ. Causal mediation analysis with survival data. Epidemiology. 2011;22:582–585. doi: 10.1097/EDE.0b013e31821db37e. doi:10.1097/EDE.0b013e31821db37e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willett JB, Singer JD. Investigating onset, cessation, relapse, and recovery: Why you should, and how you can, use discrete-time survival analysis to examine event occurrence. JCCP. 1993;61:952–965. doi: 10.1037//0022-006x.61.6.952. doi:10.1037/0022-006x.61.6.952. [DOI] [PubMed] [Google Scholar]
- Willett JB, Singer JD. Discrete-Time survival analysis. In: Kaplan D, editor. The Sage handbook of quantitative methodology for the social sciences. Sage; Thousand Oaks, CA: 2004. pp. 199–211. doi:10.4135/9781412986311.n11. [Google Scholar]
- Wright S. The method of path coefficients. The Annals of Mathematical Statistics. 1934;5:161–215. doi:10.1214/aoms/1177732676. [Google Scholar]