Synaptic Connectivity between Renshaw Cells and Motoneurons in the Recurrent Inhibitory Circuit of the Spinal Cord

Abstract

Renshaw cells represent a fundamental component of one of the first discovered neuronal circuits, but their function in motor control has not been established. They are the only central neurons that receive collateral projections from motor outputs, yet the efficacy of the excitatory synapses from single and converging motoneurons remains unknown. Here we present the results of dual whole-cell recordings from identified, synaptically connected Renshaw cell-motoneuron pairs in the mouse lumbar spinal cord. The responses from single Renshaw cells demonstrate that motoneuron synapses elicit large excitatory conductances with few or no failures. We show that the strong excitatory input from motoneurons results from a high probability of neurotransmitter release onto multiple postsynaptic contacts. Dual current-clamp recordings confirm that single motoneuron inputs were sufficient to depolarize the Renshaw cell beyond threshold for firing. Reciprocal connectivity was observed in approximately one-third of the paired recordings tested. Ventral root stimulation was used to evoke currents from Renshaw cells or motoneurons to characterize responses of single neurons to the activation of their corresponding presynaptic cell populations. Excitatory or inhibitory synaptic inputs in the recurrent inhibitory loop induced substantial effects on the excitability of respective postsynaptic cells. Quantal analysis estimates showed a large number of converging inputs from presynaptic motoneuron and Renshaw cell populations. The combination of considerable synaptic efficacy and extensive connectivity within the recurrent circuitry indicates a role of Renshaw cells in modulating motor outputs that may be considerably more important than has been previously supposed.

SIGNIFICANCE STATEMENT We have recently shown that Renshaw cells mediate powerful shunt inhibition on motoneuron excitability. Here we complete a quantitative description of the recurrent circuit using recordings of excitatory synapses between identified motoneuron and Renshaw cell pairs. We show that the excitation is highly effective as a result of a high probability of neurotransmitter release onto multiple release sites and that efficient neurotransmission is maintained at physiologically relevant firing rates in motoneurons. Our results also show that both excitatory and inhibitory connections exhibit considerable convergence of inputs. Because evaluation of the determinants of synaptic strength and the extent of connectivity constitute fundamental parameters affecting the operation of the recurrent circuit, our findings are critical for informing any future models of motor control.

Introduction

Renshaw cells are the specialized population of spinal inhibitory interneurons that receive the output from motoneurons (Renshaw, 1946) through excitatory collateral branches (Eccles et al., 1961). Projections from Renshaw cells to motoneurons (Granit et al., 1957) complete the negative feedback loop of the recurrent circuit. The biological features of Renshaw cells have been characterized in detail (Willis, 1971; Alvarez and Fyffe, 2007), yet their function in modulating motor function has been the subject of intense debate (Windhorst, 1996).

One of the first suggested roles of Renshaw cells was to suppress excessive motoneuron discharge (Eccles et al., 1954). A more sophisticated “variable gain regulator” hypothesis (Hultborn et al., 1979) proposes that the recurrent inhibitory circuit in effect provides a servomechanism that modulates gearing of motor outputs to optimize contraction of specific muscle groups over a broad range of forces. The capacity of the recurrent loop to modulate motor function depends not only on the extent of convergence within the circuit of excitatory and inhibitory inputs onto Renshaw cells and motoneurons, respectively, but also on the efficacies of individual synaptic connections in affecting postsynaptic excitability.

Indirect evaluation of motoneuron responses to Renshaw cell inputs has suggested only marginal inhibitory effects (Lindsay and Binder, 1991; Maltenfort et al., 2004). Recent direct measurements from paired recordings, however, have shown that the input from a single Renshaw cell is sufficient alone to interrupt motoneuron firing (Bhumbra et al., 2014). The capability of the recurrent circuitry depends on the efficacies of both the excitatory and the inhibitory components. Simultaneous recordings between connected pairs of presynaptic motoneurons and Renshaw cells have been made previously (Ross et al., 1975, 1976; Van Keulen, 1981), but responses were only recorded using extracellular electrodes that preclude detection and assessment of subthreshold activity. Although extracellular recordings have shown a strong increase in Renshaw cell firing in response to single motoneuron inputs, the reported paired recording (Nishimaru et al., 2005) of an EPSC of only ∼10 pA indicates a change in conductance insufficent to modulate firing.

In this paper, we present dual whole-cell paired recordings and use a recently established method of quantal analysis (Bhumbra and Beato, 2013) to evaluate the probability release, quantal size, and number of release sites at the motoneuron synapse onto Renshaw cells. We report the proportion of paired recordings that exhibit reciprocal connections, and illustrate dual current-clamp recordings performed to confirm whether single motoneuron inputs can evoke Renshaw cell firing. Finally, we present experiments that use ventral root stimulation to evoke responses recorded in Renshaw cells or motoneurons to characterize the contribution of corresponding presynaptic cell pools projecting to single neurons. We combine the results from the experiments that use stimulation of single neuron and of presynaptic cell populations to estimate the number of converging inputs from motoneurons and Renshaw cells onto their respective postsynaptic targets.

Materials and Methods

Spinal cord preparations were obtained from male or female mice at a postnatal age of 8–14 d. A transgenic strain, in which the EGFP is expressed under the control of the promoter of the neuronal glycine transporter GlyT2 (Zeilhofer et al., 2005), was used to label glycinergic interneurons. All procedures were undertaken in conformance with the Animals (Scientific Procedures) Act (United Kingdom) 1986.

After mice were anesthetized with urethane (20–30 mg i.p.), intracardiac perfusion was performed using ice-cold aCSF of identical composition used for recordings (in mm) as follows: 113 NaCl, 3 KCl, 25 NaHCO₃, 1 NaH₂PO₄, 2 CaCl₂, 2 MgCl₂, and 11 d-glucose. Following decapitation, spinal cords were extracted using standard procedures comprising a ventral laminectomy and swift dissection in oxygenated ice-cold aCSF (Beato, 2008).

An HM 650V vibrating microtome (Microm) was used to cut slices of 400 μm thickness from the caudal lumbar segment (L5) in oxygenated ice-cold solution. The slicing solution contained (in mm) the following: 130 K-gluconate, 15 KCl, 0.05 EGTA, 20 HEPES, 25 d-glucose, 3 kynurenic acid, pH 7.4 with NaOH (Dugué et al., 2005). Slices were cut obliquely at a 35° angle to the transverse plane to preserve motoneuronal axons and their collateral terminals projecting to Renshaw cells (Lamotte d'Incamps and Ascher, 2008), and ventral roots were preserved throughout the dissection procedure. After incubation at 37°C in normal extracellular solution for ∼45 min, slices were maintained at room temperature in aCSF bubbled with a 95/5% O₂/CO₂ mixture. During recordings, slices were continuously superfused at 5–8 ml/min. A suction electrode made of a glass capillary was used to evoke antidromic firing in motoneuron pools.

Whole-cell recordings were performed using an Axopatch 200B amplifier (Molecular Devices) for Renshaw cells and an ELC-03X amplifier (NPI Electronics) for motoneurons. Signals were filtered at 5 kHz, sampled at 50 kHz through an Axon 1440A interface device (Molecular Devices), and recorded using Clampex 10 software (Molecular Devices). Electrodes were pulled using a P-1000 Flaming/Brown micropipette puller (Sutter Instruments) from thick-walled borosilicate glass GC150F capillaries (Harvard Apparatus). For voltage-clamp recordings from Renshaw cells, electrodes were pulled to a resistance of ∼2 mΩ and fire polished to final resistance of ∼3 mΩ. The final resistance of electrodes used for current-clamp recordings from motoneurons was ∼4 mΩ.

For paired recordings from Renshaw cells and motoneurons, the pipette solution used for both cell types was the same and consisted of (in mm) the following: 125 K-gluconate, 6 KCl, 10 HEPES, 0.1 EGTA, 2 Mg-ATP, pH 7.3 with KOH, and osmolarity of 290–310 mOsm. The same internal solution with the addition of 3 mm QX-315 Br was used for recording Renshaw cell responses to ventral root stimulation. In a separate set of recordings (see Results) of recurrent inhibitory currents in motoneurons, we used a pipette solution consisting of (in mm) the following: 140 Cs-gluconate, 4 CsCl, 2 CaCl₂, 10 HEPES, 5 EGTA, 2 Mg-ATP, 3 QX-315 Br, pH 7.3 with CsOH, and osmolarity of 290–310 mOsm. In some experiments (see Results), the Cs-gluconate was reduced by 30 or 60 mm and replaced by equimolar concentrations of CsCl to reduce the electromotive force for chloride. Motoneurons were clamped at the reversal potential for excitatory currents, corrected for the calculated junction potential (15.8, 13.6, or 10.9 mV for 8, 38, or 68 mm total CsCl, respectively). In recordings in which the stimulus artifact could affect amplitude measurements, the final component preceding (by at least 500 μs) the onset of the evoked response was fitted with a single or double exponential function and subtracted from the remainder of the trace.

Cells were visualized using an Eclipse E600FN (Nikon) microscope equipped with a double port to allow simultaneous visualization of infrared differential interference contrast images and EGFP fluorescence detected through a laser scanning confocal unit D-Eclipse C1 (Nikon). Interneurons in the ventral horn were identified as putative Renshaw cells by the presence of EGFP and by their location in the most ventral part of lamina VIII. The identity of all the Renshaw cells recordings was confirmed functionally by orthodromic excitation in response to stimulation of the ventral root.

Motoneurons were identified by their position in the lateral motor column and by their large soma diameter (at least 20 μm) (Takahashi, 1992; Thurbon et al., 1998), or an antidromic spike in response to ventral root stimulation. While recording from one or two identified Renshaw cells, putative presynaptic motoneurons were stimulated in the loose cell-attached configuration (Barbour and Isope, 2000) using an ELC-03X amplifier as described previously (Bhumbra et al., 2012). After a connection was established, the motoneuron was repatched using a new electrode and recorded in current clamp. During paired recordings, Renshaw cells were voltage clamped at −60 mV, and the series resistance of 6–12 mΩ was compensated by 60%–80% resulting in a 1–4 kHz corner frequency range with a whole-cell capacitance of ∼30 pF. Recordings were abandoned if the series resistance increased by >20%.

Spikes were evoked in presynaptic cells every 9 s by application of a train of current pulses, with an interval of 33 ms. During paired recordings, the probability of neurotransmitter release was modulated by replacing the calcium in the perfusing aCSF with magnesium within the concentration range 1–4 mm. Quantal parameters were estimated using Bayesian quantal analysis (BQA) (Bhumbra and Beato, 2013). Like multiple probability fluctuation analysis (Silver, 2003), BQA yields estimates for the parameters from responses observed at different probabilities of release. In contrast to multiple probability fluctuation analysis, however, in which quantal parameters are estimated from quadratic fits based only on mean and variance statistics, BQA models the profiles of every amplitude distribution of responses at all observed probabilities of release. The main advantage this confers on the analysis is that reliable estimates of the quantal parameters can be obtained from small datasets (Bhumbra and Beato, 2013).

Results

Synaptic responses of Renshaw cells to inputs from single motoneurons

Simultaneous dual whole-cell recordings were performed on 30 connected pairs of motoneurons and Renshaw cells. A representative example of a paired recording is illustrated in Figure 1A–C. Spike trains were induced in motoneurons by current step applications while recording Renshaw cell responses in voltage clamp holding at −60 mV. Although electronic coupling does occur between motoneurons, the magnitude of depolarization is very small (Walton and Navarrete, 1991) and would not induce suprathreshold activation in neighboring motoneurons. Postsynaptic responses were therefore due to specific activation of the recorded motoneuron. During the course of the experiment, the probability of release was modulated by changes to the extracellular calcium concentration.

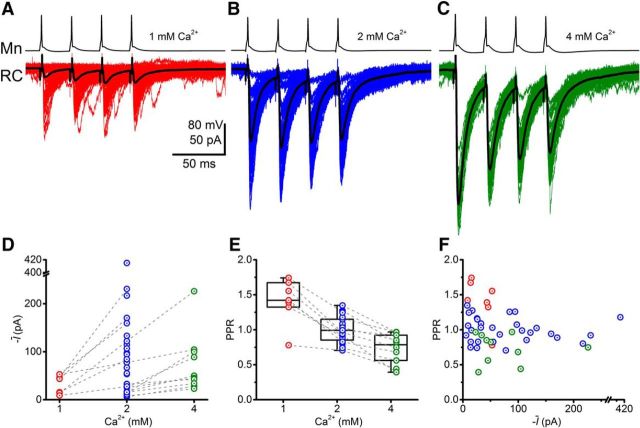
Figure 1.

Stimulation of motoneurons evokes large responses from Renshaw cells. Representative traces are shown for Renshaw cell responses to spike trains elicited from a motoneuron at extracellular calcium concentrations of 1 mm (A), 2 mm (B), and 4 mm (C). D, E, Group data for responses are represented for the mean current (Ī) and paired pulse ratio (PPR). F, Scatter distribution of the PPR against the mean current.

An example of a paired recording is shown in Figure 1. At the lowest calcium concentration (1 mm; Fig. 1A), postsynaptic responses were characteristically small with many failures and discernible potentiation. Evoked currents in control concentrations (2 mm; Fig. 1B) were typically larger with few or no failures and little or no potentiation. At the highest calcium concentration (4 mm), responses were maximal with no failures but clear depression.

Average responses for the group data are shown in Figure 1D for the calcium concentrations of 1 mm (n = 7), 2 mm (n = 30), and 4 mm (n = 10). Not all recordings were tested at every concentration. Pairwise comparisons of mean currents recorded from subgroups of recordings tested at identical concentrations, however, confirmed significant increases in size of responses with increasing calcium concentrations (Student's paired t ≤ −5.03, p ≤ 0.002), in correspondence with the example illustrated in Figure 1A–C.

The extent of short-term plasticity was quantified using the paired-pulse ratio (PPR: the response of the evoked current following the second spike divided by that following the first; Fig. 1E). Average PPRs for increasing calcium concentrations (mean ± SEM: 1.41 ± 0.12, 1.00 ± 0.03, and 0.74 ± 0.07 at 1, 2, and 4 mm calcium, respectively) showed significant reductions (Kruskal–Wallis ANOVA, χ² = 17.6, p < 0.001). PPRs distributed in a region centered at ∼1 indicate competing effects of potentiation and depression at a calcium concentration of 2 mm. The distribution of PPR plotted against the mean current (Fig. 1F) showed no correlation within any of the calcium concentrations (Spearman's |r| ≤ 0.43, p ≥ 0.373).

The results indicate that the synaptic input Renshaw cells receive from single motoneurons is typically large and characterized by few or no failures under control conditions. Although failure rates are not affected by the quantal size, they may be very low as a result of a high probability of neurotransmitter release, a large number of release sites, or a combination of the two. To evaluate the quantal parameters, we performed BQA (Bhumbra and Beato, 2013). We used responses only to the first spike to exclude possible effects of synaptic depression on quantal analysis.

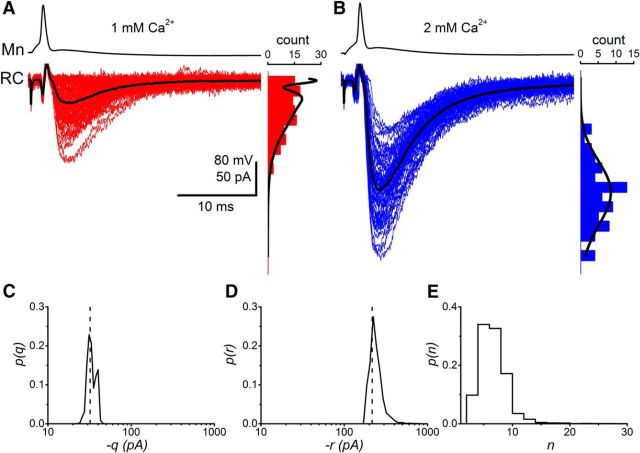
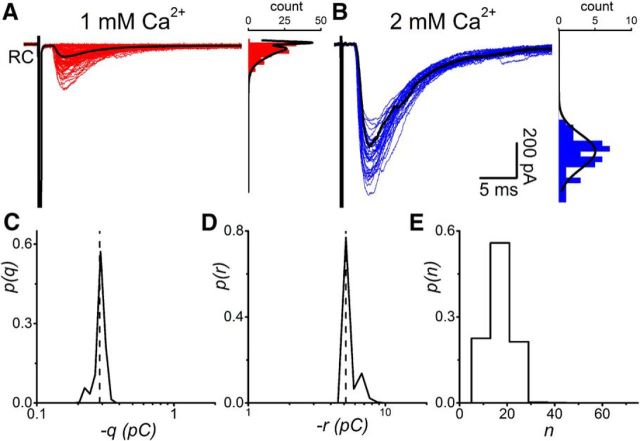
Figure 2 illustrates an example of a paired recording for which we performed BQA on the distributions of evoked currents recorded at calcium concentrations of 1 mm (Fig. 2A) and 2 mm (Fig. 2B). Alongside the traces are histograms of the corresponding amplitude distributions.

Figure 2.

BQA modeling of evoked responses from paired recordings could be used to estimate the quantal parameters from synaptic responses recorded under different conditions of release probability. Renshaw cell responses are shown alongside their respective amplitude distributions observed during applications of extracellular calcium concentrations of 1 mm (A) and 2 mm (B). Black lines indicate the amplitude distribution calculated from the BQA estimates of quantal parameters. The current artifacts recorded from the Renshaw cell electrode result from coupling between the amplifiers during the current step-induced spikes in the motoneuron and therefore precede postsynaptic responses. BQA yields probability distributions for the quantal size (C; q) and maximal response (D; r where r = nq and n is the number of release sites). E, The projected probability distribution for the number (n) of release sites.

BQA was implemented with a binomial model to calculate posterior probability distributions for the quantal parameters. The medians of the distributions were used as best estimates for each of the parameters. Posterior probability distributions are shown for the quantal size (q; Fig. 2C) and maximal response (r; Fig. 2D, where r = nq and n is the number of release sites). The projected probability distribution for the number of release sites n (Fig. 2E) was calculated from the joint probability distribution for the quantal size and maximal response (Bhumbra and Beato, 2013).

The medians represented in each of the posterior distributions were used to evaluate best estimates of the quantal parameters. In the example illustrated in Figure 2, the quantal size (q̂ = 23.1 pA) and maximal response (r̂ = 210.5 pA) yielded an estimate for the number of release sites as n̂ = 9. The amplitude distributions predicted by the BQA results, scaled for the bin width and dataset sizes, are overlaid in Figure 2A, B for illustrational purposes because the BQA procedure is based on raw rather than binned data.

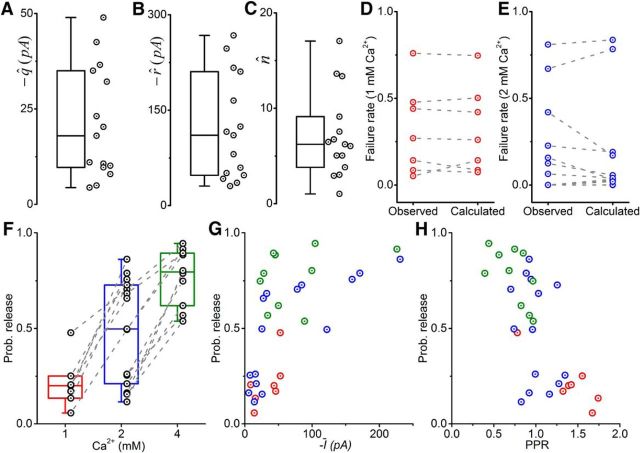
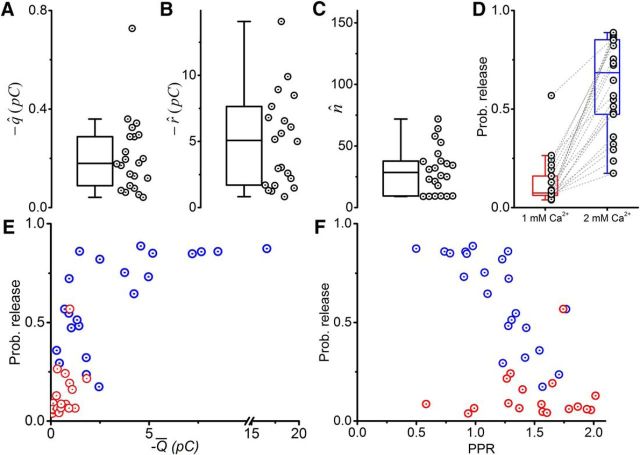
Figure 3 illustrates the group results of quantal analysis. Of the 30 paired recordings, 15 provided sufficient data for successful estimation of the quantal parameters using BQA. Averages (mean ± SEM) of the estimates were 21 ± 4 pA for the quantal size (q; Fig. 3A), 121 ± 21 pA for the maximal response (r; Fig. 3B), and 7.1 ± 1.2 sites for the number of releases sites (n; Fig. 3C).

Figure 3.

BQA demonstrates that the large magnitude of responses from Renshaw cells to inputs from single motoneurons is a result of a high probability of release from multiple release sites. Box-and-whiskers are shown for the quantal size (A; q̂), maximal response (B; r̂), and number of release sites (C; n̂). For recordings in which failures were observed, there were no significant differences in the observed failure rates and those calculated from the BQA estimates at 1 mm (D) and 2 mm (E) calcium concentrations. F, Probabilities of release at 1 mm (red), 2 mm (blue), and 4 mm (green). The probabilities of release are plotted as scatters against the mean current (G; Ī) and PPR (H).

BQA requires no classification of responses into successes and failures. We could therefore independently confirm correspondence of the observed failure rates with those estimated from the quantal parameters at calcium concentrations of 1 mm (Fig. 3D) and 2 mm (Fig. 3E) for the subset of recordings in which failures were observed. Pairwise statistical comparisons confirmed no significant differences between observed and estimated rates (Student's paired |t| ≤ 1.13, p ≥ 0.171), indicating that BQA estimates were consistent with independent observations.

Although increases in calcium concentrations (1, 2, 4 mm) were associated with increased probabilities of release (Fig. 3F), the dispersion of the estimates was greatest under control conditions (2 mm). Plotting the probabilities against the average currents (Fig. 3G) showed a positive correlation at control concentrations (Spearman's r = 0.857, p < 0.001) but no such correlation at 1 mm (r = 0.571, p = 0.207) and 4 mm (r = 0.455, p = 0.208). Pooling the data across all the three calcium concentrations (Fig. 3H), there was a negative correlation between the PPR and probability of release (r = −0.677, p < 0.001) that did not reach statistical significance for individual subsets of data within each concentration (r ≥ −0.232, p ≥ 0.060). The results indicate that the synaptic inputs Renshaw cells receive from single motoneurons are characterized by a large number of release sites and a probability of release in the region of 0.5 and are thus consistent with the minimal failure rates observed at control calcium concentrations.

Reciprocal connectivity between Renshaw cells and motoneurons

The recurrent circuit comprises a negative feedback loop, in which each pool of motoneurons excite a group of Renshaw cells that in turn inhibit the same motoneuron population. Although this pattern of connectivity is well established, the proportion of reciprocal connections between individual cell pairs is unknown. In 19 paired recordings, we tested for the occurrence of a reciprocal connection by evoking spikes in the Renshaw cell and detecting for evoked responses in the motoneuron.

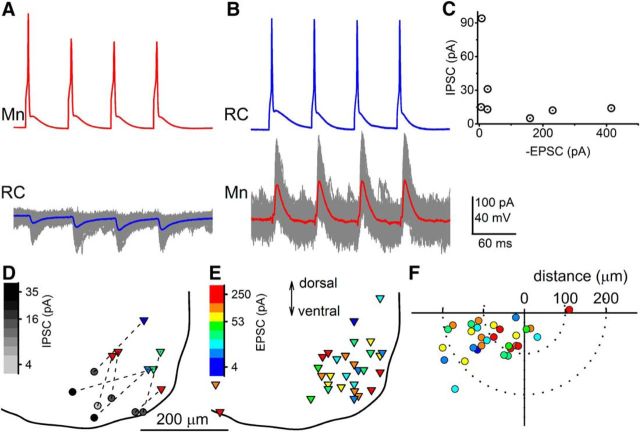
Figure 4 illustrates an example of a reciprocal connection. Spikes elicited in the motoneuron (Fig. 4A) evoked EPSCs in the Renshaw cell. Conversely, voltage clamping the motoneuron at 15 mV, IPSCs were observed in response to spikes induced in the Renshaw cell (Fig. 4B). Although electronic coupling between Renshaw cells could evoke spikelets in neighboring interneurons, their small size and duration (Lamotte d'Incamps et al., 2012) would preclude suprathreshold activation, confirming that each reciprocal connection was direct. Of the 19 paired recordings tested for reciprocity, 7 exhibited a reciprocal connection. A plot of the size of IPSCs against corresponding EPSCs (Fig. 4C) showed no statistically significant correlation (r = −0.537, p = 0.245).

Figure 4.

Reciprocal connections were observed in ∼37% of paired recordings. An example of a motoneuron-Renshaw cell pair is shown with excitatory responses from the Renshaw cell (A) and inhibitory responses from the motoneuron (B). C, Plot of the average size of the IPSC against the EPSC. D, Locations of reciprocally connected motoneurons (triangles) and Renshaw cells (circles), using pseudo-color scales to represent the size of the IPSC (grayscale) and EPSC (color scale). E, Locations of presynaptic motoneurons from all paired recordings. F, Polar plot shows the angle and distance of each Renshaw cell relative to the location of the corresponding presynaptic motoneuron.

Positions of the reciprocal Renshaw cell-motoneuron pairs are shown in Figure 4D. The size of the synaptic responses is represented on pseudo-color scales, with a grayscale for the inhibitory connection and a color scale for the excitatory responses. For all paired recordings, including those tested for reciprocity, the magnitude of EPSCs is represented on a color scale showing the location of motoneurons (Fig. 4E).

The positions of most motoneurons (Fig. 4E) were inside the regional pool innervating the gluteal and hamstring muscles, with the exception of two medial motoneurons and two located within the nuclei innervating the distal lower limb (Bácskai et al., 2014). All Renshaw cells were located within 100 μm of the gray-white matter interface near the center of the ventral part of lamina VIII (data not shown). Figure 4F illustrates the distribution of distances between the cell bodies of the connected pairs plotted against their relative angle. There was no significant correlation between the strength of the connection and the relative distance between cells (r = −0.322, p = 0.082).

Firing in Renshaw cells in response to inputs from single motoneurons

We have previously shown that the inhibitory input of a single Renshaw cell alone onto a motoneuron is sufficient to alter firing of the motoneuron (Bhumbra et al., 2014). The experiments described above provide the first measure of the change in conductance produced by the activation of a single motoneuron input onto a Renshaw cell. To determine whether such changes could affect the membrane potential and elicit firing, we performed paired recordings to compare the size of the unitary current and the probability of Renshaw cell firing following activation of a single motoneuron input.

Figure 5B illustrates voltage-clamped excitatory currents from one paired recording in which postsynaptic responses to 33 Hz spike trains were small (Fig. 5A) and another in which they were large (Fig. 5B). In dual current-clamp, corresponding responses (Fig. 5C), the first pair never reached threshold for an action potential following the first spike and occasionally after the second, as a result of temporal summation. By contrast, spikes were routinely evoked in the postsynaptic cell of the second pair following only the first and third stimulus (Fig. 5D), with failures following the second and fourth, as a result of the spike afterhyperpolarization.

Figure 5.

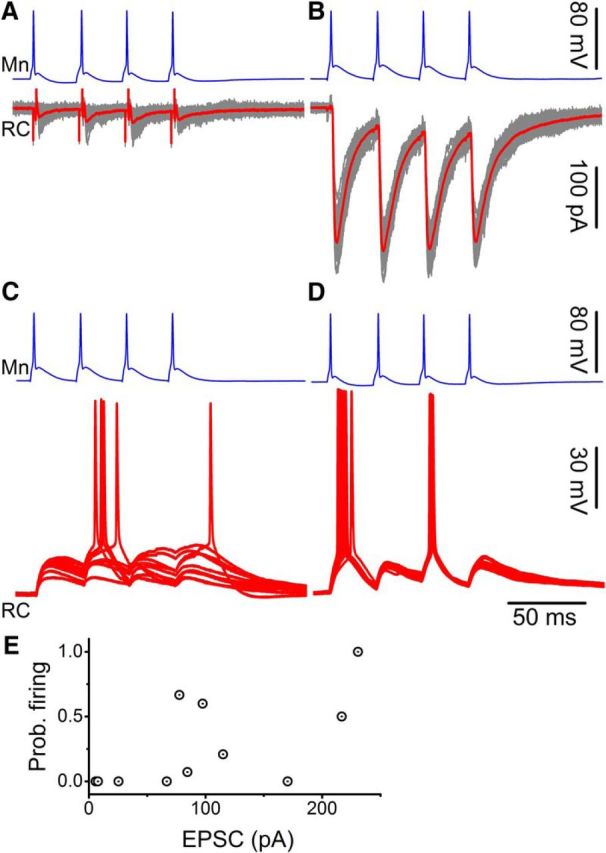
Dual current-clamp recordings demonstrated that single motoneuron inputs could drive firing in Renshaw cells. Voltage-clamp responses to spike trains are shown for two paired recordings in which the size of evoked currents was small (A) and another in which it was large (B). Respective dual current-clamp recordings showed spiking on the second pulse (and once on the fourth) for the first pair (C) and always on the first and third in the second pair (D). E, Group data showed a correlation in the scatter distribution of the probability of firing on the first spike against its corresponding EPSC.

Dual current-clamp recordings were performed on 10 motoneuron-Renshaw cell pairs. Figure 5E illustrates that the probability of generating a spike at the first response is positively correlated with the size of the corresponding postsynaptic current recorded previously in voltage clamp (r = 0.639, p = 0.038).

Responses of Renshaw cells to ventral root stimulation

Our paired recordings showed considerable variability in the size of unitary responses, which would affect the likelihood that a single input from motoneuron can depolarize the Renshaw cell above threshold for firing. Within the intact circuit, however, every Renshaw cell receives inputs from several motoneurons, belonging to the same or synergist motor nuclei (Ryall, 1981). To evaluate the efficacy of inputs from motoneuron populations, we devised experiments that could yield estimates of the degree of convergence of motoneurons onto individual Renshaw cells. Because within the oblique slice preparation most of the motoneuron axons are preserved, we used supramaximal ventral root stimulation to induce antidromic firing in motoneurons and determine the size of the compound EPSCs in Renshaw cells.

Figure 6 illustrates Renshaw cell responses to ventral root stimulation. At low calcium concentrations (Fig. 6A; 1 mm), evoked currents were small with many failures in contrast to those recorded at control concentrations (Fig. 6B; 2 mm). Some recordings exhibited multiple peaks in EPSCs due to heterogeneity in latencies in evoked responses. To ensure consistent characterization of postsynaptic currents across different cells, we measured the area over the entire duration of the synaptic event and expressed it in units of charge (pC).

Figure 6.

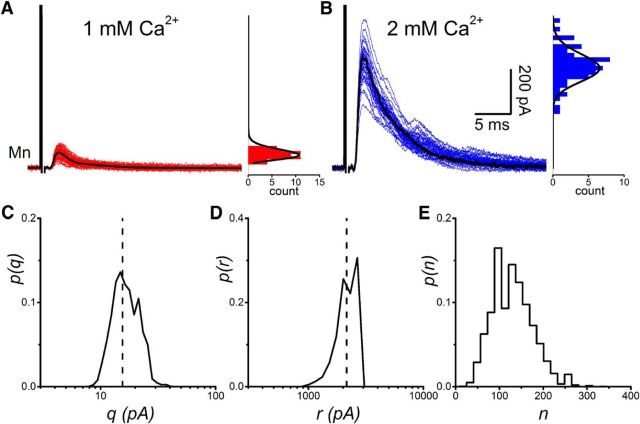
Quantal analysis of Renshaw cell responses to ventral root stimulation yielded estimates for the number of release sites from motoneuron populations. An example of Renshaw cell responses (final component of the stimulus artifact subtracted) is shown alongside their respective amplitude distributions observed during applications of extracellular calcium concentrations of 1 mm (A) and 2 mm (B). The results of BQA are represented as probability distributions for the quantal size (C; q), maximal response (D; r), and number of release sites (E; n).

For responses that were contaminated by spontaneous events, the area was evaluated in proportion to the amplitude using a scaling coefficient estimated from responses that were not. Posterior distributions for the quantal size (Fig. 6C) and the maximal response (Fig. 6D) yielded respective estimates of q̂ = 0.29 pC and r̂ = 5.15 pC. The corresponding estimate for the number of releases sites was n̂ = 18 sites (Fig. 6E).

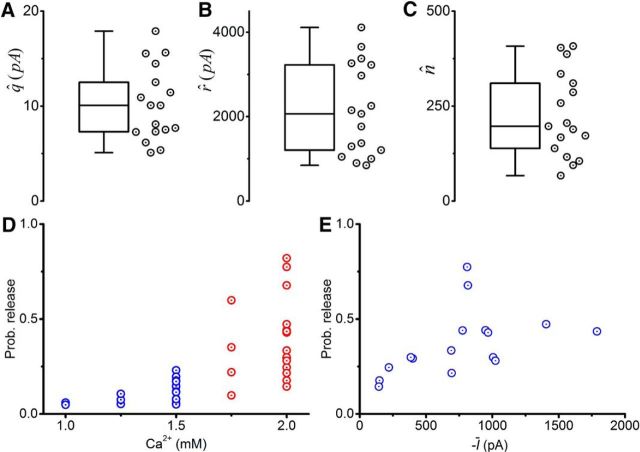
Figure 7 illustrates the group results of quantal analysis. BQA was performed on the evoked responses obtained from 22 Renshaw cell recordings. Average estimates (mean ± SEM) for the quantal parameters were 0.20 ± 0.03 pC for the quantal size (q; Fig. 7A), 5.56 ± 0.97 pC for the maximal response (r; Fig. 7B), and 30.3 ± 3.0 sites for the number of releases sites (n; Fig. 7C).

Figure 7.

BQA revealed a substantial number of release sites from ventral root inputs to Renshaw cells. Box-and-whiskers are shown for the group data for the BQA estimates of the quantal size (A; q̂), maximal response (B; r̂), number of release sites (C; n̂), and probabilities of release (D) at 1 mm (red) and 2 mm (blue) extracellular calcium concentrations. Estimates of the probabilities of release are plotted against the estimated quantal size (E; q̂) and PPR (F).

Estimates of the probabilities of release at control calcium concentrations (2 mm) were broadly distributed (Fig. 7D), with a wide range similar to that observed from the paired recordings. The average probability of release was 0.622 ± 0.050 in control conditions and decreased to 0.125 ± 0.025 in 1 mm calcium. For both concentrations, the probability of release was positively correlated with the average response (Fig. 7E; r ≥ 0.565, p ≤ 0.007) and negatively correlated with the PPR at an interstimulus interval of 30 ms (Fig. 7F; r ≤ −0.592, p < 0.001).

The extent of paired pulse modulation varied across different cells for both paired recordings (Fig. 3H) and responses to ventral root stimulation (Fig. 7F), ranging from net depression to facilitation. Because motoneurons can fire prolonged bursts of action potentials at different frequencies depending on the motor tasks, we examined the extent of short-term plasticity of EPSCs evoked in Renshaw cells in response to prolonged trains of stimulus pulses at different frequencies at control calcium concentrations (2 mm). Figure 8A–I shows Renshaw cell responses to the first, second, and 20th stimulus. Although at 3 Hz, there is a modest degree of depression, the reduction in the size of the evoked current exceeded 50% at 100 Hz. For each of the tested frequency, the extent of depression is represented as function of the pulse number in Figure 8D, F, H, J.

Figure 8.

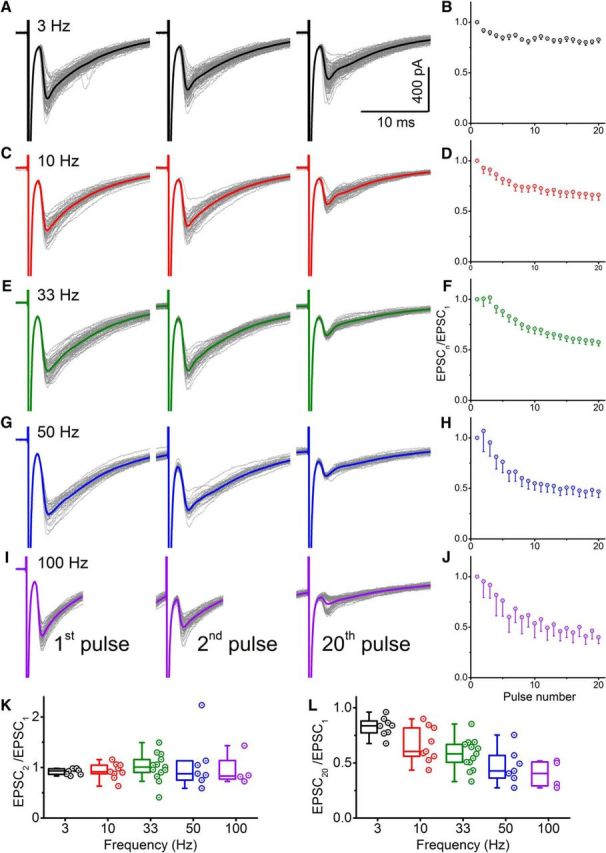
Whole-cell voltage-clamp recordings from Renshaw cells during ventral root stimulation trains showed progressive depression with increasing stimulation frequency. First, second, and 20th response within a train are shown for an example of a Renshaw cell recording while performing ventral root stimulation at 3 Hz (A), 10 Hz (C), 33 Hz (E), 50 Hz (G), and 100 Hz (I). B, D, F, H, J, Corresponding group data for evoked currents, relative to the first response. Group data across the different frequencies are also shown for the second (K) and 20th (L) response.

Group data from a total of 13 Renshaw cell recordings are represented by the quotient of the size of response to the second (Fig. 8F) or 20th (Fig. 8G) relative to the that of the first. Although there was no significant effect of stimulus frequency on the second response (Spearman's r = −0.014, p = 0.931), subsequent responses during the course of the trains consistently showed depression at all frequencies reaching a steady-state level. The extent of steady-state depression, measured at the 20th pulse, increased in correspondence with stimulus frequency (Spearman's r = −0.714, p < 0.001).

The results illustrated in Figure 8 show that, despite the frequency-dependent depression of the postsynaptic currents, even at the highest frequency tested, there was still a sustained response to ventral root stimulation. Whole-cell voltage-clamp measurements of evoked currents, however, provide no indication of whether synchronized motoneuron firing can drive spike generation in Renshaw cells. We therefore performed a separate series of experiments, in which supramaximal ventral root stimulation was performed in a similar manner, but Renshaw cells were recorded extracellularly in the loose cell-attached configuration. Although such recordings preclude measurement of subthreshold activity, the probability of evoking spikes with ventral root stimulation would not be affected by experimentally induced changes to the resting membrane potential or by dialysis of internal solutions.

Figure 9A, C, E, G shows firing in a Renshaw cell in response to ventral root stimulation with stimulus trains of 20 pulses applied at increasing frequency. The traces show that spikes are always evoked following both the first and second pulses, whereas spike failures following the 20th pulse are more likely as the stimulation frequency increases. Alongside traces are graphs showing the probability of firing for the group data from 12 cells at corresponding frequencies (Fig. 9B,D,F,H).

Figure 9.

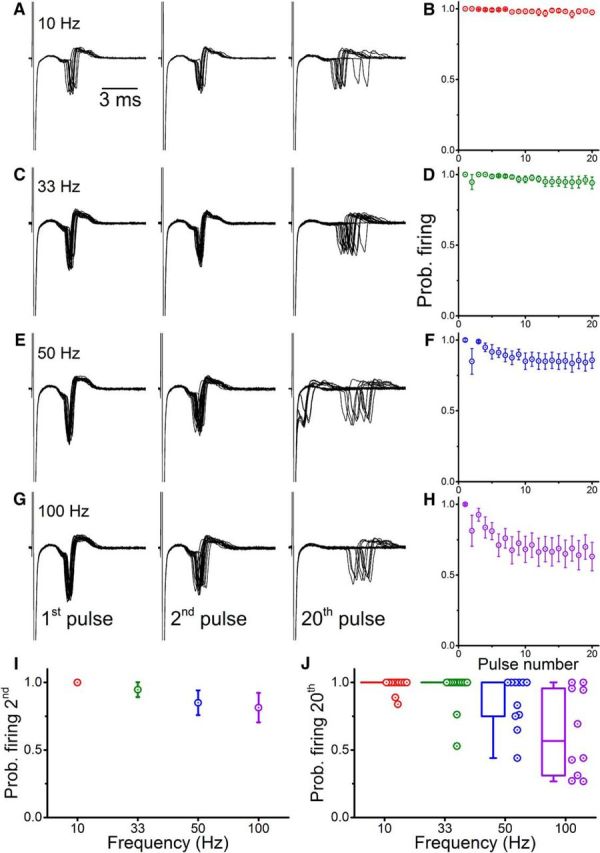
While eliciting pulse trains using ventral root stimulation, loose cell-attached recordings from Renshaw cells showed reliable spiking but with progressive depression as the stimulation frequency increased. The first, second, and 20th responses within a train are illustrated for a Renshaw cell during ventral root stimulation at 10 Hz (A), 33 Hz (C), 50 Hz (E), and 100 Hz (G). B, D, F, H, Respective group data for corresponding frequencies. Group data divided by the different frequencies are illustrated for the second (I, mean ± SEM) and 20th (J, box-and-whiskers) response .

There was a significant reduction in firing probability (calculated over 50 sweeps) during the course of the train with increasing stimulus frequency (Fig. 9I; Spearman's r = −0.528, p < 0.001). The probability of firing following the second pulse (Fig. 9J) was more variable across cells: while all 12 tested cells fired on the second stimulus at 10 Hz, 11 of 12 did so at 33 Hz, and 6 of 11 and 7 of 10 at 50 Hz and 100 Hz, respectively. There was a weak correlation between the interpulse interval and the probability of firing after the second stimulus (Spearman's r = −0.361, p = 0.016).

Inhibitory responses of motoneurons to ventral root stimulation

We have previously reported the quantal properties of the inhibitory synapses from Renshaw cells onto motoneurons (Bhumbra et al., 2014). Our measures were specific to the input from a single premotor interneuron rather than the converging inputs from Renshaw cell populations. For the present study, we used ventral root stimulation, in a similar manner as described above, to estimate the convergence of Renshaw cell inputs onto motoneurons by performing quantal analysis on the recurrent IPSCs.

Whereas the Renshaw cell response to ventral root stimulation is monosynaptic, the recurrent IPSC is evoked through a disynaptic pathway. Manipulation of external calcium concentrations would thus not only change the probability of release at the inhibitory synapses onto motoneurons but also at the excitatory synapses onto Renshaw cells. Because this could affect the probability of firing in Renshaw cells in response to ventral root stimulation, changes in calcium concentration could in effect change the number of release sites available at the inhibitory synapse as a function of release probability.

As shown in Figure 9, ventral root stimulation always evoked a spike in all the recorded Renshaw cells in control conditions. Successful estimation of the quantal parameters for the inhibitory synapses onto motoneurons can only be performed by reducing the calcium concentration because concentrations exceeding 2 mm cause multivesicular release (Bhumbra et al., 2014). We therefore confirmed whether a reduction in calcium to 1 mm changed the probability of Renshaw cell firing following single ventral root stimulation. In a set of 9 loose cell-attached recordings from Renshaw cells, ventral root stimulation elicited a spike in 100% of cases in both 1 and 2 mm calcium. We could therefore assume that the whole Renshaw cell population fires a spike after ventral root stimulation and that the size of the recurrent IPSC would not be affected by a variable number of release sites due to a variable number of Renshaw cells recruited.

In an initial set of experiments, we recorded IPSCs at a 15 mV holding potential using an internal solution with physiological chloride (see Materials and Methods) to match the reversal potential for recurrent excitatory currents (often visible in motoneurons) (Gogan et al., 1977) and maintain a substantial electromotive force for chloride. This produced very large inhibitory currents (>4 nA) that might have also resulted from activation of unclamped voltage-activated conductances in the extensive dendritic tree of the motoneuron. To reduce the size of currents, we used a nonsaturating dose of either strychnine (3–10 nm) or gabazine (30 μm). Furthermore, we increased the intracellular chloride (30–60 mm) to reduce the electromotive force. Data were pooled together, but our estimates of quantal size and maximal responses reflect an increased dispersion due to the differences in recording conditions and are not directly comparable with measures reported previously (Bhumbra et al., 2014).

Figure 10 illustrates responses of a motoneuron to ventral root stimulation. At low calcium concentrations (Fig. 10A; 1 mm), responses were small compared with those recorded at control concentrations (Fig. 10B; 2 mm), but in both cases no failures were observed, as shown by the amplitude histogram at the right of each trace. The calculated distributions for the quantal size (Fig. 10C) and the maximal response (Fig. 10C) yielded respective estimates of q̂ = 15.5 pA and r̂ = 2150 pA, with an estimate for the number of releases sites of n̂ = 139 sites (posterior illustrated in Fig. 10E).

Figure 10.

Ventral root stimulation was used to evoke recurrent IPSCs recorded in motoneurons to perform quantal analysis to estimate for the number of release sites from the population of Renshaw cells. Responses from a motoneuron (final component of the stimulus artifact subtracted) are shown alongside their respective amplitude distributions observed during applications of extracellular calcium concentrations of 1 mm (A) and 2 mm (B). BQA results are illustrated using probability distributions for the quantal size (C; q) and maximal response (D; r), and number of release sites (E; n).

Group data from the 17 motoneuron recordings are illustrated in Figure 11. Average estimates (mean ± SEM) for the quantal parameters were 10.1 ± 0.9 pA for the quantal size (q; Fig. 11A), 2146.9 ± 263.6 pA for the maximal response (r; Fig. 11B), and 225 ± 27 sites for the number of releases sites (n; Fig. 11C). Estimates for the probability of release for the different calcium concentrations are represented in Figure 11D, with an average of 0.40 ± 0.05 in control conditions (2 mm) and a significant positive correlation when plotted against the mean current (Fig. 11E; r = 0.663, p = 0.003).

Figure 11.

BQA showed a large number of release sites from Renshaw cell populations projecting to individual motoneurons. Box-and-whiskers are shown for the group data for the BQA estimates of the quantal size (A; q̂), maximal response (B; r̂), and number of release sites (C; n̂). Estimated probabilities of release (D) at control 2 mm (blue) and reduced (red) concentrations of extracellular calcium, and plotted against the mean current (E; Ī) under control conditions.

Discussion

The results of the present study show that the strong excitatory input Renshaw cells receive from motoneurons is characterized by high probabilities of neurotransmitter release at multiple release sites that enable single motoneurons to drive Renshaw cell firing. We have shown that a substantial proportion of connected pairs exhibit reciprocal connections. Finally, we have characterized responses of Renshaw cells and motoneurons to activation of converging inputs from corresponding presynaptic cell populations.

Numbers of synaptic contacts

Intracellular staining studies in the cat have revealed heterogeneity in spatial distributions of central motor axon terminals (Lagerbäck et al., 1978), with motoneurons making multiple contacts onto target neurons presumed as Renshaw cells (Lagerbäck et al., 1981). Immunohistochemical detection of the vesicular acetylcholine transporter (Alvarez et al., 1999) indicates an average of ∼70 cholinergic terminals contacting a Renshaw cell at its soma and dendrites within ∼400 μm range. Surface area-based extrapolation yields an estimated maximum of ∼450 for the total number of cholinergic contacts onto each Renshaw cell. Assuming an average of 6 contacts from single motoneurons (Alvarez et al., 1999), the extrapolation suggests a maximum of ∼75 motoneurons projecting onto one Renshaw cell.

The results of the present study indicate that the number of contacts from a motoneuron (7.1 ± 1.2) is indeed ∼6. An average estimate of ∼30 release sites from the ventral root stimulation experiments, however, is less than the extrapolated count reported previously (Alvarez et al., 1999). There are three likely reasons for the disparity. First, the extrapolation based on observations from proximal dendrites assumed a constant density of contacts throughout both proximal and distal regions and could thus only yield an upper bound. Second, although expression of the transporter identifies cholinergic terminals, its presence does not necessarily correspond to a release site directly apposed to a cluster of postsynaptic receptors that would constitute a functional synaptic contact. Finally, in our preparation, a proportion of axon collaterals might have been severed during slicing, thus reducing the number of contacts. Our estimates of both the number of contacts from all motoneurons and of the convergence of ∼4 motoneurons contacting individual Renshaw cells can therefore only represent lower bounds.

Previous paired recordings (Bhumbra et al., 2014) of the Renshaw cell to motoneuron synapse report an average of 5.5 ± 0.5 for the number of contacts. The results from the ventral root stimulation experiments of the present study yields an average of ∼225 release sites, suggesting a convergence quotient of ∼40 Renshaw cells per motoneuron. These estimates again represent lower bounds because of the slice preparation. Within the limits highlighted above, our data suggest that the degree of convergence for the inhibitory projection may be as much as 10 times greater than that of the excitatory projection.

Probabilities of release

To our knowledge, there are no reports of release probabilities from any motoneuronal targets in the mouse before this study. At the neuromuscular junction, the probability of release is in the region of 0.06–0.16 in the rat (Christensen and Martin, 1970) at low calcium concentrations (1.5 mm). In the frog, release probabilities are heterogeneously distributed (Robitaille and Tremblay, 1987) with reported values in the range of 0.32–0.65 at higher calcium concentrations (1.8 mm) (Miyamoto, 1975).

Ventral root stimulation experiments of the present study yield an average probability of neurotransmitter release onto Renshaw cells of 0.62 ± 0.05 at control calcium concentrations (2 mm). While similar results were seen from the paired recordings (0.49 ± 0.07), the range of estimates was large (0.11 ≤ p ≤ 0.85), indicating substantial heterogeneity in release probabilities from axon terminals across different motoneurons. The distribution of our estimates of release probabilities onto Renshaw cells is therefore not dissimilar from those reported for the frog neuromuscular junction.

Comparison of the motoneuron synapse onto Renshaw cells with the neuromuscular junction, however, may be limited by differences in their central and peripheral specializations. For example, although motoneurons corelease acetylcholine and glutamate (Mentis et al., 2005; Nishimaru et al., 2005) or potentially aspartate (Richards et al., 2014) at central synapses, corelease at the neuromuscular junction ceases during normal maturation (Borodinsky and Spitzer, 2007). Motor axon terminals also target motoneurons themselves through recurrent excitatory pathways (Ichinose and Miyata, 1998), but the quantal parameters for synapses between motoneurons remain unknown.

Renshaw cell firing

Extracellular recordings in cat preparations have provided initial evidence of strong excitatory motoneuronal synapses onto Renshaw cells. Continuous firing in a motoneuron can increase spiking in Renshaw cells (Ross et al., 1975) and drive discharge rates up to ≥60 Hz (Ross et al., 1976). While these observations are consistent with the reliable generation of spikes in Renshaw cells seen in our dual current-clamp recordings, we also observed alternation between successes and failures in responses to presynaptic spike trains illustrating competing effects of temporal summation and spike afterhyperpolarization.

Ventral root stimulation in decerebrated cats and rabbit preparations (Renshaw, 1946) can elicit bursts of discharges from putative Renshaw cells, and stimulation of a single motoneuron alone can be sufficient to evoke multiple spikes (Van Keulen, 1981). The bursts may result from a “priming” depolarization, mediated by AMPA and nicotinic receptors, relieving magnesium blockade and prolonging activation of NMDA receptors (Lamotte d'Incamps and Ascher, 2008).

Peripheral nerve volley experiments suggest considerable convergence onto Renshaw cells from motoneurons innervating functionally synergistic muscles (Ryall, 1981). Spectral analysis of responses to rate-modulated stimulation of peripheral nerves indicates that Renshaw cell activity is sensitive over frequency ranges characteristic of motoneuronal spiking (Christakos et al., 1987). Our recordings confirm that Renshaw cells reliably spike in response to activation of motoneuronal pools and that fidelity of transmission is maintained at frequencies up to 50 Hz. It is remarkable that, despite depression of postsynaptic responses during high-frequency trains, Renshaw cell firing is sustained during ventral root stimulation at rates as high as 100 Hz.

Our results suggest that the effects of convergence of axon collaterals, high probabilities of release at multiple release sites, and resilience to synaptic depression contribute to establish reliable spiking of Renshaw cells in response to motoneuron inputs. The term “relay” has been used describe such fidelity of responses in other CNS regions, such as the thalamus where excitatory retinal inputs drive firing of lateral geniculate nucleus outputs to the visual cortex (Sherman and Guillery, 1998). Such a relay within the recurrent inhibitory circuit would confer considerable sensitivity to motor information transmitted through axon collaterals.

Reciprocal and mutual connectivity

Experiments on cats testing for reciprocity (Van Keulen, 1981) report mutual synaptic interactions in 2 of 5 simultaneous recordings from Renshaw cells extracellularly and motoneurons intracellularly. The proportion is likely to be an underestimate because detected inhibitory responses were very small (average 12 μV) most likely as a consequence of a negligible electromotive force for chloride under the sharp electrode recording conditions. It is thus probable that inhibitory connections could remain undetected. The reciprocal proportion of approximately one-third, observed in the present study, could also be an underestimate but in this case due to severing of some connections during slice preparation because recorded cells were located within the 150 μm from the surface. It is thus possible that reciprocal connectivity represents the rule rather than the exception.

Although the slice preparation provides tractable access for studying unitary responses within the recurrent circuitry, one disadvantage is the loss of descending fibers. In addition to upper motoneurons, these may include neuromodulatory inputs that may affect the probability of release and quantal size. Even discounting external inputs, however, the quantal parameters and connectivity measures between motoneurons and Renshaw cells do not provide a complete picture of the functional circuitry within the isolated recurrent inhibitory loop. Motoneurons are coupled electrotonically (Gogan et al., 1977) and additionally interconnected by cholinergic synapses (Ichinose and Miyata, 1998). Renshaw cells are coupled electrically through gap junctions (Lamotte d'Incamps et al., 2012) and chemically through glycinergic synapses (González-Forero and Alvarez, 2005). Until the mutual interconnectivity and corresponding synaptic efficacies within each cell type have been established, the picture of the functional circuitry of the recurrent inhibitory loop remains incomplete.

Function of recurrent inhibition

Since the discovery of Renshaw cells, their function has been intensely debated (Windhorst et al., 1978). Beyond merely suppressing excessive motoneuron discharge, the recurrent circuitry may serve as a variable gain regulator of motor output (Hultborn et al., 1979). This proposal is supported by nonlinear input–output relations observed across motor pools (Hultborn et al., 1979) rather than a constant negative offset. The proposal is also supported by our recordings in which we show that the probability of Renshaw cell firing during stimulation pulses of motor inputs is markedly dependent on frequency.

Whereas recurrent inhibition is absent in mammalian motoneurons innvervating digits (Illert and Kümmel, 1999) or muscles of mastication (Shigenaga et al., 1989), it acts on motor units supplying much of the limb (Hahne et al., 1988) and diaphragm (Lipski et al., 1985). If the variable gain regulator hypothesis is true, recurrent inhibition might be expected characteristically to modulate motor outputs to muscle groups whose functions encompass wide ranges of contractile strength. In accordance, the vast majority of our paired recordings were obtained from motoneuron located within the motor pools innervating the proximal hindlimb and glutei.