Figure 6. Pairs of V1 and CA1 cells with overlapping firing fields displayed correlated lap-by-lap fluctuations in firing rate and firing location.
(A) Lap-by-lap spike raster and the average rate curves (see Figure 2 legend for details) of a pair of V1 and CA1 cells on the same trajectory. Boxes: the overlapping firing fields of the two cells. (B) The spikes within the marked laps (*) of the two cells in A are expanded and plotted together. Note the correlated lap-by-lap shifting of the V1 and CA1 cells in their spikes. (C) The lap-by-lap fluctuations in firing rate (ΔRate) and COM (ΔCOM) within the firing fields of the two CA1 and V1 cells in A. Each dot is a lap. Solid line: linear regression. R, P: Pearson's correlation between the CA1 and V1 fluctuations and the associated p-value. (D) Average correlation in ∆rate and ∆COM for overlapping, non-overlapping, and non-responsive pairs of CA1 and V1 cells (see text for definitions). (E, F) Same as C and D, but for modified ∆rate and modified ∆COM after removing the modulations of firing rate and COM by speed and head direction.
Figure 6—figure supplement 1. Two more examples of overlapping V1-CA1 cell pairs with correlated lap-by-lap fluctuations in, each from a different animal.
For each example (A or B), plotted on the left are the lap-by-lap spike raster and firing rate curves of the V1 (red) and CA1 (blue) cells, while plotted on the right are the lap-by-lap fluctuations in rate (∆rate) and COM (∆COM) for the two cells on the left, and in rate (modified ∆rate) and COM (modified ∆COM) after the modulation by speed and head direction was removed. See the main figure (Figure 6) legend for details.
Figure 6—figure supplement 2. Illustration of overlapping, non-overlapping, and non-responsive V1-CA1 cell pairs.
(A) An overlapping pair: a location-responsive V1 cell (top) and a CA1 place cell (bottom) with spatially overlapping firing fields (with 50–100% overlap). (B) A non-overlapping pair: a location-responsive V1 cell (top) and a CA1 place cell (bottom) with spatially non-overlapping firing fields. (C) A non-responsive pair: a non-location-responsive V1 cell (top) and a CA1 place cell (bottom). Boxed areas: the spatial intervals for probing the co-fluctuation of a given pair. For overlapping pair (A) and non-overlapping pairs (B), the spatial intervals were their firing fields. For Non-responsive pairs (C), the spatial interval for the location-responsive cell was its firing field, whereas for the non-location-responsive cell it was the location-responsive cell's firing field shifted with a small random distance that yielded a random overlap of 50–100% with the firing field of the other cell. The same V1 cell and CA1 place cell can be involved in multiple pairs. In this example the same CA1 place cell appeared in 3 pairs.
Figure 6—figure supplement 3. Overlapping V1-V1 and CA1-CA1 cell pairs displayed correlated lap-by-lap fluctuation in firing rate and COM within their firing fields.
(A) Average correlation in ∆rate and ∆COM for pairs of V1 location-responsive cells with overlapping firing fields (Overlapping), pairs of V1 location-responsive cells with non-overlapping firing fields (Non-overlapping), and pairs made of one location-responsive V1 cell and one non-location-responsive V1 cell (Non-responsive). (B) Same as (A), but after the modulation by speed and head direction was removed. (C, D) Same as A and B, but for CA1-CA1 cell pairs. Number of V1-V1 pairs: N = 803 overlapping pairs; 953 non-overlapping pairs; 30 non-responsive pairs. Number of CA1-CA1 pairs: N = 1621 overlapping pairs; 11,273 non-overlapping pairs; 121 non-responsive pairs. *: p < 0.05; **: p < 0.01; ***: p < 0.001; ****: p < 0.0001; t-test.
Figure 6—figure supplement 4. Modulation of V1 and CA1 firing activities by speed and head direction.
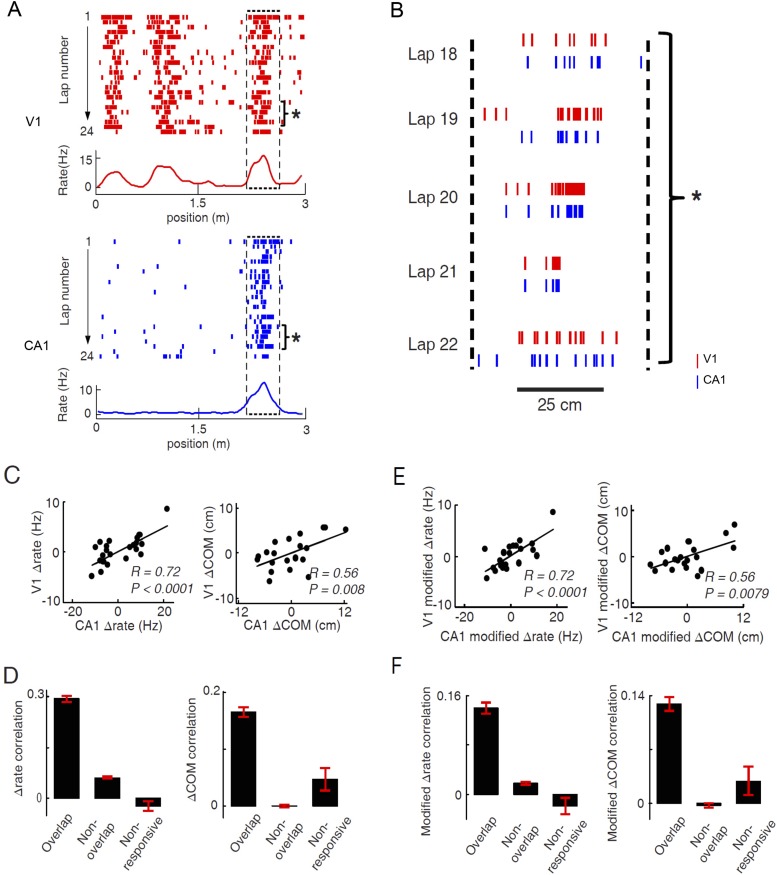
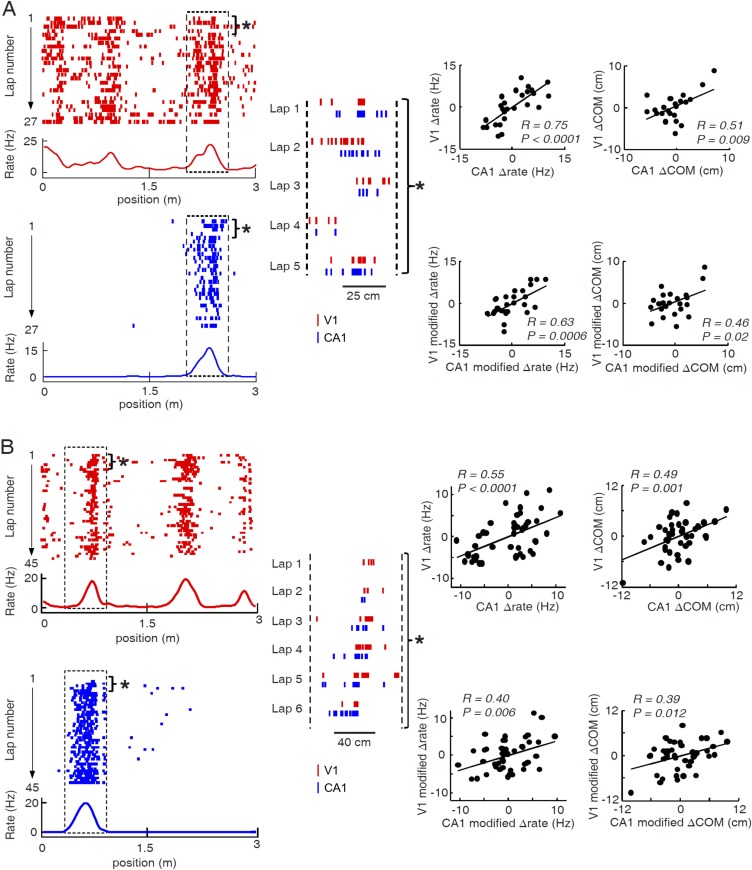
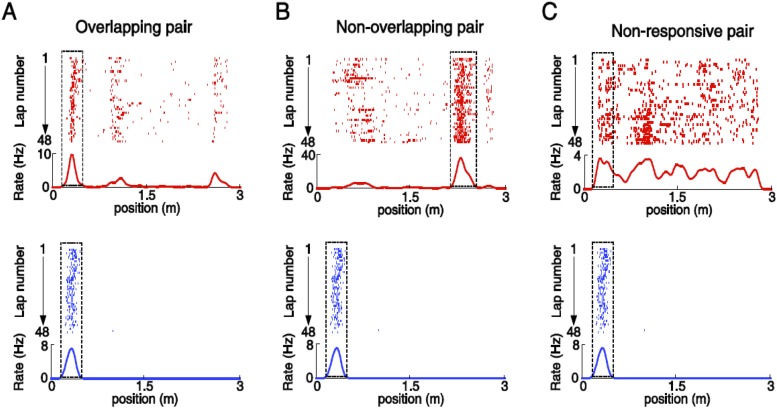
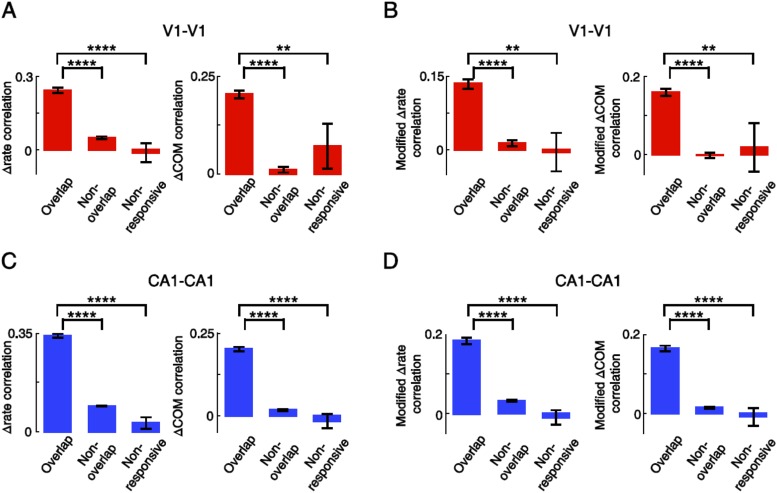
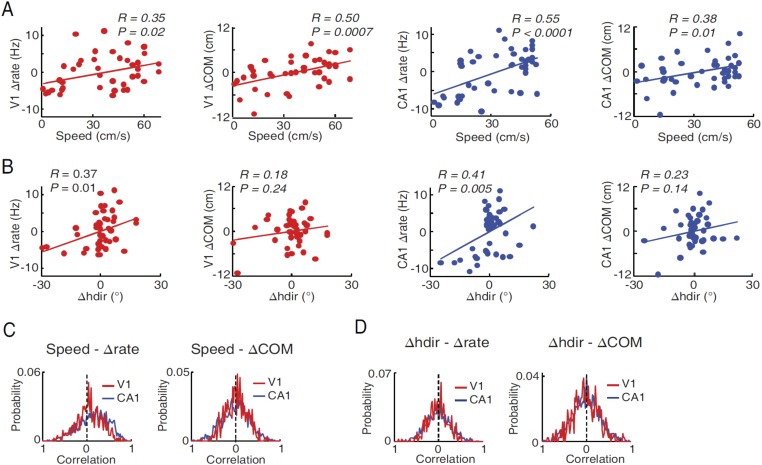
(A) Correlations between lap-by-lap speed and Δrate and between lap-by-lap speed and ΔCOM for example V1 and CA1 cells (the same as in Figure 6—figure supplement 1, panel B). Solid line: linear regression. R, P: Pearson's correlation and the associated p-value. Overall, speed was significantly correlated (p < 0.05) with Δrate in 25% (N = 107 out of 428) of V1 location-responsive cells and 41% (N = 619 out of 1510) of CA1 place cells, and with ΔCOM in 14% (N = 60) of V1 location-responsive cells and 25% (N = 378) of CA1 place cells. (B) Same as A, but between head direction fluctuation (Δhdir) and Δrate and between Δhdir and ΔCOM for the same V1 and CA1 cells in A. Δhdir was significantly correlated with Δrate in 12% (N = 51) of location-responsive V1 cells and in 21% (N = 317) of CA1 place cells, and with ΔCOM in 23% (N = 98) of location-responsive V1 cells and in 23% (N = 347) of CA1 place cells. (C) Distributions of speed-Δrate and speed-ΔCOM correlation values for all CA1 place cells and location-responsive V1 cells. Dashed lines: 0 correlation. The speed-Δrate distribution was skewed to the positive side for both V1 (0.064 ± 0.014; p < 0.0001, t-test compared with 0) and CA1 cells (0.16 ± 0.009, p < 0.0001), indicating that at the population level both V1 and CA1 cells increased their firing rates as speed increased. The speed-ΔCOM distribution was slightly but significantly skewed toward a positive mean for V1 (0.029 ± 0.011, p = 0.014), but not for CA1 cells (0.010 ± 0.008, p = 0.18), suggesting that, as speed increased, V1 cells' firing locations tended to move slightly forward along the animal's movement direction. (D) Same as (C), but for Δhdir-Δrate and Δhdir-ΔCOM distributions. The Δhdir–Δrate distribution was centered near 0 for both V1 (−0.0052 ± 0.011, p = 0.44) and CA1 (0.0057 ± 0.0073, p = 0.64) cells, indicating no systematic relationship between firing rate and head direction at the population level, even though each individual cell could increase or decrease firing rate as head direction was changed from left to right or vice versa. This result is expected if we assume that the V1 or CA1 cells as a group should not show any preferred head direction, even through individual V1 cells are tuned to particular directions. The Δhdir - ΔCOM distribution was similarly centered near 0 for both V1 (0.009 ± 0.015, p = 0.53) and CA1 (0.003 ± 0.008, p = 0.68) (right).
Figure 6—figure supplement 5. V1 location-responsive cells showed much less lap-by-lap backward shift in their firing locations than CA1 place cells.
(A) Average lap-by-lap changes in COM for V1 location-responsive cells (red, N = 670) and CA1 place cells (blue, N = 1743). The COM change of a firing field at each lap was computed relative to its stabilized value, which was the average of those values at laps #21–25. Solid lines: linear regressions between the COM change and lap numbers for the first 10 laps. It can be seen that the COMs of CA1 place fields significantly and systematically shifted backward (COM decreased with lap number) along the animal's moving direction (p < 0.0001, one-way ANOVA; Pearson's R = −0.89, p = 0.0006). The COMs of V1 firing fields appeared to shift backward during the first 5 laps or so, but fluctuated forward/backward in later laps. As a result, there was no significant change in COM (p = 0.09, one-way ANOVA) within the first 10 laps and no significant correlation between average COM change and lap number (Pearson's R = 0.10, p = 0.79). In addition, the average change in COM of V1 firing fields was significantly less than that of CA1 place fields within the first 10 laps (p < 0.0001, two-way ANOVA). (B) Same as A, but for lap-by-lap COM change of V1 and CA1 cells after removing the modulation by speed and head direction. The results are similar. There was a systematic backward shifting of the modified COM for CA1 place fields (p < 0.0001, one-way ANOVA; Pearson's R = 0.86, p = 0.0014), but not so for V1 firing fields (p = 0.13; R = 0.23, p = 0.53; comparison between CA1 and V1: p < 0.0001, two-way ANOVA). Therefore, the analysis indicates that V1 firing fields showed much less dynamics at the short-term lap-by-lap time scale than CA1 place fields.